2. 中国地质大学(北京), 北京 100083
2. China University of Geosciences (Beijing), Beijing 100083, China
在重、磁等地球物理测量中,观测数据通常呈不规则的离散分布,在测线途径较大面积的陡峭山地、滩涂沼泽时,往往还会造成数据的缺失.重磁数据处理前,需要对离散分布的观测数据进行规则网格化,而网格化后的数据也因为原始测量数据的大面积缺失而有数据空缺.如此数据在常规处理,例如延拓和滤波等,不影响数据的计算,但对于某些特殊处理,例如场源位置、物性等的反演计算时,则需要首先对缺失区域进行数据补缺处理.这种补缺处理还经常存在于网格数据的拼接过程中,相邻区域不同时期测量的数据进行拼接联合时,因为测线覆盖区域的不完全重合,在拼接区域难免造成数据的缺失,此时,后续计算也可能需要将缺失区域进行补缺处理.
对数据的补缺处理计算可采用离散点数据插值的方法,目前常用方法包括线性插值方法(郭志宏,2001)、最小曲率法(Briggs et al., 1974)、等效源法(Cordell,1992)、多元二次函数法(Hardy,1971)、样条函数法(郭志宏,1999;唐泽圣,1999)、离散光滑插值法(Mallet,1992;孟小红等, 2001, 2002;Claerbout, 2002; 李冰等,2002)、克里金法(孙洪泉等,1990)等,这些方法均有各自的理论适应性和计算特点,在不同领域计算中得到广泛应用.共同点事其具体操作为首先将测量数据于坐标结合,以网格中有数据的点为型值点,以空缺位置坐标为待插值点,计算完后再输出为网格形式以供后续计算.
本文将介绍一种更为简单直接的方法,不需要再将网格数据与坐标结合,直接将2D的网格数据进行基于傅立叶正反变换的迭代计算,可将缺失数据补齐,该方法称为凸集投影方法.凸集投影数据重建方法基于Gerchberg-Saxton迭代计算(Saxton method (Gerchberg and Saxton, 1972)发展而来,在图像和信号重建计算中得到广泛的应用(Menke, 1991; Papoulis and Chamzas, 1979),有学者将其发展到地震数据道缺失的重建中(Abma and Kabir, 2006).综合过去的研究,凸集投影总结下来具有以下的特点:(1)能够实现大间距缺失的重建,并保持较好的计算精度;(2)具有较为直接、简单和易于执行的计算过程;(3)常规数据的计算精度较其他方法而言相同或略高,因此,将其发展到重磁等地球物理数据缺失的重建中,具有重要的应用意义.
本文根据凸集投影方法的特点,设计了其在重磁网格化缺失数据重建的计算流程,结合不同实际资料的和不同插值方法进行对比分析表明,该方法具有计算精度高,计算直接、简单的特点.
1 凸集投影的计算原理凸集投影对于重磁等网格化后数据缺失的重建于2D图像缺失重建的方法类似(Menke, 1991; Papoulis and Chamzas, 1979),主要基于Gerchberg-Saxton迭代计算,每次迭代计算的核心是进行2D傅立叶变换,通过2D傅立叶变换将数据从空间域转换到波数域,给定一个门限值,振幅高于这个门限值时保留,振幅低于这个门限值则充零代替,然后对该数据进行反傅立叶变换.而在下一次迭代计算时,减小门限值,重复上述操作,直到达到结束迭代计算的条件.例如含缺失数据网格数据Dobs(x, y),其凸集投影重建计算公式为

|
(1) |
其中,Dk代表迭代重建后的数据,F-1和F代表傅立叶正反变换,M是采样矩阵,其于数据维度相同,如果某点值为1,代表该点有数据,无需插值,反之若为零,则代表该点需要进行插值计算.Tk是门限值矩阵,其值可以表示为
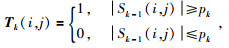
|
(2) |
其中,pk是第k次迭代的幅值门限, N为迭代次数.
pk在每次迭代次数时取值根据振幅的最大值pmax和最小值pmin,以及迭代次数N,采用线性插值获得,公式为
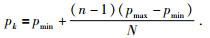
|
(3) |
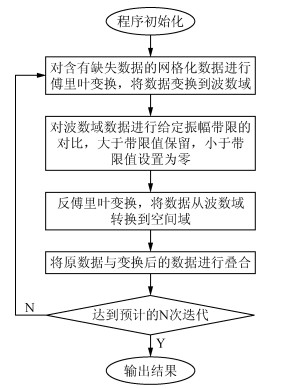
凸集投影法网格化缺失数据重建流程图如图 1所示,从中可以看出,整个计算过程简单明了,其主要计算量体现在2D的傅里叶正反变换中.
|
图 1 凸集投影网格缺失重建流程图 Figure 1 Flowchart of POCS method |
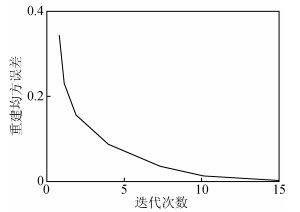
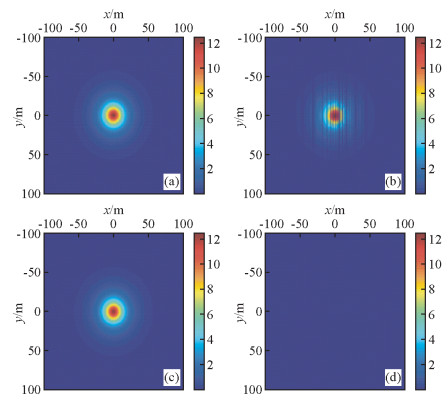
为了测试方法的正确性,本文采用单异常体正演的重力数据进行测试,观测数据点距和线距为10 m,横向和纵向侧线长度均为200 m.原始正演输入如图 2a所示,对其部分测线数据整体去掉,形成如图 2b的缺失数据,从图中可以看出,整体缺失比例在百分之三十以上,图 2c是应用本文方法的重建结果,从图 2d是图 2a与2c的差.分析得出,本文方法得到了很好的重建结果,残差在简单模型中几乎为零.图 3是重建过程的迭代曲线,在迭代10次左右时达到了较好的收敛.通过上述简单算例,验证了方法的正确性.
|
图 2 简单模型凸集投影重建结果 (a)原始数据; (b)部分缺失数据; (c)重建结果; (d) a和c的差. Figure 2 A simple model for POCS method (a) Original data; (b) Data need reconstruction; (c) Reconstructed data; (d) Error of a and c. |
2 凸集投影重建方法精度的对比分析
从上述原理论述可以看出,凸集投影法计算简单,全过程主要计算表现为2D的离散傅里叶正反变换,因此计算速度能够得到保证.为了验证本文方法的计算精度,我们采用对比分析的办法进行测试,分别采用目前应用比较广泛的最小曲率方法和克里金方法,以及计算最为稳定的反距离加权方法对特定数据进行缺失部分重建.其中缺失数据是从已知的某磁测数据中去掉一部分,分别应用上述对比方法重建,除本文方法外,均需首先将网格数据转换格式,与坐标结合,而本文方法无需坐标信息,直接读取网格数据进行计算.
应用均方误差公式衡量各重建结果,均方误差ε公式表达式为
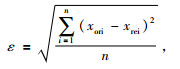
|
(4) |
其中,xori为原始数据,xrei为缺失化后重建数据,n为参与计算的数据点个数.
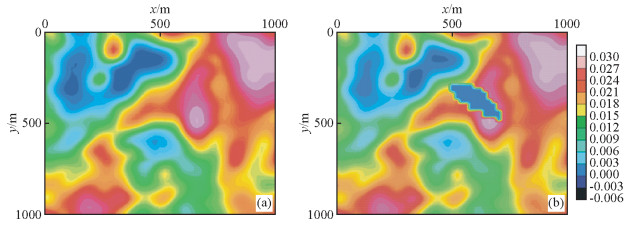
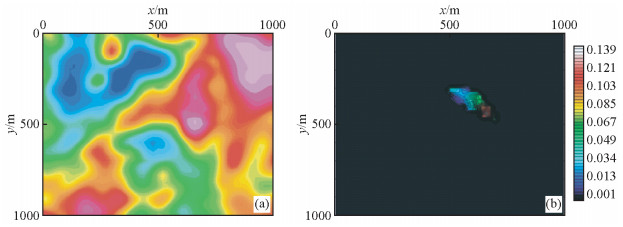
所选磁测数据如图 4a所示,测线间距和测点间距均被网格化为10 m,双向各延伸1000 m.在该数据中间部分,在异常高点区域制造缺失,用做本文测试对比的数据,如图 4b.
|
图 4 某实际磁测数据(a)和部分空缺的数据(b) Figure 4 Some real data (a) and the data need reconstruction (b) |
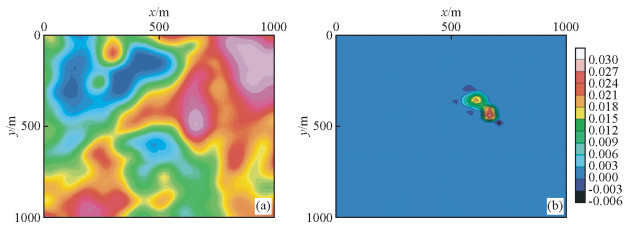
克里金、最小曲率和反距离加权方法进行重建前,需要将网格数据转化成坐标和异常数据格式,并剔除缺失部分,按照原始规则化的网格进行重建.其重建结果分别为图 5,图 6和图 7所示,其中各图中,(a)是重建的结果,(b)是原始数据和重建数据的残差,从中我们看出,克里金方法和最小曲率方法都降缺失的异常得到相对好的恢复,而反距离加权方法效果相对较差.
|
图 5 Kriging重建结果(a)及与原数据的残差(b) Figure 5 Reconstruction result with kriging method (a) and the error (b) |

|
图 6 最小曲率重建结果(a)及与原数据的残差(b) Figure 6 Reconstruction result with minimum curve method (a) and the error (b) |
|
图 7 反距离重建结果(a)及与原数据的残差(b) Figure 7 Reconstruction result with minimum curve method (a) and the error (b) |
在将网格化的数据应用本文方法重建时,无需读入坐标数据,只需将数据读入矩阵中,按图 1所示的流程进行计算,相对上述三种方法,整个计算流程变得很简单,经过30次迭代计算得出最终重建数据.图 8a是重建的结果,图 8b是与原始数据的残差.单就参差结果分析,直观上相对于上述三种方法聚焦成都较差,但其残留辅值普遍较低,对原异常幅值恢复的更好.

|
图 8 本文重建结果(a)及与原数据的残差(b) Figure 8 Reconstruction result with our method (a) and the error (b) |
为了量化对比效果,应用公式(4)对几种重建结果进行了均方误差对比,对比结果可以看出(如表 1),本文的凸集投影方法于最小曲率方法相当,而最小曲率在常规方法中效果最好,这与相关研究的结论是一致的.
|
|
表 1 插值均方误差表 Table 1 Mean squared error of different methods |
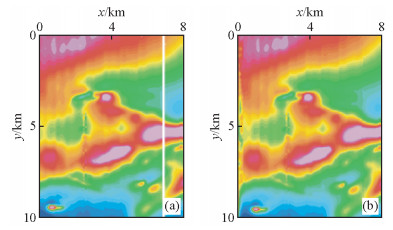
本文介绍的凸集投影方法在地震数据的缺失地震道重建中被证明具有很好的应用效果,而在航磁等测量中,通常会因为工业环境等问题造成整条测线不能完成采集,这与地震道整道缺失类似.采用了某地区航磁数据对该种情况进行测试,规则化后的航磁数据线间距为50 m,测点间距为10 m,在飞机飞行过程中,受到工业电等因素影响,甩掉了部分测线,缺失数据如图 9a所示,图中白色线状即为飞行中的缺失测线,缺失部分横向缺失10条测线,横跨间距约500 m.应用本文方法重建结果如图 9所示,迭代次数50次,达到收敛.从重建结果中可以看出,较好的恢复了缺失数据,且没有重建痕迹.证明了该方法在航磁数据整条侧线缺失时重建效果的有效性.
|
图 9 某航磁数据:失数据(a)和重建数据(b) Figure 9 Practical aeromagnetic data (a) and reconstruction result (b) |
本文将图像处理中常用的凸集投影法应用于重磁等网格化数据缺失的重建中,经过常规数据不规则缺失重建以及航磁数据整条缺失重建的计算分析,验证了其精度和有效性,方法核心是基于傅里叶变换的迭代计算,其具有方法简单、计算稳定、计算速度的特点.与常规方法的对比分析,其具有与最小曲率相近的计算精度.该方法的不足之处在于,其目前只适用于规则缺失数据的重建,没有常规的诸如最小曲率、反距离加权等方法的插值计算灵活度.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Abma R, Kabir N .2006. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 71 (6) : E91–E97. DOI:10.1190/1.2356088 |
| [] | Briggs I C .1974. Machine contouring using minimum curvature[J]. Geophysics, 39 (1) : 39–48. DOI:10.1190/1.1440410 |
| [] | Claerbout J F .2002. Image Estimation by Example[M]. San Francisco Bay Area, California: Stanford University . |
| [] | Cordell L .1992. A scattered equivalent-source method for interpolation and gridding of potential-field data in three dimensions[J]. Geophysics, 57 (4) : 629–636. DOI:10.1190/1.1443275 |
| [] | Gerchberg R W, Saxton W O .1972. A practical algorithm for the determination of phase from image and diffraction plane pictures[J]. Optik, 35 (2) : 237–246. |
| [] | GUO Zhi-Hong. 1999. Software and application of cubic spline gridding method[C].//Collection of Airborne Geophysical Prospecting and Remote Sensing (in Chinese). Beijing:Geological Publishing House. |
| [] | GUO Zhi-Hong .2001. A practical contour type data gridding technique[J]. Geophysical & Geochemical Exploration (in Chinese), 25 (3) : 203–208. |
| [] | Hardy R L .1971. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysics Research, 76 (8) : 1905–1915. DOI:10.1029/JB076i008p01905 |
| [] | LI Bing, LIU Hong, LI You-Ming .2002. 3-D seismic data discrete smooth interpolation using conjugate gradient[J]. Chinese Journal of Geophysics (in Chinese), 45 (5) : 691–699. |
| [] | LIU Cai, LI Peng, LIU Yang, et al .2013. Iterative data interpolation beyond aliasing using seislet transform[J]. Chinese Journal of Geophysics (in Chinese), 56 (5) : 1619–1627. DOI:10.6038/cjg20130519 |
| [] | LU Yan-Hong, LU Wen-Kai, ZHAI Zheng-jun .2012. An edge-preserving seismic data interpolation method[J]. Chinese Journal of Geophysics, 55 (3) : 991–997. DOI:10.6038/j.issn.0001-5733.2012.03.029 |
| [] | Mallet J L .1992. Discrete smooth interpolation in geometric modelling[J]. Computer-Aided Design, 24 (4) : 178–191. DOI:10.1016/0010-4485(92)90054-E |
| [] | MENG Xiao-Hong, HOU Jian-Quan, LIANG Hong-Ying, et al .2002. The fast realization of discrete smooth interpolation in the interpolation of potential data[J]. Geophysical & Geochemical Exploration (in Chinese), 26 (4) : 302–306. |
| [] | MENG Xiao-Hong, WANG Wei-Min, YAO Chang-Li, et al .2001. Principle and Application of Computer Aided Design of Geological Model (in Chinese)[M]. Beijing: Geological Publishing House . |
| [] | Menke W .1991. Applications of the POCS inversion method to interpolating topography and other geophysical fields[J]. Geophysical Research Letters, 18 (3) : 435–438. DOI:10.1029/90GL00343 |
| [] | Papoulis A, Chamzas C .1979. Improvement of range resolution by spectral extrapolation[J]. Ultrasonic Imaging, 1 (2) : 121–135. DOI:10.1177/016173467900100202 |
| [] | SUN Hong-Quan .1990. Geological Statistics and Its Application (in Chinese)[M]. Beijing: China University of Mining and Technology Press . |
| [] | TANG Ze-Sheng .1999. Visualization of 3D Date Sets (in Chinese)[M]. Beijing: Tsinghua University Press . |
| [] | 郭志宏. 1999.双三次样条内插网格化方法软件的研制开发及应用[C].//航空物探遥感论文集.北京:地质出版社. |
| [] | 郭志宏.2001. 一种实用的等值线型数据网格化方法[J]. 物探与化探, 25 (3) : 203–208. |
| [] | 李冰, 刘洪, 李幼铭.2002. 三维地震数据离散光滑插值的共轭梯度法[J]. 地球物理学报, 45 (5) : 691–699. |
| [] | 刘财, 李鹏, 刘洋, 等.2013. 基于seislet变换的反假频迭代数据插值方法[J]. 地球物理学报, 56 (5) : 1619–1627. DOI:10.6038/cjg20130519 |
| [] | 陆艳洪, 陆文凯, 翟正军.2012. 一种边缘保持的地震数据插值方法[J]. 地球物理学报, 55 (3) : 991–997. DOI:10.6038/j.issn.0001-5733.2012.03.029 |
| [] | 孟小红, 王卫民, 姚长利, 等.2001. 地质模型计算机辅助设计原理与应用[M]. 北京: 地质出版社 . |
| [] | 孟小红, 侯建全, 梁宏英, 等.2002. 离散光滑插值方法在地球物理位场中的快速实现[J]. 物探与化探, 26 (4) : 302–306. |
| [] | 孙洪泉.1990. 地质统计学及其应用[M]. 北京: 中国矿业大学出版社 . |
| [] | 唐泽圣.1999. 三维数据场可视化[M]. 北京: 清华大学出版社 . |
 2016, Vol. 31
2016, Vol. 31