2. 长安大学地测学院, 西安 710054
2. College of the Geological Engineering and Geomatics, Chang'an University, Xi'an 710054, China
地震波场正演模拟(裴正林和牟永光,2004)不仅能够指导野外地震数据采集,并且在数据处理中可以指导分辨波场特征,是地震数据处理中的重要环节.随着地震勘探精度的提高,常规地震勘探方法受到限制.井间地震勘探(陈世军等,2003)是一种特殊的地震观测方法,将炮点与检波点放置在相邻两口井中,地震波传播时有效避免了浅层低速带对地震波高频信号的吸收作用,提高地震勘探分辨率.井间地震勘探的波场特征也较其他勘探方法更加丰富,不仅可以获得自下而上传播的上行反射波,也可以接收到从上至下传播的下行反射波,提高反射波成像精度.
井间地震技术基于层析成像发展而来.1972年,美国《地球物理》杂志首次报道关于井间地震技术在油气开发的层析结果,将井间地震勘探方法移植到油气勘探领域(Gal’perin, 1974).20世纪80年代,美国石油界采用计算机技术将医学上的层析成像方法引入到井间地震当中.1983年G.McMachan提出的井间地震波层析成像方法引起了许多石油公司,石油院校以及大批地球物理技术人员对井间地震研究的强烈重视,取得了新的应用成果.在国内,20世纪90年代中国石油大学吴律教授首次将井间地震技术引入井间层析地震理论之中(吴律,1997),取得了较好效果.1992年,我国在胜利油田和辽河油田开展井间地震技术研究.“十五”到“十二五”期间,井间地震勘探技术(曹辉,2002)一直作为国家级重点科研项目研究专题进行研究,取得了较好的效果.井间地震技术也从二维勘探发展到三维勘探,形成了一套比较成熟的工作流程.可用于多井同步检测,既可以陆地作业也可以海上开发,接收井可以是斜井、水平井、油管井或者高温井.
井间地震还在继续发展,作为井间地震正演的方法主要包括波动方程法和射线追踪法(李强和白超英,2012).射线追踪正演的优点在于计算速度快,简单直观,地震波传播旅行时准确,但是缺少动力学特征,面对复杂构造会产生盲区.波动方程正演(金胜汶等,1994;左建军等,2005)具有动力学特征,但是计算速度慢,时效性差,在井间地震勘探中研究较少.本文基于射线追踪正演与波动方程正演的优点,采用高斯射线束方法进行三维井间地震波场正演(魏峥嵘,2014).高斯束正演算法解决了常规射线追踪正演方法缺少动力学特征以及复杂构造产生的盲区问题(吴立明等,1995).在国外,20世纪80年代初,Cerveny等人首先将电磁学领域的高斯束方法引入到地球物理领域,发展了一种将射线理论与波动方程结合的地震波正演方法.1984年Cerveny和Muler等人分别介绍了高斯束运动学与动力学合成记录的特点(Červený, 1983;Červený, 1985;Weber, 1988).1987年George将高斯束正演与有限差分正演结果进行对比,结果表明高斯束正演得到的合成记录具有较高精度.在国内,周熙襄、刘学才等人1991年介绍了二维高斯束的基本原理,并且对弹性介质地震模型进行试算(周熙襄等,1991).1997年成都理工大学基于井间地震的观测方式,开发了二维井间地震高斯束正演模块(张汝杰等,1997),并对不同模型进行试算取得较好效果. 2012年,李振春,岳玉波等人将高斯束原理应用在地震数据偏移处理当中,并对数值模型及实际资料的应用效果进行了验证(岳玉波等,2012),2013-2014年,段鹏飞等人、李辉等人分别对TI介质中地震数据偏移和高斯波包法叠前偏移做了深入研究,取得了一定效果(段鹏飞等,2013;李辉等,2014).
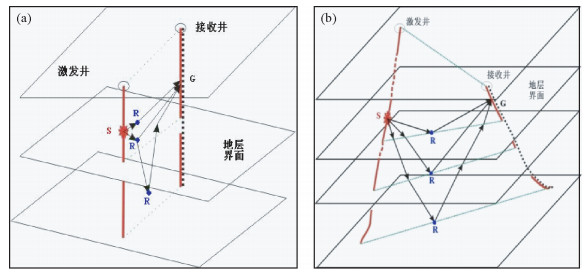
1 方法技术 1.1 地质建模 1.1.1 井轨迹建模三维井间地震勘探中,根据井轨迹的空间分布可分为共面三维井间地震(类似于二维井间地震)和非共面三维井间地震(真三维),如图 1a,1b所示.针对非共面斜井建模问题,使用三次样条插值方法进行井轨迹模拟(曹德欣和王海军,2001).
|
图 1 三维井间地震 (a)共面三维井间地震;(b)非共面三维井间地震. Figure 1 3D Cross-well seismic (a)3D Cross-well seismic in the same plane; (b)3D Cross-well seismic in the different plane. |
设一插值函数s(x)∈[a, b],根据插值点的个数将区间分为N个小单元,s(x)在每一个小区间上[xi, xi+1]上是三次多项式,a=x0 < x1 < … < xn=b,其中xi(i=0, 1, 2, …, n)为节点.若节点xi上给定函数值yi=f(xi)(i=0, 1, …, n),且插值条件s(xi)=yi(i=0, 1, 2, …, n)成立,称s(x)为三次样条插值函数.
要求出s(x),在每个小区间[xi, xi+1]上应确定4个待定系数,共有n个小区间,故要确定4n个参数.根据s(x)在[a, b]上二阶导数连续,在节点xi(i=1, 2, …, n-1)处满足连续性条件为
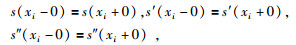
|
(1) |
共有3n-3个条件,并且s(x)满足插值条件,共有4n-2个条件,因此还需要2个条件才能确定s(x).通常在区间[a, b]端点a=x0, b=xn上各加一个条件(即边界条件),边界条件可根据实际的问题要求给定.常见的边界条件为已知两端的二阶导数,公式为
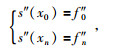
|
(2) |
特殊情况下边界条件为s″(x0)=s″(xn)=0,这种情况也称自然边界条件.
1.1.2 地层建模三维地层建模时使用薄板样条插值方法对地层进行模拟.薄板样条函数(程义军和孙海燕,2008)是一种简单方便的三维插值方法,它寻找一个通过所有的控制点的弯曲最小的光滑界面.当控制点为3个不共线的点时,薄板样条插值后是一个平面;多于三个不共线的点插值后成为一个曲面;当控制点少于三个则为未定义.
已知地层控制点集合(xi, yi, zi)i=1, 2, …, n,构造插值函数f(x, y)为
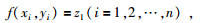
|
(3) |
(x, y)可看做控制点在xoy平面上的投影,z为该控制点的高程,根据控制点的分布及插值函数f(x, y)计算相应的高程,插值出所建立地层的所有控制点坐标.
定义函数为
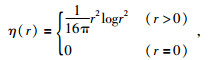
|
(4) |
设地层控制点t=[x, y]T的坐标为(x, y),定义三个函数为
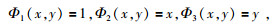
|
(5) |
则该地层上的任意线性函数均可表示为Φj的线性组合.设有3行n列的矩阵T,其元素为Tjk=Φj(tk),公式为
即
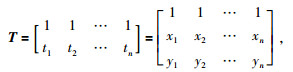
|
(6) |
用||ψ||表示两维空间的欧氏范数,即||ψ||2=tTt.若能得到合适的常数δ=[δ1, δ2, …, δn]T及a=[a1, a2, a3]T及使得
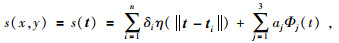
|
(7) |
满足插值条件(3),则称式(7)为点集(t1, t2, …, tn)上的薄板样条函数.如果还有
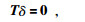
|
(8) |
成立,则称式(7)为点集(t1, t2, …, tn)上的自然薄板样条函数.
为了计算式(7)中的常数δ=[δ1, δ2, …, δn]T与a=[a1, a2, a3]T定义矩阵E,其元素为
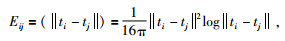
|
(9) |
线性方程组
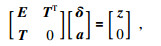
|
(10) |
的解即为所求.式中z=[z1, z2, …, zn]
1.2 高斯束正演高斯束正演方法隶属于射线类正演方法,它是将检波器周围所有有效射线能量高斯加权叠加来实现波场数值模拟(李瑞忠等,2006;邓飞等,2009;范廷恩,2014).不同于其他射线正演方法,高斯射线束是弹性波动力学方程集中于射线附近的高频近似解,不仅包含地震波传播的运动学特征,还有动力学特征.高斯束运动学追踪依赖于中心射线,求解从震源出发的地震波经过地层传播至检波器附近的射线路径和旅行时.
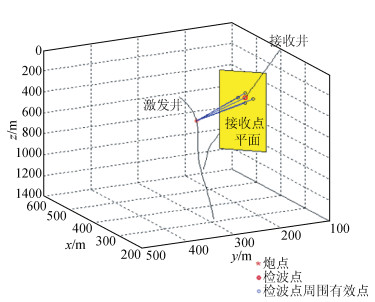
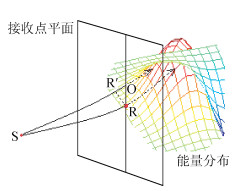
三维井间地震高斯射线束(邓飞等,2009;杨飞龙,2013)运动学追踪主要计算地震波经地层反射、透射到达每一个接收点平面的射线路径、旅行时.地震波传播时遵循斯奈尔定理、费马原理和惠更斯原理,射线以一定的角度步长发出,传播至接收点平面上记录下来.角度步长越小,射线越密.如图 2所示,对接收井上的每一道检波器拟合出射线传播至接收点的垂面(即接收点平面),震源发出地震波经地层反射、透射最终传播到接收点平面上,当到达接收点平面上的射线与接收点的距离满足接收点有效半宽度范围时,对这些射线进行高斯加权合成该接收点的地震记录.
|
图 2 井间地震接收点平面 Figure 2 Receiving plane in Cross-well seismic |
井间地震高斯束运动学追踪是通过求解程函方程得到
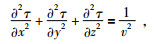
|
(11) |
式中:τ为地震波传播的旅行时;v为地震波的速度.
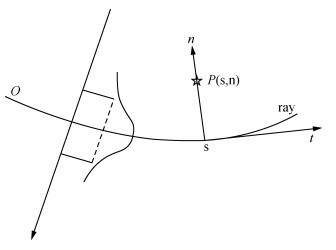
动力学追踪的核心是求取每一个接收点的p、q值,计算射线传播至接收点平面的振幅能量.高斯射线束传播依赖于中心射线,根据高斯束传播建立射线中心坐标系,该坐标系下高斯束波传播类似于球面波传播沿着一个特定的波矢量在局部点进行傍轴近似展开,沿射线中心坐标系进行傍轴近似方程的波传播.如图 3所示,射线从O点出发,ray代表中心射线路径,射线周围一定范围内任意一点可用射线中心坐标表示.空间中任一点P,过该点向射线作垂线n交射线与S点,n指向射线左侧,过S点作射线的切线t,指向与射线传播方向相同.s表示O点到S点的射线长度,这样建立一条射线的中心坐标系.在该坐标系中,点的坐标可写成(s,n),P=xi+yj=st+nn.
|
图 3 射线中心坐标系 Figure 3 Ray center coordinate system |
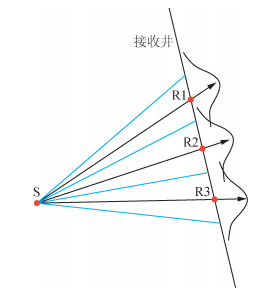
二维情况下,高斯束射线传播至接收井上,检波点处的能量由其周围有效射线加权叠加获得(杨飞龙等,2014),有效射线能量分布呈高斯包络线形态(如图 4所示).而在三维情况下,接收井分布于三维空间中,检波点处的能量由检波点三维空间中有效球面范围内所有射线加权贡献.在实际计算时为方便计算,拟合炮点与每一个检波点所构成平面的垂面(称为接收点平面),从震源发出的地震波传播至每一个接收点平面上,在接收点周围所有有效射线能量分布呈高斯形态,将检波点有效平面内的射线进行高斯加权叠加(李辉等,2012)获得检波点的能量(如图 5所示).检波点接收平面可应用在三维起伏地面高斯束正演问题当中,使得起伏地面分布的检波器能量更加准确,解决因地表起伏造成的检波点有效半宽度范围内射线传播时间误差的问题.
|
图 5 三维高斯束射线追踪 Figure 5 3D Gaussian beam ray tracing |
|
图 4 二维高斯束射线追踪 Figure 4 2D Gaussian beam ray tracing |
三维均匀介质同一层中速度不随位置发生变化,设炮点在第一层地层中,地震波传播的初始条件为
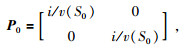
|
(12) |
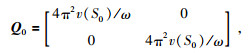
|
(13) |
v(1)为炮点所在地层的速度,ω为角频率.根据初始条件以及在线性边界上,界面曲率为0的边界条件可知检波点处P、Q值为
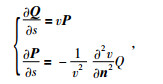
|
(14) |
其中,s为地震波传播的距离,n为中心坐标系下垂直于射线传播方向左侧的方向向量.
使用四阶龙格库塔方程对式(14)进行求解,可得到检波点处P、Q值为
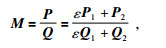
|
(15) |
P1、P2和Q1、Q2分别为接收点处P和Q的两个实数解.ε对一根射线来说是一个复常数,公式为
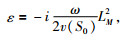
|
(16) |
其中,
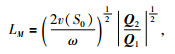
|
(17) |
检波点的有效半宽度L(s)与射线传播到检波点的P、Q有关,公式为
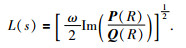
|
(18) |
当射线传播至接收点平面时,射线与接收点平面的交点与检波点的距离满足检波点有效半宽度范围时,将有效射线的波场特征叠加起来.用U(R, t)表示时间域中的波场,则每一个检波点处波场大小为
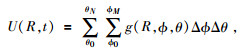
|
(19) |
式中ϕ和θ分别为地震波传播时沿XOY平面和YOZ平面的角度.ϕ0和ϕM为XOY平面内射线的起始入射角和终止入射角;θ0和θN为YOZ平面内射线的起始入射角和终止入射角,Δϕ和Δθ为入射角的间隔.g(R, ϕ, θ)是高斯束合成记录时的波包,检波点处的波场就是其周围这些波包在该点的叠加.通常我们选择Gabor子波作为波包的子波函数,利用Gabor子波公式,可以得到波包的近似表达式为
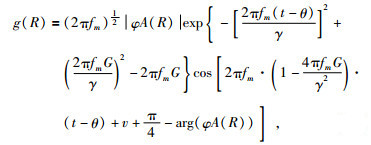
|
(20) |
影响波包的因素有子波参数(fm、γ和v)、射线传播至接收点平面时的振幅A(R)、叠加权系数φ、波场位移相位因子虚部θ和实部G以及传播时间t.
地震波传播时发生透射、反射或者受地层吸收作用振幅发生衰减变化,设炮点处振幅大小为A(S0),地震波传播至接收点平面时振幅的大小为
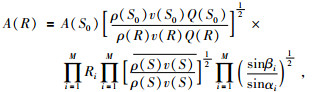
|
(21) |
式中,Ri为界面的反射或者透射系数,M为射线的节点数,ρ和v分别为地层的密度和速度,αi和βi为入射角与透射角(或反射角).考虑地层的吸收作用,设地层的吸收系数为δ,若地震波从炮点传播至接收点平面所用的距离为l,则地震波从震源传播至接收点平面时振幅为
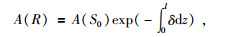
|
(22) |
叠加权系数φ、波场位移相位因子虚部θ和实部G分别为
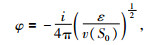
|
(23) |
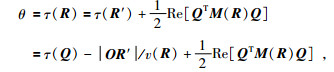
|
(24) |
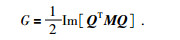
|
(25) |
如图 6所示,建立一套具有断层的三维斜井井间地质模型.地震波在地下介质中传播时遵循斯奈尔定理,费马原理.不同于常规正演方法在于检波器放置于接收井中,利用高斯射线束方法模拟地震波传播.高斯束方法的独特之处在于地震波传播的动力学特征,检波点处的能量是其周围有效射线能量的高斯加权叠加.在三维井间地震中,对于每一道检波器拟合一个检波点接收平面,地震波传播至每一个检波点接收平面上,合成该点的地震记录.炮点位于左井深度为300 m处,地层的速度分别为V1=1700 m/s,V2=2000 m/s,V3=2200 m/s,检波器的起始深度为220 m,道间距为15 m,共55道接收.以上行反射P波为例,如图 6a为上行反射波射线路径,图 6b为对应的上行反射波时距曲线,每一道检波器的能量都是由检波点平面上有效射线能量高斯加权叠加获得.图 6b中地震波传播时经过断面使得同一套地层上行反射波时距曲线发生交叉.
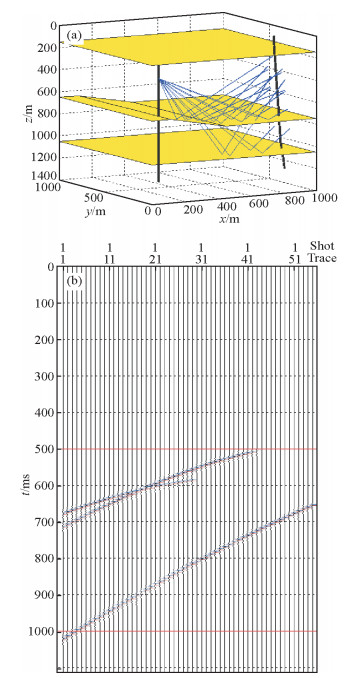
|
图 6 三维井间地震断层高斯束正演 (a)上行反射波射线路径; (b)上行反射波地震记录. Figure 6 3D Cross-well seismic Gaussian beam forward in fault model (a) The ray path of Up reflection wave; (b) The seismic record of Up reflection wave. |
图 7为反射波与地层的交点,由于高斯射线束正演是将检波点附近所有有效射线叠加起来,因此反射点的分布范围更加广泛,这样有利于进行XSP-CDP叠加成像研究,为成像提供准确的反射波信息,增大成像范围.
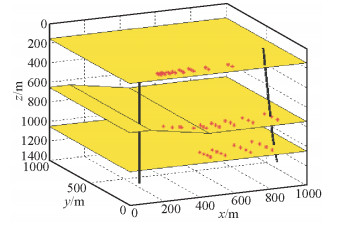
|
图 7 三维井间地震断层高斯束正演反射点位置示意图 Figure 7 3D Cross-well seismic Gaussian beam forward reflection point position in fault model |
为了验证三维井间地震高斯束正演算法的性能,将该方法与三维井间地震逐段迭代正演(王彦军,2011)算法进行了比较.建立一套具有水平地层的斜井地质模型,图 8a为两种不同正演方法在炮点与检波点相同位置的射线路径,图 8b为两种正演方法得到的正演记录,图 8c为使用不同正演方法获得的反射点位置示意图.
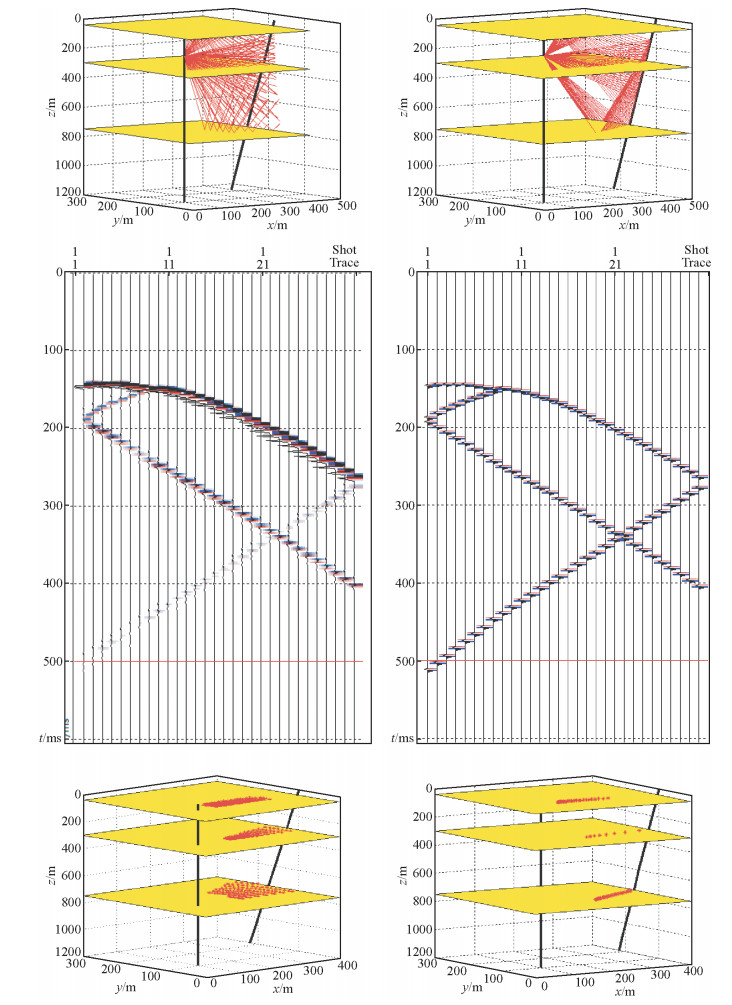
|
图 8 不同正演方法对比示意图 (a)三维井间地震正演射线路径(左:逐段迭代;右:高斯射线束); (b)三维井间地震正演地震记录(左:逐段迭代;右:高斯射线束); (c)三维井间地震正演反射点位置示意图(左:逐段迭代;右:高斯射线束). Figure 8 The contrast diagram of different forward methods (a) The ray path of 3D Cross-well seismic forward (Left: Piecewise iteration; Right: Gaussian beam); (b) Seismic record of 3D Cross-well seismic forward (Left: Piecewise iteration; Right: Gaussian beam); (c) Reflection point position of 3D Cross-well seismic forward (Left: Piecewise iteration; Right: Gaussian beam). |
高斯射线束正演方法是一种特殊的射线类正演方法,它不但包含地震波传播的运动学特征,还具有地震波传播的动力学特点.并且在三维地震勘探中,检波点处的能量不再只受传播至检波点上的射线能量影响,与其周围的有效射线都有关系.高斯射线束方法就是考虑检波点附近有效射线能量对检波点的贡献,使用高斯加权叠加合成地震记录.从图 8b中也可以清楚地看到地震波传播的动力学变化.高斯射线束正演的结果包含更多反射波信息,如图 8c所示,可以看到高斯束正演时具有更多的反射信息,有利于反射波成像研究,为进一步成像处理提供依据.
3 实际资料验证为了说明三维井间地震高斯束正演方法的效果,将该方法应用于X地区井间地震数据处理之中.根据X地区地质、钻井及测井资料建立如图 9a所示的地质模型,炮点放置于激发井中,炮点的垂直深度为1785 m,检波点的起始深度为1576.58 m,检波器间垂深2.5 m,共120道接收.通过对X区原始三维井间地震资料进行波场分离处理,下行P波反射在目地层处较为清晰,如图 9b所示.使用高斯射线束方法对该区进行三维井间地震正演,得到的正演结果与经过波场分离后的三维原始井间地震资料进行对比,如图 9c所示.通过对比发现,正演结果与原始资料较为吻合,说明该方法正演结果准确,能够指导三维井间地震数据处理,并且为进一步成像处理提供依据,应用效果较好.
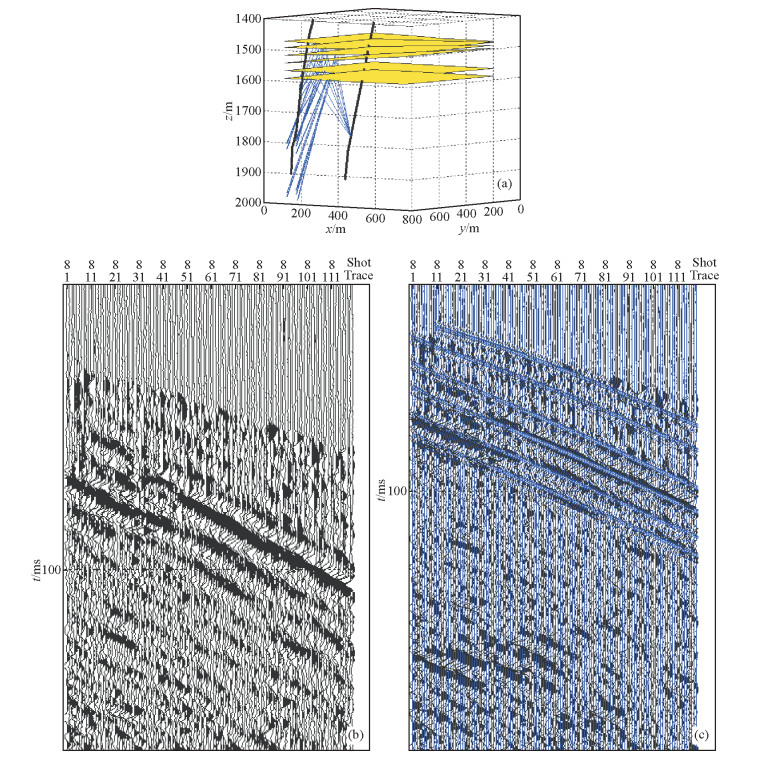
|
图 9 井间地震高斯束正演 (a)射线路径; (b)原始地震记录; (c)正演结果对比剖面. Figure 9 Cross-well seismic Gaussian beam forward (a) Ray path; (b) Original seismic record; (c) Comparing section of forward result. |
本文研究了三维情况下非共面斜井井间地震正演问题,使用高斯射线束方法解决射线传播的动力学问题以及复杂构造射线正演问题.针对三维非共面斜井,结合高斯射线束的特点,文中提出检波点接收平面.该检波点接收平面是由炮点及检波点的相对位置决定的,每一个检波点处的能量是由每一个检波点接收平面上的有效射线能量高斯加权叠加得到的,该思路亦可应用在三维起伏地面高斯射线束正演及成像问题当中.通过对理论模型模拟,实际资料应用说明该方法能够有效解决三维非共面斜井及复杂构造井间地震正演问题,也为三维起伏地面高斯束正演提供一个新的思路.通过理论与实际研究证明笔者所研究的三维非共面斜井井间地震高斯束正演方法具有一定的实用价值,在三维井间地震勘探开发领域也具有较好的应用前景.
致谢 感谢长安大学地质工程与测绘学院孙渊教授,他为本文的完成提供了大量有益的建议.西安石油大学李辉峰教授在实现该程序算法上提出宝贵的建议,在此一并感谢,同时感谢审稿专家对本文提出的意见和建议.| [] | CAO De-Xin, WANG Hai-Jun .2001. Numerical stability of interpolation functions of cobic spline[J]. Journal of China University of Mining & Technology (in Chinese), 30 (2) : 213–216. |
| [] | CAO Hui .2002. Current status of crosswell seismic technology[J]. Progress in Exploration Geophysics (in Chinese), 25 (6) : 6–10. |
| [] | Cerveny V .1983. Synthetic body wave seismograms for laterally varying layered structures by the Gaussian beam method[J]. Geophysical Journal International, 73 (2) : 389–426. DOI:10.1111/gji.1983.73.issue-2 |
| [] | Cerveny V .1985. Gaussian beam synthetic seismograms[J]. Journal of Geophysics, 58 : 44–72. |
| [] | CHEN Shi-Jun, LIU Hong, ZHOU Jian-Yu, et al .2003. The current situation and prospect of crosswell seismic technique[J]. Progress in Geophysics (in Chinese), 18 (3) : 524–529. DOI:10.3969/j.issn.1004-2903.2003.03.031 |
| [] | CHENG Yi-Jun, SUN Hai-Yan .2008. Thin plate spline interpolation and modeling of height anomaly of large area[J]. Science of Surveying and Mapping (in Chinese), 33 (4) : 42–44. |
| [] | DENG Fei, LIU Chao-Ying .2009. 3-D rapid ray-tracing and Gaussian ray-beam forward simulation[J]. Oil Geophysical Prospecting (in Chinese), 44 (2) : 158–165. |
| [] | DENG Fei, LIU Chao-Ying, ZHAO Bo, et al .2009. Gaussian beams forward simulation and migration[J]. Oil Geophysical Prospecting (in Chinese), 44 (3) : 265–269. |
| [] | Duan P F, Cheng J B, Chen S P, et al .2013. Local angle-domain ray tracing and prestack depth migration in TI medium[J]. Chinese Journal of Geophysics (in Chinese), 56 (1) : 269–279. DOI:10.6038/cjg20130128 |
| [] | FAN Ting-En, YU Lian-Yong, YANG Fei-Long, et al .2014. A method of Gaussian beam forward modeling in deviated-well VSP[J]. China Offshore Oil and Gas (in Chinese), 26 (5) : 30–35. |
| [] | Gal'perin E I. 1974. Vertical seismic profiling[R]. SEG Special publication No. 12, Tulsa, 270. |
| [] | JIN Sheng-Wen, CHEN Bi-Yuan, MA Zai-Tian .1994. Three-dimensional wave equation forward modelling by the finite-difference method[J]. Acta Geophysica Sinica (in Chinese), 37 (6) : 804–810. |
| [] | Li H, Wang H Z, Feng B, et al .2014. Efficient pre-stack depth migration method using characteristic Gaussian packets[J]. Chinese Journal of Geophysics (in Chinese), 57 (7) : 2258–2268. DOI:10.6038/cjg20140720 |
| [] | LI Hui, FENG Bo, WANG Hua-Zhong .2012. A new wave field modeling method by using Gaussian Packets[J]. Geophysical Prospecting for Petroleum (in Chinese), 51 (4) : 327–337. |
| [] | LI Qiang, BAI Chao-Ying .2012. Review on seismic wavefront and raytracing in complex media[J]. Progress in Geophysics (in Chinese), 27 (1) : 92–104. DOI:10.6038/j.issn.1004-2903.2012.01.011 |
| [] | LI Rui-Zhong, YANG Chang-Chun, CHEN Hui-Guo .2006. The Gaussian beam method and its application[J]. Progress in Geophysics (in Chinese), 21 (3) : 739–745. DOI:10.3969/j.issn.1004-2903.2006.03.009 |
| [] | PEI Zheng-Lin, MU Yong-Guang .2004. Numerical simulation of seismic wave propagation[J]. Progress in Geophysics (in Chinese), 19 (4) : 933–941. |
| [] | WANG Yan-Jun. 2011. The research of 3-D crosswell seismic kinematic forward (in Chinese)[MSc thesis]. Xi'an:Xi'an Shiyou University. |
| [] | Weber M .1988. Application of the Gaussian beam method in refraction seismology-Urach revisited[J]. Geophysical Journal, 92 (1) : 25–31. DOI:10.1111/j.1365-246X.1988.tb01117.x |
| [] | WEI Zheng-Rong, LI Hui-Feng, FAN Ting-En, et al .2014. Forward simulation method for crosswell seismic Gaussian beam of declined well[J]. Journal of Xi'an Shiyou University (Natural Science Edition) (in Chinese), 29 (1) : 10–14. |
| [] | Wu L .1997. Tomographic Fundamentals with Applications to Crosswell Seismics (in Chinese)[M]. Beijing: Petroleum Industry Press . |
| [] | WU Li-Ming, XU Yun, WUDA-BALA .1995. Applied study of Gaussian beam method in 2-D inhomogeneous media and laterally varying layered structures[J]. Acta Geophysica Sinica (in Chinese), 38 (S) : 144–152. |
| [] | Yang Fei-long. 2013. The research of 3-D crosswell seismic Gaussian beam (in Chinese)[MSc thesis]. Xi'an:Xi'an Shiyou University. |
| [] | YANG Fei-Long, SUN Yuan, LI Xu-Xuan, et al .2014. Deviatedhole VSP forward method based on the Gaussian beam[J]. Progress in Geophysics (in Chinese), 29 (6) : 2791–2799. DOI:10.6038/pg20140648 |
| [] | Yue Y B, Li Z C, Qian Z P, et al .2012. Amplitude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese Journal of Geophysics (in Chinese), 55 (4) : 1376–1383. DOI:10.6038/j.issn.0001-5733.2012.04.033 |
| [] | ZHANG Ru-Jie, HE Zhen-Hua, WANG Li .1997. Forward modeling by Gaussian beam method in crosswell seismic[J]. Computing Techniques For Geophysical and Geochemical Exploration (in Chinese), 19 (2) : 128–137. |
| [] | ZHOU Xi-Xiang, LIU Xue-Cai, JIANG Xian-Yi .1991. Seismic model made by two-dimensional Gaussian beam method[J]. Oil Geophysical Prospecting (in Chinese), 26 (4) : 452–464. |
| [] | ZUO Jian-Jun, LI Zhen-Chun, KONG Qing-Feng, et al .2005. Crosswell seismic imaging based on wave equation migration[J]. Progress in Exploration Geophysics (in Chinese), 28 (3) : 212–214. |
| [] | 曹德欣, 王海军.2001. 三次样条插值函数的数值稳定性[J]. 中国矿业大学学报, 30 (2) : 213–216. |
| [] | 曹辉.2002. 井间地震技术发展现状[J]. 勘探地球物理进展, 25 (6) : 6–10. |
| [] | 陈世军, 刘洪, 周建宇, 等.2003. 井间地震技术的现状与展望[J]. 地球物理学进展, 18 (3) : 524–529. DOI:10.3969/j.issn.1004-2903.2003.03.031 |
| [] | 程义军, 孙海燕.2008. 薄板样条与大区域高程异常插值[J]. 测绘科学, 33 (4) : 42–44. |
| [] | 邓飞, 刘超颖.2009. 三维射线快速追踪及高斯射线束正演[J]. 石油地球物理勘探, 44 (2) : 158–165. |
| [] | 邓飞, 刘超颖, 赵波, 等.2009. 高斯射线束正演与偏移[J]. 石油地球物理勘探, 44 (3) : 265–269. |
| [] | 段鹏飞, 程玖兵, 陈三平, 等.2013. TI介质局部角度域射线追踪与叠前深度偏移成像[J]. 地球物理学报, 56 (1) : 269–279. DOI:10.6038/cjg20130128 |
| [] | 范廷恩, 余连勇, 杨飞龙, 等.2014. 斜井VSP高斯射线束正演方法[J]. 中国海上油气, 26 (5) : 30–35. |
| [] | 金胜汶, 陈必远, 马在田.1994. 三维波动方程有限差分正演方法[J]. 地球物理学报, 37 (6) : 804–810. |
| [] | 李辉, 冯波, 王华忠.2012. 波场模拟的高斯波包叠加方法[J]. 石油物探, 51 (4) : 327–337. |
| [] | 李辉, 王华忠, 冯波, 等.2014. 特征高斯波包叠前深度偏移方法[J]. 地球物理学报, 57 (7) : 2258–2268. DOI:10.6038/cjg20140720 |
| [] | 李强, 白超英.2012. 复杂介质中地震波前及射线追踪综述[J]. 地球物理学进展, 27 (1) : 92–104. DOI:10.6038/j.issn.1004-2903.2012.01.011 |
| [] | 李瑞忠, 杨长春, 陈辉国.2006. 高斯束方法及其应用[J]. 地球物理学进展, 21 (3) : 739–745. DOI:10.3969/j.issn.1004-2903.2006.03.009 |
| [] | 裴正林, 牟永光.2004. 地震波传播数值模拟[J]. 地球物理学进展, 19 (4) : 933–941. |
| [] | 王彦军. 2011.三维井间地震运动学正演方法研究[硕士论文].西安:西安石油大学. http://cdmd.cnki.com.cn/Article/CDMD-10705-1012493379.htm |
| [] | 魏峥嵘, 李辉峰, 范廷恩, 等.2014. 斜井井间地震高斯射线束正演方法[J]. 西安石油大学学报(自然科学版), 29 (1) : 10–14. |
| [] | 吴立明, 许云, 乌达巴拉.1995. 高斯束射线法在二维非均匀介质复杂构造中的应用[J]. 地球物理学报, 38 (S) : 144–152. |
| [] | 吴律.1997. 层析基础及其在井间地震中的应用[M]. 北京: 石油工业出版社 . |
| [] | 杨飞龙. 2013.三维井间地震高斯射线束方法研究[硕士论文].西安:西安石油大学. http://cdmd.cnki.com.cn/Article/CDMD-10705-1014165852.htm |
| [] | 杨飞龙, 孙渊, 李绪宣, 等.2014. 基于高斯射线束的斜井VSP正演方法[J]. 地球物理学进展, 29 (6) : 2791–2799. DOI:10.6038/pg20140648 |
| [] | 岳玉波, 李振春, 钱忠平, 等.2012. 复杂地表条件下保幅高斯束偏移[J]. 地球物理学报, 55 (4) : 1376–1383. DOI:10.6038/j.issn.0001-5733.2012.04.033 |
| [] | 张汝杰, 贺振华, 王理.1997. 井间地震高斯射线束正演方法[J]. 物探化探计算技术, 19 (2) : 128–137. |
| [] | 周熙襄, 刘学才, 蒋先艺.1991. 二维高斯射线束地震模型[J]. 石油地球物理勘探, 26 (4) : 452–464. |
| [] | 左建军, 李振春, 孔庆丰, 等.2005. 波动方程法井间地震成像[J]. 勘探地球物理进展, 28 (3) : 212–214. |
 2016, Vol. 31
2016, Vol. 31

