微地震事件通常具有持续时间短、能量微弱、信噪比(signal-to-noise ratio, SNR)低的特点(赵博雄等,2014),有时微地震的有效信号甚至能被外部噪声所淹没,而微地震事件信号的信噪比极大地影响了震源定位的精度.因此,必须首先对监测到的微地震数据进行滤波去噪,提高微地震数据的信噪比,从而提高震源定位的精度.目前,已经有很多滤波方法应用于微地震数据去噪中,如卡尔曼滤波(Kalman Filter,KF)(Baziw and Weir-Jones, 2002;Baziw et al., 2004;邓小英等,2014)、自适应滤波(宋维琪等,2013)、小波分析(王正蕾,2009;Du and Zhang, 2010;宋广东等,2011),其中有些方法是基于模型的滤波技术,如KF滤波已经成功应用在基于机理模型的微地震信号处理中.
2002年,Baziw和Weir-Jones (2002)提出了一种基于微地震信号机理模型的KF滤波算法.通过对微地震信号进行机理分析,利用衰减震荡周期过程模拟微地震子波,将微地震记录的背景噪声当作高斯马尔科夫过程进行处理和建模,在一系列的假设和线性化之下得到了微地震信号的机理模型.两年后,Baziw等(2004)改进了当前检测微地震P波初至的卡尔曼滤波器的设计,进一步提高了自动识别P波初至的能力.
由于机理建模是以分析大量的信号数据为基础的,使得机理模型在实际应用中很难获得.为了克服这个难题,本文采用衰减震荡周期信号模拟微地震子波,通过辨识方法,如Steiglitz-McBride迭代方法,建立微地震信号的ARMA模型.为了在微地震信号处理过程中应用KF滤波,将ARMA模型进一步地转换为适用于卡尔曼滤波算法的状态空间模型(邓自立,2005).在此基础上,设计了适合于微地震信号去噪的KF滤波算法.在微地震信号辨识建模过程中,消除了机理模型在线性化处理过程中所存在的一些假设,提高了模型的精度,从而改善了KF滤波效果.
通过对微地震合成信号和地面监测数据进行滤波处理,基于辨识模型的KF滤波算法能够有效抑制微地震监测数据中的随机噪声,显著提高信噪比,从而验证了该辨识模型和滤波算法的准确性和可行性.
1 微地震信号辨识建模 1.1 ARMA模型自回归滑动平均模型(Auto-Regressive and Moving Average Model,ARMA)(邓自立,2005)是近代时序分析中描述离散平稳随机信号的最常用模型之一,可看做白噪声激励一个线性系统产生的时间序列模型.
离散系统的输入输出模型可用差分方程的形式表示为
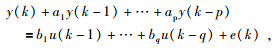
|
(1) |
将式写成更一般的形式,即
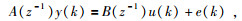
|
(2) |
式中,z-1为单位滞后算子,A(z-1)=1+a1z-1+a2z-2+…+apz-p, B(z-1)=b1z-1+b2z-2+…+bqz-q, p和q分别是自回归部分和滑动平均部分的阶数,ai(i=1, 2, …, p)和bj(j=1, 2, …, q)分别是自回归和滑动平均系数.
特殊地,当ARMA模型中输入项的各个系数bj都为0时,模型变为

|
(3) |
式(3)称为p阶自回归模型,记为AR (p).
当ARMA模型中输出项各个系数ai都为0时,模型变为

|
(4) |
式(4)称为q阶滑动平均模型,记为AM (q).
参数辨识建模需要确定辨识模型的类型,模型的阶次p和q,进而估计出模型系数ai(i=1, 2, 3…, p)和bj(j=1, 2, 3…, q).模型确定后,需要对模型的参数进行估计.与信号的分析类似,模型参数的估计方法可分为时域和频域两大类,本论文采用时域方法进行参数估计.具体方法是在确定系统为AR模型或者是ARMA模型之后,从给定的系统响应信息,或者是输入输出序列的相关性中估计出模型参数的具体值.
1.2 微地震子波辨识建模本文采用指数衰减周期震荡信号合成微地震子波(王维波等,2012),如式(5)所示,与实际监测到的微地震信号波形比较相似.公式为

|
(5) |
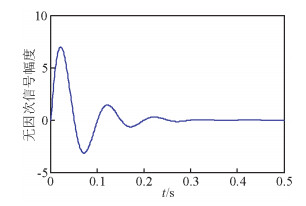
式中,A0为信号的初始振幅,h为阻尼因子,w为角频率,t0为信号的初始相位.通过对阻尼因子和角频率等参数选取合适的数值,可得如图 1所示的微地震子波.
|
图 1 数值模拟合成的微地震子波 Figure 1 Numerical simulation of microseismic wavelet |
通过对微地震合成子波的样本数据进行相关性分析(王少水等,2009),结果表明,样本数据的自相关函数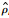


|
图 2 自相关与偏相关系数 (a)自相关系数; (b)偏相关系数. Figure 2 The autocorrelation and partial correlation coefficients (a) The autocorrelation coefficient; (b) The partial correlation coefficient. |
拖尾是指,当样本数据点数k增大时,样本数据的自相关函数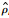


由相关分析法的分析结果可知,样本数据的自相关函数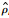

|
|
表 1 相关分析法结果与辨识模型类别关系表 Table 1 The relation between the results of correlation analysis and the category of identification model |
为了确定辨识模型的阶次,本文通过奇异值分解法(Singular Value Decomposition,SVD)判定ARMA模型的阶次(王少水等,2010;王树青等,2012).奇异值分解法是应用比较广泛的完全正交分解法,通过构造特殊矩阵并进行SVD分解,将归一化处理后的奇异值按从大到小的顺序进行排序,画出归一化奇异值曲线(图 3).通过观察和分析奇异值曲线,找出曲线趋向于水平或者突然下降的点,该点所对应的奇异值的个数即为所求的模型阶次.该方法简单实用,判定结果也较为准确.

|
图 3 SVD方法中的奇异值 Figure 3 Singular values in SVD method |
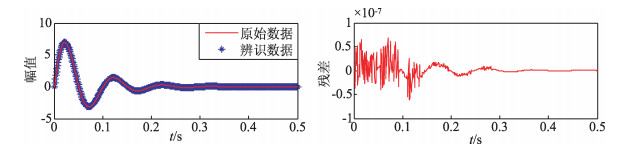
通过观察图 3所示的奇异值曲线,在第2个奇异值处曲线突然下降并趋向于水平,表明SVD法判定的模型阶次为2阶.在随后的建模仿真实验中,当辨识模型的阶次为2阶时,辨识模型的响应曲线与实验数据曲线高度吻合,所以最终选择辨识模型的阶次为2阶,即为ARMA (2, 1),其输入输出表达式如式(6)所示,辨识结果如图 4所示.公式为
|
图 4 微地震子波辨识结果 Figure 4 Identification results of the microseismic wavelet |

|
(6) |
其中
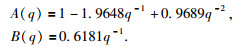
|
采用该模拟信号合成微地震信号时,在有效信号A(t)上叠加均值为0,标准差为σ的高斯白噪声N(t)~N(0, σ2).用一个表达式描述微地震监测站点接收的微地震数据,即

|
(7) |
从信号能量角度定义微地震信噪比RSN为
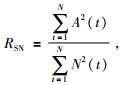
|
(8) |
即有效信号的能量与噪声能量之比.微地震记录的信噪比越高,微地震记录就越接近微地震信号,就越能有效地识别出P波、S波,从而提高震源定位的精度.
1.3 微地震子波状态空间模型为了验证辨识模型的准确性和方法的可行性,将辨识得来的ARMA模型进一步转换为状态空间模型,公式为
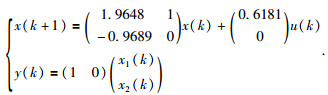
|
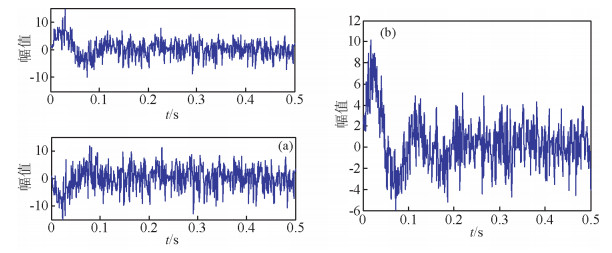
以此状态空间模型合成微地震子波,并叠加一定的高斯白噪声(图 5).
|
图 5 叠加白噪声的合成微地震子波 (a)叠加高斯白噪声的状态分量; (b)叠加高斯白噪声的观测值. Figure 5 Microseismic wavelet added with certain Gaussian white noise (a) State components added with Gaussian white noise; (b) Observations added with Gaussian white noise. |
基本KF滤波(Kalman,1960)只适用于线性离散系统,要求精确已知系统的数学模型和噪声的统计特性.假设系统中所有的噪声信号都服从高斯分布,并且相互独立.
设线性离散系统的状态空间模型(王静波,2012)为

|
(9) |
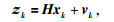
|
(10) |
其中,式(9)为系统的状态方程,式(10)为系统的观测方程.xk和zk分别为系统在k时刻的状态变量和观测变量,uk为系统在k时刻受到的控制量.A为状态转移矩阵,B为控制矩阵,H为观测矩阵.假设系统噪声wk和观测噪声vk是互不相关的零均值高斯白噪声,并且它们是相互独立的.公式为

|
式中,Q和R分别为系统噪声wk和观测噪声vk的协方差.
KF滤波在确保最小均方误差的前提下,以迭代递推的形式对信号状态进行最优估计.滤波算法由时间更新和测量更新两个过程组成,时间更新是对当前时刻的系统状态和先验误差协方差进行预测,测量更新根据系统当前时刻的观测值修正时间更新过程中的系统预测值.滤波算法(王静波,2012)简述如下:
1) 系统的先验状态估计
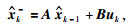
|
(11) |
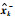
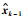
2) 先验误差协方差估计
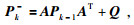
|
(12) |
Pk-为系统在k时刻的先验误差协方差估计,Pk-1为系统在k-1时刻的误差协方差,上标T表示矩阵的转置.
3) 计算卡尔曼滤波增益
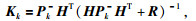
|
(13) |
Kk为卡尔曼滤波算法在k时刻的滤波增益,上标-1表示矩阵的逆.
4) 更新系统状态
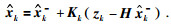
|
(14) |
5) 更新误差协方差
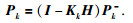
|
(15) |
单位矩阵I的维数与辨识模型的系数矩阵A保持一致.
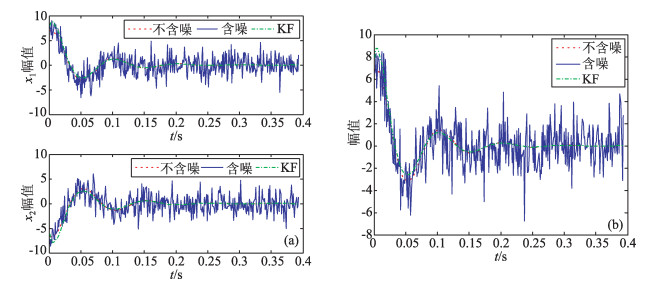
系统初始条件为
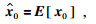
|
(16) |
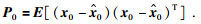
|
(17) |
Kalman滤波算法的实现步骤如下:
(1) 初始化系统状态
(2) 计算系统的先验状态估计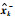
(3) 计算卡尔曼滤波增益Kk、系统状态
(4) 判断滤波算法是否结束,如果没有结束则返回步骤2,直至算法结束为止.
2.2 合成微地震信号滤波处理为验证辨识模型的准确性和KF滤波算法的应用效果,对叠加不同程度高斯白噪声后信噪比为10%、30%、50%、100%的微地震合成信号进行KF滤波.结果表明,微地震信号中的高斯白噪声均得到明显抑制,效果显著.由于篇幅限制,本文只列出信噪比100%的微地震合成信号的滤波结果(图 6).
|
图 6 微地震信号卡尔曼滤波结果 (a)状态分量滤波曲线; (b)观测值滤波曲线. Figure 6 The filtering results of the microseismic signal added with certain Gaussian white noise (a) The filtering results of state components; (b) The filtering result of observations. |
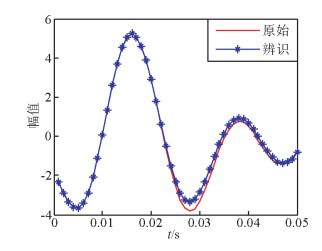
为了进一步验证辨识建模方法的适用性和辨识模型的准确性,将该辨识建模方法和滤波算法应用于实际采集到的微地震监测信号中,笔者从采集到的高信噪比的微地震数据中提取出实际微地震信号,并对提取得到的实际微地震信号采用上述建模方法进行辨识建模,可得实际微地震信号的辨识模型为ARMA (15, 14),其输入输出表达式如式(18)所示,实际微地震信号的辨识结果如图 7所示.
|
图 7 实际微地震信号辨识效果图 Figure 7 Identification results of microseismic signals |
|
(18) |
其中,

|
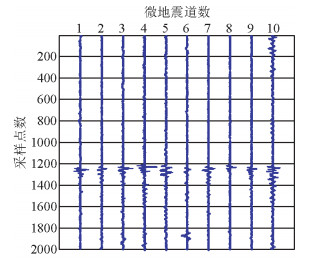
通过对实际采集到的微地震监测信号进行辨识建模,将得到的ARMA模型进一步转化为状态空间模型.在此基础上,设计了适于实际微地震监测数据去噪的卡尔曼滤波算法.为验证基于实际微地震信号辨识模型的卡尔曼滤波算法在实际微地震监测数据中的应用效果,笔者对某压裂气井的地面微地震监测信号(图 8)进行处理,滤波效果如图 9所示.
|
图 8 某气井微地震压裂信号 Figure 8 Microseismic fracturing signals of a gas well |

|
图 9 某气井微地震压裂信号滤波结果 Figure 9 The filtering results of microseismic fracturing signals of a gas well |
通过对实际采集到的微地震地面监测数据进行卡尔曼滤波处理,KF滤波对实际微地震数据中的随机噪声滤波效果明显,能够显著提高微地震记录的信噪比,从而验证了该辨识模型的准确性和滤波算法的可行性.
4 结论 4.1本文采用衰减震荡周期信号合成微地震子波,针对微地震典型信号建立了ARMA辨识模型,辨识建模过程中消除了机理模型中因假设和线性化处理而存在的模型误差.为了在实际采集到微地震监测数据中应用KF滤波,笔者将辨识得来的ARMA模型进一步转化为适于卡尔曼滤波的状态空间模型,并研究和设计了卡尔曼滤波的实现算法.根据理论模型和对微地震子波信号的辨识结果可知,本文通过参数辨识方法建立的微地震典型信号的辨识模型误差很小,精度较高.
4.2通过对叠加不同程度高斯白噪声、信噪比分别为10%、30%、50%、100%的微地震合成信号进行KF滤波,噪声得到显著抑制,滤波效果较好.实际采集到的微地震监测数据滤波结果表明,KF滤波可以较好地抑制微地震监测数据中的随机噪声,显著提高微地震监测数据的信噪比,从而验证了该辨识模型的准确性和基于辨识模型的KF滤波算法的可行性.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Baziw E, Nedilko B, Weir-Jones I .2004. Microseismic event detection Kalman filter:Derivation of the noise covariance matrix and automated first break determination for accurate source location estimation[J]. Pure and Applied Geophysics, 161 (2) : 303–329. DOI:10.1007/s00024-003-2443-8 |
| [] | Baziw E, Weir-Jones I .2002. Application of Kalman filtering techniques for microseismic event detection[J]. Pure and Applied Geophysics, 159 (1) : 449–471. DOI:10.1007/PL00001260 |
| [] | Deng X Y, Hu J, Li Y, et al .2014. A new tracking approach of the seismic record event based on Kalman filtering and its performance analysis[J]. Chinese Journal of Geophysics (in Chinese), 57 (1) : 270–279. DOI:10.6038/cjg20140122 |
| [] | Deng Z L .2005. Optimal Estimation Theory with Applications (in Chinese)[M]. Harbin: Harbin Institute of Technology Press . |
| [] | Du W J, Zhang Z P. 2010. Application of wavelet analysis in seismic data processing of volcanic rock region[C]//Proceedings of 2010 International Conference on Intelligent System Design and Engineering Application (ISDEA). Changsha:IEEE, 1:371-374. |
| [] | Kalman R E .1960. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 82 (1) : 35–45. DOI:10.1115/1.3662552 |
| [] | Song G D, Liu T Y, Wang C, et al .2011. Application of wavelet analysis in the processing of micro-seismic signal[J]. Shandong Science (in Chinese), 24 (3) : 64–68. |
| [] | Song W Q, He K, Guo Q S, et al .2013. Micro-seismic data adaptive filtering method[J]. Geophysical Prospecting for Petroleum (in Chinese), 52 (3) : 229–233. |
| [] | Wang J B, Xiong S Q, Guo Z H, et al .2012. Kalman smoothing for airborne gravity data[J]. Progress in Geophysics (in Chinese), 27 (4) : 1717–1722. DOI:10.6038/j.issn.1004-2903.2012.04.052 |
| [] | Wang S Q, Lin Y Y, Meng Y D, et al .2012. Model order determination based on singular value decomposition[J]. Journal of Vibration and Shock (in Chinese), 31 (15) : 87–91. |
| [] | Wang S S, Dai Y S, Wang F, et al .2009. The summarization of the research on the order determination of the seismic wavelet parameterized estimation model[J]. Progress in Geophysics (in Chinese), 24 (4) : 1405–1410. DOI:10.3969/j.issn.1004-2903.2009.04.031 |
| [] | Wang S S, Dai Y S, Wang F, et al .2010. Research on the ARMA model for extraction of in seismic wavelets[J]. Progress in Geophysics (in Chinese), 25 (6) : 2109–2114. DOI:10.3969/j.issn.1004-2903.2010.06.030 |
| [] | Wang W B, Zhou Y Q, Chun L .2012. Characteristics of source localization by seismic emission tomgraphy for surface based on microseismic monitoring[J]. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 36 (5) : 45–50. |
| [] | Wang Z L .2009. Detection of weak earthquake signals based on wavelet analysis[J]. Progress in Exploration Geophysics (in Chinese), 32 (3) : 182–185. |
| [] | Zhao B X, Wang Z R, Liu R, et al .2014. Review of Microseismic monitoring technology research[J]. Progress in Geophysics (in Chinese), 29 (4) : 1882–1888. DOI:10.6038/pg20140454 |
| [] | 邓小英, 胡健, 李月, 等.2014. 一种新的基于卡尔曼滤波的地震记录同相轴跟踪方法及性能分析[J]. 地球物理学报, 57 (1) : 270–279. DOI:10.6038/cjg20140122 |
| [] | 邓自立.2005. 最优估计理论及其应用:建模、滤波、信息融合估计[M]. 哈尔滨: 哈尔滨工业大学出版社 . |
| [] | 宋广东, 刘统玉, 王昌, 等.2011. 小波分析在微地震信号处理中的应用研究[J]. 山东科学, 24 (3) : 64–68. |
| [] | 宋维琪, 何可, 郭全仕, 等.2013. 微地震资料自适应滤波方法研究[J]. 石油物探, 52 (3) : 229–233. |
| [] | 王静波, 熊盛青, 郭志宏, 等.2012. 航空重力数据Kalman滤波平滑技术应用研究[J]. 地球物理学进展, 27 (4) : 1717–1722. DOI:10.6038/j.issn.1004-2903.2012.04.052 |
| [] | 王树青, 林裕裕, 孟元栋, 等.2012. 一种基于奇异值分解技术的模型定阶方法[J]. 振动与冲击, 31 (15) : 87–91. |
| [] | 王少水, 戴永寿, 王芳, 等.2009. 参数化地震子波估计模型定阶方法研究综述[J]. 地球物理学进展, 24 (4) : 1405–1410. DOI:10.3969/j.issn.1004-2903.2009.04.031 |
| [] | 王少水, 戴永寿, 王芳, 等.2010. 一种ARMA模型地震子波提取方法研究[J]. 地球物理学进展, 25 (6) : 2109–2114. DOI:10.3969/j.issn.1004-2903.2010.06.030 |
| [] | 王维波, 周瑶琪, 春兰.2012. 地面微地震监测SET震源定位特性研究[J]. 中国石油大学学报(自然科学版), 36 (5) : 45–50. |
| [] | 王正蕾.2009. 基于小波变换的微地震信号检测方法研究[J]. 勘探地球物理进展, 32 (3) : 182–185. |
| [] | 赵博雄, 王忠仁, 刘瑞, 等.2014. 国内外微地震监测技术综述[J]. 地球物理学进展, 29 (4) : 1882–1888. DOI:10.6038/pg20140454 |
 2016, Vol. 31
2016, Vol. 31

