2. 北京科胜伟达石油科技股份有限公司, 北京 100085
2. Co-Sail Petroleum Technology, Co., Beijing 100085, China
对当前微地震监测的研发进展,特别是各种方法的可行性和局限性,梁北援等(2015)已进行了综述和讨论.本文较详细地描述了微震监测的向量扫描技术(Vector Scanning—VS)的原理(Shen等,2009;Ma等,2012;Wang等,2012;Shen等,2014;Wu等,2014;Zhang等,2014<1><2>),特别是其近几年的最新进展.
为了说明技术特性,有必要首先简要列出发展VS的背景和动因(第1章),并据此明确VS的研发要求.随后,我们定义VS的应用方程(第2章).第3章各节分别讨论了方程实施中的几个问题:应用VS的先决或必要条件、使用何种波形、最小扫描台站数的估计、适度矫正速度模型引起的误差、台站权重在叠加中的使用、以及它的局限性;前两个问题是最重要、也是一些地震学家质疑、且很多应用方和服务方容易忽略的;其他问题是保证或提高VS应用的可行性与可靠性的一些工作.其中,局限性也是任何使用者应当明确的.这些定义、应用细节和过程、以及讨论均用一组人工数据的例子给与说明.
欲保证VS应用的成功,仅仅明确原理或算法是远远不够的,还必须工程化地解决在野外数据采集、数据处理、和解释各个环节中的一系列问题.任一环节上的失误或缺乏技术监管均可能造成应用失败.除对原理的讨论给予结论外,第4章也简要列出vs在工程化的过程中必须研发和解决的一系列问题,但将另文详细讨论它们.
1 研发微破裂向量扫描技术的背景和要求研发微地震压裂监测的向量扫描方法的背景或动因简列如下(梁北援等,2015):
1) 油气生产(如压裂、注水气)、矿山和油田的安全、油储构造状态、甚至油气勘探均需要或可以实施微震监测及其监测结果的应用;
2) 上述过程中可用的或它们诱发的大量岩石破裂多为微小地震(震级M<0),且它们类似于构造地震,即为剪切滑动或具有剪切成分;
3) 井中邻近监测和实施传统定位(即提取可见初至以确定震源),一般地说,在检波器阵距监测目标一至几百米外失效;何况由于台网分布缺陷、目标远处被诱发的震群和压裂井噪声的干扰、压裂时邻近介质在不断破裂而变化,对几百米内较准确的定位是一个巨大的挑战.单分量地表大规模阵列式监测并实施传统定位,使用相对横波(S)来讲频率高、振幅小的纵波(P),监测成功率只有百分之几;若使用偏移叠加处理,则计算量极大.何况这两种方法成本高、施工复杂;
4) 任何方法必须适应恶劣的微震监测环境,如复杂地貌和大批地面地下机器管线的干扰;
5) 任何监测方法必须顾及应用方基本的常规要求,如性价比高、无或较少特殊条件限制、可随压裂等生产活动迅速施工而成为日常手段、实时或近实时处理解释;等等.
上述现状和研发应用VS的经验,使我们意识到对微震监测需明确对准微小和具有剪切性质的破裂这一监测目标,改变对观测记录要求较高的传统定位思路,实施向量扫描或偏移成像,放弃可能使很多台站噪声极大的等距等角阵列,放弃使用振幅较小的P波,而使用3分量记录的S波.简单照搬监测天然大震及其余震的地震仪和常用的勘探检波器是不适宜的,应研发适于微震监测的专用微震仪.否则,一个微震监测方法的研发和实施就可能导致致命错误,或者在可行性和可靠性上大打折扣.
因而,VS的研发要求被确定如下:
1) 针对微小地震(通常记录的信噪比<1)、且考虑它们多有剪切破裂的特性;
2) 三分量地表观测;
3) 没有特殊条件限制、不破坏环境、稀疏布设台网、与适合复杂地貌;
4) 具有很强的抗干扰能力,适合一般生产的背景噪声环境;
5) 实时监测并4D处理解释;
6) 能够在地表快速施工,成为伴随生产活动的日常监测手段;
7) 性价比高;等等.
2 应用方程对辐射或反射信号微弱的目标,或者有用信号淹没在监测环境背景噪声中的情形,即信噪比(Ratio of Signal over Noise—S/N)小于1,可使用具有很多点的阵(网)实施观测,针对某种物理参数,经适当数据处理,影像目标的时空分布.常用的大规模地震勘探阵列、射电天文望远镜阵、声纳和雷达阵、医学中的各种影像手段等的数据采集和处理就是以此为基础发展起来的.因而,根据微震特性,对它们的监测也不可避免地要使用类似的物理数学手段.事实上,任何阵网所影像的,均是目标的某种物理参数的时空分布,没有所谓“直接看到”的目标.
2.1 方程定义我们沿用一般信号处理的相关性思路(例如,Press等,1997;程乾声,2003),改造和发展Semblance叠加公式(Sheriff,1991),定义VS的应用方程为
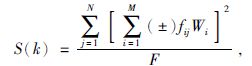
|
(1) |
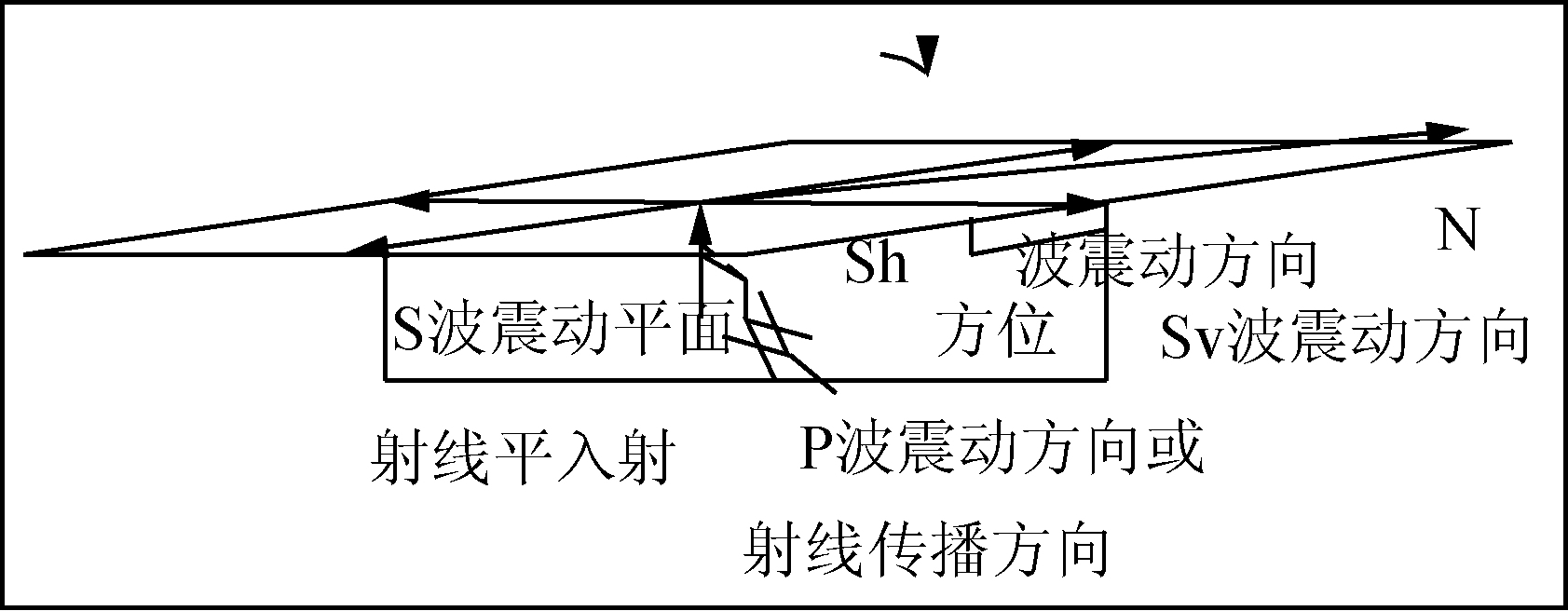
其中
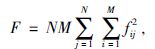
|
这里,k是被扫描的体积中第k个点;对所有台站M、各台到时算起的时窗内N个样点的某种波型fij求和,并使用归一化因子F,即得k点的S(k).因通常记录的振幅是地面运动速度,而速度的平方正比于动能,故S(k)可理解为无量纲化了的破裂辐射能量.若将式(1)写成积分形式,即为一般3D模型的深度偏移成像.当S(k)高(低)时,表示k点破裂释放能量高(低).式(1)与Semblance叠加不同的是:
1) fij由原来的标量发展为向量,为第i个台站的第j个记录样点的3D运动速度;
2) fij前面的正负号由地震剪切破裂性质或震源机制(例如,Aki 与Richards,1980;Kasahara,1981;Bullen 与 Bolt,1985)、或叠加时窗内相对于参考台的相关性(例如,Press等,1997)决定;
3) Wi为第i个台站记录在扫描叠加中的权重,由此台向量记录的S/N的大小决定.换句话说,Wi由此台向量记录在叠加中对监测目标附近的较高破裂能量分布与压制残余噪声的贡献程度决定.
上述计算使用直达的P、S、Sv、或Sh四种波型(图 1),并各自独立叠加输出;其中S波是Sv和Sh两个量的合成.在应用中使用何种波形是一个重要问题,将在第3章中专门讨论.
|
图 1 观测点处P、S、Sv和Sh波的定义 Figure 1 The definitions of P,S,Sv,and Sh at an observation point |
在扫描计算中,使用观测点的记录向量对准扫描点.建立地下速度模型后,可通过射线追踪得到观测点相应于扫描点的射线入射角、入射方位、与两点间地震波传播全路径走时;那么,就可确定对准观测点的扫描向量(P波振动方向)、S波振动平面、Sh波、和Sv波的振动方向;使用空间转向矩阵(例如,Aki 与Richards,1980),将3分量记录数据投影到一个波型的振动方向,并与其他台站的同波到时记录投影、据走时经时间上的适当错动后实施叠加,即得该波形的记录能量输出.简单地说,我们是将所有观测点的同波型的各个向量在4D空间中移到参考台点,并实施叠加.
叠加时,要依据相对于任选的参考台的记录正负相关性对各台向量赋予(1)式中的正负号.叠加各向量后,就应当反映出各台对准一个扫描点的相关性程度,而这种相关性,只要背景信号是随机的,则由有用信号控制,或说震源机制控制.因而在数学上,我们影像的是对准扫描点的各个向量间的相关程度分布;在物理上,则反映了破裂能量释放的高低程度分布.
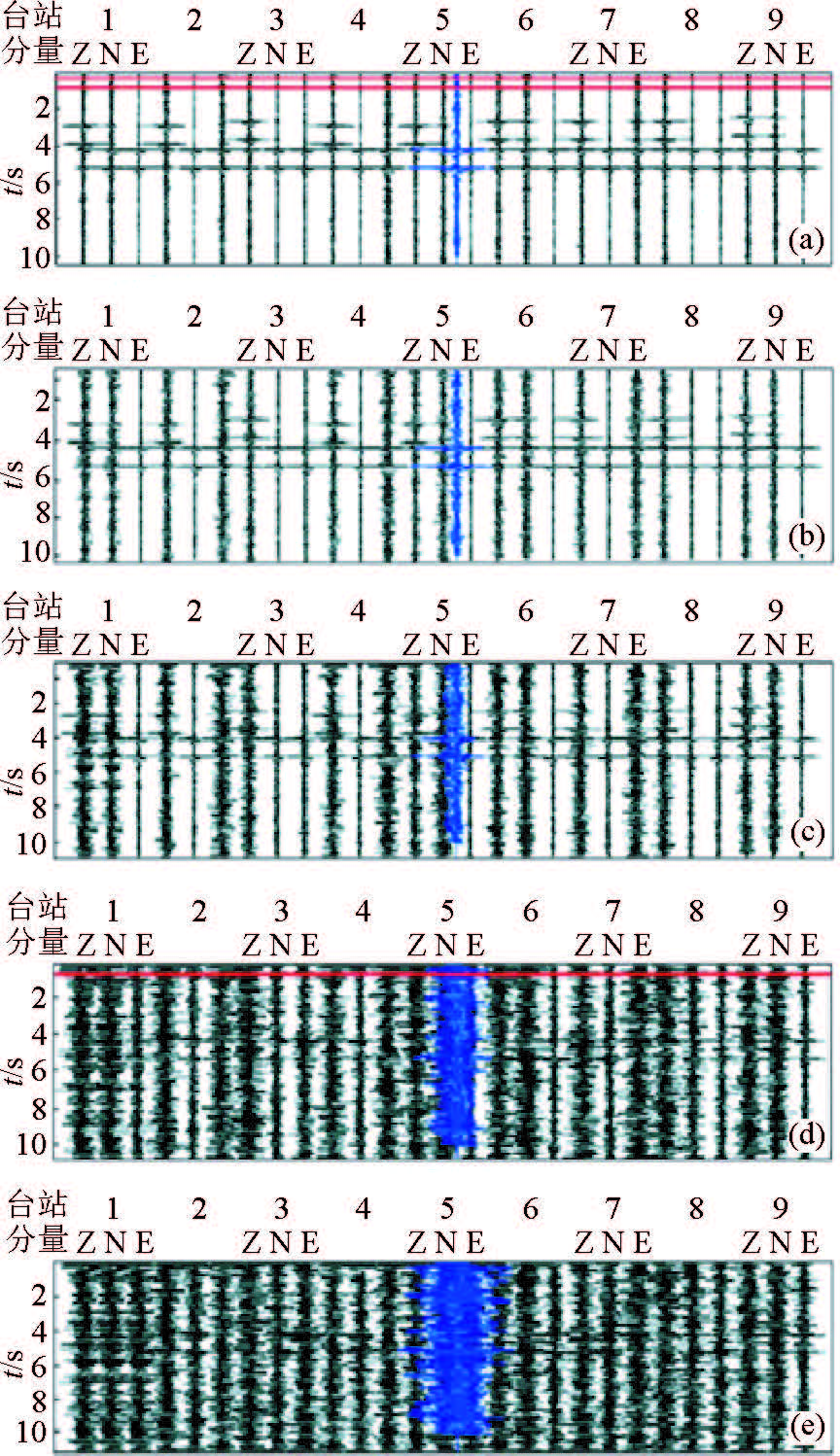
2.2 人工数据例子作为例子,我们用一组人工数据(图 2~图 4),来说明公式(1)的使用.地表台网由9个具有北(N)、东(E)、深度(Z)方向的三分量台站组成;计算扫描范围为4×4×5 km3;设传播到地表的破裂振动的主频为15 Hz,采样间隔为2 ms,扫描点距为25 m;破裂点在[1,1,4]km,由两个剪切滑动组成,期间相隔1 s;S/N=(10,5,3,1,0.5);相应的记录波形显示在图 2中.这里,S/N的定义为最大有用信号与最大随机噪声振幅之比,其中,背景随机噪声由计算机使用随机数的数值程序创造(例如,Press等,1997).各台已据射线追踪后的S波到时差在时间上错动使它们的到时对齐.地下网格的P波速度Vp分布由自地表 1.5 km/s到5 km深度的3.8 km/s的一维模型构成,设泊松比为0.25,则S波速度Vs=Vp/1.732.这里,S波最大振幅约为P波的2倍,且以Sh波为主.图 2中各蓝色线为各台指向破裂点的向量叠加后S波模振幅波形.仅对破裂点周围各方向 500 m的体积进行扫描.
|
图 2 验证微破裂向量扫描技术例子的波形.破裂振动的主频为15 Hz,样点间隔为2 ms.从上至下分别为不同信噪比S/N=(10,5,3,1,0.5)相应的波形.据射线追踪后的S波到时差在时间上错动使它们的振幅对齐,产生各台指向破裂点的向量叠加后模振幅波形(蓝色). Figure 2 The synthetic data for testing vector scanning. Where,the main frequency of 15H and sample interval of 2 ms are used. From up to down,show the ruptures signals with S/N=(10,5,3,1,0.5),respectively. Each blue wave is the stack of all vectors of the station records relative to the rapture point. |
注意图 2的波形,当S/N降到3时,尚可勉强辨认S波,但提取它们的准确到时已很困难.当S/N更小时,即使从向量相叠加后的波形(蓝色线),也很难辨认出破裂信号,这就是我们几百次在地表实际监测时的基本情形.
据射线追踪后的S波到时差,在时间上错动,以使各台的S波振幅对齐,产生各台指向破裂点的向量叠加后模振幅波形(图 2蓝色波形,这里仅是对准破裂点的叠加波形).由图 3可知:
|
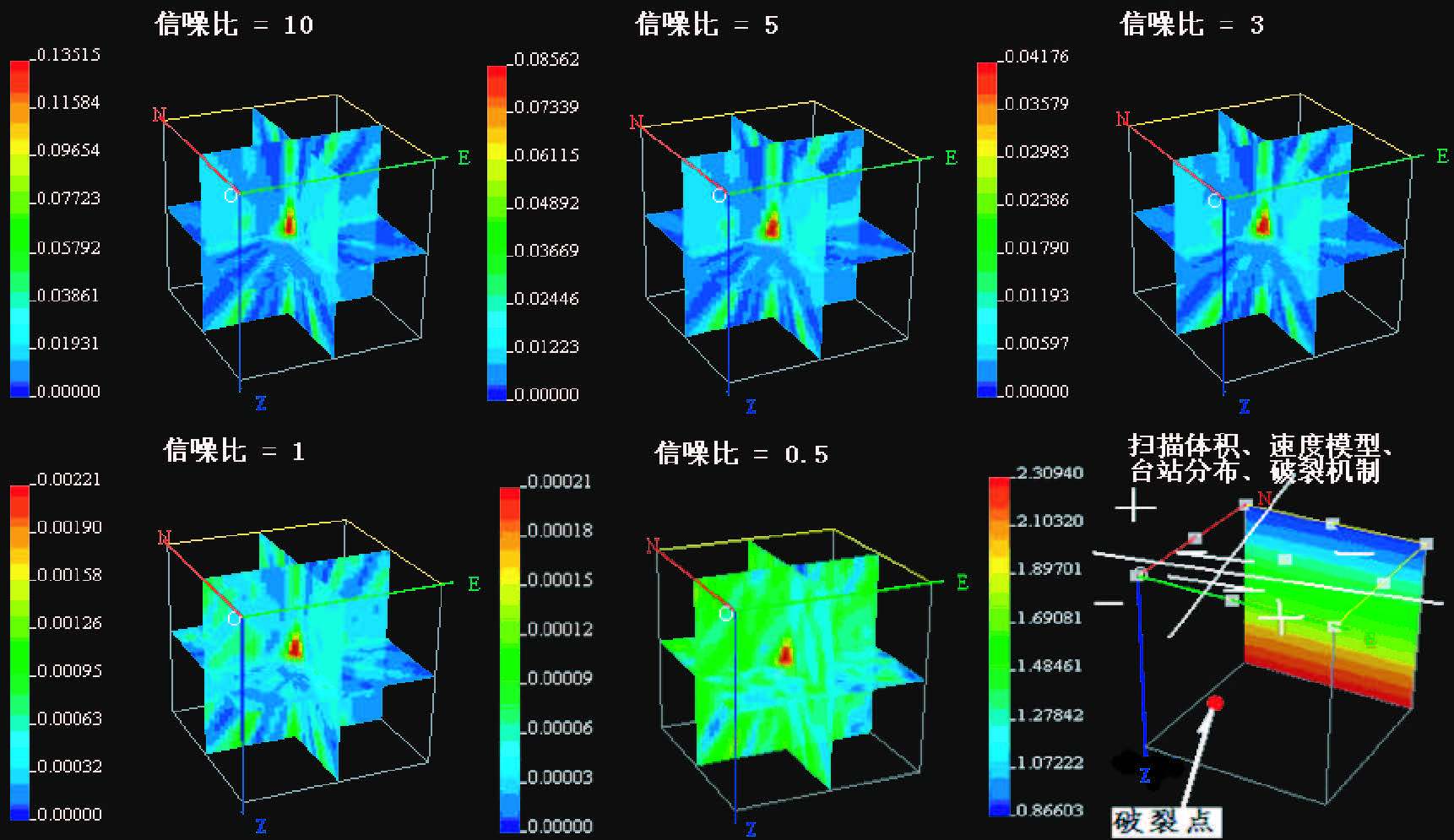
图 3 相应于图 2的各种信噪比的破裂释放能量的3D扫描输出.从上至下、从左至右分别对应信噪比为10、5、3、1、0.5的记录.最后的子图显示了台站分布、P波速度模型、与根据记录极性对 走滑机制的确定;这里,正负号仅是相对参考台而言. Figure 3 Scanning outputs of releasing energy corresponding to the data in Fig. 2. From left to right and up to down,the figures show the outputs with S/N=10,5,3,1,0.5,respectively. The last figure displays station distribution(white points),P wave velocity structure,and the mechanism of the seismic events. |
1) 破裂释放的最大能量输出均准确地发生在预定点[1,1,4]km;
2) 相应于每个计算的最大能量点,各台向量极性(以推动台站为正)同预知的一致,即当存在附近已知断层时,若台站分布较均匀,VS输出可用于解释此剪切破裂的机制(图 3第6子图);
3) 随着S/N的降低,最大能量输出值也越来越低,相应的,背景噪声的影响却逐渐升高.但直至S/N=0.5,依然可得到前两个结论.
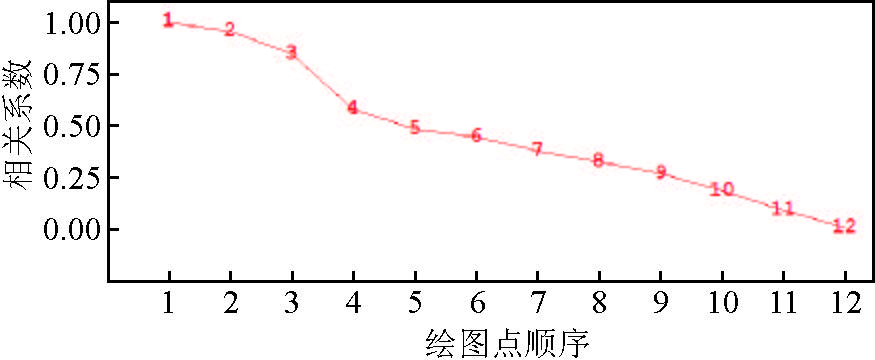
以S/N=10的情形为准,做5种S/N的相对于预定破裂点[1,1,4]km的向量相叠加波形(图 2中各蓝色线)的相关分析,即图 4中的点1至5.图 4中点6至12是S/N=0.5时沿东方向逐渐远离破裂点的情形.可见,S/N越低,相关性越差.但即使S/N=0.5,扫描到破裂点外的各点时,其相关系数相对于破裂点的更低,故仍可在空间上辨别较高能量的释放点.
|
图 4 相对信噪比=10的叠加曲线的各种情形的相关性.图中点1至5是相对于预定破裂点[1,1,4]km的相关比较.点6至12是S/N=0.5时沿Y轴逐渐远离破裂点的情形. Figure 4 Correlation between the stacks of data with S/N=10 and other S/N corresponding to the data in Fig. 2 for ruptures at [1,1,4]km(points 1 to 5).Points 6~12 show the correlations which are the cases of S/N=0.5 scanning to the locations along the Y axis gradually far from the rapture site. |
提出或应用一个算法,必须说明它的可行性和局限性,包括其可靠程度及实施条件.对此,广义地讲,我们要分析整个VS监测系统的原理、野外数据采集、数据处理、解释的全部软硬件及其关联,包括误差.对任何地面微震监测的分辨率,我们已在Shen等(2009)中初步讨论过.本章重点讨论直接涉及原理或实施方程(1)有关的几个问题.其他问题将简列于本文最后讨论与结论中,并另文详细讨论.以下几个问题,有的是某些地震学家和应用者对实施公式(1)质疑过的,有的是应用者常忽略的,有的是可以在应用中进一步改进扫描质量的.
3.1 应用向量扫描的必要条件在上述应用方程的定义和验证例子中,可以注意到,我们要求所有台站的背景噪声记录是随机的.这里所谓的随机背景噪声,应当是
1) 远处无穷个振动及观测点弱电磁干扰场的组合,其记录是无规律或时空上不可预报从而也不可能去除的波动;
2) 由于S/N<1,而公式(1)是检查各向量间的由有用信号控制的相关程度,故这些背景噪声的振幅应尽可能的小.
事实上,我们在数百次的压裂监测记录中发现,任何天然地震、生产诱发的同目标不连通的地震、人工爆破、人员或动物行走、有规律的地面机器的运行等干扰,均可能在扫描输出中的监测目标及其附近引起“高或较高破裂能量”的伪影,从而造成误判;或者这些干扰形成了占统治地位的图形,而目标附近的破裂能量不能凸显出来.若要保证监测质量,应在数据采集、数据预处理、和计算过程中,避免、去除、或压制这些同监测目标无关的携带外来能量的干扰.
另一方面,凡是背景噪声平均振幅较大的、即使看似“随机”的记录,通常隐含有不远处的有规律的振动干扰.当有用信号较小或S/N不大时,即使背景噪声是看似“随机”的,也会造成在监测目标及其附近引起“高破裂能量”的伪影.例如,在城镇中较安静处,如公园的白天,似乎背景噪声是随机的,但较野外安静处的平均振幅仍然较大,造成扫描时的S/N较小,而不能应用此方法.又例如,靠近压裂车群1 km内安放台站,尽管此类振动干扰是宽频、有时是振幅变化不大的貌似随机的,就不可能获得好的有效S/N.
简言之,我们要在应用全过程中尽一切努力提高和获得有效的S/N.因而,在安静处布设地震台网,并在处理中去除和压制干扰信号以获得较小振幅的随机记录,是应用向量扫描技术的必要条件.在实际监测中,这也是判断一个监测是否可行、置信度的高低、或能否成功的先决条件.应当指出,这种条件应当数值化地由监测的地震仪器、地震台网分布、监测环境 、检查整理数据和去噪过程判定.人员的主观感受和目视记录数据决定此条件是不可靠的.
3.2 向量扫描使用的波型地震波理论分析表明,除了爆炸、矿洞塌陷等震源仅产生较为单一的P波外,天然构造地震均为剪切破裂或具有剪切破裂的成分,它们通常产生P、Sv、和Sh三种波型(图 1).其中,Sv和Sh分别对应震源处应力场的两个剪应力分量,且它们的传播是各自独立的(Aki与Richards,1980).如若定义S波是Sv和Sh两个量的合成,一个地震就辐射出四种波型.
在分析通常的微震特性时,我们知道:油气生产(如压裂、注水气)、矿洞变形等产生的微地震,其特点之一就是它们同构造地震类似,而具有剪切成分(梁兵和朱广生,2004;梁北援等,2015).对于产生这个特性的原因,简单地说,只要应力场的三个主压应力大小不等,例如简单的重力作用下引起的应力场,就存在非0剪应力(例如,Jaeger,1979),从而剪切破裂就是不可避免的;即使水力压裂,在脱离压裂点半米至几米的短距离外,剪切破裂就一定存在,甚至可能超过张破裂占主导地位.
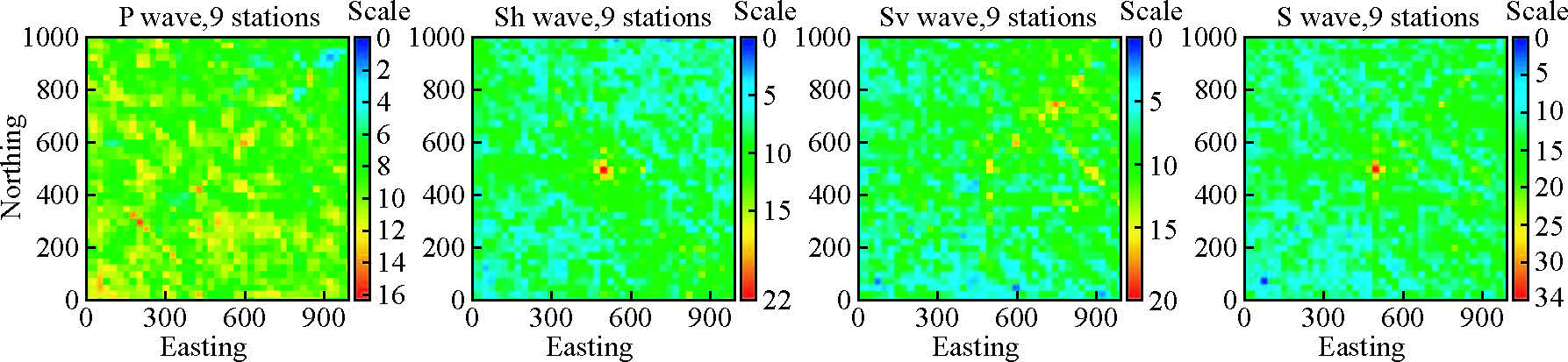
在井下邻近观测中,可以很清楚地看到S波信号(梁兵和朱广生,2004;Shapiro,2008;Maxwell,2014);与P波相比,几百米内它们就常有两三倍以上的振幅,频率显著较低,这是典型的剪切特性的记录(Aki 与 Richards,1980;Bullen 与 Bolt,1985;孟晓春,2005).由此可知,据监测目标数百至数千米的地表微震监测点可以使用由于低频、传播衰减较小、携带能量更多的S波,从而获得好得多的S/N.一个简单的推论是,微震监测应当使用三分量的地震仪,从而完整地记录波动向量.这也是为何简单地照搬垂直分量的大规模地面阵列实施微震监测的成功率极低(梁北援等,2015)的原因.图 5为第2.2节使用的人工数据例子的各种不同波型的扫描输出,用以说明:若使用振幅较小的P波,当使用9个台站时,无法获得正确影像.
|
图 5 使用人工数据对9个台站数的扫描实验的不同波形的2D平面输出.参数同第3.2节的人工数据实验, 且信噪比为0.5.4 个图形分别对应使用了P、Sh、Sv、和S波.由于人工数据的设计以Sh波为主,故Sh和S波的 输出与预想一致(图 3).由于P波振幅较小,它的输出在此例中无法正确影像破裂点.每子图的平面中, 横轴指向东,纵轴指向北.绘图时均减去了最小能量值,即以0为基准 Figure 5 Two dimensional planes of releasing energy using the synthetic data same as section 3.2 with S/N=0.5 for 4 different waves: P,Sh,Sv,and S,respectively. Each shows the horizontal section.All of energy values minus minimum so that one can compare the differences between the highest and lowest each other |
因而,在VS地面微震监测应用中,一般应当舍弃P波,使用S波实施向量扫描,从而必定可获得较高的有效S/N,大大提高监测成功率.但一般事先不知道引起S波的应力场,故应分别检查Sv、Sh、或S的扫描输出,选取最佳者实施解释.
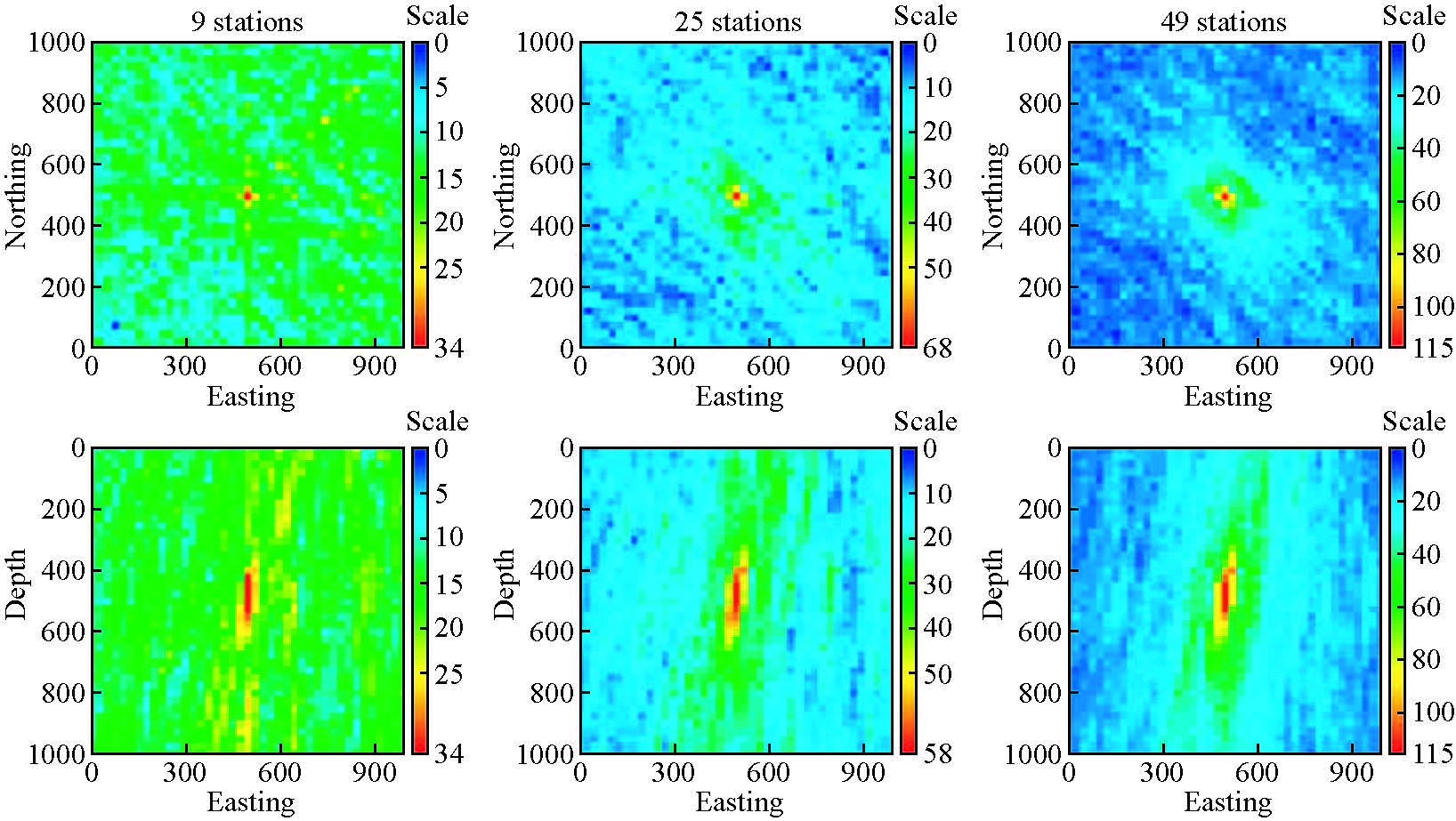
3.3 最小扫描台站数的估计在应用(1)式时,使用多少台站才能保证监测质量?当然,地震学家希望越多越好,但不得不考虑成本、施工速度、和野外监测现场所允许的布设安静点数量;否则,一个监测方法就很难成为一个日常应用手段.为此,这里继续实施了类似第2.2节中的人工数据的扫描实验,但使用了不同台站数.图 6中,参数同第2.2节的实验.三个图形分别对应使用了9、25、和49个3分量台.数据输出未加任何处理修饰,除了绘图时均减去了最小能量值,即以0为基准.可以看到,
|
图 6 使用人工数据对不同台站数的扫描实验的2D平面输出.参数同第2.2节的人工数据实验,且信噪比为0.5. 三列图形分别对应使用了9、25、和49个3分量台.每子图为包括破裂点(红色-高破裂释放能量)的平面. 上排:水平平面,横轴指向东,纵轴指向北;下排:横轴指向东,纵轴指向深度,其中深度0表示 自地表向下的3500 m.数据输出未加任何处理修饰,除了绘图时均减去了最小能量值,即以0为基准. Figure 6 Two dimensional planes of releasing energy using the synthetic data same as section 2.2 with S/N=0.5.The 3 columns correspond to the cases with 9,25,and 49 stations with rapture point(red). Up:the horizontal section; down:vertical section. All of energy values minus minimum so that one can compare the differences between the highest and lowest each other. |
1) 随着台站数的增加,高破裂释放能量点域,如80%以上的的高值域,没有显著变化;
2) 随着台站数的增加,能量最高最低差值越来越大;即反差越来越大.
事实上,有人使用了2千和1万(Shuck,2014)、以及2~3万(Chammbers等. 2008)个单分量检波器,对单个震源,包括实际射孔监测,叠加后均是上述特性.相对于他们的分量数,图 6中分别为3x(9,25,49)=(27,75,147).
可见,只要各台均是随机记录,有一定的台站基数,当使用(1)式时,就可能获得足够的高低数值或颜色反差以供辨别,且较高破裂能量的分布域变化不大,从而能够保证监测质量.因在实际中监测质量同大量因素有关,不可能确立普适的的最小扫描台站数Nmin.但根据图 6等的实验和实际监测检查,我们从扫描输出解释的角度对Nmin提出下述估计准则:
若有均含有用信号的随机背景噪声的Nmin+K个台,K=1,2,…;Nmin为统计意义上足够大的一个基数,在扫描输出中使残余干扰不占统治地位,从而能够显著地分辨出对不同点扫描时的高破裂能量点,则称Nmin为最小扫描台站数.
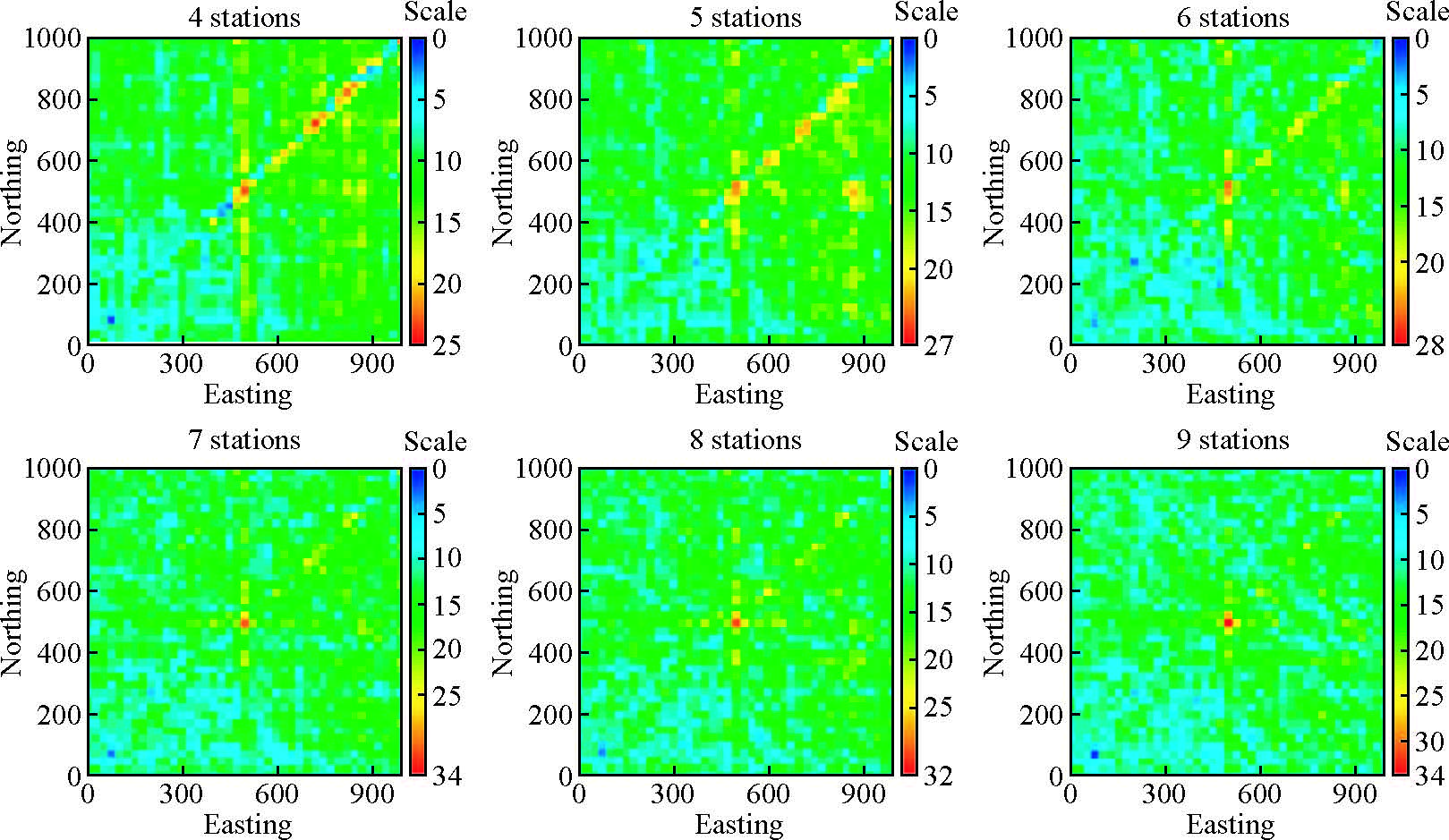
若继续进行人工数据的实验,但反向缩小使用的台站数,可以看到(图 7),当台站数逐渐缩小,使得随机噪声不能够被有效压制,偶然的或少量的伪“高破裂能量”点群显现出来.在图 7的实验情形,Nmin=7,但这是比较理想的人工数据.多个实际监测时段的检查表明(例如王磊等,2012; Wu等,2014),我们得到的Nmin大致是在近10台的范围内,通常可将Nmin估计为10.为保证监测较深的破裂点、和/或有时较弱的有用弹性波信号接收时的监测质量、再考虑总有部分台站临时受地面噪声源干扰、以及故障等因素,应至少携行布设20余台,如25.就分量而言,3分量地震台网就有至少75个分量.大于等于25台就是当前我们的携行布设台站数Nmin.当然,Nmin小了,就可能在输出中出现不占主导地位的伪影,如图 7中下排输出中的黄色斑点,促使我们在了解误差规律的基础上,在解释中辨别或压制它们.
|
图 7 同图 6上排,但6个子图分别对应使用了4至9个3分量台 Figure 7 Same as the up row of Fig. 6,but 4 to 9 stations are used,respectively |
扫描叠加需要在时间窗口内错动各台记录以便叠加,这种错动量是根据速度模型实施射线追踪得到的监测目标和接收台站的两点间走时等参数确定的.不论事先收集多少勘探处理解释、测井、构造研究、甚至现场实验测定等数据,插值出一个3D地下速度模型,在最好情况下,它总是接近或近似等效、却不等于实际的速度分布.如若已经了解了仪器特性、并有很好的监测几何设计(如地形)等,则速度模型可能是一个不可忽略的监测误差源.对于实际错动是以毫秒计的向量扫描中,可以适当矫正这个误差,或称微调计算输出.
第3.1节说明了应用向量扫描技术的必要条件.若满足它,向量之间的相关性强弱应当由隐藏在各台背景噪声中有用微震信号控制.那么,就应当在实施公式(1)时,寻求两两台站之间记录具有最大相关的修正错动样点的ΔN.反之,若没有微震信号隐藏其中,随机记录的叠加,无论如何错动,在总体上仍然是低相关的.为寻找最佳时间错动样点数,可将(1)中相对于速度模型所计算的原错动起算样点的j=1,N改为j=1±ΔN,N±ΔN,依然保持叠加样点总数为N,并选取相关性幅度最高者投入叠加.其中,ΔN的范围由网格点的间距L[m]决定,即ΔN=L/2/VL/Si,这里,VL为该点速度[m/ms],Si[ms]为样点间隔.
3.5 应用方程中台站权重的使用由于各台站距监测目标的不同距离、地震波射线在空间变化介质中的传播、环境背景噪声的差异等因素,即使实施了适当的归一化,势必造成各台向量中S/N的差异.可以预计,按照这种差异在扫描中赋予各台不同的权重Wi,将会提高扫描质量.遗憾的是,在实际监测中,我们不可能直接获得各台向量中准确的S/N.
一个替代方法是:赋予那些对监测目标附近的高破裂能量的凸显与对压制远处的残余效应贡献较大的台站以较高的权重.探索Wi的过程可为:
1)设权重Wi均为1,实施(1)式;由S波型中选出最佳者,并以此M个台的输出为基准;
2)重复步骤1),但每次使用M-1个台,即每次移走一个不同台的记录;比较扫描输出的图形与基准图的数值相关系数Ci;这里Ci越小,表示移走的这个台对扫描输出的贡献越大,即Wi越大;
3)令平均相关系数
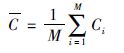
|
则每台的权重
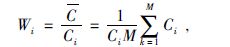
|
(2) |
最后应用Wi完成(1)式的计算.
上述步骤对一个时段会引起M倍的扫描计算量,即使仔细地编制程序也至少可能有两三倍的计算量.事实上,若在野外数据采集和处理上确实满足了实施(1)式的先决条件(第3.1节),Wi很可能差别不大.故可仅对重要时段实施(2)式以完善或进一步提高扫描质量.
3.6 微破裂向量扫描技术的局限性同任何地面监测一样,VS的最大局限性是垂直方向误差是水平方向的2~3倍以上.这由图 3和图 6下排可以很清楚地看到.这种情形,不是仅发生在我们的数十台3分量仪器的台网监测中,对于使用了2千和1万(Shuck,2014)、以及2~3万(Chammbers等. 2008)个单分量检波器,均是同一结论.这是为提高性价比和加快施工速度的地面监测所付出的代价.因而,任何地面微震监测一般不可能给出监测目标垂直向上的精确到20~30 m以内的解释.如果垂直向的高破裂能量分布,特别是峰值处,覆盖了已知监测目标位置,如压裂起裂点或巷洞变形处,可用其作为约束给予解释,同时指明监测误差或联合其他方法(如测温、地质雷达等)给予弥补.
4 实施向量扫描的其他技术保障与结论 4.1 实施向量扫描的其他技术保障仅仅明确一个监测方法的原理及其先决条件等,还不能保证其应用的可行与可靠.在实施微震监测的各个环节中,应当尽可能地提高野外记录数据中的信噪比S/N.它涉及到两个方面的研发:专用微震监测仪器和确立记录到最好S/N的地震台网布设原则,使它们满足微震监测特性与监测环境要求.有此基础,一般的微震监测质量就比较可靠.
此外,在投入扫描计算前,为尽可能的使用较多的台站记录,获得好的扫描质量,必须进行扫描几何设计等准备和必要的数据预处理,尽可能地消除地面的地形、最常见的机器(如抽油机)等对计算的干扰和误差.在很多情况下,这类预处理能够大大提高投入扫描的台站数或有效记录量,从而获得高质量的扫描输出.
最后,在解释中,应当研究4D扫描输出与监测目标(如压裂裂缝、注水气前缘等)的各种关联的细节;例如,对于压裂监测,在解释中常遇到的一系列问题包括
1) 高破裂释放能量与确定裂缝(带)几何;
2) 残余干扰的扫描叠加特性;
3) 周期性数据叠加的特性和伪影的辨别与压制;
4) 压裂段附近和较远处的破裂活动特性;
5) 主裂缝形状位置和多次多段压裂特性;
6) 主裂缝各子段随时间发展的顺序;
7) 压裂裂缝4D分布同压裂施工参数的关联;以及
8) 破裂几何的多解可能性;等等.
上述任一个环节上的失误或缺乏技术监管均可能造成应用失败.我们将另文详细讨论它们.
4.2 结 论微破裂向量扫描原理是为了充分适应微震监测的目标特性、恶劣的地表监测环境、和一般的应用方的监测要求,不得不放弃记录要求较高的传统定位处理方法与可能使绝大多数台站噪声极大的等距等角阵列,而逐步发展起来的.它依然继承了监测微弱有用信号的阵观测理念,但改变了原有的各种等距阵为离散稀疏台网,并处理分析完整的空间记录向量;在数学上,它影像的是各台记录对准扫描点的向量间的相关性程度分布;在物理上,则反映了破裂能量释放的高低程度分布.
在安静处布设地震台网并在数据预处理中去除和压制干扰信号以获得较小振幅的随机记录,是应用向量扫描技术的必要条件.在实际监测中,这也是判断一个监测是否可行、置信度的高低或能否成功的先决条件,且这种条件应当数值化地由监测的地震仪器、地震台网分布、监测环境以及数据处理过程等确定.
一般情况下,为了保证监测质量,我们放弃振幅较小的P波而使用到达地表时衰减较小的携带能量较多的S波;也为了提高性价比和使监测成为生产的日常手段,在满足应用先决条件的基础上,估计了最小扫描台站数和最大携行布设台站数.同样,我们仍然利用相关性的概念,对可能的速度模型引起的误差进行适度校正;以及为进一步完善和提高检测质量,对扫描计算使用的台站记录附加以不同的权重.
微破裂向量扫描是专门针对微小破裂、三分量浅地表埋设观测、稀疏布设台阵、实时监测并4D处理解释、且考虑了微震多有剪切破裂特性的地震学监测方法; 它扩展了传统定位方法的监测范围,能够在地表快速施工并“看到”微震破裂,性价比高,可发展成为伴随生产过程的日常监测手段.
致谢 作者感谢中石化和中石油及其有关所属单位在十余年内提供的科研实验项目,以及他们的技术专家在我们整个研发过程中给与的有益建议、质疑、和讨论.作者感谢《地球物理学进展》的辛勤编辑工作和审稿者严格细致的审查.作者特别致谢微破裂向量扫描技术研发团队的地震学家、地质学家、工程师、和管理者,感谢他们十余年间坚持不懈的、严格的、和艰苦的工作.| [1] | Aki K, Richards P.G..1980. Quantitative Seismology: Theory and Methods[M]. Freeman and Company . |
| [2] | Bullen K.E and Bolt B.1985. An introduction to the theory of Seismology[M]. 4th edition, Cambridge . |
| [3] | Chambers K, Brandsberg-Dahl S, Kendall M, et al. 2008. Testing the ability of surface arrays to locate microseismicity[C]. //SEG Annual Meeting. Las Vegas, Nevada: SEG. |
| [4] | Cheng Q.2003. Digital signal processing[M]. Peking University Press . |
| [5] | Jaeger J. C. and N.G.W. Cook, 1979, Fundamentals of rock mechanics, 3rd edition: London Chapman and Hall. |
| [6] | Kasahara K.1981. Earthquake mechanics[M]. Press Syndicate of the University Cambridge . |
| [7] | Liang B., Shen C., Leng C., Xu J., Li H., Guo B, Yang Y., Zheng B.2015. Development of microseismic monitoring for hydro-fracturing[J]. Progress in Geophysics, 30 (1) : 401–410. |
| [8] | Ma L., Wang L., Shen Y., Zhou Y., Liang B. 2012. Vector Scanning: Hydro-fracture Monitoring With Surface Microseismic Data[C]. SPE-152913, Copenhagen, Denmark. |
| [9] | Maxwell S. 2014. Microseismic imaging of hydraulic fracturing: Improved Engineering of unconventional shalereservoirs[C]. Distinguished instructor short course, SEG. |
| [10] | Meng X.2005. Analysis of Seismological data[M]. Beijing: Seismological Press . |
| [11] | Press W, Teukolsky S., Vetterling W., Flannery B.1997. Numerical Recipes in C, the art of scientific computing[M]. 2nd Edition. Cambridge . |
| [12] | Shapiro S.A.2008. Microseismicity-a tool for reservoir characterization[M]. Education Tour Series CIS, EAGE Publications bv . |
| [13] | Shen C., Liang B., Li Z..2009. Principle of vector scanning technique for micro-fractures[J]. Acta Petrolei Sinica, 30 (5) : 744–748. |
| [14] | Shen C., Z. Wu, J. Lu, B. Liang, 2014, Vector Scanning: Instruments and Seismic Network: Presented at SEG 1st International Microseismic Technology Workshop. |
| [15] | Sheriff R.E.1991. Encyclopedic Dictionary of Exploration Geophysics[M]. Third Edition, SEG . |
| [16] | Shuck T., 2014, Advantages of Patch Acquisition and Processing for Surface Microseismic Data: Presented at SEG 1st International Microseismic Technology Workshop. |
| [17] | Wang L., Yang S., Liu H., Zhang D., Huang G., Liang B.2012. Application of vector scanning for fracture monitoringwith surface microseismic data[J]. Geophysical Prospecting for Petroleum, 51 (6) : 613–619. |
| [18] | Wu Z, J. Lu, C. Shen, B. Liang, 2014, Data Processing in Vector Scanning: Presented at SEG 1st International Microseismic Technology Workshop. |
| [19] | Zhang Q., Ren Z., Zheng B. Wang L., Yang S., Liang B.2014. Hydro-Fracture MonitoringUsing Vector Scanning With Surface Microseismic Data[C], AAPG-1948512, Istanbul, Turkey. |
| [20] | Zhang Q, Ren Z, Zheng B, Zuo J, Liang B, 2014, For 86 Stages of Yan227 in Shengli Oil Field, China: Presented at SEG 1st International Microseismic Technology Workshop. |
| [21] | 程乾声.2003. 数字信号处理[M]. 北京: 北京大学出版社 . |
| [22] | 梁北援, 沈琛, 冷传波, 许建明, 李洪川, 郭炳平, 杨英才, 郑彬涛.2015. 微地震压裂监测技术研发进展[J]. 地球物理学进展, 30 (1) : 401–410. |
| [23] | 梁兵, 朱广生编著.2004. 油气田勘探开发中的微震监测方法[M]. 北京: 石油工业出版社 . |
| [24] | 孟晓春.2005. 地震信息分析技术[M]. 北京: 地震出版社 . |
| [25] | 沈琛, 梁北援, 李宗田.2009. 微破裂向量扫描原理[J]. 石油学报. 2009, 30 (5) : 744–748. |
| [26] | 王磊, 杨世刚, 刘宏, 张德顺, 黄光军, 梁北援.2012. 微破裂向量扫描技术在压裂监测中的应用[J]. 石油物探, 51 (6) : 613–619. |
 2016, Vol. 31
2016, Vol. 31

