2. 国家山区公路工程技术研究中心 重庆 400067
3. 公路隧道建设技术国家工程实验室 重庆 400067
4. 长安大学 地质工程与测绘学院 西安 710054
5. 广东省南粤交通投资建设有限公司, 广州 510101
2. Country mountain area highway engineering technology research center, Chongqing 400067, China
3. National engineering laboratory of highway tunnel construction technology, Chongqing 400067, China
4. School of Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China
5. Guangdong Nanyue Transportation Investment & Construction Co.Ltd., Guangzhou 510101, China
电磁测深法包括主动源法和被动源法,被动源法是以天然交变电磁场做场源的电磁测深法,包括大地电磁法(MT)和音频大地电磁法(AMT)等;主动源法是以人工建立的场做源的电磁测深法,包括可控源音频大地电磁法(CSAMT)和瞬变电磁法(TEM)等(刘国栋,1994).其中MT法工作频率范围为10-4~104 Hz,具有探测深度大的特点,广泛的应用于地壳及上地幔探测等领域(林长佑等,1984;孔祥儒等,1991;詹艳等,2004;彭淼等2012);AMT法取MT的高频部分0.1~104 Hz进行探测,具有较大勘探深度,较强分辨能力,观测效率高的特点,主要应用于中深部地质构造探测和寻找隐伏型矿体(杨进和安海忠,1995;杨承志等,2013;冯兵等,2014;阮帅等,2015);CSAMT法与MT法和AMT相比,克服了场源的随机性,测量信号强度也有所提高,用于解决几十米到3 km深度范围内的地质问题,具有工作效率高、精度高和分辨率高等优点,因此该方法在金属矿、水文、地热和环境等领域广泛应用(吴璐苹等,1996;于昌明,1998;孙英勋,2005;成江明,2008;王绪本等,2013;陈玉玲等,2015).由于采用了人工场源,为了保证信号强度,CSAMT法在离场源几公里到十几公里的地方进行测量,存在非平面波效应,使得波区视电阻率在非平面波区不能正确、真实的反应地电结构,一般要做近场校正,近场校正在一定程度上可以削弱非平面波效应,但在很多情况下,校正结果往往并不可靠,且缺乏灵活性和系统性(王军和王庆乙,1992).
为此人们定义了全区视电阻率,使视电阻率不拘泥于波区条件,同样适用于过渡区,增加该方法的实际探测深度和扩大数据采集范围.何继善院士(2010)在CSAMT法的基础上提出了广域电磁测深方法并定义了广域视电阻率,采用该法可以在过渡区进行测量,利用较小的收发距便可达到较大的深度,该方法已经广泛的应用于油气资源勘探和深部找矿等领域(朱裕振和许聪悦,2011;邓锋华等,2013;刘春明等,2013;何继善等,2014).关于全区视电阻率的定义及计算,诸多学者做了研究:殷长春和朴华荣(1991)利用数值逼近的方法讨论了电偶源FEMS法中水平电场观测的全区视电阻率定义问题;黄皓平和朴华荣(1992)用均匀大地上电磁场的三个分量来定义磁偶源全区视电阻率;方文藻等(1992)将电偶源远区定义的视电阻率乘上校正系数K,求得全区视电阻率值;汤井田和何继善(1994)利用等效电阻率法来定义水平电偶极子场的全区视电阻率;汤井田等(2011)和冯兵等(2013)分别研究了CSAMT法中电场y方向视电阻率的定义和电场x方向定义的全区视电阻率;关于广域电磁法中的广域视电阻率,研究最多的是电场E-Ex定义的全区视电阻率(李帝铨等,2013;王宏宇等,2014;胡涂和李帝铨,2014),上述全区视电阻率的计算以迭代法为主.用上述各方法定义并计算的全区视电阻率均能够较好的反映地电断面结构,但各有优缺点和适用性.总体来说全区视电阻率常用的计算方法一般有迭代法和逆插值法,迭代法步骤简单,但存在迭代发散的情况;逆插值的影响因素较少,计算过程稳定,但要求插值目标函数单调(王顺国和熊彬,2012).
笔者在前人的基础上,研究了一种能够快速、准确、稳定的计算电性双极源频率域全区视电阻率的方法并分析了应用效果.
1 电性双极源的电磁场和大地电阻率的关系在人工源频域电磁法中,CSAMT法和广域电磁法的发射源一般为一对接地电极,长为1~4 km,不能看作电偶极子源,是电性双极源,此时要通过对电偶极子场沿双极源的长度方向进行积分来获得双极源场(殷长春,1994).设双极源的长度为L,双极源的起点为坐标原点,方向沿x轴方向,大地电阻率为ρ1,μ为磁导率,${{k}_{1}}=\sqrt{-\text{i}\omega \mu /\rho }$为波数,供电电流为I,(x,y,0)为接收点坐标,(x*,0,0)为电偶极子坐标.均匀半空间上的水平电偶极子的电磁场表达式为
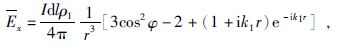
|
(1) |
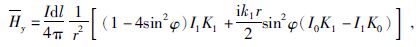
|
(2) |
式(1)~(2)中$r=\sqrt{{{x}^{2}}+{{y}^{2}}}$,φ为r与x轴的夹角,I0,K0,I1,K1分别是宗量为ik1r/2的零阶和一阶的第一类和第二类修正贝塞尔函数.
均匀半空间上的双极源电磁场表达式为

|
(3) |
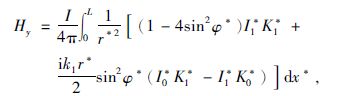
|
(4) |
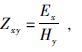
|
(5) |
式(3)~(4)中${{r}^{*}}=\sqrt{{{(x-{{x}^{*}})}^{2}}+{{y}^{2}}}$,φ*为r*与x轴的夹角, I0*,K0*,I1*,K1* 分别是宗量为ik1r*/2的零阶和一阶的第一类和第二类修正贝塞尔函数.式(5)为电磁波阻抗表达式.对于式(3)和式(4)中的外层积分,可通过高斯勒让德求积方法求解.
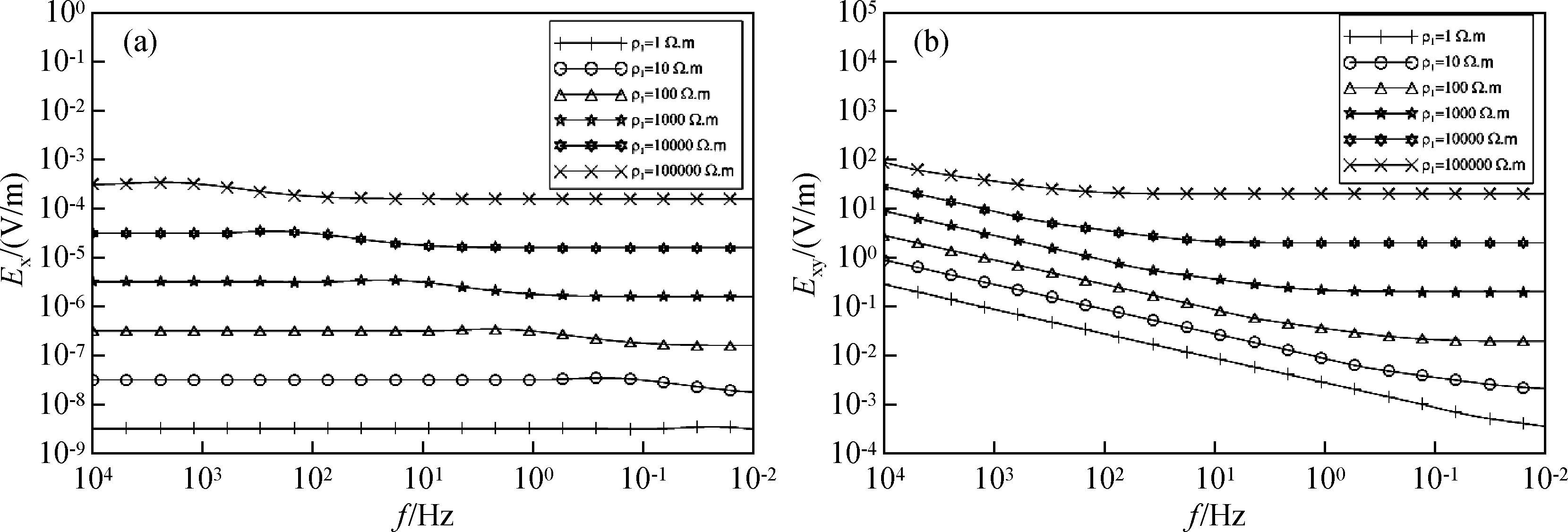
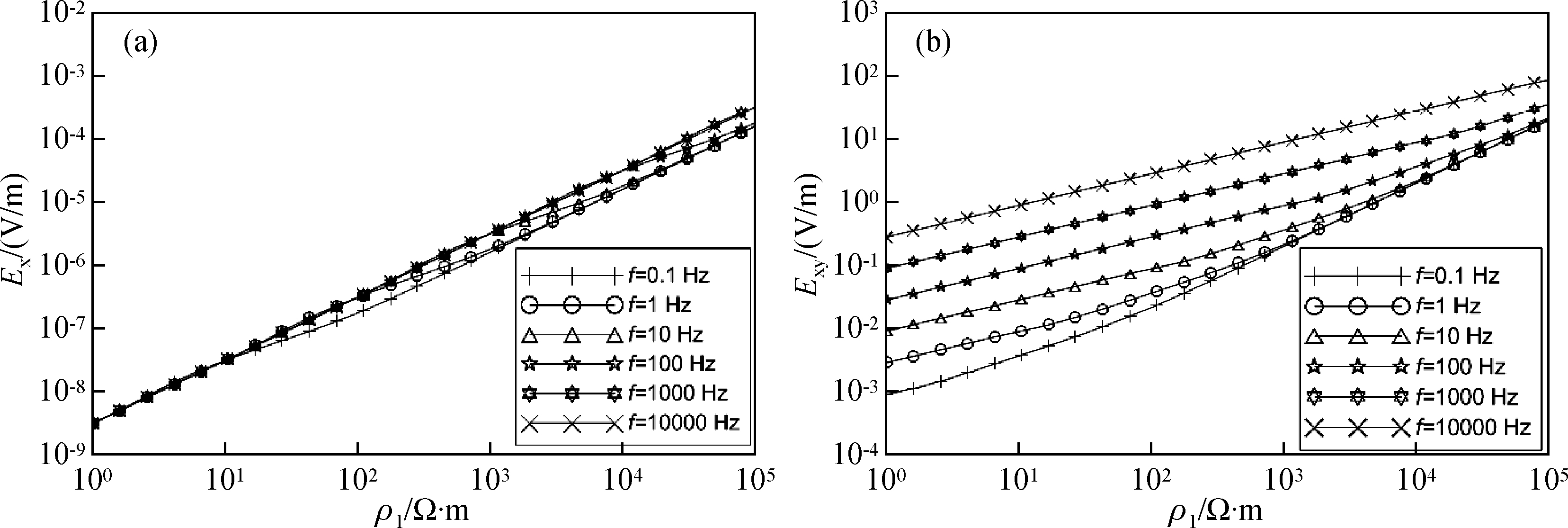
为了研究双极源电磁场与大地电阻率的关系,这里设双极源长度为1 km,电流为10 A,接收点坐标为(500 m,10 km,0).图 1为不同大地电阻率Ex和Zxy频率特性曲线,可见Ex和Zxy随着大地电阻率的增大而增大,且Ex和Zxy与大地电阻率呈一一对应关系.由于常见岩石电阻率变化范围为1~105Ω·m之间,所以在此范围内取不同的大地电阻率值,并分别取不同频点计算Ex和Zxy如图 2,可见在高频、中频和低频,Ex和Zxy都是大地电阻率的单调递增函数.
|
图 1 不同大地电阻率Ex和Zxy的频率特性曲线 (a)Ex;(b)Zxy. Figure 1 Ex and Zxy frequency characteristic curve of different earth resistivity (a)Ex;(b)Zxy. |
|
图 2 Ex和Zxy随大地电阻率变化 (a)Ex;(b)Zxy. Figure 2 The Ex and Zxy over the earth resistivity changing (a)Ex;(b)Zxy. |
二分法是非线性方程求根的一种常用方法,具有算法简单,总是稳定收敛的优点,但要求在求根区间内只有一个单根或奇数个重根.由于双极源的Ex和Zxy都是大地电阻率的单调递增函数,因此双极源的Ex和Zxy与大地电阻率具有一一对应关系,若把全区视电阻率当做非线性方程式(3)和式(4)的根,则在求根区间内式(3)和式(4)只有一个单根.因此结合二分法的思想,可把求取全区视电阻率的过程当作一个用二分法对非线性方程求根的过程,求得的根即为全区视电阻率.下面以Ex为例说明具体实现过程:
首先要确定求根范围,该范围为工区地层最大电阻率ρmax和最小电阻率ρmin之间,即[ρmin,ρmax],如果工区地层的最大电阻率和最小电阻率未知,则取常见岩石电阻率变化范围1~105 Ω·m.
(1) 取求根范围的中点位置ρ=(ρmax+ρmin)/2作为初始值,带入均匀半空间双极源Ex的表达式(1.3),计算出场值Ex与实测场值Ex0进行比较;
(2) 若Ex=Ex0,则ρ为要求的根,即全区视电阻率;
(3) 若Ex>Ex0,依据单调递增的性质,改变求根范围为[ρmin,ρ];
(4) 若Ex<Ex0,依据单调递增的性质,改变求根范围为[ρ,ρmax];
(5) 再二分求根范围,重复(1)~(4),直到Ex和Ex0的差异小于一个界限ε为止,此时的ρ为要求的全区视电阻率.利用Zxy计算全区视电阻率的方法和Ex类似.
为了快速计算,在实际计算第一个高频频点对应的全区视电阻率时,步骤(1)中的初始值并不是ρ=(ρmax+ρmin)/2,而是取波区视电阻率,高频时波区视电阻率和全区视电阻率理论上是非常接近的.由于体积效应的存在,相邻频点之间电阻率不会相差太大,因此在计算第二个频点时,以第一个频点的全区视电阻率作为初始值,以此类推,直到计算完所有频点.据此作者编制相应的处理程序,在普通计算机上利用该方法计算40个频点的全区视电阻率测深数据仅需约0.2 s,计算速度相对较快且稳定.
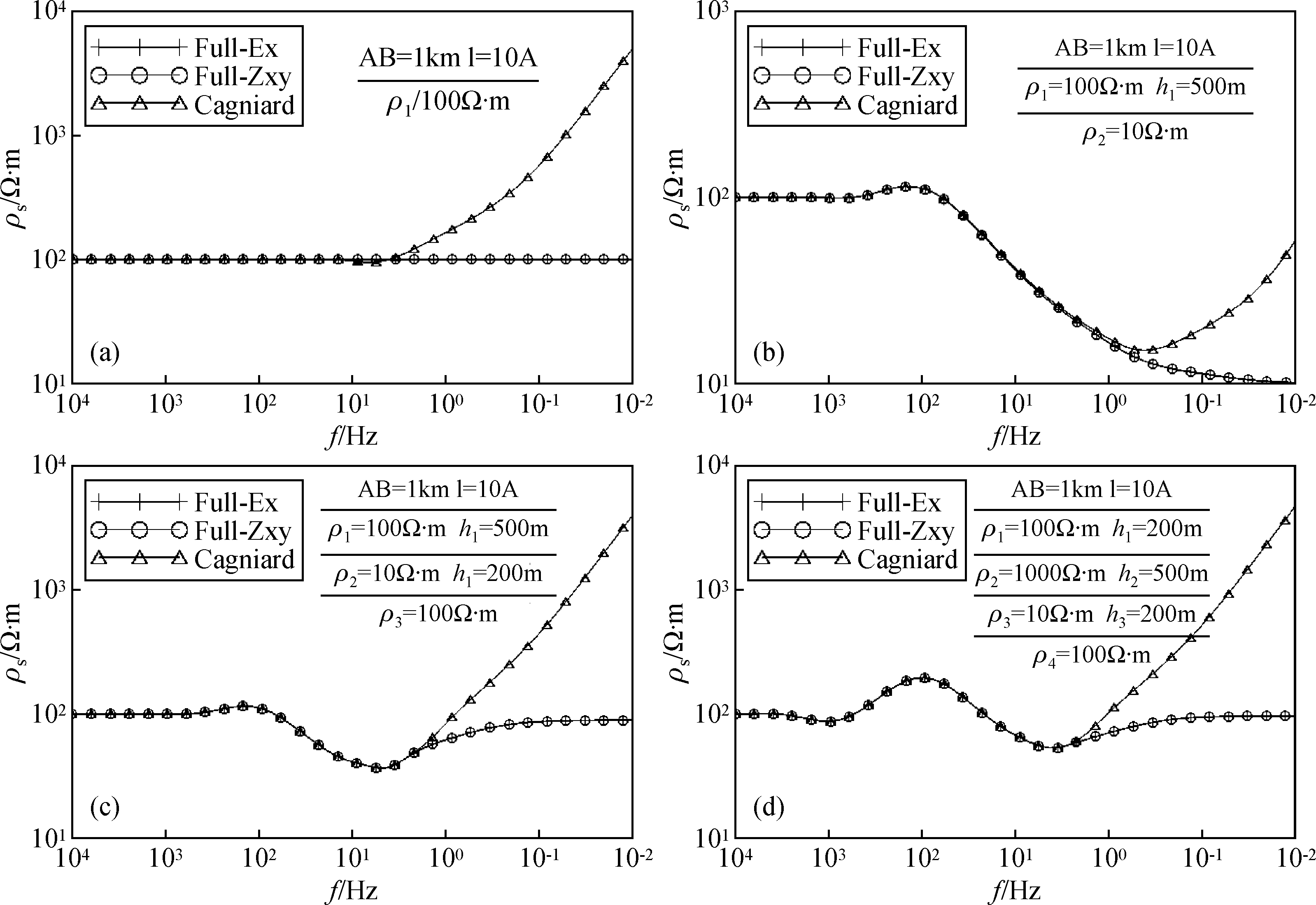
3 理论模型计算结果取双极源长1 km,电流为10 A,接收点坐标为(500 m,10 km,0),用二分法计算一维理论模型的全区视电阻率并和卡尼亚视电阻率对比.图 3a为均匀半空间模型计算结果,可见均匀半空间模型的全区视电阻率曲线和卡尼亚视电阻率曲线在频率较高的波区是重合的,随着频率降低,进入过渡带和近区,卡尼亚视电阻率曲线呈上升趋势,全区视电阻率曲线真实的反映了地电结构;对于理论模型,Ex和Zxy定义的全区视电阻率曲线在整个频率范围内是重合的.从图 3b和图 3c为层状D型和H型模型计算结果,和均匀半空间结果类似,在频率较高的波区,全区视电阻率和卡尼亚视电阻率是重合的,能够真实的反映第一层的电阻率;随着频率降低,进入过渡带,卡尼亚视电阻率与实际不符,全区视电阻率不仅能很好的反映出中间低阻层的存在,而且对基底也有较好的反映;对于图 3d KH模型,全区视电阻率对中间高阻层下的低阻层有很好的反映,且尾支趋近于基底的电阻率,真实客观的反映了地电断面特征.
|
图 3 一维理论模型视电阻率曲线 (a)均匀半空间;(b)D;(c)H;(d)KH. Full-Ex:Ex定义的全区视电阻率;Full-Zxy:Zxy定义的全区视电阻率;Cagniard:卡尼亚视电阻率. Figure 3 The apparent resistivity curves of 1D theoretical models (a)Uniform earth;(b)D;(c)H;(d)KH. Full-Ex:Full-zone apparent resistivity defined by Ex;Full-Zxy:Full-zone apparent resistivity defined by Zxy;Cagniard:Cagniard apparent resistivity. |
就理论模型,只有在波区Ex和Zxy定义的全区视电阻率和卡尼亚视电阻率曲线重合,对地电断面的分辨能力也一致.但在进入过渡区以后,Ex和Zxy定义的全区视电阻率和卡尼亚视电阻率曲线不重合,Ex和Zxy定义的全区视电阻率较卡尼亚视电阻率对地电断面的分辨能力高,探测深度也大于卡尼亚视电阻率.该特性对于断面的定性解释具有重要的意义.
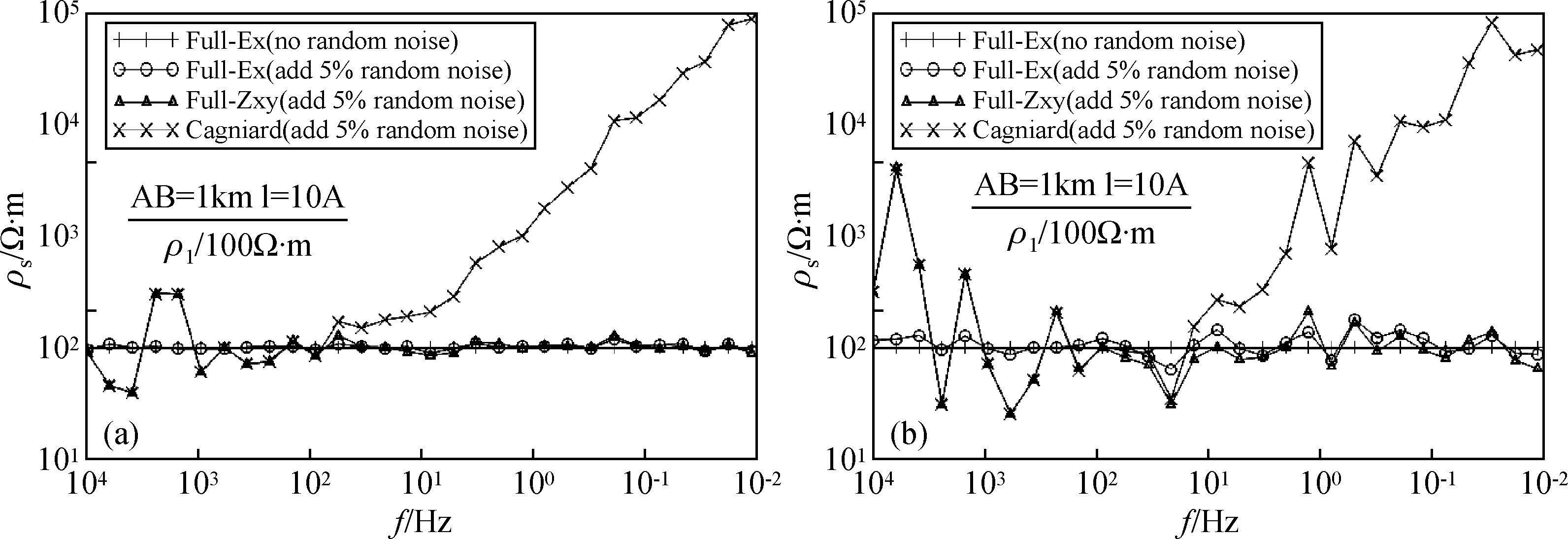
利用比值方法定义的视电阻率并不比场分量定义的视电阻率提供更多的地电信息,它们只是放大或压制了场分量视电阻率的某些特征,由于采取了比值原则,理论上它们比场分量视电阻率具有更强的抗干扰能力.为此对理论数据分别加入5%和10%的随机噪声,来研究Ex和Zxy定义的全区视电阻率及卡尼亚视电阻率的抗干扰能力.由图 4可知,在加入了随机噪声后,Zxy定义的全区视电阻率并没有起到压制干扰的作用,在很多情况下都是放大了干扰,且所加噪声越大,对干扰越放大;卡尼亚视电阻率对噪声的放大作用和Zxy定义的全区视电阻率对噪声的放大作用是一致的;Ex定义的全区视电阻率对噪声的压制最强.可见就压制随机噪声而言,Ex定义的全区视电阻率的计算结果优于Zxy定义的全区视电阻率及卡尼亚视电阻率.
|
图 4 加入随机噪声后Ex和Zxy定义的全区视电阻率 (a)加5%随机噪声;(b)加10%随机噪声. Full-Ex:Ex定义的全区视电阻率;Full-Zxy:Zxy定义的全区视电阻率; Cagniard:卡尼亚视电阻率. Figure 4 Full-zone apparent resistivity defined by Ex and Zxy after add random noise (a)Add 5% random noise;(b)Add 10% random noise. |
工区位于山西省于都县,该区域集中了多处已开发和在开发的矿田,区内岩浆活动强烈,地质构造发育,有色金属资源集中,是赣南地区有名的成矿有利区域.本次勘探的目的是在该区域试验多种电法勘探技术手段,探索适宜该区的电法勘探方法,尽可能地获取地下与深部找矿有关的地质构造信息,为后续开展钻探等工作提供物探依据.
工区地层出露比较齐全,从老到新为元古界青白口系、震旦系;古生界泥盆系、石炭系、二叠系;中生界侏罗系、白垩系;新生界第四系.工区位于华南板块南华活动带华夏褶皱系武夷—云开褶皱带,晚期的构造活动改变了早期的构造,并对区内的成岩成矿提供了良好的空间,也控制了它们的展布,后期的构造活动又破坏了它们的连续性.工区岩浆活动比较强烈,主要有加里东,燕山两个活动时期;岩石类型简单,侵入岩均为花岗岩类.
针对区内出露的主要岩(矿)石进行了物性标本采集和物性测定和收集,统计结果见表 1.可以看出,工区内花岗闪长岩和石英砂岩的电阻率相对较高,平均值分别为6128.73 Ω·m和5410 Ω·m;其次为凝灰岩,电阻率均值为3838 Ω·m;石英斑岩的电阻率最低,平均值为452 Ω·m;花岗斑岩的电阻率数值也较低,平均值为969.52 Ω·m.因此工区内不同岩(矿)石之间存在一定的电性差异,具备开展电法勘探的地球物理前提.
|
|
表 1 工区岩(矿)石电性参数测定统计表 Table 1 Work area rock(ore)stone electrical parameter table |
可控源音频大地电磁法(CSAMT)和音频大地电磁法(AMT)均具有勘探深度大,分辨率高的特点,已广泛的应用于地质勘查;基于岩(矿)石存在电阻率差异的地球物理前提,本次工作选择CSAMT法的AMT法进行试验研究.采用V8多功能电法工作站进行原始数据采集,利用全区视电阻率、二维反演等技术方法进行数据处理,以达到探索适宜该区的电法勘探方法,尽可能地获取地下与深部找矿有关的地质构造信息的研究目的.
本次CSAMT工作采用TM模式标量观测方法,发射极距1 km,收发距为6 km,且发射方向平行于测线方向,接收电极距40 m;测线点距为40 m;工作中使用的最低频率为1 Hz,最高频率为7680 Hz,共40个频点;供电电流达到了10 A.本次AMT工作采用仪器设备和CSAMT相同,接收电极距为100 m,测线点距100 m,观测参数为Ex,Ey,Hx,Hy.为了提高观测数据的质量,本次工作采用多次叠加和重复观测等技术,有效的抑制了工业电流及人为设施干扰,确保了采集数据的质量.
4.3 CSAMT全区视电阻率应用效果分析选用800线960~1400点的CSAMT数据和AMT数据进行处理比对,研究全区视电阻率在CSAMT数据处理中的应用效果,分析CSAMT法和AMT法在该工区的优越性.首先对实测数据进行干扰消除、滤波等处理;再对CSAMT数据计算全区视电阻率和卡尼亚视电阻率,对AMT数据计算TM模式下的卡尼亚视电阻率,由于AMT卡尼亚视电阻率采用阻抗定义,为了进行更好的对比两种方法,CSAMT全区视电阻率也采用阻抗Zxy定义;其次进行静态效应校正;最后对视电阻率进行二维反演.
理论上来说,AMT方法的源为天然场源,不存在非平面波效应;CSAMT方法采用人工源,存在非平面波效应,采用卡尼亚视电阻率只能反映波区地电特征,探测深度浅;全区视电阻率既可以反映波区地电特征,还可以反映过渡区地电特征,增加了探测深度.在未进入近区场之前,CSAMT全区视电阻率的探测能力和AMT方法的探测能力是一致的,但实际探测能力可能会有差异.下面将分析800线960~1400点CSAMT法探测结果和AMT法探测结果.
图 5为800线960~1100点AMT和CSAMT视电阻率反演断面图及实测地质剖面图.图 5a为AMT卡尼亚视电阻率反演断面图,根据花岗斑岩岩体(γπ)相对于细粒少斑黑云母花岗闪长岩(K1G)呈相对低阻划分了岩性分界面,结果与图 5d实测地质剖面图中的岩性分界面相吻合;根据断裂破碎带相对围岩呈低阻、且低阻异常呈线性走向,推断了三条隐伏断裂破碎带F1、F2和F3,推断断裂F1和F2与岩性分界面倾向大体一致、F3断裂与岩性分界面倾向大体相反;在深部存在一低阻异常.
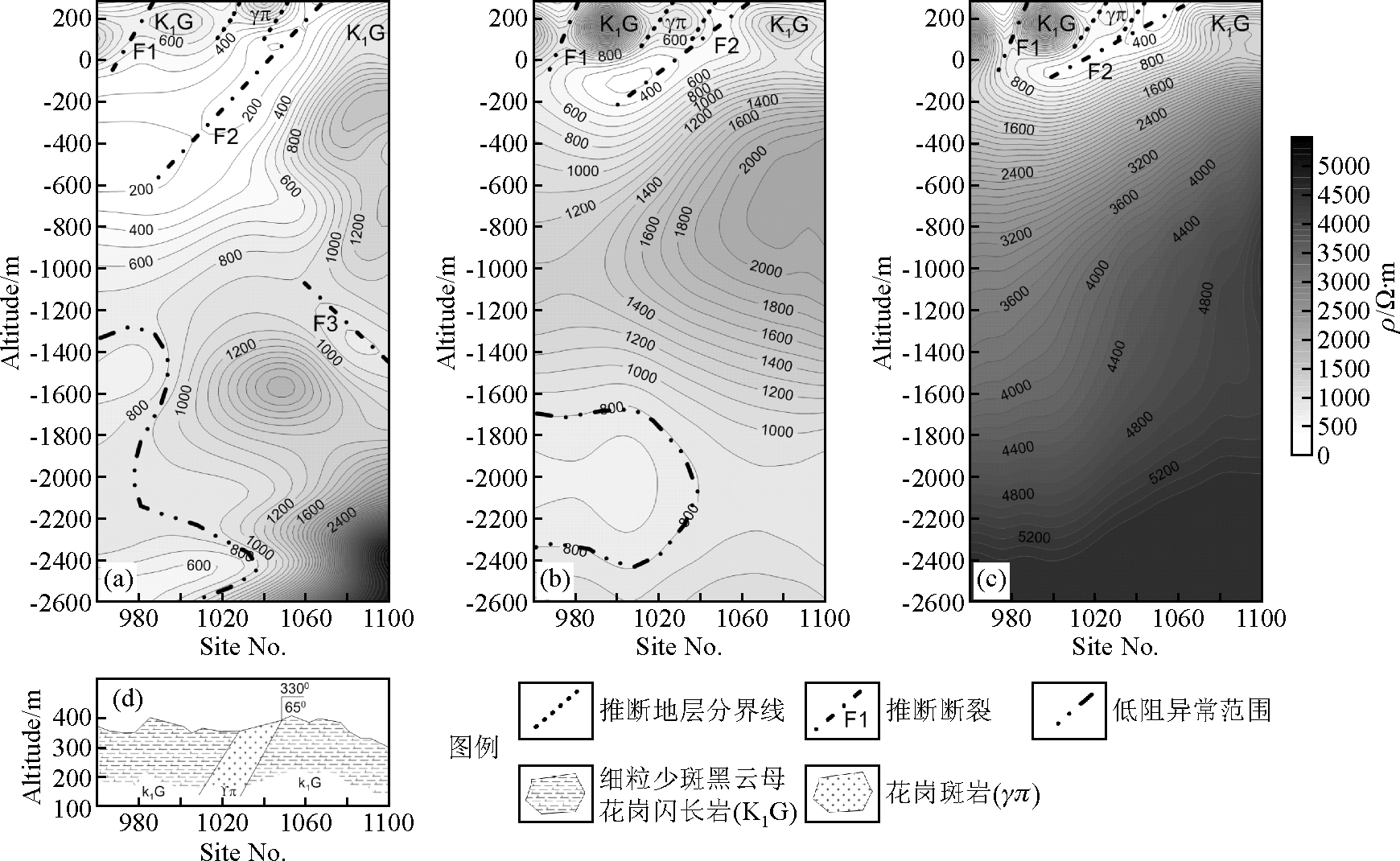
|
图 5 800线960~1100点AMT和CSAMT视电阻率反演断面图及实测地质剖面图 (a)AMT卡尼亚视电阻率反演断面图;(b)CSAMT全区视电阻率反演断面图; (c)CSAMT卡尼亚视电阻率反演断面图;(d)实测地质剖面图. Figure 5 AMT and CSAMT apparent resistivity inversion profiles and the measured geological profile of Line 800 point 960~1100 (a)AMT Cagniard apparent resistivity inversion profile;(b)CSAMT full-zone apparent resistivity inversion profile; (c)CSAMT Cagniard apparent resistivity inversion profile;(d)Measured geological profile. |
图 5b为CSAMT全区视电阻率反演断面图,可见在浅部海拔-1 km以上,地电分布规律和AMT结果大体一致,可反映出同样的地质信息;但CSAMT法浅部高阻异常显得更加突出、低阻异常范围收缩,纵、横向分辨率均有所提高;花岗斑岩岩体(γπ)的相对低阻特征和细粒少斑黑云母花岗闪长岩(K1G)的高阻特征在CSAMT全区视电阻率结果中表现的更为明显,探测效果优于AMT结果.在深部-1 km以下,CSAMT全区视电阻率探测结果和AMT探测结果存在较大差异,虽然在深部均存在低阻异常,但异常形态和异常范围都不同;在AMT结果中,深部高低阻分明,对高低阻异常刻画的更为具体;在CSAMT全区视电阻率探测结果中,深部低阻异常范围扩大,对F3断裂异常没有反映,可见分辨率低于AMT探测结果.
图 5c为CSAMT卡尼亚视电阻率反演断面图,可见在浅部海拔-400 m以上,异常形态和图(b)基本一致,其探测能力和CSAMT全区视电阻率基本一致,随着深度加大,CSAMT卡尼亚视电阻率很快不满足波区条件,进入过渡区和近区,电阻率呈一直增大趋势,对深部地电构造失去分辨能力.
在本次勘探中,CSAMT全区视电阻率探测结果和AMT卡尼亚视电阻率探测结果在浅中部存在很好的一致性,证明计算的全区视电阻率对CSAMT方法的非平面波效应有很好的改善作用;利用CSAMT全区视电阻率探测1 km范围以内的地质构造具有分辨率高、保真度高、不受过渡带和近区场影响的特点,证明CSAMT全区视电阻率方法可进行大深度第二深度找矿勘探.
5 结 论对均匀半空间上电性双极源频域的电磁场研究结果表明,均匀大地表面上双极源电场x方向分量Ex、阻抗Zxy是大地电阻率的单调递增函数.
利用二分法计算Ex和Zxy定义的全区视电阻率,理论模型计算结果表明,该计算方法是可行的、结果是可靠的;计算得到的全区视电阻率不受过渡带影响,较真实客观的反映了地电断面的电性变化.对理论模型数据加入随机噪声后计算结果表明,Ex定义的全区视电阻率对随机噪声的抑制是最强的,Zxy定义的全区视电阻率及卡尼亚视电阻率放大了噪声.
对某工区实测CSAMT和AMT数据处理结果表明,CSAMT全区视电阻率探测结果在浅部海拔-1 km以上较AMT探测结果具有更高的纵、横向分辨率,探测结果优于AMT探测结果;在深部海拔-1 km以下,AMT探测结果具有更高的分辨能力;CSAMT卡尼亚视电阻率探测结果在浅部海拔-400 m以上和CSAMT全区视电阻率探测结果一致,很快进入过渡区和近区,电阻率呈一直增大趋势,对深部地电构造失去分辨能力.
在本次勘探中,计算的全区视电阻率对CSAMT方法的非平面波效应有很好的改善作用;利用CSAMT全区视电阻率探测1 km范围以内的地质构造具有分辨率高、保真度高、不受过渡带和近区场影响的特点,证明CSAMT全区视电阻率方法可进行大深度第二空间找矿勘探.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持.| [1] | Chen Y L, Han K, Chen Y X, et al.2015. The application of CSAMT in Karst collapse investigation[J]. Progress in Geophysics (in Chinese), 30 (6) : 2616–2622. DOI:10.6038/pg20150620 |
| [2] | Cheng J M.2008. Application of CSMAT method in hidden coalmine[J]. Progress in Geophysics (in Chinese), 23 (4) : 1269–1272. |
| [3] | Deng F H, Yang Y, Li D Q.2013. The application of wide-field electromagnetic method to hidden gold deposit[J]. Chinese Journal of Engineering Geophysics (in Chinese), 10 (3) : 357–362. DOI:10.3969/j.issn.1672-7940.2013.03.015 |
| [4] | Fang W Z, Li X, Li Y G, et al.1992. The whole-zone definition of apparent resistivity used in the frequency domain electromagnetic methods[J]. Journal of Xi'an College of Geology (in Chinese), 14 (4) : 81–86. |
| [5] | Feng B, Wang J L, Zhou X W, et al.2013. Application of full-region apparent resistivity of CSAMT Ex in exploration[J]. Coal Geology & Exploration (in Chinese), 41 (6) : 78–82. DOI:10.3969/j.issn.1001-1986.2013.06.019 |
| [6] | Feng B, Li J G, Zhao B, et al.2014. The application of audio magnetotelluric method (AMT) in Nanling Yudu-Gan county ore-concentrated area Yinkeng demonstration plot to survey deep mineral resources[J]. Acta Geologica Sinica (in Chinese), 88 (4) : 669–675. |
| [7] | He J S.2010. Wide field electromagnetic sounding methods[J]. Journal of Central South University (Science and Technology) (in Chinese), 41 (3) : 1065–1072. |
| [8] | He J S, Li D Q, Dai S K.2014. Shale gas detection with wide field electromagnetic method in North-western Hunan[J]. Oil Geophysical Prospecting (in Chinese), 49 (5) : 1006–1012. |
| [9] | Hu T, Li D Q.2014. Distinguish ability on thin resistant layered structure of E-Ex mode of wide field electromagnetic sounding method[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 36 (3) : 297–303. DOI:10.3969/j.issn.1001-1749.2014.03.08 |
| [10] | Huang H P, Piao H R.1992. Full-wave apparent resistivity from vertical magnetic dipole frequency soundings on a layered earth[J]. Acta Geophysica Sinica (in Chinese), 35 (3) : 389–395. |
| [11] | Kong X R, Liu S J, Zhang J J.1991. Magnetotelluric sounding studies in the eastern area of Fujian province[J]. Acta Geophysica Sinica (in Chinese), 34 (6) : 724–735. |
| [12] | Li D Q, Xie W, Cheng D X.2013. Three-dimensional modeling for E-Ex wide field electromagnetic methods[J]. The Chinese Journal of Nonferrous Metals (in Chinese), 23 (9) : 2459–2470. |
| [13] | Lin C Y, Zhang Y L, Si Y L, et al.1984. On the Magnetotelluric research in the eastern region of the He-Xi corrido[J]. Acta Geophysica Sinica (in Chinese), 27 (2) : 131–143. |
| [14] | Liu C M, Tong T G, He J S.2013. Exploration of various electromagnetic method in some gold mine[J]. The Chinese Journal of Nonferrous Metals (in Chinese), 23 (9) : 2422–2429. |
| [15] | Liu G D.1994. Development of magnetotelluric method in china[J]. Acta Geophysica Sinica (in Chinese), 37 (S1) : 301–310. |
| [16] | Peng M, Tan H D, Jiang M, et al.2012. Joint inversion of receiver functions and magnetotelluric data: Application to crustal and mantle structure beneath central Namche Barwa, eastern Himalayan syntaxis[J]. Chinese Journal of Geophysics (in Chinese), 55 (7) : 2281–2291. DOI:10.6038/j.issn.0001-5733.2012.07.014 |
| [17] | Ruan S, Zhang J, Sun Y B, et al.2015. AMT impedance phase invariant correction based on 3D MT modeling technology[J]. Chinese Journal of Geophysics (in Chinese), 58 (2) : 685–696. DOI:10.6038/cjg20150229 |
| [18] | Sun Y X.2005. Application of CSAMT electromagnetic image system in survey of deeply-buried long tunnels for expressways[J]. Progress in Geophysics (in Chinese), 20 (4) : 1184–1189. |
| [19] | Tang J T, He J S.1994. A new method to define the full-zone resistivity in horizontal electric dipole frequency soundings on a layered earth[J]. Acta Geophysica Sinica (in Chinese), 37 (4) : 543–552. |
| [20] | Tang J T, Zhou C, Zhang L C.2011. A new apparent resistivity of CSAMT defined by electric field y-direction[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 41 (2) : 552–558. |
| [21] | Wang H Y, Cheng D X, Yang X.2014. Study on apparent resistivity of wide field electromagnetic defined by E-Eφ component[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 36 (1) : 9–15. DOI:10.3969/j.issn.1001-1749.2014.01.02 |
| [22] | Wang J, Wang Q Y.1992. A fast method for calculating the frequency-domain EM response of a finitely long grounded wire over a layered earth[J]. Geology and Prospecting (in Chinese), 28 (3) : 30–38. |
| [23] | Wang S G, Xiong B.2012. Numerical Calculation methods of wide field apparent resistivity[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 34 (4) : 380–383. DOI:10.3969/j.issn.1001-1749.2012.04.02 |
| [24] | Wang X B, Chen J C, Guo Q S, et al.2013. Research of the CSAMT exploration mode and experiment for the coalbed methane enrichment region in the north Qinshui basin[J]. Chinese Journal of Geophysics (in Chinese), 56 (12) : 4310–4323. DOI:10.6038/cjg20131233 |
| [25] | Wu L P, Shi K F, Li Y H, et al.1996. Application of CSAMT to the search for groundwater[J]. Acta Geophysica Sinica (in Chinese), 39 (5) : 712–717. |
| [26] | Yang C Z, Deng J Z, Chen H.2013. Research on effect of acquisition parameters on audio-frequency magnetotelluric 2D inversion results using nonlinear conjugate gradients algorithm[J]. Progress in Geophysics (in Chinese), 28 (3) : 1346–1354. DOI:10.6038/pg20130328 |
| [27] | Yang J, An H Z.1995. Geological effects of audio-frequency magnetotelluric method in Qinling region[J]. Geophysical & Geochemical Exploration (in Chinese), 19 (4) : 286–290. |
| [28] | Yin C C, Piao H R.1991. A study of the definition of apparent resistivity in electromagnetic sounding[J]. Geophysical & Geochemical Exploration (in Chinese), 15 (4) : 290–299. |
| [29] | Yin C C.1994. One-dimensional modelling of CSAMT method and evaluation of calculation precision[J]. Journal of Changchun University of Earth Sciences (in Chinese), 24 (4) : 438–453. |
| [30] | Yu C M.1998. The application of CSAMT method in looking for hidden gold mine[J]. Acta Geophysica Sinica (in Chinese), 41 (1) : 133–138. |
| [31] | Zhan Y, Zhao G Z, Chen X B, et al.2004. Crustal structure from magnetotelluric profiling in the Haiyuan earthquake area, Ningxia Hui Autonomous Region, China[J]. Chinese Journal of Geophysics (in Chinese), 47 (2) : 274–281. DOI:10.3321/j.issn:0001-5733.2004.02.014 |
| [32] | Zhu Y Z, Xu C Y.2011. The experimental application of wider field electromagnetic method to the prospectiang for deep ore deposits[J]. Geophysical & Geochemical Exploration (in Chinese), 35 (6) : 743–746. |
| [33] | 陈玉玲, 韩凯, 陈贻祥, 等.2015. 可控源音频大地电磁法在岩溶塌陷勘察中的应用[J]. 地球物理学进展, 30 (6) : 2616–2622. DOI:10.6038/pg20150620 |
| [34] | 成江明.2008. 可控源音频大地电磁法在隐伏煤矿区的应用[J]. 地球物理学进展, 23 (4) : 1269–1272. |
| [35] | 邓锋华, 杨洋, 李帝铨.2013. 广域电磁法在隐伏金矿中的应用[J]. 工程地球物理学报, 10 (3) : 357–362. DOI:10.3969/j.issn.1672-7940.2013.03.015 |
| [36] | 方文藻, 李貅, 李予国, 等.1992. 频率域电磁法中视电阻率全区定义[J]. 西安地质学院学报, 14 (4) : 81–86. |
| [37] | 冯兵, 王珺璐, 周祥文, 等.2013. CSAMT探测中电场Ex全区视电阻率定义及应用[J]. 煤田地质与勘探, 41 (6) : 78–82. DOI:10.3969/j.issn.1001-1986.2013.06.019 |
| [38] | 冯兵, 李建国, 赵斌, 等.2014. 音频大地电磁法在南岭于都-赣县矿集区银坑示范区深部矿产资源探测中的应用[J]. 地质学报, 88 (4) : 669–675. |
| [39] | 何继善.2010. 广域电磁测深法研究[J]. 中南大学学报(自然科学版), 41 (3) : 1065–1072. |
| [40] | 何继善, 李帝铨, 戴世坤.2014. 广域电磁法在湘西北页岩气探测中的应用[J]. 石油地球物理勘探, 49 (5) : 1006–1012. |
| [41] | 胡涂, 李帝铨.2014. E-Ex广域电磁法对低阻薄层分辨能力探讨[J]. 物探化探计算技术, 36 (3) : 297–303. DOI:10.3969/j.issn.1001-1749.2014.03.08 |
| [42] | 黄皓平, 朴化荣.1992. 水平多层大地上垂直磁偶极频率测深的全波视电阻率[J]. 地球物理学报, 35 (3) : 389–395. |
| [43] | 孔祥儒, 刘士杰, 张建军, 等.1991. 福建东部地区大地电磁测深研究[J]. 地球物理学报, 34 (6) : 724–735. |
| [44] | 李帝铨, 谢维, 程党性.2013. E-Ex广域电磁法三维数值模拟[J]. 中国有色金属学报, 23 (9) : 2459–2470. |
| [45] | 林长佑, 张云琳, 司玉兰, 等.1984. 河西走廊东部地区的大地电磁测深研究[J]. 地球物理学报, 27 (2) : 131–143. |
| [46] | 刘春明, 佟铁钢, 何继善.2013. 多种电磁法在某金矿的野外勘探应用[J]. 中国有色金属学报, 23 (9) : 2422–2429. |
| [47] | 刘国栋.1994. 我国大地电磁测深的发展[J]. 地球物理学报, 37 (S1) : 301–310. |
| [48] | 彭淼, 谭捍东, 姜枚, 等.2012. 利用接收函数和大地电磁数据联合反演南迦巴瓦构造结中部地区壳幔结构[J]. 地球物理学报, 55 (7) : 2281–2291. DOI:10.6038/j.issn.0001-5733.2012.07.014 |
| [49] | 阮帅, 张炯, 孙远彬, 等.2015. 基于三维正演的音频大地电磁阻抗相位不变量校正技术[J]. 地球物理学报, 58 (2) : 685–696. DOI:10.6038/cjg20150229 |
| [50] | 孙英勋.2005. CSAMT法在高速公路长大深埋隧道勘察中的应用研究[J]. 地球物理学进展, 20 (4) : 1184–1189. |
| [51] | 汤井田, 何继善.1994. 水平电偶源频率测深中全区视电阻率定义的新方法[J]. 地球物理学报, 37 (4) : 543–552. |
| [52] | 汤井田, 周聪, 张林成.2011. CSAMT电场y方向视电阻率的定义及研究[J]. 吉林大学学报(地球科学版), 41 (2) : 552–558. |
| [53] | 王宏宇, 程党性, 杨旭.2014. 广域电磁法E-Eφ 视电阻率研究[J]. 物探化探计算技术, 36 (1) : 9–15. DOI:10.3969/j.issn.1001-1749.2014.01.02 |
| [54] | 王军, 王庆乙.1992. 层状大地有限长接地导线频域电磁响应的快速计算方法[J]. 地质与勘探, 28 (3) : 30–38. |
| [55] | 王顺国, 熊彬.2012. 广域视电阻率的数值计算方法[J]. 物探化探计算技术, 34 (4) : 380–383. DOI:10.3969/j.issn.1001-1749.2012.04.02 |
| [56] | 王绪本, 陈进超, 郭全仕, 等.2013. 沁水盆地北部煤层气富集区CSAMT勘探试验研究[J]. 地球物理学报, 56 (12) : 4310–4323. DOI:10.6038/cjg20131233 |
| [57] | 吴璐苹, 石昆法, 李荫槐, 等.1996. 可控源音频大地电磁法在地下水勘查中的应用研究[J]. 地球物理学报, 39 (5) : 712–717. |
| [58] | 杨承志, 邓居智, 陈辉.2013. 采集参数对音频大地电磁法二维非线性共轭梯度反演结果的影响研究[J]. 地球物理学进展, 28 (3) : 1346–1354. DOI:10.6038/pg20130328 |
| [59] | 杨进, 安海忠.1995. 音频大地电磁法在秦岭地区的地质效果[J]. 物探与化探, 19 (4) : 286–290. |
| [60] | 殷长春, 朴化荣.1991. 电磁测深法视电阻率定义问题的研究[J]. 物探与化探, 15 (4) : 290–299. |
| [61] | 殷长春.1994. 可控源音频磁大地电流法一维正演及精度评价[J]. 长春地质学院学报, 24 (4) : 438–453. |
| [62] | 于昌明.1998. CSAMT方法在寻找隐伏金矿中的应用[J]. 地球物理学报, 41 (1) : 133–138. |
| [63] | 詹艳, 赵国泽, 陈小斌, 等.2004. 宁夏海原大震区西安州-韦州剖面大地电磁探测与研究[J]. 地球物理学报, 47 (2) : 274–281. DOI:10.3321/j.issn:0001-5733.2004.02.014 |
| [64] | 朱裕振, 许聪悦.2011. 广域电磁法深部找矿实验效果[J]. 物探与化探, 35 (6) : 743–746. |
 2016, Vol. 31
2016, Vol. 31

