2. 中国地震局第二监测中心, 西安 710054
2. Second Monitoring Center, China Earthquake Administration, Xi'an 710054, China
青藏高原东北缘在印度板块和欧亚板块发生冲撞之后发生了一系列的复杂连续变形,并逐渐隆升.六盘山位于青藏高原东北缘与鄂尔多斯地块的交界地带,隆起于晚上新世(Zhang et al.,1991; Lin et al.,2001).在隆升过程中,六盘山地区发生多期地壳缩短,吸收了来自海原断裂带的部分走滑位移形变,其主要吸收方式为逆断裂和褶皱(邓起东等,1989).GPS观测表明,目前青藏高原北缘地区仍维持较高的滑动速率,但在向青藏高原东北缘延伸的过程中,滑动速率逐渐减小,至六盘山地区,主要断裂带不再沿高原边界继续延伸,表明六盘山地区是吸收青藏高原北部断裂左滑位移的挤压带,青藏高原东北缘的变形主要是逆冲变形和地壳增厚(Zhang et al.,2007;郑文俊等,2009).六盘山以东的鄂尔多斯地区莫霍面变化平缓,六盘山西侧地区莫霍面西高东低,靠近六盘山呈现汇聚挤压、明显缩短的特征(李洪强等,2013).综上所述,六盘山地区地表形变、莫霍面起伏特征以及区域挤压构造在总体上是互洽的.
目前关于六盘山地区地壳隆升的形成机制主要有三类:
(1) 青藏高原隆升后由于重力势能的累积而向外部生长(Tapponnier et al.,2001);
(2) 青藏高原下地壳物质由于放射性物质的作用,导致其具有了流变性质,其在深部地壳中的活动导致了青藏高原东北缘的连续变形(即下地壳流)(Royden et al.,2008);
(3)青藏高原岩石圈地幔的迁移导致了其东北部的复杂变形(Molnar et al.,1993).
迄今为止,六盘山地区地壳隆升的形成机制尚存争议,没有明确的答案,部分学者甚至认为,上述三种机制的共同作用才导致了现今青藏高原东北缘的复杂形变(Yuan et al.,2013).
综上可知,六盘山地区的隆升主要是由于印度板块对欧亚板块的挤压作用,引起青藏高原地壳内部连续变形而导致的结果,但具体隆升机制仍需进一步的研究.此外,由于六盘山地区的构造背景与龙门山地区类似,阐明六盘山地区隆升机制,对于该地区未来的构造活动以及地震危险性的评估都具有重要意义.鉴于此,我们在六盘山地区展开流动重力/GPS联合剖面观测,结合EGM2008重力数据,使用Airy均衡理论和重力导纳方法,分析了青藏高原东北缘地区的重力异常和地壳均衡,研究六盘山地区岩石圈有效弹性厚度与隆升机制,并结合弹性板均衡模型与Airy均衡模型对六盘山地区岩石圈挠曲的承载量进行估计,深化人们对六盘山地区隆升机制的认识.
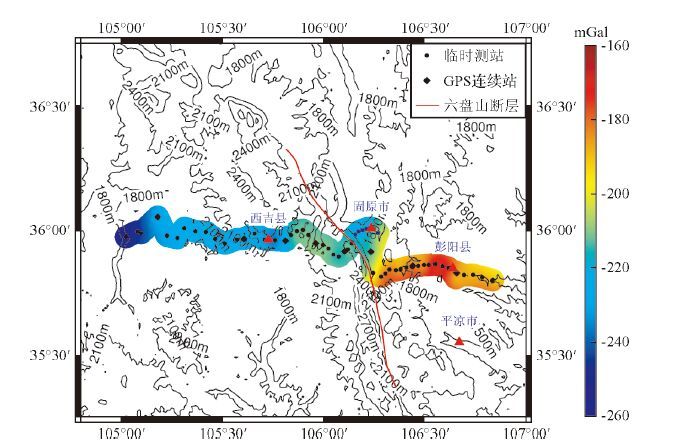
1 六盘山地区重力/GPS数据采集、处理与重力异常2014年8月在六盘山地区沿北纬36°,从东经105°至106.8°的测线上进行了包含58个测点的流动重力观测(图 1),其中50个为临时观测站,8个为GPS连续观测站.测站间隔为2~4 km,使用的重力仪为1台Burris重力仪和1台LaCoste-Romberg G重力仪.两种重力仪的分辨率为0.01 mGal(10-5 ms-2),观测精度约为0.03 mGal(朱仲芬等,1988;付广裕等,2013).在观测过程中,采取A-B-C…-C-B-A形式的往返串联观测方式,以减少流动重力观测过程中无法回避的传递误差,互差超过0.1 mGal的测段需要重新测量.观测结果使用中国地震局流行的流动重力平差软件(LGADJ软件)进行平差计算,平差结果的总体精度为0.02 mGal.
|
图 1 流动重力/GPS联测测线及布格重力异常 圆点代表临时测站,菱形代表GPS连续站,红线代表六盘山东麓断层,红色三角代表城镇. Figure 1 Gravity and GPS hybrid survey line and the distribution of bouguer gravity anomalies The points denote the temporary observation points. The diamonds denote GPS continuous observation stations. Red line denotes the fault of eastern Liupan Shan. Red triangles denote towns. |
配套的GPS观测使用Leica GX1230双频GPS接收机和LEIAX1202双频天线,每一测站的观测时长为40分钟,采样间隔为30秒,使用GAMIT/GLOBK软件进行基线解算,基线精度中误差为5 cm,保证了分米级的高程观测精度.依据GPS高程观测结果,对平差后的重力数据进行归算,使用WGS84参考椭球作为重力归算的基准面,进行自由空气改正,获取了该测线的自由空气重力异常,之后再进行布格改正,并使用ASTER GDEM 2011数据分别以1″×1″、5″×5″、10″×10″网格数据对近场(0~2 km),中场(2~20 km)和远场(20~167 km)进行地形改正,最后获取了此测线上58个观测点的布格重力异常数据(图 1).
EGM2008地球重力模型是美国国家地理空间局NGA于2008年4月发布的全球超高阶地球重力场模型,其展开至2190阶,2159次.此模型一直在持续更新中,Satellite Geodesy网站(http://topex.ucsd.edu/)可以直接下载最新版本(V23.1)分辨率为1′×1′的自由空气重力异常数据和高程数据.使用Kriging插值法提取了与观测点位置相同的模型自由空气重力异常数据,并使用ASTER GDEM 2011模型高程数据,进行了布格改正和地形改正,获取了模型布格重力异常.模型布格重力异常的重力改正方法与地表观测数据的改正方法一致.
经比较发现,六盘山地区实测自由空气重力异常与EGM2008模型给出的自由空气重力异常虽然变化趋势较为一致.但是,两组数据的平均差值为-18.8 mGal,其标准偏差为-8.5 mGal,最大差值为-35.9 mGal,最小差值为-0.3 mGal,且模型数据均大于实测数据.六盘山以西测点的差值均小于-25 mGal,六盘山地区部分测站出现大于-30 mGal的差值,六盘山以东差值逐渐减小.川西盆地实测自由空气重力异常与EGM2008模型结果之间的差异约为-10 mGal(付广裕等,2013),比六盘山地区的差异要小,可能是由于川西盆地较为平坦所致.经过六盘山以及川西盆地实测值与模型值对比,发现实测与模型的偏差随地形的坡度增加而增大.
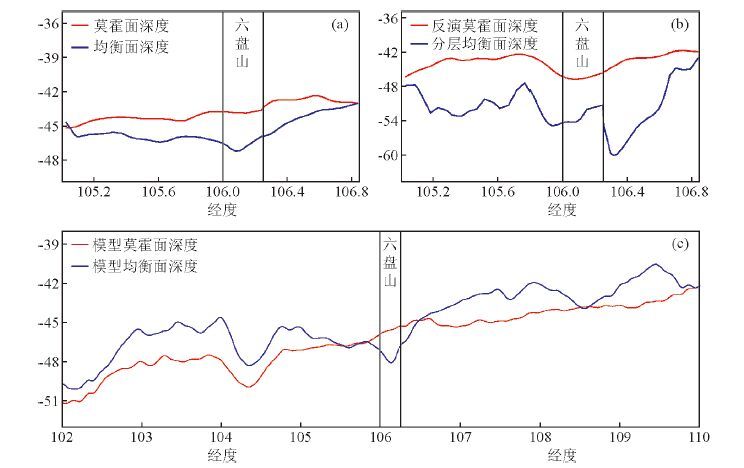
2 六盘山地区地壳重力均衡地壳均衡的研究对象是岩石圈深部静水压平衡状态的问题,因此有必要通过滤波的方式从观测数据中消除浅部地壳物质的影响.鉴于此,首先对51个测站对应的布格重力异常与GPS高程信息进行了10公里的低通滤波处理,固原市内的7个测点偏离了测线,被弃用.使用滤波后的数据基于Airy均衡模型计算图 1所示测线对应的地壳均衡面.假设地幔密度为3.27 g/cm3,地壳密度为2.67 g/cm3,且六盘山地区东侧稳定的鄂尔多斯地块已经处于均衡状态,并依据Fu等(2014)的研究思路进行地壳均衡研究.地震反射波资料显示,鄂尔多斯中部地区的平均地壳厚度为40~43 km(Jia et al.,2005;Pan et al.,2011;李多等,2012),因此本文取41 km作为鄂尔多斯中部的平均地壳厚度.从ASTER GDEM 2011中提取鄂尔多斯中部地震波剖面(Jia et al.,2005)的高程,取其平均值为1200 m.依据Airy均衡模型计算,在高程为零时地壳厚度应为35.7 km,然后依据测线滤波后的高程数据计算测线位置的均衡深度即图 2a蓝线,再根据布格板公式(Fu et al.,2014)和滤波后的布格重力异常计算莫霍面深度.本文取图 1所示测线最东端的均衡深度为莫霍面的起算深度,结果如图 2a红线所示.图 2a中红线为莫霍面,蓝线为地壳均衡面,其反映的是研究区域的地壳均衡状态.地壳均衡面深度大于莫霍面深度,表明该区域处于正均衡异常.
|
图 2 依据地表实测数据与EGM2008数据计算的均衡面深度和莫霍面深度 (a)均一地壳情况下莫霍面与均衡面深度;(b)考虑地壳密度结构情况下莫霍面与均衡面深度;(c)均一地壳情况下使用EGM2008数据计算的莫霍面与均衡面深度,红线代表莫霍面深度;蓝线代表均衡面深度,黑色竖线代表六盘山位置,黄色竖线代表测线位置. Figure 2 The Moho and isostasy depths calculated from observed and EGM2008 modeled gravity data (a)the Moho and isostasy depths based on a homogeneous crust model;(b)the Moho and isostasy depths based on a crust model considering the density structure;(c)the Moho and isostasy depths based on a homogeneous crust and EGM2008 model data. Red lines denote the Moho depths. Blue lines denote the isostasy depths. Black vertical lines denote the position of Liupan Shan. Yellow vertical lines denote the position of the survey line. |
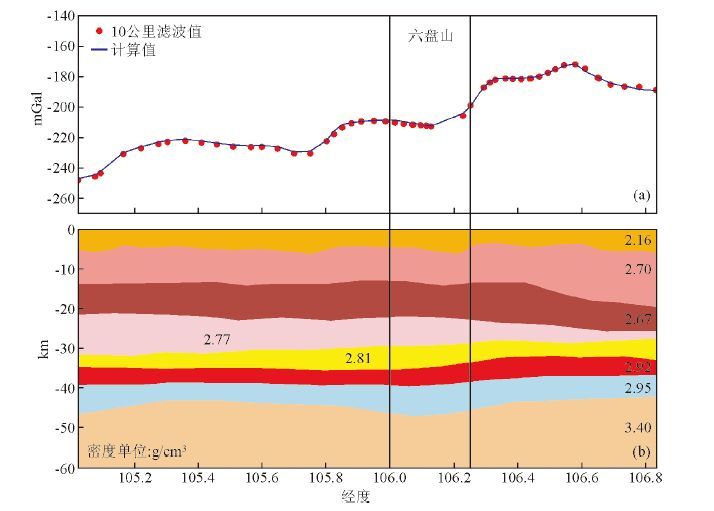
为了考虑实际地壳的密度分层结构的影响,更精细地研究六盘山地区的地壳均衡状态,本文利用布格重力异常数据反演区域的地壳密度构造.具体地说,使用滤波后的布格重力异常以二维多边棱柱体模型(Talwani et al.,1959)作为正演模型,反演方法使用非线性最小二乘方法(Marquardt et al.,1963),并用该区域的地壳P波分层结构和以P波速度换算的密度(Zhang et al.,2014)作为反演的初始密度分层模型.进行多次迭代计算数据标准差小于0.01 mGal之后,便得到六盘山地区的密度分层结构,如图 3所示.本文反演选取的初始地壳分层模型是人工地震深反射剖面资料给出的P波波速结构(Zhou et al.,2000),此人工地震剖面与本文使用的重力剖面都经过西吉县并向东延伸穿过六盘山,因此使用此剖面来约束重力反演的多解性是合理的.以 P波波速结构为起始模型,用最新的重力观测数据进行拟合,可得到更为准确的地壳结构模型.
反演得到的莫霍面深度在测线东端为41 km,在西端为47 km,六盘山下部为46 km.CRUST1.0提供了分辨率为1°×1°全球地壳模型,从此模型中提取的测线东端莫霍面深度为42 km左右,西端为50 km左右,六盘山下部为49 km左右,而背景噪声层析成像方法得到该区域的莫霍面深度在测线东端为41 km,在西端为46 km,六盘山下部为44 km(Zheng et al.,2010).Shen等(2011)和Yue等(2013)利用接受函数方法得到研究区域西部莫霍面深度为52和51 km,东部为42和41 km.综上所述,本文反演的莫霍面深度与前人研究结果接近.
参考图 3的地壳密度分层结构,本文利用Airy模型,使用公式(1)计算包含地壳分层结构的均衡面深度Hiso.公式(1)中,ρt为地面到参考面的密度值,ρ1~ρn为地壳各层的密度值,ρm为地幔的密度值.h为高程值,H1~Hn代表各层深度值,带有0角标的项为均衡起算点相应的地面高度和各层深度值,在此我们取测线最东端作为起算点.图 2b绘制了分层结构均衡面深度Hiso与使用滤波后的布格重力异常反演的莫霍面深度Hmoho,可以看出,考虑地壳分层结构后,六盘山地区地壳处于正均衡异常状态.公式(1)为

|
(1) |
|
图 3 跨六盘山地区布格重力异常与地壳密度结构反演结果 (a)跨六盘山地区布格重力异常,红点代表 10公里滤波后的布格重力异常值,蓝线为计算的布格重力异常值;(b)地壳密度结构反演结果,数字代表各层密度值,单位是g/cm3. Figure 3 Bouguer gravity anomalies across the Liupan Shan area and the inversed density structure of the crust (a)Bouguer Gravity Anomalies across Liupan Shan area. Red points denote the Bouguer Gravity Anomalies with 10 kilometers low-pass filter processing. Blue line denotes calculated Bouguer Gravity Anomalies;(b)Result of the inversion of the density structure of the crust. The numbers denote the density of the layers. The unit is g/cm3. |
上述研究表明,无论使用均一密度地壳模型还是密度分层地壳模型,计算结果均显示六盘山地区地壳处于正均衡状态.此外,图 1所示的测线长度只有200多公里,测线的长度是否满足六盘山地区地壳均衡研究的需要,尚需进一步确认.鉴于此,本文沿实测数据剖面的走向,从EGM2008模型数据和相应的高程数据中提取了一条经度从102°至110°的重力剖面,保证剖面东端延伸至稳定的鄂尔多斯地块中部地区,并对此剖面数据进行了20公里低通滤波处理,去除了高频成分的影响.使用此数据,在假设地壳密度均一的前提下,基于Fu等(2014)的方法,计算出六盘山地区地壳均衡面深度和莫霍面深度(见图 2c).从图 2c可知,六盘山地区的地壳确实处于均衡正异常状态.
综上所述,六盘山及周边地区的地壳处于正均衡异常状态,即该区域的地壳均衡面深于莫霍面.该异常可能与六盘山地区岩石圈处于挤压状态有关,来自青藏高原的挤压作用使六盘山地区地表隆起,但是并没有形成足够补偿隆起高度的山根.
3 六盘山地区岩石圈有效弹性厚度与加载机制小节3对于六盘山地区地壳均衡的分析是建立在Airy均衡模型的基础上展开的.Airy均衡模型是表述地壳处于静水压力平衡状态下均衡模型,即其考虑的是地壳不具有弹性性质且地幔为流体的情况下,地壳对于加载的响应情况.然而,实际情况是较为坚硬的岩石圈是具有弹性性质的,可以承担一定量的加载.在此情况下,地形波长较短的区域不会达到Airy均衡状态,只有长波长的区域可以达到Airy均衡状态(Watts et al.,2001).换句话说,岩石圈由于具有弹性属性,在短波长区域也就是范围较小的局部地区,对于加载,其难以达到Airy均衡的挠曲,而在长波长区域,其更易发生挠曲,也就可以达到Airy均衡状态.据此可知,我们可以通过建立模型来计算研究区域岩石圈有效弹性厚度,以及造成其挠曲的加载位置.利用有效弹性厚度Te和加载位置以及研究区域的高程数据和重力数据可以计算该区域弹性地壳模型下均衡重力异常.使用实测数据计算该区域的岩石圈有效弹性厚度,目前流行的做法是利用弹性板模型重力异常与实测的剖面重力异常数据进行拟合计算Te(Turcotte and Schubert,2002).六盘山地区实测数据的长度有限,不适合使用上述方法进行研究.因此,我们使用二维重力与地形模型数据计算研究区域的有效弹性厚度和加载机制.虽然模型数据与实测数据存在一定偏差,但整体变化趋势是一致的,因此可用EGM2008模型数据进行计算.
近年来使用较多的频域方法是自由空气重力导纳方法,该方法是通过分析自由空气重力异常和相应地区地形的波数域相关性估计Te和形成挠曲的加载位置.采用自由空气异常估计有效弹性厚度,可有效避免风化剥蚀作用在计算重力导纳中造成的误差.在弹性板模型下,布格重力异常导纳具有随波长减小而变小的变化特征.发生在短波长的风化剥蚀造成导纳变化的频段向长波长偏移,进而造成计算误差,使计算的Te较厚.自由空气异常导纳随波长减小而增大,且不论是否发生风化剥蚀其值在短波长都很高,不存在布格重力异常导纳由于风化剥蚀而产生的偏移问题(McKenzie and Fairhead,1997; McKenzie,2003).
本文使用McKenzie(2003)给出的方法计算模型导纳Zcf(k).McKenzie(2003)的导纳模型将岩石圈分为上地壳,下地壳和地幔三部分,并且考虑了加载发生在不同位置对于模型导纳的影响.其方法的实质是利用实测重力数据和地形数据计算的重力导纳与弹性板模型导纳在波数域(k=2π/λ,k为波数,λ为波长)中拟合,求解岩石圈挠曲的初始加载位置和有效弹性厚度,因此该方法需要对重力数据与高程数据进行二维的频域计算,也就是说使用的重力数据和高程数据必须是二维数据.在此使用EGM2008自由空气重力异常数据以及SRTM V18.1 DEM数据(研究区域为E102°-110°,N33°-38°)作为实测值进行导纳的计算.在计算中高频部分的信号会增大导纳值,这样会造成计算的误差,所以选择滤除高频信号会提高结果的精度.具体地说,为了压制数据中高频成分的影响,分别对重力数据和DEM数据在频率域进行了50 km和20 km的低通滤波处理(Fielding and McKenzie,2012).采取不同的波长进行滤波的原因是在确保去除高频成分的同时,使用公式(2)计算可以得到较高的重力异常与地形的相关性.在对EGM2008自由空气重力异常Δgof(x,y)与DEM数据ho(x,y)进行谱估计的计算中,使用多窗谱分析方法(MTM)(Thomson,1982; Scheirer et al.,1995)将空间域的数据转换为波数域数据ΔGof(k)和Ho(k).该方法可减小频谱泄露,同时可增加频峰的宽度,从而提高频谱分辨率,使丢失的信息尽量减少,在此沿x方向和y方向均取3个窗口进行重力数据和高程数据频域计算,McKenzie(1997,2013)和Fielding(2012)使用此方法均得到了较好的结果.实测重力导纳可通过公式(2)计算,该公式中,*为取共轭,波数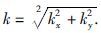
在模型导纳计算中取岩石圈泊松比σ为0.25,杨氏模量E为1.4×1011 Pa.利用小结3反演的地壳密度分层结构,设定六盘山地区的上地壳厚度为10 km,下地壳厚度为30 km,上地壳密度为2.60 g/cm3,下地壳密度为2.80 g/cm3,地幔密度为3.40 g/cm3.不同的Te和加载比F1~3(F1、F2和F3分别代表地表加载、上地壳和下地壳界面加载以及地幔与下地壳界面加载在总加载中所占比例,且F1+F2+F3=1)对应不同的模型导纳Zcf(k).
依据上述参数设定,使用公式(3)计算Zof(k)与Zcf(k)的不符合度HMisfit.
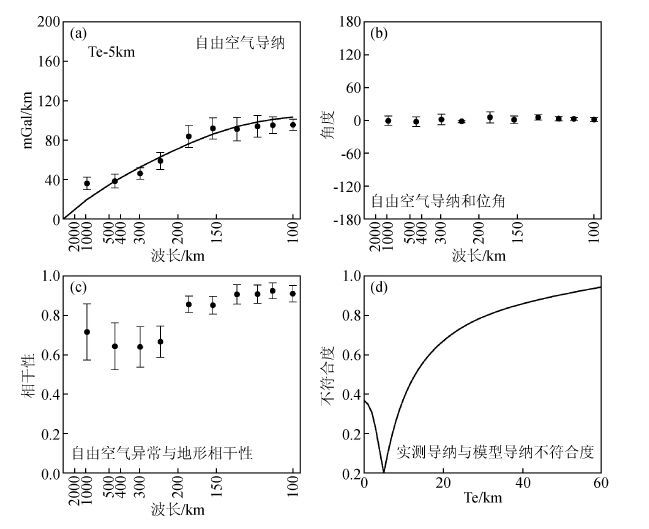
Te在1~100 km范围内迭代,步长为1 km,F1、F2和F3在0~1之间迭代,步长为0.01.经全局迭代计算后发现,当Te=5 km,F1=0.95,F2=0.05,F3=0时HMisfit最小.图 4a为EGM2008自由空气导纳与模型导纳的拟合图,图 4b和4c分别为自由空气重力导纳的相位角和自由空气异常数据与DEM数据的相干性,图 4d为拟合的不符合度,当Te=5 km时,不符合度最小.图 4a,b,c中的导纳值、相位值与相关值及其误差使用Forsyth(1985)和McKenzie(1997,2003)的方法计算.导纳值、相位值和相关值与波数k是一一对应的关系,取图中对应的k值为中心,以Δk为波数段宽度,计算k-Δk与k+Δk范围中每一个k所对应的导纳值、相位值与相关值的平均值,并计算其标准差,作为图中对应k值的平均值和标准差.相位角越接近于0,相干性越接近1,表示自由空气重力异常数据与高程数据的相关性越好,(McKenzie and Fairhead,1997; McKenzie,2003).在所有波段,六盘山地区的导纳相位角接近0,相干性较高,表明六盘山地区的加载确实主要来自于地形的加载.
|
图 4 自由空气导纳方法计算结果 (a)自由空气导纳,横轴代表波长;(b)自由空气导纳相位角;(c)自由空气异常与地形相干性;(d)实测导纳与模型导纳不符合度,Te=5 km,不符合度最小;实点代表EGM2008与SRTM V18.1 DEM数据估计得到的观测值,误差棒取一个标准差. Figure 4 Result of free-air admittance method (a)Free-air admittance. The x-axis denotes wavelength;(b)Phase angle of free-air admittance;(c)Coherence between the free-air anomaly and topography;(d)Misfits between Observation admittance and model admittance. When Te=5 km, the misfit is the minimum. Black points denote the observation values estimated from EGM2008 model data and SRTM V18.1 DEM data. Error bars are 1 standard deviation. |
六盘山地区岩石圈加载参数F1=0.95,F2=0.05,F3=0表明,六盘山地区挠曲加载的位置主要来自于地表,地幔和下地壳不存在加载贡献.换句话说,以六盘山为中心的青藏高原东北缘地区的隆起主要是由于地表加载而形成的.杨亭等(2013)和Deng等(2014)使用布格重力异常数据计算获取的研究区域有效弹性厚度为40~50 km左右,两者的工作均未考虑上地壳与下地壳的分层,也未提及风化剥蚀对于计算的影响.在有效弹性的厚度的估计中采用了空间窗口的方法来计算区域的有效弹性厚度分布,其结果并未提及弹性地壳挠曲的加载情况.以上两者的工作主要在于获取其研究区域的有效弹性厚度分布,进而分析地壳的横向不均匀性.本文的工作是建立在地壳为横向均一的基础上,对该区域的隆起机制和均衡异常进行讨论,并未涉及该区域的Te分布研究.采用自由空气异常导纳方法所获取的Te相比布格重力异常导纳的结果较低,且其估计的Te小于地震深度(McKenzie and Fairhead,1997).研究区域中大于5级(Mw)的地震震源深度在10~15 km,所以本文采用自由空气异常数据所估算的Te具有其合理性.公式为
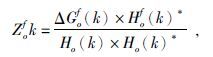
|
(2) |

|
(3) |
以上为考虑岩石圈为弹性板的前提下,通过频域分析的方法来估计岩石圈Te和其起始加载位置.在得到估计的Te与加载比分布后,依据岩石圈弹性板均衡模型和DEM数据,使用公式(4)可以计算区域弹性板均衡重力异常(陈石等,2011).公式(4)中,Δgiso为均衡重力异常,Δg为观测重力异常,Δgc为弹性板模型给出的布格重力异常,由模型布格重力导纳值Z(k)与波数域地形H(k)的乘积再经过二维快速傅里叶逆变换得到.在具体应用于六盘山地区时,Δg为EGM2008模型给出的自由空气重力异常数据,经过布格改正和地形改正后获得的布格重力异常数据.由于采样点较密集,在进行地形重力校正时,将近场(0~2 km)、中场(2~20 km)和远场(20~167 km)的网格地形数据分别定义为5″×5″、25″×25″、50″×50″,以减少计算时间,地形数据为ASTER GDEM 2011数据.为了避免快速傅里叶变换的边缘效应对于区域均衡异常计算精度的影响,我们将计算区域扩大至E100°-E112°,N31°-N40°范围,最后只截取E102°- E110°,N33°-N38°的均衡重力异常.利用上述方法得到的弹性板模型重力异常(图 5)比Airy均衡模型给出的结果更接近于实际情况.公式为
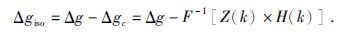
|
(4) |
|
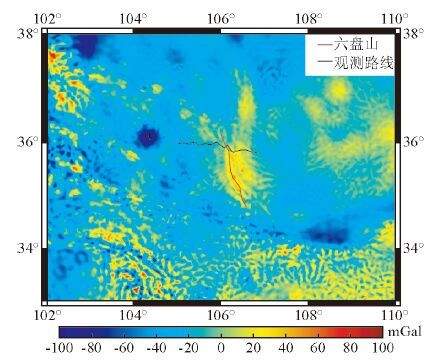
图 5 基于弹性板模型的青藏高原东北缘均衡重力异常场.棕线代表六盘山位置,黑线代表观测路线 Figure 5 Gravity isostasy anomalies of northeastern margin of Tibetan Plateau based on elastic plate model. Brown line denotes the position of Liupan Shan. Black line denotes the survey line |
图 5为弹性板模型给出的六盘山地区均衡重力异常.正均衡异常代表均衡面比莫霍面深,负均衡异常代表均衡面比莫霍面浅.图 5的东北部是较为稳定的鄂尔多斯地块,其在弹性板模型假设下依旧保持均衡状态.图 5的西南部分地区呈现不均衡状态,可能是由于弹性板模型采用的是横向均匀的地壳模型,而实际地壳是横向不均匀的,因而在局部地区出现较大的均衡异常.换句话说,相对研究区域西南部的青藏高原地区,稳定的鄂尔多斯地块的地壳横向变化较小,从而出现图 5所示的弹性板均衡重力异常场.图 5显示,六盘山两侧较远地区处于负均衡异常状态,但六盘山脉却处于正均衡异常状态,该分布与上文使用Airy 均衡分析的结果在分布形态上类似,但异常幅度较小,这是由于采用了弹性板模型,地壳在小尺度范围内具有一定的承载能力,可以抵消部分加载而不发生变形,或者发生较小的挠曲.
为了量化六盘山地区岩石圈的实际承载情况,有必要对弹性板模型均衡异常与Airy均衡异常进行对比分析.首先,从弹性板均衡异常中提取与小节2中观测点相对应的值作为弹性板均衡异常值;其次,计算Airy模型对应的均衡异常,将依据Airy模型得到的均衡面深度与莫霍面深度的差值通过布格板公式换算为重力值;不同模型的均衡异常差值即可反映测线处岩石圈承载情况.
为了更直观的比较弹性板均衡异常与Airy模型均衡异常的差异及其承载状况,本文使用布格板公式(地壳与地幔密度差取700 kg/m3)将两个模型的均衡异常换算为深度.图 6a中,紫线为均一地壳结构对应的Airy均衡异常,蓝线为考虑地壳密度结构的Airy均衡异常,这两种情况都假设固体地壳没有弹性,且上浮于较重的流体地幔之上,相对而言,后者由于考虑了地壳的密度结构,其结果应更精确.相对于均一地壳的Airy均衡异常和考虑地壳密度结构的Airy均衡异常,弹性板均衡异常(图 6a中黑线)明显偏小,而且总体接近于零,表明在弹性板模型下,测线区域基本上处于均衡状态,即岩石圈承载了其自身的加载.

|
图 6 弹性板模型与Airy模型均衡异常的对比 (a)弹性板模型与Airy模型均衡异常,黑线代表弹性板均衡异常,紫线代表均一地壳情况下的Airy均衡异常,蓝线代表考虑地壳密度结构情况下的Airy均衡异常;(b)弹性板均衡异常与考虑地壳密度结构Airy均衡异常的差异,红色垂线代表六盘山东麓断裂位置,蓝色代表岩石圈承载量. Figure 6 Contrast of isostasy anomalies between elastic plate model and Airy model (a)Isostasy anomalies of elastic plate model and Airy model. Black line denotes isostasy anomalies of elastic plate model. Purple line denotes Airy isostasy anomalies based on homogeneous crust. Blue line denotes Airy isostasy anomalies based on density structure of the crust;(b)Differences between isostasy anomalies of elastic plate and Airy isostasy anomalies based on density structure of the crust. Red vertical lines denote the fault of eastern Liupan Shan. Blue area denotes load capacity. |
需要注意的是,六盘山东麓存在一条高角度断裂(张秉良和向宏发,2000),表明该地区的岩石圈不是连续的,但是我们的连续弹性板模型计算结果表明该地区接近于均衡状态,该结论显示六盘山东麓断裂带处于耦合状态.地表GPS数据反演结果显示六盘山断裂带处于闭锁状态(李强等,2014),该结论被本文的重力研究所证实.
比较Airy模型和岩石圈弹性板模型给出的均衡异常可研究六盘山地区岩石圈的承载力.Airy模型给出的均衡异常是地壳物质重量与所受浮力之差,而岩石圈弹性板模型给出的均衡异常则为地壳物质重量与其所受浮力外加弹性板承载力之和的差异.因此,Airy模型给出的均衡异常减去岩石圈弹性板模型给出的均衡异常等效于弹性板所受的承载力.
图 6b为图 5所示测线对应的岩石圈弹性板所承载的加载值,该加载值等效为考虑地壳密度分层的Airy均衡异常(图 6a中的蓝色线条)减去岩石圈弹性板模型给出的均衡异常(图 6a中的黑色线条),该结果由地壳地幔密度差异布格板厚度等效表示,反映了图 5所示测线岩石圈承载情况.加载量梯度变化最大值处于六盘山东麓断裂带上,表明该断裂带吸收了比较大的应变能,因此该断层存在发生强震的可能.
5 结 论本文采用Airy地壳均衡理论,基于2014年8月在六盘山地区观测的流动重力/GPS联合观测数据,结合EGM2008重力模型数据,研究了六盘山地区的地壳均衡状态.使用实测数据进行岩石圈挠曲的计算要优于模型数据,但由于本文使用的实测数据量有限,不适合用来研究该区域的岩石圈挠曲,所以使用EGM2008重力数据与SRTM V18.1 DEM数据基于自由空气重力异常导纳方法研究六盘山区域的岩石圈有效弹性厚度和加载机制.主要结论如下:
(1) 比较了六盘山地区实测自由空气重力异常与EGM2008模型结果,发现两者之间的平均差异为-18.8 mGal(10-5 ms-2),标准差为-8.5 mGal,最大差异为-35.9 mGal,超过30 mGal的差异主要集中在六盘山山区,实测与模型的偏差随地形的坡度增加而增大.模型数据和实测数据整体较为接近,但模型自由空气重力异常均大于实测结果.
(2) 依据地表流动重力/GPS联测数据和Airy均衡理论,基于均一地壳模型和密度分层地壳模型,分别计算了跨六盘山剖面的地壳均衡状态,同时利用EGM2008重力场模型数据计算了更长空间尺度的地壳均衡状态.各种结果均表明六盘山区处于均衡正异常状态.该结果表明,六盘山地区地壳底部并没有形成足够补偿地表隆起的山根.
(3) 基于EGM2008自由空气重力异常数据与SRTM数字高程数据,通过重力导纳方法计算了青藏高原东北缘地区的岩石圈有效弹性厚度Te,分析了六盘山地区岩石圈加载机制.研究发现,当Te取5 km,加载比F1、F2和F3分别取0.95、0.05和0时,实测导纳与模型导纳符合度最高.该结果表明,六盘山地区的岩石圈加载位置集中在地表,上下地壳界面以及地幔与下地壳界面基本上不存在起始加载.上述结果表明,以六盘山地区为中心的青藏高原东北缘的隆起主要是由于区域地壳挤压增厚、并在重力势能的作用下向外部生长造成的.
(4) 依据弹性板模型展开均衡重力异常研究,发现弹性板模型下六盘山地区基本处于均衡状态.对比Airy均衡异常与弹性板均衡异常,获得跨六盘山断裂带的岩石圈承载情况,发现六盘山东麓断层处地壳承载梯度值最大,表明该断裂带吸收了较多的应变能,具有发生较强地震的可能.
致谢 感谢审稿专家提出的宝贵意见和支持.| [1] | Chen S, Wang Q S, Zhu Y Q, et al.2011. Temporal and spatial features of isostasy anomaly using gravitational admittance model at eastern margin of Tibetan Plateau[J]. Chinese Journal Geophysics, 54 (1) : 22–34. DOI:10.3969/j.issn.0001-5733.2011.01.004 |
| [2] | Deng Q D, Zhang W, Zhang P Z.1989. Haiyuan strike-slip fault zone and its compressional structures of the end[J]. Seismology and Geology. (in Chinese), 11 (1) : 1–14. |
| [3] | Deng Y, Zhang Z, Fan W, et al.2014. Multitaper spectral method to estimate the elastic thickness of South China: Implications for intracontinental deformation[J]. Geoscience Frontiers, 5 (2) : 193–203. DOI:10.1016/j.gsf.2013.05.002 |
| [4] | Fielding E J, McKenzie D.2012. Lithospheric flexure in the Sichuan Basin and Longmen Shan at the eastern edge of Tibet[J]. Geophysical Research Letters, 39 (9) . |
| [5] | Forsyth, D. W.1985. Subsurface loading and estimates of the flexural rigidity of continental lithosphere[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 90 (B14) : 12623–12632. DOI:10.1029/JB090iB14p12623 |
| [6] | Fu G Y, Gao S H, Freymueller J T, et al.2014. Bouguer gravity anomaly and isostasy at western Sichuan Basin revealed by new gravity surveys[J]. Journal of Geophysical Research: Solid Earth, 119 (4) : 3925–3938. DOI:10.1002/2014JB011033 |
| [7] | Fu G Y, Zhu Y Q, Gao S H, et al.2013. Discrepancies between free air gravity anomalies from EGM2008 and the ones from dense gravity/GPS observations at west Sichuan Basin[J]. Chinese Journal Geophysics, 56 (11) : 3761–3769. DOI:10.6038/cjg20131117 |
| [8] | Jia S X, Zhang X K.2005. Crustal structure and comparison of different tectonic blocks in North China[J]. Chinese Journal of Geophysics, 48 (3) : 672–683. DOI:10.1002/cjg2.700 |
| [9] | Li D, Zhou S Y, Chen Y S, et al.2012. 3-D lithospheric structure of upper mantle beneath Ordos region from Rayleigh-wave tomography[J]. Chinese Journal Geophysics (5) : 1613–1623. DOI:10.6038/j.issn.0001-5733.2012.05.019 |
| [10] | Li H Q, Gao R, Wang H Y, et al.2013. Extracting the Moho structure of Liupanshan by the method of near vertical incidence[J]. Chinese Journal Geophysics, 56 (11) : 3811–3818. DOI:10.6038/cjg20131122 |
| [11] | Li Q, Jiang Z S, Wu Y Q, et al.2014. Inversion of Locking and Distribution of Slip Deficit in Haiyuan-Liupan Fault Zone Using GPS Data[J]. Geomatics and information science of Wuhan university, 39 (5) : 575–580. |
| [12] | Lin A, Yang Z, Sun Z, et al.2001. How and when did the Yellow River develop its square bend?[J]. Geology, 29 (10) : 951–954. DOI:10.1130/0091-7613(2001)029<0951:HAWDTY>2.0.CO;2 |
| [13] | Marquardt D W.1963. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial & Applied Mathematics, 11 (2) : 431–441. |
| [14] | McKenzie D, Fairhead D.1997. Estimates of the effective elastic thickness of the continental lithosphere from Bouguer and free air gravity anomalies[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 102 (B12) : 27523–27552. DOI:10.1029/97JB02481 |
| [15] | McKenzie D.2003. Estimating Te in the presence of internal loads[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 108 (B9) . |
| [16] | Molnar P, England P, Martinod J.1993. Mantle dynamics, uplift of the Tibetan Plateau, and the Indian monsoon[J]. Reviews of Geophysics, 31 (4) : 357–396. DOI:10.1029/93RG02030 |
| [17] | Pan S Z, Niu F L.2011. Large contrasts in crustal structure and composition between the Ordos plateau and the NE Tibetan plateau from receiver function analysis[J]. Earth and Planetary Science Letters, 303 (3) : 291–298. |
| [18] | Royden L H, Burchfiel B C, Robert D H.2008. The geological evolution of the Tibetan Plateau[J]. science, 321 (5892) : 1054–1058. DOI:10.1126/science.1155371 |
| [19] | Scheirer D, Forsyth D. W. Hosford A.1995. Multitaper estimates of the lithospheric strength of the Basin and Range province[J]. Eos Trans. AGU, 76 : 17. |
| [20] | Shen X Z, Mei X P, Zhang Y S.2011. The crustal and upper-mantle structures beneath the northeastern margin of Tibet[J]. Bulletin of the Seismological Society of America, 101 (6) : 2782–2795. DOI:10.1785/0120100112 |
| [21] | Talwani M, Worzel J L, Landisman M.1959. Rapid gravity computations for two-dimensional bodies with application to the Mendocino submarine fracture zone[J]. Journal of Geophysical Research, 64 (1) : 49–59. DOI:10.1029/JZ064i001p00049 |
| [22] | Tapponnier P, Xu Z Q, Roger F, et al.2001. Oblique stepwise rise and growth of the Tibet Plateau[J]. science, 294 (5547) : 1671–1677. DOI:10.1126/science.105978 |
| [23] | Thomson D J.1982. Spectrum estimation and harmonic analysis[J]. Proceedings of the IEEE, 70 (9) : 1055–1096. DOI:10.1109/PROC.1982.12433 |
| [24] | Turcotte D. L, Schubert G.2002. Geodynamics[M]. Cambridge University Press . |
| [25] | Watts A B.2001. Isostasy and Flexure of the Lithosphere[M]. Cambridge University Press . |
| [26] | Yang T FU Rong-Shan, HUANG Jin-Shui.2013. Effective elastic thickness of continental lithosphere in China with Moho topography admittance method[J]. Chinese Journal Geophysics, 56 (6) : 1877–1886. DOI:10.6038/cjg20130610 |
| [27] | Yuan D Y, Ge W P, Chen Z W, et al.2013. The growth of northeastern Tibet and its relevance to large-scale continental geodynamics: A review of recent studies[J]. Tectonics, 32 (5) : 1358–1370. DOI:10.1002/tect.v32.5 |
| [28] | Y ue, H, Chen Y. J, Sandvol E, et al.2012. Lithospheric and upper mantle structure of the northeastern Tibetan Plateau[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 117 (B5) . |
| [29] | Zhang B L, Xiang H F.2000. The fabric of fault gouge from the eastern Liupanshan piedmont fault zone and their implication[J]. Seismology and Geology, 22 (1) : 47–52. |
| [30] | Zhang P Z, Molnar P, X u, X W.2007. Late Quaternary and present-day rates of slip along the Altyn Tagh Fault, northern margin of the Tibetan Plateau[J]. Tectonics, 26 (5) . |
| [31] | Zhang P, Burchfiel B C, Molnar P, et al.1991. Amount and style of late Cenozoic deformation in the Liupan Shan area, Ningxia Autonomous Region, China[J]. Tectonics, 10 (6) : 1111–1129. DOI:10.1029/90TC02686 |
| [32] | Zhang Y Q, Teng J W, Wang Q S, et al.2014. Density structure and isostatic state of the crust in the Longmenshan and adjacent areas[J]. Tectonophysics, 619 : 51–57. |
| [33] | Zhen W J, Zhang P Z, Yuan D Y, et al.2009. Deformation on the northern of the Tibetan plateau from GPS measurement and geologic rates of Late Quaternary along the major fault[J]. Chinese Journal Geophysics, 52 (10) : 2491–2508. DOI:10.3969/j.issn.0001-5733.2009.10.008 |
| [34] | Zheng Y, Yang Y, Ritzwoller M. H, et al.2010. Crustal structure of the northeastern Tibetan plateau, the Ordos block and the Sichuan basin from ambient noise tomography[J]. Earthquake Science, 23 (5) : 465–476. DOI:10.1007/s11589-010-0745-3 |
| [35] | Zhou M D, Lü T Y, Zhang Y S, et al.2000. A. The geological structure background and the crustal structure in the northeastern margin of the Qinghai-Tibetan plateau[J]. Acta Seismologica Sinica, 13 (6) : 687–697. DOI:10.1007/s11589-000-0071-2 |
| [36] | Zhu Z F, Chen D S.1988. Discussion on some problems of LaCoste-Romberg G Gravimeter[J]. Crustal Deformation and Earthquake, 1 : 004. |
| [37] | 陈石, 王谦身, 祝意青, 等.2011. 青藏高原东缘重力导纳模型均衡异常时空特征[J]. 地球物理学报, 54 (1) : 22–34. DOI:10.3969/j.issn.0001-5733.2011.01.004 |
| [38] | 邓起东, 张维岐.1989. 海原走滑断裂带及其尾端挤压构造[J]. 地震地质, 11 (1) : 1–14. |
| [39] | 付广裕, 祝意青, 高尚华, 等.2013. 川西地区实测自由空气重力异常与EGM2008模型结果的差异[J]. 地球物理学报, 56 (11) : 3761–3769. DOI:10.6038/cjg20131117 |
| [40] | 嘉世旭, 张先康.2005. 华北不同构造块体地壳结构及其对比研究[J]. 地球物理学报, 48 (3) : 611–620. DOI:10.1002/cjg2.700 |
| [41] | 李多, 周仕勇, 陈永顺, 等.2012. 鄂尔多斯地区上地幔岩石圈三维速度结构面波反演研究[J]. 地球物理学报 (5) : 1613–1623. DOI:10.6038/j.issn.0001-5733.2012.05.019 |
| [42] | 李洪强, 高锐, 王海燕, 等.2013. 用近垂直方法提取莫霍面——以六盘山深地震反射剖面为例[J]. 地球物理学报, 56 (11) : 3811–3818. DOI:10.6038/cjg20131122 |
| [43] | 李强, 江在森, 武艳强, 等.2014. 利用 GPS 资料反演海原一六盘山断裂带闭锁程度与滑动亏损分布[J]. 武汉大学学报: 信息科学版, 39 (5) : 575–580. |
| [44] | 杨亭, 傅容珊, 黄金水.2013. 利用Moho地形导纳法(MDDF)反演中国大陆岩石圈有效弹性厚度[J]. 地球物理学报, 56 (6) : 1877–1886. DOI:10.6038/cjg20130610 |
| [45] | 张秉良, 向宏发.2000. 六盘山东麓断裂断层泥的组构特征及其意义[J]. 地震地质, 22 (1) : 47–52. |
| [46] | 周民都, 吕太乙, 张元, 等.2000. 青藏高原东北缘地质构造背景及地壳结构研究[J]. 地震学报, 22 (6) : 645–653. |
| [47] | 郑文俊, 张培震, 袁道阳, 等.2009. GPS观测及断裂晚第四纪滑动速率所反映的青藏高原北部变形[J]. 地球物理学报, 52 (10) : 2491–2508. DOI:10.3969/j.issn.0001-5733.2009.10.008 |
| [48] | 朱仲芬, 陈冬生.1988. 关于 LaCoste-Romberg G 型重力仪几个问题的探讨[J]. 地壳形变与地震, 1 : 004. |
 2016, Vol. 31
2016, Vol. 31


