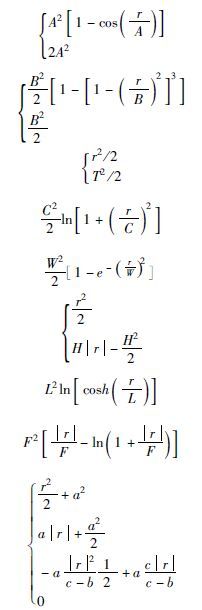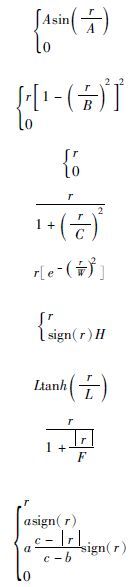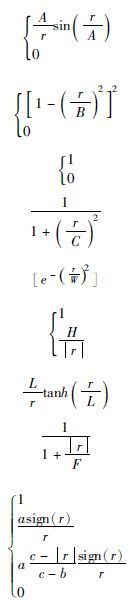扩频激电法是一种通过向大地发送扩频m序列,对测点电位信息进行接收测量的新型频谱激电法.由于m序列具有类似于随机信号的宽频谱特性(赵璧如等,2006;汤井田和罗维斌,2008;罗维斌等,2012;淳少恒等,2014;罗延钟等,2015),扩频激电法可以实现一次发射,同时获得多个频点复电阻率信息,通过计算视极化率、相对相位等参数来进一步获取激电信息.近年来,扩频激电法广泛应用于藏南罗布莎矿区铬铁矿勘探,为控制超过200万吨铬铁矿储量发挥了关键作用(Xi et al.,2013,2014).
但是因为激电法都是在野外通过接地电极来测量电位差,很容易受到大地电流、工业游散电流和高压电力线等干扰.当测区位于生产矿区周边时,尤其会有高幅值的尖峰脉冲干扰持续出现.脉冲噪声是野外电磁探测中经常出现的干扰,其振幅远远大于正常信号与高斯噪声.主要来自于测区附近电动力设备引起的脉冲型游散电流和强天电干扰(娄远清等,1994).脉冲干扰的频率范围非常宽,与扩频激电信号的频谱相互重叠.如果在数据预处理阶段未能对其进行有效压制,则会给后期的复电阻率计算与激电参数求取产生不利影响.
传统的激电数据处理方法主要包括周期叠加(瞿德福和张云尔,1996;崔燕丽,2002;姚红春,2012)与数字滤波(陈儒军,2003;刘春明,2006;李荡等,2011;姚红春,2012).周期叠加可有效压制高斯噪声.当环境中有少量脉冲噪声出现时,也可以通过延长观测时间,增大叠加次数来对其进行压制.但是当环境干扰严重,脉冲噪声在各周期持续出现时,周期均值叠加不再有效.基于傅里叶方法的数字滤波在各种激电观测系统中都有广泛应用,通过设置高通、低通、带通、陷波、梳状等滤波器可对观测数据中的噪声进行压制.但是脉冲噪声的频率与有用信号的频率在很大范围内相互重叠,导致数字滤波去噪效果很不理想.另外平滑滤波和小波分析等也被用于激电叠后数据的噪声压制(刘春明,2006).但是,当脉冲干扰严重时,会带来信号的失真.
应用统计分析方法压噪除平均值法外,还有中值法、截割均值法、设置阈值剔除异常点等方法(王宏禹,2008).中值法虽然对脉冲噪声也有一定的抑制作用,但其并没有进行叠加,保留的仍是受随机干扰影响的采样点.截割均值法需要人为设置截割比例,当截割比例过大时,损失有用信号,截割比例过小时,噪声压制不彻底.设置阈值剔除异常点的方法通常要对整体的数据分布有一个先验了解,根据“3倍标准差”准则,设置阈值,剔除异常点.但“3倍标准差”方法在求取平均值与标准差的同时就已经受到了原始数据中离群值的影响,所以该方法稳健性并不好.
稳健统计是一个广泛的定义(Huber, 1981).稳健统计方法在地球物理信号处理中已得到较广泛的应用,除了在天然源MT阻抗估计中已成为常规处理方法外(Egbert and Booker, 1986;Chave and Thomson, 1989).近年来在可控源电磁(Streich et al.,2013)、瞬变电磁(Buselli and Cameron, 1996)、地震信号监测(Lyubushin Jr, 2002)等数据处理中都有了进一步的应用.本文针对传统处理方法在压制脉冲干扰中的不足,提出将稳健统计方法用于扩频激电数据预处理,以压制脉冲噪声,提高数据预处理质量.主要包括两方面的应用:一是将稳健最小二乘回归用于去趋势项处理.二是将稳健M估计用于周期叠加.通过选用合适的影响函数与迭代算法,以抑制原始数据中由脉冲干扰引起的离群值对预处理结果的影响.将其应用于甘肃白银地区实测的扩频激电数据预处理,对计算结果及误差分布进行对比分析,发现稳健统计方法对高斯噪声与脉冲噪声都有较好的压制作用.相比于均值叠加,稳健统计可以降低计算误差,提高数据预处理质量.同时提高计算结果随叠加次数的收敛速度,节省观测时间.
1 稳健统计稳健或鲁棒(Robust)性的英文含义是强壮、健康、坚韧、能经受住逆境考验.获得观测数据的过程中由于误差和干扰的影响,数据中不可避免地存在反常值,称为离群值(outlier)(Huber, 1981).有些统计方法对离群值相当敏感,个别离群值的出现就会使统计结果发生较大的变化,导致不合理甚至完全错误的结论.稳健统计方法基本思想就是实现一种方法能够合理地处理假定模型,降低模型中少量异常点对统计结果引起的偏离(Huber, 1981;王宏禹,2008).
1.1 稳健M估计基本原理Huber(1964) 提出稳健M估计法,类似于最大似然估计.在用统计方法解决问题时,首先要通过多次观测得到原始数据{yi},其中yi=θ+ξi,i=1,2,3,4…N, ξ1,ξ2,ξ3,…,ξN为误差序列.为了由多次观测值y1,y2,y3,…,yN估计真实值θ,根据最大似然估计准则(Fisher, 1950;王宏禹,2008),选用分段连续的可微凸函数ρ(z)构造目标函数为



如果在上述过程中,若目标函数选为:ρ(z)=z2/2,则ψ(z)=z, 可求得: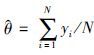 .统计过程成为常见的最小二乘估计,即平均值法.平均值法受观测数据中离群值的影响很大.
.统计过程成为常见的最小二乘估计,即平均值法.平均值法受观测数据中离群值的影响很大.
稳健M估计的基本原理就是令ψ(x)为一个有界奇函数.即:ψ(-x)=-ψ(x),且当x很小时接近于ψ(x)=x, 但是当x的值很大时,函数就变成一个常量或者衰减到0.从而实现对于偏离位置参数的观测点给予低权值,降低其对统计过程的影响.在稳健M估计中,ψ(x)函数有多种类型(Holland and Welsch, 1977),如:“Andrews”,“Beaton”,“Talwar”,“Cauchy”,“Welsch”,“Huber”,“Logistic”,“Fair”,“Hampel”等,各ψ函数形式见表 1.
|
|
表 1 稳健M估计影响函数与稳健回归权重函数 Table 1 The influence function of robust M estimate and weight function of robust regression |
通过求解非线性方程(3) 可以得到稳健估值θ.Huber(1981) 给出了两种较为简单的求解算法:改进残差法(Modified Residuals)和改进权重法(Modified Weights).
(1) 改进残差法(Modified Residuals)
对于该迭代算法,首先定义初值,令观测序列{yi,i=1,2,…,N}的中值为位置参数初始值θ0,中位数绝对离差为尺度参数初始值σ0,即:



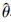 .Huber对该迭代算法的收敛性予以了证明.
.Huber对该迭代算法的收敛性予以了证明.
(2) 改进权重法(Modified Weights)
同样利用公式(4) 和(5) 定义位置参数和尺度参数的初始值.迭代公式定义为


除了上述两种迭代算法,Huber(1981) 还给出了位置参数和尺度参数的联合M估计.Englund等(1988) 也提出了在动态测量数据中求解M估计位置参数和尺度参数的递归算法.算法比较复杂,本文不再赘述.
1.2 稳健最小二乘回归基本原理稳健最小二乘回归(Robust least squares regression)是稳健M估计的进一步发展,可用于二元或多元线性回归(Holland and Welsch, 1977;Street et al.,1988).
对于含观测误差ε的回归模型:

回归估计就是求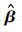 令下式目标函数最小,公式为
令下式目标函数最小,公式为

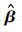 应满足公式为
应满足公式为
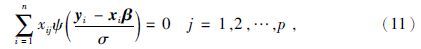
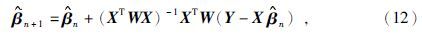
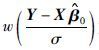 为对角线的n×n对角方阵.权重函数为M估计中的影响函数ψ(r)与自变量的比值,公式为
为对角线的n×n对角方阵.权重函数为M估计中的影响函数ψ(r)与自变量的比值,公式为

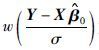 ,确定权重矩阵W, 再利用公式(12) 迭代求解参数
,确定权重矩阵W, 再利用公式(12) 迭代求解参数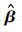 .与稳健M估计类似,根据目标函数ρ和影响函数ψ的不同,权重函数有很多种,具体形式见表 1.可以证明迭代重加权算法与M估计的改进权重迭代法实际上是一致的,本文不再赘述.
.与稳健M估计类似,根据目标函数ρ和影响函数ψ的不同,权重函数有很多种,具体形式见表 1.可以证明迭代重加权算法与M估计的改进权重迭代法实际上是一致的,本文不再赘述.
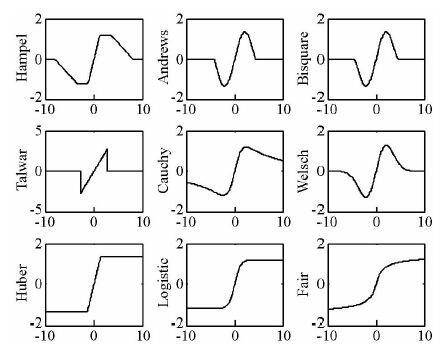
表 1中,A、B、T、C、W、H、L、F、a、b、c等为常数,称为调节常数(Holland and Welsch, 1977).取Holland和Welsch(1977) 建议的各调节常数,绘制影响函数ψ(x)的曲线,如图 1所示.各种ψ(x)函数虽然形式不同,但都为有界奇函数.
|
图 1 不同影响函数ψ的函数曲线 Fig. 1 Function curve of different Influence function |
为了在稳健统计中选择最佳的影响函数与迭代算法.首先利用计算机产生模拟噪声数据进行测试.因为迭代重加权最小二乘算法与改进权重法是一致的.所以只需对比M估计中改进残差法和改进权重法在各种不同影响函数下的效果即可.模拟噪声由两部分合成,一部分代表均值θ0近似为0,标准差σ0近似为1的高斯噪声,另一部分代表脉冲噪声,脉冲噪声的标准差从0到10变化,均值从0到5变化.脉冲噪声可以看做背景高斯噪声中的离群值,脉冲噪声在总的合成噪声信号中所占的百分比值从0到35%变化,相当于背景噪声中离群值所占的比例依次增大.
分别利用改进残差法与改进权重法对模拟噪声数据进行叠加估计,然后对估计结果进行对比分析.估计结果的绝对值|θi|越接近0,证明对脉冲噪声与高斯噪声的压制效果越好.下表 2给出了当环境噪声中脉冲信号出现的比例逐渐增大时,采用改进残差法迭代,各种不同影响函数的估计结果.下表 3给出了采用改进权重法迭代时,各种不同影响函数的估计结果.其中“Mean”,“Median”分别代表传统的均值法与中值法估计结果.
|
|
表 2 采用改进残差法迭代时各种不同影响函数的M估计结果 Table 2 The estimator of different influence functions using Modified Residuals |
|
|
表 3 采用改进权重法迭代时各种不同影响函数的M估计结果 Table 3 The estimator of different influence functions using Modified Weights |
通过对比表 2和表 3,可以发现,平均值法估计结果受离群值的影响最大,随着离群值比例增大,估计结果严重偏离了0值.对于改进残差法迭代,“Huber”“Logistic”“Fair”三种函数的估计误差最大,效果不如中值法好.而其他六种函数估计效果好于中值法.其中,影响函数“Talwar”的估计结果最接近0,受离群值影响最小.对于改进权重法迭代,“welsch”函数估计误差最小,受离群值影响最小.“welsch” “Cauchy”两种函数的估计效果都好于中值法,其他函数估计误差略大于中值法.
其实离群值对估计结果的影响,与ψ(x)函数的形态有很大关系.“Hampel”“Andrews” “Bisquare”“Talwar”四种函数当x的值很大时,函数直接等于0. “Cauchy”“Welsch” 两种函数当x的值很大时,函数逐渐趋近于0,但并不完全等于0. “Huber”“Logistic”“Fair”三种函数当x的值很大时,变成一个常量.三类影响函数对离群值的抑制程度不同,所以在不同迭代算法下出现了不同的效果.
通过对模拟数据进行测试,可以得出,对于稳健M估计采用该进残差法进行迭代,影响函数选用“Talwar”,降噪效果更佳.对于稳健最小二乘回归,由于其是采用迭代重加权算法,类似于稳健M估计中的改进权重法,所以选用“Welsch”函数效果更佳.
2 实际资料应用湖南强军科技公司的85321A-SIP分布式激电仪采集站,采取大规模分布式同步采集激电数据.2014年在甘肃白银地区获得了多周期观测的扩频激电实测数据(Liu et al.,2015).测区位于正在生产的矿区周边,高幅值的尖峰脉冲干扰持续出现.最大的干扰源为钻井钻机,其采用大功率发电机供电,位于测区附近.另一个干扰源是金属冶炼厂,在测区附近有3家大型有色金属冶炼厂,24小时昼夜不停地工作.除此之外,矿山附近的人员活动以及大型机组设备等也带来严重的噪声干扰.侧线旁钻机施工如下图 2所示:

|
图 2 大功率钻机正在测线旁开钻 Fig. 2 Drilling machine near data acquisition station |
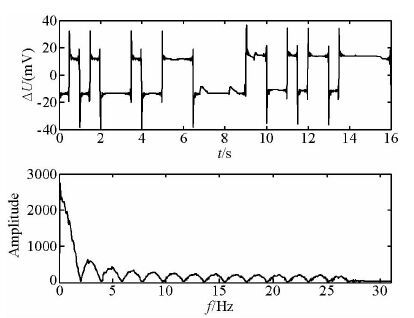
此次观测发送电流为5阶扩频m序列,码元宽度为0.5 s, 采样频率为64 Hz, 每周期16 s.每测点观测160周期,观测时间超过40分钟.供电电流幅值8A左右.取干扰严重的一个测点的实测数据利用稳健统计方法进行处理.下图 3为扩频激电实测数据一个周期内的时间域波形与振幅谱.
|
图 3 扩频激电观测电压时间域波形与振幅谱 Fig. 3 Observed voltage signal of spread spectrum induced polarization in time domain and frequence domain |
稳健最小二乘回归可用于扩频激电数据的线性趋势项消除.实测电压信号随时间延长会产生漂移,这就是趋势项.去趋势项是扩频激电数据预处理必不可少的一项内容.产生趋势项的原因主要有:电极极差变化,自然电位,放大器零漂,大地电流,环境温度变化,其他不明低频干扰等.趋势项会干扰实测数据傅里叶变换的结果及相关参数的计算.去除趋势项的方法主要有:平均值法、线性拟合法、多项式拟合法等(陈儒军,2003;刘春明,2006).
在扩频激电数据预处理中主要用到平均值法和线性拟合法,多项式拟合只用在某些特殊情况下.首先令原始数据整体减去平均值以消除直流分量.再利用Robust最小二乘回归对各采样点进行拟合,得到拟合直线的参数.在原始测量数据中减去拟合直线对应的线性成分,消除线性趋势项.下面分别将普通最小二乘回归与稳健最小二乘回归应用于实测的扩频激电数据去除线性趋势项,以说明Robust回归的效果.Robust回归采用迭代重加权算法,权重函数采用“Welsch”.
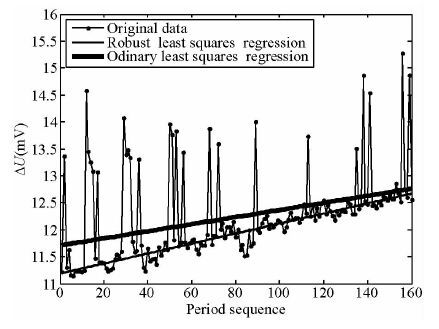
取某测点多周期实测数据.图 4为同一个采样点在不同周期中的观测值,原则上,不同周期对同一个点的观测值应该是相同的.或者由于随机噪声的存在,应该是围绕真实值上下波动.但是由于线性漂移的存在,除了上下波动,还存在线性趋势项.而且因为该测点脉冲干扰严重,采样点中有大量离群值.普通最小二乘线性拟合,拟合结果受离群值影响很大.去趋势项不合理,对后续数据处理产生不利影响.Robust最小二乘拟合,拟合结果受离群值影响较小.
|
图 4 同一采样点在不同周期中的观测值与不同方法线性趋势项拟合 Fig. 4 The observed value of a sample in different periods and the linear trend fitting by different methods |
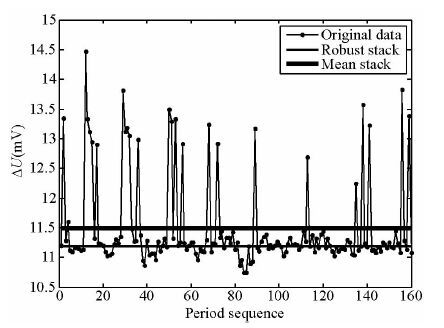
利用稳健最小二乘回归去除趋势项之后,线性分量已经消除,但离群值依然存在.这时对该测点数据进行周期叠加.Robust周期叠加就是利用前述的稳健M估计,通过改进残差法进行迭代,ψ(r)函数选用“Talwar”函数.处理结果见图 5.可以看到,平均值周期叠加,叠加结果受离群值影响很大,已经偏离了真实值.Robust周期叠加,叠加结果受离群值影响很小.说明稳健M估计对高斯随机噪声和尖峰脉冲噪声都有较好的压制效果.由图 5也可以看出,脉冲干扰在整个观测时间内持续出现,而且都是幅值远大于正常数据的正值.在这种情况下,对于常规均值叠加,单靠延长观测时间,增大叠加次数无法压制脉冲干扰,引入稳健叠加方法可以抑制脉冲干扰引起的离群值对最终结果的影响.
|
图 5 同一采样点在去趋势项之后平均值叠加与Robust叠加对比 Fig. 5 The comparison of mean stack and Robust stack after reducing linear trend |
频率域激电法的复电阻率计算公式为

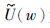 为观测电压频谱,
为观测电压频谱,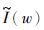 为发送电流频谱.
为发送电流频谱.
对于扩频激电实测原始数据,先对原始数据整体减去平均值以去除直流分量.再利用Robust最小二乘回归对各采样点做去趋势项处理.然后可以在时间域对电压数据和电流数据进行Robust叠加,然后对叠加后的电压、电流进行傅里叶变换,再通过公式(13) 计算复电阻率的振幅和相位,此即为时间域Robust方法.也可以先将各周期电压、电流道原始数据进行傅里叶变换,然后通过公式(13) 计算复电阻率的振幅和相位,在频率域对复电阻率相位、幅值进行Robust周期叠加,此即为频率域Robust方法.虽然扩频激电的频谱比较丰富,但为了保证信号强度,只取复电阻率频谱在1/16 Hz~1 Hz范围内(前2-17个样点)的值.每4个点做一次平均,作为对应于0.1563 Hz、0.4063 Hz、0.6563 Hz、0.9063 Hz四个频点的复电阻率计算结果.
同时为了对数据质量有一个直观评价.取同一测点前后重复观测所得两批数据处理结果的相对误差为计算误差.复电阻率计算结果如下表所示:
在表 4中后标1、2、3的各量分别表示常规平均值叠加方法、时间域Robust叠加方法、频率域Robust叠加方法所得计算结果.
|
|
表 4 某测点复电阻率相位与幅值计算结果 Table 4 The calculated results of complex resistivity in a survey point |
Phase(mrad)表示所得复电阻率相位值.
Error(mrad)表示复电阻率相位值计算误差,取绝对误差.
|ρs1|(Ω·m)表示所得复电阻率幅值.
Relative Error(%)表示复电阻率幅值计算误差,取相对误差.
由表 4可以看出,常规算法计算复电阻率,得相位误差在4 mrad以内,幅值误差在0.4%以内.采用Robust方法后,可以进一步降低复电阻率相位与幅值的计算误差,相位误差降到2 mrad以内,幅值误差降到0.2%以内.相对而言,相位的处理效果比幅值明显,频率域Robust叠加比时间域Robust叠加效果明显.把稳健回归和稳健叠加引入到扩频激电数据预处理有利于提高数据预处理质量.
2.3.2 计算结果随叠加次数收敛情况
此次甘肃白银地区实测扩频激电数据,电流道和电压道数据共有160个周期.前面对比了叠加160次时,复电阻率的计算结果及计算误差.下面依次对比叠加10次、20次、30次、40次、50次、60次、70次、80次、90次、100次、110次、120次、130次、140次、150次、160次时,利用不同方法所得复电阻率在4个频点上对应的计算结果及计算误差.来研究计算结果随叠加次数的收敛情况.图 6,图 7,图 8,图 9给出了不同处理方法下,各频点复电阻率的相位、幅值计算结果及误差棒分布随叠加次数的收敛情况.
图 6~图 9,分别对比了在频点f=0.1563 Hz、 f=0.4063 Hz、 f=0.6563 Hz、f=0.9063 Hz时,复电阻率相位、幅值计算结果和计算误差随叠加次数的收敛情况.因为整个测区脉冲干扰非常严重.可以发现,均值叠加计算结果收敛情况较差,不同叠加次数时,计算结果也不相同,说明传统处理方法受噪声干扰影响较大.相对而言,时间域Robust叠加方法和频率域Robust叠加方法,无需人为设置阈值,克服了传统方法的不稳健性,可以自动原始根据数据分布情况,分配权重,对离群值进行降权或剔除之后再进行叠加平均,如此既可以压制尖峰脉冲噪声,又可以压制高斯随机噪声,计算结果随叠加次数的收敛情况较好.
3.1 本文将稳健统计引入扩频激电数据预处理,以压制常规均值叠加和数字滤波无法消除的尖峰脉冲噪声.介绍了稳健M估计与稳健最小二乘回归的基本原理.通过模拟数据对不同影响函数和迭代算法的应用效果进行了测试,针对脉冲干扰选取了最佳的影响函数和迭代算法.将稳健统计方法应用于实测的受强脉冲干扰影响的扩频激电数据处理,对计算结果和误差分布进行对比分析.试验结果表明:稳健最小二乘回归可有效用于扩频激电数据的线性趋势项消除,以抑制脉冲干扰引起的离群值对拟合结果带来的偏差.稳健M估计可有效用于扩频激电数据的周期叠加,其对高斯随机噪声与尖峰脉冲噪声都有较好的压制作用.对于传统均值叠加,在脉冲干扰严重的地区,单靠延长观测时间,增大叠加次数难以实现降噪效果.将稳健统计引入扩频激电数据预处理,有两方面的优势:一是可降低复电阻率计算误差,提高数据预处理质量.二是可有效提高计算结果随叠加次数的收敛速度,节省观测时间. 3.2 虽然稳健统计方法在此次扩频激电实测数据中取得了明显的效果.但是其主要是针对于尖峰脉冲干扰.当原始数据主要是受高斯随机干扰时,稳健统计相对于普通最小二乘并没有明显优势.而且,当测区干扰特别严重时.仅靠在数据预处理中引入稳健统计还是不够的.需要研究更多的后续数据处理方法以提高数据质量.另外,扩频激电法所用m序列不仅具有宽频谱特性,还具有良好的自相关、互相关特性.可以进一步研究基于相关检测等技术的扩频激电数据处理方法.
致 谢 感谢国防科技大学信息地球物理协同创新中心和湖南强军科技有限公司吴宏、姚红春、申瑞杰、石红华、仇洁婷等在扩频激电方法、仪器和数据处理研究方面给予的帮助.
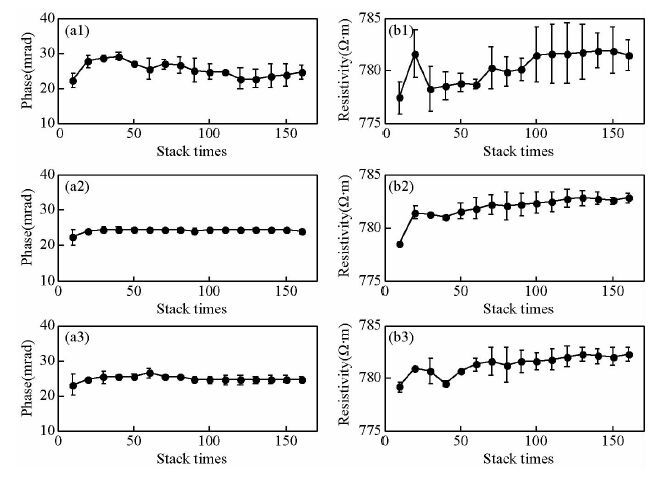
图 6 频点f=0.1563 Hz对应复电阻率的相位、幅值计算结果随叠加次数收敛情况
(a1)采用平均值叠加所得相位计算结果;(b1)采用平均值叠加所得幅值计算结果;(a2)采用时间域Robust叠加所得相位计算结果;(b2)采用时间域Robust叠加所得幅值计算结果;(a3)采用频率域Robust叠加所得相位计算结果;(b3)采用频率域Robust叠加所得幅值计算结果.
Fig. 6 Convergence of complex resistivity with stack times increasing at f=0.1563 Hz
(a1)Phase by mean stack;(b1)Amplitude by mean stack;(a2)Phase by Robust stack in time domain; (b2)Amplitude by Robust stack in time domain;(a3)Phase by Robust stack in frequency domain; (b3)Amplitude by Robust stack in frequency domain.
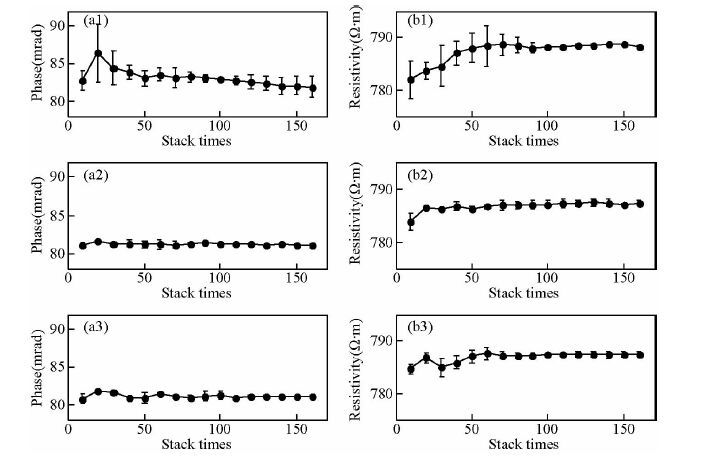
图 7 频点f=0.4063 Hz对应复电阻率的相位、幅值计算结果随叠加次数收敛情况
(a1)采用平均值叠加所得相位计算结果;(b1)采用平均值叠加所得幅值计算结果;(a2)采用时间域Robust叠加所得相位计算结果;(b2)采用时间域Robust叠加所得幅值计算结果;(a3)采用频率域Robust叠加所得相位计算结果;(b3)采用频率域Robust叠加所得幅值计算结果.
Fig. 7 Convergence of complex resistivity with stack times increasing at f=0.4063 Hz
(a1)Phase by mean stack;(b1)Amplitude by mean stack;(a2)Phase by Robust stack in time domain;(b2)Amplitude by Robust stack in time domain;(a3)Phase by Robust stack in frequency domain;(b3)Amplitude by Robust stack in frequency domain.
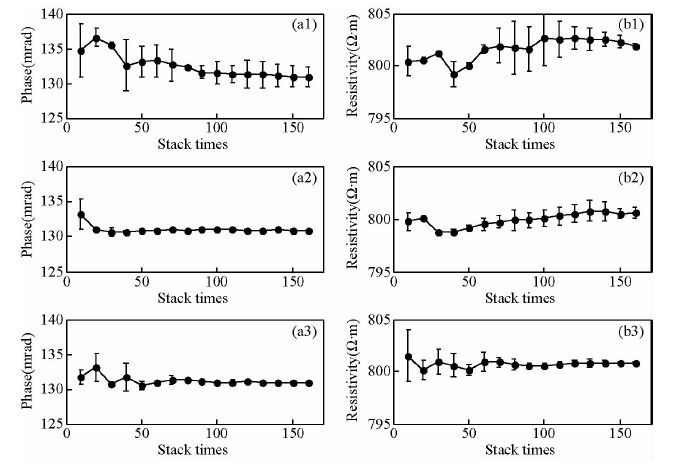
图 8 频点f=0.6563 Hz对应复电阻率的相位、幅值计算结果随叠加次数收敛情况
(a1)采用平均值叠加所得相位计算结果;(b1)采用平均值叠加所得幅值计算结果;(a2)采用时间域Robust叠加所得相位计算结果;(b2)采用时间域Robust叠加所得幅值计算结果;(a3)采用频率域Robust叠加所得相位计算结果;(b3)采用频率域Robust叠加所得幅值计算结果.
Fig. 8 Convergence of complex resistivity with stack times increasing at f=0.6563 Hz
(a1)Phase by mean stack;(b1)Amplitude by mean stack;(a2)Phase by Robust stack in time domain;(b2)Amplitude by Robust stack in time domain;(a3)Phase by Robust stack in frequency domain;(b3)Amplitude by Robust stack in frequency domain.
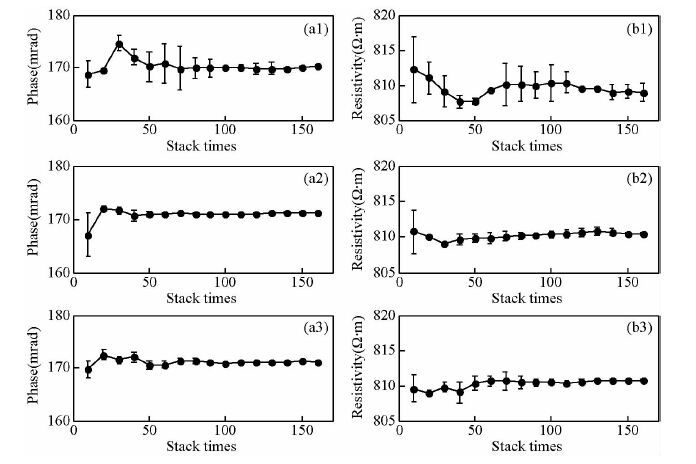
图 9 频点f=0.9063 Hz对应复电阻率的相位、幅值计算结果随叠加次数收敛情况
(a1)采用平均值叠加所得相位计算结果;(b1)采用平均值叠加所得幅值计算结果;(a2)采用时间域Robust叠加所得相位计算结果;(b2)采用时间域Robust叠加所得幅值计算结果;(a3)采用频率域Robust叠加所得相位计算结果;(b3)采用频率域Robust叠加所得幅值计算结果.
Fig. 9 Convergence of complex resistivity with stack times increasing at f=0.9063 Hz
(a1)Phase by mean stack;(b1)Amplitude by mean stack;(a2)Phase by Robust stack in time domain;(b2)Amplitude by Robust stack in time domain;(a3)Phase by Robust stack in frequency domain;(b3)Amplitude by Robust stack in frequency domain.
| [1] | Buselli G, Cameron M. 1996. Robust statistical methods for reducing sferics noise contaminating transient electromagnetic measurements[J]. Geophysics, 61(6): 1633-1646. |
| [2] | Chave A D, Thomson D J. 1989. Some comments on magnetotelluric response function estimation[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 94(B10): 14215-14225. |
| [3] | Chen R J. 2003. The study on pseudo-random multi-frequency electromagnetic prospecting system (in Chinese)[Ph. D. thesis]. Changsha: Central South University. |
| [4] | Chun S H, Chen R J, Geng M H. 2014. Review of the pseudo-random m sequence and its application in electrical prospecting of exploration geophysics[J]. Progress in Geophysics (in Chinese), 29(1): 439-446, doi: 10.6038/pg20140164. |
| [5] | Cui Y L. 2002. The study on data processing of pseudo-random multi-frequency electromagnetic prospecting system (in Chinese)[Ph. M. thesis]. Changsha: Central South University. |
| [6] | Egbert G D, Booker J R. 1986. Robust estimation of geomagnetic transfer functions[J]. Geophysical Journal International, 87(1): 173-194. |
| [7] | Englund J E, Holst U, Ruppert D. 1988. Recursive M-estimators of location and scale for dependent sequences[J]. Scandinavian Journal of Statistics, 15(2): 147-159. |
| [8] | Fisher R A. 1950. On the Mathematical Foundations of Theoretical Statistic[M]. New York: Jone Wiley & Sons. |
| [9] | Holland P W, Welsch R E. 1977. Robust regression using iteratively reweighted least-squares[J]. Communications in Statistics-Theory and Methods, 6(9): 813-827. |
| [10] | Huber P J. 1964. Robust estimation of a location parameter[J]. The Annals of Mathematical Statistics, 35 (1): 73-101. |
| [11] | Huber P J. 1981. Robust Statistics[M]. New York: John & Sons Press. |
| [12] | Ilyichev P V, Bobrovsky V V. 2015. Application of pseudonoise signals in systems of active geoelectric exploration (Results of mathematical simulation and field experiments)[J]. Seismic Instruments, 51(1): 53-64. |
| [13] | Li D, Li Z H, Zeng X. 2011. Receiver of dual-frequency IP instrument[J]. Journal of Electronic Measurement and Instrument (in Chinese), 25(12): 1078-1085. |
| [14] | Liu C M. 2006. The study about multiparameter spectrum pseudo-random IP method (in Chinese)[Ph. D. thesis]. Changsha: Central South University. |
| [15] | Liu W Q, Chen R J, Wu H, et al. 2015. High precision FDIP exploration in productive mine with strong EM interference[C].//Symposium on the Application of Geophysics to Engineering and Environmental Problems. Austin, Texas, USA: SEG, 65-73. |
| [16] | Luo W B, LI Q C, Tang J T. 2012. Coded source electromagnetic sounding method[J]. Chinese Journal of Geophysics (in Chinese), 55(1): 341-349, doi: 10.6038/j.issn.0001-5733.2012.01.035. |
| [17] | Luo Y Z, Lu Z G, Sun G L, et al. 2015. New generation of instruments for electrical and electromagnetic prospecting-instruments using pseudo random signal[J]. Progress in Geophysics (in Chinese), 30(1): 411-415, doi: 10.6038/pg20150159. |
| [18] | Lyubushin Jr A A. 2002. A robust wavelet-aggregated signal for geophysical monitoring problems[J]. Izvestiya Physics of the Solid Earth, 38(9): 745-755. |
| [19] | Qu D F, Zhang Y E. 1996. Outline of induced polarization industry standard and level of instruments at home and abroad[J]. Foreign Geoexploration Technology (in Chinese), (6): 12-22. |
| [20] | Street J O, Carroll R J, Ruppert D. 1988. A note on computing robust regression estimates via iteratively reweighted least squares[J]. The American Statistician, 42(2): 152-154. |
| [21] | Streich R, Becken M, Ritter O. 2013. Robust processing of noisy land-based controlled-source electromagnetic data[J]. Geophysics, 78(5): 237-247. |
| [22] | Tang J T, Luo W B. 2008. Pseudo-random electromagnetic exploration based on Invert-Repeated m-Sequence correlation identification[J]. Chinese Journal of Geophysics (in Chinese), 51(4): 1226-1233, doi: 10.3321/j.issn:0001-5733.2008.04.034. |
| [23] | Wang H Y. 2008. Signal Processing method and Application (in Chinese)[M]. Beijing: China Machine Press. |
| [24] | Xi X L, Yang H C, He L F, et al. 2013. Chromite mapping using induced polarization method based on spread spectrum Technology[C].//Symposium on the Application of Geophysics to Engineering and Environmental Problems. Austin, Texas, USA: SEG, 13-19. |
| [25] | Xi X L, Yang H C, Zhao X F, et al. 2014. Large-scale distributed 2D/3D FDIP system based on Zigbee network and GPS[C].//Symposium on the Application of Geophysics to Engineering and Environmental Problems. Austin, Texas, USA: SEG, 130-139. |
| [26] | Yao H C. 2012. The design and implementation of distributed 3D-SIP acquisition system (in Chinese)[Ph. M. thesis]. Changsha: Central South University. |
| [27] | Zhao B R, Zhao J, Zhang H K, et al. 2006. The PS100 high precision earth-electricity instrument system (IP to IP) with controllable source-application of CDMA technology to the measurement of earth-resistivity for the first time[J]. Progress in Geophysics (in Chinese), 21(2): 675-682. |
| [28] | 陈儒军. 2003. 伪随机多频电磁法观测系统研究[博士论文]. 长沙: 中南大学. |
| [29] | 淳少恒, 陈儒军, 耿明会. 2014. 伪随机m序列及其在电法勘探中的应用进展[J]. 地球物理学进展, 29(1): 439-446, doi: 10.6038/pg20140164. |
| [30] | 崔燕丽. 2002. 伪随机多功能多频观测系统的数据处理研究[硕士论文]. 长沙: 中南大学. |
| [31] | 李荡, 李志华, 曾信. 2011. 双频激电仪接收机[J]. 电子测量与仪器学报, 25(12): 1078-1085. |
| [32] | 刘春明. 2006. 伪随机激电多参数谱法研究[博士论文]. 长沙: 中南大学. |
| [33] | 罗维斌, 李庆春, 汤井田. 2012. 编码电磁测深[J]. 地球物理学报, 55(1): 341-349, doi: 10.6038/j.issn.0001-5733.2012.01.035. |
| [34] | 罗延钟, 陆占国, 孙国良,等. 2015. 新一代电法勘查仪器-伪随机信号电法仪[J]. 地球物理学进展, 30(1): 411-415, doi: 10.6038/pg20150159. |
| [35] | 瞿德福, 张云尔. 1996. 概述我国激电仪行业标准和国内外仪器水平[J]. 国外地质勘探技术, (6): 12-22. |
| [36] | 汤井田, 罗维斌. 2008. 基于相关辨识的逆重复m序列伪随机电磁法[J]. 地球物理学报, 51(4): 1226-1233, doi: 10.3321/j.issn:0001-5733.2008.04.034. |
| [37] | 王宏禹. 2008. 信号处理方法与应用[M]. 北京: 机械工业出版社. |
| [38] | 姚红春. 2012. 三维谱激电分布式采集系统的设计与实现[硕士论文]. 长沙: 中南大学. |
| [39] | 赵璧如, 赵健, 张洪魁,等. 2006. PS100型IP到端可控源高精度大地电测仪系统-CDMA技术首次在低电阻率测量中的应用[J]. 地球物理学进展, 21(2): 675-682. |
 2016, Vol. 31
2016, Vol. 31