本世纪以来,瞬态多道瑞利面波勘探方法(Park et al.,1999;Aki and Richards, 2002)以其可在复杂干扰波场条件下能够有效的分离和提取瑞利面波信息的能力,从而具有的高勘探精度和勘探效率,在浅层工程地质勘探和工程质量检测等领域中得到了广泛应用.实验室物理模拟研究(张碧星和鲁来玉,2005;鲁来玉等,2006)是认识和发展瞬态多道瑞利面波理论和方法的主要手段之一.瑞利面波实验室物理模拟主要采用超声实验技术(赵鸿儒等,1986;彭一民和孙进忠,1987;孙进忠等,1997),即在超声波频段范围内,采用小尺度模型进行模拟实验.显然,由于模型尺度的有限性,难以满足基于理想半无限空间条件下的瞬态多道瑞利面波勘探理论和方法.因此,研究模型尺度对瑞利面波实验数据的影响特征以及潜在的消除方法,将促进瞬态多道瑞利面波勘探模型实验的理论和方法的发展和完善.本文应用商用Abaqus有限元数值模拟软件,基于均匀介质和两层介质模型,分析和研究了实际三维条件下有限尺度模型的瑞利面波波场特征,及模型尺度的主要影响因素,提出了基于视速度τ-p滤波,分离来自侧边界瑞利面波干扰的方法.本文最后以一瑞利面波物理模型的实际观测数据的实例分析,验证了本文提出的问题和解决方案的可行性.
1 数值模拟分析为较系统的分析模型尺度的影响,本节首先以3个不同宽度的均匀介质的三维数值模型,研究了简单条件下模型尺度影响因素;然后基于3个不同层厚的两层介质模型,分析了复杂条件下模型尺度影响因素.并针对模型尺度影响因素特征,提出了在不改变模型尺度条件下,运用τ-p变换的分离模型尺度影响因素的处理方法.
1.1 均匀介质模型 1.1.1 模型和观测参数基于实验室中常用的模型材料,本文主要采用了花岗岩和有机玻璃两种材料的物性参数进行数值模拟建模,具体材料参数见表 1.
|
|
表 1 模型材料参数 Table 1 Model material parameters |
依据表 1中的花岗岩模型材料参数,建立了3个均匀介质数值模型,其长度和厚度(或深度)相同,但模型的宽度不同,具体模型尺度参数见表 2.数值模拟中均采用和下一节物理模型实验中激发声源相近主频——即主频为48 kHz的雷克子波作为波场激发源.由模型参数可计算,对于两类材料的模型,激发的面波主波长分别为5 cm和3 cm左右,远小于上述均匀介质模型的9 cm厚度.因此,对于瑞利面波的传播,建立的数值模型在深度尺度上是可视为均匀介质模型的.在综合考虑近场效应、空间假频影响和三维模拟的有限元计算量问题后,选用了如图 1所示的瞬态多道瑞利面波实验观测排列,以及1.024 ms采样窗长,0.25 μs采样间隔的观测参数.
|
|
表 2 均匀介质模型尺度 Table 2 The size parameters of homogeneous medium models |
|
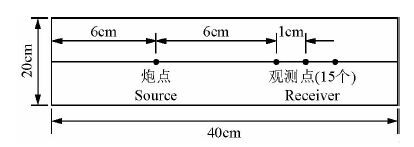
图 1 花岗岩模型观测排列示意图 Fig. 1 The observation layout on the top surface of the granite model |
分别对这表 2中的三个花岗岩参数的均匀介质数值模型进行模拟计算,以各模型模拟结果的垂直分量的波场快照和剖面记录为数据基础,分析了有限尺度模型侧边界对瑞利面波传播的影响.不失一般性,以图 2所示的模型1观测表面上的波场垂直位移数据的波场快照进行分析.
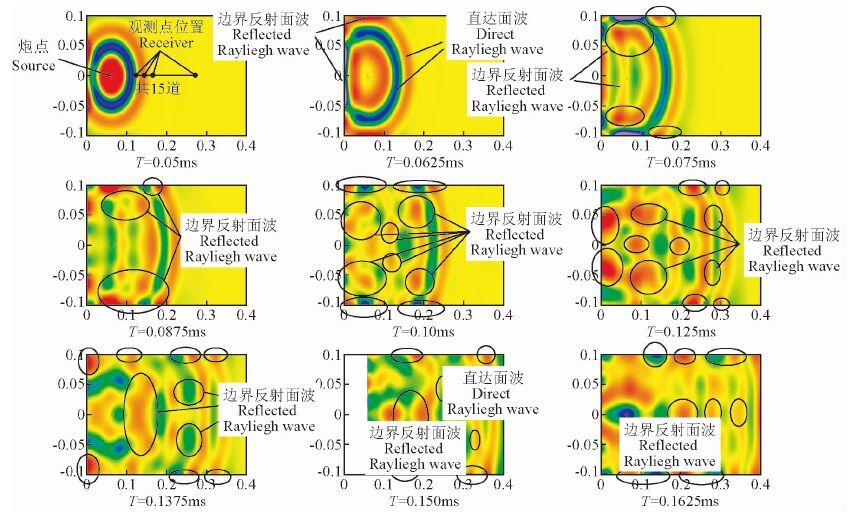
图 2显示,由点震源激发的瑞利面波以柱面波的波阵面向外传播,当面波传播到模型侧边界时,部分能量将被反射回来,导致瑞利面波波场传播特征复杂化.首先分析与观测排列平行的两侧边界的影响.由图可看到,由点源激发的直达面波与来自侧边界反射的面波将先后到达观测排列位置.如果模型宽度较小,就会导致直达面波和侧边界反射的面波先后到达观测排列的时间间隔较短,观测排列记录的面波强能量会是这两类面波在时间上的叠加,而不是只有均匀半无限介质假设条件下的直达面波.特别应注意的是:当观测排列位于模型的中心轴线上时,来自两侧边界的反射面波在观测排列处是相互干涉的,这将进一步增大记录处来自侧边界的反射面波干扰复杂性.但这种侧边界反射面波不同于直达面波的线性时距关系,其具有双曲的时距关系,因此表现远为更高的视速度.此外,图 2中也可看出,来自观测排列两端的界面也会产生反射面波.来自左端近源点侧的边界反射面波相当于新震源激发的直达面波,其具有和由震源激发的直达面波相似的波场传播特征.来自右端远离源点侧的边界反射面波也相当于新震源激发的直达面波,但其传播方向相反.因此,在有限尺度模型的模拟实验中,观测排列记录到的不仅是半无限空间假设条件下的直达面波,也将不可避免的记录到来自侧边界的反射面波.这种面波波场的复杂叠加记录,显然不满足常规的二维傅里叶变换(或频率-波数域变换)中依据在半无限空间传播的直达面波的图象能量极值提取瑞利面波频散曲线的假设条件.
|
图 2 模型1观测表面上的垂直分量波场快照 Fig. 2 The wave field snapshots of the vertical components on the model surface |
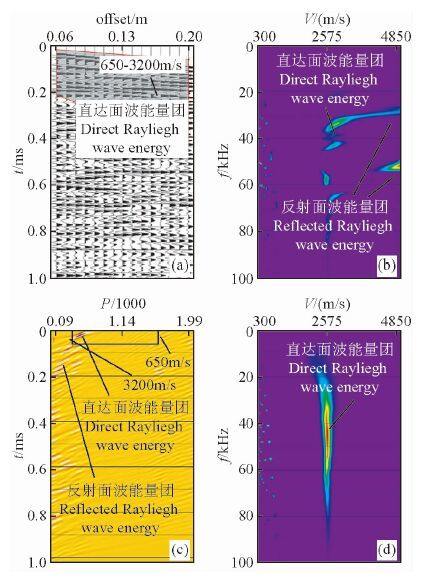
图 3a,4a, 5a分别显示了模型1,2,3数值模拟单炮观测排列记录的垂直分量剖面.由图可识别出直达面波初至到达时间,但由于来自边界的反射面波的叠加,后续的面波记录波形十分复杂.采用常规的视速度开窗滤波(单炮记录剖面中的阴影区)对各模型的单炮记录进行干扰波切除处理,再采用二维傅里叶变换将时间-距离(t-x)域中的单炮记录转换到频率-速度(f-v)域中(张碧星等,2002;王朝令,2012).图 3b,4b, 5b为各模型单炮记录变换后的频率-速度(f-v)域的面波能量分布图或称为面波频散谱.由理论分析可知,常规的视速度开窗滤波一般可以有效的切除来自观测排列左端近源点侧的边界反射面波;且由于在频率-速度(f-v)域中,直达面波位于正视速度区域,而来自观测排列右端远离源点侧的边界反射面波位于负视速度区,故右端边界反射面波对在正视速度区域拾取频散曲线不会有干扰.但这些不同半宽度模型的瑞利面波能量分布并未完全依照均匀半无限空间的特征分布,即表现出能量分布无频散特征,而是在低频段出现明显的速度随频率迅速增大的频散现象,在高速度区出现局部强干扰能量团现象,且面波的能量分布随频率变化不能保持连续性,成断续的带状分布.这种能量随频率成断续的带状分布的现象可由波的干涉理论(马文蔚等,2006)解释:由模型的对称性,两侧边界反射的面波将同时到达观测排列处,两侧边界点发出的波具有相同的频带、同相位或恒定的相位差、和相同的振动方向(垂直)的特性,因此将产生干涉现象,形成了某些频率信号相干(振幅或能量加强)、某些频率信号相消(振幅或能量减弱)的带状分布特征.但也可看出,随着模型半宽度由10 cm增大到25 cm, 即模型半宽度由大于面波主波长(5 cm)的2倍增大到5倍,低频段的速度频散和局部强干扰能量团逐渐消失,面波的能量分布随频率变化的连续性也逐渐改善.由此可以进一步证实,这些干扰主要是由平行于观测排列方向的两侧边界所产生,且这类干扰会给依据能量团拾取瑞利面波速度频散曲线带来严重的不确定性.
|
图 3 均匀介质模型1数值模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 3 The shot records and the dispersion analysis of the Rayleigh waves of the homogeneous medium model 1 with numerical data (a)the common shot records.(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
|
图 4 均匀介质模型2数值模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 4 The shot records and the dispersion analysis of the Rayleigh waves of the homogeneous medium model 2 with numerical data (a)the common shot records.(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
|
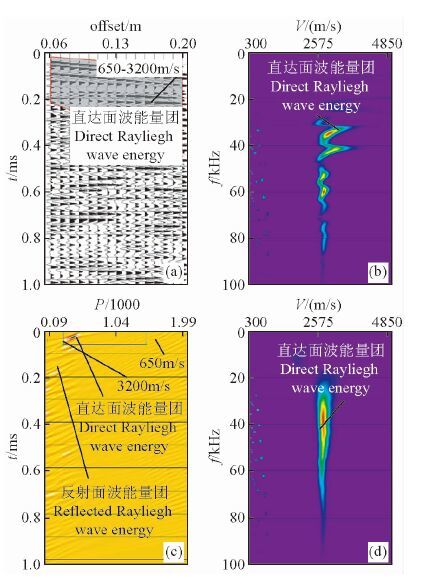
图 5 均匀介质模型3数值模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 5 The shot records and the dispersion analysis of the Rayleigh waves of the homogeneous medium model 3 with numerical data (a)the common shot records.(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
以上的研究表明,在多道瞬态瑞利面波的物理模拟实验中,物理模型半宽度若远大于(本实验为5~10倍)模拟波场的主波长,则来自侧边界的反射面波与来自点震源的直达面波在时间上足以清楚分离,就可极大的削弱常规的频率-速度(f-v)域中频散曲线拾取中的侧边界反射面波的干扰.但另一方面,侧边界距离或模型宽度过大,会带来物理建模效率和数值建模计算量大的问题.注意到直达面波和来自侧边界的反射面波时距关系的几何特征的不同性,前者为直线关系,而后者为双曲关系,并具有高于前者的视速度,显然采用可分离不同几何特征时距关系波组的τ-p变换(吴律等,1986)可以有效的分离直达面波和反射面波.图 3b,4b, 5b分别是模型1,2,3的单炮记录在τ-p域中的图像,由图可以清楚看到,来自侧边界的反射面波在到达时间上和直达面波有重合区段,但由于高视速度的差异,其在p值上完全可以分离.应用前述常规视速度开窗的上,下视速度限为p的左右限,以τ值分别等于零和直达面波传播结束时间为τ值的上下限,构成τ-p域中的视速度滤波通过窗口(图中的矩型框内区域),进行τ-p滤波,分离出直达面波.图 3d,4d, 5d是分离出的直达面波在f-v域中的能量分布图像,其具有典型的均匀半无限空间的频散特征,即无频散,信号频带内所有的频率都具有相同的传播速度——约2400 m/s, 非常接近于表 1中的花岗岩模型的理论面波速度2412 m/s.这表明,应用τ-p变换,可有效的分离直达面波和来自侧边界的反射面波,从而可避免建立模型的尺度过大,带来的物理建模效率和数值建模计算量大的问题.
1.2 两层介质模型以下,我们以速度递增型的两层介质模型的数值模拟结果来分析复杂条件下模型尺度的影响(张立和刘争平,2013).
1.2.1 模型和观测参数表 3为由有机玻璃参数为上层,花岗岩参数为下层,上层有机玻璃厚度依次递增的三个数值模型,模型的总尺寸均为40 cm×20 cm×9 cm, 具体的模型材料参数见表 1.在数值模拟中,采用的观测排列参数和激发震源参数与上节中均匀介质模型完全一致.由于模型只有深度上的变化,数值模拟发现两层介质模型观测表面的瑞利面波的波场快照特征与均匀介质模型中相似,因此本节仅以数值模拟的单炮记录剖面数据结果展开分析.
|
|
表 3 两层模型组合参数和材料性质 Table 3 Model structure parameters of two layered models |
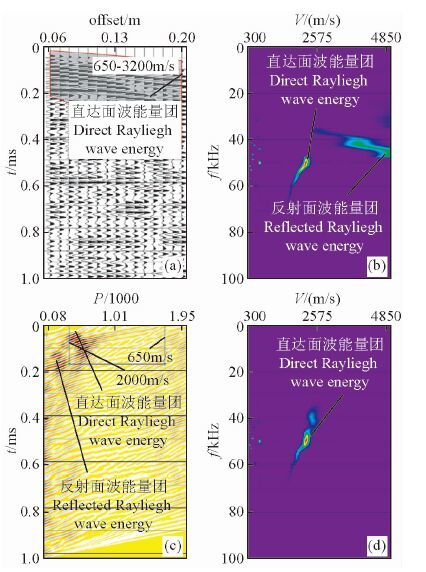
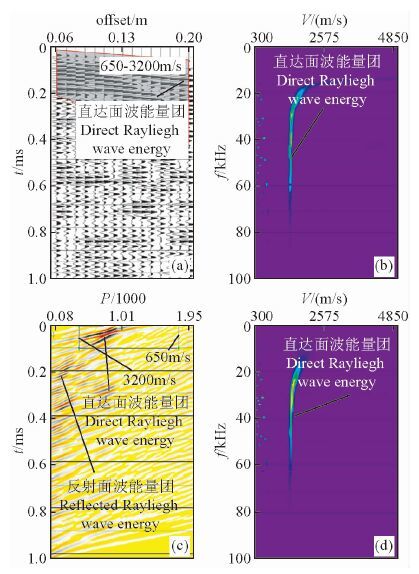
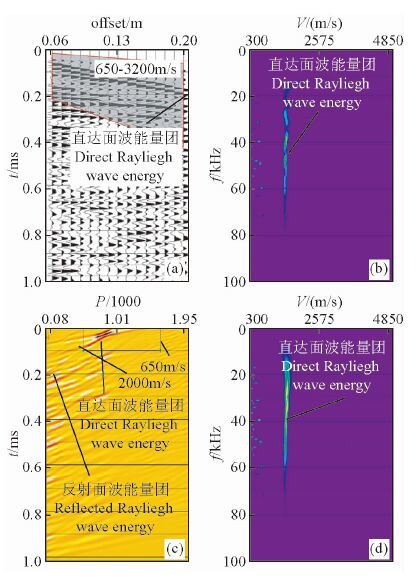
图 6a,7a, 8a分别为表 3中模型1,2,3数值模拟的垂直分量单炮记录.与前述的均匀介质模型类似,图中可识别出直达面波的初至到达,但是来自边界的反射面波的叠加,导致后续的面波记录波形十分复杂.图 6b,7b, 8b为经简单的视速度开窗滤波(单炮记录图中的阴影区)进行干扰波切除处理后,各模型单炮记录的频率-速度(f-v)域的面波能量分布图.由图可看出,面波高速能量团和频散曲线的不连续现象仍然存在,这进一步证明通过简单的视速度开窗滤波不能有效的切除来自侧边界的反射面波的干扰.另一方面,由表 1中有机玻璃参数和激发雷克子波的主频可计算,在低速有机玻璃中传播波场的主波长为2.5 cm, 远较高速花岗岩中传播波场的主波长5 cm短.若以波长量度模型宽度,对于同样的半宽度为10 cm的模型,前者模型宽度为4倍波长,而后者的只有4倍.图中低速有机玻璃中侧边界的影响明显的小于上节中的同尺度的高速花岗岩模型的侧边界的影响.这也可很好的解释随着两层介质模型的上层低速有机玻璃的增厚,图 6b,7b, 8b对应的频率-速度(f-v)域中的侧边界干扰面波影响逐渐减弱的现象.类似的,图 6c,图 7c, 图 8显示来自侧边界的反射面波与来自震源的直达面波在τ-p域得到很好的分离.按均匀介质模型一节中的思路设计τ-p滤波窗口,分别分离出图 6c,7c, 8c中的矩型框内的直达面波.分离后的直达面波的频率-速度(f-v)域图像频散分析结果如图 6d,7d, 8d中所示.由图 6d可看到来自侧边界的反射面波干扰已被有效的消除,直达面波的频散特征明显的表现出在高频端趋于上层有机玻璃的低面波速度1206 m/s, 低频段侧趋于下层花岗岩的高面波速度2412 m/s.图 7d、8d显示,随着上层有机玻璃的厚度接近或大于面波的主波长,能量频散逐渐表现出均匀半无限介质中的典型特征,即面波速度与频率无关,所有频率都以趋于有机玻璃材料的理论面波速度1206 m/s传播.由此也可以推导图 6d中的频散间断点应是由两层介质模型1的浅界面所引起的.
|
图 6 两层介质模型1数值模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 6 The records and the dispersion analysis of the Rayleigh waves of the two-layered model 1 with numerical data (a)the common shot records.(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
|
图 7 两层介质模型2数值模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除的视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 7 The records and the dispersion analysis of the Rayleigh waves of the two-layered model 2 with numerical data (a)the common shot records;(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
|
图 8 两层介质模型3数值模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除的视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 8 The records and the dispersion analysis of the Rayleigh waves of the two-layered model 3 with numerical data (a)the common shot records.(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
我们最初是在多道瞬态瑞利面波的物理实验中观测到模型的有限尺度所引起的边界反射干扰,尤其是与观测排列平行的两侧边界的尺度对实验结果的干扰问题的(Xiong et al.,2010;Xiong et al.,2013),在此基础上展开了前述的数值模拟研究.
本节以我们实验中一花岗岩模型的物理实验数据和相应分析结果来验证模型尺度的干扰影响和本文提出的消除干扰的方法的有效性.取一块尺度为40 cm×20 cm×9 cm的、可视为均匀介质的整块花岗岩作为物理模型,该物理模型的尺度、物性参数、观测排列布置参数等参数与1.1节均匀介质的数值模型完全相同(图 1);事实上,数值模型相关参数是依该物理模型的实测结果而取值的.
物理模拟中采用一对48 kHz的超声波换能器分别作为声激发源和接收检波器,记录窗长与数值模拟中记录窗长相同,即:1.024 ms, 采样间隔为1 μs.考虑到物理实验中存在随机噪声干扰,物理实验中每道采样记录均以1024次重复激发-采样记录的叠加结果作为最终记录,该重复激发-采样记录和叠加过程由计算机控制的虚拟仪器自动完成的.
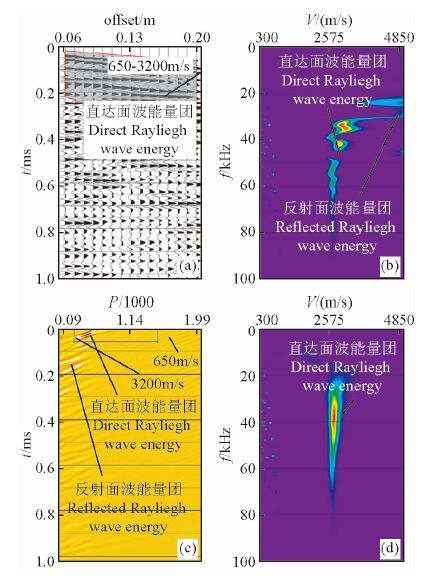
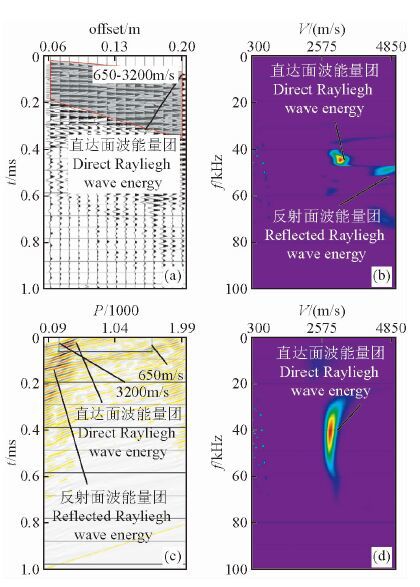
图 9为对此模型进行观测后得到的单炮记录及按数值模拟研究中的相同数据处理流程进行数据处理后的结果图像.与1.1节中相同模型参数的均匀介质模型1的数值模拟结果(图 3)对比,图 9a中的物理模拟单炮记录表现出类似的边界反射面波的干扰特征.类似的,图 9b显示经简单视速度窗切除后的f-v域面波能量分布图中存在来自两侧边界反射面波的高速能量团干扰特征,其显然会干扰频散曲线的正确提取.图 9c显示:在τ-p域内,直达面波与来自两侧边界的反射干扰面波依据视速度的差异,在p值上能够很好的被分离开.我们以上一节相同的思路来设计τ-p滤波窗口(图 9c中的矩形框区),按此滤波窗口分离后的直达面波的f-v域能量图像(图 9d)表现出与图 3d中相近的均匀介质频散特征.
|
图 9 物理模拟记录和面波频散分析图 (a)数值模拟单炮记录和干扰波切除的视速度窗口;(b)干扰波切除后的f-v域图像;(c)单炮记录的τ-p域图像和设计的视速度滤波窗口;(d)τ-p滤波后的f-v域图像. Fig. 9 The records and the dispersion analysis data of the Rayleigh waves of the homogeneous medium model with physical modeling (a)the common shot records.(b)the image of direct arrival Rayleigh wavesin the f-v domain;(c)image of the records in the τ-p domain;(d)the image of direct arrival Rayleigh waves (shown in the box with black line in the(c))in the f-v domain. |
需指出的是,相对于数值模拟中宽带激发雷克子波和宽带接收,实验中的声激发和接收换能器均为窄带的,因此不同于图 3,图 9中数据表现出具有时间域中的长波列,频率域中的窄带宽的典型窄带信号特征.这是由实验室的仪器设备所决定的.
3 结 论本文基于数值模拟和实验模拟研究了多道瞬态瑞利面波物理模拟实验中,模型尺度对频散曲线提取的影响,并提出了在不改变模型尺度的硬件条件下,应用τ-p变换波场分离方法有效消除模型尺度影响的数据处理方法.本文研究结果表明:
(1) 实验室条件下进行瑞利面波物理模拟时,模型尺度的有限性难以满足瞬态多道瑞利面波勘探理论和方法基于的理想半无限空间条件.多道观测排列结果不仅记录到来自激发震源的直达面波,还会记录到来自有限的尺度模型侧边界的反射面波.
(2) 来自观测排列两端侧面的反射面波可以由常规面波处理方法:视速度开窗滤波(单炮记录剖面中的阴影区)和常规二维频率-速度(f-v)域变换被有效的切除或消除,对f-v域中直达面波的频散曲线提取没有影响.
(3) 如果模型的半宽度与实验激发波场的主波长的量级相近,则来自平行观测排列两侧面边界的反射面波将与直达面波在时间上混叠和干涉,其在f-v域面波能量分布图像中表现为出现高速能量团,频散谱发生错断等现象,并难以在常规面波处理流程中被消除,严重的干扰了面波频散曲线的正确拾取.若模型的半宽度近似大于实验激发波场的主波长一个量级时(5~10倍),则来自平行观测排列两侧面边界的反射面波将与直达面波在到达时间上显著分离,常规面波处理流程可消除该侧边界面的影响.
(4) 对于本文的研究模型,根据平行观测排列两侧面边界的反射面波与直达面波在的时距关系几何形态上的差异,应用τ-p滤波可以有效的消除前者的干扰影响,避免增大模型宽度所带来的物理建模难度问题.
本文的研究结果对野外瞬态多道瑞利面波观测中,沿排列方向的侧表面地形起伏对观测记录的影响分析也具有参考意义.
致 谢 本项目由国家自然科学基金—山区深部岩体结构的瑞利面波椭圆极化特征研究(批准号:41274107)资助.在数值模型的设计、研究方法和论文书写方面,得到了于文福师兄和熊自英师姐的热心帮助,在此深表谢意.对于文福师兄前期工作和平台的搭建所作的贡献,衷心感谢.
| [1] | Aki K, Richards P G. 2002. Quantitative Seismology[M]. Sansalito, CA: University Science Books. |
| [2] | Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes[J]. Chinese J. Geophys. (in Chinese), 49(4): 1082-1091, doi: 10.3321/j.issn:0001-5733.2006.04.021. |
| [3] | Park C B, Miller R D, Xia J H. 1999. Multichannel analysis of surface waves[J]. Geophysics, 64(3): 800-808. |
| [4] | Sun J Z, Guo T S, Tang W B, et al. Theory, practice and application of ulltrasonic seismic modeling experiment in China[J]. Acta Geophysica Sinica (in Chinese), 40(S1): 266-274. |
| [5] | Wang Z L. 2010. The numerical simulation research on separation of wave field and inversion method in tunnel seismic prediction (in Chinese)[Ph. D. thesis]. Chengdu: Southwest Jiaotong University. |
| [6] | Wu L, Wu K F, Sun L. The method of τ-p transformation and its application in seismic data processing, Part I[J]. Geophysical Prosecting for Petroleum (in Chinese), 25(1): 37-53. |
| [7] | Xiong Z Y, Liu Z P, Song B, et al. 2010. Physical experiments for Rayleigh surface wave field[C].//Near-Surface Geophysics and Geohazards--Proceedings of the 4th International Conference on Environmental and Engineering Geophysics (Volume 1). Chengdu, China. |
| [8] | Xiong Z Y, Liu Z P, Zhang K. 2013. An experimental research of Rayleigh wave based on the acoustic-electric conversions effect[C].//Near Surface Geophysics Asia Pacific Conference. Beijing, China: SEG, 258-261. |
| [9] | Zhang B X, Lu L Y, Bao G S. 2002. A study on zigzag dispersion curves in Rayleigh wave exploration[J]. Chinese Journal of Geophysics (in Chinese), 45(2): 263-274, doi: 10.3321/j.issn:0001-5733.2002.02.013. |
| [10] | Zhang B X, Lu L Y. 2005. Investigation on the dispersion curves of Rayleigh wave by frequency-wavenumber analysis method[J]. Chinese Journal of Engineering Geophysics (in Chinese), 2(4): 245-255. |
| [11] | ZHANG Li, LIU Zheng-Ping. 2013. A study of the elliptic polarization characteristics of fundamental mode rayleigh wave based on numerical simulation[J]. Chinese Journal of Geophysics (in Chinese), 56(5): 1686-1695, doi: 10.6038/cjg20130526. |
| [12] | Zhou B Z, Greenhalgh S A. 1994. Linear and parabolic τ-p transforms revisited[J]. Geophysics, 59(7): 1133-1149. |
| [13] | 鲁来玉, 张碧星, 汪承灏. 2006. 基于瑞利波高阶模式反演的实验研究[J]. 地球物理学报, 49(4): 1082-1091, doi: 10.3321/j.issn:0001-5733.2006.04.021. |
| [14] | 马文蔚, 解希顺, 周雨青. 2006. 物理学教程(下册)[M]. 第二版. 北京: 高等教育出版社. |
| [15] | 彭一民, 孙进忠. 1987. 超声地震模型实验相似准则[J]. 勘察科学技术, (5): 58-61, 52. |
| [16] | 孙进忠, 郭铁栓, 唐文榜,等. 1997. 我国超声地震模型试验的理论研究与实践[J]. 地球物理学报, 40(S1): 266-274. |
| [17] | 王朝令. 2012. 隧道地震超前预报中波场分离与反演方法的数值模拟研究[博士论文]. 成都: 西南交通大学. |
| [18] | 吴律, 武克奋, 孙力. 1986. τ-p变换方法及其在地震资料处理中的应用(Ⅰ)[J]. 石油物探, 25(1): 37-53. |
| [19] | 张碧星, 鲁来玉, 鲍光淑. 2002. 瑞利波勘探中“之”字形频散曲线研究[J]. 地球物理学报, 45(2): 263-274, doi: 10.3321/j.issn:0001-5733.2002.02.013. |
| [20] | 张碧星, 鲁来玉. 2005. 用频率-波数法分析瑞利波频散曲线[J]. 工程地球物理学报, 2(4): 245-255. |
| [21] | 张立, 刘争平. 2013. 水平层状介质中基阶瑞利面波椭圆极化特征数值分析与研究[J]. 地球物理学报, 56(5): 1686-1695, doi: 10.6038/cjg20130526. |
| [22] | 赵鸿儒, 唐文榜, 郭铁栓. 1986. 超声地震模型试验技术及应用[M]. 北京: 石油工业出版社. |
 2016, Vol. 31
2016, Vol. 31

