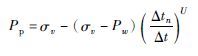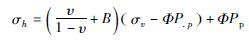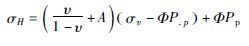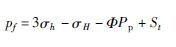地应力是地球固体介质受重力及多种地球构造力等在地球内部引起的相应变形的力学参数，直接影响着固体介质及其蕴含的各种流体的力学行为，已广泛应用于油田开发工程中.水力压裂法、应力恢复法、应力解除法等(马寅生，1997)是获取地应力数据较为直接的测试手段，理论上它比其他方法有更高的精度，但却存在测量数据有限、地应力剖面不连续、成本高等问题(葛洪魁等，1998).研究表明：利用井中测量的纵横波速度、岩层密度、岩层孔渗特征等信息，可以计算出连续的地应力剖面(黄荣樽和邓金根，1996；余雄鹰等，1996)，由于声波成像测井资料可以测量横波波速，已被广泛用于计算地层水平主应力(高坤等，2006；王晓杰等，2008).鉴于声波成像测井资料的非普及性，以成像测井资料测量的横波传播速度为基础，采用优化技术建立常规测井计算横波波速的方法(张美玲等，2014)，使常规测井资料计算连续水平地应力得以有效实现.

油田开发过程中的套损预测、压裂设计等工作的有效实现需要已知岩层地应力的平面及纵向分布，而从经济角度很难实现某一油田全面的地应力测量.练章华(2009) 依据有限元技术，针对含断层的层状均匀地层模型进行应力计算，从理论角度研究了岩层应力变化与套管损坏的对应关系.

尽管国内外在应力计算方面的研究成果较多，但如何应用常规测井资料确立地层应力公式尚缺乏系统具体的论述.结合国内外相关研究成果，形成了利用常规测井资料计算岩石力学参数、垂直应力、最大最小水平应力、破裂压力的计算方法及步骤.

在地下岩体中存在着三个在方向上相互垂直的主地应力，即由岩体自重引起的纵向地应力和两个水平方向的主地应力.

瑞士地质学家Heim认为纵向地应力σ_v是由上覆地层的重力引起的，它是随着地层密度和深度而变化的，因此可用密度测井资料来求出(丰成君等，2013)，公式为

式(1) 中的积分范围为(0，H)，则依据研究区构造特点，分别在研究区的东部、西部、北部、南部及中部各设计一口井，要求这5口井的补偿密度测量井段为井口至葡萄花层组底部.考虑到研究区葡萄花层组井段约为60 m(Zhang et al.，2013)，以每口井葡顶开始，每加深1 m为一个深度单元，分别计算(1) 式的垂向地应力，得到5×60个数据，以深度H与σ_v(H)建立关系，相关系数为0.9996.可以看出，研究区葡I油藏垂直应力与地层深度有非常好的对应关系式为

地层孔隙压力是进行地层主应力分析的关键参数.在地层正常压实条件下，地层孔隙压力可以根据静水柱高度法计算，实际上地层中的孔隙压力不仅是地层深度的变化函数，采用声波时差法计算地层孔隙压力的有效应力法是传统且实用的(黄荣樽，1981)，公式为

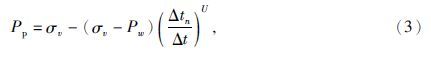
对于单一岩性的泥岩地层，声波波速度主要反映垂直主应力，可以利用泥岩段声波时差确立正常孔隙压力条件下声波时差趋势线.在Δt_n具体计算过程中，按照以下规则选取研究区井的泥岩段声波测量值：

a)有比较平直的、低自然电位的、均匀低电阻率的和高自然伽马值的泥岩层段；b)厚度大于2 m的泥岩层段；c)非缩径的或井径扩大不超过6 cm的泥岩层段.以深度为自变量，建立正常孔隙压力条件下声波时差的计算公式(4) .公式相关系数为0.9987，公式为

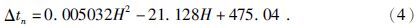
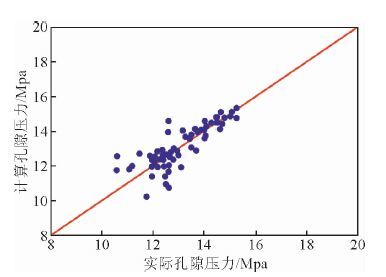
(3) 式中系数U的求解，以研究区78个单试油测试层测量的地层孔隙压力数据为约束，采用一维搜索优化方法(王德人，1979)，确定U=2.46，一维搜索区间为[1，5]，以相对均方根误差＜5%为搜索截止误差.图 1为计算的孔隙压力与实际孔隙压力精度对比图，平均相对误差3.69%.

图 1

Fig. 1

图 1 地层孔隙压力计算精度对比图 Fig. 1 Calculation accuracy of the formation pore pressure

1.3.1 水平主应力计算模型

水平地应力计算模型主要分为两种(余雄鹰等，1996；张风达等，2015)：一种是最大水平应力和最小水平应力相等计算模型，该模型认为在水平面上的地应力相等，不存在构造应力；二是水平应力不相等的计算模型，认为地层的构造应力在各方向上是不相等的.第一种模型因不符合地层实际状况而使计算的地应力结果不合理.因此本文主要采用第二种地应力计算模型，并结合水力压裂资料及井壁崩落数据综合反演模型中的参数，效果较好，公式为

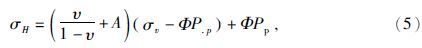
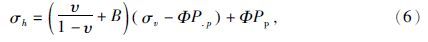
该模型的优点在于，一方面考虑了上覆岩层的重力、地层孔隙压力、地层岩石的泊松比以及构造应力对水平地应力的影响；另一方面模型中的各参数比较容易获取，与实际压裂数据结合较容易，模型简单实用(李光泉等，2012；曾顺鹏等，2015).

研究区横波时差值采用文献(张美玲等，2014)中方法进行构建，纵波时差值取为补偿声波测量值.其中，岩石泊松比ν的计算公式为

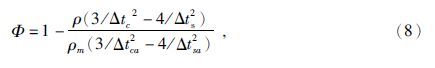
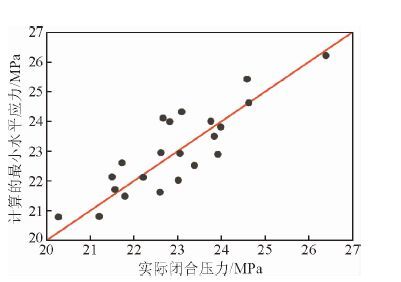
水力压裂是向测试层段泵入高压流体直至孔壁岩石发生破裂，在孔壁周围地层中诱发形成水力裂缝(谢富仁等，2007).根据能量最低原理，裂缝起裂后总是沿着垂直最小主应力的方向扩展.当注入的流体量足以使裂缝扩展长度达到一定程度时停泵，关闭水力压裂系统.停泵后裂缝逐渐闭合，当裂缝处于临界闭合状态时，裂缝内的流体压力与垂直裂缝平面的最小主应力相平衡，此时所对应的裂缝闭合压力就近似等于最小水平主应力(刘子晋，1985).在实际计算时，选取研究区单压裂层(共计24层)，从压裂测试曲线上读取岩层压裂后的闭合压力(已校正到地下压力)，作为最小水平应力代入式(6) 中，采用一维优化搜索技术，确定B=0.209，一维搜索区间为(0，1)，以相对均方根误差＜5%为搜索截止误差.图 2为计算的最小水平应力与实测闭合压力精度对比图，平均相对误差3.19%.

图 2

Fig. 2

图 2 计算的最小水平应力与实测闭合压力精度对比图 Fig. 2 Accuracy comparison between the minimum horizontal stress and closed pressure

最大水平应力的精确计算是目前地应力研究的难点.地下岩层构造的不均匀性导致岩层的最小与最大水平应力并不相同(吴满路等，2005)，(5) 式中的最大水平应力构造系数往往依据构造规律估计给出(黄荣樽和邓金根，1996；余雄鹰等，1996).最大与最小水平应力的差异往往会造成钻孔的椭圆状变化(Barton et al.，1988).Mohr-Coulomb破坏准则指出井眼的坍塌状况与地层水平应力大小密切相关(张保平等，2003).陈朝伟等(2014) 给出了由井眼坍塌形状预测最大水平主应力的计算流程，并利用一口井的成像测井所反映的井眼坍塌状况预测了该井2个深度点的最大水平应力值.Aadnoy等(2013) 给出了由崩落的椭圆井眼的长短半轴比值，结合最小水平应力来计算最大水平应力的公式，见(9) .这样，依据四臂井径测井资料就可以计算出最大水平应力值(王成虎等，2014)，公式为

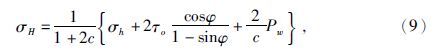
考虑研究区葡I储层为砂泥岩剖面的情况，储层为中等致密砂岩，依据刘建中等(1993) 、McLean和Addis(1990) 基于岩石的Mohr-Coulomb圆实验结果，确立中等致密砂岩的τ₀、φ分别取为6.5 MPa、36.5度；收集研究区10口测量四臂井径测井资料.研究中，首先排出由于钻井液浸泡垮塌、泥岩等软地层膨胀缩径、钻井工程等因素造成的不规则井眼状况，而选择层厚较大、井眼椭圆状态较稳定的砂岩(硬)地层，作为分析的对象.给出这10口井15层中符合条件层双井径长短轴之比、最小水平应力由(6) 、孔隙压力由(3) 式计算，最大水平应力由(9) 式计算.计算结果见表 1.

表 1 (Table 1)

表 1 计算得到的最大水平应力表 Table 1 The maximum horizontal stress table is obtained by calculating 井号 层号 井段/m 孔隙压力/MPa 短轴/长轴 最小水平主应力/MPa 最大水平应力/MPa W2#1 PI6 1450.0~1454.0 14.89 0.975 21.3 26.32 T#2 PI9 1259.8~1264.4 12.71 0.989 18.7 23.57 T#1 PI2 1223.0~1225.2 12.34 0.9673 19.8 24.23 T#1 PI4 1242.2~1245.4 12.56 0.991 18.1 23.22 W#6 PI6 1371.2~1373.2 13.98 0.978 20.3 25.26 W#9 PI4 1296.0~1300.0 12.88 0.923 17.2 24.91 W#9 PI7 1311.6~1316.2 13.19 0.911 17.3 25.53 W#9 PI9 1321.0~1326.4 13.27 0.901 17.4 25.93 W2-#4-#9 PI5 1234.8~1237.0 12.66 0.987 19.6 23.89 W2-#4-#9 PI7 1250.6~1254.2 12.69 0.998 18.5 23.27 W2-#9-#2 PI3 1232.4~1235.2 12.53 0.993 18.5 23.28 W2-#9-#2 PI6 1253.6~1257.4 12.69 0.991 18.4 23.41 W2-#9-#6 PI8 1395.4~1400.2 14.15 0.989 23.6 26.19 W2#2 PI6 1456.4~1459.4 14.56 0.954 22.5 27.10 W2#2 PI7 1463.4~1468.4 14.39 0.963 21.9 26.51

表 1 计算得到的最大水平应力表 Table 1 The maximum horizontal stress table is obtained by calculating

将表 1中的最大水平应力计算结果代入公式(5) 中，采用一维优化搜索技术，确定A=0.441，一维搜索区间为(0，1)，以相对均方根误差＜5%为搜索截止误差，迭代误差为2.34%.迭代精度高与研究区构造相对简单(Shi Qi Zhang, 2012)密切相关.

地层破裂压力是指某一深度地层发生破碎和形成裂缝时所承受的压力.在油气井水力压裂过程中，地层是沿最小地应力方向诱发人工裂缝.如果地层沿水平方向的地应力最小，那么水力压裂将会诱发垂直人工裂缝；如果地层沿垂直方向的地应力最小，那么水力压裂将会诱发水平人工裂缝.实践证明，卫星油田葡I层组水平方向的应力最小，利用经典弹性理论证明，最大水平应力σ_H、最小水平应力σ_h、破裂压力p_f之间存在的关系为

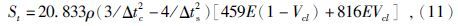
归纳总结前文所述的地应力计算方法(见表 2)，可以看出，应用岩层深度、补偿声波时差(或纵波时差)、横波时差、补偿密度、自然伽马等常规测井资料就可较容易地实现研究区所有井的连续地应力曲线的计算，进而给出地应力的水平分布.

表 2 (Table 2)

表 2 卫星油田PI层组地应力计算公式汇总表 Table 2 A summary of the formulas of the stress calculation of the PI layer in Wei Xing Oilfield 地应力MPa 输入参数 计算公式 计算公式建立的关键基础 垂直主应力σv 岩层深度 σv=0.0222H－0.6782 合理选择典型井，并进行全井段补偿密度测井，通过密度的积分计算，建立应力值与深度的对应关系式 孔隙压力Pp 垂直主应力、补偿声波时差(或纵波时差)、岩层深度 利用稳定、厚泥岩段补偿声波时差值建立地层压力正常趋势线计算公式；利用试油测试的地层孔隙压力值约束优化伊顿公式系数 最小水平主应力σh 垂直主应力、补偿声波时差(或纵波时差)、横波时差、补偿密度测井资料 利用施工压裂曲线的瞬时停泵压力数据作为最小水平应力计算公式的约束，优化参数B 最大水平主应力σH 垂直主应力、补偿声波时差(或纵波时差)、横波时差、补偿密度测井资料 由应力造成的井眼的坍塌反映为多臂井径的长短轴半径之比上，由实验提供内摩擦角及黏滞力参数计算最大水平应力，并以此为约束反演计算出参数A 破裂压力pf 补偿声波时差(或纵波时差)、横波时差、补偿密度、自然伽马、最大及最小水平应力、 最大水平应力的精确确定，岩石泥质含量的计算

表 2 卫星油田PI层组地应力计算公式汇总表 Table 2 A summary of the formulas of the stress calculation of the PI layer in Wei Xing Oilfield

利用表 2步骤，对卫星地区512口井进行了地应力计算.表 3给出了全区葡I层组9个砂体的地应力值分布范围和平均值.全区最小水平应力的分布范围为16.96～23.01 Ma, 最大水平应力的分布范围20.79～28.09 MPa, 破裂压力梯度分布范围为0.0152～0.0202 MPa/m.由表 3可看出，同一层组不同的平面位置主应力值不同，而且同一平面位置纵向各小层的主应力值也不相同.这样通过井资料就可构建出地层主应力的空间分布.

表 3 (Table 3)

表 3 卫星油田葡Ⅰ层组9个砂体应力值范围 Table 3 Stress value range of 9 sand bodies of the PI layer in the Wei Xing Oilfield 层组 最小水平地应力/MPa 最大水平地应力/MPa 破裂压力梯度/MPa/m 范围 平均 范围 平均 范围 平均 PI1 16.96~22.75 19.36 20.79~27.49 23.59 0.0155~0.0198 0.0175 PI2 17.08~22.36 19.18 21.07~27.31 23.32 0.0157~0.0192 0.0169 PI3 17.22~22.83 19.39 21.12~27.47 23.62 0.0156~0.0197 0.0173 PI4 17.28~22.67 19.32 21.15~27.54 23.86 0.0156~0.0195 0.0174 PI5 17.59~22.69 19.51 21.76~27.60 24.01 0.0152~0.0202 0.0173 PI6 17.53~22.23 19.25 21.21~27.28 23.53 0.0150~0.0196 0.0172 PI7 17.55~22.83 19.93 22.16~27.89 24.28 0.0153~0.0200 0.0173 PI8 18.09~23.17 20.12 22.08~27.95 24.46 0.0158~0.0198 0.0174 PI9 18.17~23.01 20.24 22.34~28.09 24.64 0.0155~0.0199 0.0173

表 3 卫星油田葡Ⅰ层组9个砂体应力值范围 Table 3 Stress value range of 9 sand bodies of the PI layer in the Wei Xing Oilfield

国内各油田普遍存在油水井套管损坏问题，且已严重影响油田的开发工作.套管损坏实际上就是套管受周围地应力场的作用而发生破坏，因此，分析井周围地应力场特征，有助于套管损坏的预测.代丽和徐守余(2005) 指出断层带附近是应力集中带，在外界作用下局部应力条件改变，利于地层变形和断块相对移动，容易产生套管损坏现象.宋杰(2014) 指出泊松比、剪切模量、破裂压力等岩石本身力学特征是油层部位发生套损的内因，而地应力场和地层压力场的改变是油层部位发生套损的外因.练章华(2009) 从理论角度证实了高压注水更容易在油层段产生套损现象.

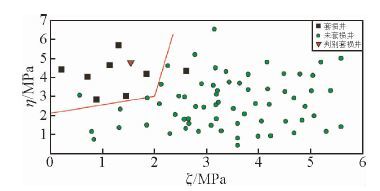
卫星油田PI层段开发至今共计8口注水井发生套损(连续注水时间均在5年以上)，套损位置均发生在射孔层段下部的泥岩处.若射孔层段与其下部泥岩段的最小水平主应力差值为ζ；射孔段下部泥岩处最大、最小主应力差为η；射孔层段与其下部泥岩段破裂压力差值为δ；射孔段注水压力与孔隙压力差值为θ.图 3为“射孔层段与其下部泥岩段的最小水平主应力差值为ζ～下部泥岩处最大、最小主应力差为η”交会图版.

图 3

Fig. 3

图 3 关于参量ζ～η的注水井套损预测图版 Fig. 3 The forecast figure of casing damage on parameters ζ～η in water injection well

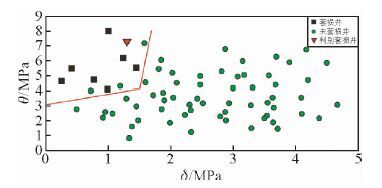
ζ～η交会图表明：射孔层段与其下部泥岩段最小水平主应力相差不大，而下部泥岩段的最大、最小水平应力差距较大的情况，反映了岩层中应力分布不均匀的状况，注入水的长期浸入破坏加剧了这种不均衡性，套管在这种不均衡力作用下，极易产生套损.图 3图版判别套损的条件为：当η>0.45ξ+2.1且η>9.43ξ－15.86时，射孔层段下部的泥岩段容易发生套损现象.图 4为“射孔层段与其下部泥岩段破裂压力差值为δ～射孔段注水压力与孔隙压力差值为θ”交会图版.δ～θ交会图表明：当射孔段与其下部泥岩段破裂压力较相近情况下，以远大于岩层孔隙压力的注水压力进行注水时，容易使下部岩层产生裂隙，注入水浸入到下部泥岩段，使岩层形成憋压，增大套管的受力而造成套损.图 4图版判别套损的条件为：当θ>0.6667δ+3.1且θ>19.5δ－25.15时，射孔层段下部的泥岩段容易发生套损现象.

图 4

Fig. 4

图 4 关于参量δ～θ的注水井套损预测图版 Fig. 4 The forecast figure of casing damage on parameters δ～θ in water injection well

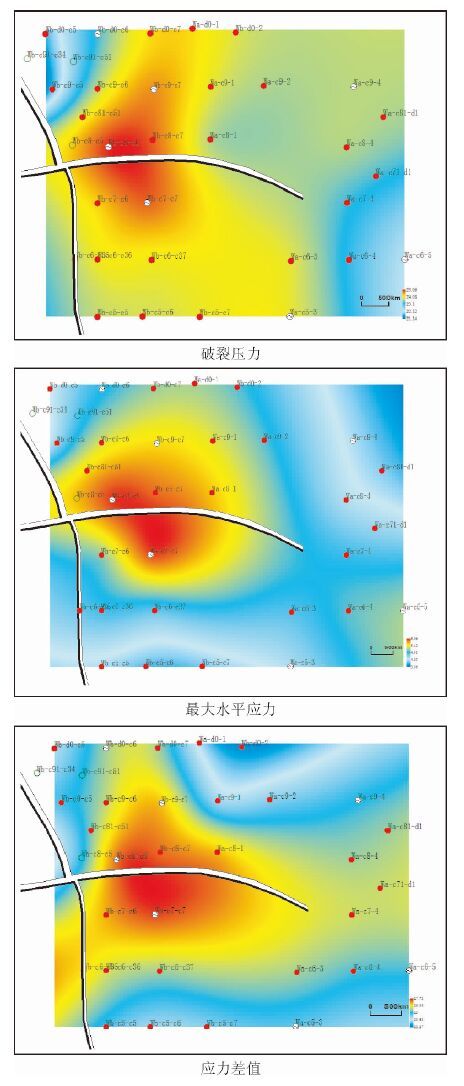
Wc-c8-c6井及Wb-c7-c7井两口邻近断层的注水井在注水开发5年后均在PI1-PI2层间的泥岩段发生套损，绘制这两口井及其邻近井PI1与PI2间泥岩段的最大水平应力、破裂压力、最大与最小水平应力差的平面分布(见图 5)，可以看出这两口井所在的区域呈现出异常，正是这种平面区域的不均衡性造成了套管的损坏.(下图中井号简化)

图 5

Fig. 5

图 5 套损水井Wb-c8-c6及Wb-c7-c7的PI1与PI2间泥岩段应力分布 Fig. 5 The stress distribution of PI1 and PI2 in casing damage well Wb-c8-c6 and Wb-c7-c7

位于研究区的井Wb-c9-c7是一口2009年转注的注水井，我们利用上文提供的应力计算公式，对该井的最大、最小水平应力、破裂压力进行计算.得到了PI1-PI2段泥岩层对应的ξ、η、δ、θ分别为1.53、4.8、1.3、7.2，如图 6所示.利用ξ～η与δ～θ井筒套损预测交会图版进行预测，预测井段数据点落在交会图版套损区域内(见图 3、图 4)，理论上说明在现阶段注水开发条件下该段井筒套损.实际中，在注水开发5年后，该井在2015年9月进行检修，结果显示在PI1-PI2段井筒发生变形，在脆弱点处发生错断.

图 6

Fig. 6

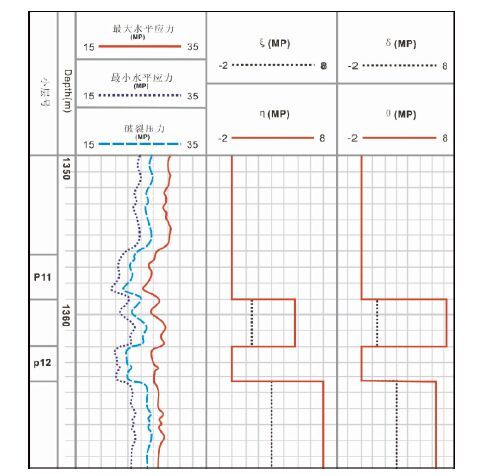
图 6 井Wb-c9-c7地应力参数 Fig. 6 The in-situ stress parameters of well Wb-c9-c7

油田开发过程中具有大量的常规测井资料，若能合理建立针对这些资料的地应力计算公式，则可有效地从平面和纵向上给出地层主应力分布.建立这些公式的关键思路是以较成熟的实验理论公式为基础，以复杂测量方式获得的应力数据为约束，采用优化反演技术，给出适合的公式系数.由研究过程可以得出：

(1) 公式建立过程中，应用的基础数据要完备.这样，即使最终建立的计算公式相对简单，但也具备实用性.如，采用5口从井口至目的层底的密度测量数据来计算目的层段的垂直应力值，这与垂直应力即为岩层上覆压力的物理意义完全吻合，也进一步保障了由深度计算垂直应力公式的精度.

(2) 基于经济成本原因，油田开发一般只进行常规资料的测量，只有将应力计算公式落脚到常规稳定的测量值上，才能合理计算各主应力的纵向与平面分布，进而有效地解决套损预测等工程问题.如，油田中测量的多臂井径资料较少、且能应用于计算的椭圆井段识别存在难度，因此以多臂井径资料求取的最大水平应力值为基础，优化建立由补偿声波、密度计算最大水平应力的公式是非常有必要的.

(3) 论文系统具体地建立了地层主应力的计算公式，实现过程具备可操作性，实现方法具备可推广性.而利用岩石力学参数可以对油田井筒套损进行有效的预测，具有显著的生产应用价值.

致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持！