地球物理学进展  2016, Vol. 31 Issue (3): 1257-1261   PDF    
引用本文
杨修超, 林年添, 张栋, 文博, 宁旋旋. 2016. 利用全波形反演提高逆时偏移成像的精度[J]. 地球物理学进展, 31(3): 1257-1261, doi: 10.6038/pg20160344  
YANG Xiu-chao, LIN Nian-tian, ZHANG Dong, WEN Bo, NING Xuan-xuan. 2016. Using full waveform inversion to improve the accuracy of inverse time migration imaging. Progress in Geophysics, 31(3): 1257-1261, doi: 10.6038/pg20160344   
利用全波形反演提高逆时偏移成像的精度
杨修超1, 林年添1 , 张栋1, 文博1, 宁旋旋2    
1. 山东省沉积成矿作用与沉积矿产重点实验室, 山东科技大学地球科学与工程学院, 青岛 266590;
2. 国家海洋局南海分局, 广州 510300
收稿日期: 2015-07-10 修回日期: 2015-12-11.
基金项目: 国家自然科学基金项(41174098,41374126)和国家高技术研究发展计划(863)(2013AA064201,2012AA061202)联合资助.
作者简介: 杨修超,男,1991年生,山东聊城人,硕士研究生,主要从事全波形反演研究.(E-mail:1648337556@qq.com)
通讯作者: 林年添,男,1962年生,博士,教授,主要从事地震成像、反演及地球物理综合解译分析方法研究等.(E-mail:linnt@sina.com)
摘要: 逆时偏移对速度模型有较强的依赖性,速度模型精度高低决定着偏移效果的好坏,速度模型越准确,偏移效果越好.因此,如何获取高精度的速度模型是实现有效逆时偏移的关键步骤.全波形反演方法利用叠前地震波场的运动学和动力学信息重建地下速度结构能够得到高精度的速度模型.为了验证全波形反演能否提高逆时偏移效果,本论文以OVERTHRUST速度模型为例,在频率域进行全波形反演,并实现了速度模型的更新.逐步缩小了初始速度模型与真实速度模型的残差,提高了速度模型的准确度.然后使用初始OVERTHRUST速度模型以及经过反演的速度模型分别进行逆时偏移,应用结果表明, 使用经过全波形反演后的速度模型进行逆时偏移,其成像效果较好.因此,逆时偏移结合全波形反演可以有效的提高成像精度.
关键词: 全波形反演     逆时偏移     提高精度    
Using full waveform inversion to improve the accuracy of inverse time migration imaging
YANG Xiu-chao1, LIN Nian-tian1 , ZHANG Dong1, WEN Bo1, NING Xuan-xuan2    
1. Shandong Provincial Key Laboratory of Depositional Mineralization & Sedimentary Minerals, College of Geological Sciences & Engineering, Shandong University of Science and Technology, Qingdao 266510, China;
2. South China Sea Branch, State Oceanic Administration, Guangzhou 510300, China
Abstract: Reverse-time migration has strong dependence on speed,The accuracy of velocity model decides the migration effect is good or bad,The more accurate velocity model, migration imaging effect is better.Therefore, how to achieve high precision velocity model is the key step in the reverse-time migration.Full waveform inversion method by using prestack seismic wave field in the kinematic and dynamic information reconstruction underground velocity structure can get high accuracy of velocity model.In order to verify whether the full waveform inversion can apply to reverse-time migration,In the case of OVERTHRUST velocity model,Implementation of the full waveform inversion in frequency domain, and implements the velocity model updating.Gradually narrowed the residual of initial velocity model and the real velocity model, improve the accuracy of the velocity model.Then use the inversion speed model respectively for reverse-time migration,And then use the initial speed of OVERTHRUST model and the inversion velocity model respectively for migration imaging.By comparing the draw, use after full waveform inversion velocity model to get the reverse-time migration precision is higher.Migration imaging of complex structure area more precisely.Therefore, the combination of reverse-time migration and full waveform inversion can effectively improve the imaging accuracy.
Key words: full waveform inversion     reverse-time migration     improve accuracy    
0 引 言

20世纪80年代首次提出基于双程波动方程的逆时偏移技术(Baysal et al.，1983).近年来随着计算机技术的快速发展，地震波逆时偏移成像技术逐步成为目前复杂构造成像中最精确、理论较为成熟的成像方法之一，并从单程波波动方程发展到双程波波动方程(张美根和王妙月，2002; Mulder and Plessix, 2003; Bednar et al.，2003a, 2003b; Yoon et al.，2004).如何提高叠前逆时偏移成像精度是当前地球物理学界关注的核心之一，逆时偏移对速度比较敏感(杨勤勇和段心标，2010)，对速度模型有较强的依赖性，当速度模型不准确时，逆时偏移的优势并不明显，因此提高速度模型的准确度是提高逆时偏移成像精度的关键.

20世纪80年代，提出了基于广义最小二乘的时间域全波形反演(Tarantola, 1984，1986)，这一方法的产生推动了全波形反演的发展，到20世纪90年代，理论由时间域发展到了频率域(Pratt, 1990，1999;Shin et al.，1998)，频率域反演相对时间域反演具有计算高效性、数据选择灵活性等优势，且具有低频到高频的反演策略，可以更好地解决全频段反演遇到的局部极小值，由此奠定了频率域全波形反演发展的基础.在发展的过程当中，相关的应用实例(李国平等，2011)证明了全波形反演是一种高精度的建模手段，具有精细刻画地下及岩性构造的能力，能够反演出接近真实速度的速度模型.

我国独有的油气地质特点，决定了我国油气勘探面临诸多世界级难题.结合对世界物探技术发展现状的描述(王西文等，2013)，为了解决逆时偏移速度模型不准确，影响逆时偏移精度的问题，本文利用全波形反演优化逆时偏移所需的速度模型，经初步验证，取得良好的效果.

1 全波形反演理论以及算例分析 1.1 频率域全波形反演理论

本文采用频率-空间域声波方程在频率域进行全波形反演，公式为

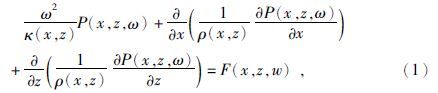
上式中ρ(x, z)代表密度，F(x, z, ω)代表频率域震源函数，κ(x, z)代表体积模量，P(x, z, ω)表示频率域波场，采用混合网格进行有限差分离散可以将上述式子整理成矩阵方程为
其中A代表阻抗矩阵，P代表波场向量，F代表震源向量，求解上述矩阵方程，可以求得频率为ω的波场数值.

为了得到计算波场数据与观测波场数据之差，另Pcal代表计算波场数据，Pobs表示观测波场数据，则波场差值为

为了使计算波场数据与观测波场数据之差达到最小，即使下面目标函数达到最小，公式为

其中T代表矩阵转置；*为复数矩阵的共轭.本文采用共轭梯度法更新参数模型，公式为
上式中m代表迭代的模型，k为迭代次数；α为迭代步长；ΔmC表示目标函数对模型参数的梯度，其中：
上式中：Re{ }表示取复数实部；JT表示Frechet导数矩阵的转置.对方程(2.2)两边同时对模型mi求导，因为震源与模型无关，可得：
继而可得：
展开方程式(2.6)可得：

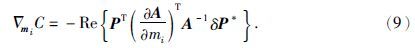
从而可以得到某一频率多炮目标函数对模型参数mi的梯度为

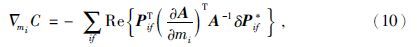
上述方程式中if代表第if炮，Pif代表第if炮该频率对应的波场，同样，δPis代表第if炮计算波场数据与观测波场数据之差.

1.2 OVERTHRUST 算例分析

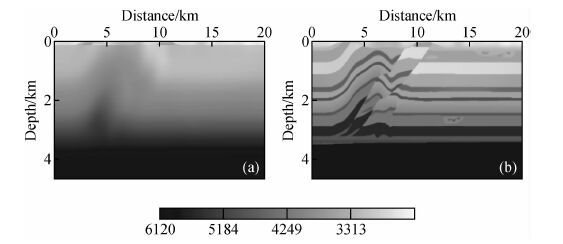
为了检验全波形反演具有高精度的建模能力，并且具有适应复杂介质和速度横向剧烈变化的适应能力，本文以OVERTHRUST模型为例进行反演模拟.如图 1分别给出OVERTHRUST速度模型的初始速度模型(v0)与真实速度模型(vtrue)，将模型大小设为20 km×4 km, 在801×187的网格上进行反演，网格间距25 m, 本文采用主频为10 Hz的雷克子波，在频带范围3.5~20.6 Hz内选取7个频率数据进行组间串行反演，频率分别为3.5 Hz、5.75 Hz、8.20 Hz、9.66 Hz、13.12 Hz、16.39 Hz和20.00 Hz, 限定每组最大迭代次数为80次，目标函数收敛阈值设定为0.01以内，以保证各组数据都能在给定的最大迭代次数范围内充分迭代.

图 1 OVERTHRUST 初始速度模型(a)和真实速度模型(b) Fig. 1 OVERTHRUST：The Starting velocity model and The true velocity model for FWI

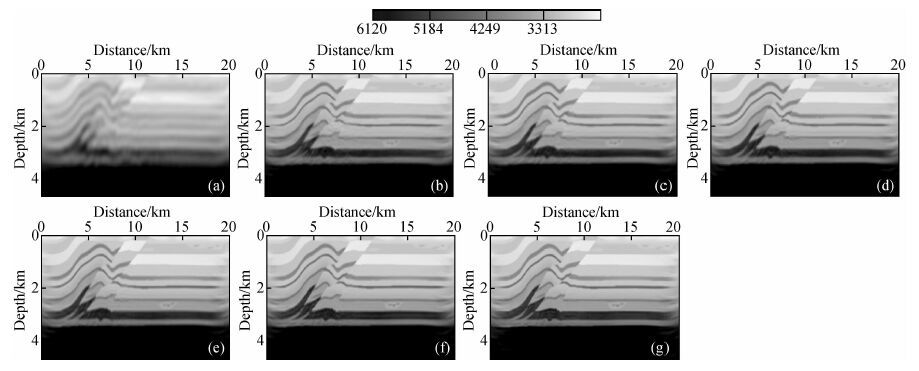
图 2中给出了七个频率迭代80次后所得到的反演结果.与图 1中的初始模型(υ0)相比，图 2中的反演模型的分辨率有不同程度的提高.由图 2中的各反演模型可知，当频点较低时，大尺度的速度信息可以显示出其轮廓；随着频点的升高，反演得到的大尺度速度信息更加精确，一些小尺度的速度构造信息也逐渐凸显出来，当频点较高时，这些小尺度的速度信息也越来越准确.由于大孔径和震源频带较窄现象的存在，导致观测系统的照明度较差，模型左右两侧边界在反演中未得到充分更新，因此模型左、右边侧边界区域内存在边界划弧现象.

图 2 七个频点分别反演的结果从(a)-(g)依次: 3.5 Hz, 5.75 Hz, 8.20 Hz, 9.66 Hz, 13.12 Hz, 16.39 Hz, 20.00 Hz. Fig. 2 The FWI model with 7 different frequencies from(a)to(g)is:3.5 Hz, 5.75 Hz, 8.20 Hz, 9.66 Hz, 13.12 Hz, 16.39 Hz, 20.00 Hz.

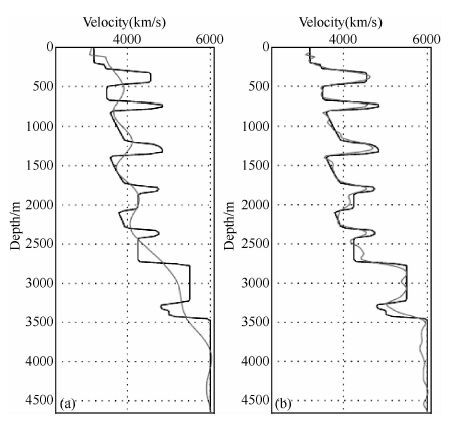
由于，x=6.25 km处是逆冲断层的位置，速度变化剧烈，因此分别给出了初始速度模型(a)和最终速度模型(b)与真实速度模型在水平方向x=6.25 km处提取的速度曲线对比图(图 3). 其中黑色实线代表真实速度，灰色曲线代表反演模型的速度.相比于初始速度模型，最终反演速度模型速度曲线与真实速度曲线几乎完全重合；但随着深度范围的增加，由于观测系统的照明度变差，误差还是相对明显.OVERTHRUST模型分析证明了全波形反演是一种高精度的建模手段，具有精细刻画地下及岩性构造的能力，能够反演出接近真实速度的速度模型.

图 3 速度曲线比较图 Fig. 3 Comparison of the velocity curve
2 逆时偏移理论及模型运算 2.1 逆时偏移理论

二维情况下，各向同性介质中的双程声波方程为

式中：vx和vz分别代表质点在x和z方向的振动速度，p为位移；v为纵波速度；ρ为密度.

对式(11) 通过交错网格空间(董良国等，2000)的高阶差分，得到其高阶差分格式为

其中Δx, Δz分别为x和z方向的差分步长；Δt为时间差分步长；N为差分阶数的一半；i, j为空间点序号；n代表时间点序号；Dk(N)为差分系数.

为了保证波场能够正常传播，式(3.2)需满足稳定性条件为

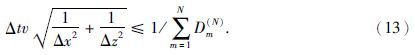
本文采用PML来消除由于边界反射而引起的反射波场问题，依据PML方程分裂思路(Berfenger, 1994)可得：

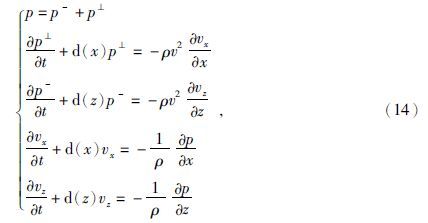
其中p⊥和p－分别代表p分量在x和z方向的分裂算子；d(x)、d(z)分别代表x和z方向的衰减因子.

由于逆时延拓算法具有一定的误差，在深部地层，检波点波场逆时延拓能量会出现衰减，采用上、下行波互相关成像条件(Claerbout, 1971)，偏移效果不好，因此本文采用归一化互相关成像条件(Kaelin and Guitton, 2007)(3.5)来优化偏移效果，公式为

上式称为归一化互相关成像条件.

2.2 OVERTHRUST模型分析比较

为了验证全波形反演对逆时偏移的影响，本文选取图 1中OVERTHRUST未经过反演的初始速度模型(v0)，真实速度模型vtrue, 和图 2中反演频率为9.66 Hz的反演速度模型(v4)，反演频率为20.00 Hz的反演速度模型(v7).选用主频为25 Hz的雷克子波作为震源，共35炮，每炮101道接受，在801*187的网格上采用上、下行波互相关成像条件对上述四种速度模型分别进行偏移.然后比较逆时偏移成像效果. 图 4依次展示了v0，v4，v7以及vtrue速度模型的偏移效果图，我们可以直观的看出，断层以及薄层的刻画随着速度模型精度的提高越来越清晰，分层越来越明显.

图 4 OVERTHRUST速度模型偏移结果从(a)-(d)依次为v0，v4，vfinal, 和vtrue. Fig. 4 the result of migration imaging of OVERTHRUST model From(a)to(g)is:v0，v4，vfinal, and vtrue.
3 结 论

本文把全波形反演与逆时偏移成像结合起来，通过对OVERTHRUST速度模型分析验证了全波形反演是一种高精度的建模手段，具有精细刻画地下介质分层以及岩性构造的能力，能够反演出接近真实速度的速度模型.对于复杂构造地区，为逆时偏移提供高精度的速度，理论上能够大大提高逆时偏移成像的精度，这种高精度速度建模对于我国复杂地区的油气勘探有重大意义.但是由于实际地区采集数据量比较大，全波形反演和逆时偏移计算量也比较大，对于计算机性能要求比较高，因此对实际地区数据处理存在一定困难.

致 谢 感谢丁仁伟老师、王守进等同学的大力支持和帮助，感谢审稿专家对文章提出的修改意见和编辑部老师的大力支持！

参考文献
[1] Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration[J]. Geophysics, 48(11): 1514-1524.
[2] Bednar J B, Stein J, Yoon K, et al. 2003a. An up and down walk in the two-way park[C].//2003 SEG Annual Meeting. Dallas, Texas: SEG, 877-880.
[3] Bednar J B, Yoon K, Shin C, et al. 2003b. One way vs two way wave equation imaging. Is two-way worth it?[C].//65th EAGE Annual Conference and Exhibition. BGS, EAGE.
[4] Berfenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 114(2): 185-200.
[5] Bian A F, Yu W H, Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics (in Chinese), 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037.
[6] Claerbout J F. 1971. Toward a unified theory of reflector mapping[J]. Geophysics, 36(3): 467-481.
[7] Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics (in Chinese), 43(3): 411-419.
[8] Du Q Z, Zhu Y T, Zhang M Q, et al. 2013. A study on the strategy of low wavenumber noise suppression for prestack reverse-time depth migration[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2391-2401, doi: 10.6038/cjg20130725.
[9] Gao F X, Liu C, Feng X, et al. 2013. Comparisons and analyses of several optimization methods in the application of frequency-domain full waveform inversion[J]. Progress in Geophysics (in Chinese), 28(4): 2060-2068, doi: 10.6038/pg20130450.
[10] He B S, Zhang H X, Wei X C, et al. 2010. Imaging conditions for two-way acoustic wave equation pre-stack reverse-time depth migration[J]. Oil Geophysical Prospecting (in Chinese), 45(2): 237-243.
[11] Kaelin B, Guitton A. 2007. Imaging condition for reverse time migration[C]./. 2006 SEG Annual Meeting. New Orleans, Louisiana: SEG, 2594-2598.
[12] Li G P, Yao F C, Shi Y M, et al. 2011. Pre-stack wave equation inversion and its application in frequency domain[J]. Oil Geophysical Prospecting (in Chinese), 46(3): 411-416.
[13] Liu L, Liu H, Zhang H, et al. 2013. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2447-2451, doi: 10.6038/cjg20130730.
[14] Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 49(5): 533-549.
[15] McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 31(3): 413-420.
[16] Mulder W A, Plessix R E. 2003. One-way and two-way wave-equation migration[C].//SEG Technical Program Expanded Abstracts 2003. SEG, 881-884.
[17] Pratt R, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 133(2): 341-362.
[18] Pratt R G. 1990. Frequency-domain elastic wave modeling by finite differences: a tool for crosshole seismic imaging[J]. Geophysics, 55(5): 626-632.
[19] Pratt R G. 1999. Seismic waveform inversion in the frequency domain, part I: theory and verification in a physical scale model[J]. Geophysics, 64(3): 888-901.
[20] Shi Y M, Zhang Y, Yao F C, et al. 2014. Methodology of seismic imaging for hydrocarbon reservoirs based on acoustic full waveform inversion[J]. Chinese Journal of Geophysics (in Chinese), 57(2): 607-617, doi: 10.6038/cjg20140224.
[21] Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 49(8): 1259-1266.
[22] Tarantola A. 1986. Strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 51(10): 1893-1903.
[23] Wang X W, Yang W Y, Lv B, et al. 2013. Grasp of the world geophysical technology development status, to promote seismic data processing and interpretation of technological progress[J]. Progress in Geophysics (in Chinese), 28(1): 224-239, doi: 10.6038/pg20130124.
[24] Whitmore N D. 1983. Iterative depth migration by backward time propagation[C].//SEG Technical Program Expanded Abstracts 1983. SEG, 382-385.
[25] Xu L, Meng X H, Liu G F. 2012. Reverse time migration and removing artifacts[J]. Progress in Geophysics (in Chinese), 27(4): 1548-1556, doi: 10.6038/j.issn.1004-2903.2012.04.031.
[26] Yang Q Y, Duan X B. 2010. Development status and trend of reverse time migration technology[J]. Geophysical Prospecting for Petroleum (in Chinese), 49(1): 92-98.
[27] Yoon K, Marfurt K J, Starr W. 2004. Challenges in reverse-time migration[C].//SEG Technical Program Expanded Abstracts 2004. SEG, 1057-1060.
[28] Zhang M G, Wang M Y. 2002. Poststack reverse-time depth migration for anisotropic elastic waves[J]. Geophysical Prospecting for Petroleum (in Chinese), 41(3): 259-263.
[29] 卞爱飞, 於文辉, 周华伟. 2010. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037.
[30] 董良国, 马在田, 曹景忠,等. 2000. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 43(3): 411-419.
[31] 杜启振, 朱钇同, 张明强,等. 2013. 叠前逆时深度偏移低频噪声压制策略研究[J]. 地球物理学报, 56(7): 2391-2401, doi: 10.6038/cjg20130725.
[32] 高凤霞, 刘财, 冯晅,等. 2013. 几种优化方法在频率域全波形反演中的应用效果及对比分析研究[J]. 地球物理学进展, 28(4): 2060-2068, doi: 10.6038/pg20130450.
[33] 何兵寿, 张会星, 魏修成,等. 2010. 双程声波方程叠前逆时深度偏移的成像条件[J]. 石油地球物理勘探, 45(2): 237-243.
[34] 李国平, 姚逢昌, 石玉梅,等. 2011. 频率域叠前波动方程反演及其应用[J]. 石油地球物理勘探, 46(3): 411-416.
[35] 刘璐, 刘洪, 张衡,等. 2013. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 56(7): 2447-2451, doi: 10.6038/cjg20130730.
[36] 石玉梅, 张研, 姚逢昌,等. 2014. 基于声学全波形反演的油气藏地震成像方法[J]. 地球物理学报, 57(2): 607-617, doi: 10.6038/cjg20140224.
[37] 王西文, 杨午阳, 吕彬,等. 2013. 把握世界物探技术发展现状, 促进地震资料处理、解释技术进步[J]. 地球物理学进展, 28(1): 224-239, doi: 10.6038/pg20130124.
[38] 许璐, 孟小红, 刘国峰. 2012. 逆时偏移去噪方法研究进展[J]. 地球物理学进展, 27(4): 1548-1556, doi: 10.6038/j.issn.1004-2903.2012.04.031.
[39] 杨勤勇, 段心标. 2010. 逆时偏移技术发展现状与趋势[J]. 石油物探, 49(1): 92-98.
[40] 张美根, 王妙月. 2002. 各向异性弹性波叠后逆时深度偏移[J]. 石油物探, 41(3): 259-263.