常规地震反演不能有效识别较薄的储层,不能满足生产的需要.研究者利用两种方法提高地震反演的分辨率.一种方法是将高频先验信息加入到地震反演中,如宽带约束反演(Mansfield,1983;杨谦和李正文,1996)、随机反演(Sams et al.,1999;Francis,2005;Srivastava and Sen.,2010;王保丽等,2015)等.宽带约束反演综合利用地质及测井资料,建立高分辨率阻抗作为初始模型,将地震资料作为约束条件,利用随机迭代算法对初始模型进行修正,从而得到高分辨率反演结果.该方法对初始模型的依赖性强,容易陷入局部极小值,在井少的工区,反演结果不可靠.随机反演也称为地质统计学反演.其实质是基于地震资料约束的测井信息的内插和外推,并利用随机模拟技术将不同尺度和方向上的数据相融合,反演结果分辨率较高,但多解性强、运算效率低,制约着该技术的应用.
另一种方法是拓宽地震频带减弱薄层调谐作用,从而提高反演结果的分辨率.这种方法对初始模型依赖较小,在少井的地区也可以得到较为合理的高分辨率反演结果,一直是地震反演的重点研究领域.谱反演技术(Puryear and Castagna,2008;Chopra et al.,2009;刘万金等,2013)在频域建立目标函数,充分利用地震资料中被压制的相对高频和相对低频信息,反演结果具有较高的分辨率,但也存在抗噪性差,可信度低,运算速度慢等问题.较为成熟的方法是分频反演,把地震资料分成多个频段,使用岭回归法分别进行反演并将反演结果累加,提高了反演分辨率(宿淑春和王晓华,2000).在这之后,研究者将振幅与频率的关系(AVF)作为独立信息引入叠后反演,获得了分辨率较高的反演结果(于建国等,2006);提出了多井约束分频非线性地震波阻抗反演算法,获得了低、中、高全频段合成波阻抗剖面(崔炯成等,2007);发展了AVA多频信息同时反演技术,将分频反演方法推广到叠前(张繁昌等,2014).分频反演虽然可以提高分辨率,但带通滤波产生的多频带数据体地质意义不明确,在拓宽频带的同时也引入了高频假象,降低了反演精度,分频和反演方法仍需改进.
层序地层学认为(Vail et al.,1977),层序体是组成沉积地质体的基本单元.地震资料是不同尺度层序体的综合响应,以较大级别层序体响应为主(杜世通,1998),低级别层序体受薄层调谐作用的影响,反射能量被压制而难以识别.小波变换(Chakraborty and Okaya,1995;高静怀等,1996,2006)具有良好的时频局部化性质,高频部分有较好的时间分辨率,低频部分有较好的频率分辨率.通过小波变换将地震数据转换为时频域,可以清晰地划分不同级别的层序体,识别较低级别的层序体(夏竹等,2005;赵军龙和李娜,2008;任金峰等,2013),在此基础上可将层序体的地震响应进行多尺度分解,并进行频谱特征分析,为后续地震反演奠定了基础.
本文将小波多尺度分频技术与贝叶斯反演算法(Li et al.,1996;黄捍东等,2011)相结合,通过典型沉积旋回模型分析,研究了沉积旋回体及地震响应的多尺度特征,阐明了多尺度反演的可行性.利用Morlet小波将地震资料分解为大、中、小三个层序尺度的数据体,在拓宽频带的同时,有效避免了高频假象,使得分频结果具有明确的地质意义.基于贝叶斯理论,根据先验信息与似然函数的关系,令后验概率最大化,建立目标函数,首先反演大尺度地震数据,突出地震低频信息,识别大套层序体;随后利用大尺度反演结果作为中尺度地震反演的约束项,得到中尺度反演波阻抗,还原了地震主频信息;最后利用中尺度反演结果作为约束项,进行小尺度地震反演得到最终结果.理论模型测试和实际地震资料反演表明,同常规稀疏脉冲反演相比,基于贝叶斯理论的多尺度反演对薄储层的分辨率有实质性提升.
1 多尺度地震反演原理 1.1 沉积旋回的多尺度特征由于沉积环境的影响,油气储集空间及地震响应具有多尺度特征.不同级别的层序体对应着不同的地震频带范围,满足镶嵌原理(杜世通,2004),用时频分析的方法可以将地震资料分解成反映不同尺度沉积旋回的地震数据体.本文通过对正旋回、反旋回、正反旋回、反正旋回等4种典型沉积旋回模型的研究,阐明了沉积旋回与地震响应的对应关系,为地震资料的分频及层序尺度的划分奠定了理论基础.
正旋回沉积模型见(图 1),自下而上沉积物颗粒由粗变细,地层厚度由厚变薄,底部厚层对应着大尺度地震同相轴,顶部薄层对应着小尺度地震同相轴.随着尺度的变小,其主频逐渐升高.模型顶部薄层由于调谐作用能量被压制,合成记录上难以被识别.分频技术能够把被压制的小尺度高频段提取出来,从而提高地震分辨率.
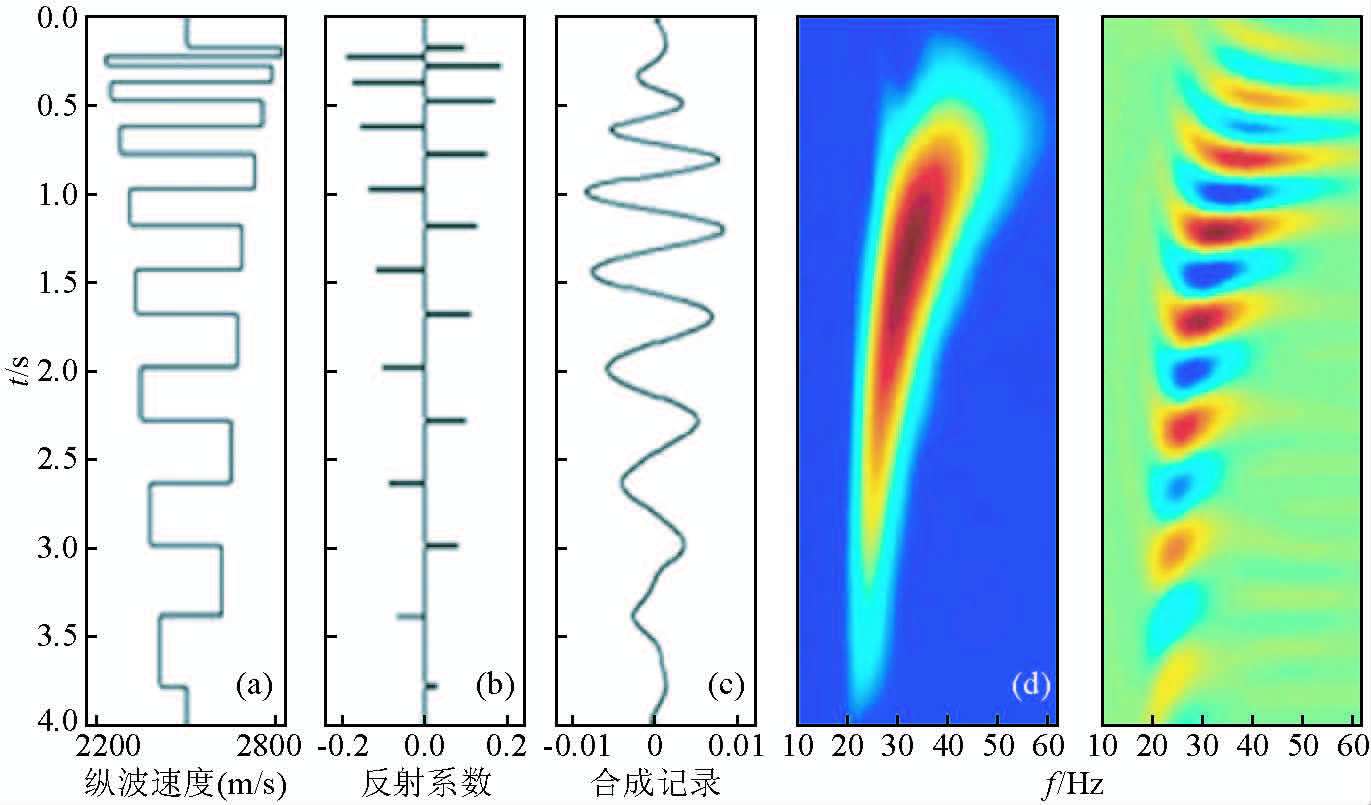
|
图 1 正旋回沉积模型
(a)速度模型;(b)反射系数;(c)合成记录;(d)时频分布. Fig. 1 Positive cycle sedimentary model (a)Velocity model;(b)Reflection coefficient;(c)Synthetic seismogram;(d)Time-frequency distribution. |
反旋回沉积模型见(图 2),自下而上,沉积物粒度由细变粗,地层厚度由薄变厚,相应的主频逐渐降低,地震同相轴逐渐变粗,底部薄层部分受调谐作用影响严重,合成记录无法识别,需要做分频处理.
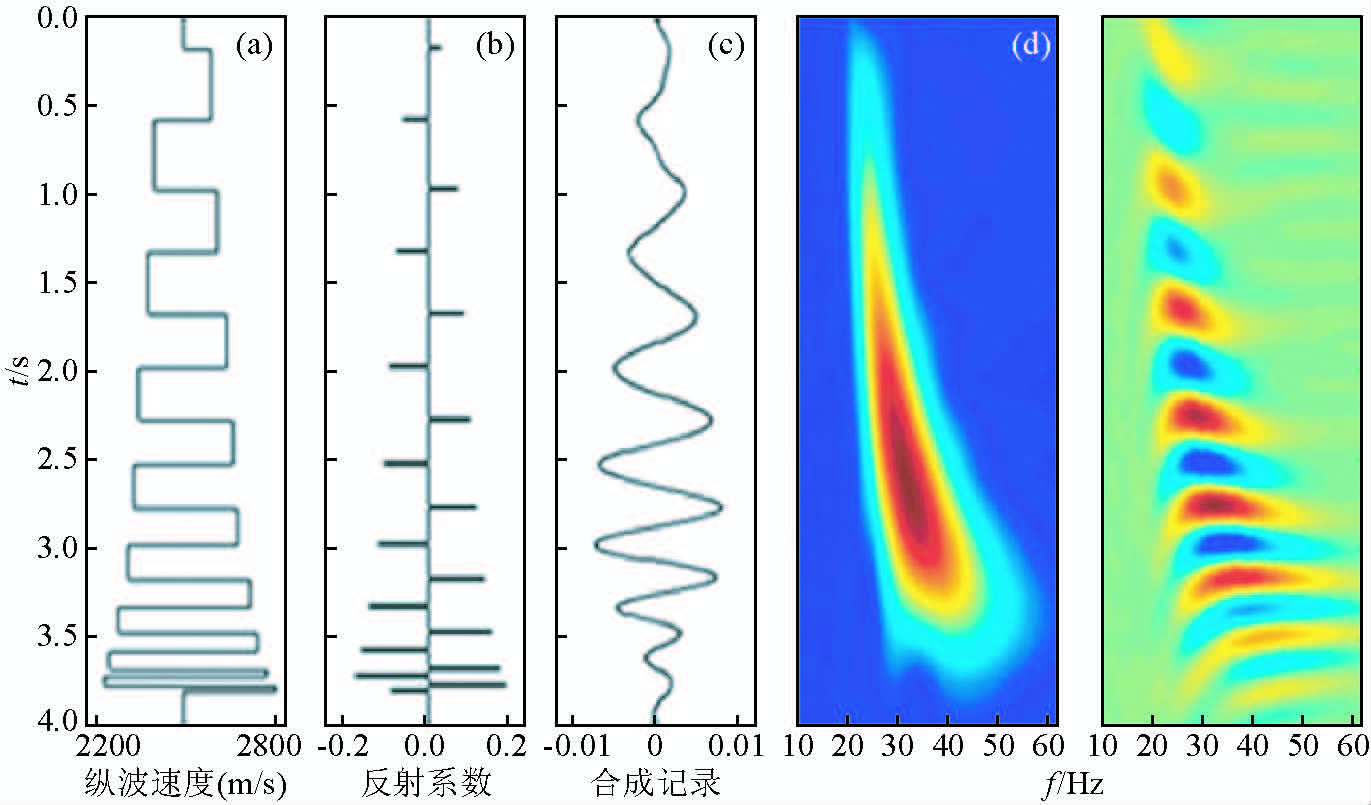
|
图 2 反旋回沉积模型
(a)速度模型;(b)反射系数;(c)合成记录;(d)时频分布. Fig. 2 Reverse cycle sedimentary model (a)Velocity model;(b)Reflection coefficient;(c)Synthetic seismogram;(d)Time-frequency distribution. |
正反旋回模型和反正旋回模型如图 3、图 4所示,从结构上看,两种旋回都是正旋回和反旋回的组合,其地震响应和频谱特征具有正旋回和反旋回的特点.时频分析表明,地震记录的低频信息主要反映大层序沉积组合(大尺度厚层),具有宏观性;高频信息主要反映大层序背景下的小层序沉积组合(小尺度薄层)具有微观性.这种对应关系是多尺度地震反演的理论依据.
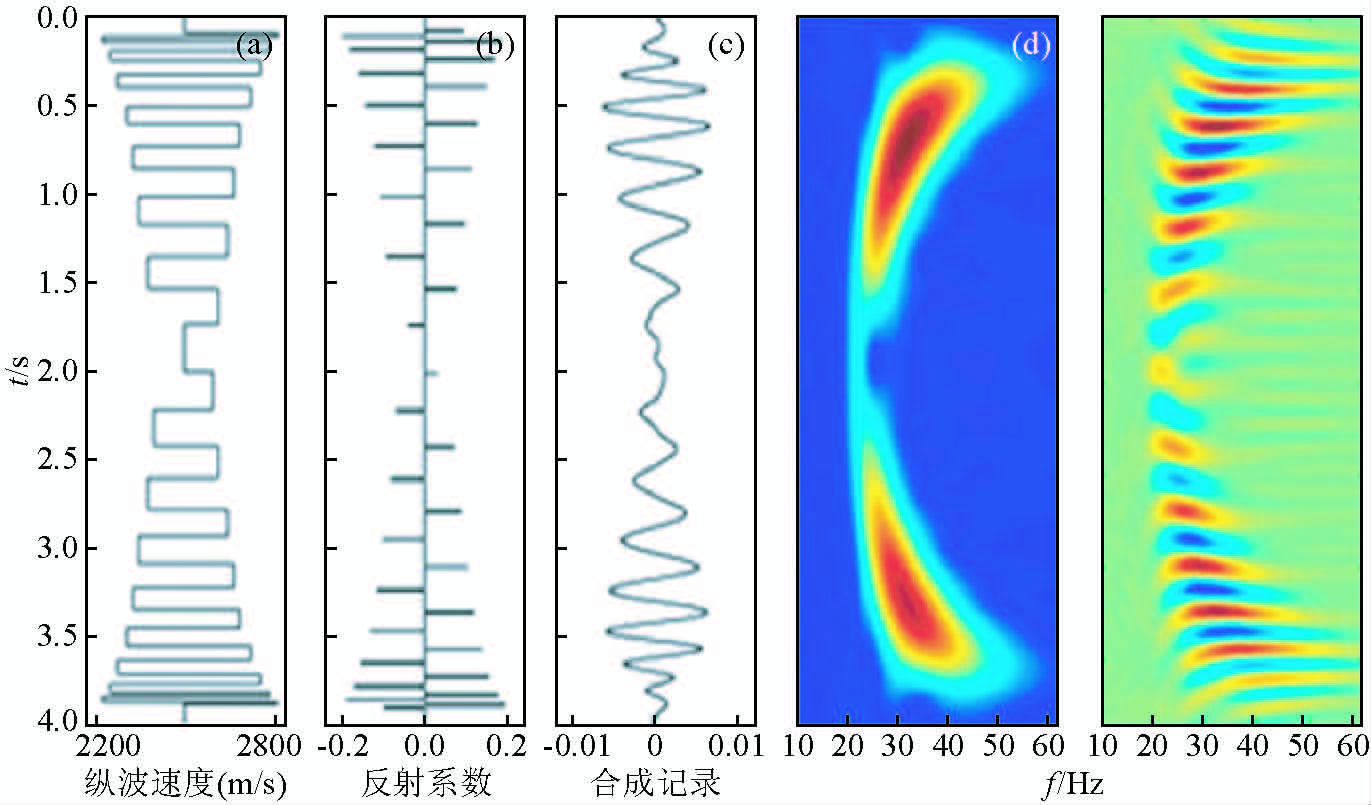
|
图 3 反正旋回沉积模型
(a)速度模型;(b)反射系数;(c)合成记录;(d)时频分布. Fig. 3 Reverse cycle and positive cycle combination sedimentary model (a)Velocity model;(b)Reflection coefficient;(c)Synthetic seismogram;(d)Time-frequency distribution. |
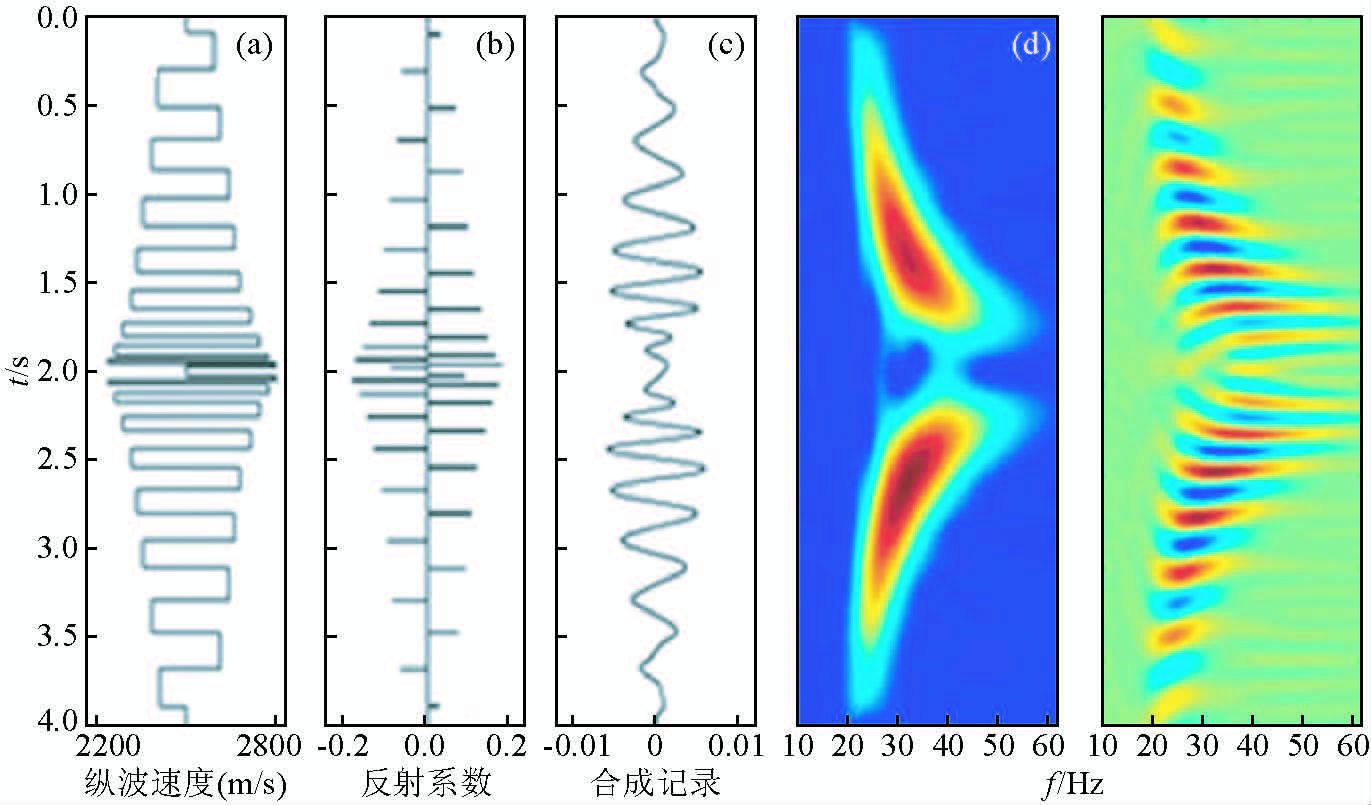
|
图 4 正反旋回沉积模型
(a)速度模型;(b)反射系数;(c)合成记录;(d)时频分布. Fig. 4 Positive cycle and reverse cycle combination sedimentary model (a)Velocity model;(b)Reflection coefficient;(c)Synthetic seismogram;(d)Time-frequency distribution. |
贝叶斯属于古老而又经典的数理统计学派,已被广泛应用在自然科学、经济心理学及市场研究等领域.八十年代末引入地震反演(Tarantola,1987),近些年受到了越来越多的关注(陈建江,印兴耀,2007;邸海滨等,2011;宋维琪等,2013;候栋甲等,2014),基于贝叶斯理论框架,将模型参数先验分布和观测数据结合起来形成后验概率密度分布,通过对后验分布优化求解得到唯一解,并对反演进行不确定性分析,验证反演的可靠性,为反演的目标函数构建赋予明确的数理意义.地震记录的褶积模型为
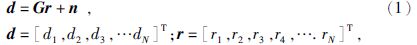
其中:d是实际观测地震数据,r为地层反射系数,G表示子波褶积矩阵,n表示噪声.在地震反演中,根据贝叶斯理论,反射系数的后验概率可以表示为
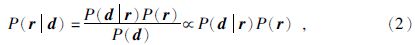
P(r|d)为反射系数的后验概率分布函数,是在观测地震数据基础上求得反射系数的概率分布.P(r)表示反射系数先验概率分布,表示人们在取得观测数据之前对反射系数模型参数的了解程度,在这里可以看成为使反演结果稳定而进行的约束.P(d|r)为似然函数,表示反射系数r与地震数据d之间的匹配程度.假设噪声表示人们在取得观测数据之前对反射系数模型参数的了解程度,假设观测噪声服从高斯分布,其似然函数可以为
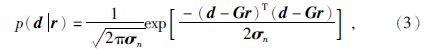
σn为噪声均方差.假设反射系数分布服从柯西分布,由此得到反射系数先验概率为
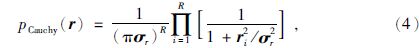
σr表示反射系数标准差,R为地层反射系数序列长度.为了反演结果更适定,引入先验信息如测井阻抗模型对反射系数做进一步约束.令I为地层波阻抗,在反射系数较小的条件下,反射系数表示为
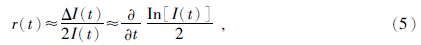
对上式两边积分,得到相对阻抗为
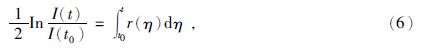
I(t0)为初始阻抗,将积分写成矩阵形式:ξ=Cr,其中:

根据(3)式,反射系数计算出来的相对阻抗与先验模型之间的误差满足方差为σw的高斯分布,在此条件下先验分布为
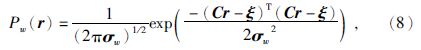
与(4)式相乘,得到整体先验分布表达式为
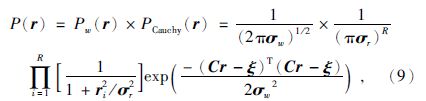
结合(9)式与(3)式代入(2)得到
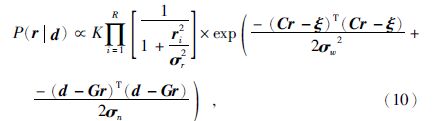
令后验概率最大化,最终推导反演方程为
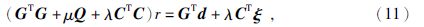
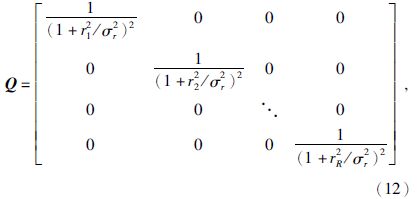
μ和λ分别为稀疏约束和阻抗约束因子,式(12)中对角线元素分母项加上了平方,与传统柯西分布推导出的Q不同,称之为修正柯西约束项(张繁昌等,2008).这样可以更好地保护弱反射系数,提高反演准确性.求解(11)式得到反射系数r之后,通过道积分(式13)即可得到波阻抗为
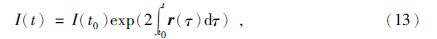
本文采用Morlet小波(Morlet et al.,1982;马朋善等,2007)作为基函数,将地震数据分解成大尺度低频地震数据体、中等尺度优势频带数据体、小尺度高频数据体.Morlet小波具有对称性及零相位特征,分解前后地震反射同相轴位置不发生变化.其表达形式为
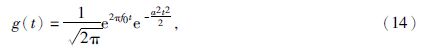
式中a为小波系数,控制小波的时频特征.利用贝叶斯反演算法,结合地层及井资料中的低频信息反演大尺度地震数据,得到大尺度的波阻抗体;将大尺度的波阻抗数据作为中等尺度地震数据反演的约束项(低频模型),得到中等尺度的波阻抗数据;最后用中等尺度的波阻抗数据作为小尺度地震数据反演的约束项(低频模型),最终得到小尺度的波阻抗数据作为最终波阻抗反演的结果.其反演过程如图 5所示.
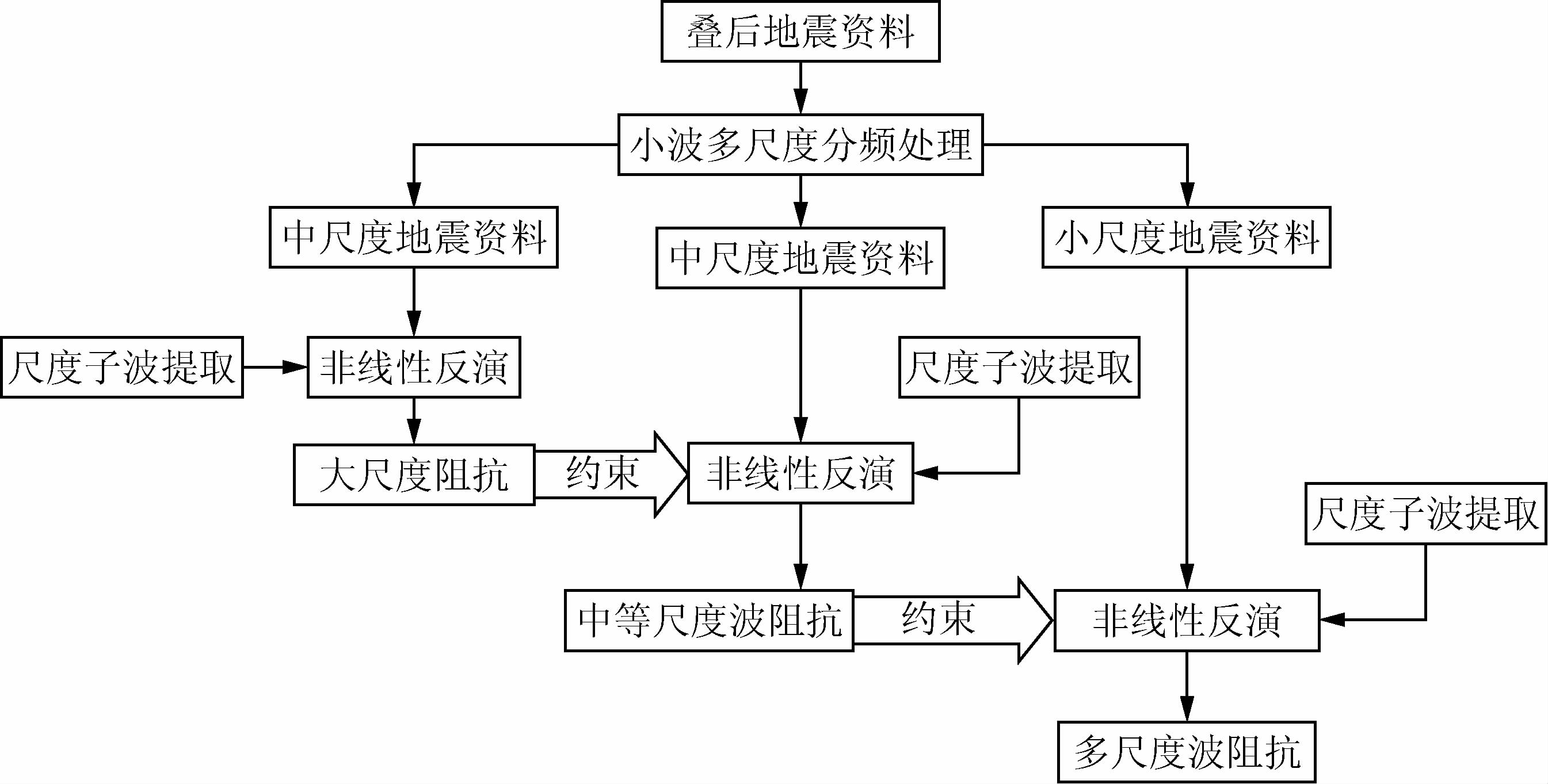
|
图 5 多尺度反演技术流程 Fig. 5 Multi-scale inversion technical process |
该方法首先将较大尺度的地质信息反演出来,以趋势约束的形式加入到较小尺度地震资料反演中,增强了较小尺度地震资料反演的可靠性.同多尺度联合反演(曹丹平等,2009)相比,这种逐级多尺度反演虽然加大了数据处理量,但由于反演是分尺度进行的,大尺度地震数据较平缓,反演结果准确,将其作为先验信息约束较小尺度反演,在一定程度上避免了之后的反演受局部极小点所困扰.整个反演过程是通过不断收缩目标函数尺度,逼近全局极小点实现的,这与多尺度逐级寻优思想相似(Bunks et al.,1995;朱成宏,1999;Sirgue and Pratt,2004;魏哲枫等,2014).从理论上来讲,本文方法较常规反演有更高的分辨率和准确性.
1.4 理论模型测试(1)选择测井原始波阻抗曲线作为模型数据,利用30 Hz的雷克子波与地层反射系数序列褶积合成地震记录,并加入30%的随机噪声以测试结果的稳定性.相关曲线及合成记录的时频分析结果如图 6所示.
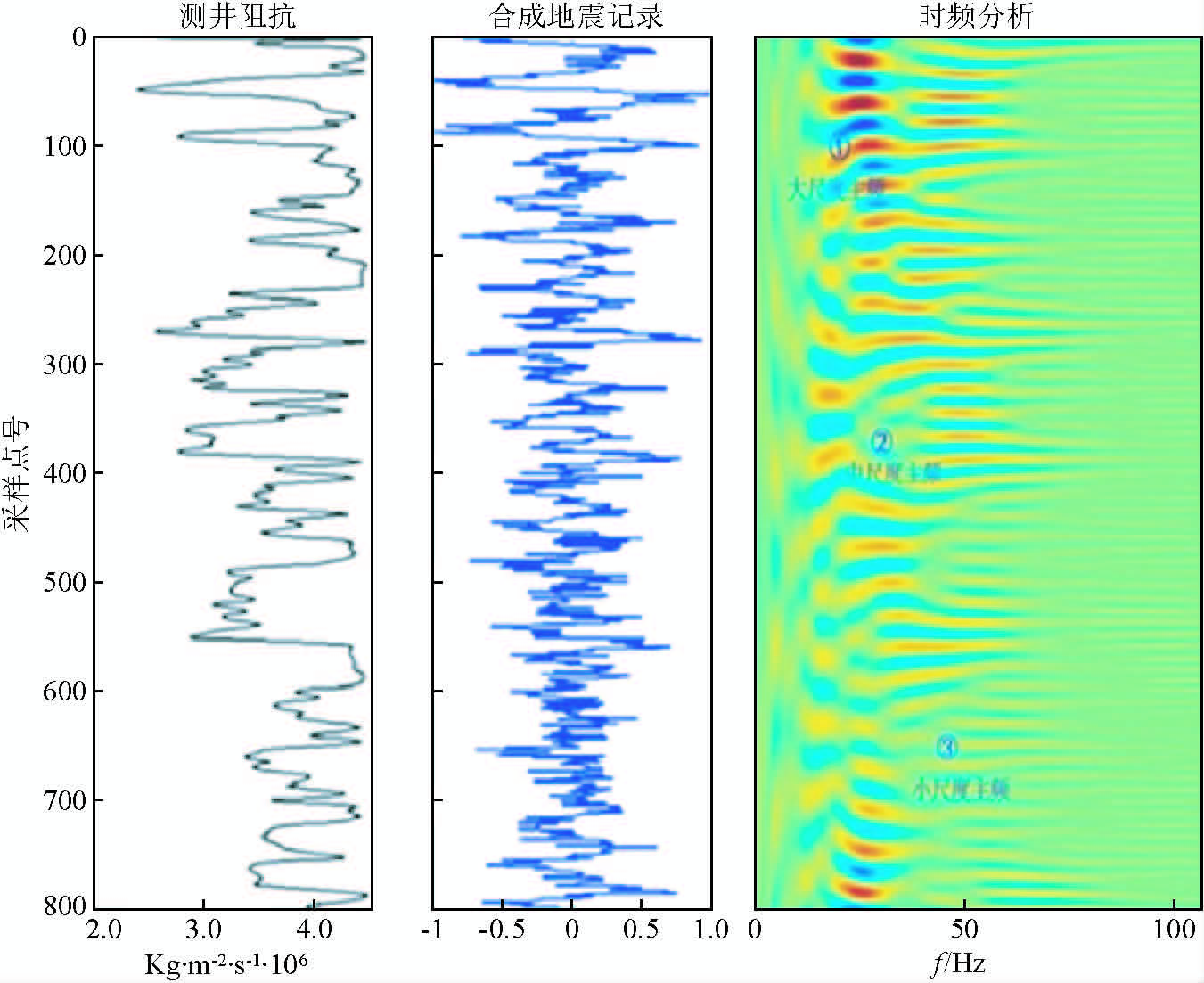
|
图 6 波阻抗模型及合成记录数据时频分析 Fig. 6 Impedance model and synthetic seismogram data time-frequency analysis |
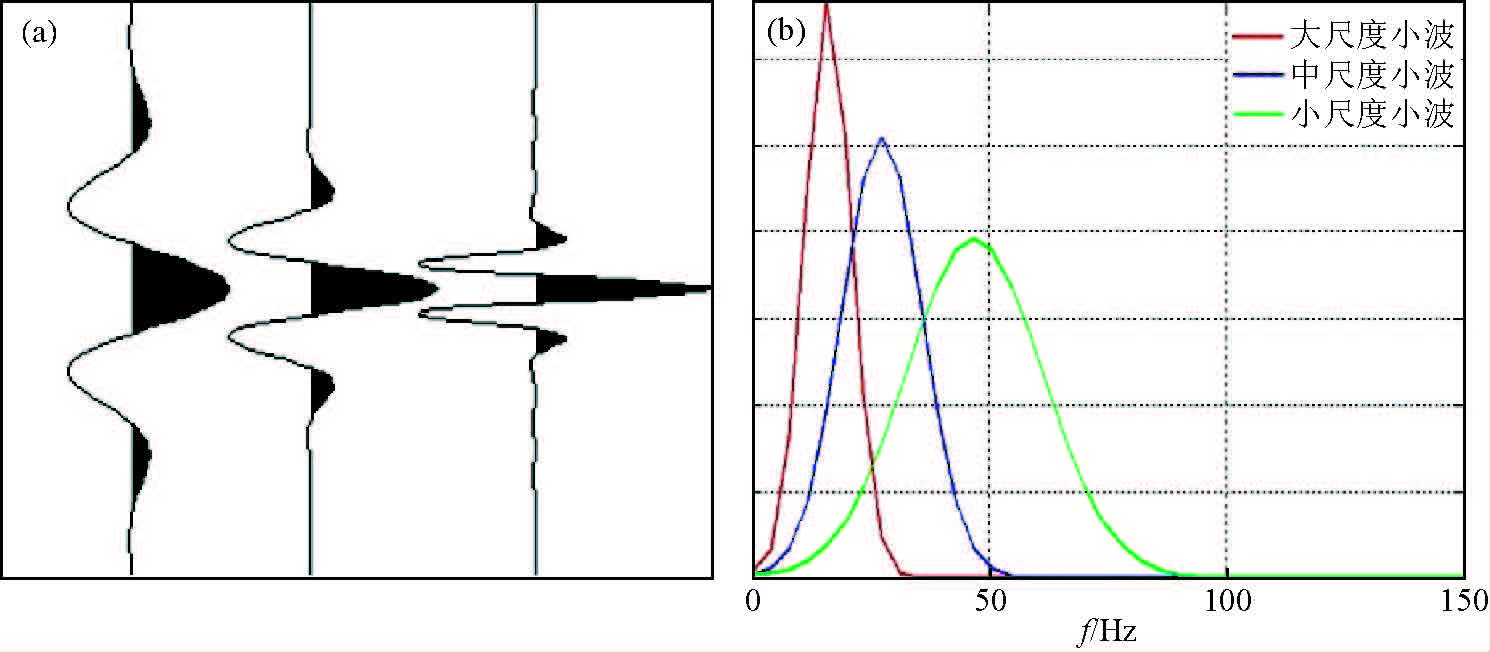
(2)时频分析结果表明,地震频带可划分为三个层序尺度,大尺度(10~25 Hz)、中尺度(25~40 Hz)、小尺(40 Hz以上),选取三个中心频带与三个层序尺度对应频带一致的Morlet小波作为滤波器如图 7所示,与地震记录褶积(高静怀等,1997),得到三个尺度的模型数据如图 8所示.
|
图 7 多尺度小波及频率分布
(a)多尺度的小波;(b)多尺度小波的频率分布. Fig. 7 Multi-scale wavelets and wavelet frequency distribution (a)Multi-scale wavelets;(b)Frequency distribution of multi-scale wavelet. |
|
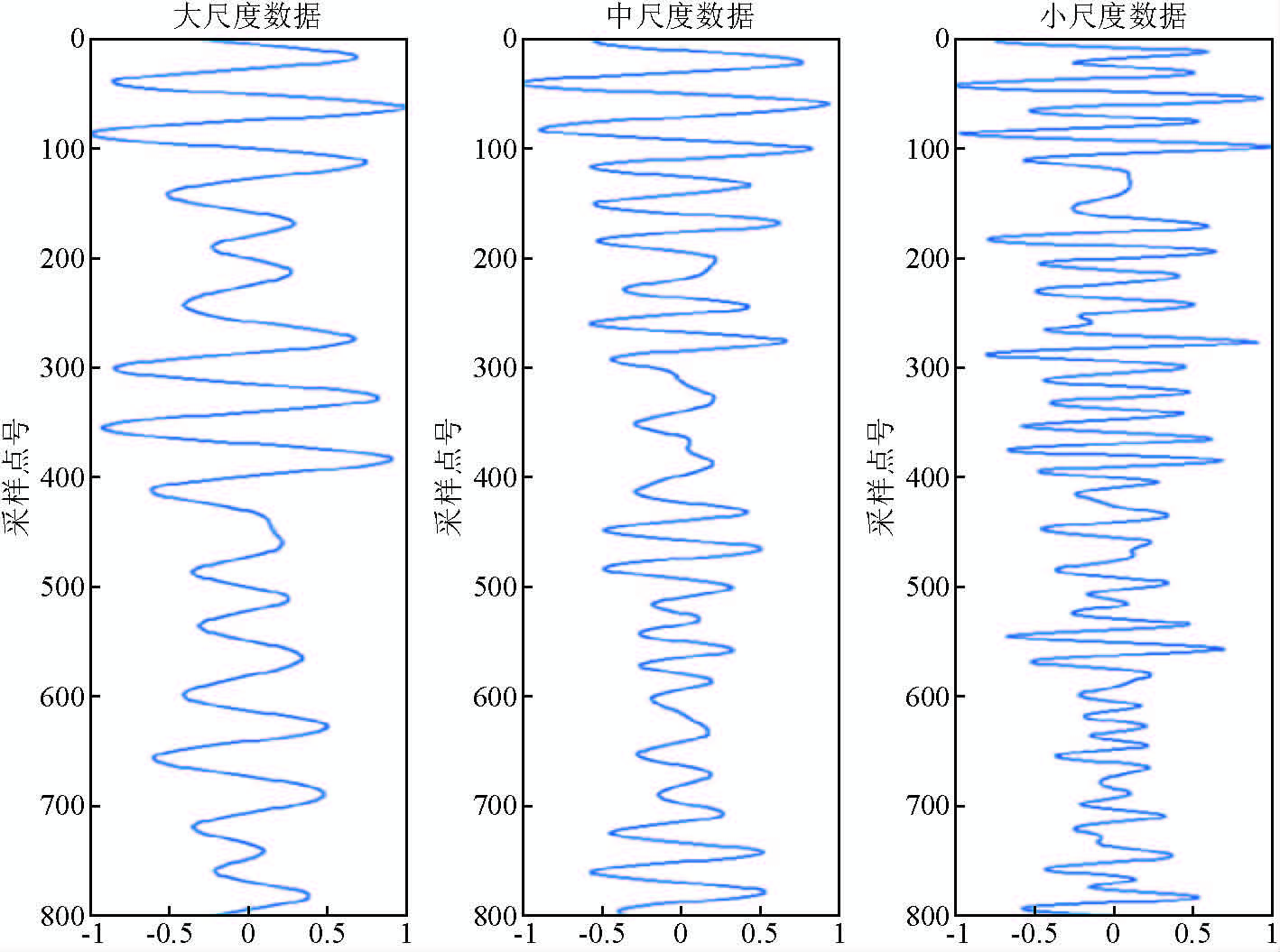
图 8 模型数据的多尺度分频结果 Fig. 8 Model data multi-scale frequency division results |
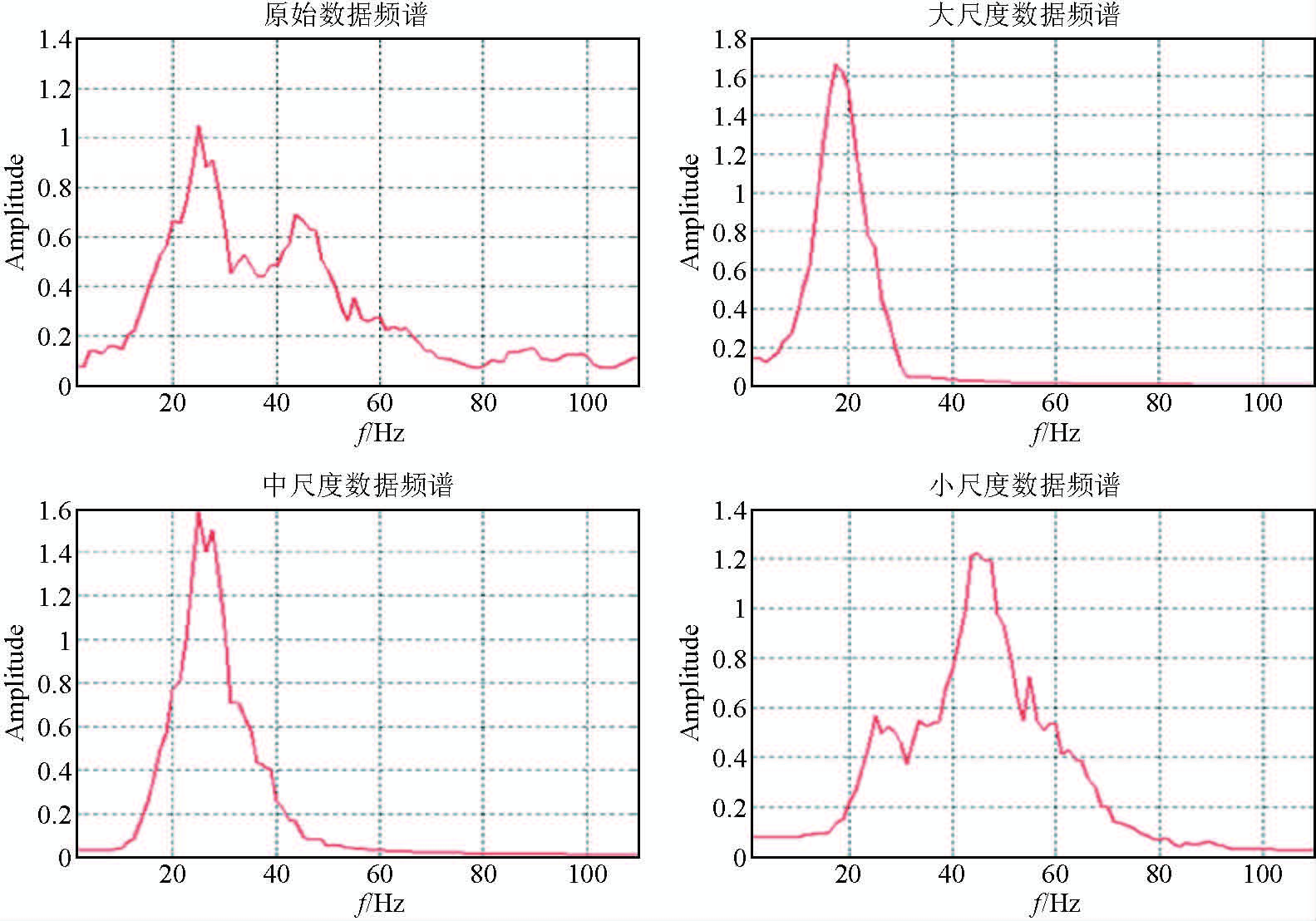
(3)小尺度数据在突出高频的同时也兼顾中低频信息,避免了高频假象,频谱分析如图 9所示,70 Hz以后的噪声能量被有效压制.小波分频不但可以提高分辨率,也在一定程度上压制了随机噪声.
|
图 9 多尺度模型数据的频谱 Fig. 9 Multi-scale model data frequency spectrums |
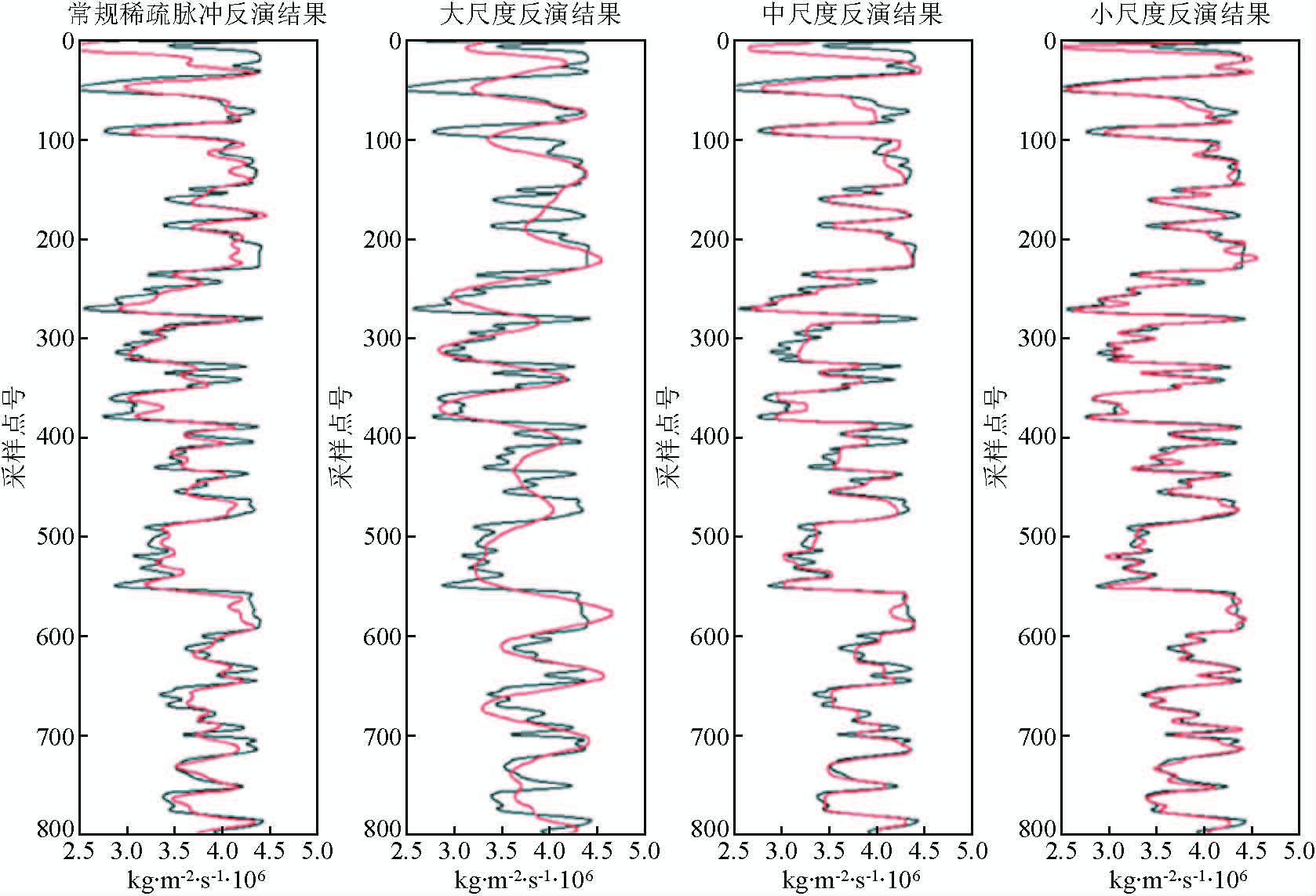
(4)多尺度反演与常规稀疏脉冲反演结果比较如图 10所示.图中黑色曲线表示测井阻抗,红色曲线为反演阻抗.多尺度反演阻抗逐步逼近真实值,验证了其逐级寻优特性,最终结果与原始模型吻合良好,能够有效识别较薄的小层,效果明显优于常规反演.
|
图 10 传统稀疏脉冲反演和多尺度反演阻抗的对比 Fig. 10 Conventional sparse pulse inversion with multi-scale inversion impedance contrast |
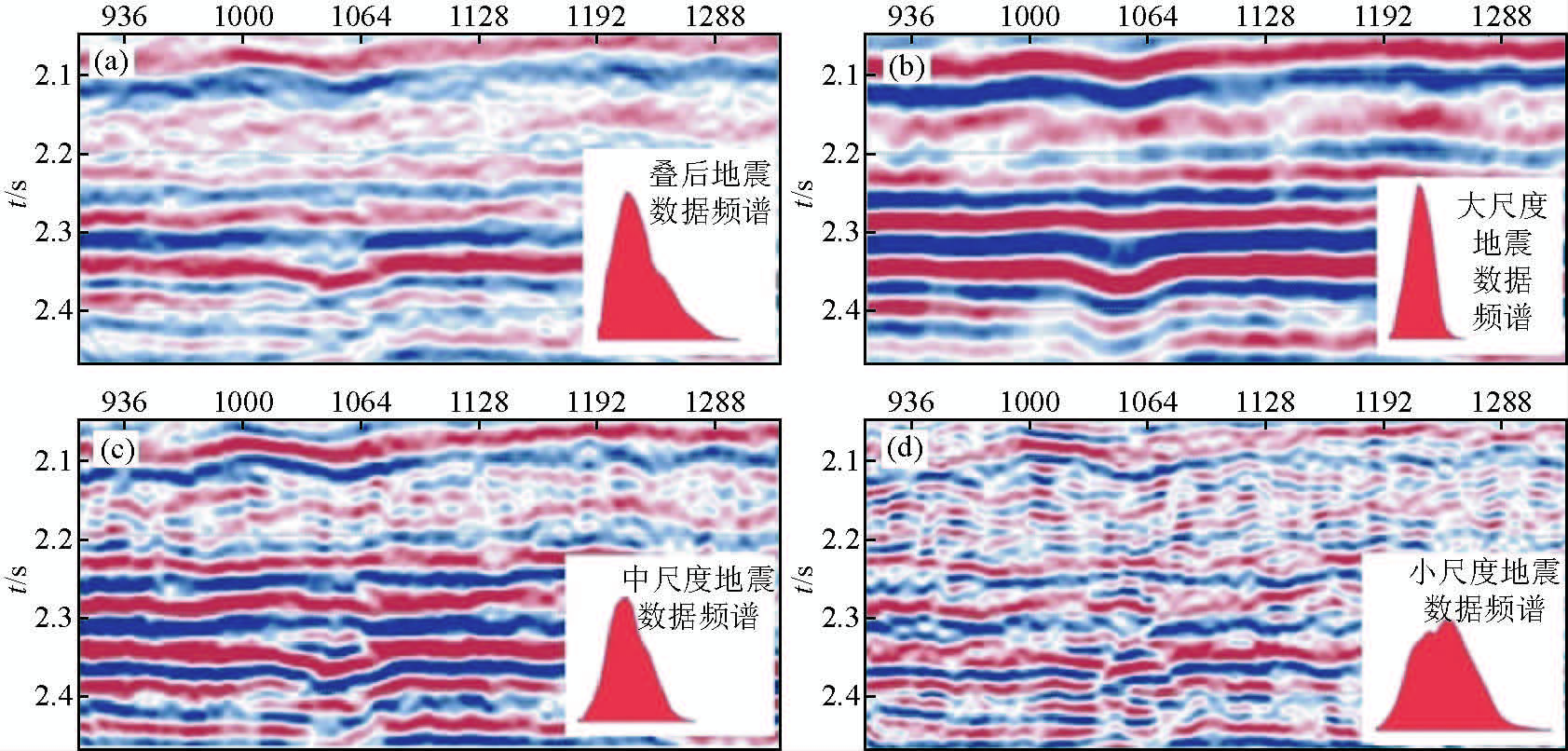
利用Morlet小波分析技术将实际地震资料进行分频处理,不同尺度的分频结果如图 11所示.不同尺度的地震资料对应着不同的频带范围,大尺度地震资料相对低频部分能量突出,反映大套地层沉积格架;中尺度为地震数据优势频带,分辨率比大尺度高反演中起衔接作用;小尺度剖面频带较宽,在提升高频信息的同时也适当保留了相对低频的信息,有效避免了高频假象.
|
图 11 叠后地震剖面与多尺度地震剖面
(a)叠后地震剖面图;(b)大尺度地震剖面图;(c)中尺度地震剖面图;(d)小尺度地震剖面图. Fig. 11 Post-stack seismic profile and multi-scale seismic sections (a)Post-stack seismic profile;(b)Large scale seismic profile;(c)Middle scale seismic profile;(d)Small scale seismic profile. |
叠后地震资料的大尺度和中尺度反演结果如图 12所示,反演阻抗与井的纵波阻抗曲线相一致,同大尺度反演结果相比,中尺度反演结果反映中厚层地层纵波阻抗的分布特征,频率明显升高;小尺度反演阻抗和常规方法反演结果的比较如图 13、图 14所示.多尺度反演纵波阻抗分辨率有很大提升,而且连续性好、抗噪性强,同井的波阻抗曲线吻合性好.
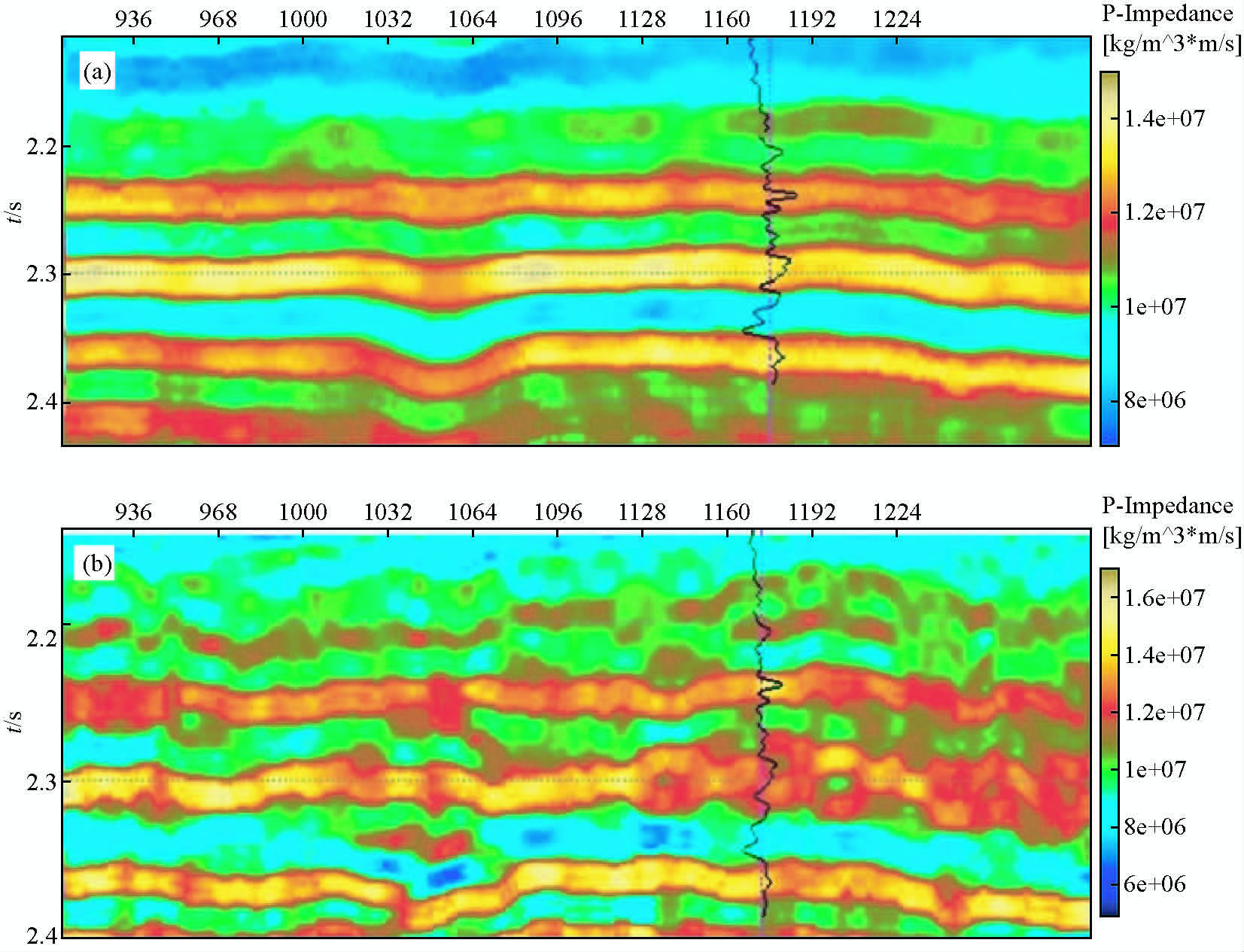
|
图 12 大尺度和中尺度纵波阻抗反演结果
(a)反演的大尺度纵波阻抗;(b)反演的中尺度纵波阻抗. Fig. 12 Large scale and middle scale P-wave impedance inversion results (a)Large-scale P-wave impedance inversion;(b)Middle scale P-wave impedance inversion. |
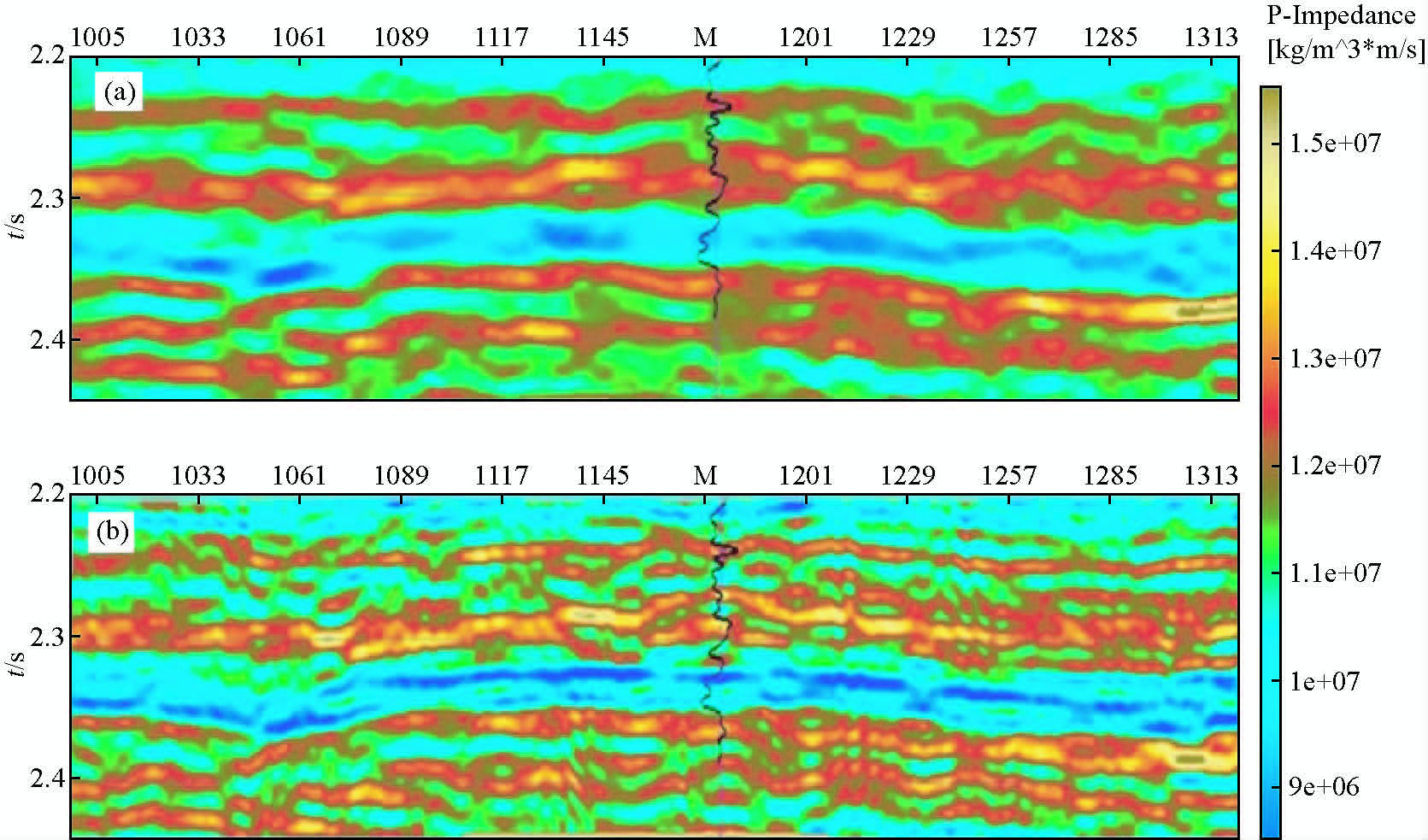
|
图 13 多尺度反演与常规反演阻抗对比剖面图
(a)常规反演的纵波阻抗剖;(b)多尺度反演的纵波阻抗. Fig. 13 Multi-scale inversion compared with the conventional inversion impedance section (a)Conventional inversion P-wave impedance;(b)Multi-scale inversion P- wave impedance. |
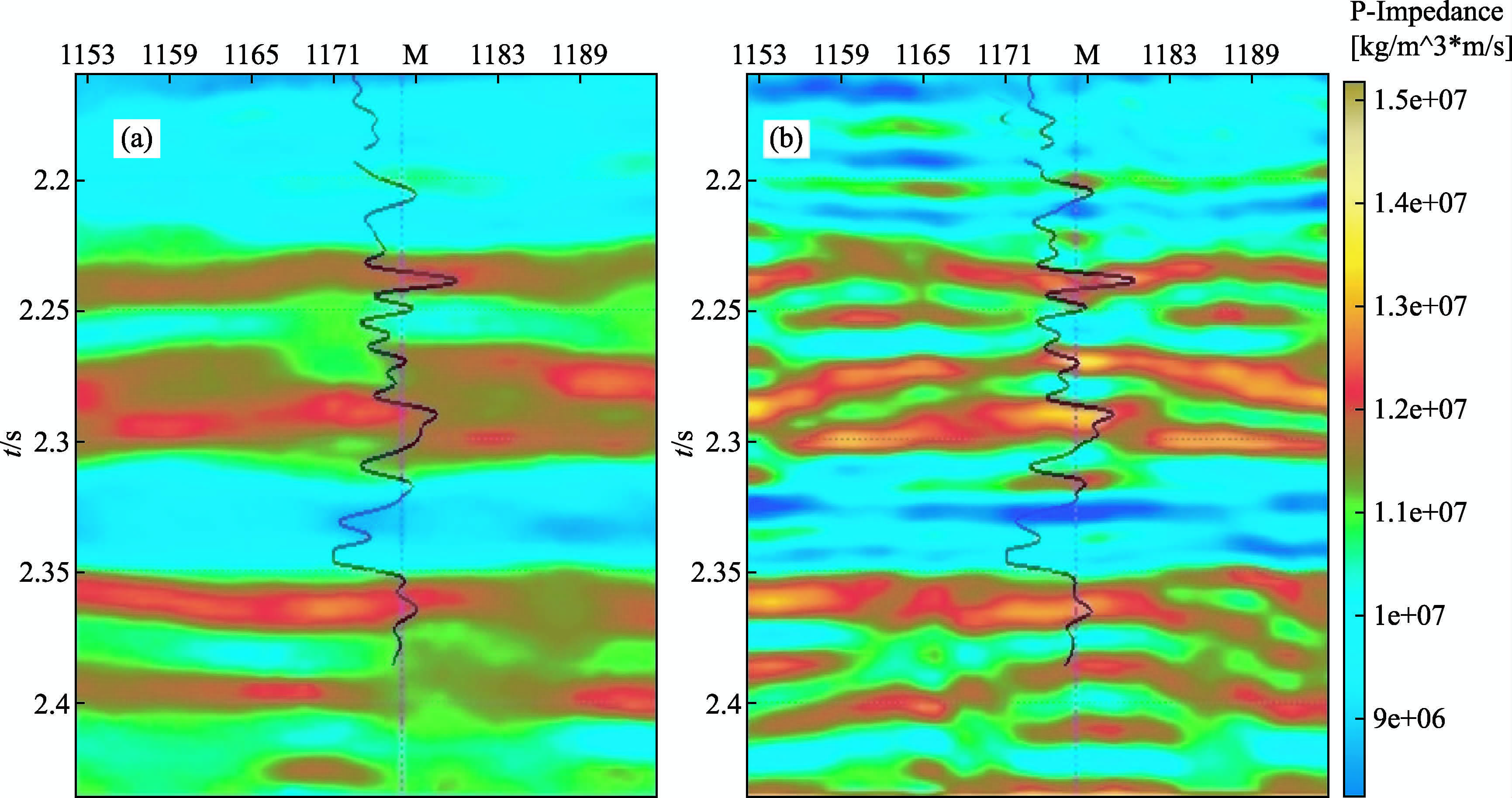
|
图 14 井旁多尺度反演与常规反演结果比较
(a)常规反演纵波阻抗;(b)多尺度反演纵波阻抗. Fig. 14 Multi-scale inversion compared with the conventional inversion impedance near the well (a)Conventional inversion P-wave impedance;(b)Multi-scale inversion P-wave impedance. |
M井的纵波阻抗、密度及岩性的交汇图,如图 15所示.砂岩为相对高阻抗,泥岩为相对低阻抗,纵波阻抗能够识别砂岩和泥岩.由于本工区为河流相沉积,砂岩物性差、厚度薄、连续性不好,常规稀疏脉冲反演的纵波阻抗受分辨率限制,难以有效识别薄层砂岩如图 16a所示,而多尺度反演纵波阻抗能够有效识别该砂岩如图 16b(图中标注位置).这些反演结果验证了本文方法的有效性.
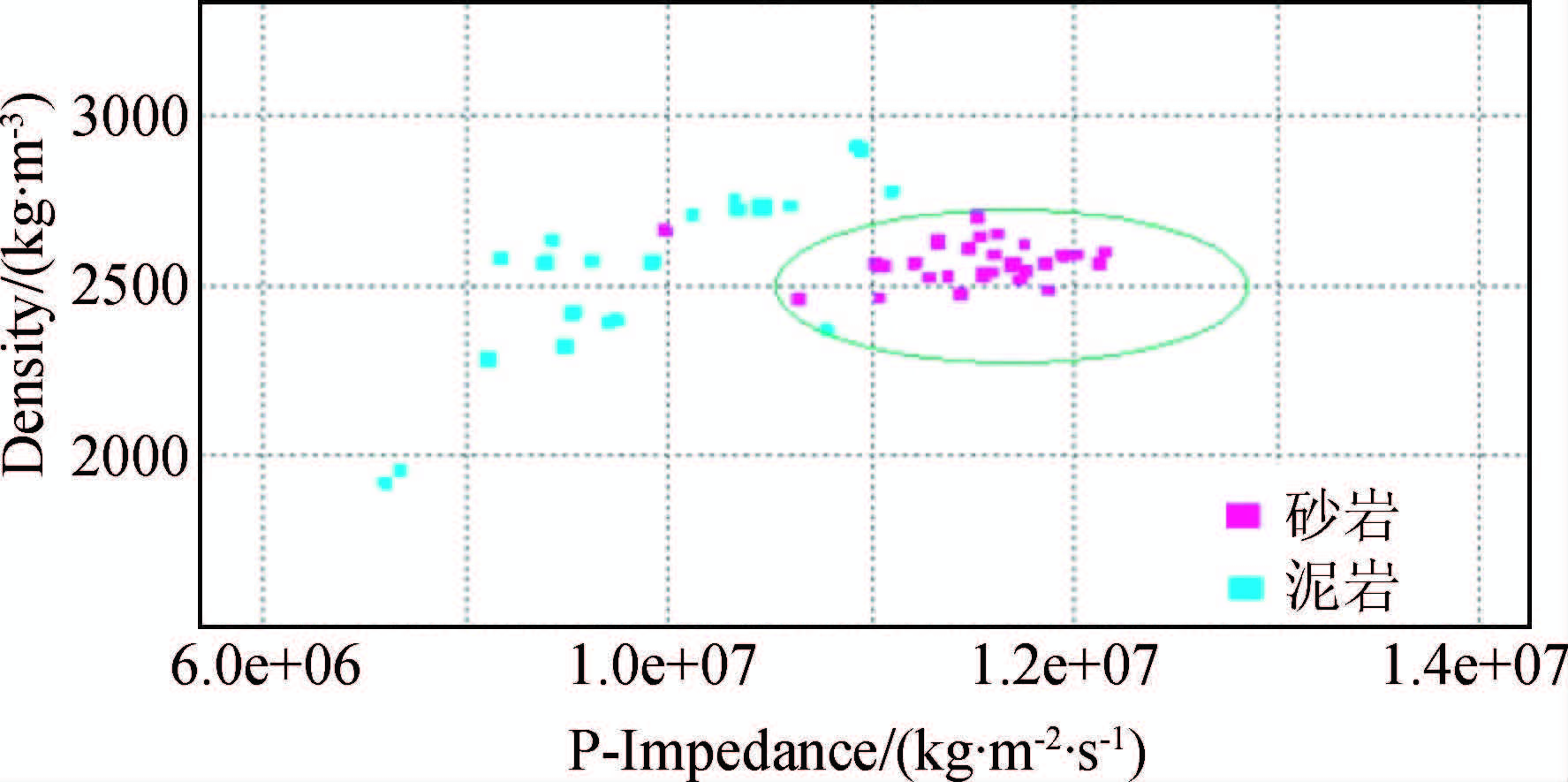
|
图 15 M井交汇图分析 Fig. 15 M well cross-plots analysis figure |

|
图 16 反演纵波阻抗和井的岩性对比剖面
(a)常规反演纵波阻抗;(b)多尺度反演纵波阻抗. Fig. 16 P-wave impedance inversion and well the lithology contrast section (a)Conventional inversion P-wave impedance;(b)Multi-scale inversion P-wave impedance. |
沉积层序体及其地震响应具有多尺度特征,不同尺度的层序体对应着不同频带范围的地震资料.在时频分析的基础上,本文利用Morlet小波分频技术把地震数据分解为三个尺度的数据体,有效避免了高频假象,保护了相对低频,恢复了调谐作用压制的相对高频信息,提升了地震资料的分辨率,为获得高分辨率的反演成果奠定了基础.基于贝叶斯理论的多尺度反演方法,将较大尺度的反演结果作为先验信息约束较小尺度的反演,在一定程度上避免了后续反演受局部极小点的困扰,逐级寻优逼近全局极小点,增强了反演的抗噪性和稳定性,对初始模型的依赖性较小.理论模型测试和实际应用表明,同常规稀疏脉冲反演相比,该方法反演结果对较薄储层的识别能力有实质性提升,验证了方法的先进性及实用性.
致 谢 感谢审稿专家和编辑部老师的辛勤工作!
| [1] | Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale Seismic waveform inversion[J]. Geophysics, 60(5): 1457-1473. |
| [2] | Cao D P, Yin X Y, Zhang F C, et al. 2009. A study on the method of joint inversion of multiscale seismic data[J]. Chinese J. Geophys. (in Chinese), 52(4): 1050-1067. |
| [3] | Chakraborty A, Okaya D. 1995. Frequency-time decomposition of seismic data using wavelet-based methods[J]. Geophysics, 60(6): 1906-1916. |
| [4] | Chen J J, Yin X Y. 2007. Three-parameter AVO waveform inversion based on Bayesian theorem[J]. Chinese Journal of Geophysics (in Chinese), 50(4): 1251-1260. |
| [5] | Chopra S, Castagna J, Xu Y. 2009. Thin-bed reflectivity inversion and some applications[J]. First Break, 27: 17-24. |
| [6] | Cui J C, Wu M, Li W X, et al. 2007. Nonlinear high-resolution impedance inversion method and its application[J]. Geophysical Prospecting for Petroleum (in Chinese), 46(1): 1-12. |
| [7] | Di H, Guo Y Q, Liu X W. 2011. Relative acoustic impedance inversion based on Cauchy sparseness constraint Bayesian estimation[J]. Geophysical Prospecting for Petroleum (in Chinese), 50(2): 124-128. |
| [8] | Du S T. 1998. Sequence model and seismic data high-resolution processing[J]. Petroleum Explorationist (in Chinese), (3): 17-23. |
| [9] | Du S T. 2004. The high-resolution seismic interpretation in the sequence framework[J]. Petroleum Geophysics (in Chinese), 2(4): 66-77. |
| [10] | Francis A. 2005. Limitations of deterministic and advantages of stochastic seismic inversion[J]. CSEG Recorder, 30(2): 5-11. |
| [11] | Gao J H, Wan T, Chen W C, et al. 2006. Three parameter wavelet and its applications to seismic data processing[J]. Chinese J. Geophys. (in Chinese), 49(6): 1802-1812. |
| [12] | Gao J H, Wang W B, Zhu G M, et al. 1996. On the choice of wavelet functions for seismic data processing[J]. Acta Geophysica Sinica (in Chinese), 39(3): 392-400. |
| [13] | Gao J H, Wang W B, Zhu G M. 1997. Wavelet transform and instantaneous attributes analysis[J]. Acta Geophysica Sinica (in Chinese), 40(6): 821-832. |
| [14] | Hou D J, Liu Y, Hu G Q, et al. 2014. Prestack multiwave joint inversion for elastic moduli based on Bayesian theory[J]. Chinese J. Geophys. (in Chinese), 57(4): 1251-1264, doi: 10.6038/cjg20140422. |
| [15] | Huang H D, Zhao D, Ren D Z, et al. 2011. A thin bed inversion method based on Bayes theory[J]. Oil Geophysical Prospecting (in Chinese), 46(6): 919-924. |
| [16] | Li X G, Sachhi M D, Ulrych T J. 1996. Wavelet transform inversion with prior scale information[J]. Geophysics, 61(5): 1379-1385. |
| [17] | Liu W J, Zhou H, Yuan S Y, et al. 2013. Applications of spectral inversion in the seismic attribute interpretation[J]. Oil Geophysical Prospecting (in Chinese), 48(3): 423-428. |
| [18] | Ma P S, Wang J Q, Liu L X, et al. 2007. Application of Morlet wavelet frequency-division processing in enhancing the seismic data resolution[J]. Geophysical Prospecting for Petroleum (in Chinese), 46(3): 283-287. |
| [19] | Mansfield G. 1989. Interactive broadband constrained inversion[J]. Exploration Geophysics, 20(2): 253-255. |
| [20] | Morlet J, Arens G, Fourgeau E, et al. 1982. Wave propagation and sampling theory: Part I ---Complex signal and scattering in multilayered media[J]. Geophysics, 47(2): 203-221. |
| [21] | Puryear C I, Castagna J P. 2008. Layer-thickness determination and stratigraphic interpretation using spectral inversion: theory and application[J]. Geophysics, 73(2): R37-R48. |
| [22] | Ren J F, Liao Y T, Sun M, et al. 2013. A method for quantitative division of sequence stratigraphy with high-resolution based on wavelet transform and its application[J]. Progress in Geophysics (in Chinese), 28(5): 2651-2658, doi: 10.6038/pg20130546. |
| [23] | Sams M S, Atkins D, Siad N, et al. 1999. Stochastic inversion for high resolution reservoir characterisation in the Central Sumatra Basin[C].// SPE Asia Pacific Improved Oil Recovery Conference. Kuala Lumpur, Malaysia: Society of Petroleum Engineers, 257-260. |
| [24] | Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 69(1): 231-248. |
| [25] | Song W Q, Gao Y K, Zhu H W. 2013. The differential evolution inversion method based on Bayesian theory for micro-seismic data[J]. Chinese J. Geophys. (in Chinese), 56(4): 1331-1339, doi: 10.6038/cjg20130427. |
| [26] | Srivastava R P, Sen M K. 2010. Stochastic inversion of prestack seismic data using fractal-based initial models[J]. Geophysics, 75(3): R47-R59. |
| [27] | Su S C, Wang X H. 2000. Development of dividing frequency impedance inversion and its application [J]. Journal of China University of Petroleum, China (in Chinese), 24(1): 85-87. |
| [28] | Tarantola A. 1987. Inverse problem theory: Methods for data fitting and model parameter estimation[M]. America: Elsevier Science Publ. Co., 245-357. |
| [29] | Wang B L, Yin X Y, Ding L X, et al. 2015. Study of fast stochastic inversion based on FFT-MA spectrum simulation [J]. Chinese J. Geophys. (in Chinese), 58(2): 664-673, doi: 10.6038/cjg20150227. |
| [30] | Wei Z F, Gao H W, Zhang J F. 2014. Time-domain full waveform inversion based on an irregular-grid acoustic modeling method[J]. Chinese J. Geophys. (in Chinese), 57(2): 586-594, doi: 10.6038/cjg20140222. |
| [31] | Xia Zhu, Liu Chao-Ying, Wei Wen-Bo, et al. 2005. Frequency attributes characters of seismic traces in time domain and division of stratigraphic sequence[J]. Oil Geophysical Prospecting (in Chinese), 40(5): 550-560. |
| [32] | Yang Q, Li Z W. 1996. Broadband constrained inversion of data and its application[J]. Geophysical Prospecting for Petroleum (in Chinese), 35(4): 37-42. |
| [33] | Yu J G, Han W G, Liu L H. 2006. Frequency-divided inversion and application[J]. Oil Geophysical Prospecting (in Chinese), 41(2): 193-197. |
| [34] | Zhang F C, Liu J, Yin X Y, et al. 2008. Modified Cauchy-constrained seismic blind deconvolution[J]. Oil Geophysical Prospecting (in Chinese), 43(4): 391-396. |
| [35] | Zhang F C, Dai R H, Liu H Q, et al. 2014. Multi-frequency information joint inversion of AVA prestack seismic data[J]. Oil Geophysical Prospecting (in Chinese), 43(4): 453-460. |
| [36] | Zhao J L, Li N. 2008. Application of wavelet transform to high resolution sequence analysis[J]. Progress in Geophysics (in Chinese), 23(4): 1230-1235. |
| [37] | Zhu C H. 1999. Multiscale acoustic impedance inversion using poststack seismic data[J]. Geophysical Prospecting for Petroleum (in Chinese), 38(2): 20-30. |
| [38] | 曹丹平, 印兴耀, 张繁昌,等. 2009. 多尺度地震资料联合反演方法研究[J]. 地球物理学报, 52(4): 1059-1067. |
| [39] | 陈建江, 印兴耀. 2007. 基于贝叶斯理论的AVO三参数波形反演[J]. 地球物理学报, 50(4): 1251-1260. |
| [40] | 崔炯成, 吴眉, 李维新,等. 2007. 高分辨率非线性地震波阻抗反演方法和应用[J]. 石油物探, 46(1): 1-12. |
| [41] | 邸海滨, 郭玉倩, 刘喜武. 2011. 基于稀疏约束贝叶斯估计的相对波阻抗反演[J]. 石油物探, 50(2): 124-128. |
| [42] | 杜世通. 1998. 层序模型与地震资料高分辨率处理[J]. 勘探家, (3): 17-23. |
| [43] | 杜世通. 2004. 层序框架下的地震高分辨率资料解释[J]. 油气地球物理, 2(4): 66-77. |
| [44] | 高静怀, 万涛, 陈文超,等. 2006. 三参数小波及其在地震资料分析中的应用[J]. 地球物理学报, 49(6): 1802-1812. |
| [45] | 高静怀, 汪文秉, 朱光明,等. 1996. 地震资料处理中小波函数的选取研究[J]. 地球物理学报, 39(3): 392-400. |
| [46] | 高静怀, 王文秉, 朱光明. 1997. 小波变换与信号瞬时特征分析[J]. 地球物理学报, 40(6): 821-832. |
| [47] | 候栋甲, 刘洋, 胡国庆,等. 2014. 基于贝叶斯理论的叠前多波联合反演弹性模量方法[J]. 地球物理学报, 57(4): 1251-1264, doi: 10.6038/cjg20140422. |
| [48] | 黄捍东, 赵迪, 任敦占,等. 2011. 基于贝叶斯理论的薄层反演方法[J]. 石油地球物理勘探, 46(6): 919-924. |
| [49] | 刘万金, 周辉, 袁三一,等. 2013. 谱反演在地震属性解释中的应用[J]. 石油地球物理勘探, 48(3): 423-428. |
| [50] | 马朋善, 王继强, 刘来祥,等. 2007. Morlet小波分频处理在提高地震资料分辨率中的应用[J]. 石油物探, 46(3): 283-287. |
| [51] | 任金峰, 廖远涛, 孙鸣,等. 2013. 基于小波变换的高精度层序地层定量划分研究及其应用[J]. 地球物理学进展, 28(5): 2651-2658, doi: 10.6038/pg20130546. |
| [52] | 宋维琪, 高艳珂, 朱海伟. 2013. 微地震资料贝叶斯理论差分进化反演方法[J]. 地球物理学报, 56(4): 1331-1339, doi: 10.6038/cjg20130427. |
| [53] | 宿淑春, 王晓华. 2000. 分频波阻抗反演方法及其应用[J]. 石油大学学报, 24(1): 85-87. |
| [54] | 王保丽, 印兴耀, 丁龙翔,等. 2015. 基于FFT-MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 58(2): 664-673, doi: 10.6038/cjg20150227. |
| [55] | 魏哲枫, 高红伟, 张剑锋. 2014. 基于非规则网格声波正演的时间域全波形反演[J]. 地球物理学报, 57(2): 586-594, doi: 10.6038/cjg20140222. |
| [56] | 夏竹, 刘超颖, 魏文博,等. 2005. 地震道时间域频率属性特征和地层层序划分[J]. 石油地球物理勘探, 40(5): 550-560. |
| [57] | 杨谦, 李正文. 1996. 地震资料宽带约束反演方法及应用[J]. 石油物探, 35(4): 37-42. |
| [58] | 于建国, 韩文功, 刘力辉. 2006. 分频反演方法及应用[J]. 石油地球物理勘探, 41(2): 193-197. |
| [59] | 张繁昌, 刘杰, 印兴耀,等. 2008. 修正柯西约束地震盲反褶积方法[J]. 石油地球物理勘探, 43(4): 391-396. |
| [60] | 赵军龙, 李娜. 2008. 小波变换在高分辨率层序地层分析中的应用[J]. 地球物理学进展, 23(4): 1230-1235. |
| [61] | 朱成宏. 1999. 地震资料波阻抗多尺度反演[J]. 石油物探, 38(2): 20-30. |
 2016, Vol. 31
2016, Vol. 31

