2. 中国石油化工股份有限公司勘探分公司, 四川成都 610041;
3. 中国石油大学(华东)地球物理系, 山东青岛 266580
2. Sinopec Exploration Company, Chengdu 610041, China;
3. Department of Geophysics, China University of Petroleum, Shandong Qingdao 266580, China
渤海地区区块运动复杂,走滑断裂纵贯南北,多期构造反转使得其构造格局异常复杂.该地区的地震成像存在两个典型的难点和挑战:
(1)高陡构造较多,地层横向速度差别较大.
(2)浅层次生断层广为发育,常规偏移成果往往断点不清,剖面层次不清.
(3)潜山结构复杂,信噪比较低,往往成像质量较差.
因此,需要找到灵活、高效且具有较高精度的偏移方法来解决复杂构造的成像问题.Kirchhoff偏移是当前工业界普遍使用的深度域成像方法(Wiggins,1984; Docherty,1991; 徐升和Gilles,2006; 王华忠等,2010),具有灵活和高效的特点,但其依赖于常规的射线方法来计算地震波的旅行时.一方面,常规的射线方法存在焦散区及阴影区等缺陷,使得射线振幅参数所表示的加权函数的可靠性大打折扣;另一方面,若地下介质复杂,震源、接收点与地下成像点之间往往存在多次波至,现今大部分Kirchhoff偏移算法只选择其中的单次波至(最小走时或最大振幅),而单次波至往往难以对复杂构造进行有效成像,且其导致偏移算子的截断会造成大量的偏移噪声.虽然基于多值走时的Kirchhoff偏移算法在成像质量上得到了明显的提高(Operto et al.,2000; Koren et al.,2008),但是其计算效率明显降低.
作为一种多路径的成像方法,高斯束偏移兼具Kirchhoff偏移和波动方程偏移的优势,具有高效、灵活和较高精度的特点.Hill(1990,2001)先后提出了叠后与叠前高斯束偏移方法.Nowack等(2003)和Gray(2005)分别针对Hill方法对观测系统适应性的不足,提出共炮域高斯束偏移.Albertin等(2004)则提出了适用于共偏移距、窄方位角数据的真振幅高斯束偏移.在国内,李振春等(2010)提出了角度域高斯束保幅偏移,并且提取了角度域共成像点道集.岳玉波等(2011)基于反褶积成像条件提出了共炮域的保幅高斯束偏移方法.岳玉波等(2012)通过考虑起伏地表平面波的传播特点,直接在起伏地表进行局部平面波的分解,实现了一种适用于起伏地表的保幅高斯束偏移方法.黄建平等(2015a,2015b)先后基于声波介质和弹性波介质发展了一种更适应复杂地表情况的非倾斜叠加精确束偏移方法.袁茂林等(2015)则定性定量地分析了不同参数对高斯束偏移成像质量和计算效率的影响.
为了弥补高斯束偏移在处理低信噪比数据上的不足,Vinje等(2008)将提出了控制束偏移方法,并将其运用于盐丘底部成像、裂缝基底成像、宽方位角数据成像、低覆盖次数数据成像等方面.Casasanta等(Casasanta and Grion,2012;Casasanta et al.,2013)先后提出了共偏移距域和共炮域(共接收点域)的PS转换波控制束偏移成像方法.本文在高斯束偏移理论的基础上,通过在τ-p域进行相似度扫描并分析地震数据的能量分布特征,从而设定阈值以提取有效信号进行偏移.在实现这种改进的束偏移方法基础上,将其应用于渤海某探区实际资料处理.
1 高斯束偏移理论在二维标量各向同性介质中,假设地表水平,xs为震源,xr为接收点,x为成像点,u(xs,xr,ω)为接收到的地震波场.局部角度域高斯束叠前深度偏移的基本过程主要包括:1)由高斯束叠加积分表征向下延拓的震源波场;2)通过倾斜叠加,将地震记录分解为不同初始方向的局部平面波场;3)将震源波场和反向的记录波场进行延拓并成像.
首先,格林函数G(x,x0,ω)通过点源处x0出射的高斯束uGB(x,x0,ω)的叠加积分来表示(Hill,2001)公式为
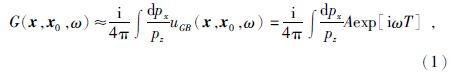
上式中,px,pz分别为中心射线初始慢度的水平和垂直分量;A,T为高斯束的复值振幅和走时.式(1)表示从点源x0到点x的地震波场,此地震波场由一系列高斯束叠加形成.
其次,反向延拓的地震波场U(x,xs,ω)可以通过Rayleigh II积分来表示,公式为
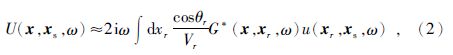
其中,G(x,xr,ω),θr分别为由接收点xr到成像点x的格林函数以及射线的出射角;Vr为接收点处的速度;*代表复共轭.
根据式(1),通过引入一个相位校正因子将格林函数G(x,xr,ω)由点xr附近束中心位置L出射的高斯束uGB(x,L,ω)的叠加积分来近似表征(Hill,2001).只需在相对于接收点xr更为稀疏的的束中心位置L处进行高斯束计算和波场延拓成像,从而有效的减少计算量.当xr同L距离较远时,反向延拓波场会存在一定的误差.为了减少误差,可以通过对地表观测排列加入一系列重叠的高斯窗,高斯窗的中心即为束中心.因此反向延拓的地震波场可以重写为
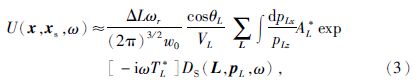
上式中,DS(L,pL,ω)为以束中心位置L为中心的高斯窗内地震波场的倾斜叠加,ΔL为束中心间隔,ωr为参考频率,w0为初始束宽.
最后,应用如下互相关成像条件进行偏移成像,公式为
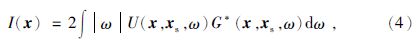
其中,U(x,xs,ω)和G(x,xs,ω)分别为反向延拓波场和震源格林函数,I(x)为单炮成像值.
利用式(1)表示震源格林函数,并结合式(3)表征的反向延拓波场,考虑到水平地表情况,根据最速下降法,可以得到高斯束偏移成像公式为
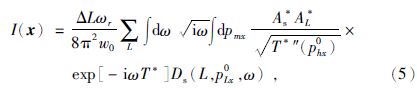
其中,T=Ts+TL为成像点处总的复值走时;Ts和As分别为成像点处对应着震源高斯波束的走时和振幅;TL和AL分别为成像点处对应着波束中心高斯波束的走时和振幅;T*″(phx0)为走时T的二阶导数项;pmx,phx为中心点和偏移距射线参数的水平分量,其与震源和波束中心射线参数的水平分量psx和pLx存在关系为
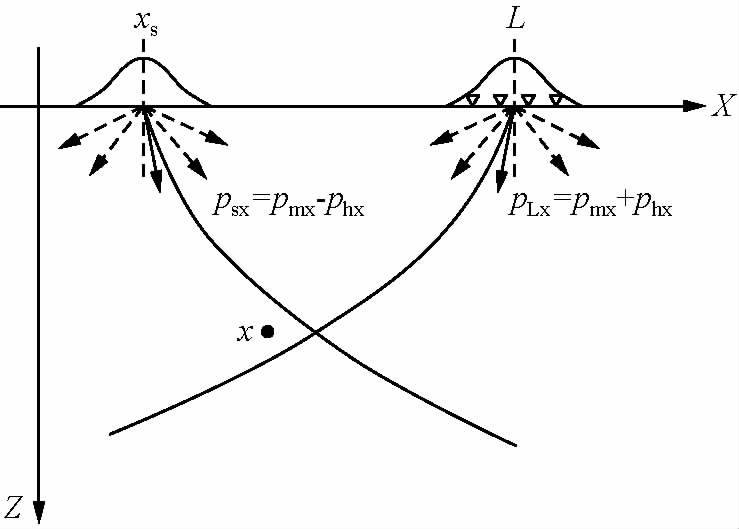
图 1为叠前高斯束偏移示意图.对于地下成像点x,对于一个固定的pmx,扫描phx,寻找使走时T的虚部最小的临界值phx0,根据式(6)求出对应的临界值pLx0、psx0,然后计算出psx0对应的高斯束振幅As和走时Ts,并计算出pLx0对应的倾斜叠加数据Ds(L,pLx0,ω)以及高斯束振幅AL和走时TL,最终可以得到一个束中心位置L的成像值.单炮偏移的成像值是所有束中心位置成像结果的叠加.
|
图 1 叠前高斯束偏移示意图 Fig. 1 The sketch of prestack Gaussian beam migration |
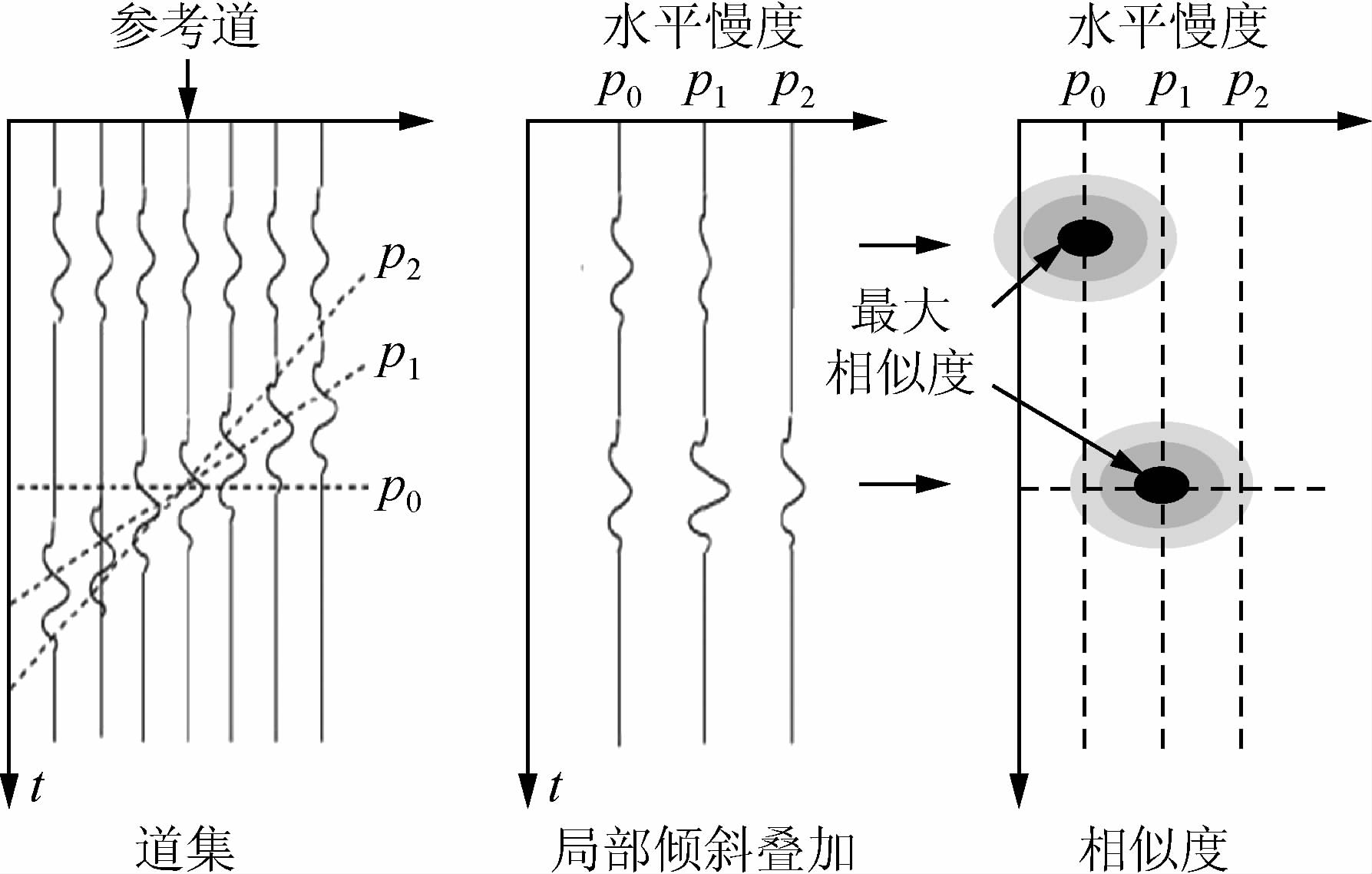
如图 2所示,首先选定束中心位置为参考道,接着对高斯窗内地震数据进行局部倾斜叠加,对于窗内任一时间t,依次按不同斜率(水平慢度)p0、p1、p2等对窗内地震道进行叠加,对一系列t重复以上步骤,就得到了τ-p域数据.在此基础上,对τ-p域数据进行相似度扫描得到相似谱,其中,与最大相似度对应的斜率就是高斯束在该束中心位置主要的出射方向,不同的斜率对应着不同的时刻.
|
图 2 τ-p域相似谱分析 Fig. 2 The coherent spectrum analysis in τ-p domian |
常规高斯束偏移方法与本文改进的束偏移方法对比:前者是对τ-p域内每一个采样点进行偏移,后者是选择相似谱中的能量峰值进行偏移.相似谱中的能量峰值为图 2上相对振幅较强的样点,其意味着存在局部相干同相轴,这个同相轴可能是来自地下的某一反射段,相反,一些相对较弱的能量团,可能是随机噪声干扰.通过阈值滤波设计对束形成进行有效控制,达到去除随机噪声的目的,从而实现一种改进的束偏移方法.
3 处理流程结合渤海某探区地震数据特点和以上理论分析,本文提出叠前深度域的海洋地震数据成像处理流程,该处理流程的核心是建立较准确的速度模型.
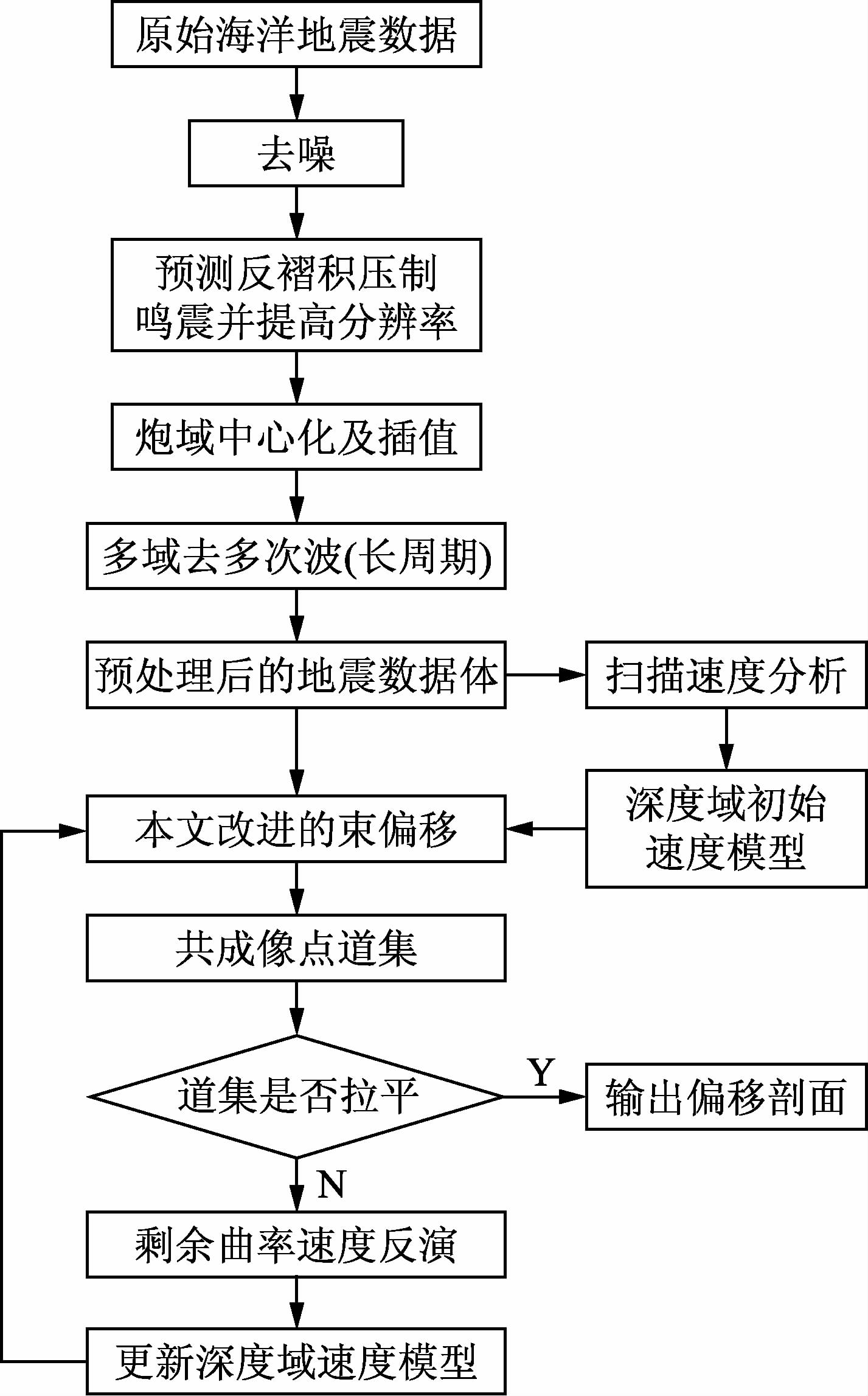
渤海地区区块运动复杂,走滑断裂纵贯南北,多期构造反转使得其构造格局异常复杂.该地区高陡构造较多,地层横向速度差别较大;除此之外,浅层次生断层广为发育且潜山结构复杂.复杂的地下构造以及低信噪比的海洋地震数据给叠前偏移成像以及速度建模带来很大的困难.因此,本文发展了一种精确、高效且适用于低信噪比数据的束偏移方法,并将其应用于速度建模.图 3是结合渤海某探区地震数据特点和前述理论分析建立的一套叠前深度域的海洋地震数据成像处理流程,此流程主要包含两个环节,第一个环节是预处理,首先针对原始海洋地震数据,需要进行去噪和去多次波处理;第二个环节是速度建模,首先通过扫描速度分析得到均方根速度场,并将其转换成深度域层速度场,以此作为初始速度模型,然后基于剩余曲率速度反演方法,以初始速度场作为输入,采用本文改进的束偏移方法提取共成像点道集,以道集是否拉平为标准,决定是否终止速度模型更新.如果道集没拉平,进一步拾取剩余曲率,并根据剩余曲率进行速度反演,得到更新的速度模型.以此循环,直到道集拉平、偏移剖面理想为止.
|
图 3 海洋地震数据成像处理基本流程图 Fig. 3 The basic flowchart of marine seismic data |
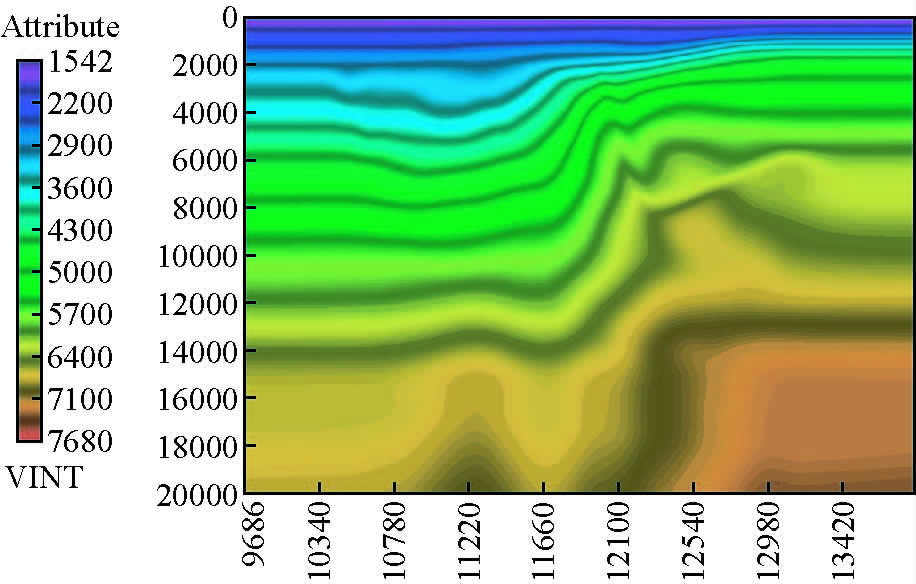
为了体现改进的束偏移在实际生产中的应用前景,首先选取渤海某探区M测线实际资料进行成像处理.基于前述速度建模流程,最终得到如图 4所示的深度域速度模型.图 5为共成像点道集,其同相轴基本拉平,说明建立的深度域速度模型较为准确.在速度建模过程中,成像道集中深层能量较弱且信噪比较低是影响速度模型精度的重要因素,由此也会对深层构造的偏移成像造成不利影响.
|
图 4 深度域偏移速度场 Fig. 4 The migration velocity in depth domain |

|
图 5 共成像点道集 Fig. 5 Common image gathers |
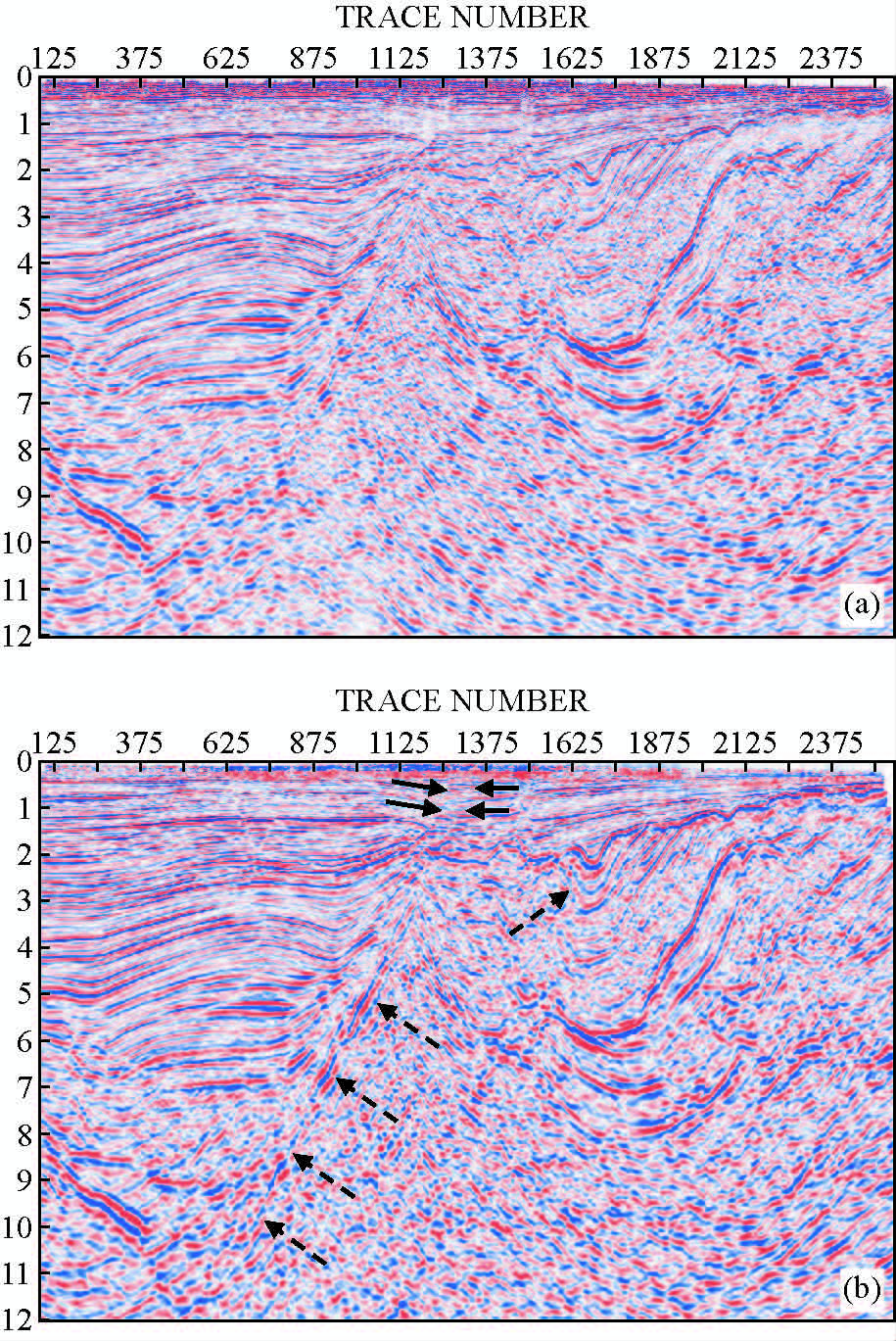
图 6为M测线实际资料偏移成像结果.其中,图 6a为Kirchhoff偏移结果,图 6b为束偏移结果.两种偏移算法均采用相同的输入数据和偏移速度场.从单路径的Kirchhoff偏移结果(如图 6a所示)中可以看出,不仅浅层次生断层断点不清晰,而且深层高陡构造也被偏移噪声覆盖.与其相比,多路径的束偏移不仅有效地成像浅层次生断层(实线箭头所示),而且增强了剖面信噪比,使得中深层高陡构造的同相轴连续性更好(虚线箭头所示).总体而言,束偏移通过改善信噪比以及提高同相轴连续性,可以提供更详细的构造特征.
|
图 6 M测线实际资料偏移成像结果 (a)Kirchhoff偏移;(b)改进的束偏移. Fig. 6 Migrated images with real data along M line (a)Kirchhoff migration;(b)Improved beam migration. |
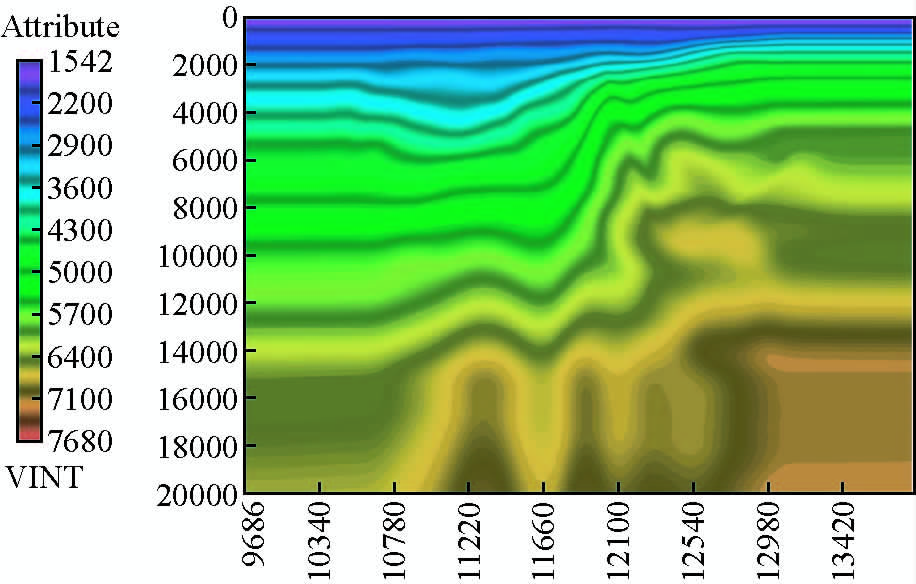
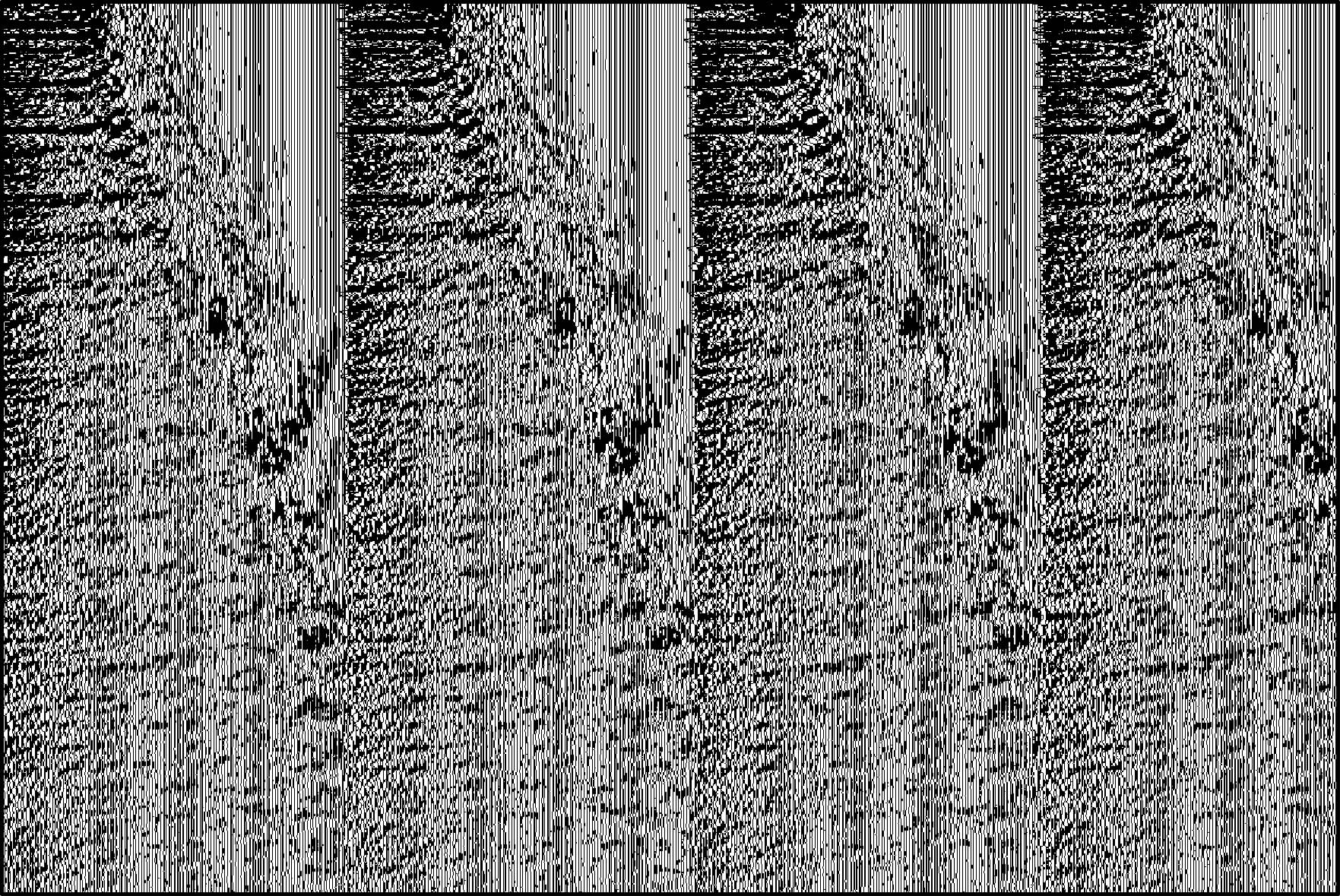
为了进一步体现束偏移在成像潜山构造的优势,选取渤海某探区N测线实际资料进行成像处理.同样地,基于前述速度建模流程,最终得到如图 7所示的深度域速度模型.图 8为潜山左边界附近的共成像点道集,其中浅层同相轴基本拉平,说明中浅层区域的速度场较为准确.但是,成像道集中深层能量较弱且信噪比较低等因素加大了速度建模和深层构造成像的难度,往往对深层构造成像产生不利影响.
|
图 7 深度域偏移速度场 Fig. 7 The migration velocity in depth domain |
|
图 8 共成像点道集 Fig. 8 Common image gathers |
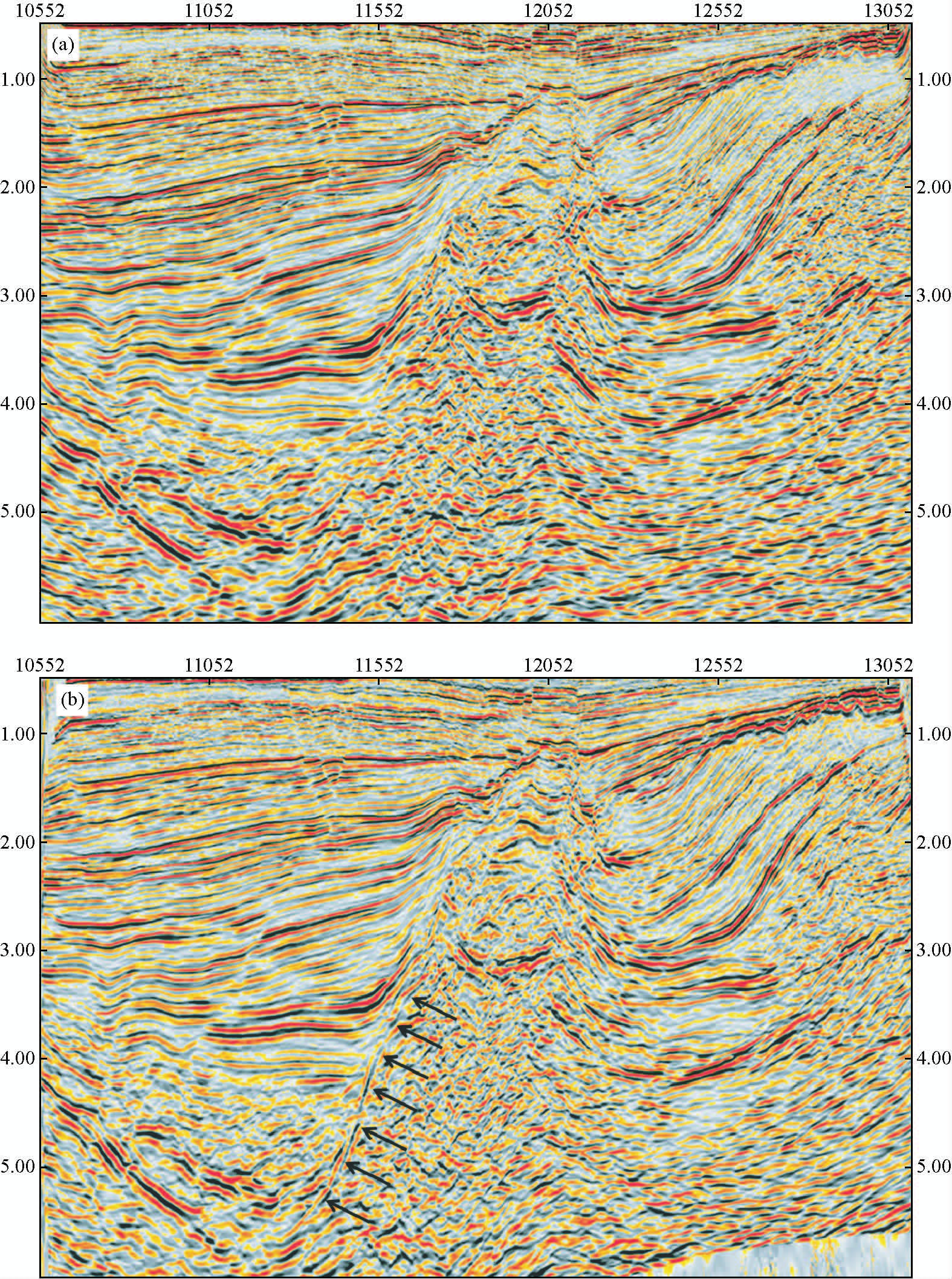
图 9为N测线实际资料偏移成像结果.其中,图 9a为Kirchhoff偏移结果,图 9b为束偏移结果.两种偏移算法均采用相同的输入数据和偏移速度场.与单路径的Kirchhoff偏移相比,束偏移增强了剖面信噪比,使得潜山内幕的同相轴更加连续,潜山侧翼高陡构造(箭头所指)更加清晰.
|
图 9 N测线实际资料偏移成像结果 (a)Kirchhoff偏移;(b)改进的束偏移. Fig. 9 Migrated images with real data along N line (a)Kirchhoff migration;(b)Improved beam migration. |
5.1 在传统高斯束偏移方法的基础上,将地震数据变换到τ-p域,进行相似度扫描形成相似谱,再根据能量分布特征设定阈值对束形成过程进行有效控制,实现一种改进的束偏移方法.在此基础上,将改进的束偏移方法运用到速度建模中,建立了一套海洋地震数据的成像处理流程.通过对渤海某探区实际资料的成像处理表明,多路径的束偏移作为Kichhoff偏移的一种替代方法,不仅运算效率较高,而且能够明显改善剖面信噪比,有效地成像高陡、潜山等复杂构造,在实际生产中具有广泛的应用前景.
5.2 根据束偏移兼具效率和成像精度的特点,在今后的研究中,可以进一步将算法扩展应用到三维数据中.另外,可以基于Yuan等(2014,2015)提出的最小二乘高斯束反演算法,实现保幅成像.
致 谢 感谢SWPI(Seismic Wave Propagation and Imaging)课题组对本项研究的支持.
| [1] | Albertin U, Yingst D, Kitchenside P. 2004. True-amplitude beam migration[C].//74th SEG Annual International Meeting. Expanded Abstracts, 398-401. |
| [2] | Casasanta L, Grion S. 2012. Converted-wave controlled-beam migration for vector-offset volumes[C].//83rd SEG Annual International Meeting. Expanded Abstracts, 1-5. |
| [3] | Casasanta L, Gray S, Grion S. 2013. Converted-wave controlled beam migration with sparse sources or receivers[C].//75th EAGE Conference & Exhibition incorporating SPE EUROPEC. Expanded Abstracts. |
| [4] | Docherty P. 1991. A brief comparison of some Kirchhoff integral formulas for migration and inversion [J]. Geophysics, 56(8): 1164-1169. |
| [5] | Gray S H. 2005. Gaussian beam migration of common-shot records[J]. Geophysics, 70(4): S71-S77. |
| [6] | Hill N R. 1990. Gaussian beam migration[J]. Geophysics, 55(11): 1416-1428. |
| [7] | Hill N R. 2001. Prestack Gaussian-beam depth migration[J]. Geophysics, 66(4): 1240-1250. |
| [8] | Huang J P, Yuan M L, Li Z C, et al. 2015a. The accurate beam migration method without slant stack under dual-complexity conditions and its application (I): Acoustic equation[J]. Chinese Journal of Geophysics (in Chinese), 58(1): 267-276, doi: 10.6038/cjg20150124. |
| [9] | Huang J P, Yuan M L, Li Z C, et al. 2015b. An accurate elastic beam migration method without slant stack for complex surface and subsurface geological conditions[J]. Geophysical Prospecting for Petroleum (in Chinese), 54(1): 56-63. |
| [10] | Koren, Z, Ravve I, Ragoza E, et al. 2008. Full-azimuth angle domain imaging[C].//78th SEG Annual International Meeting. Expanded Abstracts, 2221-2225. |
| [11] | Li Z C, Yue Y B, Guo C B, et al. 2010. Gaussian beam common angle preserved-amplitude migration[J]. Oil Geophysical Prospecting (in Chinese), 45(3): 360-365. |
| [12] | Nowack R L, Sen M K, Stoffa P L. 2003. Gaussian beam migration for sparse common-shot and common-receiver data[C].//73th SEG Annual International Meeting. Expanded Abstracts, 1114-1117. |
| [13] | Operto M S, Xu S, Lambarß G. 2000. Can we quantitatively image complex structures with ray?[J]. Geophysics, 65(4): 1223-1238. |
| [14] | Vinje V, Roberts G A, Taylor R. 2008. Controlled beam migration: a versatile structural imaging tool[J]. First Break, 26(9): 109-112. |
| [15] | Wang H Z, Cai J X, Kong X N, et al. 2010. An implementation of Kirchhoff integral prestack migration for large-scale data[J]. Chinese Journal of Geophysics (in Chinese), 53(7): 1699-1709, doi: 10.3969/j.issn.0001-5733.2010.07.021. |
| [16] | Wiggins J W. 1984. Kirchhoff integral extrapolation and migration of nonplanar data[J]. Geophysics, 49(8): 1239-1248. |
| [17] | Xu S, Gilles L. 2006. True amplitude Kirchhoff prestack depth migration in complex media[J]. Chinese Journal of Geophysics (in Chinese), 49(5): 1431-1444, doi: 10.3321/j.issn:0001-5733.2006.05.022. |
| [18] | Yuan M L, Huang J P, Jia L X, et al. 2014. Implementation of Gaussian-beam based demigration and its adjoint operator[J]. Electronic Journal of Geotechnical Engineering, 19(Z4): 17073-17087. |
| [19] | Yuan M L, Huang J P, Li Z C. 2015. Least-squares Gaussian beam migration[C].//77th EAGE Annual International Meeting. Expanded Abstracts. |
| [20] | Yuan M L, Huang J P, Li Z C, et al. 2015. Parameters optimization in local angle-domain Gaussian beam migration[J]. Geophysical Prospecting for Petroleum (in Chinese), 54(5): 602-612. |
| [21] | Yue Y B, Li Z C, Liu W, et al. 2011. Preserved amplitude shot domain Gaussian beam migration[J]. Journal of China University of Petroleum (in Chinese), 35(1): 52-55. |
| [22] | Yue Y B, Li Z C, Qian Z P, et al. 2012. Amplitude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1376-1383, doi: 10.6038/j.issn.0001-5733.2012.04.033. |
| [23] | 黄建平, 袁茂林, 李振春,等. 2015a. 双复杂条件下非倾斜叠加精确束偏移方法及应用I——声波方程[J]. 地球物理学报, 58(1): 267-276, doi: 10.6038/cjg20150124. |
| [24] | 黄建平, 袁茂林, 李振春,等. 2015b. 双复杂条件下弹性波非倾斜叠加精确束偏移方法研究[J]. 石油物探, 54(1): 56-63. |
| [25] | 李振春, 岳玉波, 郭朝斌,等. 2010. 高斯波束共角度保幅深度偏移[J]. 石油地球物理勘探, 45(3): 360-365. |
| [26] | 王华忠, 蔡杰雄, 孔祥宁,等. 2010. 适于大规模数据的三维Kirchhoff积分法体偏移实现方案[J]. 地球物理学报, 53(7): 1699-1709, doi: 10.3969/j.issn.0001-5733.2010.07.021. |
| [27] | 徐升, Gilles L. 2006. 复杂介质下保真振幅Kirchhoff深度偏移[J]. 地球物理学报, 49(5): 1431-1444, doi: 10.3321/j.issn:0001-5733.2006.05.022. |
| [28] | 袁茂林, 黄建平, 李振春,等. 2015. 局部角度域高斯束偏移参数优选研究[J]. 石油物探, 54(5): 602-612. |
| [29] | 岳玉波, 李振春, 刘伟,等. 2011. 保幅炮域高斯波束偏移[J]. 中国石油大学学报(自然科学版), 35(1): 52-55. |
| [30] | 岳玉波, 李振春, 钱忠平,等. 2012. 复杂地表条件下保幅高斯束偏移[J]. 地球物理学报, 55(4): 1376-1383, doi: 10.6038/j.issn.0001-5733.2012.04.033. |
 2016, Vol. 31
2016, Vol. 31


