固定翼航空电磁系统具有探测深度深、工作效率高等特点,目前已广泛用于矿产资源勘查以及地下水、油气探测等领域.由于固定翼航空电磁探测采用连续测量方式,数据量巨大,通常利用电导率深度转换和电导率深度成像快速获得地下介质分布信息(Liu and Asten, 1993;Huang et al.,2008),但这些成像方法均采用半空间模型近似大地模型,不能准确的描述地质体信息.为得到准确的地电信息分布,需要对航空电磁数据进行反演解释.
一维航空电磁反演技术较为成熟,2005年,Sattel将直流电法中Zohdy反演方法应用于航空电磁数据中.Yin和Hodges(2007) 提出航空电磁模拟退火反演算法.Vallée和Smith(2009) 将Occam反演方法应用于时域航空电磁数据反演当中,获得了比较稳定的反演结果.周道卿等(2010) 利用Marquardt方法对频域航空电磁数据进行反演,取得了较好的结果.朱凯光等(2012) 提出了基于主成分的航空时间域神经网络反演方法.罗勇等(2014) 研究了时间域航空电磁一维阻尼特征参数反演方法.一维反演的弊端在于把每个测点的地下介质都看作是层状模型,与实际地质情况不符,忽略了相邻测点的相关性,使相邻测点间的反演结果不连续,产生较大的误差.
二维、三维反演算法虽然已见相关文献(Alumbaugh and Newman, 2000; Haber et al.,2004;刘云鹤和殷长春,2013;殷长春等,2014),但是算法复杂,计算量大,尤其是对于高度密集连续采样的海量航空电磁数据,因此在实际应用中很少采用.近年来,基于一维反演的横向约束反演(laterally-constrained inversion, LCI)得到了广泛关注与应用,2004年,Auken将横向约束反演方法应用于直流电法数据中,利用模型的横向粗糙度对相邻测点间的地电信息进行约束,反演出多个测点的地电参数,提高了反演结果的横向连续性.Monteiro Santos(2004) 将LCI方法应用于地面频域电磁数据中.Tartaras和Beamish(2006) 、Siemon等(2009) 分别将其应用于固定翼和直升机频率域航空电磁数据中,均取得了良好的效果.在此基础上,殷长春等(2014) 提出了加权横向约束反演方法(WLCI),并应用于频率域航空电磁数据.上述LCI反演方法中均对反演问题进行了约束,使不适定问题具有稳定的反演结果,但是在反演迭代过程中,由于约束项系数不变,容易出现数据过拟合或模型过光滑等问题.Brodie(2010) 提出了基于一维Occam 反演的固定翼航空电磁拟二维反演方法,在反演迭代过程中动态选取正则化因子,平衡了模型的光滑度与数据的拟合度,但Occam反演采用24层定厚度大地模型,导致反演速度较慢.
本文针对上述问题,基于多层变厚度大地模型,提出了整条测线同时反演的固定翼航空电磁数据拟二维整体反演算法.首先阐述了整体反演目标函数以及反演迭代方程组的推导过程,并采用超松弛迭代的预处理共轭梯度算法进行求解.其次对比研究了利用一维反演算法及拟二维整体反演算法对大地模型仿真数据的反演结果,最后给出了加入实测噪声数据的反演结果.
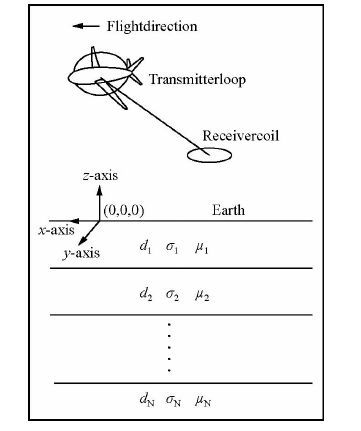
1 固定翼航空电磁正演固定翼航空电磁系统如图 1所示,惯性坐标系平行于地表(Brodie, 2010),原点位于发射线圈中心在地面的投影,x轴方向为飞机飞行方向.
|
图 1 固定翼航空电磁系统示意 Fig. 1 The fixed-wing time-domain electromagnetic system |
设激励为阶跃电流,发射电流关断后,x分量和z分量接收线圈内的归一化感应电动势分别为
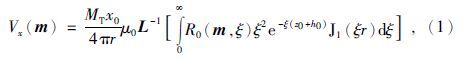
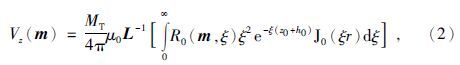
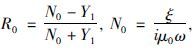 Y1通过递推公式:Yk=Nk
Y1通过递推公式:Yk=Nk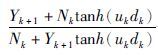 计算,k=N-1,N-2,...,1,YN=NN,
计算,k=N-1,N-2,...,1,YN=NN,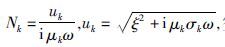 空气磁导率μ0=4π×10-7 H/m.L-1为拉普拉斯逆变换算符,利用G-S变换计算(Knight and Raich, 1982).零阶和一阶贝赛尔函数的无限积分(汉克尔变换)分别利用Guptasarma120点和140点数字滤波算法计算(Guptasarma, 1982; Guptasarma and Singh, 1997).
2 拟二维整体反演
2.1 整体反演基本原理
空气磁导率μ0=4π×10-7 H/m.L-1为拉普拉斯逆变换算符,利用G-S变换计算(Knight and Raich, 1982).零阶和一阶贝赛尔函数的无限积分(汉克尔变换)分别利用Guptasarma120点和140点数字滤波算法计算(Guptasarma, 1982; Guptasarma and Singh, 1997).
2 拟二维整体反演
2.1 整体反演基本原理
整体反演算法的目标函数Φ(m)由观测数据的目标函数Φd(m),模型先验信息目标函数Φr(m),模型纵向粗糙度目标函数Φv(m)和横向粗糙度目标函数Φh(m)构成,公式为
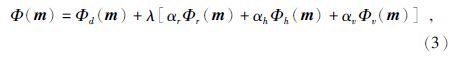
数据的目标函数为
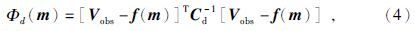
先验信息目标函数Φr(m)=[mr-m]TCr-1[mr-m],mr为测线各测点对应的先验信息,可根据已知的地质资料或CDI获得,Cr为Nr×Nr的对角阵(Nr为模型先验信息参数个数),对角线元素Cr(i, i)为第i个先验信息对应的不确定度的方差.
横向粗糙度目标函数Φh(m)=mTRhTRhm, 本文采用二阶导数计算模型参数的横向粗糙度,对相邻测点间的地电信息约束,则横向粗糙度矩阵为
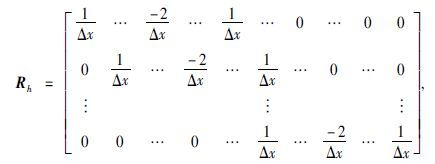
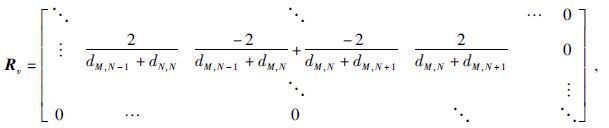
在反演迭代过程中,λ通过线性搜索自适应迭代的方式自动确定.αr、αh、αv在初始反演时由人工决定,迭代过程中并不改变.
为求得目标函数的最优解,以第n+1次迭代为例,令目标函数对待求模型参数mn+1的偏导等于零,公式为
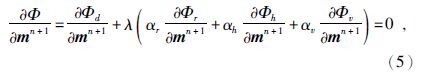
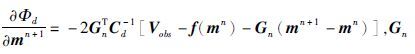 为雅克比矩阵,
为雅克比矩阵,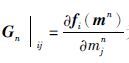 为第i个数据对第j个模型参数的导数,
为第i个数据对第j个模型参数的导数,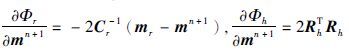
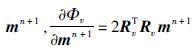 ,代入式(5) ,可得第n+1次迭代方程为
,代入式(5) ,可得第n+1次迭代方程为

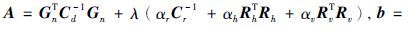
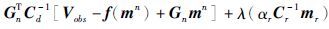 .求解此线性方程组,得到第n+1次迭代所求得的新模型向量mn+1.
.求解此线性方程组,得到第n+1次迭代所求得的新模型向量mn+1.
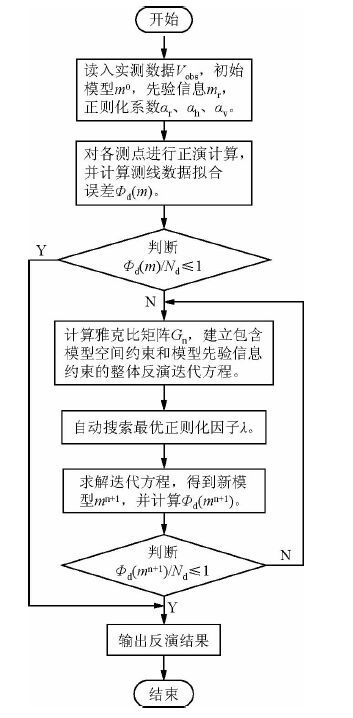
反演的终止条件为:Φd(m)/Nd≤1,Nd为测线电磁数据个数.具体流程如图 2所示.
|
图 2 拟二维整体反演流程图 Fig. 2 Flowchart of quasi 2D holistic inversion |
在反演过程中,若正则化因子λ太小,起不到提高反演稳定性的作用.λ太大,求得的模型过于光滑,数据拟合效果差.因此本文采用线性搜索自适应迭代的方法选取正则化因子,即在每次迭代过程中,通过线性搜索的方法自动选取最优的正则化因子λ.在实际反演中,首先给定初始值λ1t和搜索步长Δ.对于一个确定的λ1t通过求解式(6) 可得到m|λ=λ1t,根据式(4) 计算λ1t对应的数据拟合目标函数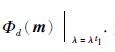 为保证数据的拟合误差逐阶减小,定义数据拟合目标项,Φt=κΦd,系数κ通常选取[0,1]区间内较大的值,可以有效的避免数据拟合误差减小过快在反演结果中引入的多余构造.
为保证数据的拟合误差逐阶减小,定义数据拟合目标项,Φt=κΦd,系数κ通常选取[0,1]区间内较大的值,可以有效的避免数据拟合误差减小过快在反演结果中引入的多余构造.
首先利用包围法(Press et al.,2002),根据正则化参数初始值λ1t及搜索步长Δ,计算λnt=λ1t-(n-1)Δ对应的数据拟合目标函数,直到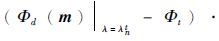
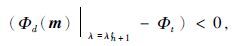 则[λnt,λn+1t]确定为满足
则[λnt,λn+1t]确定为满足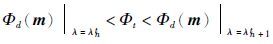 条件的单谷区间,在该区间内,利用二分法逐步减小搜索空间,直至正则化参数λ′满足如下条件:
条件的单谷区间,在该区间内,利用二分法逐步减小搜索空间,直至正则化参数λ′满足如下条件:
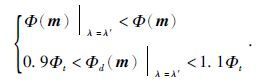
则λn+1=λ′为本次迭代的最优正则化参数,相应的mn+1=m′即为本次迭代的最优模型.若对于所有的λ值均不满足Φd(m, λ)<Φt,采用黄金分割法寻找到最小值min[Φd(mg,λg)],以λg为此次迭代的正则化参数,mg为其对应的最优模型.
2.3 超松弛预处理共轭梯度算法本文提出的拟二维整体反演算法将一条测线数据同时参与计算,推导的反演迭代方程式(6) 中A为大型病态稀疏矩阵.若一条测线有1000个测点,每个测点为5层大地模型,则式(6) 中A的维数是9000×9000,b的维数是9000×1.为降低系数矩阵的条件数,改善方程的病态程度,以加快收敛速度,本文采用超松弛预处理共轭梯度算法(successive over relaxation preconditioned conjugate gradient, SOR-PCG)求解式(6) 线性方程组(胡家赣,1991;Benzi, 2002),以第n+1次反演迭代方程为例,求解方式如下:
首先选取预处理矩阵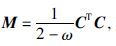 其中C=D-1(D2+L),L为A的严格上三角矩阵,对角阵D中元素Dij=
其中C=D-1(D2+L),L为A的严格上三角矩阵,对角阵D中元素Dij=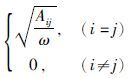 Aij为式(6) 中矩阵A的第i行第j列元素,ω为超松弛因子,默认值为1.根据第n次反演迭代方程的解mn,设置SOR-PCG算法迭代初始模型m0=mn,计算m0的负梯度方向r0=b-Am0,同时可求得z0=M-1r0,并令p0=z0.
Aij为式(6) 中矩阵A的第i行第j列元素,ω为超松弛因子,默认值为1.根据第n次反演迭代方程的解mn,设置SOR-PCG算法迭代初始模型m0=mn,计算m0的负梯度方向r0=b-Am0,同时可求得z0=M-1r0,并令p0=z0.
SOR-PCG算法在第k(k=0,1,2,…)次迭代时,迭代格式如下:
第一步:计算最优步长因子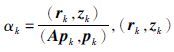 表示rk和zk的内积;
表示rk和zk的内积;
第二步:计算新的模型参数,mk+1=mk+αkpk;
第三步:计算残差rk+1=rk-αkApk.若rk+1满足精度条件,则求得式(6) 的解,令mn+1=mk+1,输出结果,否则更新下列参数zk+1=M-1rk+1,βk=(zk+1,pk+1)(zk,pk),pk+1=zk+1+βkpk,转至第一步,继续迭代.
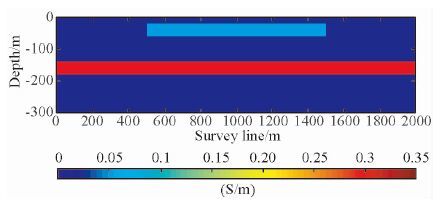
3 数据反演与分析为验证本文提出的拟二维整体反演算法的正确性,首先对理论模型数据进行反演.仿真构造如图 3所示的理论模型,测线总长2000 m, 在500~1500 m处的地下埋深20 m有一个厚度为40 m电导率为0.05 S/m的异常体,同时在埋深120 m处有一个厚度60 m电导率为0.3 S/m的异常体,围岩的电导率为0.01 S/m.固定翼电磁探测系统发射高度为100 m, 收发距为70 m, 接收高度为70 m.利用二维有限元数值模拟方法,采用三角形剖分网格,沿测线每隔10 m为一个测点,计算了图 3中大地模型的z分量电磁响应.
|
图 3 拟二维大地理论模型 Fig. 3 Quais 2D earth model |
本文采用5层大地模型,对仿真数据进行拟二维整体反演.反演数据Vobs由200个测点组成,总数为200×14个,反演参数m由200个测点的5层大地模型电导率和4个厚度组成,维数是1800×1.正则化系数αr、αh、αv分别选取1、40、1,κ为0.7,先验信息mr采用CDI结果(朱凯光等,2010),初始模型m0选择电导率为0.1 S/m的均匀半空间,将上述参数代入式(6) ,即得到整体反演迭代方程.当Φd(m)/2800≤1时,停止迭代.
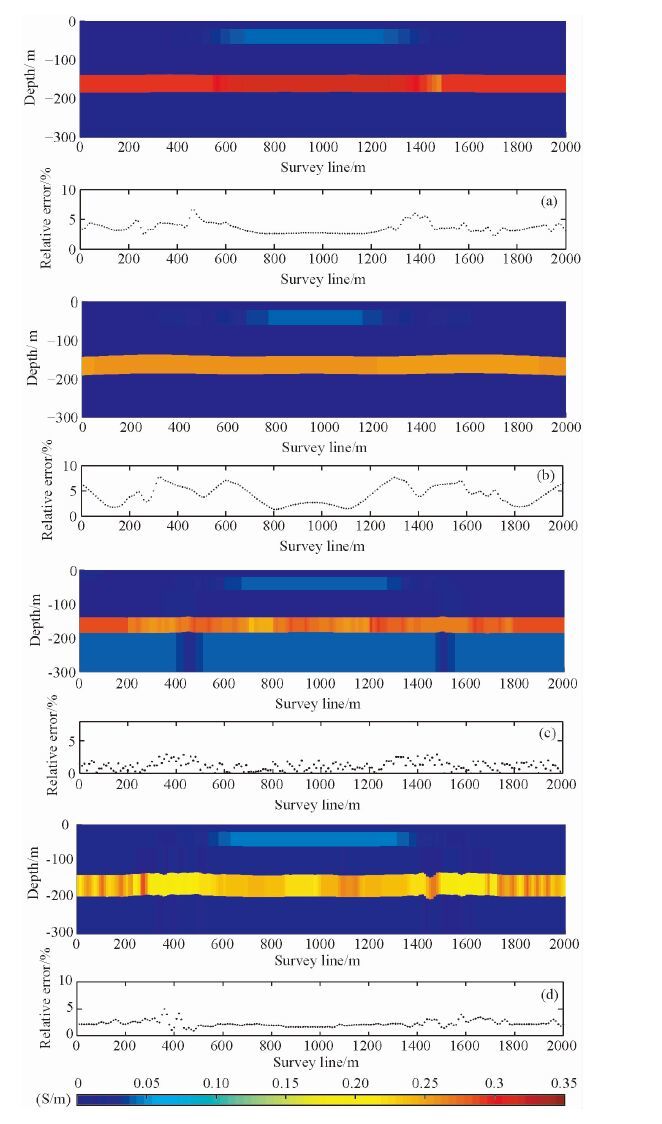
为仿真实测数据,在上述正演数据中,按各道中心时间t-1/2比例,加入2%的高斯噪声(Munkholm and Auken, 1996).拟二维整体反演算法和一维Marquardt反演算法的反演结果及各测点数据拟合误差如图 4所示.其中正则化因子λ的初始值设为1000,在迭代过程中利用线性搜索算法自适应选取最优的正则化因子,拟二维整体反演结果如图 4a所示;应用定正则化因子(迭代过程中正则化因子保持恒定不变)进行反演,当λ等于50和500时,拟二维整体反演结果分别如图 4b、4c所示.一维5层Marquardt反演结果如图 4d所示.可以看出拟二维整体反演结果和一维Marquardt反演结果均能反映出大地的电性分布,但图 4d中,反演结果横向连续性较差,受浅层导体及模型边界影响,埋深120m处的异常体在测线400~1600 m处,反演结果电导率与真实模型存在一定偏差,而图 4a、图 4b、4c反演结果横向分布相对均匀,与模型的吻合度较好.由于一维反演只考虑单一测点的地电信息,反演结果只是利用层状大地模型简单的拼接来描述地下介质的电性信息,而整体反演算法同时将相邻测点间的地电信息进行约束,对于浅层高导覆盖下的导体有更好的分辨率.因此拟二维整体反演算法优于一维Marquardt反演算法,更适用于描述复杂的真实大地模型.
|
图 4 加入2%高斯噪声,拟二维大地模型反演结果 (a)拟二维整体反演,线性搜索λ;(b)拟二维整体反演,λ=500; (c)拟二维整体反演,λ=50;(d)一维Marquardt反演. Fig. 4 Quais 2D earth model inversion result, with 2% Gaussian noise (a)Quasi 2D holistic inversion, λ is selected by a linear search method automatically; (b)Quasi 2D holistic inversion, λ=500;(c)Quasi 2D holistic inversion, λ=50;(d)1D Marquart inversion. |
对比图 4a、4b和4c可得,图 4a在每次迭代中采用自适应线性搜索选取正则化因子的反演结果与模型的吻合度更好,且数据拟合误差除浅层异常边界附近均保持在5%以下;图 4b中正则化因子选取过大,导致反演结果电导率横向过度光滑,浅层异常体异常体明显小于理论模型,埋深120 m处电导率小于模型值,电导率的平均相对误差达到31%;图 4c中正则化因子选取过小,虽然数据拟合程度较好,但横向粗糙度目标函数没有起到很好的约束作用,在测线500~1500 m处,浅层导体覆盖下的深部良导体电导率值略小于模型的真实值,且深层电导率值明显大于模型值.因此,在每次反演迭代过程中,自动搜索自适应正则化因子不仅避免了定正则化因子反演算法中数据过拟合和模型过光滑,同时克服了定正则化因子在反演时需要根据地质条件进行人为干涉的问题.
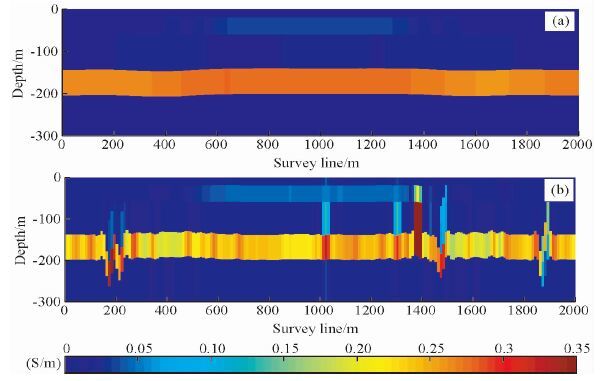
同样根据Munkholm和Auken(1996) 给出的加噪方法,在仿真数据各时间道中加入5%的高斯噪声.采用上述相同初始反演参数对其进行反演,拟二维整体反演和一维Marquardt反演结果分别如图 5a和5b所示.可以看出,一维Marquardt反演结果基本能反映出地下电性分布,但空间连续性较差,反演结果与模型值存在较大偏差.而拟二维整体反演方法反演结果能够很好的反映出两个异常体的电导率及厚度信息,且各层界面光滑,反演结果横向连续性较好.
|
图 5 加入5%高斯噪声,拟二维大地模型反演结果 (a)拟二维整体反演;(b)一维Marquardt反演. Fig. 5 Quais 2D earth model inversion result, with 5%Gaussian noise (a)Quasi 2D holistic inversion;(b)1D Marquart inversion. |
对比图 4a,4d和图 5a,5b可以看出,加入较大的高斯噪声,一维Marquardt反演结果所得到的电导率连续性较差,受噪声影响严重,而拟二维整体反演结果无明显变化,仅电导率略小于加入2%高斯噪声数据的反演结果.可以得出,相同水平的高斯噪声,相对于一维Marquardt反演方法,拟二维整体反演算法受高斯噪声的影响较小.由于拟二维整体反演算法相邻测点间的地电信息受横向约束目标函数约束,对于相邻测点间数据不相关的高斯噪声起到抑制作用,更适用于信噪比较低的航空电磁数据.
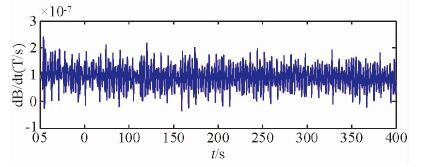
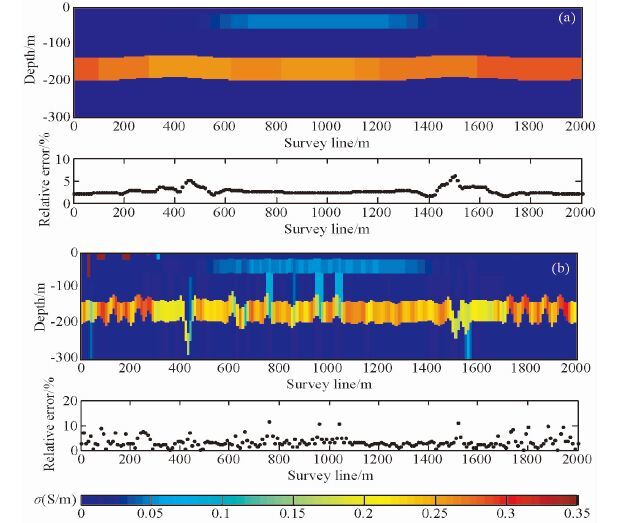
3.2 加入实测噪声反演结果由于国内尚无可直接用于飞行实验的固定翼时间域航空电磁系统,为模拟实测飞行实验数据,本文在仿真数据中加入幅度约为10%实测飞行背景噪声.飞行背景噪声数据为吊舱式直升机电磁系统在河南某地野外飞行实验时飞机在1000 m高空,发射磁矩为170000 A·m2,接收机采样频率为50 kHz情况下测得的,归一化后如图 6所示.分别利用一维Marquardt反演和拟二维整体反演算法对其进行反演,反演结果和各测点数据拟合误差如图 7所示.可以得出,加入约为10%的实测噪声后,一维Marquardt反演算法结果连续性很差,部分测点数据拟合误差达10%以上,对模型中埋深120 m处异常体不能准确描述,埋深120 m的异常体在测线500~1500 m处,电导率信息的平均相对误差已达40%,且在浅层异常模型边界处(测线500 m, 1500 m),受噪声影响,反演结果的平均相对误差为52%.而拟二维整体反演算法可以正确描述出模型的地电信息,埋深120 m的异常体的连续性及数据拟合程度得到很大改善,不存在假异常信息,反演结果的平均相对误差为21.4%.
|
图 6 直升机航空电磁探测系统在河南某地进行飞行实验的高空噪声 Fig. 6 Helicopter time domain electromagnetic noise data collect in Henan Province |
|
图 7 加入航空实测噪声反演结果 (a)拟二维整体反演;(b)一维Marquardt反演. Fig. 7 Quais 2D earth model inversion result, with survey noise (a)Quasi 2D holistic inversion;(b)1D Marquart inversion. |
4.1 本文针对连续密集采样的航空电磁海量数据,提出了整条测线数据同时反演的拟二维整体反演算法.在反演过程中,引入了模型参数的粗糙度目标函数,对相邻测点之间模型参数进行横向约束,不仅克服了一维反演方法对二维目标体反演时存在的横向连续性较差的问题,而且减小了观测数据噪声对反演结果的影响.因此拟二维整体反演算法更适用于横向分辨率较高、信噪比较低的航空电磁数据.通过对比利用拟二维整体反演算法和传统的一维Marquardt反演算法对加入实测噪声数据的反演结果,证明了拟二维整体反演算法的有效性.
4.2 本文在反演迭代中,采用线性搜索自适应迭代的方法选取正则化因子,避免了由于正则化因子选取不当而造成的反演结果过光滑和过拟合问题,提高了反演结果的可靠性和稳定性.利用基于超松弛的预处理共轭梯度算法求解反演迭代方程,不仅预条件矩阵容易求得,而且对系数矩阵做预处理后,矩阵条件数降为原来的平方根,加快迭代收敛速度,提高了反演的计算效率.
4.3 拟二维整体反演方法虽然在反演精度方面不及二维反演,但由于其反演计算速度快、内存需求少,所以在实际工作中,可以对实测航空电磁数据进行快速反演解释,具有重要的实际应用意义.该方法可推广到直升机电磁、海洋电磁等测量系统的海量数据反演算法中.
致 谢 感谢吉林大学地球信息探测仪器教育部重点实验室提供了研究平台.感谢吉林大学张博同学在二维正演计算中给予的帮助.
| [1] | Alumbaugh D L, Newman G A. 2000. Image appraisal for 2-D and 3-D electromagnetic inversion[J]. Geophysics, 65(5): 1455-1467. |
| [2] | Auken E, Christiansen A V. 2004. Layered and laterally constrained 2D inversion of resistivity data[J]. Geophysics, 69(3): 752-761. |
| [3] | Benzi M. 2002. Preconditioning techniques for large linear systems: A survey[J]. Journal of Computational Physics, 182(2): 418-477. |
| [4] | Brodie R C. 2010. Holistic inversion of airborne electromagnetic data[Ph. D. thesis]. Canberra: Australian National University. |
| [5] | Cai J, Qi Y F, Yin C C. 2014. Weighted Laterally-constrained inversion of frequency-domain airborne EM data[J]. Chinese Journal of Geophysics (in Chinese), 57(3): 953-960, doi: 10.6038/cjg20140324. |
| [6] | Guptasarma D. 1982. Computation of the time-domain response of a polarizable ground[J]. Geophysics, 47(11): 1574-1576. |
| [7] | Guptasarma D, Singh B. 1997. New digital linear filters for Hankel J0 and J1 transforms[J]. Geophysical Prospecting, 45(5): 745-762. |
| [8] | Haber E, Ascher U M, Oldenburg D W. 2004. Inversion of 3D electromagnetic data in frequency and time domain using an inexact all-at-once approach[J]. Geophysics, 69(5): 1216-1218. |
| [9] | Huang H P, Rudd J. 2008. Conductivity-depth imaging of helicopter-borne TEM data based on a pseudolayer half-space model[J]. Geophysics, 73(3): F115-F120. |
| [10] | Knight J H, Raich A P. 1982. Transient electro-magnetic calculations using the Gaver-stehfest inverse Laplace transform method[J]. Geophysics, 47(1): 47-50. |
| [11] | Liu G, Asten M. 1993. Conductance-depth imaging of airborne TEM data[J]. Exploration Geophysics, 24(4): 655-662. |
| [12] | Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data[J]. Chinese Journal of Geophysics (in Chinese), 56(12): 4278-4287, doi: 10.6038/cjg20131230. |
| [13] | Luo Y, Lu C D, Wang Y H. 2014. 1D inverse method based on damped eigenparameter for airborne time domain electromagnetic data[J]. Progress in Geophysics (in Chinese), 29(6): 2723-2729, doi: 10.6038/pg20140638. |
| [14] | Mao L F, Wang X B, Chen B. 2011. Study on an adaptive regularized 1D inversion method of helicopter TEM data[J]. Progress in Geophysics (in Chinese), 26(1): 300-305, doi: 10.3969/j.issn.1004-2903.2011.01.035. |
| [15] | Monteiro Santos F A. 2004. 1-D laterally constrained inversion of EM34 profiling data[J]. Journal of Applied Geophysics, 56(2): 123-134. |
| [16] | Munkholm M S, Auken E. 1996. Electromagnetic noise contamination on transient electromagnetic soundings in culturally disturbed environments[J]. Journal of Environmental and Engineering Geophysics, 1(2): 119-127. |
| [17] | Press W H, Teukolsky S A, Vetterling W T, et al. 2002. Numerical Recipes in C++: The Art of Scientific Computing[M]. 2nd ed. Cambridge: Cambridge University Press. |
| [18] | Sattel D. 2005. Inverting airborne electromagnetic (AEM) data with Zohdy's method[J]. Geophysics, 70(4): G77-G85. |
| [19] | Siemon B, Auken E, Christiansen A V. 2009. Laterally constrained inversion of helicopter-borne frequency-domain electromagnetic data[J]. Journal of Applied Geophysics, 67(3): 259-268. |
| [20] | Tartaras E, Beamish D. 2006. Laterally constrained inversion of fixed-wing frequency-domain AEM data[C].//Proceedings of Near Surface 2006. Netherlands: EAGE. |
| [21] | Vallße M A, Smith R S. 2009. Application of Occam's inversion to airborne time-domain electromagnetics[J]. The Leading Edge, 28(3): 284-287. |
| [22] | Wang J Y. 2002. Inverse Theory in Geophysics (in Chinese)[M]. 2nd ed. Beijing: Higher Education Press. |
| [23] | Yin C C, Hodges G. 2007. Simulated annealing for airborne EM inversion[J]. Geophysics, 72(4): F189-F195. |
| [24] | Yin C C, Qi Y F, Liu Y H, et al. 2014. Trans-dimensional Bayesian inversion of frequency-domain airborne EM data[J]. Chinese Journal of Geophysics (in Chinese), 57(9): 2971-2980, doi: 10.6038/cjg20140922. |
| [25] | Zhou D Q, Tan L, Tan H D, et al. 2010. Inversion of frequency domain helicopter-borne electromagnetic data with Marquardt's method[J]. Chinese Journal of Geophysics (in Chinese), 53(2): 421-427, doi: 10.3969/j.issn.001-5733.2010.02.020. |
| [26] | Zhu K G, Lin J, Han Y H, et al. 2010. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network[J]. Chinese Journal of Geophysics (in Chinese), 53(3): 743-750, doi: 10.3969/j.issn.0001-5733.2010.03.030. |
| [27] | Zhu K G, Ma M Y, Che H W, et al. 2012. PC-based artificial neural network inversion for airborne time-domain electromagnetic data[J]. Applied Geophysics, 9(1): 1-8. |
| [28] | 蔡晶, 齐彦福, 殷长春. 2014. 频率域航空电磁数据的加权横向约束反演[J]. 地球物理学报, 57(3): 953-960, doi: 10.6038/cjg20140324. |
| [29] | 胡家赣. 1991. 线性代数方程组的迭代解法[M]. 北京: 科学出版社. |
| [30] | 李永兴, 强建科, 汤井田. 2009. 航空瞬变电磁法一维反演新方法研究[C]. //第九届中国国际地球电磁学术讨论会论文集. 桂林: 中国地球物理学会. |
| [31] | 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究[J]. 地球物理学报, 56(12): 4278-4287, doi: 10.6038/cjg20131230. |
| [32] | 罗勇, 陆从德, 王宇航. 2014. 时间域航空电磁一维阻尼特征参数反演方法[J]. 地球物理学进展, 29(6): 2723-2729, doi: 10.6038/pg20140638. |
| [33] | 毛立峰, 王绪本, 陈斌. 2011. 直升机航空瞬变电磁自适应正则化一维反演方法研究[J]. 地球物理学进展, 26(1): 300-305, doi: 10.3969/j.issn.1004-2903.2011.01.035. |
| [34] | 王家映. 2002. 地球物理反演理论[M]. 第2版. 北京: 高等教育出版社. |
| [35] | 殷长春, 齐彦福, 刘云鹤,等. 2014. 频率域航空电磁数据变维数贝叶斯反演研究[J]. 地球物理学报, 57(9): 2971-2980, doi: 10.6038/cjg20140922. |
| [36] | 周道卿, 谭林, 谭捍东,等. 2010. 频率域吊舱式直升机航空电磁资料的马奎特反演[J]. 地球物理学报, 53(2): 421-427, doi: 10.3969/j.issn.001-5733.2010.02.020. |
| [37] | 朱凯光, 林君, 韩悦慧,等. 2010. 基于神经网络的时间域直升机电磁数据电导率深度成像[J]. 地球物理学报, 53(3): 743-750, doi: 10.3969/j.issn.0001-5733.2010.03.030. |
 2016, Vol. 31
2016, Vol. 31


