2. 西安石油大学 电子工程学院, 西安 710065
2. School of Electronic Engineering, Xi'an Shiyou University, Xi'an, 710065, China
水资源是人类赖以生存和发展的最重要的自然资源,随着人口增长,工业化、农业化进程加快,世界水资源日趋匮缺.研究有效的找水方法,探寻潜在的地下水源,对缓解水资源短缺,保障人民生活,促进经济可持续发展具有十分重要的意义.
地球物理方法已经广泛应用于地下水的勘探,常见的有激电法、视电阻率法、瞬变电磁法等.激电法利用激电二次场的大小与衰减快慢的不同推断岩体的含水情况,视电阻率法通过探测地层、岩性在垂直方向的电性变化,寻找位移稳定的含水层(苏永军等,2015).瞬变电磁法通过观测激发场感应的地下涡流所产生的二次电磁场的时空分布,勘探地质体构造,查找地下水源(葛燕燕等,2014).反射地震法依据岩层弹性参数的差异,通过地质构造和岩性对比确定含水层(宋希利等,2012).以上这些方法主要通过寻找含水构造或低阻异常来间接达到找水的目的,但是对于构造或者低阻异常是否一定含水以及含有多少水无法明确判断,还需要对含水层的含水率和赋存状态进行评价,一般的物探方法难以实现.
核磁共振是目前唯一用于直接勘探地下水的地球物理方法,通过测量水体中的氢原子旋进运动中释放的电磁信号,可以直接描述含水率的空间变化,与传统的地球物理勘测方法相比具有高分辨率、高效率、信息量丰富和解唯一性等优点.核磁共振探测地下水的思想最早由美国人Russell Varian提出的,20世纪70年代末前苏联科学家研制出了第一台核磁共振地下水探测仪,并在大量试验的基础上形成了一套核磁共振正反演的数学模型(潘玉玲和张昌达,1999).法国、美国、德国的研究人员在核磁共振探测水体的正、反演以及应用方面取得了大量卓有成效的工作,商业化的核磁共振地下水探测仪得到了推广(Yaramanci et al.,2002;Legchenko et al.,2008,2011; Greben et al.,2011).国内,潘玉玲和张昌达(1999)、张昌达和潘玉玲(2006)、潘玉玲等(2003)、李振宇(2002,2003)、林君(2010)、林君等(2012)、易晓峰等(2013)、翁爱华等(2002,2004)、胡祥云(2006,2012)等学者在核磁共振理论、线圈设计以及仪器研制等方面展开了一系列研究,推动了国内核磁共振技术的发展,目前地面核磁共振找水的一维正、反演已经成熟,应用研究也多以此为理论基础,然而对于储存结构较为复杂的三维水体,目前方法很难获得较好的探测效果,为了进一步提高找水定位的准确度,三维核磁共振探测方法的研究显得很有必要.本文讨论了回线源条件下三维空间核磁共振响应的正演问题,由麦克斯韦方程组推导了有源条件下频率域三维磁场方程与边界条件,给出泛函表达式,应用有限元法实现了正演计算,分析了不同含水体参数对核磁共振响应的影响,为含水体的反演提供了依据.
1 基本理论 1.1 核磁共振现象核磁共振研究的基础是原子核的磁性及其与外加磁场的相互作用,当原子核置于静磁场中时,其自旋系统将被极化,并且在外加磁场力矩的作用下,以固有的拉莫尔频率绕外加磁场方向进动,此时在垂直静磁场方向施加一个相同频率的交变磁场,根据量子力学理论,处于低能级的原子核通过吸收交变磁场的能量跃迁至较高能级,从而出现核磁共振现象.
1.2 核磁共振信号的测量地面核磁共振找水以地磁场作为静磁场,在地面线圈中通入频率为质子进动频率的谐变电流,在地下形成交变电磁场,在垂直地磁场的分量作用下,水中氢核宏观磁矩发生偏离,撤去外加激发场后,水中氢核释放出自由衰减信号,信号的初始振幅表示为
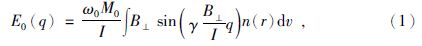
式中,ω0为拉莫尔频率,M0为宏观磁矩,I为发射电流,B⊥为激发场垂直于地磁场的分量,n为含水率,γ为磁旋比,q为脉冲矩.当ω0,M0,I,γ等观测参数确定时,信号的初始振幅直接反映了含水体的分布及含水率,而求解初始振幅的关键是确定B⊥,因此首先需要计算电磁场在三维空间中的分布.
2 三维核磁共振正演 2.1 三维空间的电磁场分布通过对时间域内的麦克斯韦方程组作傅里叶变换,得到含源情况下的谐变电磁场方程为

式中,E和H分别为电场和磁场矢量,ω为激励回线源的角频率,ε,μ,σ分别为介电常数、磁导率及电导率,Js为外加电流源的电流密度.对(2)式中的磁场两边取旋度,得到只关于磁场的方程为
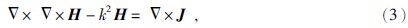
其中,k2=ω2εμ+iωμσ,由于不存在磁荷和面电流密度,磁场在内部电性界面上,同时具有法向和切向连续性,因此通过外边界S2上的第三类边界条件给出方程(3)所满足的边界条件为
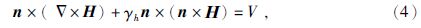
其中n为S2的外法向单位向量,V,γh为关于边界条件的已知量.
为了获得满足方程(3)和边界条件(4)的磁场解,根据变分原理,构造如下形式的泛函为

利用有限元法计算磁场值,将体积V划分为M个小单元,以第e个小单元为例,令R=Δ×Js,将(5)式写为标量分量形式,在第e个小单元内,有:
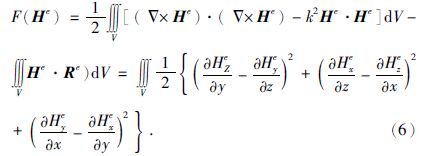
假定剖分单元内部物性均匀,对剖分后的所有单元求解变分问题的驻点等价于求解以下方程组:
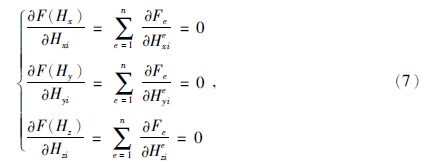
其中n为剖分单元个数,e为单元编号,Hxi,Hyi,Hzi为单元节点i上的磁场的三个分量,在每个小单元内:
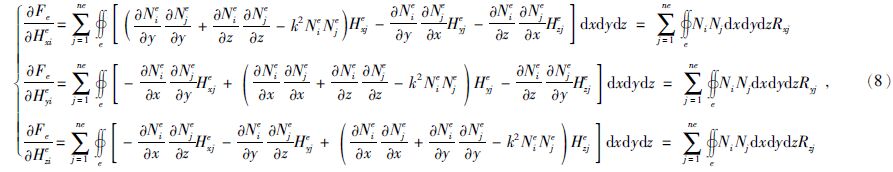
其中Nie为单元内i号节点的形函数,ne为单元内节点个数.对所有单元进行组合并强加驻点条件得:
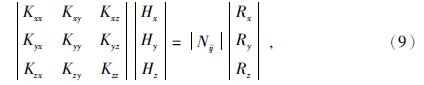
求解上式可以得到空间中任意点的磁场强度.
2.2 源的加载对于细导线产生的场源,往往使用δ函数进行处理,考虑到场源附近场值的奇异性以及背景构造的复杂性,利用近似函数等效场源的作用,将源分布于一定范围内,直接求解总场值.本文中的近似函数采用Herrmann(1979)提出的伪δ函数,公式为
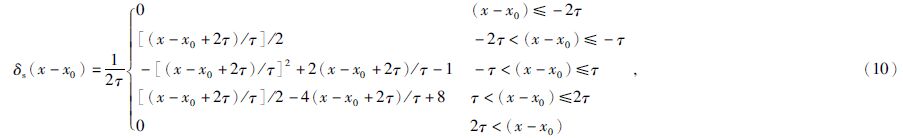
其中参数τ是控制源分布宽度和幅值的参数,x为某一空间维度的坐标,x0为源所在位置的坐标.而式(8)中对电流密度求旋度的运算,可转换为对伪δ函数的导数运算.
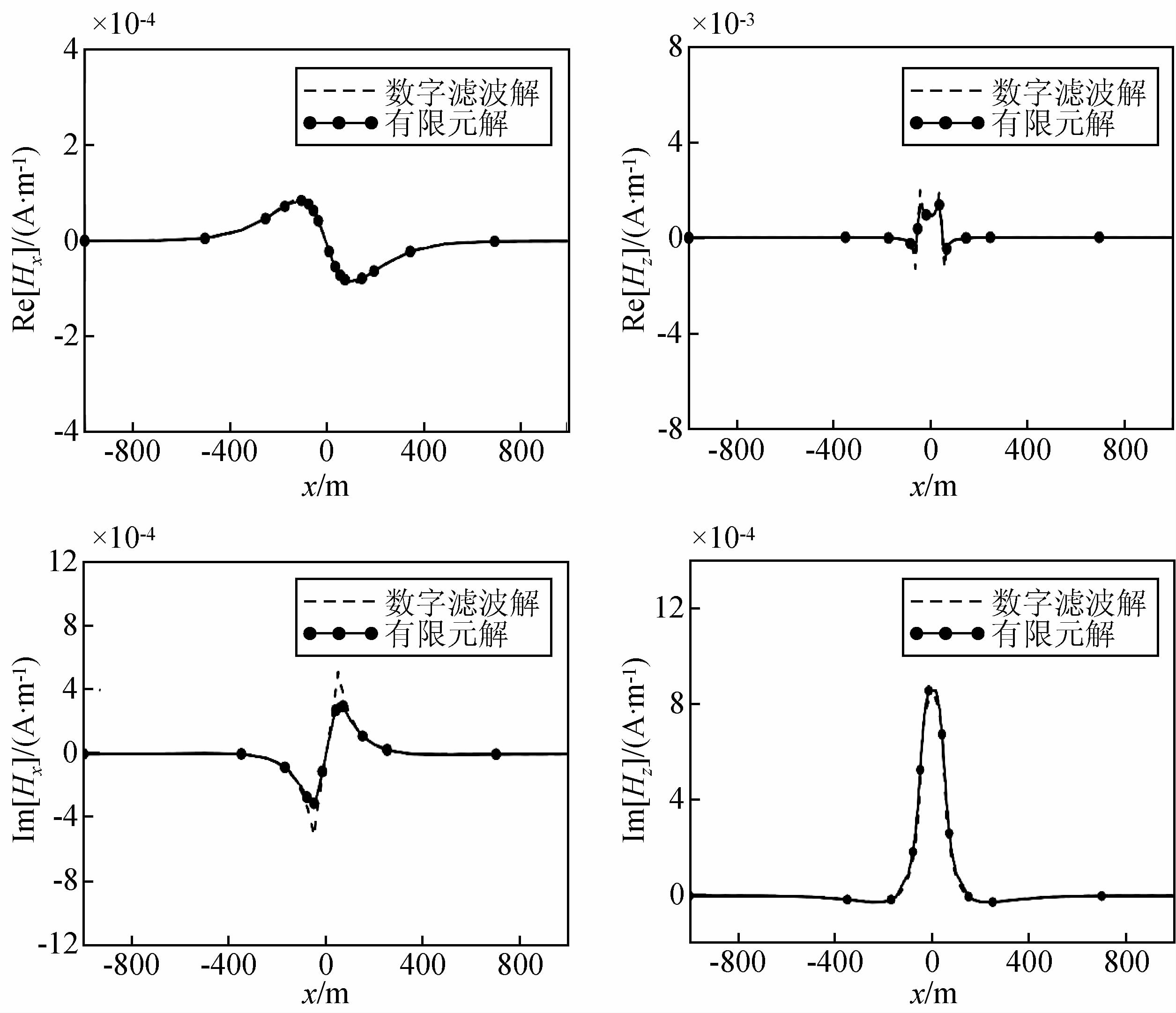
2.3 磁场计算结果验证计算了l=100 m的回线源在ρ=100 Ω·m的均匀半空间上产生的磁场,并在地表沿x轴设计了一条测线,与数字滤波解进行了对比.如图 1所示,除导线附近位置,有限元计算结果和数字滤波解基本一致,进而了验证有限元解的正确性.
|
图 1 有限元解和数字滤波解比较 Fig. 1 Comparison of FEM solution and digital filtering solutions |
由于地磁场同时包含地磁倾角I和地磁偏角D,感应磁场垂直分量B⊥的表示较为复杂.为了简化计算,对坐标系进行旋转,首先以z轴为旋转轴,x轴和y轴沿顺时针旋转角度D,记为坐标系x′y′z′.其次以y′轴为旋转轴,x′轴和z′轴沿顺时针旋转角度I,记为坐标系x″y″z″.此时新坐标系下的感应磁场BT″与原坐标系下B⊥的关系可表示如下:

由于BT″的x″轴方向与地磁场方向B0重合,因此垂直分量由y″轴和z″轴分量合成,即:
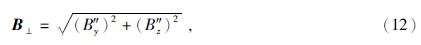
同理,当线圈的法向偏度αn和法向倾度βn发生变化时,通过旋转坐标系可推导出坐标旋转之后的感应磁场B""为

其中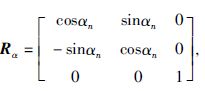
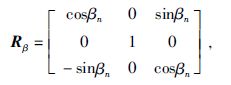
式中Rα和Rβ都是正定的,有
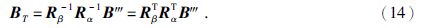
计算线圈坐标系下感应磁场的矢量值B"",通过四个旋转矩阵可得到地磁场坐标系下B″=RIRDRβTRαTB"",最终利用式(12)计算出感应磁场垂直分量B⊥.
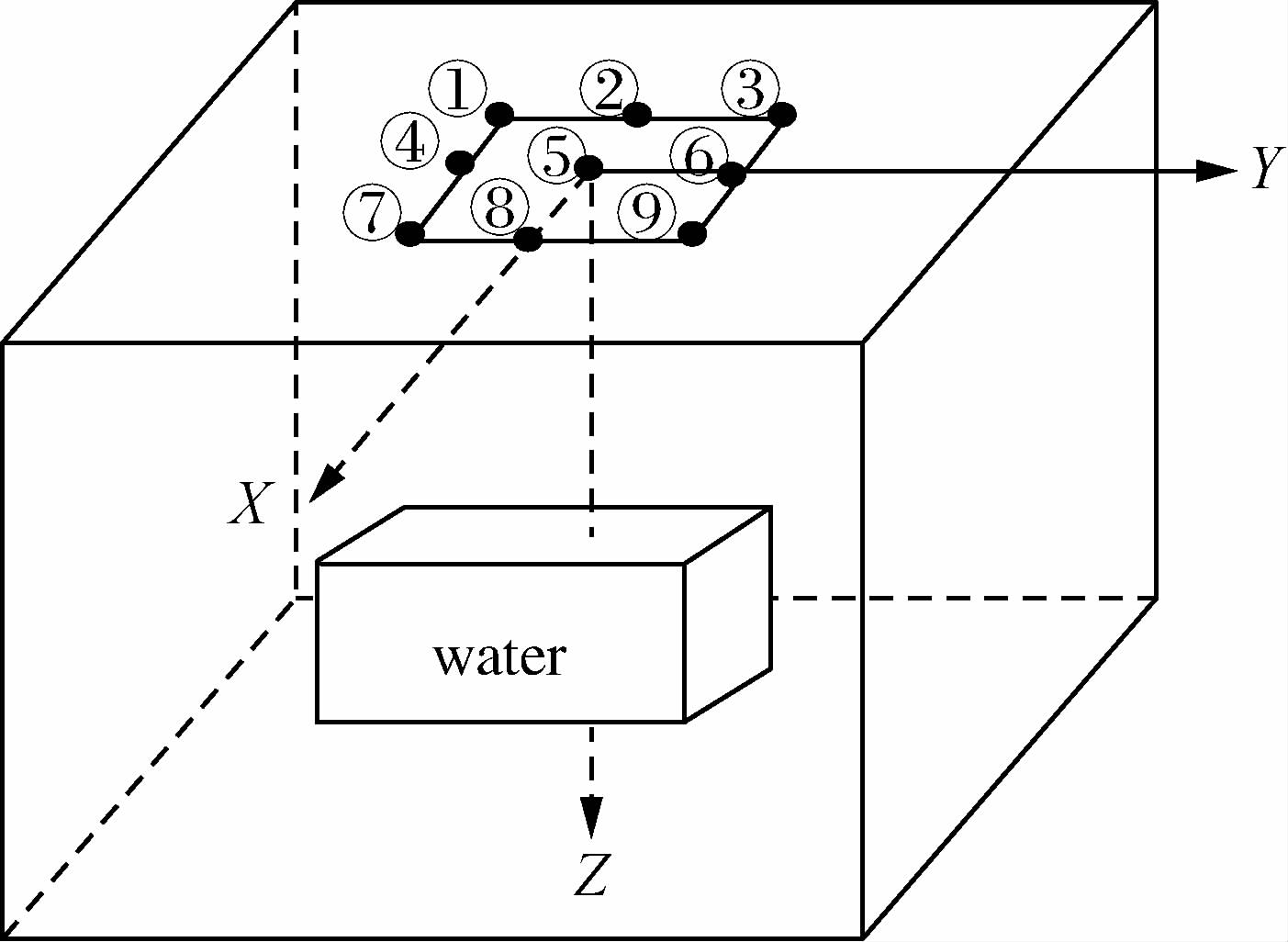
3 含水体参数对核磁共振响应的影响为了研究三维含水体的核磁共振响应特征,对含水体在不同埋藏深度、水平位置、以及电阻率情况下的磁共振响应进行了数值模拟.设计模型如图 2所示,在电阻率为100 Ω·m 的均匀介质中,安放了一个10 m×10 m×1 m 的含水六面体,六面体在空间上的边界位置分别是x:-5~5 m,y:-5~5 m,含水体中心点设在z轴上,测点坐标(单位为m)定为①(-2.5,-2.5,0)、②(-2.5,0,0)、③(-2.5,2.5,0)、④(0,-2.5,0)、⑤(0,0,0)、⑥(0,2.5,0)、⑦(2.5,-2.5,0)、⑧(2.5,0,0)⑨(2.5,2.5,0).计算中,地磁场强度为48000 nT,磁倾角为60°,磁偏角为0°,发射电流1 A,拉莫尔频率为2350 Hz.
|
图 2 含水体模型 Fig. 2 The mode of aquifer |
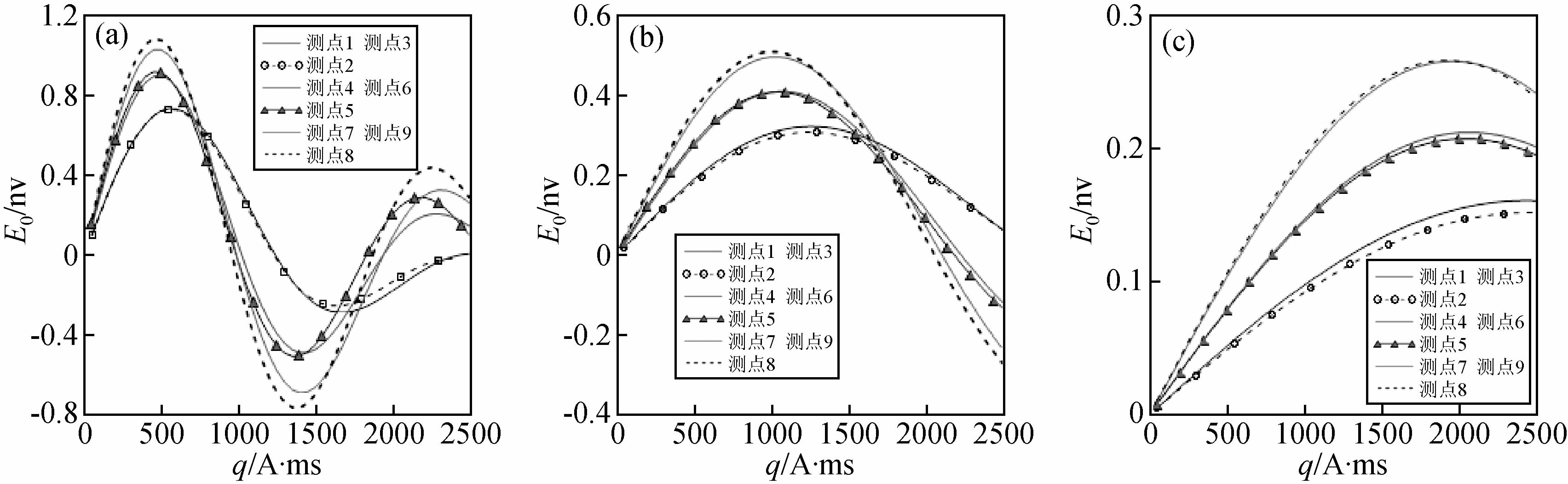
设含水体电阻率为5 Ω·m,当含水体中心深度分别取6 m,9 m,12 m时,脉冲矩(q)与初始振幅(E0)的关系如图 3所示.
|
图 3 含水体深度对初始振幅的影响
(a)含水体中心点深度为6 m;(b)含水体中心点深度为9 m;(c)含水体中心点深度为12 m. Fig. 3 The effect of aquifer depth on the NMR response (a)The depth of the center is 6 m;(b)The depth of the center is 9 m;(c)The depth of the center is 12 m. |
由图 3可以看出:当含水体中心点深度为6 m时,核磁共振响应信号的初始振幅幅值为1.2 nv左右,当含水体中心点深度增加为9 m和12 m时,响应信号的初始振幅幅值降低为0.55 nv和0.28 nv,随着含水体深度的增加,各测点的响应振幅均逐渐减小,分辨率不断降低,而最大初始振幅对应的脉冲矩却不断变大,这说明核磁共振信号可以反映含水体的深度变化,增加发射信号的脉冲矩可以扩大勘探深度,获得深部地层的含水信息.
3.2 含水体水平位置对初始振幅的影响设含水体电阻率为5 Ω·m,含水体中心点在z=6 m的平面上沿x轴移动,中心点坐标依次为(-2.5,0,6),(0,0,6),(2.5,0,6)时,不同水平位置的对比关系如图 4所示.

|
图 4 含水体水平位置对初始振幅的影响
(a)含水体中心点(-2.5,0,6);(b)含水体中心点(0,0,6);(c)含水体中心点(2.5,0,6). Fig. 4 The effect of aquifer horizontal position on the NMR response (a)The Center coordinate is(-2.5,0,6),(b)The Center coordinate is(0,0,6),(c)The Center coordinate is(2.5,0,6). |
从图 4可以看出:不同水平位置上,各个测点响应曲线的变化趋势基本相同,呈现为有两个极大值的双峰型.含水体水平位置的变化对响应振幅的影响不大,但对于各测点曲线之间的差异影响较大.随着含水体中心点在x轴上的移动,具有相同x坐标测点间的曲线差异逐渐减小,而不同x坐标测点之间的曲线差异逐渐增大,由图 4c中可以明显看到因测点x坐标差异而出现的曲线分组现象,根据这样的变化规律,可以实现对含水体水平位置的定位.
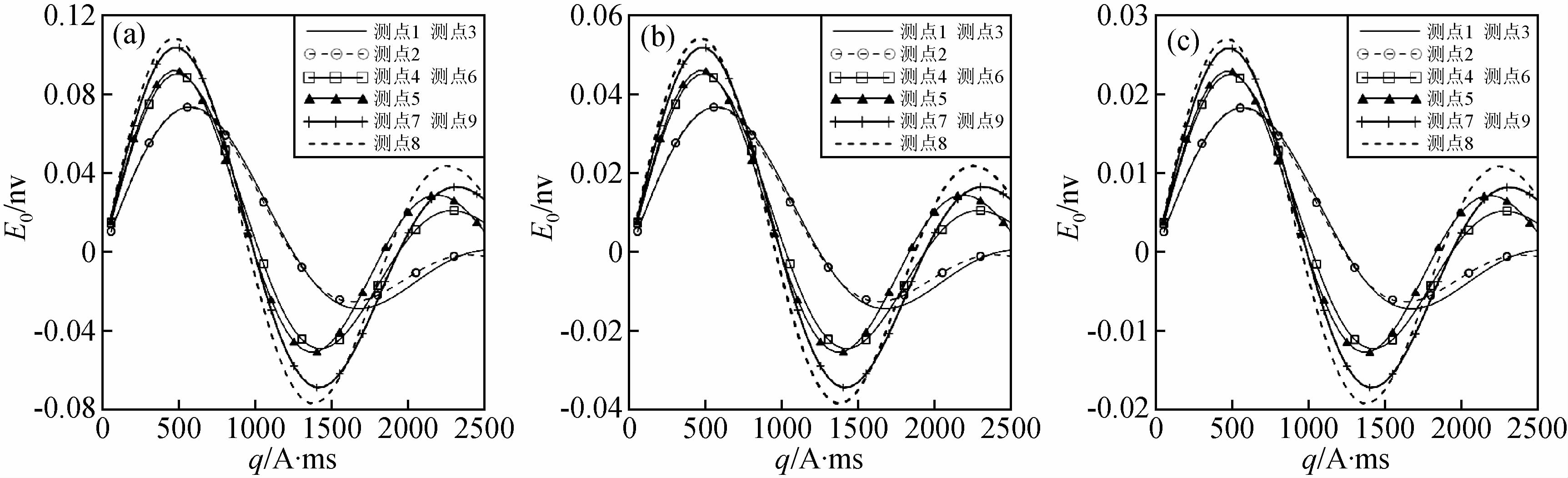
3.3 含水体电阻率对初始振幅的影响设含水体中心点位置坐标为(0,0,6),改变含水体电阻率,分别取50 Ω·m,100 Ω·m,200 Ω·m时,含水体电阻率对初始振幅的影响如图 5所示.
|
图 5 含水体电阻率对初始振幅的影响
(a)含水体电阻率为50 Ω·m;(b)含水体电阻率为100 Ω·m;(c)含水体电阻率为200 Ω·m. Fig. 5 The effect of aquifer resistivity on the NMR response (a)The aquifer resistivity is 50 Ω·m;(b)The aquifer resistivity is100 Ω·m;(c)The aquifer resistivity is 200 Ω·m. |
从图 5中可以看出,模型中含水体电阻率的改变对各测点的曲线形态以及曲线之间的差异影响较小,初始振幅与脉冲距的对应关系基本不变,但是各曲线的振幅对电阻率的变化较为敏感,相同脉冲矩下,含水体电阻率越大,响应振幅越小,最大初始振幅与含水体电导率近似呈线性关系,这说明浅层地下含水体电导率的变化对于频域电磁场的分布影响较大,利用响应曲线的振幅特性可以实现地下含水体的电阻率反演.
4 结 论4.1 频域激发磁场的分布是三维核磁共振响应计算的关键,本文从谐变磁场所满足的变分问题出发,通过求变分的驻点得到了有限元方程.通过引入伪δ函数解决了细导线中电流密度的旋度计算问题,实现了电流源的直接加载,通过与数字滤波解的对比,验证了文中三维频率正演方法的有效性和准确性.
4.2 通过模型计算研究了核磁共振响应特征和含水体参数之间的关系.结果表明,核磁共振响应对含水体的埋藏深度和水平位置的变化是敏感的,其中脉冲矩的大小决定了核磁共振探测深度,水平位置的变化会对不同测点之间的曲线差异产生影响,说明核磁共振探测对于含水体位置和边界的圈定是有效的.
4.3 含水体电性对核磁共振响应的影响主要取决于其对于频率域磁场分布的改变程度,对于浅层含水体,含水体的电性对于频率域磁场分布影响较大,核磁共振的初始振幅与含水体的电导率近似成正比,这一点对地下含水体的电阻率反演研究具有重要的参考价值.
致 谢 感谢戚志鹏老师在本文研究中的帮助,感谢审稿人及编辑部老师给予文章内容与格式上的建议指导!
| [1] | Chalikakis K, Nielsen M R, Legchenko A. 2008. MRS applicability for a study of glacial sedimentary aquifers in Central Jutland, Denmark[J]. Journal of Applied Geophysics, 66(3-4): 176-187, doi: 10.1016/j. jappgeo.2007.11.005. |
| [2] | Ge Y Y, Fu X H, She J Z, et al. 2014. Research of transient electromagnetic method detection on groundwater response during coalbed methane well drainage [J]. Coal Science and Technology (in Chinese), 42(12): 98-101. |
| [3] | Greben J M, Meyer R, Kimmie Z. 2011. The underground application of magnetic resonance soundings [J]. Journal of Applied Geophysics, 75(2): 220-226, doi: 10.1016/j. jappgeo.2011.06.010. |
| [4] | Grunewald E, Knight R. 2011. A laboratory study of NMR relaxation times in unconsolidated heterogeneous sediments [J]. Geophysics, 76(4): G73-G83, doi: 10.1190/1.3581094. |
| [5] | Herrmann R B. 1979. SH-wave generation by dislocation sources—a numerical study[J]. Bulletin of the Seismological Society of America, 69(1): 1-15. |
| [6] | Jiang C D, Lin J, Duan Q M, et al. 2011. A study on 2D magnetic resonance sounding with an array loop for groundwater exploration [J]. Chinese Journal of Geophysics (in Chinese), 54(11): 2973-2983, doi: 10.3969/j.issn.0001-5733.2011.11.028. |
| [7] | Legchenko A, Ezersky M, Girard J F, et al. 2008. Interpretation of magnetic resonance soundings in rocks with high electrical conductivity[J]. Journal of Applied Geophysics, 66(3-4): 118-127, doi: 10.1016/j.jappgeo.2008.04.002. |
| [8] | Legchenko A, Vouillamoz J M, Roy J. 2010. Application of the magnetic resonance sounding method to the investigation of aquifers in the presence of magnetic materials[J]. Geophysics, 75(6): L91-L100, doi: 10.1190/1. 3494596. |
| [9] | Li Z Y, Li J L, Pan Y L. 2002. Summary of groundwater detection with surface nuclear magnetic resonance method [J]. Progress in Exploration Geophysics (in Chinese), 25(6): 55-58. |
| [10] | Li Z Y, Pan Y L, Zhang B, et al. 2003. Using NMR method research the hydrogeology problems and practical examples[J]. Hydrogeology & Engineering Geology (in Chinese), 30(4): 50-54. |
| [11] | Lin J. 2010. Situation and progress of nuclear magnetic resonance technique for groundwater investigations [J]. Progress in Geophysics (in Chinese), 25(2): 681-691, doi: 10.3969/j.issn.1004-2903.2010.02.043. |
| [12] | Lin J, Jiang C D, Duan Q M, et al. 2012. The situation and progress of magnetic resonance sounding for groundwater investigations and underground applications [J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 42(5): 1560-1570. |
| [13] | Liu D H, Hu X Y, Li Y G. 2012. Understanding the effect of elliptical polarization in surface nuclear magnetic resonance method[J]. Applied Geophysics, 9(4): 365-377, doi: 10.1007/s11770-012-0348-y. |
| [14] | Pan Y L, He H, Li Z Y, et al. 2003. Surface detection of groundwater with the nuclear magnetic resonance method and its application results in China [J]. Regional Geology of China (in Chinese), 22(2): 135-139. |
| [15] | Pan Y L, Zhang C D. 1999. New sphere of nuclear magnetic resonance technology application[J]. CT Theory and Applications (in Chinese), 8(4): 5-8. |
| [16] | Roy J, Rouleau A, Chouteau M, et al. 2008. Widespread occurrence of aquifers currently undetectable with the MRS technique in the Grenville geological province, Canada[J]. Journal of Applied Geophysics, 66(3-4): 82-93, doi: 10.1016/j.jappgeo.2008.04.006. |
| [17] | Song X L, Song P, Tian M Y, et al. 2012. Geophysical prospecting method in intrusive rocks area fight a drought to find water wells set [J]. Progress in Geophysics (in Chinese), 27(3): 1280-1286, doi: 10.6038/j.issn.1004-2903.2012.03.057. |
| [18] | Su Y J, Ma Z, Meng L S, et al. 2015. Application of high-density resistivity method and induced polarization method to determine a good well location in groundwater prospecting [J]. Geoscience (in Chinese), 29(2): 265-271. |
| [19] | Wang X M, Guo D, Li J. 2011. The integrated electrical prospecting technology and its application to water resource exploration [J]. Geophysical and Geochemical Exploration (in Chinese), 35(1): 65-69. |
| [20] | Weng A H, Li Z B, Wang X Q. 2002. Numerical simulation of surface NMR[J]. Computing Techniques For Giophysical and Geochenical Exploration (in Chinese), 24(2): 97-101. |
| [21] | Weng A H, Li Z B, Wang X Q. 2004. A study on surface nuclear magnetic resonance over layered conductive earth [J]. Chinese Journal of Geophysics (in Chinese), 47(1): 156-163. |
| [22] | Yaramanci U, Lange G, Hetrich M. 2002. Aquifer characterisation using surface NMR jointly with other geophysical techniques at the Nauen/Berlin test site[J]. Journal of Applied Geophysics, 50(1-2): 47-65, doi: 10.1016/S0926-9851(02)00129-5. |
| [23] | Yi X F, Li P F, Lin J, et al. 2013. Simulation and experimental research of MRS response based on multi-turn loop [J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2484-2493, doi: 10.6038/cjg20130734. |
| [24] | Zhang C D, Pan Y L. 2006. Some views on petrophysical interpretation of SNMR data[J]. Chinese Journal of Engineering Geophysics (in Chinese), 23(1): 1-8. |
| [25] | Zhang R, Hu X Y, Yang D K, et al. 2006. Review of development of surface nuclear magnetic resonance [J]. Progress in Geophysics (in Chinese), 21(1): 284-289. |
| [26] | 葛燕燕, 傅雪海, 舍建忠,等. 2014. 煤层气井排采时地下水响应瞬变电磁法探测研究[J]. 煤炭科学与技术, 42(12): 98-101. |
| [27] | 蒋川东, 林君, 段清明,等. 2011. 二维阵列线圈核磁共振地下水探测理论研究[J]. 地球物理学报, 54(11): 2973-2983, doi: 10.3969/j.issn.0001-5733.2011.11.028. |
| [28] | 李振宇, 李俊丽, 潘玉玲. 2002. 地面核磁共振找水方法综述[J]. 勘探地球物理进展, 25(6): 55-58. |
| [29] | 李振宇, 潘玉玲, 张兵,等. 2003. 利用核磁共振方法研究水文地质问题及应用实例[J]. 水文地质工程地质, 30(4): 50-54. |
| [30] | 林君. 2010. 核磁共振找水技术的研究现状与发展趋势[J]. 地球物理学进展, 25(2): 681-691, doi: 10.3969/j.issn.1004-2903.2010.02.043. |
| [31] | 林君, 蒋川东, 段清明,等. 2012. 复杂条件下地下水磁共振探测与灾害水源探查研究进展[J]. 吉林大学学报, 42(5): 1560-1570. |
| [32] | 潘玉玲, 贺颢, 李振宇,等. 2003. 地面核磁共振找水方法在中国的应用效果[J]. 地质通报, 22(2): 135-139. |
| [33] | 潘玉玲, 张昌达. 1999. 核磁共振技术应用的新领域──探查地下水[J]. CT理论与应用研究, 8(4): 5-8. |
| [34] | 宋希利, 宋鹏, 田明阳,等. 2012. 物探方法在侵入岩地区抗旱找水定井中的应用[J]. 地球物理学进展, 27(3): 1280-1286, doi: 10.6038/j.issn.1004-2903.2012.03.057. |
| [35] | 苏永军, 马震, 孟利山,等. 2015. 高密度电阻率法和激发极化法在抗旱找水定井位中的应用[J]. 现代地质, 29(2): 265-271. |
| [36] | 王星明, 郭栋, 李嘉. 2011. 水资源勘查中综合电法勘探方法技术与应用[J]. 物探与化探, 35(1): 65-69. |
| [37] | 翁爱华, 李舟波, 王雪秋. 2002. 地面核磁共振响应数值模拟研究[J]. 物探化探计算技术, 24(2): 97-101. |
| [38] | 翁爱华, 李舟波, 王雪秋. 2004. 层状导电介质中地面核磁共振响应特征理论研究[J]. 地球物理学报, 47(1): 156-163. |
| [39] | 易晓峰, 李鹏飞, 林君,等. 2013. 基于多匝环形线圈的核磁共振信号响应计算与试验研究[J]. 地球物理学报, 56(7): 2484-2493, doi: 10.6038/cjg20130734. |
| [40] | 张昌达, 潘玉玲. 2006. 关于地面核磁共振方法资料岩石物理学解释的一些见解[J]. 工程地球物理学报, 3(1): 1-8. |
| [41] | 张荣, 胡祥云, 杨迪琨,等. 2006. 地面核磁共振技术发展述评[J]. 地球物理学进展, 21(1): 284-289. |
 2016, Vol. 31
2016, Vol. 31


