由于测井资料具有纵向分辨率高、地震资料具有横向连续性强的鲜明特点，因此，基于二者融合的井震联合反演技术是用于储层预测最行之有效的地震反演方法之一.而声波测井资料作为井震联合反演技术的核心资料之一，显得尤为重要.当没有在井筒内采集声波测井资料时，便给井震联合技术进行储层参数反演、储层精细描述、剩余油分布预测等工作造成了较大的障碍.因此，纵、横波测井曲线的预测或重构成为了井震联合反演技术前期一项必不可少的工作.在大部分情况下，纵波测井曲线有实测数据，因此，前人更多的是在横波测井曲线的预测方面开展工作，而进行纵波测井曲线预测的研究工作相对较少，随钻纵波曲线的预测则少之又少(张学芳等，2005；陈钢花和王永刚，2005；杨少虎等，2006；贺懿等，2008；崔健和张星，2008；龙国清等，2008；袁全社等，2009；郭永恒，2010；张亚斌等，2011；熊冉等，2012).

X油田有20口评价井和开发井，其中1口井有电缆纵波测井曲线，1口井为随钻纵波测井曲线，而另外18口井均缺乏纵、横波测井资料，这给后期该油田剩余油分布预测及井位优化研究工作带来较大困难.因此，本文针对这一问题，基于聚类分析算法、岩石物理模型和多元线性拟合三种方法，开展了随钻纵波测井曲线的预测工作；基于Han公式、Greengerg-Castagna(GC)公式和Xu-White模型，进行了随钻横波测井曲线的预测工作.随钻纵、横波测井曲线的准确预测对该油田剩余油分布预测及井位优化研究工作具有很强的现实意义.

聚类分析是将物理或抽象对象的集合分成相似对象类的过程(Kohonen，1989; Konhonen，1990; Ultsch，1993; Krishnapuran et al.，1995; Ye and Philippe，2000; Mahamed et al.，2005; Abdelhamid and Witold，2006; Han and Micheline，2006; Carlotta et al.，2007; Vilalta et al.，2007)，它是一种在“无监督”情况下根据对象间的相似程度自动地将其分割为一组“有意义”的类的处理过程.“无监督”是指待分类对象没有预先给定的类标识；“有意义”是指聚类的结果应该反映原始数据的自然结构特征.聚类分析问题的实质是一个全局最优问题，可以描述为：给定n维空间Rⁿ中的m个向量，将每个向量归属到c聚类中的某一个，使得每个向量与其聚类中心的距离最小，其中n为参与聚类的属性个数，m为参与聚类的样本个数，c为类别数.聚类分析的三要素分别为：相似性测度、聚类准则和聚类算法.相似性测度是根据相似系数或距离函数来衡量两个样本之间的相似性；聚类准则是保证聚类循环过程直到聚类质量满足要求，结束聚类算法所遵循的准则；聚类算法是为了达到聚类目的所采用的算法，主要包括划分方法、层次方法、密度方法、网格方法和模型方法等五种.

本文基于Multi-Resolution Graph Based Clustering(MRGC)、Dynamic Clustering(DC)、Ascendant Hierarchical Clustering(AHC)、Self-Organizing Map(SOM)和ARtificial Neural Network(ANN)五种聚类算法，以预测精度和泛化能力作为衡量指标，通过对比分析来优选构建随钻纵波测井曲线预测模型的聚类算法.

岩石物理模型是进行岩石物理研究的重要基础和主要方法之一，它通过一定的假设条件，将实际岩石中的颗粒与孔隙的几何形状、排列方式等关键因素进行理想化，然后基于该理论模型，采用物理学原理和数学方法来建立通用的函数关系.基于实际岩石不同的理想化过程，岩石物理模型主要包括层状模型、球形孔隙模型、包含体模型和接触模型等(李庆忠，1992；云美厚和管志宁，2002；李维新等，2007；马淑芳等，2010；张佳佳等，2010；谢月芳和张纪，2012).

岩石物理模型在正演得到弹性参数的过程中，会受到岩石性质、地层压力、地层温度、流体类型等诸多因素的综合影响.在采用岩石物理模型正演纵、横波测井曲线的过程中，其预测精度受这些参数的影响也相对较大.

因此，基于岩石物理模型预测纵、横波测井曲线的过程也是岩石物理模型正演得到弹性参数的过程；同时，岩石物理模型的选择、岩石相关参数的设置成为了制约纵、横波测井曲线预测精度的关键环节.

在线性拟合中，如果有两个或两个以上的自变量，就称为多元线性拟合.由于一种现象往往是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更准确、更有效和更实际.因此，在大部分情况下，多元线性拟合比单元线性拟合在准确性、有效性和实用性方面均更强一些.尽管与聚类分析算法和岩石物理模型相比，多元线性拟合的基本原理和操作过程均显得相对简单，但在很多领域的实际操作过程中，多元线性拟合的准确性、稳定性和实用性常常会更强一些.

在采用多元线性拟合方法来预测纵波测井曲线的过程中，多个自变量分别是反映岩性的自然伽马、泥质含量，刻画物性的孔隙度，及评价含油性的电阻率和饱和度等相关参数(雍世和和张超谟，2007).基于不同的参数组合，以预测精度为主要的衡量指标，参考每组参数实际的物理含义，优选最佳的纵波测井曲线预测模型.

在X油田的20口井中，A井为电缆纵波测井曲线，B井为随钻纵波测井曲线，另外18口井均缺乏纵、横波测井资料.以A、B井为模型井，分别采用聚类分析算法、岩石物理模型和多元线性拟合三种方法构建纵波测井曲线预测模型.

基于不同的参数组合，尝试多种建模算法之后，聚类分析算法的参数组合为自然伽马(GR，API)、体积密度(RHOB，g/cm³)和深电阻率(R_t，Ω·m)；对该油田的数据体而言，基于不同聚类算法的基本原理和试验分析之后，确定MRGC为构建纵波预测模型最优的聚类分析算法.多元线性拟合中有三组自变量的组合，分别是自然伽马和体积密度，自然伽马、体积密度和深电阻率，泥质含量(V_sh， v/v)和有效孔隙度(φ，v/v).其中聚类分析算法和多元线性拟合模型井、预测井的相对误差分别见表 1、表 2.

表 1 (Table 1)

表 1 聚类分析算法的相对误差 Table 1 Relative error of cluster analysis algorithm 模型井 预测井 累积频率为80%时所对应的相对误差 K=1 K=5 K=10 A A 0.40% 8.11% 8.99% B 13.66% 9.81% 9.22% B A 12.46% 11.66% 11.42% B 0.40% 3.48% 3.86%

表 1 聚类分析算法的相对误差 Table 1 Relative error of cluster analysis algorithm

表 2 (Table 2)

表 2 多元线性拟合的相对误差 Table 2 Relative error of multilinear fitting 模型井 预测井 累积频率为80%时所对应的相对误差 GR，RHOB GR，RHOB，Rt Vsh，φ A A 10.18% 10.01% 12.06% B 7.66% 7.51% 6.42% B A 11.36% 12.04% 11.49% B 5.44% 5.21% 4.07%

表 2 多元线性拟合的相对误差 Table 2 Relative error of multilinear fitting

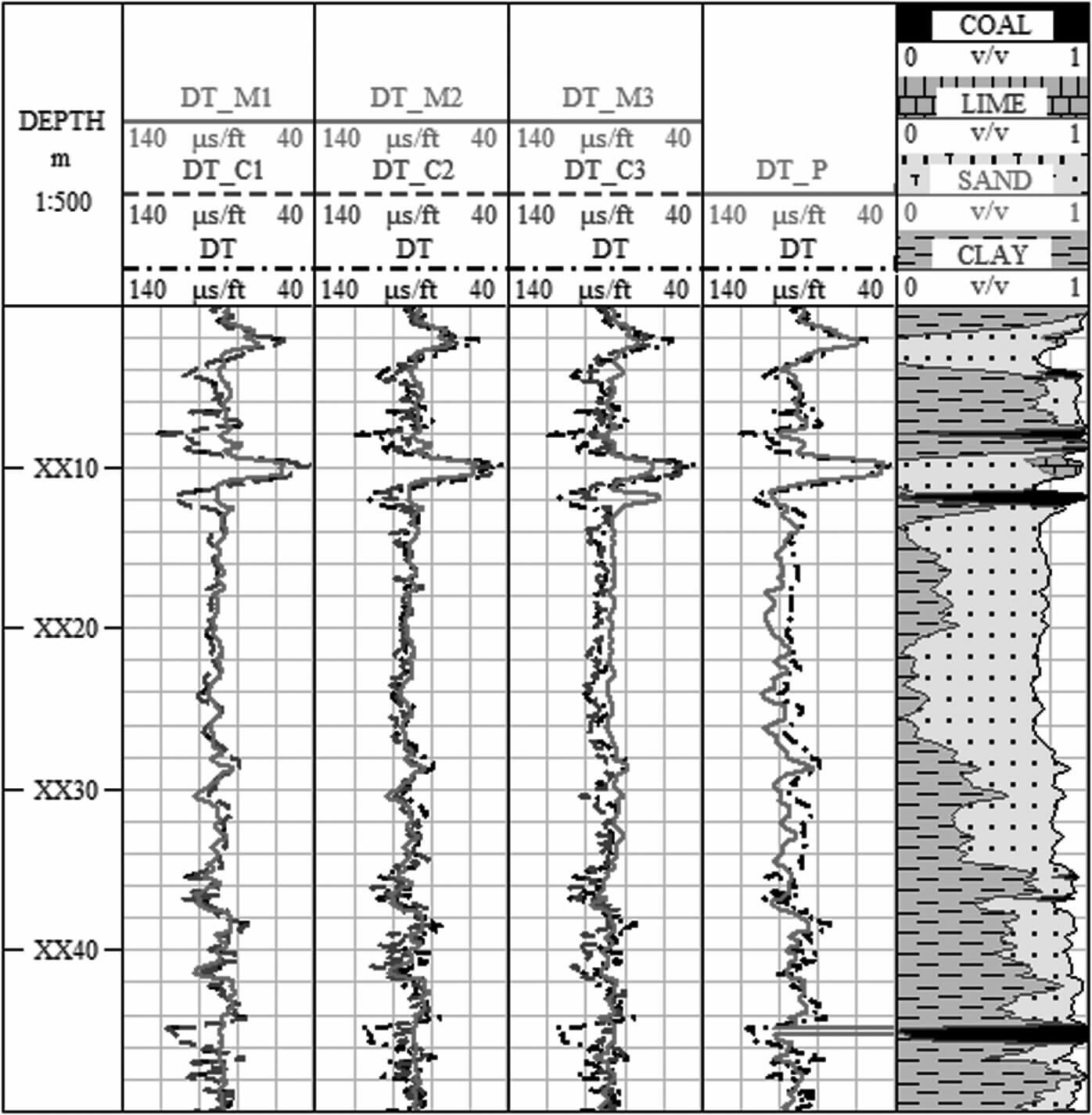
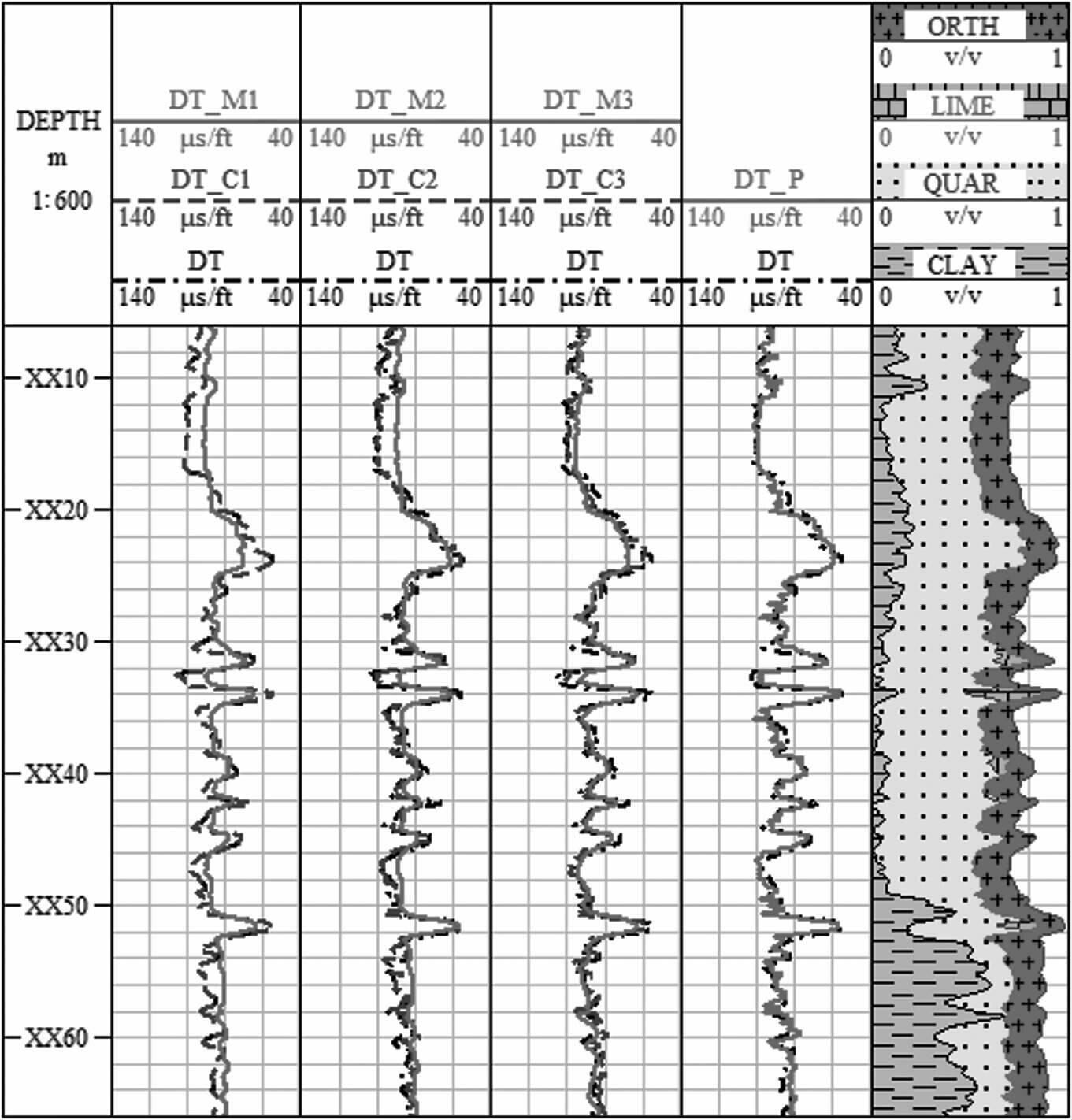
A、B井预测纵波测井曲线与实测纵波测井曲线的对比分析分别见图 1、图 2；其中DT为实测纵波测井曲线，DT_C、DT_P、DT_M分别为聚类分析算法、岩石物理模型、多元线性拟合方法所预测的纵波测井曲线.

图 1

Fig. 1

图 1 A井实测与预测的纵波测井曲线对比 Fig. 1 Comparison of measured and forecasted compression wave logging of well A

图 2

Fig. 2

图 2 B井实测与预测的纵波测井曲线对比 Fig. 2 Comparison of measured and forecasted compression wave logging of well B

聚类分析算法、岩石物理模型和多元线性拟合三种方法基于不同的参数设置、组合所构建纵波预测模型的误差分析见表 3.

表 3 (Table 3)

表 3 纵波预测模型的相对误差 Table 3 Relative error of forecasting model of compression wave logging 序号 方法 参数选取 对应曲线 累积频率为80%时所对应的相对误差 A井 B井 1 聚类分析算法 GR，RHOB，Rt K=1 DT_C1 0.40% 0.40% K=5 DT_C2 8.11% 3.48% K=10 DT_C3 8.99% 3.86% 2 岩石物理模型 — DT_P 12.51% 4.99% 3 多元线性拟合 GR，RHOB DT_M1 10.18% 5.44% GR，RHOB，Rt DT_M2 10.01% 5.21% Vsh，φ DT_M3 12.06% 4.07%<

表 3 纵波预测模型的相对误差 Table 3 Relative error of forecasting model of compression wave logging

一般情况下，预测模型相对误差的累积频率为80%时所对应的相对误差小于10%时，那么基于该预测模型所重构的纵波测井曲线便能满足实际勘探开发的生产需求.

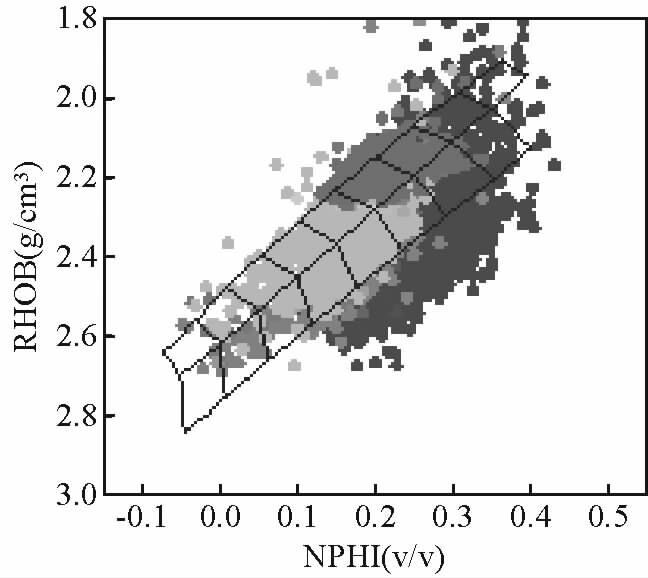
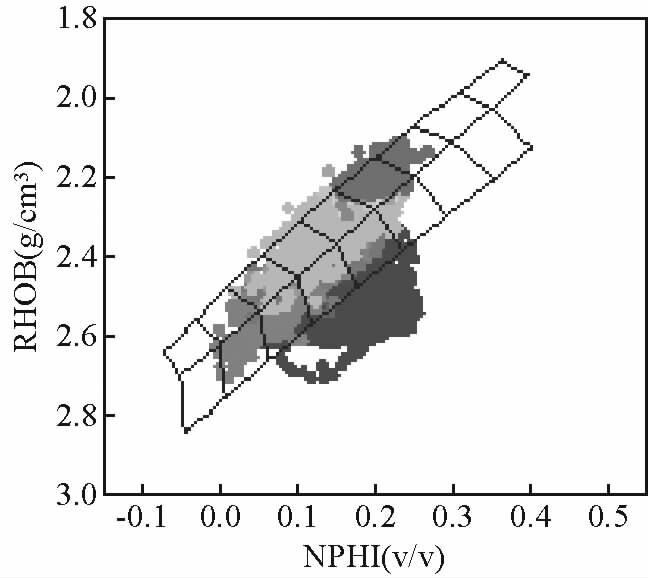
由表 3可知，与A井相比，基于B井所建立纵波预测模型的相对误差相对较小，其主要原因是由于二者的岩性存在一定的差异.A、B井密度和中子的交会图分别见图 3、图 4，通过对比分析可知，A井存在碳质泥岩.碳质泥岩是介于煤层和泥岩之间的一种岩性.就测井曲线的响应特征而言，煤层为低伽马、低密度的特征，泥岩为高伽马、高密度的特征，而碳质泥岩则表现为高伽马、低密度的特征.

图 3

Fig. 3

图 3 A井的交会图 Fig. 3 Cross plot of well A

图 4

Fig. 4

图 4 B井的交会图 Fig. 4 Cross plot of well B

基于前人的研究可知，随钻与电缆纵波测井资料之间的误差小于3%(Paul et al.，1998; Rama et al.，2004)，因此，测井系列之间的差异是A、B井纵波预测模型相对误差存在较大的差异的次要因素.

由于缺少纵、横波测井曲线的18口井均为随钻测井，因此，选择以B井为模型井来预测这18口井的纵波测井曲线.

由表 3可知，对于研究靶区以砂泥岩为主的地层，就方法的预测效率和准确度而言，聚类分析算法和多元线性拟合优于岩石物理模型.另外，由于聚类分析算法存在一定程度的不稳定性，因此，基于GR、RHOB和R_t的参数组合，K分别取1、5、10时来预测纵波测井曲线，分别见图 5、图 6、图 7；基于V_sh、φ的参数组合，多元线性拟合预测的纵波测井曲线见图 8.

图 5

Fig. 5

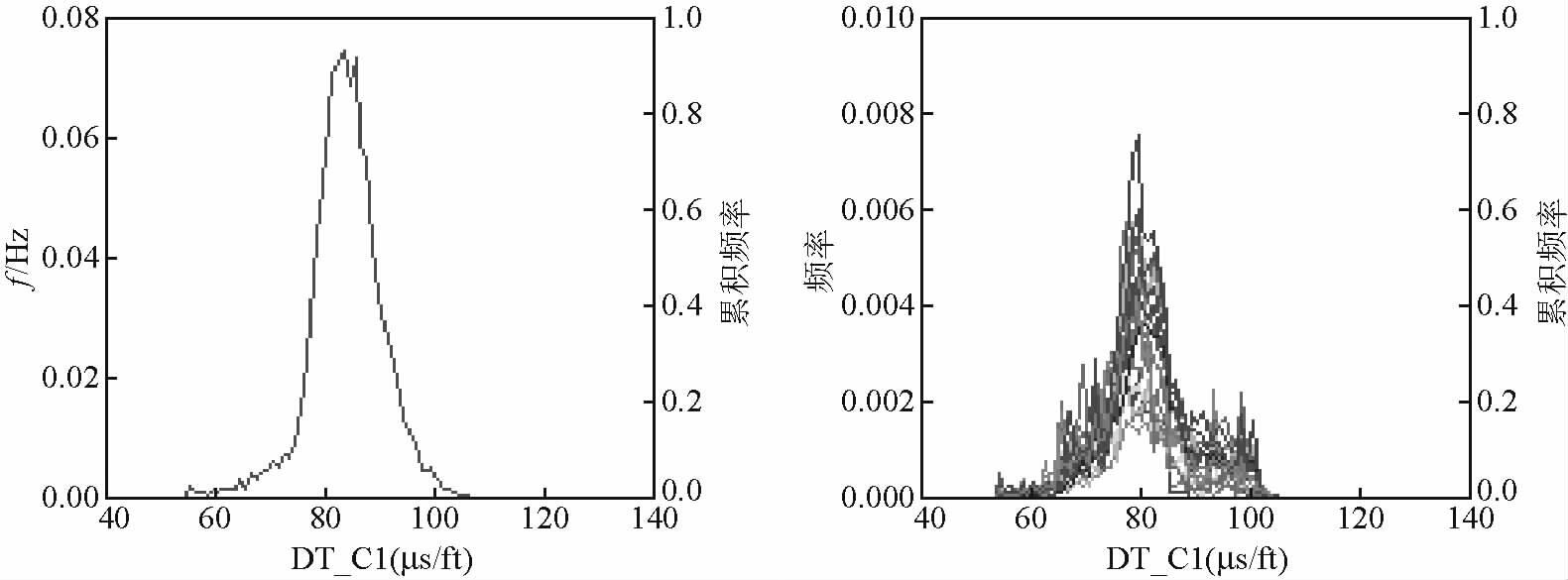
图 5 聚类分析算法K=1时预测的纵波测井曲线 Fig. 5 Forecasted compression wave logging with K is equal to 1 based on cluster analysis algorithm

图 6

Fig. 6

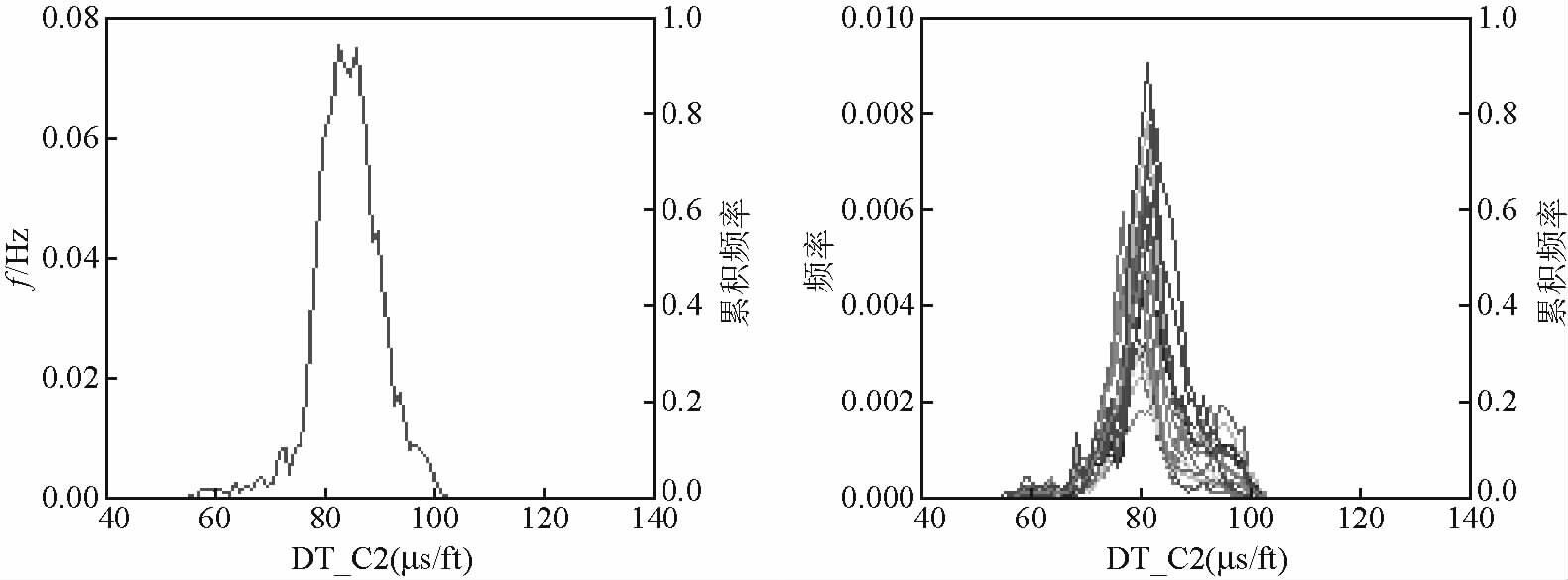
图 6 聚类分析算法K=5时预测的纵波测井曲线 Fig. 6 Forecasted compression wave logging with K is equal to 5 based on cluster analysis algorithm

图 7

Fig. 7

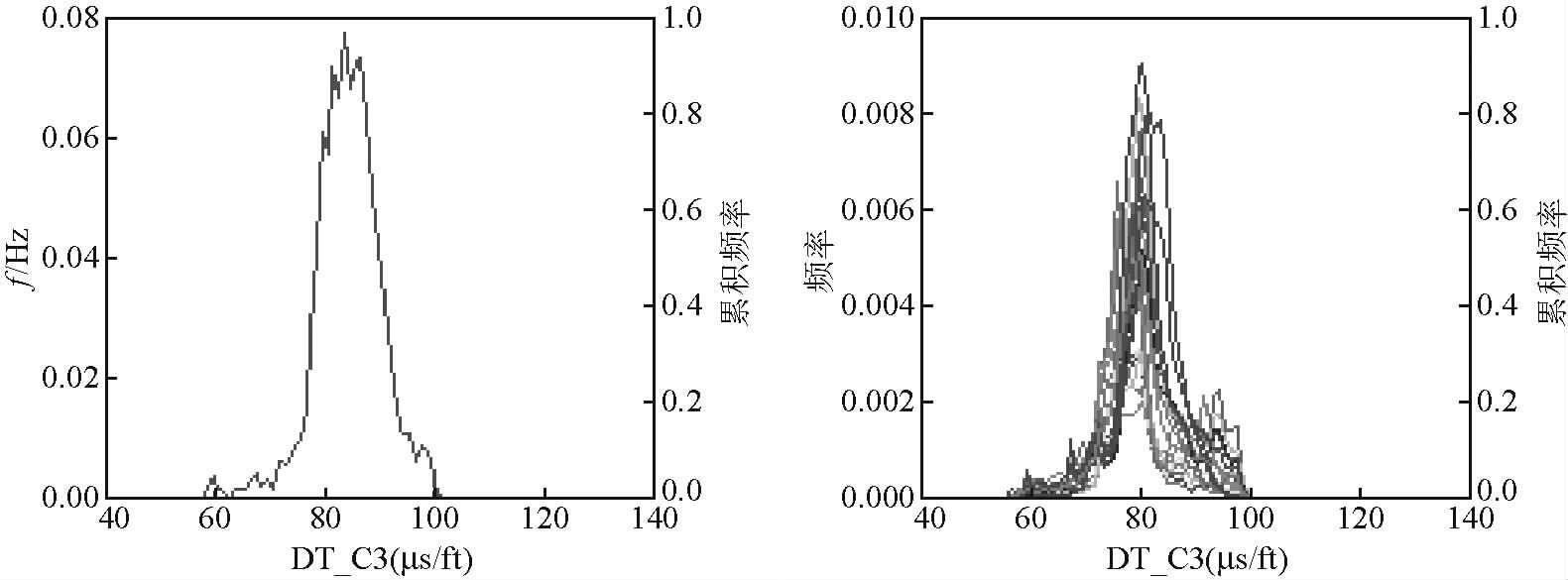
图 7 聚类分析算法K=10时预测的纵波测井曲线 Fig. 7 Forecasted compression wave logging with K is equal to 10 based on cluster analysis algorithm

图 8

Fig. 8

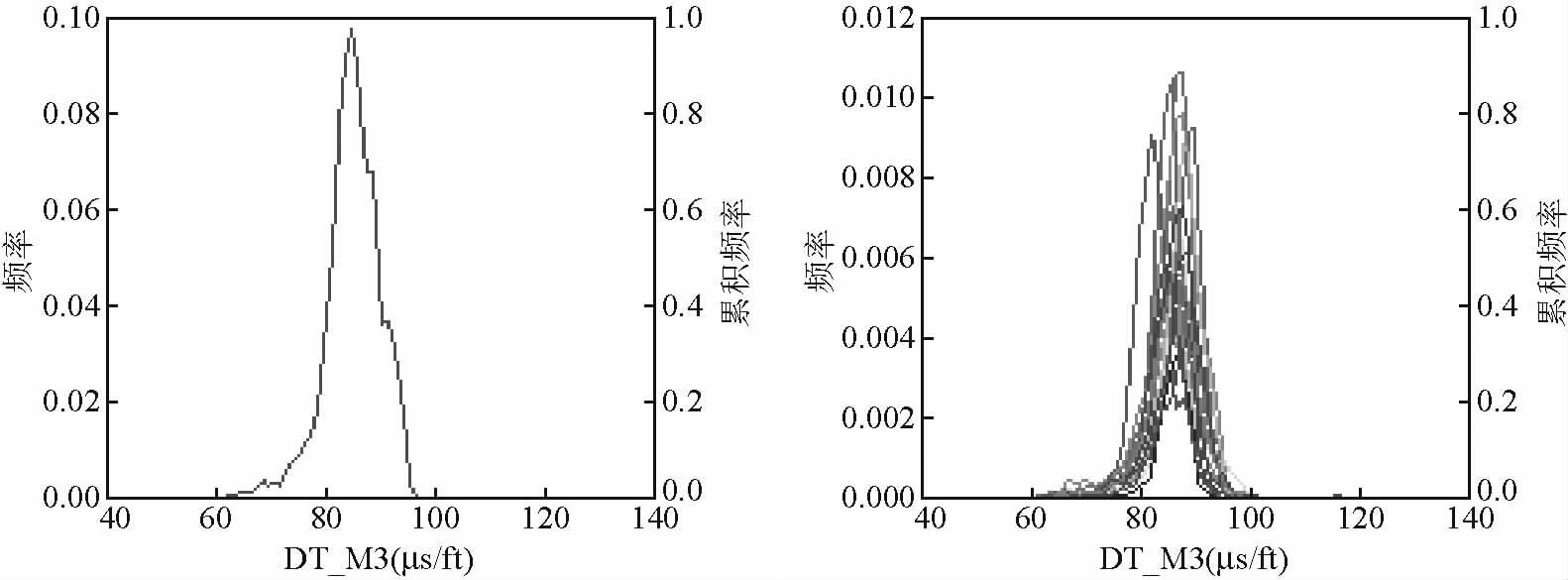
图 8 多元线性拟合预测的纵波测井曲线 Fig. 8 Forecasted compression wave logging based on multilinear fitting

预测纵波测井曲线累积频率为50%所对应的纵波时差值见表 4，预测的B井与其他18口井纵波测井曲线累积频率为50%所对应的纵波时差，多元线性拟合基于V_sh、φ的参数组合所对应的值最小.

表 4 (Table 4)

表 4 预测纵波测井曲线累积频率为50%所对应的纵波时差 Table 4 Forecasted compression wave logging when cumulative frequency is equal to 50% 类型 DT_C1 (μs/ft) DT_C2 (μs/ft) DT_C3 (μs/ft) DT_M3 (μs/ft) B井 83.84 84.20 84.28 84.99 预测的18口井 80.82 80.91 80.88 85.93

表 4 预测纵波测井曲线累积频率为50%所对应的纵波时差 Table 4 Forecasted compression wave logging when cumulative frequency is equal to 50%

因此，参考并结合所预测纵波曲线的曲线形态，及模型井与预测井的差值，采用多元线性拟合基于V_sh、φ的参数组合所预测的纵波测井曲线为最终采用的纵波测井曲线.

X油田20口井纵波测井曲线的标准化时的差值见表 5，标准化后的曲线形态见图 9.标准化后的纵波测井曲线无论是曲线形态，还是累积频率为50%所对应的纵波时差，均存在较好的一致性，因此，可用于后期储层参数反演、储层精细描述、剩余油分布预测等相关的工作.

表 5 (Table 5)

表 5 预测纵波测井曲线的标准化 Table 5 Standardization of forecasted compression wave logging 序号 井名 累积频率为50%对应 纵波时差(μs/ft) 标准化时的差值 (μs/ft) 1 A 84.60 1.30 2 A1 86.21 -0.31 3 A2 86.09 -0.19 4 A3 85.75 0.15 5 A4 84.88 1.02 6 A5 86.94 -1.04 7 A6 85.62 0.28 8 A7 85.00 0.90 9 A8 86.45 -0.55 10 A9 86.36 -0.46 11 B 83.84 2.06 12 B1 81.96 3.94 13 B2 84.90 1.00 14 B3 88.08 -2.18 15 B4 87.64 -1.74 16 B5 86.00 -0.10 17 B6 86.96 -1.06 18 B7 84.35 1.55 19 B8 87.89 -1.99 20 B9 85.90 0.00

表 5 预测纵波测井曲线的标准化 Table 5 Standardization of forecasted compression wave logging

对于砂泥岩地层横波测井曲线的预测，主要基于Han公式、Greengerg-Castagna(GC)公式和Xu-White模型等.其中Han公式是分析了孔隙度、泥质含量对纵、横波速度的影响，给出了纵、横波速度的经验关系(Han et al.，1986)；与Han公式相似，GC公式是根据岩石样品纵、横波速度之间的关系，用统计方法建立了横波速度预测方法(Castagna et al.，1985; Greenberg and Castagna，1992)；而Xu-White模型则是建立在Kuster-Toksoz和Gassmann方程基础之上的一种理论岩石物理模型(Xu and White，1995; Xu and White，1996).

由于X油田20口井均没有横波测井资料，而邻区的C井有实测的横波测井资料，故以C井为模型井，分别采用Han公式、GC公式和Xu-White模型来重构C井的横波测井曲线，通过与C井实测的横波测井曲线进行对比，从而优选合适的方法来预测X油田20口井的横波测井曲线.

Han公式、GC公式和Xu-White模型所重构C井的横波测井曲线，与实测横波测井曲线之间的相对误差分别为4.80%、4.36%和9.51%，见图 10.在图 10中，DTSM是实测的横波测井曲线，DTSM_Han是Han公式所预测的横波测井曲线，DTSM_GC是GC公式所预测的横波测井曲线，DTSM_XW是Xu-White模型所预测的横波测井曲线.

图 10

Fig. 10

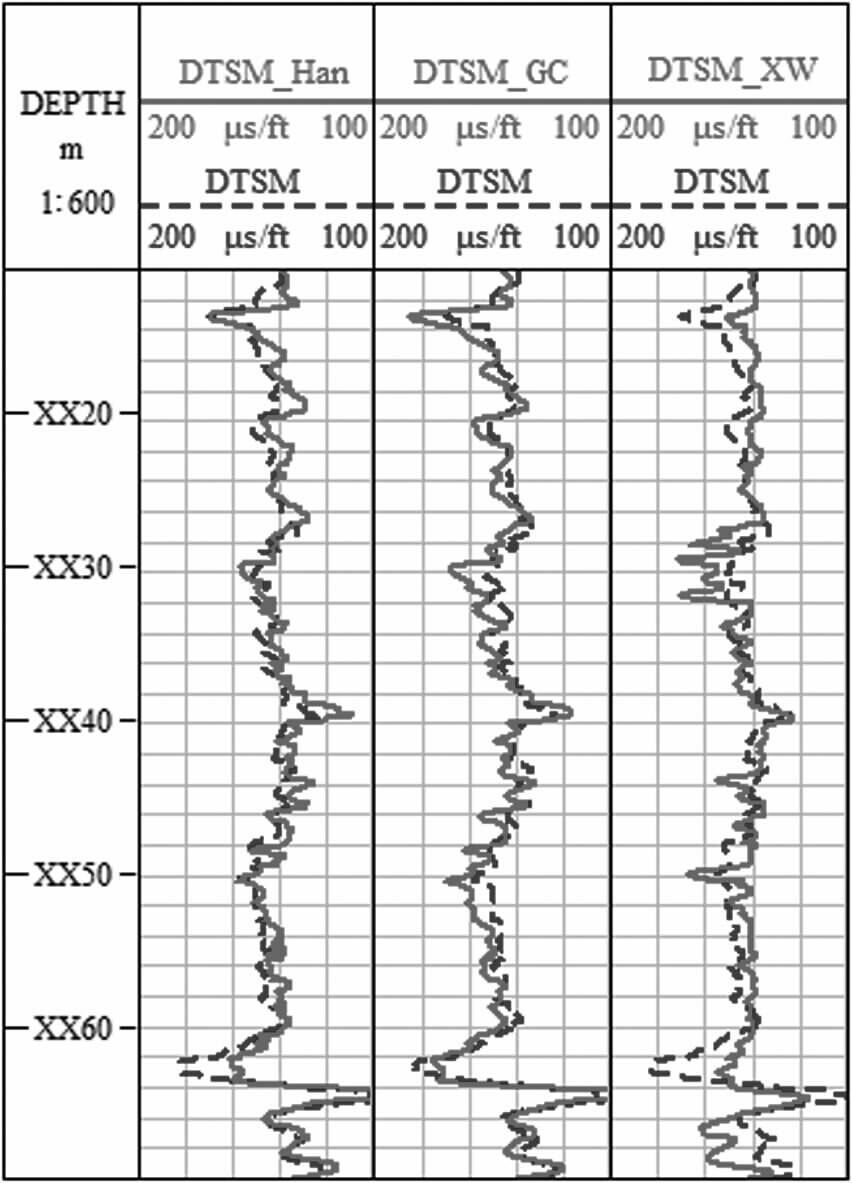
图 10 C井实测与预测的横波测井曲线对比 Fig. 10 Comparison of measured and forecasted shear wave logging of well C

尽管Han公式、GC公式属于经验公式，但对X油田砂泥岩地层和中高孔中高渗储层的横波预测具有较好的预测效果.Xu-White模型由于在横波预测的过程中需要一系列的参数，且这些参数难以准确给出，从而造成其预测横波的相对误差相对较高.因此，选用相对误差相对较低的GC公式来预测X油田20口井的横波测井曲线.

X油田20口井横波测井曲线的预测见图 11.由图 11可知，所预测横波测井曲线的值域分布范围存在较好的一致性，因此，可用于后期储层参数反演、储层精细描述、剩余油分布预测等相关的工作.

图 11

Fig. 11

图 11 预测X油田20口井的横波测井曲线 Fig. 11 Forecasted shear wave logging of 20 wells

3.1 在纵波测井曲线预测的方法中，聚类分析算法构建模型的精度相对较高，但其泛化能力相对较差，存在较大的不稳定性；岩石物理模型需要较多的背景参数，更适用于岩性相对复杂的地层；多元线性拟合的原理相对简单，但只要基于最敏感、最合适的参数组合进行拟合，便能取得较好的效果；基于多元线性拟合所建立的预测模型精度最高，其相对误差约为3.18%；因此，采用多元线性拟合方法预测纵波测井曲线.

3.2 在横波测井曲线预测的方法中，Han公式、GC公式和Xu-White预测模型的相对误差分别为4.80%、4.36%和9.51%；对于X油田砂泥岩地层和中高孔中高渗储层，属于经验公式的Han公式、GC公式的预测效果相对较好，而Xu-White模型由于一系列参数难以准确赋值，致使其预测效果相对较差.

3.3 在纵、横波测井曲线的预测过程中，针对不同的地层或储层类型，诞生了一系列的预测方法或模型，故每一种方法都有其最佳的适用对象.因此，应根据实际的地层或储层类型，选用合适的方法或模型来预测纵、横波测井曲线即可.

致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持！