2. 国家山区公路工程技术研究中心, 重庆 400067;
3. 公路隧道建设技术国家工程实验室, 重庆 400067
2. Country mountain area highway engineering technology research center, Chongqing 400067, China;
3. National engineering laboratory of highway tunnel construction technology, Chongqing 400067, China
国内瞬变电磁勘探常用的方法有:中心回线法、重叠回线法和大回线源法等,这些方法在找水、工程地质调查、环境灾害地质调查等勘察领域均取得了较好的效果(李貅,2002).其中大回线源法用较长边的回线作为发射源,在回线中心地带一定的范围内观测,一旦布好回线后,可采用多台接收机同时工作,具有工作效率高的特点(薛国强等,2007).
随着近地表矿产资源的枯竭,大量的国家和社会资源将融入到深部勘探中去,地球物理方法将发挥重要的作用,此外诸多环境工程问题愈来愈依赖地球物理勘探.这就客观的要求地球物理方法能够高精度、定量的解决地质问题.而快速、高精度的实现地球物理场的正演则是进行地球物理异常定性识别认识和定量反演解释的基础.因此研究地球物理场的正演问题具有重要意义.目前用于回线源瞬变电磁场三维正演计算的方法主要为数值计算方法:有限差分法,有限元法和积分方程法(薛国强等,2008).岳建华等(2007)利用Mur吸收边界条件和均匀全空间电偶极源作为初始激发源,实现了矿井瞬变电磁法三维时域有限差分数值模拟;孙怀凤等(2013)在瞬变电磁三维正演中实现了回线源的加入,并计算了考虑关断时间的瞬变三维响应;邱稚鹏等(2013)采用非正交网格时间域有限差分算法实现了带地形瞬变电磁场的正演计算;李建慧等(2012)利用矢量有限元法对回线源激发的时域电磁响应进行了数值模拟.可见回线源瞬变电磁场三维正演已经取得了很大的进展,但对于三维数值结果的正确性,需要一维解进行验证.因此研究高精度、快速的实现回线源瞬变场的一维正演依然非常重要,同样是实现其一维反演的前提.
回线源瞬变电磁场一维正演有诸多方法,其基本的思想是先求回线源频率域的响应,再通过某种时频变换方法变换到时间域.常用的时频变换方法主要有正余弦变换算法和Gaver-Stehfest算法等,前者计算精度高,但计算速度慢;后者的计算速度快,但计算精度不如前者.孙业发等(2014)研究发现在晚期,正弦变换的计算精度要高于余弦变换;李大俊等(2014)用折线逼近的方法研究了余弦变换的频率范围,使得正余弦变换用于时频转换趋近于成熟.大回线源任意一点的电磁场是包含双贝塞尔函数的积分,需要用近似求解方法来实现.最早在国外,Ryu等(1970)讨论了计算双贝塞尔函数积分的方法,进而得到回线源的电磁场响应;Poddar(1982)用水平电偶极子TE模式表达式沿回线边做积分,得到矩形回线的电磁响应;纳比吉安(1992)在“勘察地球物理电磁法”一书中提出用磁偶极子表达式沿回线边做数值积分可得到回线源的响应.而在国内,李建平等(2012)和李建慧等(2008)沿用了国外偶极子合成回线源的思想计算并获得大回线的瞬变响应;华军等(2001)将双贝塞尔函数积分的区间分成两段,分别用不同的数值计算方法进行求解.
本文分别利用垂直磁偶极子和水平电偶极子的一维时域电磁场表达式沿回线边做积分获取矩形大回线的瞬变电磁场,并与圆回线中心点解析解和数值解进行对比,并讨论了这两种方法的计算精度问题.
1 正演方法 1.1 水平电偶极子合成回线源方式水平电偶极子在均匀水平层状大地表面上的频率域垂直磁场分量表达式为(米萨克,1992)
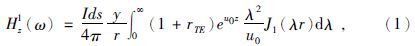
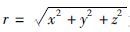 为收发距;Ids为电偶极矩;μ0为自由空间磁导率,rTE为反射系数,u0=
为收发距;Ids为电偶极矩;μ0为自由空间磁导率,rTE为反射系数,u0=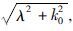 准静态条件下<
准静态条件下<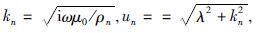 ,
,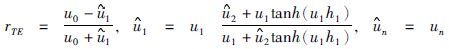
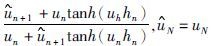 ,n=1,2,…,N共层.
,n=1,2,…,N共层.
式(1)是关于贝塞尔函数的无穷积分,一般用数字滤波法求其数值解.本文则采用Guptasarma和Singh(1997)给出的120点J0滤波系数和140点J1滤波系数(阮百尧,2005),公式为
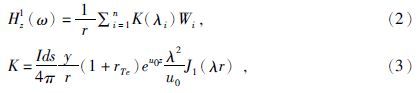
式(2)为频域表达式,需要用G-S变换或者正余弦变换变换到时间域.本文则是对频率域表达式用正弦变换得到时间域表达式(李貅,2002),则时间域垂直磁场随时间变化率可表示为
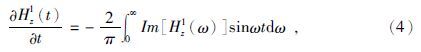
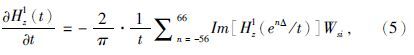
当N=1时,即水平电偶极子位于均匀大地上的时间域垂直磁场随时间变化率为(李貅,2002)
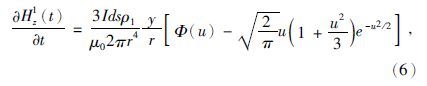
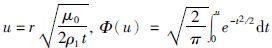 ,ρ1为均匀大地的电阻率.
,ρ1为均匀大地的电阻率.
对于矩形回线源,一条边产生的垂直磁场随时间的变化率可由水平电偶极子产生的时间域垂直磁场随时间变化率沿回线边做积分得到

则矩形大回线任意位置的时间域垂直磁场随时间变化率为
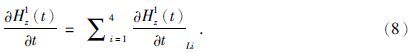
垂直磁偶极子在均匀水平层状大地表面上的频率域垂直磁场为(纳比吉安,1992)
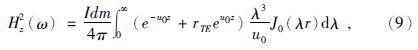
有了式(9),可利用1.1节中的方法获得时间域垂直磁偶极子位于均匀水平层状大地表面上的垂直磁场随时间变化率
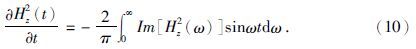
当N=1时,即垂直磁偶极子位于均匀半空间上的时间域垂直磁场随时间变化率为(李貅,2002)
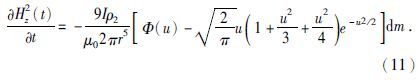
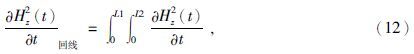
回线位于均匀水平层状大地表面上的中心点频域垂直磁场为(纳比吉安,1992)
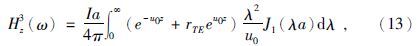
有了式(13),同样用1.1节中的方法获得回线位于均匀水平层状大地表面上中心点的时间域垂直磁场随时间变化率
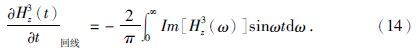
当N=1时,即回线位于均匀半空间上中心点的时间域垂直磁场随时间变化率(李貅,2002)
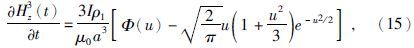
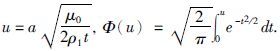 1.4 部分计算方法改进
1.4 部分计算方法改进
在上述公式中,式(6),(11),(15)中都包含有误差函数项:Φ(u)=$\sqrt{\frac{2}{\pi }}$∫0ue-t2/2dt.误差函数项计算一般是采用数值积分法,但从的物理含义可以看出,其变化范围较大,当积分上限变化范围较大时,误差函数积分计算耗时且不准确.陈清礼(2009)利用一种改进的积分算法用来计算误差函数,使得求取一个测点的全区视电阻率仅需1 min左右.本文作者研究发现利用自变量复杂化的双曲正切函数来近似误差函数,将避免直接数值积分的耗时和不稳定,可快速、稳定、高精度的实现误差函数的计算(韩自强等,2015).
对于式(7)中和式(12)中的积分,为了提高积分的精度,用复化的高斯-勒让德求积法进行计算:对于电偶极子合成回线正演方式,先把矩形回线的四条边分别分成若干段,再对每一小段进行高斯-勒让德求积,然后将每一小段激发的瞬变响应相叠加;对于磁偶极子合成回线正演方式,先把矩形回线分成若干个小回线,再对每个小回线进行高斯-勒让德求积,然后将每个小回线激发的瞬变响应相叠加.
电偶极子合成回线正演方式,式(7)可表示为
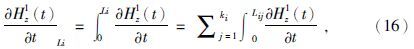
磁偶极子合成回线正演方式,式(12)可表示为
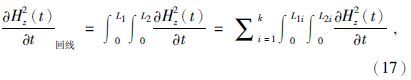
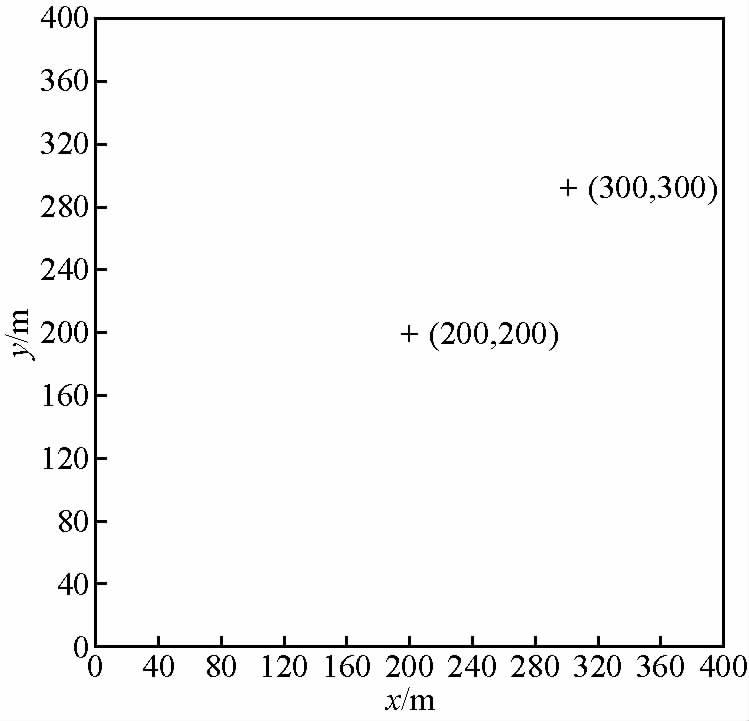
在瞬变电磁场一维正演计算的过程中,电流为1 A;时间测道有25道;采样窗口为0.01~1000 ms;回线框和测量点位置见图 1,回线中心点位置为(200,200).如果接收在回线的中心点或回线外一较远的距离上,则圆型回线与面积相同的方型回线是一个很好的近似(纳比吉安,1992).因此,对于同一理论模型,对比偶极子合成方回线中心点正演计算结果和等效面积相同的圆回线中心点公式计算结果,分析利用偶极子合成方回线正演计算回线源瞬变场的计算精度,以及积分计算方式和回线框大小对计算精度的影响.
|
图 1 发射回线框和测量点位置示意图 Fig. 1 Sketch map of loop source and measurement points |
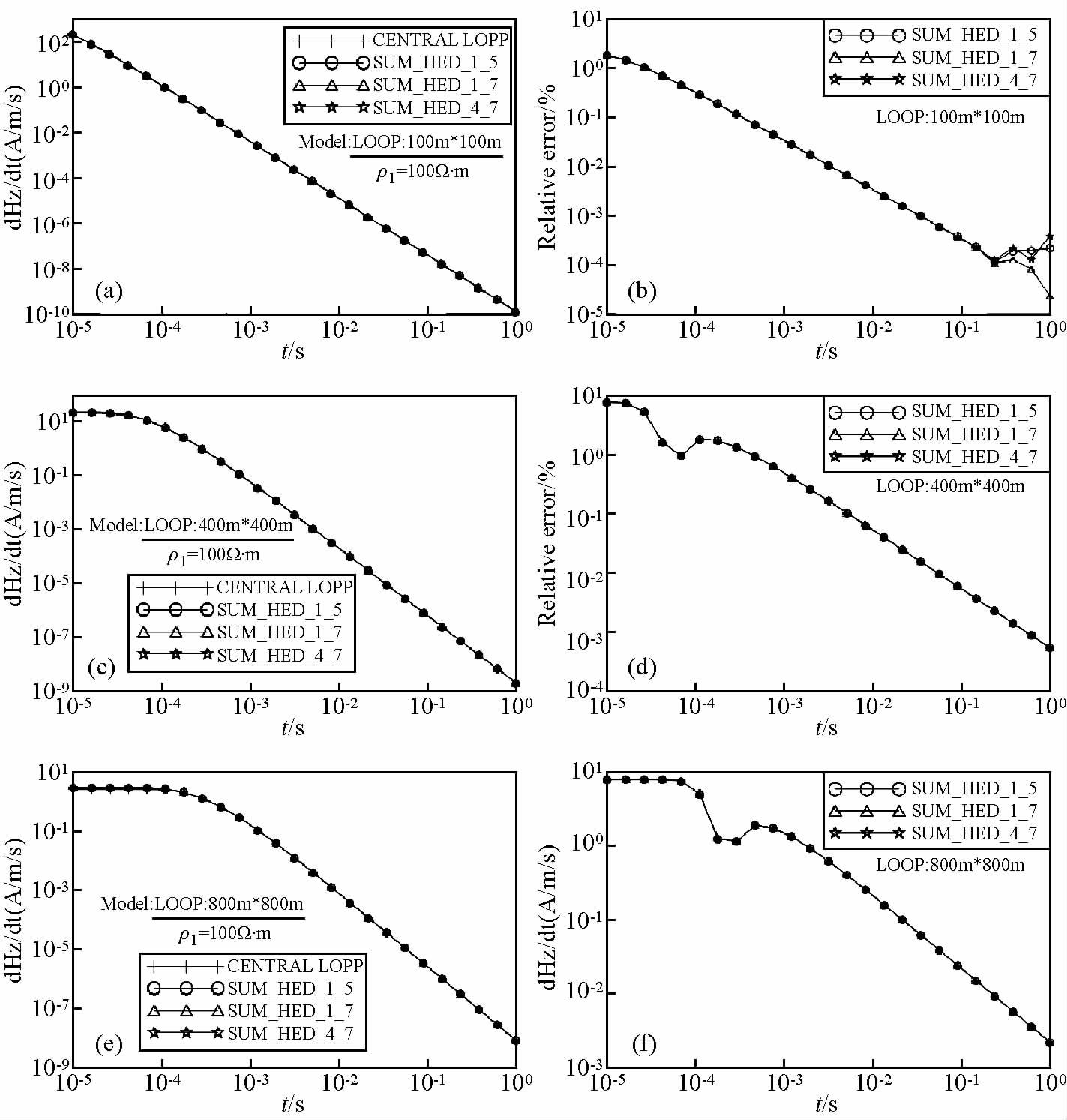
图 2为均匀半空间模型水平电偶极子合成方回线中心点正演与等效面积相同的圆回线中心解析解对比图.可见,对于100×100 m的回线,如(a)图和(b)图,当采用高斯-勒让德5点求积时,在早期道的相对误差较大,最大为1.28%,随着测量时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线基本一致;不同积分方式计算结果的相对误差曲线在早期重合,在晚期有所波动,因此当采用更加精细的积分时,相对误差没有明显的减小,计算精度基本保持不变.
|
图 2 均匀半空间模型水平电偶极子合成方回线中心点正演与等效面积相同圆回线中点解析解对比图 (a)、(c)、(e):不同回线大小的场值;(b)、(d)、(f):相对中心回线解析解的相对误差 CENTRAL LOOP:中心回线解析解;SUM_HED_1_5:高斯-勒让德5点求积; SUM_HED_4_7:每条回线边分成4段,高斯-勒让德7点求积. Fig. 2 Contrast of horizontal electric dipoles synthesis square loop center pointforward and the same area circularcentral loop analytic solutions for uniform half space model (a),(c),(e): Field value of different loop area;(b),(d),(f): Relative error to central loop analytic solutions CENTRAL LOOP: Central loop analytic solutions; SUM_HED_1_5: Gauss-Legendre 5 points quadrature; SUM_HED_4_7: Every loop sideis divided into 4 sections,Gauss-Legendre 7points quadrature. |
对于400×400 m的回线,如(c)图和(d)图,当采用高斯-勒让德5点求积时,在早期道相对误差较大,最大为7.73%;其相对误差曲线变化规律和积分方式对计算精度的影响均与100×100 m回线计算结果基本一致,但相对误差曲线在晚期没有波动.对于800×800 m的回线,如(e)图和(f)图,当采用高斯-勒让德5点求积时,在早期道相对误差较大,最大为7.73%,其相对误差曲线变化规律和积分方式对计算精度的影响均与400×400 m回线计算结果一致.
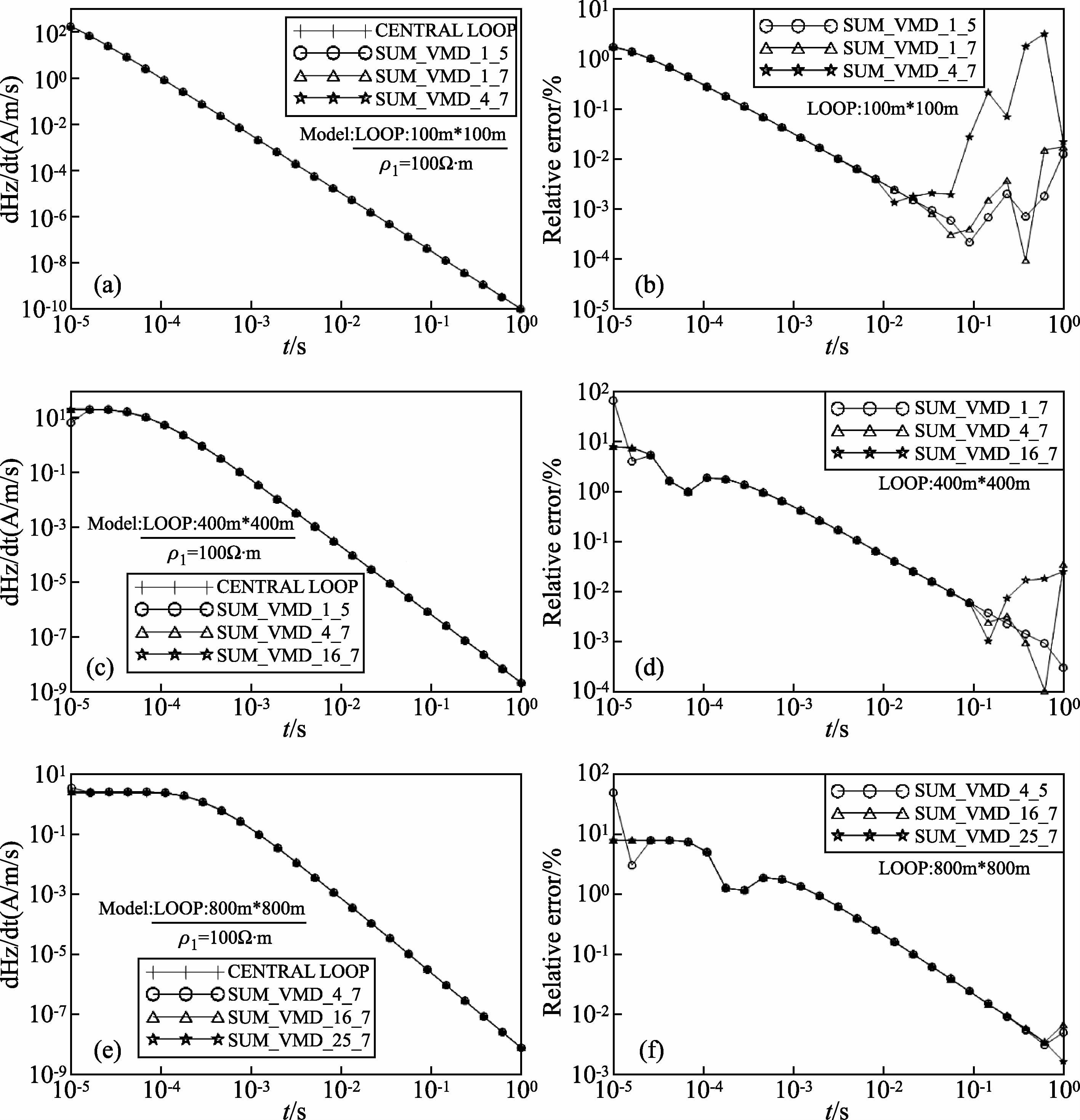
图 3为均匀半空间模型垂直磁偶极子合成方回线中心点正演与等效面积相同圆回线中心解析解对比图.可见对于100×100 m的回线,如(a)图和(b)图,当采用高斯-勒让德7点求积时,在早期道相对误差较大,最大为1.82%,在早期,不同积分方式的计算结果的相对误差曲线重合,随着测量时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线一致;在晚期采用更精细的积分时,相对误差出现较大波动且无规律,当采用将回线分成4个小回线、高斯-勒让德7点求积时,晚期的相对误差最大值达到了3.35%.
|
图 3 均匀半空间模型垂直磁偶极子合成方回线中心点正演与等效面积相同圆回线中心解析解对比图 (a)、(c)、(e):不同回线大小的场值;(b)、(d)、(f):相对中心回线解析解的相对误差 SUM_VMD_4_7:大回线分成4个小回线,高斯-勒让德7点求积计算结果. Fig. 3 Contrast ofvertical magnetic dipoles synthesis square loop center pointforward and the same area circularcentral loop analytic solutions for uniform half space model (a),(c),(e): Field value of different loop area;(b),(d),(f): Relative error to central loop analytic solutions SUM_VMD_4_7: Loop is divided into 4small loops,Gauss-Legendre 7points quadrature. |
对于400×400 m的回线,如(c)图和(d)图,当采用高斯-勒让德7点求积时,在早期道,相对误差非常大,达到66.36%,但随着测量时间道的增加,相对误差减小;当采用将回线分成4个小回线、高斯-勒让德7点求积时,在早期道相对误差较大,最大为7.79%,随着测量时间道的增加,相对误差减小;当采用将回线分成16个小回线、高斯-勒让德7点求积时,在早期道相对误差较大,最大为7.79%,随着测量时间道的增加,相对误差减小,计算精度并没有再提高;当采用更精细的积分时,相对误差在晚期出现较大波动且无规律.
对于800×800 m的回线,如(e)图和(f)图,当采用将回线分成4个小回线、高斯-勒让德7点求积时,在早期道,相对误差非常大,达到48.88%,随着测量时间道的增加,相对误差减小;当采用将回线分成16个小回线、高斯-勒让德7点求积时,在早期道相对误差较大,最大为7.79%,随着测量时间道的增加,相对误差减小;当采用将回线分成25个小回线、高斯-勒让德7点求积时,在早期道相对误差较大,最大为7.79%,随着测量时间道的增加,相对误差减小,计算精度并没有再提高;和400×400 m回线计算结果类似,在晚期采用更精细的积分时,相对误差出现较大波动且无规律.
可见对于电偶极子合成方回线正演方式,在早期道相对误差较大,随着测量时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线基本一致;不同积分方式计算结果的相对误差曲线在早期重合;一般采用高斯-勒让德5点求积便可达到最高精度,当采用更精细的积分时,相对误差没有明显的减小,且在晚期有所波动.对于磁偶极子合成方回线正演方式,在早期道相对误差较大,随着测量时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线基本一致;对于不同大小的回线,为了达到最高计算精度,所需要的积分方式不同,一般回线框越大,便需要更精细的积分.采用更精细的积分时,相对误差在晚期出现较大波动且无规律.
当回线框较小,如100×100 m时,二次磁场衰减速度快,回线框形状对二次磁场早期的衰减影响小,因此等效面积相等的方回线和圆回线在早期(10-5s)时,二次磁场衰减情况较接近,故等效面积相等的方回线和圆回线激发的二次磁场在10-5 s时差异较小为1.28%或者1.82%.当回线框较大,如400×400 m和800×800 m时,二次磁场衰减速度较慢,回线框的形状对二次磁场早期的衰减影响大,因此等效面积相等的方回线和圆回线在早期(10-5 s)时,二次磁场衰减情况差异较大,故等效面积相等的方回线和圆回线激发的二次磁场在10-5 s时误差较大为7.73%或者7.79%.可见偶极子合成回线方式正演在早期较大的误差并非由计算方法本身导致,而是等效面积相等的方回线和圆回线激发的二次磁场本身存在差异所致.
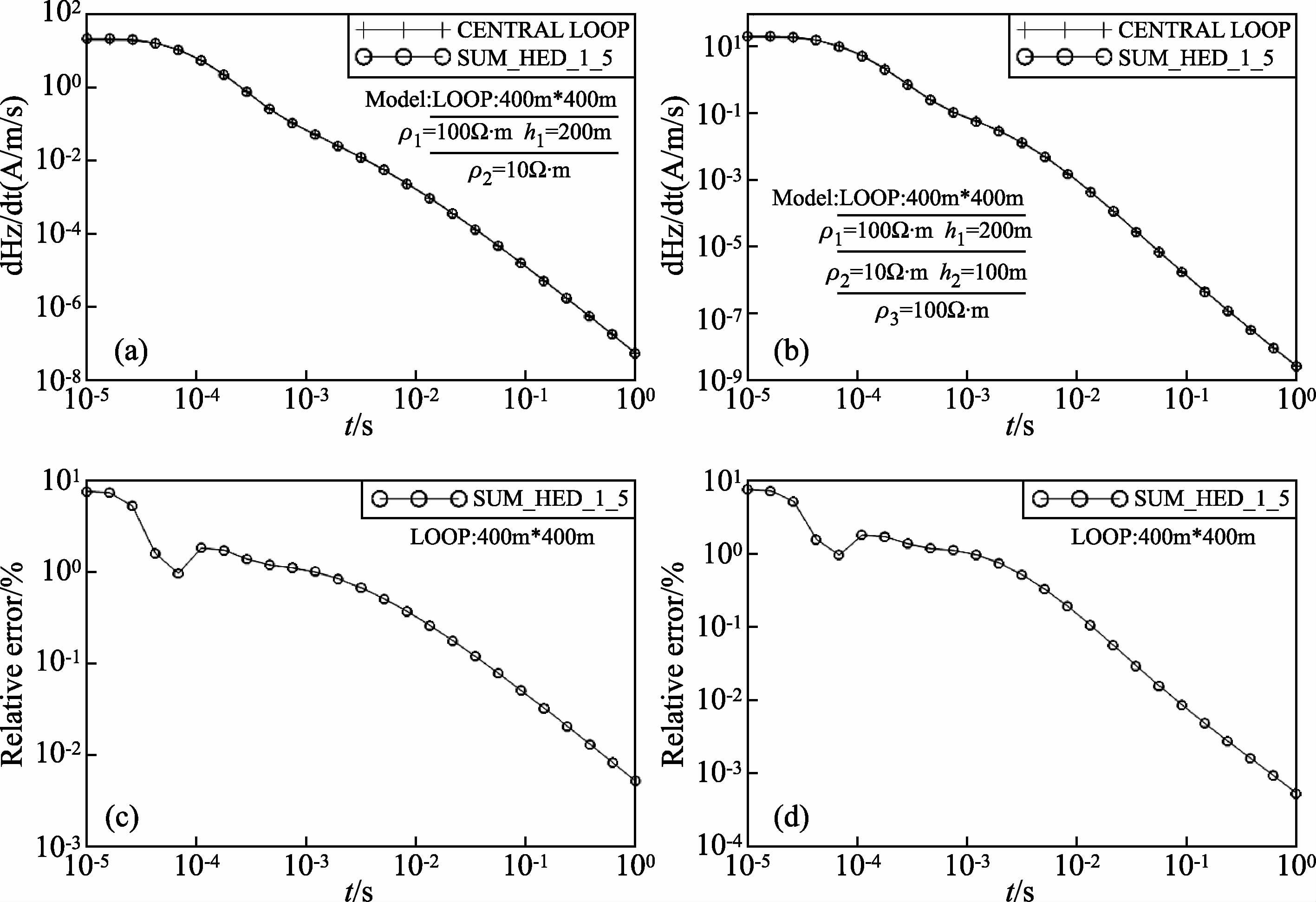
2.2 层状模型回线中心点计算结果分析图 4为层状模型水平电偶极子合成方回线中心点正演与等效面积相同圆回线中心点数值解对比图,这里采用高斯-勒让德5点求积,和均匀半空间模型类似,层状D型和H型模型在早期道相对误差较大,最大为7.73%;随着测量时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线基本一致.
|
图 4 层状模型水平电偶极子合成方回线中心点正演与等效面积相同圆回线中心点数值解对比图 (a)、(b):不同模型的场值;(c)、(d):相对圆回线中心点数值解相对误差. Fig. 4 Contrast of horizontal electric dipoles synthesis square loop center pointforward and the same area circularcentral loop numerical solutions for layered models (a),(b): Field value of different models;(c),(d): Relative error to central loopnumerical solutions. |
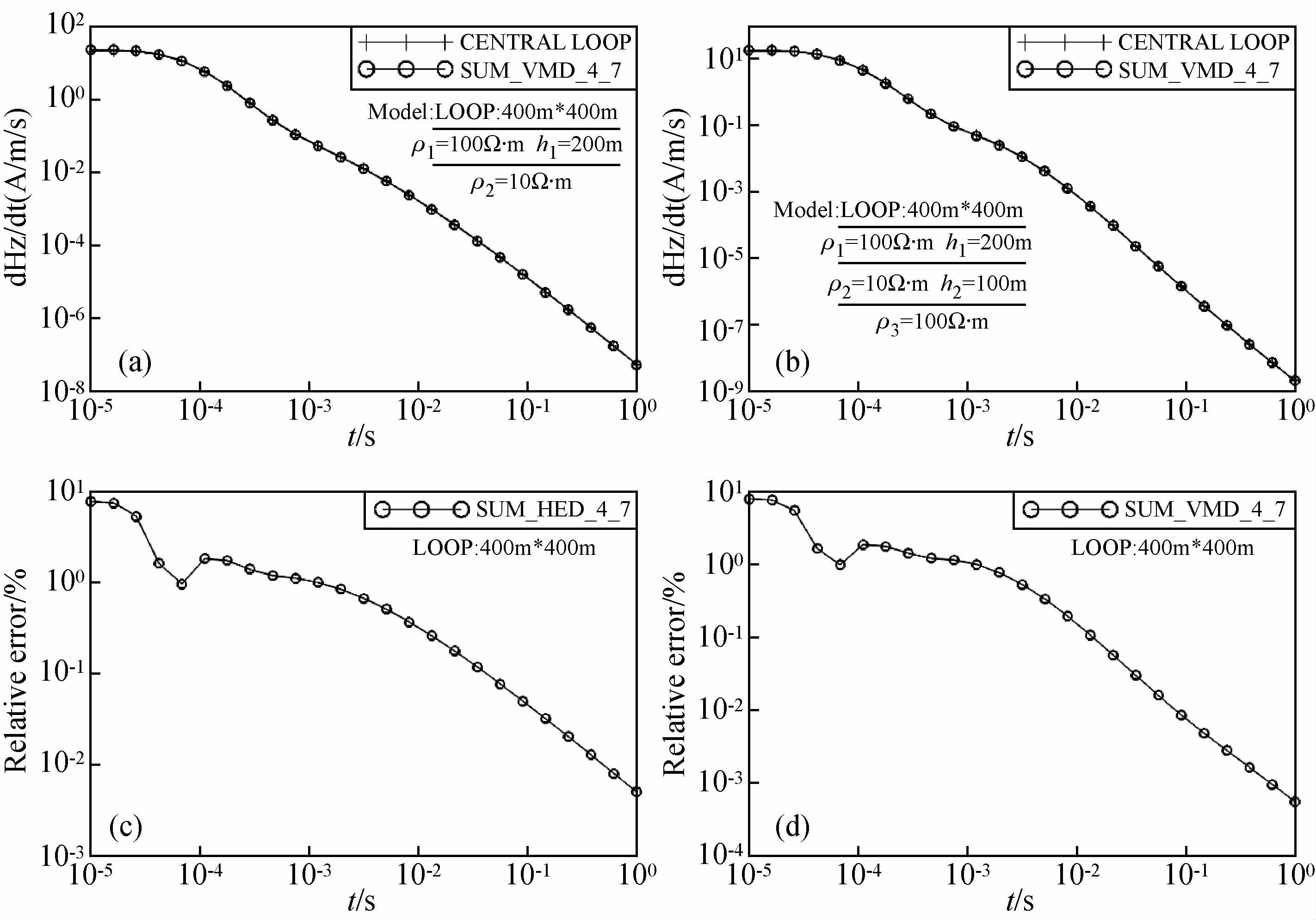
图 5为层状模型垂直磁偶极子合成方回线中心点正演与等效面积相同圆回线中心点数值解对比图,由于是400×400 m的回线,故采用将回线分成4个小回线、高斯-勒让德7点求积,和均匀半空间模型类似,层状D型和H型模型在早期道相对误差较大,最大为7.79%,随着测量时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线基本一致.
|
图 5 层状模型垂直磁偶极子合成方回线中心点正演与等效面积相同圆回线中心点数值解对比图 (a)、(b):不同模型的场值;(c)、(d):相对圆回线中心点数值解相对误差. Fig. 5 Contrast of vertical magnetic dipoles synthesis square loop center point forward and the same area circularcentral loop numerical solutions for layered models (a),(b): Field value of different models;(c),(d): Relative error to central loopnumerical solutions. |
和均匀半空间模型类似,层状D型和H型模型具有同样的特征:由于回线框较大,为400×400 m,故二次磁场衰减速度较慢,回线框的形状对二次磁场早期的衰减影响大,因此等效面积相等的方回线和圆回线在早期(10-5s)时,二次磁场衰减情况差异较大,故等效面积相等的方回线和圆回线激发的二次磁场在10-5s时误差较大为7.73%或者7.79%.
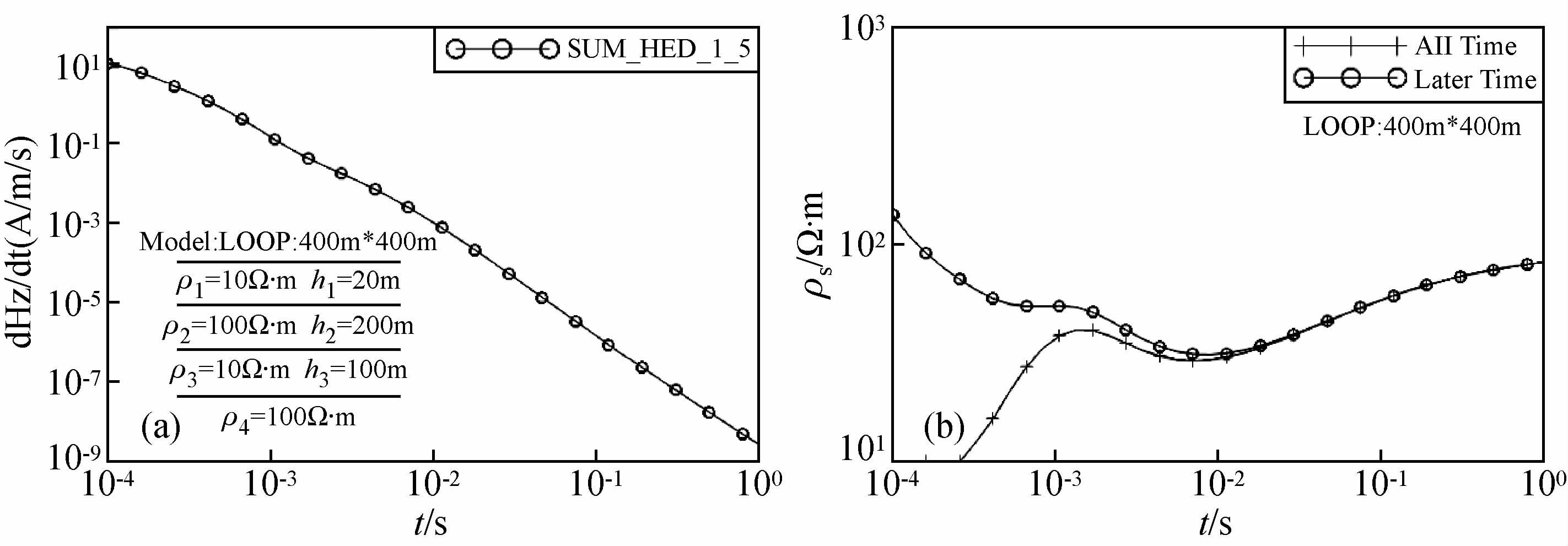
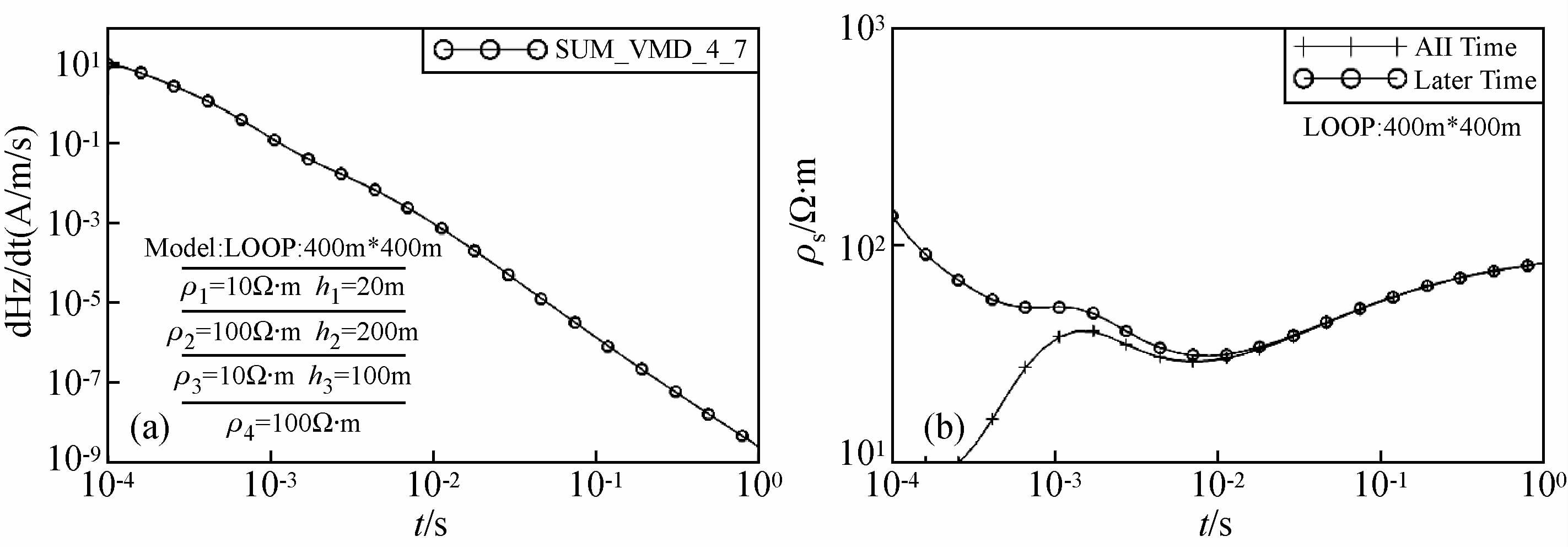
2.3 非回线中心点计算结果分析图 6为KH型模型电偶极子合成方回线非中心点正演计算结果,采用高斯-勒让德5点求积;图 7为KH型模型磁偶极子合成方回线非中心点正演计算结果,由于是400×400 m的回线,故采用将回线分成4个小回线、高斯-勒让德7点求积.并求取了晚期和全区视电阻率.可以看出,晚期视电阻率在早期比实际偏大,且对地电模型的反映不如全区视电阻率具体;在晚期,晚期视电阻率和全区视电阻率基本重合,对地电模型的反映基本一致.全区视电阻率曲线是一条明显的KH型曲线,真实客观的反映了地电断面.
|
图 6 KH型模型电偶极子合成方回线正演在非中心点(300,300)计算结果:(a)场值;(b)视电阻率 Fig. 6 Horizontal electric dipoles synthesis square loop forward results at non center point(300,300)forward for KH model:(a)Field value;(b)Apparent resistivity |
|
图 7 KH型模型磁偶极子合成方回线正演在非中心点(300,300)计算结果:(a)场值;(b)视电阻率 Fig. 7 Vertical magnetic dipoles synthesis square loop forward results at non center point(300,300)forward for KH model:(a)Field value;(b)Apparent resistivity |
可见偶极子合成方回线源正演可以较准确的计算方回线框内外任意一点的一维瞬变电磁场,用该方法计算的理论模型数据来计算全区视电阻率,结果较好的反映了一维模型的地电特征.该计算方法将为回线源瞬变电磁全区勘探和一维反演提供理论基础.
3 结 论
3.1 在偶极子合成回线的计算结果中,早期道相对误差较大,但随着观测时间道的增加,相对误差减小,相对误差曲线的变化趋势和场值曲线基本一致.
3.2 对于电偶极子合成回线正演方式,一般采用高斯-勒让德5点求积便可达到最高精度;对于磁偶极子合成回线正演方式,不同大小的回线,为了达到最高计算精度,所需要的积分方式不同,一般回线框越大,便需要更精细的积分.当采用更精细的积分时,两种方式计算结果的相对误差在晚期均出现较大波动且无规律.
3.3 选取能达到最高精度的积分方式后,研究发现偶极子合成回线正演方式在早期存在较大的误差并非由计算方法导致,而是等效面积相等的方回线和圆回线激发的二次磁场本身存在差异所致.
3.4 偶极子合成回线正演方式可以较准确的计算回线框内外任意一点的瞬变电磁场,将为回线源瞬变电磁全区勘探和一维反演提供理论指导.
| [1] | Chen Q L. 2009.Searching algorithm for full time apparent resistivity from tem electromotive force data[J]. Journal of Oil and Gas Technology (in Chinese), 31(2): 45-49. |
| [2] | Han Z Q, Liu T, Ouyang J, et al. 2015. Application of large rectangular loop source TEM all-time apparent resistivity on colliery goafexploration[J]. Progress in Geophysics (in Chinese), 30(1): 342-349, doi: 10.6038/pg20150150. |
| [3] | Hua J, Jiang Y S, Wang W B. 2001. The numerical integration of dual hankeltransformation[J]. Coal Geology & Exploration (in Chinese), 29(3):58-62. |
| [4] | Li D J, Weng A H, Yang Y, et al. 2014.Frequency range discussion of use polygonal line approximations method to calculate the cosine transform[J]. Progress in Geophysics (in Chinese), 29(4): 1689-1694, doi: 10.6038/pg20140426. |
| [5] | Li J H, Liu S C, Li F, et al. 2008.Electromagnetic field transmitted by rectangular loop in large fixed TEM[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 30(2):154-157. |
| [6] | Li J H, Zhu Z Q, Zeng S H, et al. 2012. Progress of forward computation in transient electromagnetic method[J]. Progress in Geophysics (in Chinese), 27(4): 1393-1400, doi: 10.6038/j.issn.1004-2903.2012.04.013. |
| [7] | Li J P, Li T L, Zhang Y D. 2012. TEM forward and inversion of arbitrary shape loop source in layered media[J]. Geophysical & Geochemical Exploration(in Chinese), 36(2):256-259. |
| [8] | Li X. 2002. Theory and Application of Transient Electromagnetic Sounding (in Chinese)[M]. Xi'an: Shanxi Science Technology Press. |
| [9] | NabighianM N. 1992. Electromagnetic Methods in Applied Geophysics[M]. Zhao J X, Wang Y JTrans.Beijing: Geological Publishing House. |
| [10] | Poddar M. 1982. A rectangular loop source of current on a two-layered earth[J]. GeophysicalProspecting, 30(1):101-114. |
| [11] | Poddar M. 1983. A rectangular loop source of current on multilayered earth[J]. Geophysics, 48(1): 107-109. |
| [12] | Qiu Z P, Li Z H, Li D Z, et al. 2013. Non-orthogonal-Grid-based three dimensional modeling of transientelectromagnetic field with topography[J]. Chinese J.Geophys.(in Chinese), 56(12): 4245-4255, doi: 10.6038/cjg20131227. |
| [13] | Ruan B Y. 2005. Digital filter method of evaluating electromagnetic field from a vertical magnetic dipole above the homogeneous earth[J]. Journal of GuilinUniversity of Technology(in Chinese), 25(1): 14-18. |
| [14] | Ryu J, Morrison HF, Ward SH. 1970. Electromagnetic fields about a loop source of current[J]. Geophysics, 35(5):862-896. |
| [15] | Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese J.Geophys.(in Chinese), 56(3): 1049-1064, doi: 10.6038/cjg20130333. |
| [16] | Sun Y F, Li T L, Fan C S, et al. 2014. Research on frequency-time domain transform method in central-loop transient electromagnetic field response computation[J]. Progress in Geophysics (in Chinese), 29(3): 1243-1247, doi: 10.6038/pg20140333. |
| [17] | Xu Z P, Hu W B. 2011. A high-accuracy numerical filtering algorithm for calculating transient electromagneticresponses[J]. Geophysical Prospecting for Petroleum(in Chinese), 50(3): 213-218. |
| [18] | Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics (in Chinese), 23(4): 1165-1172. |
| [19] | Xue G Q, Li X, Guo W B, et al. 2007. Characters of response of large-loop transient electro-magnetic field[J]. Oil Geophysical Prospecting (in Chinese), 42(5): 586-590. |
| [20] | Yue J H, Yang H Y, Hu B. 2007. 3D finite difference time domain numerical simulation for TEM in-mine[J]. Progress in Geophysics (in Chinese), 22(6): 1904-1909. |
| [21] | 陈清礼. 2009. 瞬变电磁法全区视电阻率的二分搜索算法[J]. 石油天然气学报, 31(2): 45-49. |
| [22] | 韩自强, 刘涛, 欧阳进,等. 2015. 矩形大定源回线TEM法全区视电阻率在煤田采空区勘探中的应用[J]. 地球物理学进展, 30(1): 342-349, doi: 10.6038/pg20150150. |
| [23] | 华军, 蒋延生, 汪文秉. 2001. 双重贝塞尔函数积分的数值计算[J]. 煤田地质与勘探, 29(3):58-62. |
| [24] | 李大俊, 翁爱华, 杨悦,等. 2014. 用折线逼近法计算余弦变换的频率范围讨论[J]. 地球物理学进展, 29(4): 1689-1694, doi: 10.6038/pg20140426. |
| [25] | 李建慧, 刘树才, 李富,等. 2008. 大定源瞬变电磁法矩形发射回线激发的电磁场[J]. 物探化探计算技术, 30(2):154-157. |
| [26] | 李建慧, 朱自强, 曾思红,等. 2012. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 27(4): 1393-1400, doi: 10.6038/j.issn.1004-2903.2012.04.013. |
| [27] | 李建平, 李桐林, 张亚东. 2012. 层状介质任意形状回线源瞬变电磁场正反演[J]. 物探与化探, 36(2):256-259. |
| [28] | 李貅. 2002. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社. |
| [29] | 米萨克N纳比吉安. 1992. 勘查地球物理电磁法[M]. 赵经祥,王艳君译.北京: 地质出版社. |
| [30] | 邱稚鹏, 李展辉, 李墩柱,等. 2013. 基于非正交网格的带地形三维瞬变电磁场模拟[J]. 地球物理学报, 56(12): 4245-4255, doi: 10.6038/cjg20131227. |
| [31] | 阮百尧. 2005. 均匀水平大地上频率域垂直磁偶源电磁场数值滤波解法[J]. 桂林工学院学报, 25(1): 14-18. |
| [32] | 孙怀凤, 李貅, 李术才等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J]. 地球物理学报, 56(3): 1049-1064, doi: 10.6038/cjg20130333. |
| [33] | 孙业发, 李桐林, 范翠松,等. 2014. 中心回线瞬变电磁响应计算的频-时域转换方法研究[J]. 地球物理学进展, 29(3): 1243-1247, doi: 10.6038/pg20140333. |
| [34] | 徐振平, 胡文宝. 2011. 一种高精度瞬变电磁响应正演的数值滤波算法[J]. 石油物探, 50(3): 213-218. |
| [35] | 薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 23(4): 1165-1172. |
| [36] | 薛国强, 李貅, 郭文波,等. 2007. 大回线源瞬变电磁场响应特性[J]. 石油地球物理勘探, 42(5): 586-590. |
| [37] | 岳建华, 杨海燕, 胡搏. 2007. 矿井瞬变电磁法三维时域有限差分数值模拟[J]. 地球物理学进展, 22(6): 1904-1909. |
 2016, Vol. 31
2016, Vol. 31

