2. 中国地质科学院地球物理地球化学勘查研究所, 廊坊 065000;
3. 中国科学院地质与地球物理研究所, 北京 100029
2. Chinese Academy of Geological Sciences Institute of Geophysical and Geochemical Exploration, Langfang 065000, China;
3. Institute of Geology and Geophysics, Chinese Academy of Science, Beijing 100029, China
大地电磁测深法(MT)是金属矿、石油、天然气等资源勘查的重要方法之一,其正演计算是反演解释的基础,不论是线性反演还是非线性反演,其计算过程需要一次或多次正演,然后利用正演响应修正模型参数,归根结底需要解决其正演计算的精度和速度.因此,有必要研究高精度、高效快速的MT数值模拟算法.
通过几十年的研究,高精度的二维MT数值模拟算法已取得很大进展。刘小军(2007)针对电磁场的计算精度问题实现了基于二次场的正演计算方法,将非均匀地电结构中传播的大地电磁场分解为一次场和二次场之和,提高了计算精度;徐世浙等(1995)、李予国等(1996)、刘云和王绪本(2012)等实现了电导率分块连续变化的二维MT有限元计算方法,使得MT模拟更加适应大地介质参数连续变化的特点。同时,并行计算也在地球物理领域得到了广泛应用。刘羽等(2006)在PC机群上实现了大地电磁Occam反演并行计算;顾观文等(2010)实现了基于多处理器多核工作站的CSAMT拟二维反演并行计算,但是这些计算都需要较高的计算成本。为了实现更加高效的计算方法,陈召曦等(2012a,2012b)和林巍等(2013)将GPU并行计算技术应用到重力资料的正反演计算中;戴云峰等(2012)将GPU并行计算技术应用到了汉克儿滤波计算中,并且都获得了较好的加速效果;毛玉蓉(2014)将GPU并行计算技术应用到时间域电磁响应三维计算中,在TeslaTMC1060架构上获得了25倍多的加速效果;李炎等(2010)基于MPI实现了二维大地电磁正演的并行计算.但是,基于GPU并行计算的大地电磁二维有限元数值模拟计算方法尚无文献报导.
本文在前人工作成果的基础上,实现了基于CUDA并行计算的大地电磁二维有限元数值模拟方法.首先对二维MT有限元正演及串行代码的并行化进行叙述;然后在PGI Visual Fortran+CUDA4.2环境下编写基于CPU+GPU的CUDA并行代码,并通过与解析解的计算结果对比验证方法和程序编制的有效性;最后对理论地电模型的MT异常进行正演计算,分析异常特征,对比分析不同节点下计算程序的执行效率,测试结果表明本文所实现的计算程序是可行的、高效的,加速比可达20多倍,从而为基于CUDA并行计算的MT反演技术奠定基础.
1 CUDA技术及简介CUDA是一种新型的硬件和软件架构,用于将GPU作为数据并行计算设备并在CPU上进行计算的发放和管理,而无需将其映射到图像API.GPU可以容纳成百上千个没有逻辑关系的数值计算线程,它的优势是无逻辑关系数据的并行计算.
CUDA编程模型将CPU作为主机(Host),而GPU作为协处理器或者设备(Device).在一个系统中可以存在一个主机和若干个设备.GPU计算的模式就是在异构协同处理计算模型中,将CPU与GPU结合起来加以利用,CPU负责进行逻辑性强的事务处理和串行计算,GPU则执行高度并行的线程任务.
基于GPU的通用计算能够提供强大的计算能力和存储器带宽,同时具有良好的可编程性,较低的成本和较短的开发周期.因此,MT正演并行算法与GPU高速实现研究,对MT高速并行正演计算系统的建立、完善和推广具有重要的意义.
CUDA是NIVIDA的技术,能支持Fortran CUDA并行编程.在MT有限单元正演计算中会遇到许多的频率,基于CPU的算法是将每个频点依次计算,当频点较多时务必会比较耗时,造成计算速度慢.如果将多个频点的正演分成多个模块的线程来进行独立计算,这样就可以提高计算速度,从而缩短计算时间.基于GPU的CUDA并行计算具有多核多线程的特点,因此,本文将在PGI Visual Fortran环境下编程实现MT的并行计算.程序将计算过程分成M个块来进行计算,每个块又可以为N个计算线程组成,块与块之间彼此无关,独立执行,在同一个块中数据可以共享,这些块将组织成一个一维或者二维线程块网格.
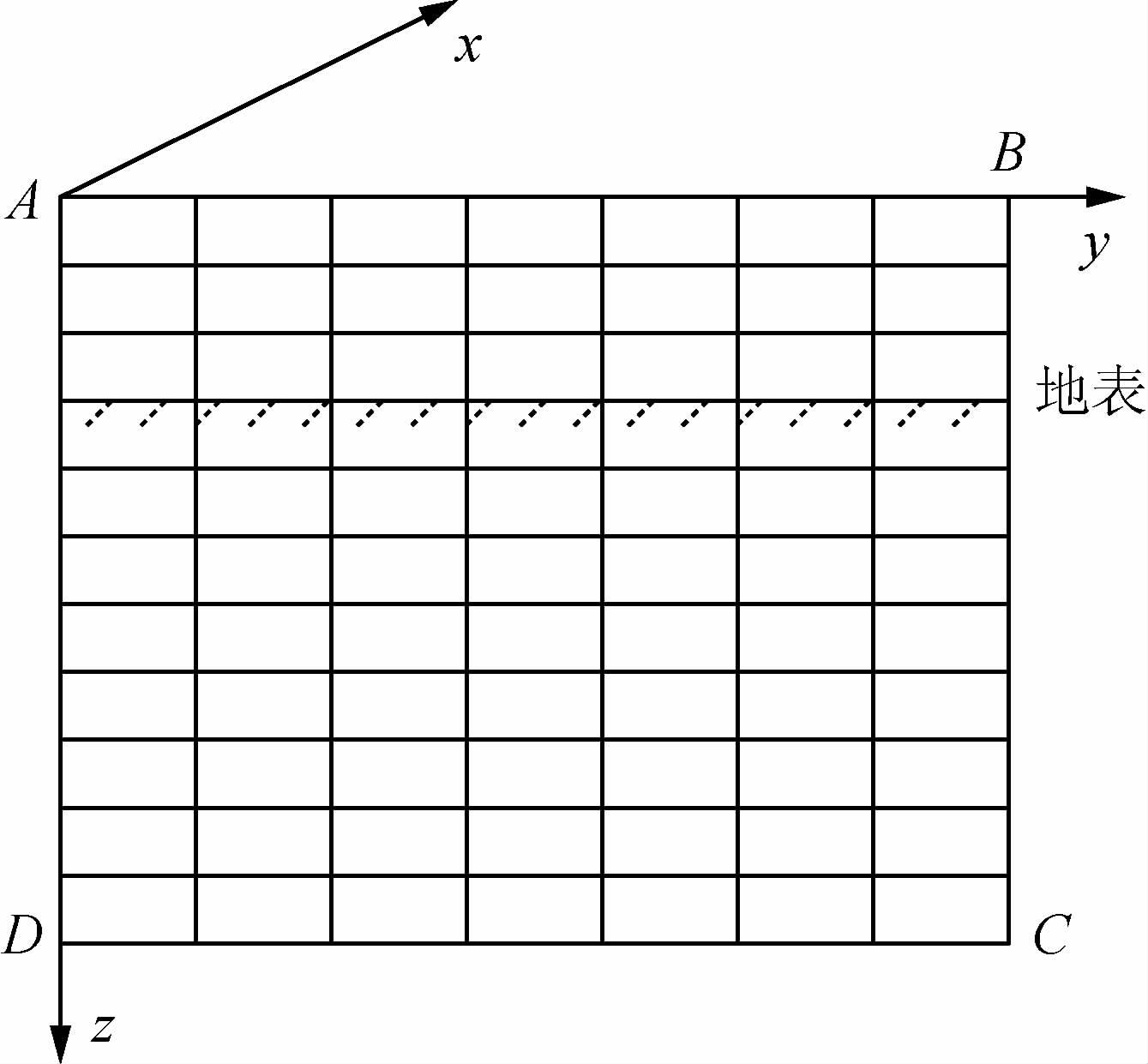
2 MT二维有限元数值模拟 2.1 变分问题在大地电磁(MT)中,对一般二维各向同性介质,若取坐标系x方向为地质体走向(即电性沿此方向不变),z轴垂直向下,如图 1所示,则与之对应边值问题的变分问题为
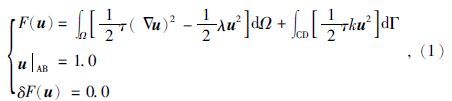
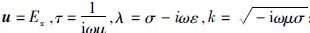 ;而对于TM模式,
;而对于TM模式,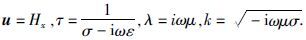
|
图 1 求解区域示意图 Fig. 1 Diagram of computation area |
二维正演中,TE、TM的上边界AB选取不同.对于TE模式,上边界位于空气中,并且离地表足够远,对于TM模式则位于地表.
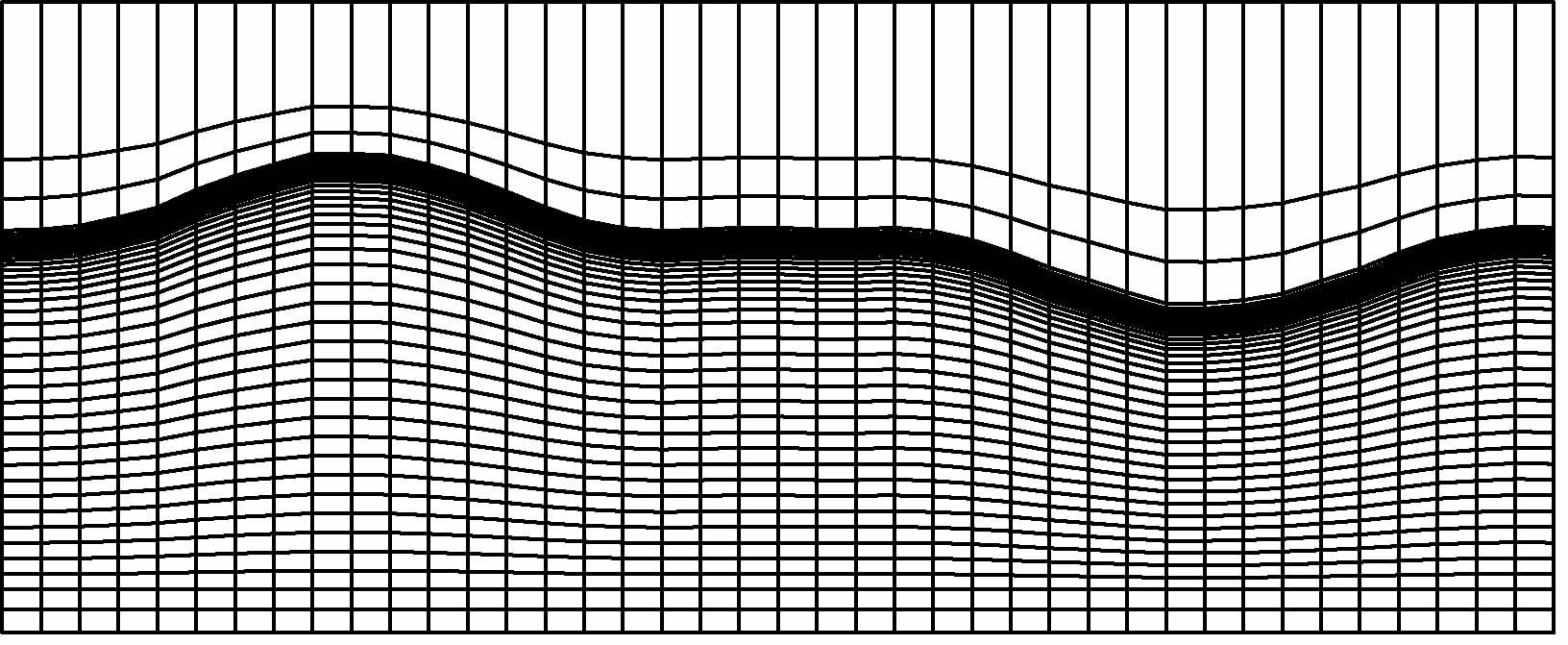
2.2 有限单元法为了适应地形变化,本文使用双线性任意四边形单元对区域Ω进行剖分,如图 2所示,将求解区域剖分为多个四边形单元,在离散的每个单元上进行线性化处理对(1)式进行求解,离散化后的公式为
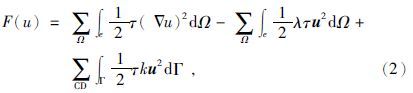
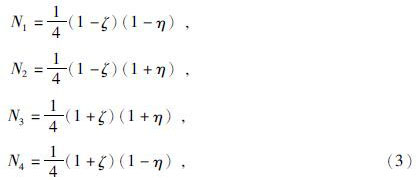
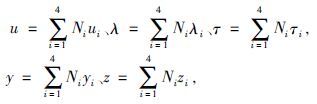
|
图 2 四边形网格自适应地形剖分示意图 Fig. 2 Adaptive topography and quadratic grids |
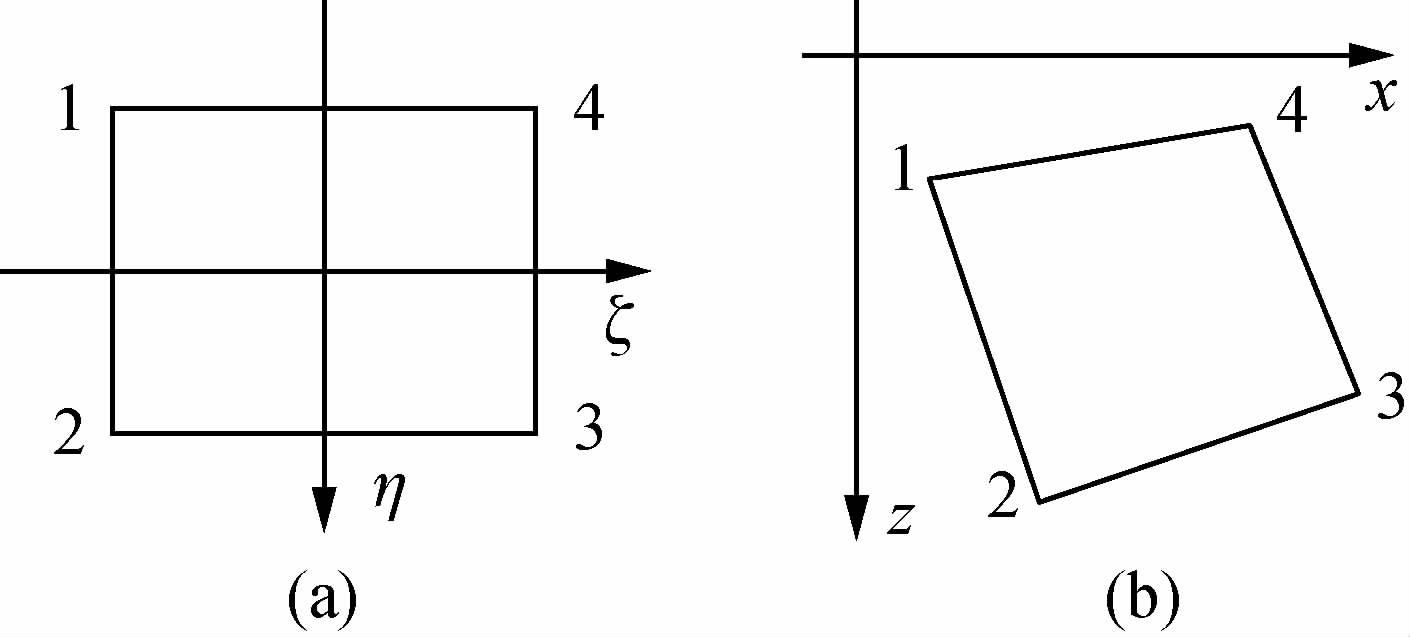
|
图 3 双线性插值单元示意图 (a)母单元;(b)子单元. Fig. 3 Bilinear interpolation element (a)Element;(b)Sub-element. |
则有
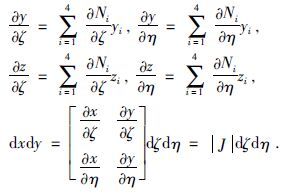
由此(2)中的第一项积分为
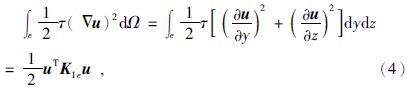
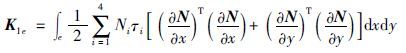
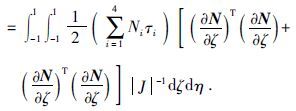
第二项积分为
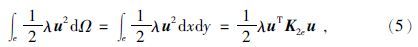
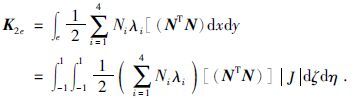
当单元23边界落在研究区域底边界时,第三项线积分为
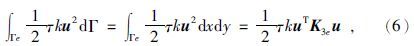
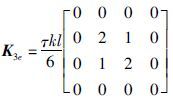
使用3点式高斯积分可计算出式(4)、(5)的积分值,将式(4)、(5)、(6)的积分值相加,再扩展到求解区域的所有单元,合成总体系数矩阵.
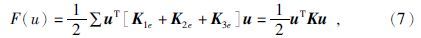

方程中的矩阵K是稀疏对称正定的,为了节约内存空间按变带宽存储.本文采用宋滔和王绪本(2013)提出的稀疏矩阵快速回代的Cholesky分解法求解方程,详细过程可直接参考文献.
3 并行计算实现策略 3.1 MT串行程序并行化并行程序开发通常需要先获得一个问题的串行算法,然后对它并行化,其并行化的方法如下.
(1) 深入分析串行程序的结构和功能,将比较独立、计算量又比较大的部分作为并行化的首选部分,要求顺序执行的部分不能并行化.在执行过程中数据依赖性太大的部分,即使并行化以后,效果也不会太好,因为消息传递太多,导致通信开销太大.
(2) 分析程序各模块计算时间的比率.在源程序中增加一些时间函数,了解各部分运行所需的时间,将计算比重最大、独立性较大的部分进行并行化.
(3) 确定并行方案.先粗颗粒度,再细颗粒度.如果并行任务划分得太细(即细粒度),那么并行任务的调用占用的时间将不可忽略,有可能反而会降低并行性能.
(4) 确定线程分配,单个线程块还是多个,每个线程块设置多少个线程,每个线程块需要传输的是什么数据.
(5) 根据以上信息,通过CPU按分配好的线程调用GPU内核(GLOBAL),给GPU分配线程及下达执行命令,等待计算结果传回.
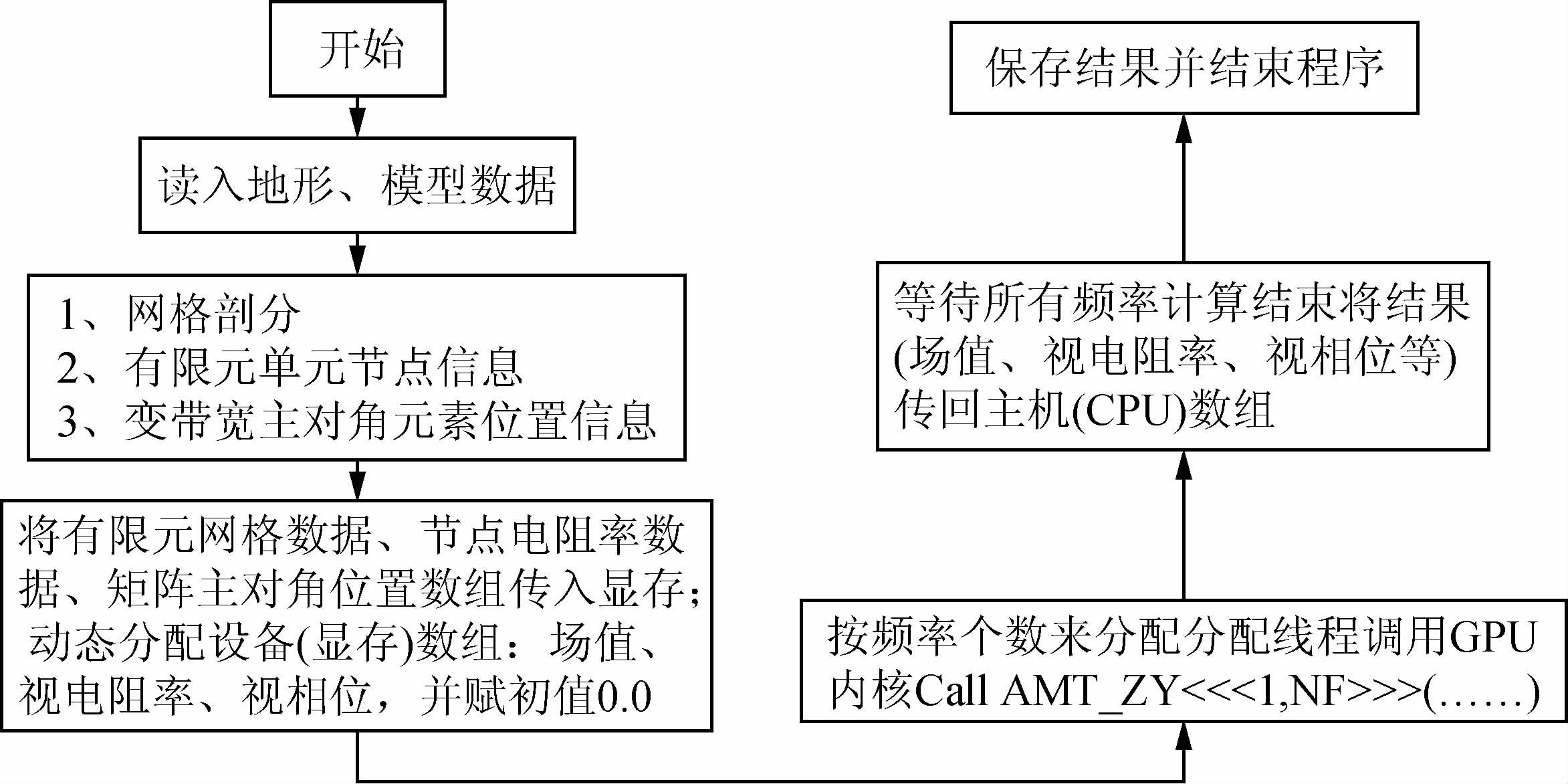
3.2 MT二维正演并行算法策略通过对程序的深入分析发现,二维正演计算中,频率循环部分为主要的计算时间,是需要并行的部分.MT二维正演是对每个频率分别进行计算的,各频率对应的电磁场值间是相互独立的,根据这个特点可以将程序按频率分粒度,将每个频点分配到各个进程同时进行计算,并行执行.程序采用主从并行模式,分主进程和子进程,主进程维持全局数据结构,负责任务的划分、派发、计算结果的回收及输出结果,子进程负责给定任务的计算并把结果回传给主进程.具体的实现过程是:主进程读入网格剖分数据及网格节点电阻率值,并将其广播给子进程,按频率分组给子进程各自计算模型的响应,子进程将计算的结果传给主进程,主进程整合所有计算的结果,并将其输出.图 4为二维正演并行计算简化流程图.在MT并行计算中,CUDA并行计算需要CPU来对GPU分配计算线程,由GPU来执行计算,最终再将计算结果返回CPU.GPU作为设备来完成设备(Device)代码命令部分,这部分代码中CPU分配的进程与GPU的计算众核对应位置关系是随机的,并且独立完成,CPU作为主机(Host)对GPU下达线程分配命令,并等待GPU计算返回结果,如图 4所示.
|
图 4 音频大地电磁法CPU+GPU并行计算流程图 Fig. 4 Flowchart of parallel computing based on CPU+GPU for MT forwarding |
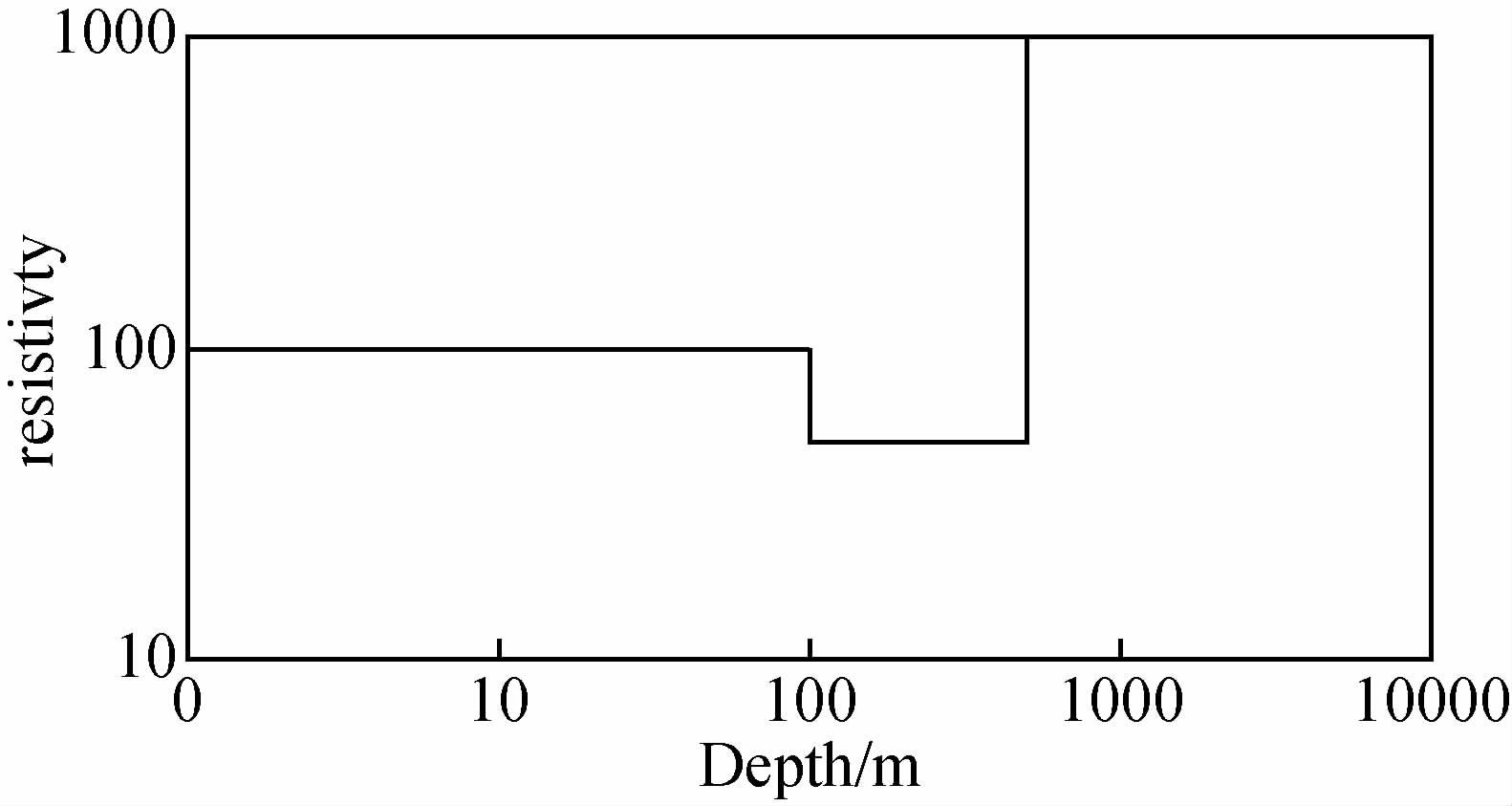
为了说明程序算法的正确性,先设计了一个三层模型,电阻率和厚度分别为ρ1=100 Ω·m,ρ2=50 Ω·m,ρ3=1000 Ω·m,d1=100 m,d2=400 m,如图 5所示.正演计算测点间隔为30 m,两边按1.2倍往外扩展,x方向网格数为108,z方向网格数为83,网格剖分坐标为-10000.0,-7000.0,-5000.0,-3000.0,-1000.0,-500.0,-100.0,-50.0,-20.0,-10.0,0.0,10.0,20.0,30.0,40.0,50.0,60.0,70.0,80.0,90.0,100.0,120.0,140.0,160.0,180.0,200.0,220.0,240.0,260.0,280.0,300.0,320.0,340.0,360.0,380.0,400.0,420.0,440.0,460.0,480.0,500.0,520.0,540.0,560.0,580.0,600.0,620.0,640.0,660.0,680.0,700.0,725.0,750.0,780.0,810.0,840.0,870.0,900.0,930.0,960.0,1000.0,1050.0,1110.0,1180.0,1260.0,1350.0,1450.0,1600.0,1800.0,2000.0,2300.0,2700.0,3200.0,3800.0,4500.0,5300.0,6200.0,7200.0,8500.0,10000.0,14000.0,20000.0,30000.0.计算频率为55个,最高频率为120160323.0 Hz,最低频率为0.0001 Hz,每个数量级按6个频点对数等间隔取值.
|
图 5 三层模型 Fig. 5 Three layered model |
计算结果如图 6所示,基于CUDA并行计算的大地电磁二维有限元数值模拟计算结果与解析计算结果曲线吻合,另外,从视电阻率相对误差曲线和阻抗相位绝对误差曲线也表明基于GPU的CUDA并行计算满足计算精度.

|
图 6 三层模型计算结果与解析结果对比 (a)视电阻率;(b)相位;(c)视电阻率相对误差;(d)相位相对误差. Fig. 6 Results of numerical solution and analytical solution |
为了说明CDUA并行计算方法在正演计算速度上的优越性,与基于CPU串行计算的有限单元法计算程序进行了对比,同时测试了4种不同网格剖分在不同GPU硬件环境下的执行效率(硬件环境分别为Intel core(TM)i5 CPU M480 2.67Ghz及GeForce G105、GeForce GT425、GeForce GTX580),测试结果如表 1、表 2所示.从表中可以看出无论在何种硬件环境下,GPU计算速度都要比CPU的计算速度快很多,其中 GTX580执行速度最快可达20多倍加速.可以看出,GPU的配置越高加速比越高,计算网格越大加速比越高,其加速比的计算公式为
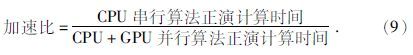
|
|
表 1 TE模式加速测试表 Table 1 Accelerate ratio for TE mode |
|
|
表 2 TM模式加速测试表 Table 2 Accelerate ratio for TM mode |
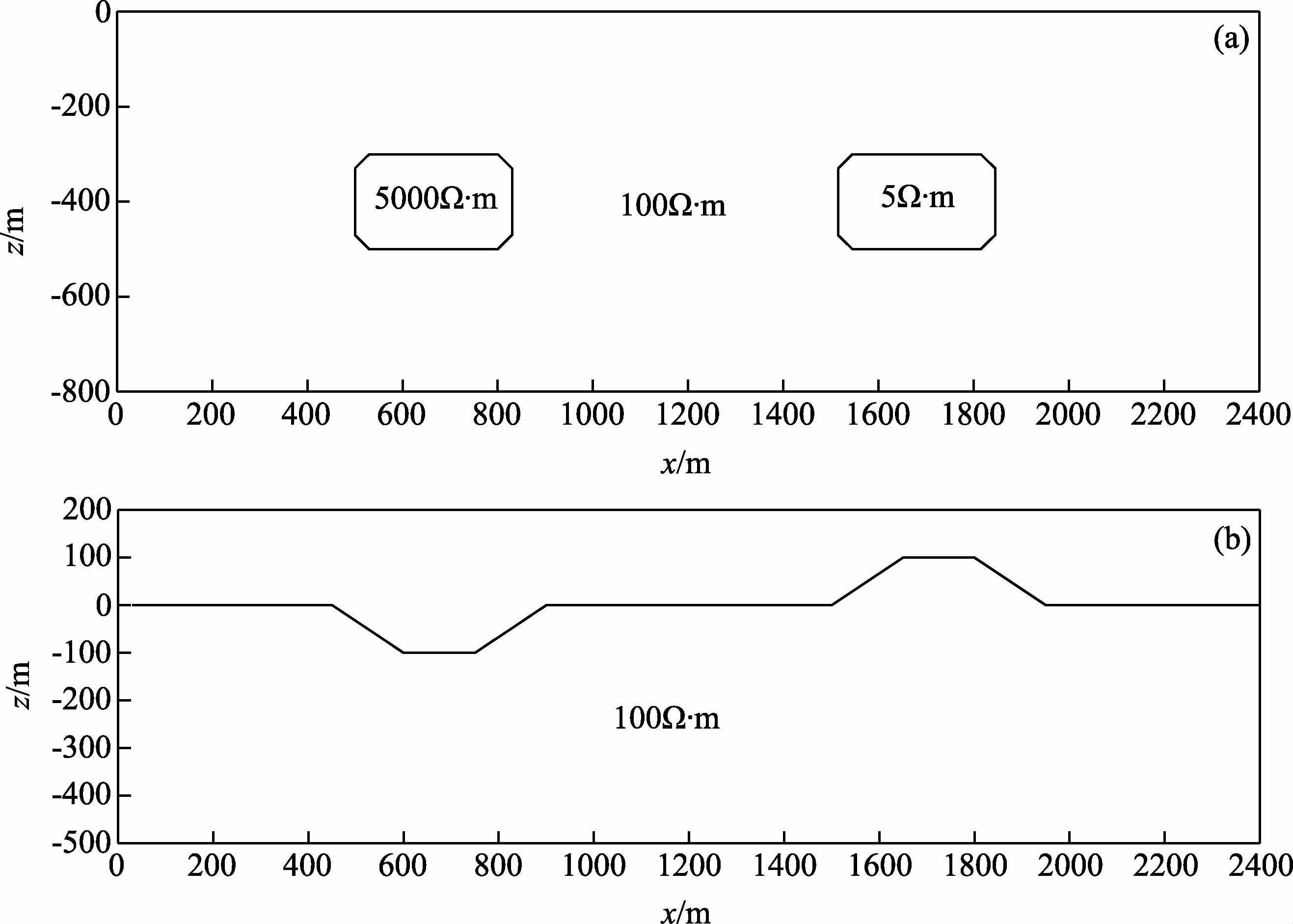
为了进一步说明GPU程序对二维地电断面计算结果的可靠性,设计了模型A和模型B两个模型,其中模型A为均匀大地(ρ=100 Ω·m)中分别存在一个高阻体(ρ1=500 Ω·m)和一个低阻体(ρ1=5 Ω·m),模型B为均匀大地(ρ=100 Ω·m)中存在一个地形凹形和一个地形凸起的模型(如图 7a、b所示).并分别使用CPU串行代码和CUDA并行代码进行测试,并对两种代码执行的结果进行对比分析.
|
图 7 理论地电模型 (a)异常体模型;(b)地形起伏模型. Fig. 7 Computation models (a)Abnormal bodies model;(b)Undulate terrain model. |
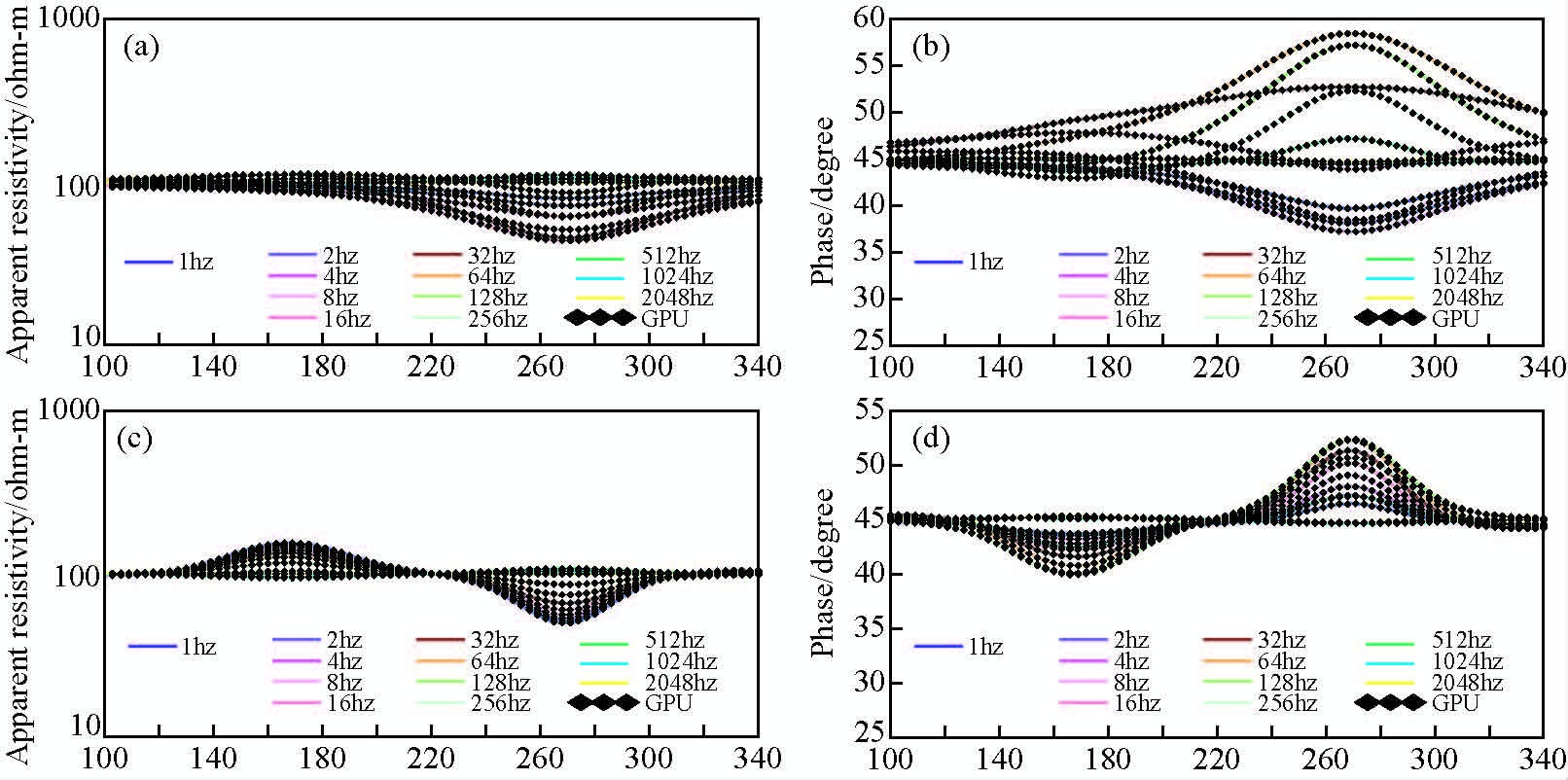
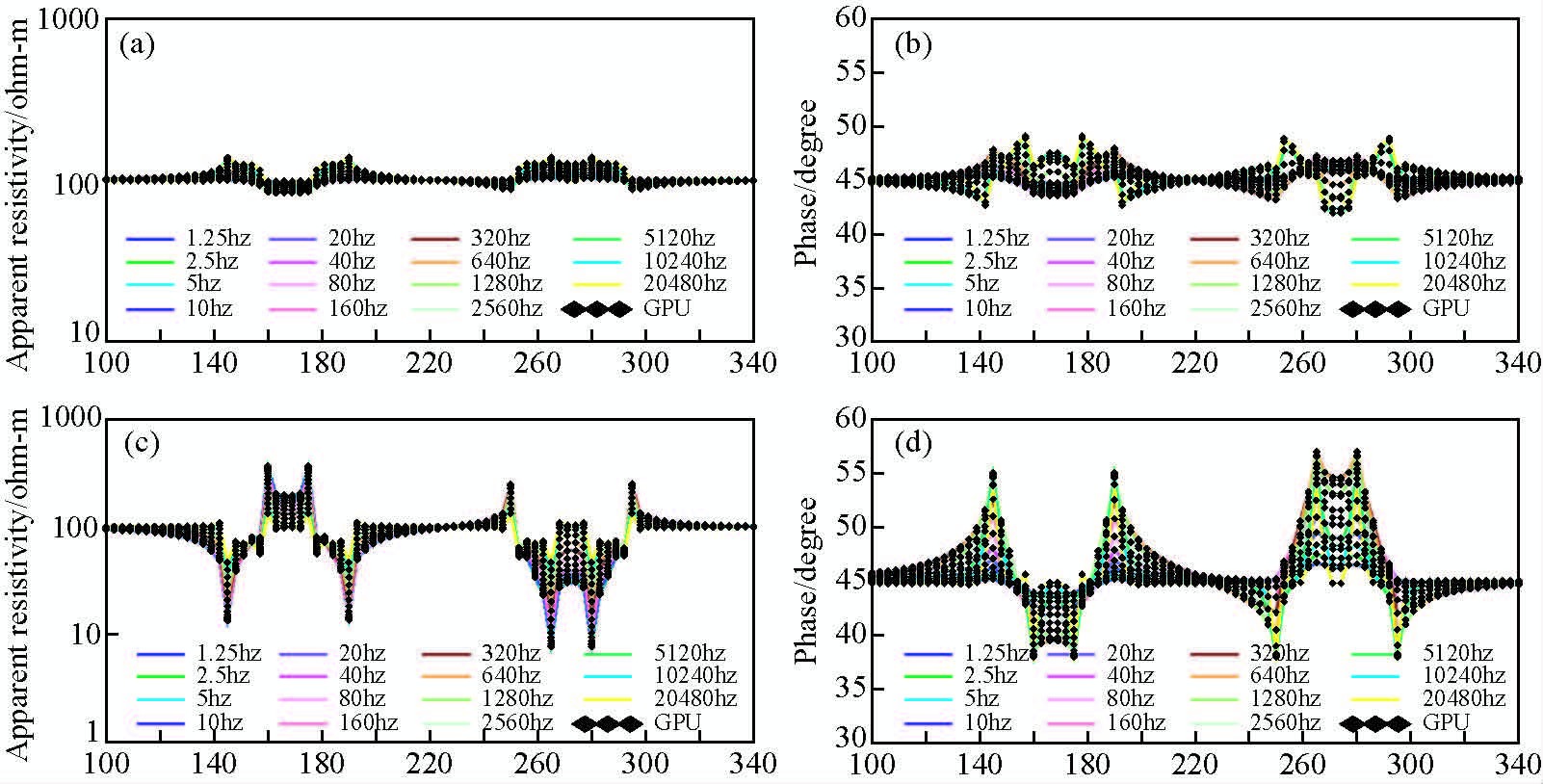
对于模型A和模型B的测试对比结果(如图 8和图 9)可以发现CUDA并行代码计算的结果和CPU串行代码计算的结果一致,由此可以证明CUDA并行计算对于MT正演计算来说具有较高的精度,完全可以使用CUDA并行算法来计算MT正演问题.分析曲线形态和模型异常位置可以发现:对于模型A测试结果,MT中TE模式对于高阻反应不灵敏,对于低阻体则相对较为灵敏,而TM模式不论对于高阻体还是低阻体相对都较为灵敏.对于模型B测试结果我们可以发现MT中地形的变化对TE模式的数据影响较小,而对TM模式的数据则影响比较大.这些也是我们通常在实际矿产勘探中TM模式测量的数据对横向地电参数变化反应比较灵敏,且对地形起伏反应比较灵敏的原因,再次说明程序计算结果和实际是相符的.
|
图 8 异常体模型正演计算对比 (a)TE模式视电阻率;(b)TE模式视相位;(c)TM模式视电阻率;(d)TM模式视相位. Fig. 8 Computation results of abnormal bodies models (a)Apparent resistivity in TE mode;(b)Apparent phase in TE mode; (c)Apparent resistivity in TM mode;(d)Apparent phase in TM mode. |
|
图 9 地形起伏模型正演计算对比 (a)TE模式视电阻率;(b)TE模式视相位;(c)TM模式视电阻率;(d)TM模式视相位. Fig. 9 Computation results of undulate terrain model (a)Apparent resistivity in TE mode;(b)Apparent phase in TE mode; (c)Apparent resistivity in TM mode;(d)Apparent phase in TM mode. |
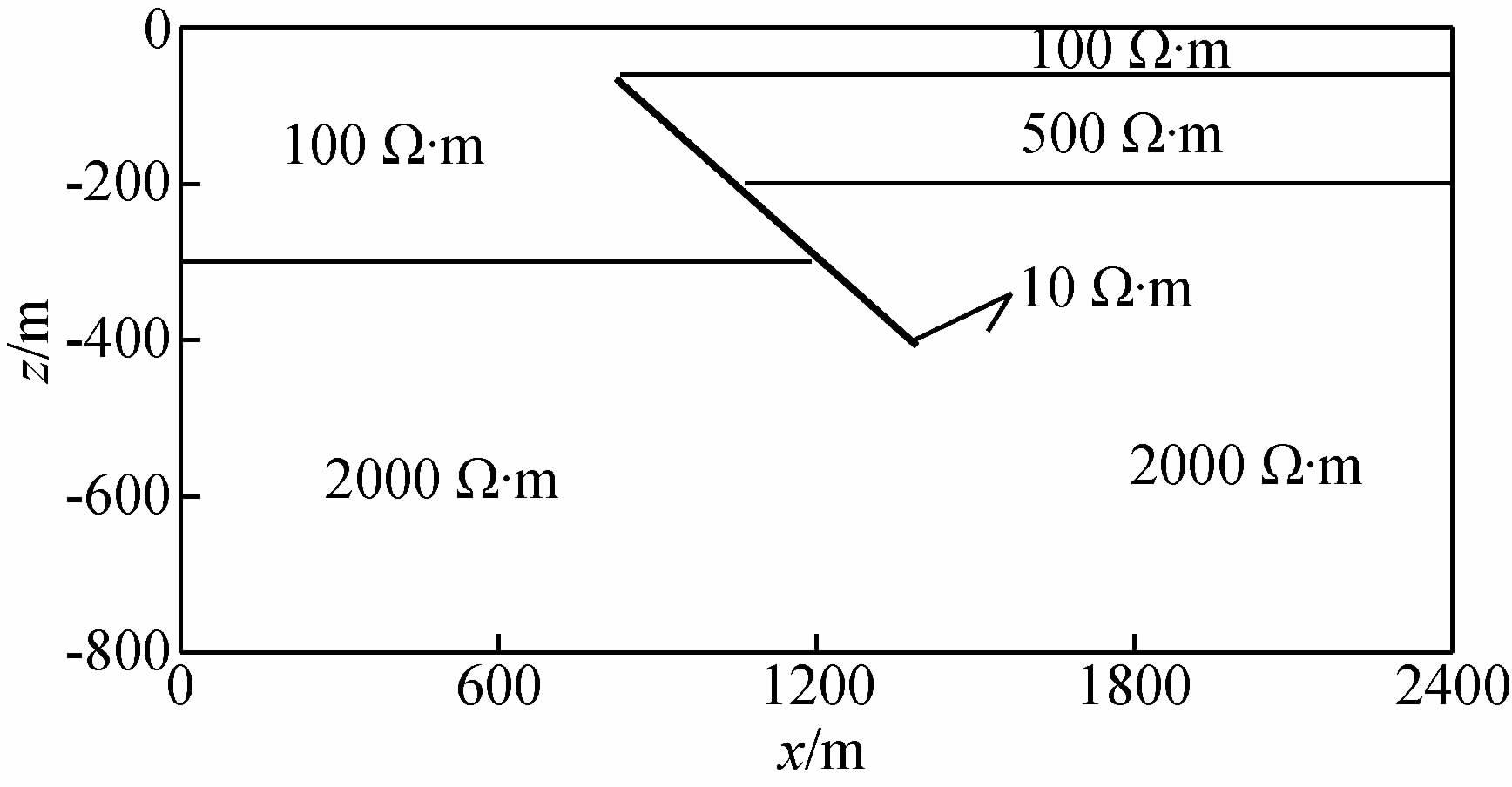
对于矿产勘查的实际应用中,地下介质的变化是复杂的,在此设计了一个更加贴切实际矿产勘探的模型C(如图 9所示)并进行了计算.模型主要为两层大地,顶层电阻率为100 Ω·m,底层电阻率为2000 Ω·m,岩层被一隐伏逆断层破坏之后上盘的顶部岩层被破坏,电阻率为500 Ω·m,底部不变为2000 Ω·m,断层面上电阻为10 Ω·m.
利用GeForce GTX580 GPU计算环境进行测试,TE模式CPU耗时214.027s,GPU耗时9.863s,TM模式CPU耗时144.615s,GPU耗时7.817s,依然具有18.5~21.7倍的加速.图 10为正演的视电阻率和视相位等值线图,纵坐标为频率,横坐标为测点号.由视电阻率和视相位等值线图可以发现在30~40号点之间(对应模型900~1200 m)横向均发生了变化,这就是模型中逆断层的响应.由此可以说明CUDA并行加速算法对MT有限单元正演计算是完全适应的,能够实现和CPU相仿的计算结果,而且具有较高的加速效果.
|
图 10 计算模型 Fig. 10 Computation model |

|
图 11 视电阻率和相位等值线图 (a)TE模式视电阻率;(b)TE模式视相位;(c)TM模式视电阻率;(d)TM模式视相位. Fig. 11 Contours of apparent resistivity and apparent phase (a)Apparent resistivity in TE mode;(b)Apparent phase in TE mode; (c)Apparent resistivity in TM mode;(d)Apparent phase in TM mode. |
针对频率域MT正演计算适用并行计算的特点,提出CUDA并行加速算法,并将其应用于二维MT有限元数值模拟计算.通过不同模型的计算结果对比,表明CUDA并行计算在MT有限单元二维正演中能够在保证计算精度的前提下显著提高MT正演的速度,在GPU硬件为GTX580环境下加速比可达20倍,随着GPU硬件设备的发展,以及支持双精度计算方法的出现,加速比有望进一步提高.因此,CUDA并行技术具有广阔的应用前景,下一步将开展基于CUDA并行技术的大地电磁反演计算.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Chen Zhaoxi, Meng Xiaohong, Guo Linghui, et al. 2012a. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU[J]. Chinese J. Geophys. (in Chinese), 55(12): 4069-4077, doi: 10.6038/j.issn.0001-5733.2012.12.019. |
| [2] | Chen Zhaoxi, Meng Xiaohong, Liu Guofeng, et al. 2012b. The GPU-based parallel calculation of gravity and magnetic anomalies for 3D arbitrary bodies[J]. Geophysical & Geochemical Exploration (in Chinese), 36(1): 117-121. |
| [3] | Dai Yunfeng, Zhou Zhifang, Qiang Jianke, et al. 2012. Realize the parallel computing of Hankel transform on GPU[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 34(5): 614-618. |
| [4] | Gu Guanwen, Liang Meng, Wu Wenpeng. 2010. Pseudo-2D inversion interpretation of CSAMT data based on parallel computation[J]. Geophysical & Geochemical Exploration (in Chinese), 34(3): 399-402. |
| [5] | Li Yan, Hu Xiangyun, Wu Guiju, et al. 2010. Parallel computation of 2-D magnetotelluric forward modeling based on MPI[J]. Seismology and Geology (in Chinese), 32(3): 392-401. |
| [6] | Li Yuguo, Xu Shizhe, Liu Bin, et al. 1996. The finite element method for modeling 2-D MT field on a geoelectrical model with continuous variation of conductivity within each block (II)[J]. Geological Journal of Universities (in Chinese), 2(4): 448-452. |
| [7] | Lin Wei, Zhang Jian, Li Jiabiao. 2013. 3D inversion of gravity anomaly with GPU in the mesozoic residual basins of Nansha Thitu island and reefs area[J]. Journal of Tropical Oceanography (in Chinese), 32(4): 36-42. |
| [8] | Liu Xiaojun. 2007. Focusing inversion images of magnetotelluric data (in Chinese) [Ph. D. thesis]. Nanjing: Tongji University. |
| [9] | Liu Yu, Wang Jiaying, Meng Yongliang. 2006. PC cluster based magnetotelluric 2-D Occam's inversion parallel calculation[J]. Geophysical Prospecting for Petroleum (in Chinese), 45(3): 311-315. |
| [10] | Liu Yun, Wang Xuben. 2012. The FEM for modeling 2-D MT with continuous variation of electric parameters within each block[J]. Chinese J. Geophys. (in Chinese), 55(6): 2079-2086. |
| [11] | Mao Yurong. 2014. Three-dimensional forward modeling of time-domain electromagnetic response on GPUs (in Chinese) [Ph. D. thesis]. Jingzhou: Yangtze University. |
| [12] | Song Tao, Wang Xuben. 2013. Cholesky decomposition method of fast back substitution for spare matrix[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 35(3): 293-296. |
| [13] | Xu Shizhe, Yu Tao, Li Yuguo, et al. 1995. The finite element method for modeling 2-D MT field on a geoelectrical model with continuous variation of conductivity within each block (I)[J]. Geological Journal of Universities (in Chinese), 1(2): 65-73. |
| [14] | 陈召曦, 孟小红, 郭良辉,等. 2012a. 基于GPU并行的重力、重力梯度三维正演快速计算及反演策略[J]. 地球物理学报, 55(12): 4069-4077, doi: 10.6038/j.issn.0001-5733.2012.12.019. |
| [15] | 陈召曦, 孟小红, 刘国峰,等. 2012b. 基于GPU的任意三维复杂形体重磁异常快速计算[J]. 物探与化探, 36(1): 117-121. |
| [16] | 戴云峰, 周志芳, 强健科,等. 2012. 基于GPU实现汉克尔变换并行计算[J]. 物探化探计算技术, 34(5): 614-618. |
| [17] | 顾观文, 梁萌, 吴文鹏. 2010. 基于并行处理的CSAMT拟二维反演解释[J]. 物探与化探, 34(3): 399-402. |
| [18] | 李炎, 胡祥云, 吴桂桔,等. 2010. 基于MPI的二维大地电磁正演的并行计算[J]. 地震地质, 32(3): 392-401. |
| [19] | 李予国, 徐世浙, 刘斌,等. 1996. 电导率分块连续变化的二维MT有限元模拟(Ⅱ)[J]. 高校地质学报, 2(4): 448-452. |
| [20] | 林巍, 张健, 李家彪. 2013. 南沙中业群礁地区中生代残留盆地GPU重力异常三维反演[J]. 热带海洋学报, 32(4): 36-42. |
| [21] | 刘小军. 2007. 大地电磁聚焦反演成像方法研究[博士论文]. 南京: 同济大学 . |
| [22] | 刘羽, 王家映, 孟永良. 2006. 基于PC机群的大地电磁OCCAM反演并行计算研究[J]. 石油物探, 45(3): 311-315. |
| [23] | 刘云, 王绪本. 2012. 电性参数分块连续变化二维MT有限元数值模拟[J]. 地球物理学报, 55(6): 2079-2086. |
| [24] | 毛玉蓉. 2014. 时间域电磁响应三维正演计算及GPU实现[博士论文]. 荆州: 长江大学 . |
| [25] | 宋滔, 王绪本. 2013. 稀疏矩阵快速回代的Cholesky分解法[J]. 物探化探计算技术, 35(3): 293-296. |
| [26] | 徐世浙, 于涛, 李予国,等. 1995. 电导率分块连续变化的二维MT有限元模拟(Ⅰ)[J]. 高校地质学报, 1(2): 65-73. |
 2016, Vol. 31
2016, Vol. 31


