可控源音频大地电磁法(CSAMT)是基于大地电磁法和音频大地电磁法发展演变而来的人工源频率域电磁测深方法,在改变频率条件下测量卡尼亚视电阻率达到测量目的.CSAMT方法最早由Goldstein和Strangway提出,是为了解决MT信号强度弱的问题发展起来的.由于使用人工源,具有信噪比高,抗干扰能力强,测量深度大(通常可达到2 km左右)的特点(胡英才,2015).由于其对良导介质分辨能力强,能有效划分断层,确定地热靶区,近年来广泛应用于地热资源勘探开发中(花蕾,2012).
目前,国内外学者关于CSAMT方法对地质体的识别和分辨能力进行了大量的探讨.徐广春研究总结了CSAMT法一维反演和二维反演的优缺点及适用条件(许广春,2011);张国鸿、李仁和在已知矿体上应用CSAMT法进行试验,讨论了在地质构造走向不清楚时,在TE和TM两种模式下进行二维反演,结果表明,两种模式的反演结果差别较大并分析了产生原因(张国鸿等,2009);汤井田、周聪通过改变三层和五层介质模型各层的电性参数和各层厚度,研究了CSAMT方法对各层信息的识别分辨能力(汤井田等,2010);王显祥、底青云建立同埋深不同体积,同体积不同埋深,同体积同埋深不同背景电阻率,同体积同埋深间隔距离不同的四组三维模型进行三维积分方程正演模拟,实验结果表明异常体体积、埋深、异常体与围岩电阻率差异对异常响应影响明显(王显祥等,2014).现阶段由于受资金和地形条件限制,在实际工作中CSAMT方法一般采用一磁道多电道的测量方式,该方式不满足三维张量测量而进行标量测量,仅观测Ex和Hy,进行一维和二维反演处理分析.在玄武岩覆盖地区,无法判断地下构造断裂走向,测线很难满足垂直构造走向布测.当测线方向与构造走向不垂直或者地下异常体为三维复杂异常体时,应用测量的标量数据进行反演,无法判断一维、二维反演的准确性.因此建立三维地质模型,进行测线与构造走向平行,呈45°以及垂直三种情况下的正演模拟和一维、二维反演结果的对比分析.通过实验结果总结规律对实际测量结果会有更深的认识,对实际工作有一定的指导作用.
本文首先介绍了CSAMT三维正演理论,接着建立三维地质模型,进行测线与异常体构造走向垂直,呈45°以及平行三种情况的三维CSAMT数值模拟及正演结果和一维、二维反演结果的对比分析.
1 CSAMT三维正演理论
为降低CSAMT三维数值模拟直接计算电磁场总场的难度,将总场分解为背景场(一次场)和感应场(二次场),将总场表示为一次场和二次场的和,公式为

三维正演计算基于二次场的偏微分方程(刘云鹤和殷长春,2013),公式为
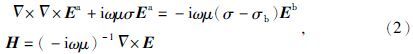
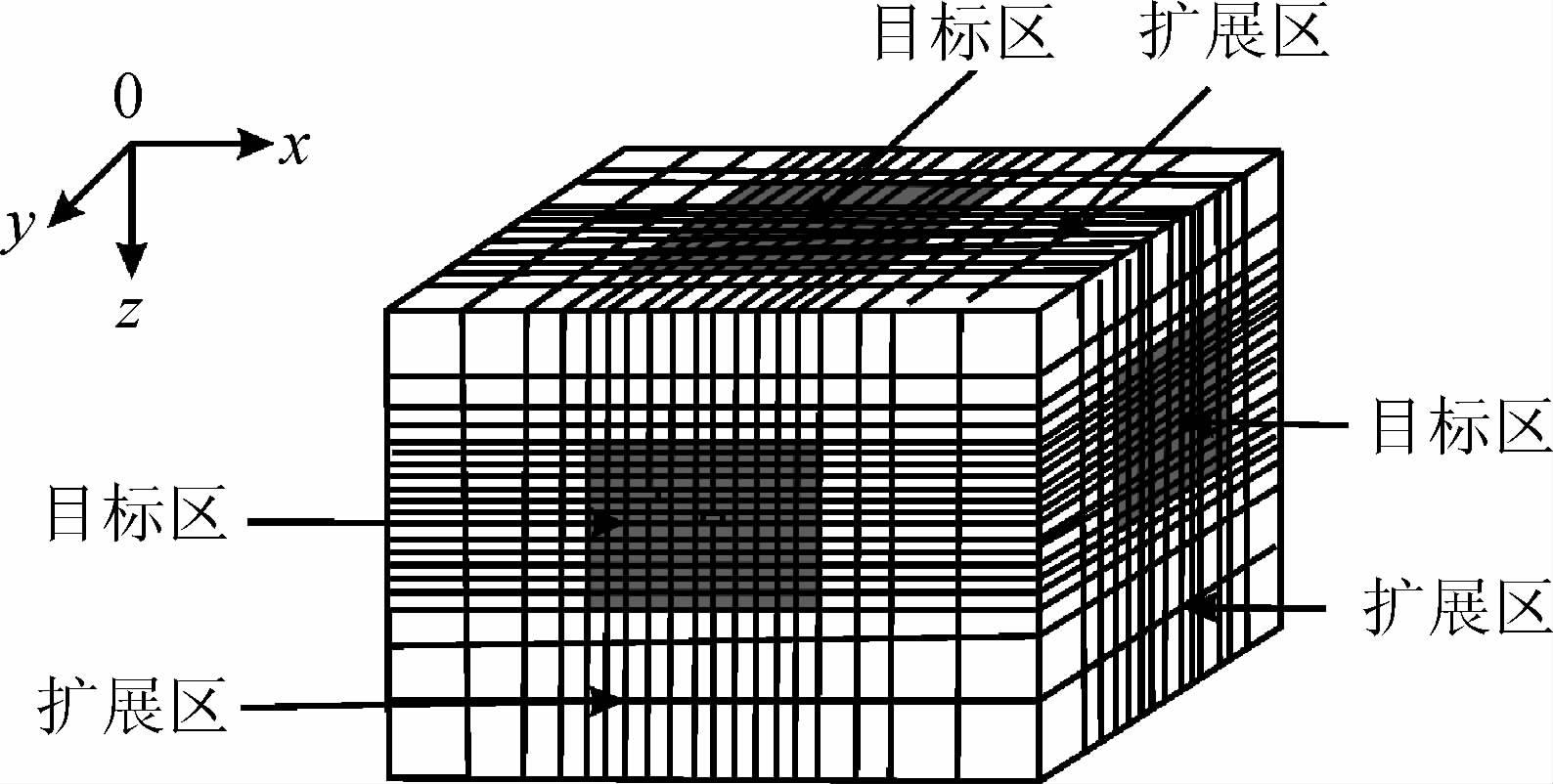
数值模拟采用交错网格有限差分的方法(Mackie et al.,1993),网格剖分如图 1所示,将空间剖分成多个六面体,遵从中心区密集剖分,向外剖分逐渐稀疏的原则,扩展区剖分的足够大,以满足边界处电磁场衰减为零.
|
图 1 三维网格剖分图 Fig. 1 3D meshing division |
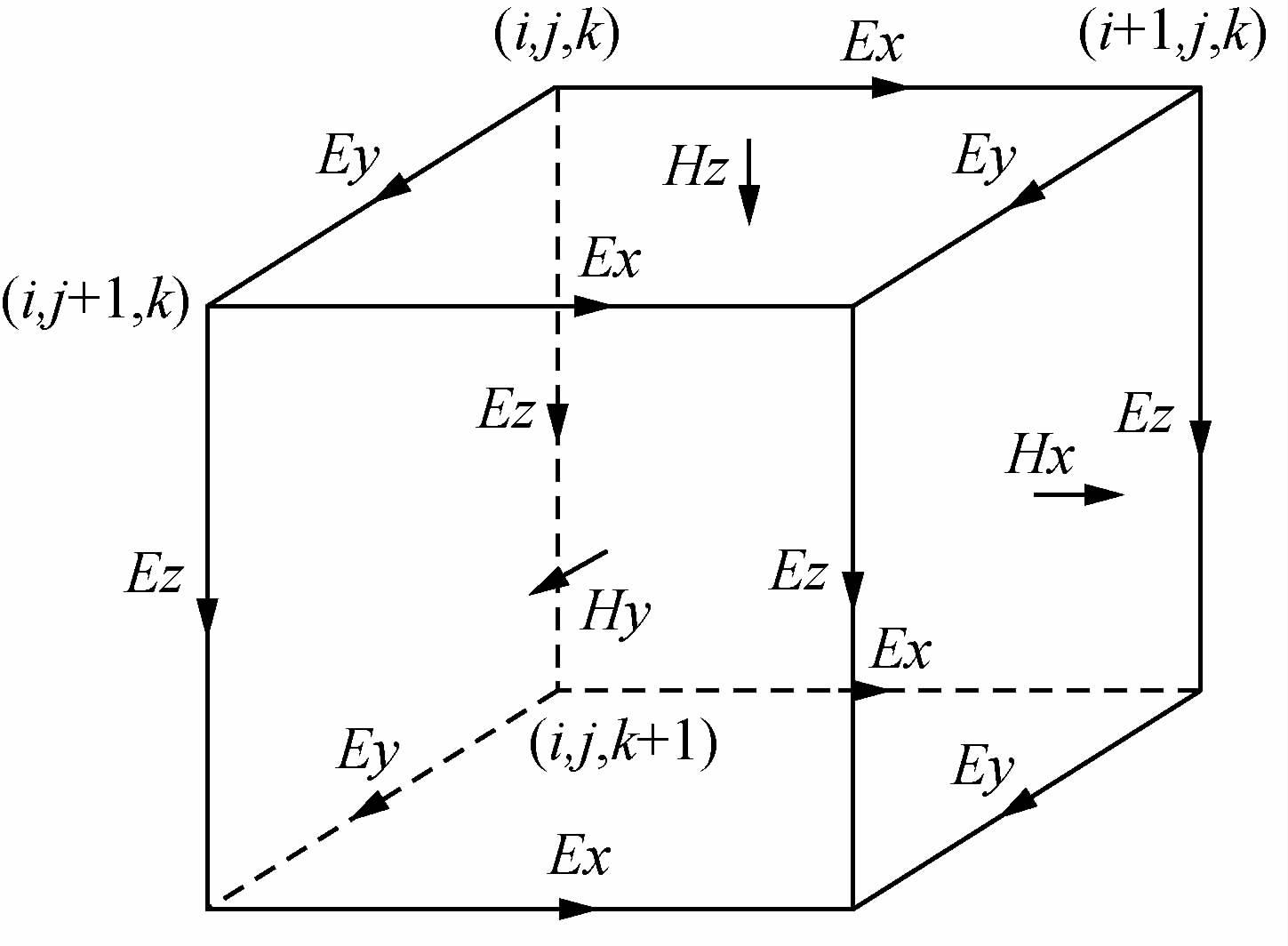
剖分后的任意网格,采用交错网格采样,如图 2所示.电场取在各网格单元边缘的中点,磁场取在各网格单元表面的中心,这种采样方式符合右手螺旋法则,能保证电磁场分布遵循能量守恒定律.
|
图 2 采用交错网格的电场分量采样图 Fig. 2 Staggered grid electric field componentsampling figure |
当地下按交错网格剖分进行离散化后,对二次场满足的偏微分方程(2)进行离散化处理可得到电场和磁场的六个关系式,通过变换替代可消去六个关系式中的电场分量或磁场分量,得到关于磁场或者电场分量的单参数线性方程组(谭捍东等,2003),最终形成的大型方程组采用拟最小残差法(QMR)求解.
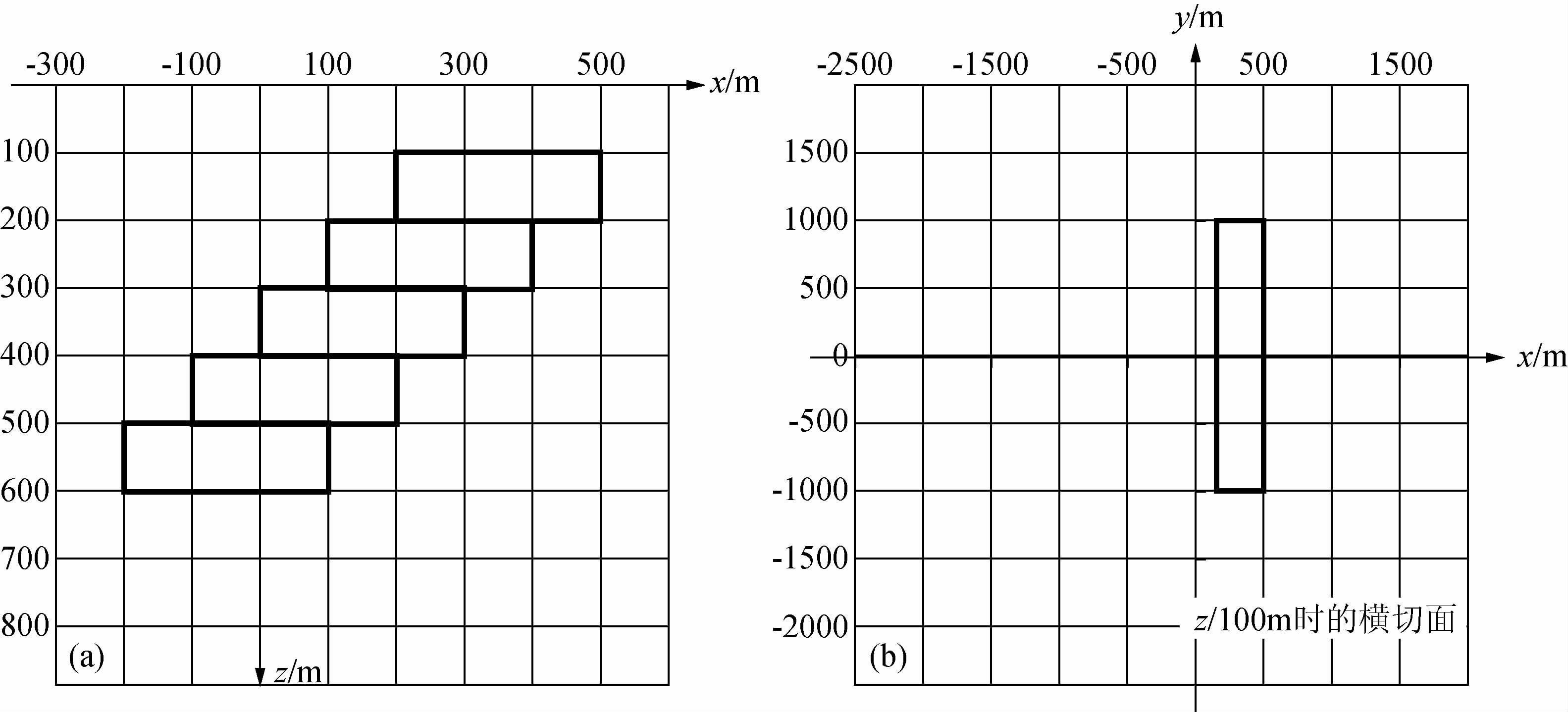
2 理论模型及正、反演分析建立三维正演模型如图 3所示.图 3a给出XZ方向上阶梯状异常体的二维剖面图,其中异常体电阻率为10 Ω·m,背景电阻率为100 Ω·m.图 3b给出XY方向上Z=100 m时的横切面,异常体沿Y轴的延伸长度±1000 m. 发射接收位置如图 4所示,发射源1与接收1沿垂直异常体的走向展布,发射源2和接收2与异常体的走向呈45°展布,发射源3和接收3平行异常体走向展布.发射源长1000 m,发射电流强度为10 A,轴向接收16 Hz,64 Hz,128 Hz,256 Hz,512 Hz,102 Hz,1448 Hz,2048 Hz对应的Ex和Hy,求取卡尼亚视电阻率.
|
图 3 三维正演模型 Fig. 3 3-D model |

|
图 4 发射接收位置图 Fig. 4 Launch receiving locations |
对三种不同情况进行正演模拟,拟断面图如图 5所示.图 5a、图 5b、图 5c分别为测线与构造走向垂直,呈45°,平行三种情况的正演拟断面图.
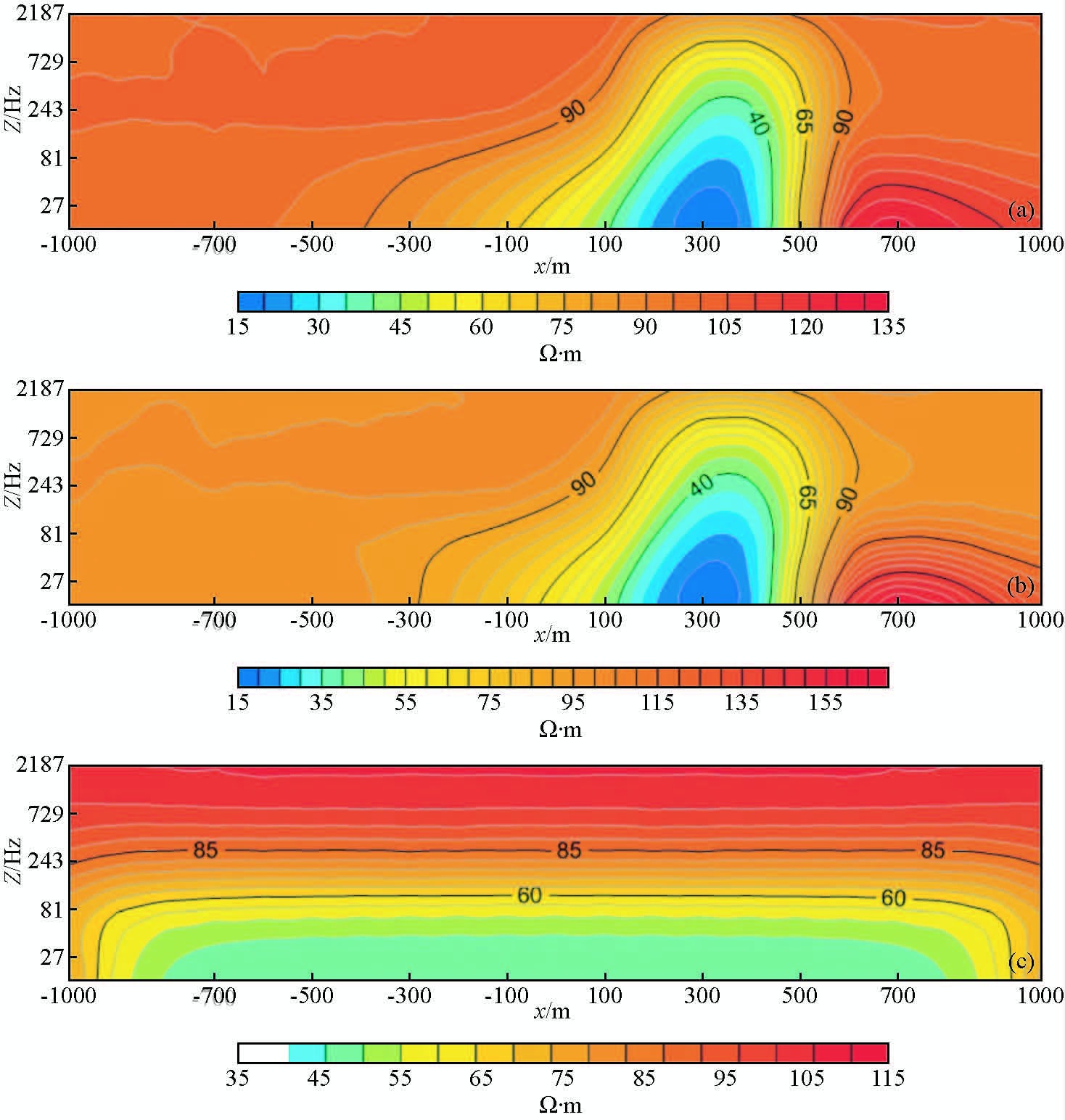
|
图 5 异常体沿Y轴±延伸1000 m的正演拟断面图 Fig. 5 Anomalies extending along the Y axis ±1000 mForward pseudosection figure |
当异常体沿Y轴的延伸增大到±2000 m,正演拟断面图如图 6所示.图 6d、图 6e、图 6f分别为测线与构造走向垂直,呈45°,平行三种情况的正演拟断面图.

|
图 6 异常体沿Y轴±延伸2000 m的正演拟断面图 Fig. 6 Anomalies extending along the Y axis ±2000 m Forward pseudosection figure |
利用Occam反演软件对异常体沿Y轴±延伸1000 m的正演模拟结果进行一维、二维反演处理.图 7给出了一维、二维反演结果比较图,图 7g、图 7h是测线垂直异常体走向时的一维、二维反演结果,一维反演结果的地电断面异常表现为上下延伸的条带状,并在异常体右侧伴生出明显的高阻假异常,二维反演结果的地电断面异常表现为平缓渐变的趋势.与正演结果对比,可看出在测线垂直异常体走向时,二维反演比一维反演对于低阻异常体的埋深、形状、大小、电性参数反演的更准确.究其原因,CSAMT一维反演只能模拟简单水平层状地质模型.当异常体为二维,三维结构时,电流流过异常体两侧会产生电荷效应.一维反演没有考虑电荷效应的影响,依然按水平层状分析,因此反演结果在异常体附近产生了高阻假异常.二维反演考虑了电荷效应的影响,因此反演效果优于一维反演结果.图 7i,图 7j为测线与异常体走向呈45°的一维、二维反演结果,在一维和二维反演异常体右侧都出现了高阻假异常,并且高阻异常与垂直情况相比都发生明显的增大,一维反演增大了90 Ω·m左右,二维反演增大了30 Ω·m左右.图 7k、图 7l为测线平行异常体走向的一维、二维反演结果,一维二维反演结果相似,一维与二维情况相比,反演出的异常体视电阻率偏大一些,并与实际情况相比,有一定程度的上下延伸.由于异常体沿Y轴的正负延伸长度与测线长度相同,在异常体两侧产生电荷效应,在一维和二维反演异常体两侧边缘都出现高阻假异常.

|
图 7 一维、二维反演结果比较图,g、h为测线平垂直异常体走向的一维、二维反演图,i、j为测线与异常体走向呈45°时的一维、二维反演图,k、l为测线平行异常体走向一维、二维反演图 Fig. 7 A one-dimensional,two-dimensional inversion results comparison chart,g、h are vertical to the line of abnormal body to one and two dimensional inversion figure,i、j are the measured line and the anomaly was 45° to one-dimensional,two-dimensional inversion fig,k、l are parallel to the line of abnormal body to one and two dimensional inversion figure |
在此基础上,研究增加异常体延伸长度对反演结果的影响.保持其他变量不变,将异常体沿Y轴±延伸1000 m增加至±延伸2000 m,进行一维二维反演.图 8给出了一维、二维反演结果比较图,图 8m、图 8n为测线垂直异常体走向时一维、二维反演图,通过与图 7g、图 7h比较发现,增大异常体的延伸长度对测线垂直异常体走向布测情况的影响不大.图 8o,图 8p为测线与异常体走向呈45°时的一维、二维反演图.通过与图 7i,图 7j进行比较发现,当增大异常体的延伸长度后,消除了二维反演右侧明显的高阻假异常,同时对于一维反演右侧的高阻假异常,异常值减小了100 Ω·m左右.图 8q、图 8r为测线平行异常体走向时的一维、二维反演图,增大异常体沿Y轴的延伸长度后,可以忽略电荷效应对反演结果的影响.一维、二维反演结果相似程度增加.
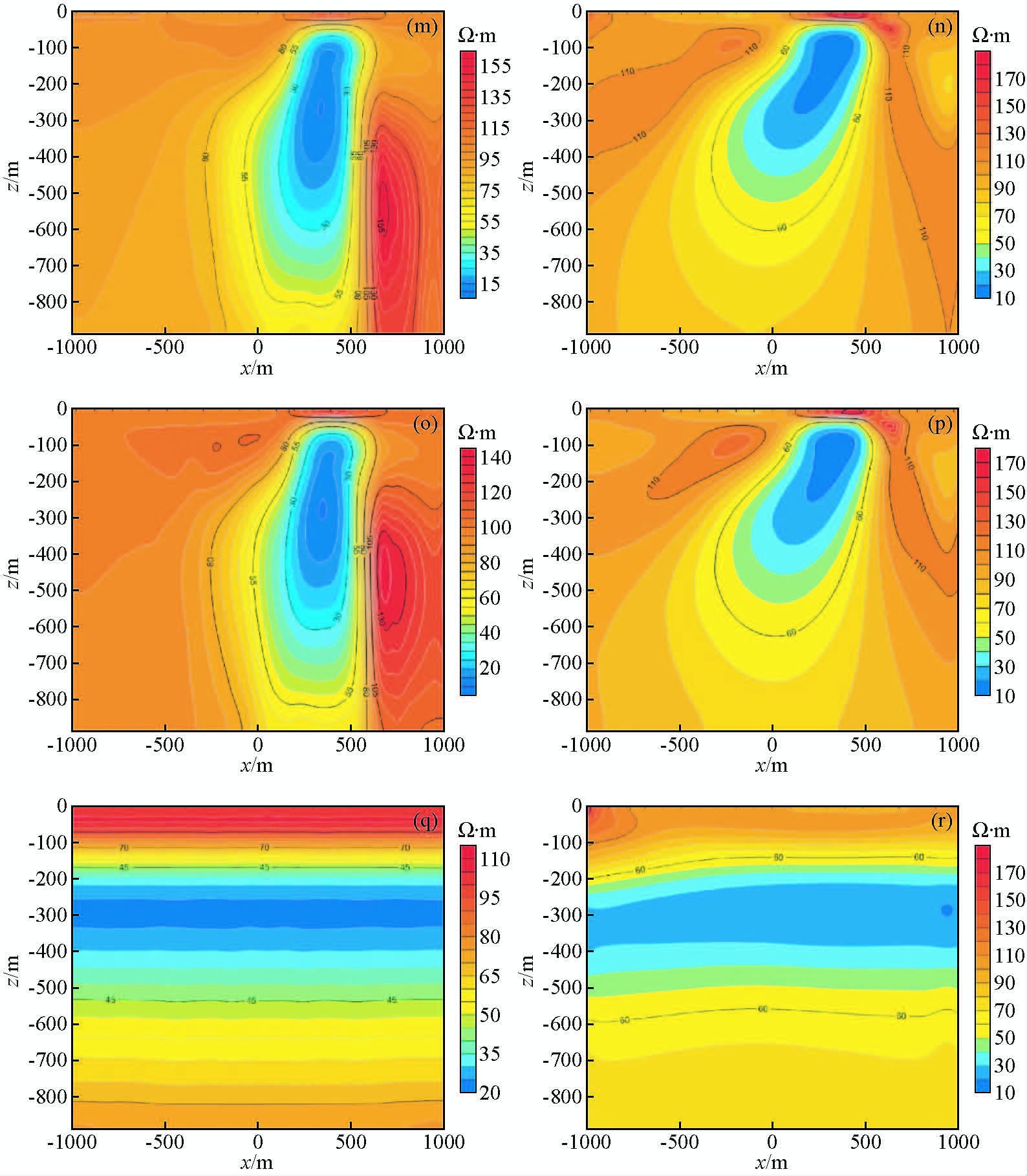
|
图 8 增加延伸长度的一维二维反演结果比较图,m、n为测线平垂直异常体走向的一维、二维反演图,o、p为测线与异常体走向呈45°时的一维、二维反演图,q、r为测线平行异常体走向一维、二维反演图 Fig. 8 Increasing the length of stretchone-dimensional,two-dimensional inversion results comparison chart,m、n are vertical to the line of abnormal body to one and two dimensional inversion figure,o、p are the measured line and the anomaly was 45° to one-dimensional,two-dimensional inversion fig,q、r are parallel to the line of abnormal body to one and two dimensional inversion figure |
通过建立三维模型进行正演分析和反演比较分析,得到如下结论:
(1) 当测线垂直构造走向时,二维反演比一维反演对于异常体的埋深,形状,电性参数反演更为准确,增加异常体延伸长度对该情况影响不大.
(2) 当测线与异常体走向呈45°时,二维反演和一维反演结果与垂直情况反演出的异常体效果基本一致,在异常体右侧一维、二维反演都反演出高阻假异常,与垂直情况相比,高阻异常值会有所增大,增加异常体延伸长度,一维反演异常体右侧高阻异常值明显减小,二维反演异常体右侧高阻异常消失.
(3) 当测线与异常体走向平行时,二维反演与一维反演结果近似,都表现出层状构造.二维反演与一维反演相比反演出的异常体电阻率值更接近实际情况.
致 谢 感谢审稿专家和编辑部的支持帮助.
| [1] | Hu Y C. 2015. Three dimensional tensor controlled source electromagnetic modeling based the vector finite element method (in Chinese)[Ph. D. thesis]. Changchun: Jilin University. |
| [2] | Hua L. 2012. CSAMT and MT looking for geothermal resources application-Taking Jiayin area as an example (in Chinese)[MSc thesis]. Changchun: Jilin University. |
| [3] | Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data[J]. Chinese Journal of Geophysics (in Chinese), 56(12): 4278-4287, doi: 10.6038/cjg20131230. |
| [4] | Mackie R L, Madden T R. 1993. Conjugate direction relaxation solutions for 3-D magnetotelluric modeling[J]. Geophysics, 58(7): 1052-1057. |
| [5] | Mackie R L, Madden T R, Wannamaker P E. 1993. Three-dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions[J]. Geophysics, 58(2): 215-226. |
| [6] | Tang H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics (in Chinese), 46(5): 705-711, doi: 10.3321/j.issn:0001-5733.2003.05.019. |
| [7] | Tang J T, Zhou C, Deng X H. 2010. Identification and discrimination of the horizontal layered Earth by using CSAMT apparent resistivity curves[J]. Geology and Exploration (in Chinese), 46(6): 1079-1086. |
| [8] | Wang X X, Di Q Y, Tang J, et al. 2014. CSAMT resolution in 3D geoelectric structures[J]. Progress in Geophysics (in Chinese), 29(5): 2258-2265, doi: 10.6038/pg20140540. |
| [9] | Xu G C. 2011. A discussion on some problems concerning practical application of CSAMT method[J]. Geophysical & Geochemical Exploration (in Chinese), 35(6): 809-812. |
| [10] | Zhang G H, Li R H, Zhang L M. 2009. Discussion of several technical issues with CSAMT method[J]. Geology of Anhui (in Chinese), 19(2): 119-123. |
| [11] | 胡英才. 2015. 矢量有限元三维张量CSAMT正演模拟研究[博士论文]. 长春: 吉林大学. |
| [12] | 花蕾. 2012. CSAMT与MT在寻找地热资源中的应用-以嘉荫地区为例[硕士论文]. 长春: 吉林大学. |
| [13] | 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究[J]. 地球物理学报, 56(12): 4278-4287, doi: 10.6038/cjg20131230. |
| [14] | 谭捍东, 余钦范, Booker J,等. 2003. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 46(5): 705-711, doi: 10.3321/j.issn:0001-5733.2003.05.019. |
| [15] | 汤井田, 周聪, 邓晓红. 2010. CSAMT视电阻率曲线对水平层状大地的识别与分辨[J]. 地质与勘探, 46(6): 1079-1086. |
| [16] | 王显祥, 底青云, 唐静,等. 2014. 三维地电结构下CSAMT分辨能力研究[J]. 地球物理学进展, 29(5): 2258-2265, doi: 10.6038/pg20140540. |
| [17] | 许广春. 2011. CSAMT法在实际应用中的若干问题[J]. 物探与化探, 35(6): 809-812. |
| [18] | 张国鸿, 李仁和, 张良敏. 2009. 可控源音频大地电磁法若干方法技术问题的探讨[J]. 安徽地质, 19(2): 119-123. |
 2016, Vol. 31
2016, Vol. 31


