地球物理反演按照方法的不同可以分为线性反演和非线性反演两大类.非线性反演问题,是指观测数据d和模型参数m之间不存在简单的线性关系,而是复杂的非线性关系,这种非线性关系既可能呈显式,也可能呈隐式.对于解决非线性反演问题,一直存在两种不同的观点(Tarantola and Valette,1982;Curtis and Lomax,2001;杨文采,2002;王家映,2007),即确定性方法和随机反演方法,确定性方法是将观测数据和模型参数全部看成是确定的量,反演过程就是利用最优化方法求出数据拟合差函数的全局最小值.而随机反演是将所有变量都看成随机变量,反演问题的求解就是利用统计学原理确定解所服从的概率分布.
地球物理反演问题普遍存在着不适定性,正则化方法和贝叶斯公式都是解决上述问题的有力工具.正则化方法通过加入模型光滑约束能降低解的不确定性,但是怎样的光滑(或者说怎样选择正则化因子)才是合适的也是一个争议性的问题.然而,反演问题的目的不仅仅是寻找到一个拟合数据的最佳模型,而且还要能描绘解的不确定性,即对结果进行评价(Sen and Stoffa,1996).随机反演方法天生适合对解的不确定性进行描述.随机反演方法的优点在于结果以后验概率密度的形式给出.尽管目前大部分的随机反演方法都是采用的高斯先验或均匀先验以及数据误差相互独立的简单假设,但是这种方法的结果依然是有其物理含义的.
本文阐述了几种常见的非线性贝叶斯反演方法的发展历程及研究现状,对每种方法的局限性、适用性、优缺点进行了分析总结.最后探讨了非线性贝叶斯方法今后的发展方向.
1 贝叶斯原理贝叶斯概率公式区别于经典概率公式的关键在于对先验信息的利用,对于模型参数与观测数据的关系,贝叶斯后验概率可以通过先验信息和似然函数给出,公式为
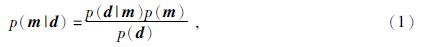
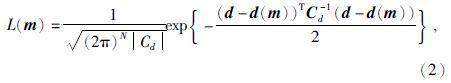
贝叶斯反演的基本流程如图 1所示,在已知先验信息和似然函数的情况下,利用贝叶斯公式来获得后验分布,根据后验分布就可以获得解的一切信息,包括期望、方差等等统计特征,如取其最大值所对应的那组模型即为最大后验解或最大似然解.

|
图 1 贝叶斯反演基本流程图 Fig. 1 Bayesian inversion schematic |
贝叶斯反演的最终目的是希望获得解的后验概率分布,但是直接通过计算获得后验分布这并不现实,因为大多数情况下,后验分布都是高维空间的积分,很难得到解析表达式,只有满足两个条件时才能给出简单的解析表达式(Grandis et al.,1999):(1)数据和参数都满足高斯分布;(2)正演模型是线性的.因此,需要利用非线性方法对模型参数空间直接采样.由于计算机技术的限制,早期的贝叶斯反演仅仅只为获得最大似然估计解就需要大量的计算时间.
2.1 从蒙特卡洛到马尔科夫链蒙特卡洛长期以来,地球物理反演的模式都是利用线性化技术解决非线性问题.基于梯度和导数的线性化迭代方法本质上是单点估计,能够给出满足目标函数的“最佳”解,无法对解进行评价.很多时候由于反演问题的多解性,会产生多个完全不同类型的模型同时满足目标函数.这时就需要基于统计理论的贝叶斯反演方法对解进行评价.
蒙特卡洛方法(Monte Carlo,MC)是一种随机搜索方法,是对穷举法的改进,相对于穷举法对全空间所有点进行采样的方式,MC方法通过随机采样的方式大大降低了计算量(Sambridge and Mosegaard,2002).MC方法早在20世纪60-70年代就被引入到地球物理反演中,分别用于目标函数的最优化搜索和后验分布的采样(Mosegaard and Sambridge,2002).最早MC方法是被用于对模型空间的随机搜索寻优,本质上是一种随机最优化方法.直到80年代,Rothman(1985)首次利用MC方法采样获得反射地震参数的后验分布,Tarits等(1994)利用MC方法对合成数据和实际资料进行了一维大地电磁贝叶斯反演,选择每层电阻率和层厚度作为反演参数,层数已知并作为先验信息,对整个参数空间随机采样获得参数的后验概率分布,并讨论了不同层数对反演结果的影响.Mosegaard和Tarantola(1995)利用MC方法对重力数据进行了反演,并且讨论了不同的随机游走(Random Walk,RW)策略对反演结果的影响.
相对于穷举法,MC方法已经有了很大的进步,但是面对高维非线性问题,MC方法基于空间均匀采样,所需要的计算量对于现有的计算机来说还是非常的耗时.并且高维问题很多时候并不是均匀分布的,均匀采样会导致大量的采样点集中在对计算贡献不大的点,降低计算效率.重要性采样技术的出现为上述问题的解决提供了可能.
马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC)是一种更加智能的随机采样方法.该算法基于马尔科夫链的性质,通过Metropolis-Hastings接受准则建立一个平稳分布为π(x)的马尔科夫链来得到π(x)的大量样本,是一种动态的蒙特卡洛方法.MCMC方法是贝叶斯反演使用最多的经典采样方法,应用范围广泛(Grandis et al.,2002;Malinverno and Leaney,2005;Rabben et al.,2008),Grandis等(1999)对Tarits等(1994)的方法进行了改进,加入了光滑约束,利用MCMC对一维电阻率模型进行反演.Hong和Sen(2009)将遗传算法引入到MCMC方法中,提出了一种多尺度的基于实数编码遗传算法的MCMC方法,并利用该方法进行了叠前地震波形反演.Chen等人(2012)利用MCMC方法进行了大地电磁数据锐边界二维反演并与三维反演结果进行了对比.Buland和Kolbjørnsen(2012)利用MCMC方法,同时运行多条马尔科夫链,对CSEM数据和大地电磁数据进行联合反演.国内学者也做了大量研究,大部分集中在对地震参数的估计.王文涛和朱培民(2009)利用Metropolis采样方法进行速度和波阻抗反演.张广智等(2011)利用Metropolis-Hastings采样方法对叠前地震资料进行反演,获得了横、纵波阻抗反射系数以及密度反射系数的后验分布.张繁昌等人(2014)通过贝叶斯理论将地震资料、测井资料和地质统计学信息融合为地层模型参数的后验概率分布,利用马尔科夫链扰动模拟方法实现对后验概率的分布采样,相对于常规确定性地震反演方法,随机反演方法提高了反演精度,实现了储层的精细描述.王保丽等人(2015a,2015b)结合FFT-MA算法和GDM更新算法得到地质统计先验信息,并引入Metropolis算法对后验概率密度进行抽样.杨迪琨和胡祥云(2008)最早利用贝叶斯公式,将一维大地电磁数据作为随机变量进行反演,并在模型空间直接引入地质信息,对反演结果有很好的约束效果.郭荣文(2011)对层状介质大地电磁数据进行贝叶斯反演,通过贝叶斯信息准则确定层参数,然后利用改进的自适应纯形下降模拟退火算法计算得到最大后验概率作为初始模型,并且加入了温度信息,加快马尔科夫链的收敛速度,取得了不错的效果.
2.2 从固定维数到变维反演由于采样算法的限制,早期的贝叶斯反演参数个数都是固定的,这就会产生拟合不足或过度拟合的问题.为了解决上述问题,地球物理学家最初将统计学中的贝叶斯信息准则(Bayesian Information Criteria,BIC)引入到地球物理反演中,BIC是基于贝叶斯模型选择理论的方法,通过计算并比较不同模型的BIC信息来推断模型的最佳参数个数,使得贝叶斯反演的应用范围更加广泛(Sambridge et al.,2006;Gallagher et al.,2009).BIC模型选择方法已经应用于海洋声学反演(Dosso and Dettmer,2011)、多模态界面波频散曲线反演(李翠琳等,2012)以及具有频率和空间相关性噪声的大地电磁一维反演(Guo et al.,2014).
BIC的不足之处在于需要对整个参数维度利用最优化方法进行寻优,Green(1995)对MCMC方法和BIC进行了改进,提出了可逆跳跃马尔科夫链蒙特卡洛(Reversible jump MCMC,RJMCMC)方法,将参数个数也当成未知量,使得采样算法可以直接对不同维数的参数空间进行搜索.RJMCMC反演方法已经大量应用于地球物理非线性反演中,取得了不错的效果.Malinverno(2002)最早将RJMCMC方法引入到地球物理反演中,首次利用“birth-death”过程对模型进行扰动,利用该方法进行一维直流电阻率反演.Bodin和Sambridge(2009)将RJMCMC应用到地震层析成像问题.Agostinetti和Malinverno(2010)和Bodin等(2012)将变维反演用于地震接收函数反演.Tkalcˇic′等(2013)对内地核速度结构进行了变维反演研究.最近关于变维反演方法在反演电磁数据上有不少研究进展,Minsley(2011)利用变维方法反演一维频率域航空电磁数据.最新的研究已经从一维反演发展到二维反演,从陆地发展到海洋CSEM(Ray and Key,2012;Ray et al.,2014).国内关于变维反演的研究比较少,殷长春等(2014)对该算法进行了改进,加入了模型约束项,对比了不同约束项对反演结果的影响,利用RJMCMC进行航空电磁数据的贝叶斯变维反演.
2.3 从少量参数估计到直接二维反演完全非线性方法的应用离不开计算机技术的发展,上述方法都是基于单条马尔科夫链来实现的.然而面对高维、复杂多极值的参数空间,仅仅通过增加单条马尔科夫链采样次数也无法收敛到满意结果.目前,并行计算思想的引入使得多条链同时计算成为可能.其中“温度”和“进化”的思想是两种不同的指导原则.
并行回火(Parallel Tempering,PT)算法也叫做Metropolis-coupled Markov Chain Monte Carlo 或是副本交换算法(replica exchange algorithm)(Earl and Deem,2005,Atchadé et al.,2011).高维非线性反演问题大多是多峰的(存在许多局部极值),为了避免陷入局部极值,将“温度”加入到似然函数中,同时运行N条马尔科夫链,每条链的似然函数变为
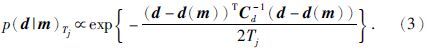
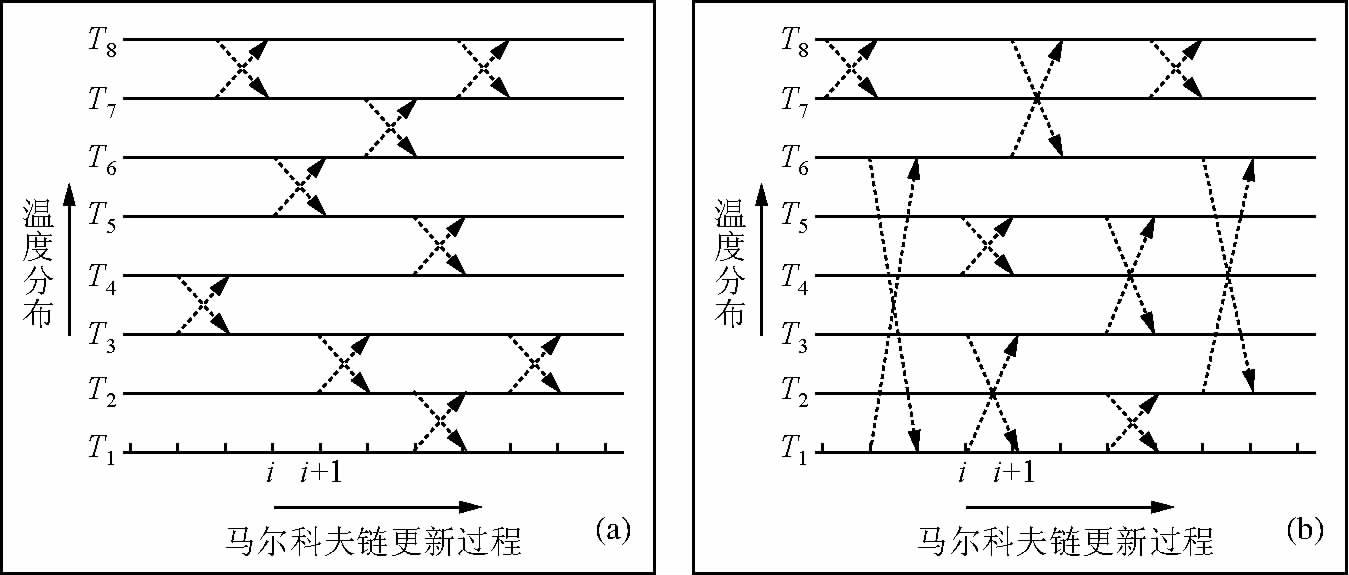
温度的引入使得我们可以从更加平滑的似然函数中进行采样.计算时每条链称为一个副本(replica),每个副本与相邻副本之间通过Metropolis-Hastings准则进行交换,这种以一定概率交换副本的方法,可以使单个副本能够大大克服能量壁垒的影响(Xu et al.,2012),加速收敛.Dosso等(2012)利用并行回火技术进行海洋声学反演,首先利用优化方法获得最大似然解,并将其设置为初始模型,加快收敛速度.Ray等(2013)在对CSEM一维层状介质数据进行反演时,应用标准并行回火方法对RJMCMC算法进行加速.Sambridge(2014)对标准并行回火技术进行了改进并应用于地震接收函数,让副本可以与任意其他副本随机进行交换,从而进一步提高了采样效率(图 2).
差分进化马尔科夫链(Differential Evolution Markov Chain,DEMC)算法(Ter Braak,2006)将“进化”的思想融入马尔科夫链,吸收了进化算法中种群和变异的概念,将进化算法的变异过程引入到采样更新中,同时运行N条马尔科夫链x1,…,xN,每一条链的更新相当于种群中每个个体的变异过程,差分的含义来源于变异时随机选择种群中的两个个体间的差值,并将差值作为个体更新的步长.Vrugt等(2008)提出了DREAM(DiffeRential Evolution Adaptive Metropolis)算法,是对DEMC方法采样效率的改进:(1)采用了随机子空间采样策略;(2)在进化过程中设置了无用链;(3)初始阶段(burn-in)交叉概率自动更新.Vrugt将其用于水文模型中的参数估计.
|
图 2 (a)标准并行回火算法;(b)改进并行回火算法 Fig. 2 (a)standard parallel tempering;(b)improved parallel tempering |
DEMC方法较好的解决了传统MCMC方法中采样步长取值和确定采样方向的问题,使得建议分布能有效的朝着后验分布进化.而缺点就在于需要同时运行的链的数目过多(N=d-2d),当参数过多时,计算量成倍增加.Laloy和Vrugt(2012)提出了MT-DREAM方法(Multiple Try DREAM),该方法结合了DREAM方法以及多点Metropolis(Multiple Try Metropolis,MTM)方法,保留了两种方法的优点:(1)对搜索步长和方向能够自适应调整;(2)通过在当前点同时产生多个候选点,能够对高维概率空间更加全面的探索;(3)算法的结构决定了它非常适合并行计算,大大提高计算效率.采样效率的提高和算法的智能化使得其直接用于二维反演成为可能,目前该类方法更多的是应用于水文学(Linde and Vrugt,2013),在地球物理反演中应用较少,但是有很大的发展空间.Rosas-Carbajal等(2014)将二维剖面划分成像素网格,利用MT-DREAM方法反演电磁数据.
3 结论及展望本文详细介绍了贝叶斯反演的原理及几种重要的非线性数值计算方法,阐述了每种方法的原理、优缺点以及在地球物理反演中的应用.贝叶斯框架为地球物理反演提供了一条不同于以往确定性反演技术的新途径,现在越来越受到学者的关注,虽然已有学者对一维和二维真实数据进行贝叶斯反演,但是面对复杂地质条件以及二维,三维反演,贝叶斯方法离实用化还有一段距离,需要在以下方面加强研究:
3.1 提高计算效率对于一维反演,由于参数相对较少,贝叶斯反演已经取得了许多不错的效果.然而非线性贝叶斯反演是建立在对大量模型的采样计算基础上,面对二维、三维等复杂模型,模型参数个数及正演计算所需的计算时间会快速增加,反演过程中绝大部分计算量是正演计算,如能提高模型正演计算速度,将大大减少贝叶斯反演所需时间.另外,并行化计算也是提高计算效率的一种方法,通过MPI、OpenMP等工具在PC机群甚至多核个人电脑的条件下同时运行多条马尔科夫链,提高计算速度.其中,并行回火算法和并行计算的联合应用(Ray et al.,2013;Sambridge,2014)是目前使用较多的一种提高计算效率的方法.目前对于高维空间的快速采样算法研究也是计算统计学现在的研究热点.
3.2 多数据联合反演联合反演一直是地球物理反演理论关注的热点,其目的是希望不同类型的数据能够相互提供参考、约束并取长补短,从而减少结果的非唯一性(杨辉等,2002;何委徽等,2009;韩波等,2012).对于贝叶斯反演而言,多种数据的联合本质上是先验信息的增加,这对反演结果的收敛和评价是有帮助的.因此,如何建立地球物理联合反演模型实现多种地球物理数据的融合以及如何通过地质构造信息的量化获取更多的先验信息都将是今后需要关注的问题.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Agostinetti N P, Malinverno A. 2010. Receiver function inversion by trans-dimensional Monte Carlo sampling[J]. Geophysical Journal International, 181(2): 858-872. |
| [2] | Atchadß Y, Roberts G, Rosenthal J S. 2011. Towards optimal scaling of metropolis-coupled Markov chain Monte Carlo[J]. Statistics and Computing, 21(4): 555-568. |
| [3] | Bodin T, Sambridge M. 2009. Seismic tomography with the reversible jump algorithm[J]. Geophysical Journal International, 178(3): 1411-1436. |
| [4] | Bodin T, Sambridge M, Tkalčić H, et al. 2012. Transdimensional inversion of receiver functions and surface wave dispersion[J]. Journal of Geophysical Research: Solid Earth, 117(B2): B2301. |
| [5] | Buland A, Kolbjørnsen O. 2012. Bayesian inversion of CSEM and magnetotelluric data[J]. Geophysics, 77(1): E33-E42. |
| [6] | Chen J S, Hoversten G M, Key K, et al. 2012. Stochastic inversion of magnetotelluric data using a sharp boundary parameterization and application to a geothermal site[J]. Geophysics, 77(4): E265-E279. |
| [7] | Curtis A, Lomax A. 2001. Prior information, sampling distributions, and the curse of dimensionality[J]. Geophysics, 66(2): 372-378. |
| [8] | Dosso S E, Dettmer J. 2011. Bayesian matched-field geoacoustic inversion[J]. Inverse Problems, 27(5): 55009-55031. |
| [9] | Dosso S E, Holland C W, Sambridge M. 2012. Parallel tempering for strongly nonlinear geoacoustic inversion[J]. The Journal of the Acoustical Society of America, 132(5): 3030-3040. |
| [10] | Earl D J, Deem M W. 2005. Parallel tempering: Theory, applications, and new perspectives[J]. Physical Chemistry Chemical Physics, 7(23): 3910-3916. |
| [11] | Gallagher K, Charvin K, Nielsen S, et al. 2009. Markov chain Monte Carlo (MCMC) sampling methods to determine optimal models, model resolution and model choice for Earth Science problems[J]. Marine and Petroleum Geology, 26(4): 525-535. |
| [12] | Grandis H, Menvielle M, Roussignol M. 1999. Bayesian inversion with Markov chains—I. The magnetotelluric one-dimensional case[J]. Geophysical Journal International, 138(3): 757-768. |
| [13] | Grandis H, Menvielle M, Roussignol M. 2002. Thin-sheet electromagnetic inversion modeling using Monte Carlo Markov Chain (MCMC) algorithm[J]. Earth, Planets and Space, 54(5): 511-521. |
| [14] | Green P J. 1995. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination[J]. Biometrika, 82(4): 711-732. |
| [15] | Guo R W, Dosso S E, Liu J X, et al. 2011. Non-linearity in Bayesian 1-D magnetotelluric inversion[J]. Geophysical Journal International, 185(2): 663-675. |
| [16] | Guo R W, Dosso S E, Liu J X, et al. 2014. Frequency- and spatial-correlated noise on layered magnetotelluric inversion[J]. Geophysical Journal International, 199(2): 1205-1213. |
| [17] | Han B, Hu X Y, He Z X, et al. 2012. Mathematical classification of magnetotelluric inversion methods[J]. Oil Geophysical Prospecting (in Chinese), 47(1): 177-187. |
| [18] | He W H, Wang J L, Yu P. 2009. Overview of the status and prospect of geophysical joint inversion[J]. Progress in Geophysics (in Chinese), 24(2): 530-540, doi: 10.3969/j.issn.1004-2903.2009.02.022. |
| [19] | Hong T C, Sen M K. 2009. A new MCMC algorithm for seismic waveform inversion and corresponding uncertainty analysis[J]. Geophysical Journal International, 177(1): 14-32. |
| [20] | Laloy E, Vrugt J A. 2012. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM(ZS) and high-performance computing[J]. Water Resources Research, 48(1): 182-205. |
| [21] | Li C L, Dosso S E, Dong H F, et al. 2012. Interface-wave dispersion curves inversion based on nonlinear Bayesian theory[J]. Acta Acustica (in Chinese), 37(3): 225-231. |
| [22] | Linde N, Vrugt J A. 2013. Distributed soil moisture from crosshole ground-penetrating radar travel times using stochastic inversion[J]. Vadose Zone Journal, 12(1), doi: 10.2136/vzj2012.0101. |
| [23] | Malinverno A. 2002. Parsimonious Bayesian Markov chain Monte Carlo inversion in a nonlinear geophysical problem[J]. Geophysical Journal International, 151(3): 675-688. |
| [24] | Malinverno A, Leaney W S. 2005. Monte-Carlo Bayesian look-ahead inversion of walkaway vertical seismic profiles[J]. Geophysical Prospecting, 53(5): 689-703. |
| [25] | Minsley B J. 2011. A trans-dimensional Bayesian Markov chain Monte Carlo algorithm for model assessment using frequency-domain electromagnetic data[J]. Geophysical Journal International, 187(1): 252-272. |
| [26] | Mosegaard K, Tarantola A. 1995. Monte Carlo sampling of solutions to inverse problems[J]. Journal of Geophysical Research: Solid Earth, 100(B7): 12431-12447. |
| [27] | Mosegaard K, Sambridge M. 2002. Monte Carlo analysis of inverse problems[J]. Inverse Problems, 18(3): R29-R54. |
| [28] | Rabben T E, Tjelmeland H, Ursin B. 2008. Non-linear Bayesian joint inversion of seismic reflection coefficients[J]. Geophysical Journal International, 173(1): 265-280. |
| [29] | Ray A, Key K. 2012. Bayesian inversion of marine CSEM data with a trans-dimensional self parametrizing algorithm[J]. Geophysical Journal International, 191(3): 1135-1151. |
| [30] | Ray A, Alumbaugh D L, Hoversten G M, et al. 2013. Robust and accelerated Bayesian inversion of marine controlled-source electromagnetic data using parallel tempering[J]. Geophysics, 78(6): E271-E280. |
| [31] | Ray A, Key K, Bodin T, et al. 2014. Bayesian inversion of marine CSEM data from the Scarborough gas field using a transdimensional 2-D parametrization[J]. Geophysical Journal International, 199(3): 1847-1860. |
| [32] | Rosas-Carbajal M, Linde N, Kalscheuer T, et al. 2014. Two-dimensional probabilistic inversion of plane-wave electromagnetic data: Methodology, model constraints and joint inversion with electrical resistivity data[J]. Geophysical Journal International, 196(3): 1508-1524. |
| [33] | Rothman D H. 1985. Nonlinear inversion, statistical mechanics, and residual statics estimation[J]. Geophysics, 50(12): 2784-2796. |
| [34] | Sambridge M. 2014. A Parallel Tempering algorithm for probabilistic sampling and multimodal optimization[J]. Geophysical Journal International, 196(1): 357-374. |
| [35] | Sambridge M, Gallagher K, Jackson A, et al. 2006. Trans-dimensional inverse problems, model comparison and the evidence[J]. Geophysical Journal International, 167(2): 528-542. |
| [36] | Sambridge M, Mosegaard K. 2002. Monte Carlo methods in geophysical inverse problems[J]. Reviews of Geophysics, 40(3): 3-1-3-29. |
| [37] | Sen M K, Stoffa P L. 1996. Bayesian inference, Gibbs' sampler and uncertainty estimation in geophysical inversion[J]. Geophysical Prospecting, 44(2): 313-350. |
| [38] | Tarantola A, Valette B. 1982. Inverse problems=quest for information[J]. Journal of Geophysics, 50(3): 159-170. |
| [39] | Tarits P, Jouanne V, Menvielle M, et al. 1994. Bayesian statistics of non-linear inverse problems: Example of the magnetotelluric 1-D inverse problem[J]. Geophysical Journal International, 119(2): 353-368. |
| [40] | Ter Braak C J F. 2006. A Markov Chain Monte Carlo version of the genetic algorithm differential evolution: Easy Bayesian computing for real parameter spaces[J]. Statistics and Computing, 16(3): 239-249. |
| [41] | Tkalčić H, Bodin T, Young M, et al. 2013. On the nature of the P-wave velocity gradient in the inner core beneath Central America[J]. Journal of Earth Science, 24(5): 699-705. |
| [42] | Vrugt J A, ter Braak C J F, Clark M P, et al. 2008. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation[J]. Water Resources Research, 44(12): W00B09. |
| [43] | Wang B L, Sun R Y, Yin X Y, et al. 2015. Nonlinear inversion based on Metropolis sampling algorithm[J]. Oil Geophysical Prospecting (in Chinese), 50(1): 111-117. |
| [44] | Wang B L, Yin X Y, Ding L X, et al. 2015. Study of fast stochastic inversion based on FFT-MA spectrum simulation[J]. Chinese Journal of Geophysics (in Chinese), 58(2): 664-673, doi: 10.6038/cjg20150227. |
| [45] | Wang J Y. 2007. Lecture on Nonlinear inverse methods in geophysics (II): Monte Carlo method[J]. Chinese Journal of Engineering Geophysics (in Chinese), 4(2): 81-85. |
| [46] | Wang W T, Zhu P M. 2009. Research on Bayesian inversion method applied to predict seismic reservoirs[J]. Journal of Oil and Gas Technology (in Chinese), 31(5): 263-266. |
| [47] | Xu S, Zhou X, Ou-Yang Z C. 2012. Parallel tempering simulation on generalized canonical ensemble[J]. Communications in Computational Physics, 12(5): 1293-1306. |
| [48] | Yang D K, Hu X Y. 2008. Inversion of noisy data by probabilistic methodology[J]. Chinese Journal of Geophysics (in Chinese), 51(3): 901-907, doi: 10.3321/j.issn:0001-5733.2008.03.032. |
| [49] | Yang H, Dai S K, Song H B, et al. 2002. Overview of joint inversion of integrated geophysics[J]. Progress in Geophysics (in Chinese), 17(2): 262-271, doi: 10.3969/j.issn.1004-2903.2002.02.011. |
| [50] | Yang W C. 2002. Non-linear geophysical inversion methods: Review and perspective[J]. Progress in Geophysics (in Chinese), 17(2): 255-261, doi: 10.3969/j.issn.1004-2903.2002.02.010. |
| [51] | Yin C C, Qi Y F, Liu Y H, et al. 2014. Trans-dimensional Bayesian inversion of frequency-domain airborne EM data[J]. Chinese Journal of Geophysics (in Chinese), 57(9): 2971-2980, doi: 10.6038/cjg20140922. |
| [52] | Zhang F C, Xiao Z B, Yin X Y. 2014. Bayesian stochastic inversion constrained by seismic data[J]. Oil Geophysical Prospecting (in Chinese), 49(1): 176-182. |
| [53] | Zhang G Z, Wang D Y, Yin X Y, et al. 2011. Study on prestack seismic inversion using Markov Chain Monte Carlo[J]. Chinese Journal of Geophysics (in Chinese), 54(11): 2926-2932, doi: 10.3969/j.issn.0001-5733.2011.11.022. |
| [54] | 韩波, 胡祥云, 何展翔,等. 2012. 大地电磁反演方法的数学分类[J]. 石油地球物理勘探, 47(1): 177-187. |
| [55] | 何委徽, 王家林, 于鹏. 2009. 地球物理联合反演研究的现状与趋势分析[J]. 地球物理学进展, 24(2): 530-540, doi: 10.3969/j.issn.1004-2903.2009.02.022. |
| [56] | 李翠琳, Dosso S E, Dong H F. 2012. 根据非线性贝叶斯理论的界面波频散曲线反演[J]. 声学学报, 37(3): 225-231. |
| [57] | 王保丽, 孙瑞莹, 印兴耀,等. 2015a. 基于Metropolis抽样的非线性反演方法[J]. 石油地球物理勘探, 50(1): 111-117. |
| [58] | 王保丽, 印兴耀, 丁龙翔,等. 2015b. 基于FFT-MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 58(2): 664-673, doi: 10.6038/cjg20150227. |
| [59] | 王家映. 2007. 地球物理资料非线性反演方法讲座(二): 蒙特卡洛法[J]. 工程地球物理学报, 4(2): 81-85. |
| [60] | 王文涛, 朱培民. 2009. 地震储层预测中贝叶斯反演方法的研究[J]. 石油天然气学报, 31(5): 263-266. |
| [61] | 杨迪琨, 胡祥云. 2008. 含噪声数据反演的概率描述[J]. 地球物理学报, 51(3): 901-907, doi: 10.3321/j.issn:0001-5733.2008.03.032. |
| [62] | 杨辉, 戴世坤, 宋海斌,等. 2002. 综合地球物理联合反演综述[J]. 地球物理学进展, 17(2): 262-271, doi: 10.3969/j.issn.1004-2903.2002.02.011. |
| [63] | 杨文采. 2002. 非线性地球物理反演方法: 回顾与展望[J]. 地球物理学进展, 17(2): 255-261, doi: 10.3969/j.issn.1004-2903.2002.02.010. |
| [64] | 殷长春, 齐彦福, 刘云鹤,等. 2014. 频率域航空电磁数据变维数贝叶斯反演研究[J]. 地球物理学报, 57(9): 2971-2980, doi: 10.6038/cjg20140922. |
| [65] | 张繁昌, 肖张波, 印兴耀. 2014. 地震数据约束下的贝叶斯随机反演[J]. 石油地球物理勘探, 49(1): 176-182. |
| [66] | 张广智, 王丹阳, 印兴耀,等. 2011. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 54(11): 2926-2932, doi: 10.3969/j.issn.0001-5733.2011.11.022. |
 2016, Vol. 31
2016, Vol. 31

