2. 中国科学院大学, 北京 100049
2. University of the Chinese Academy of Science, Beijing 100049, China
大地电磁测深法(Magnetotelluric,简称MT)是一种重要的地球物理勘探方法,具有不受高阻屏蔽和对低阻层反映灵敏的优点,探测深度可以到达下地壳和上地幔.自从20世纪50年代初由A.N.Tikhonov和L.Cagnird分别提出来后,其在国内外发展迅速.
有限单元法是20世纪50年代发展起来的一种求解偏微分方程有力的数值方法.其最早可追溯到Courant(1943)在一个子域上采用逐段连续函数来确定接近未知函数,使用了一组三角形单元和最小势能原理去分析扭转问题.将研究区域剖分成许多子单元,用古典变分原理和多项式插值的方式进行数值分析.有限元法的整体刚度矩阵是一个维度很大的矩阵,使得计算量很大,所以开始并没有得到广泛的应用.直到1960年以后,随着电子数值计算机的广泛应用和发展,有限元法的发展速度才显著加快(王勖成和邵敏,1997).
1971年Coggon提出用有限元法进行大地电磁场的数值模拟(Coggon,1971).他从电磁场最小能量原理出发推导出了赫姆霍兹方程的有限元格式,实现了二维大地电磁有限元正演计算.此后,有许多的学者和专家在大地电磁有限元正演方面进行了研究.Rodi将有限元法引入到MT正演计算中,采用矩形单元进行二维大地电测正演问题(Rodi,1976).Rijo用通用性网格剖分的有限元法,进行大地电磁正演模拟,给出了相应的程序(Rijo,1977).1981年,Pridmore发表了三维大地电磁有限元正演的研究成果(Pridmore et al.,1981).Wanamaker采用三角网格剖分进行了带地形的有限元正演(Wannamaker et al.,1986),另外还给出了能直接解出平行走向的二次场有限元算法(Wannamaker et al.,1987).Franke等用自适应网格进行了各向异性介质大地电磁二维有限元正演(Franke et al.,2004).自从有限元法在大地电磁中的应用引入到国内后(徐世浙,1982),越来越多的学者也在这方面进行了研究(徐世浙和刘斌,1995;史明娟等,1997;陈小斌等,2000;冯德山和王珣,2013;毕武和刘云,2014);带地形的二维大地电磁正演问题的研究(王绪本等,1999;刘树才等,2005;刘云和王绪本,2010);基于计算二次场响应的方法,进行二维大地电磁数值模拟(刘小军等,2007).随后许多学者开始逐渐研究如何提高有限元正演过程中大型线性方程组的计算精度和效率.如陈小斌研究出的有限元直接迭代算法,避开了传统有限元算法中的刚度矩阵的形成(陈小斌,1999;陈小斌和胡文宝,2002;陈小斌和赵国泽,2004);使得正演过程速度快、稳定性好、正演结果精度更高的不完全LU分解预处理的BICGSTAB算法(柳建新等,2009;徐凌华等,2009).
这些有关文献中,很少见到二维大地电磁有限元正演的推导过程,以及节点编码的详细描述.本文基于前人的研究,介绍了二大地电磁有限元正演的原理、方法过程,详细反复推导,特别是形象描述了单元刚度矩阵合成整体刚度矩阵的过程,使得方法原理和过程实现变得更加清晰.
1 二维大地电磁的基本原理
二维模型是指介质的电学性质除深度外还沿一个水平坐标轴方向有变化,而沿另一个水平坐标方向保持不变(走向).本文中取x轴为二维介质的走向方向,z轴为深度方向,y轴为电学性质变化的方向(倾向).
1.1 方法原理在大地电磁测深方法中,考虑到应用的观测频率范围一般为10-4~103 Hz,构成地壳浅部的介质的电阻率一般取1~1000 Ω·m,所以可以忽略位移电流的影响(陈乐寿和王光锷,1990).其麦克斯韦方程组(取时域中的谐变因子为e-iωt)为
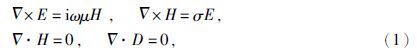
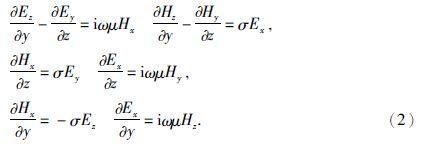
将上式展开得到二维地电模型的偏微分方程
TE模式为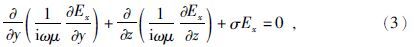
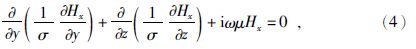

可知在忽略位移电流的情况下,空气中的Hx为常量.即使考虑位移电流,由于对大地电磁来说,有$\frac{\sigma }{\omega \varepsilon }\gg 1$,Hx也近似为常量.所以TM模式的研究区域为地下.对于TE模式,在高频时,不能忽略空气中的位移电流,因此研究区域为空气和地下.为方便起见本文取TM模式进行有限元法的正演数值模拟,令
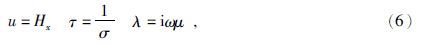

TM极化模式外边界条件(区域示意见图 1):
|
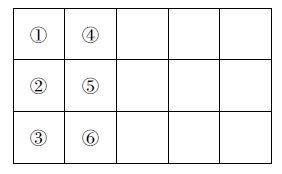
图 1 节点编号和单元编号示意图 1 ,2,…代表节点号 ①,②,…代表单元号 Fig. 1 Node number and unit number |
(1) 上边界AB直接取在地面上,并以该处的u为1单位,则有

(2) 下边界CD以下为均质的岩石,局部不均匀体所产生的异常场在CD上为零,电磁波在CD以下的传播方程为

 ,σ是CD以下岩石的电导率.对u求导
,σ是CD以下岩石的电导率.对u求导 ,因为CD处有
,因为CD处有 ,所以CD处的边界条件为
,所以CD处的边界条件为

(3) 取左右边界AD、BC离局部不均匀体足够远,电磁场在AD、BC上左右对称,其上的边界条件是

上述大地电磁的边界问题归纳为
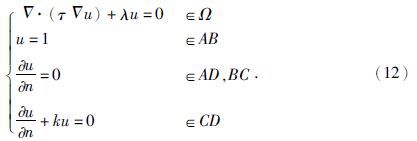
根据边值问题与变分问题的关系,(12)式与下列问题等价:
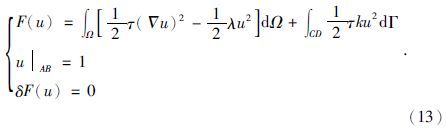
二维有限元的网格剖分常用三角形单元或者矩形单元,本文采用矩形单元对整个区域进行剖分,整体节点编号和单元编号的顺序示意见图 1.
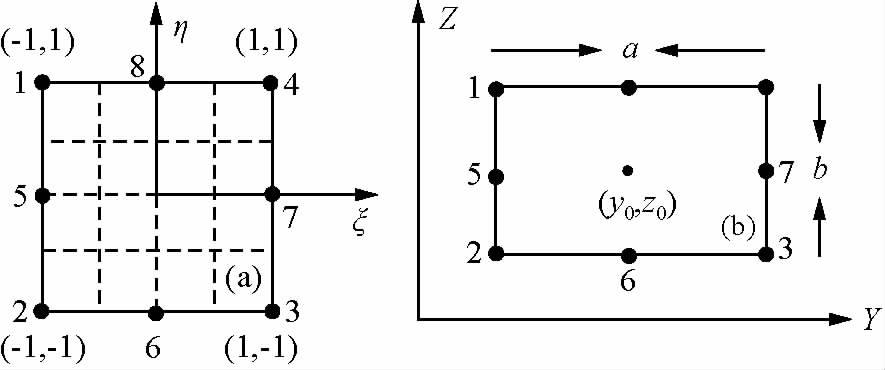
对于每个矩形单元内部,取8个点(4个顶点和4条边的中点),进行双二次插值.单元内局部节点编号和坐标如图 2所示.
|
图 2 母单元与子单元(a)母单元;(b)子单元. Fig. 2 Mother unit and sub unit |
在图 2a所示的正方形单元(母单元)上构造如下的形函数:
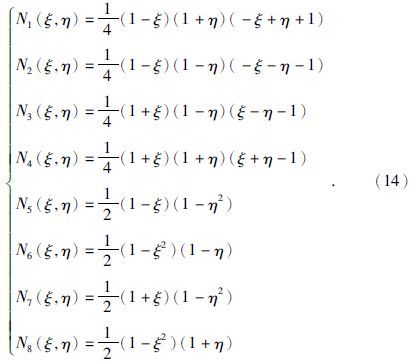
形函数(14)式满足:

子单元上的u可表示为

由(15)可知
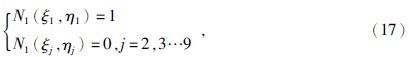
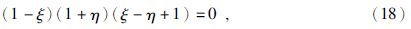
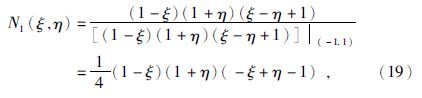
母单元和子单元间的坐标变换关系为

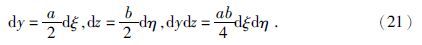
有限元法研究区域的场值问题的重要一步就将整个区域的积分分解个各单元的积分之和,因此在对区域进行单元剖分后,将(13)的F(u)的积分进行分解,公式为
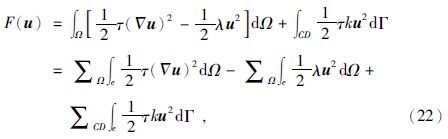
对(22)式分别进行单元积分,公式为
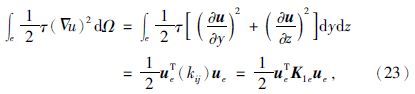
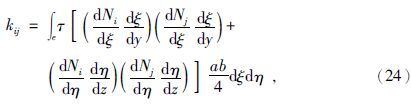
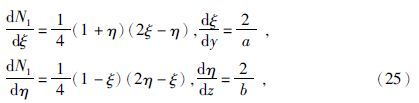
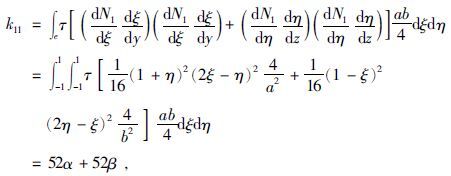
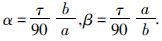
同理可得:

单元积分为
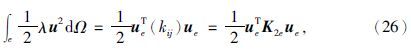

其中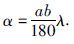
式(22)最后一项线积分只对边界单元进行,当单元的 $\overline{263}$ 边落在无穷远边界CD上时,线积分为


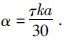 2.4 整体合成
2.4 整体合成
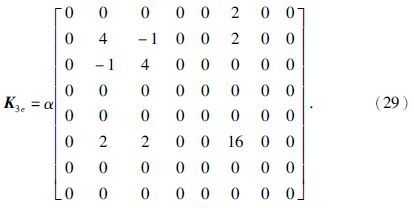
以上过程得到的K1e、K2e和K3e为各单元的刚度矩阵,之后需要将各个单元的刚度矩阵进行合成,得到整体刚度矩阵.各个单元中的元素在整体刚度矩阵中的位置,是由网格中的整体编码和单元中局部节点编码的关系决定的.
以图 1中的①单元为例,其局部编码如图 2a所示.即单元①局部节点编码1、2、3、4、5、6、7和8在整体结构中的编码分别为1、3、14、12、2、9、13和8.①单元的单元刚度矩阵中的元素在整体刚度矩阵中的位置如下图所示.
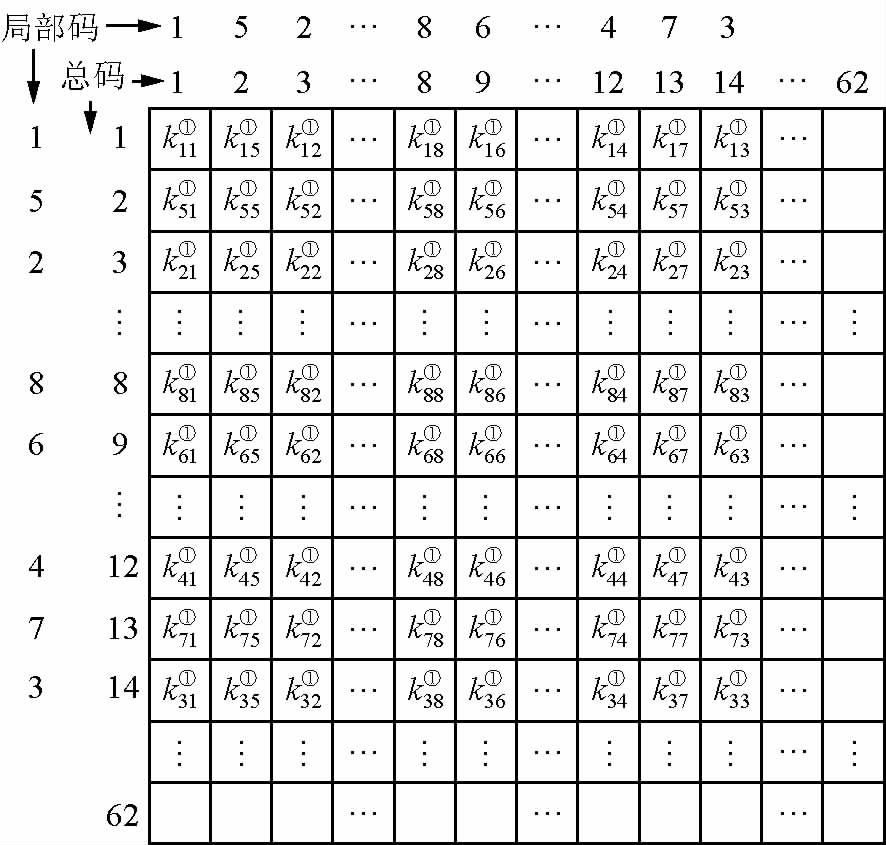
|
图 3 局部编码和总体编码的关系 Fig. 3 The relationship between local coding and global coding |
图中k11①表示①单元的单元刚度矩阵中的元素.将K1e、K2e和K3e扩展成全部节点组成的矩阵,再将3个扩展矩阵相加得
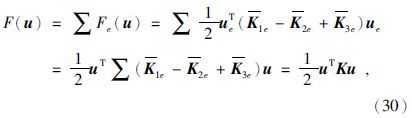

将上边界值代入,接线性方程组即得节点的u,它代表个节点的Hx.
3 编程实现MATLAB软件是一种功能强大,运算效率高的数字工具软件.它允许用户以数学形式的语言编写程序,使用上比C、Fortran和Basic等高级语言都要方便得多.
本文用MATLAB软件,编程实现上述二维有限元正演过程,给出了两组模型的正演响应.模型一和其响应如图 4所示,求解区域为4 km,异常体和围岩的电阻率分别是 10 Ω·m和100 Ω·m.模型二和其响应如图 5所示.
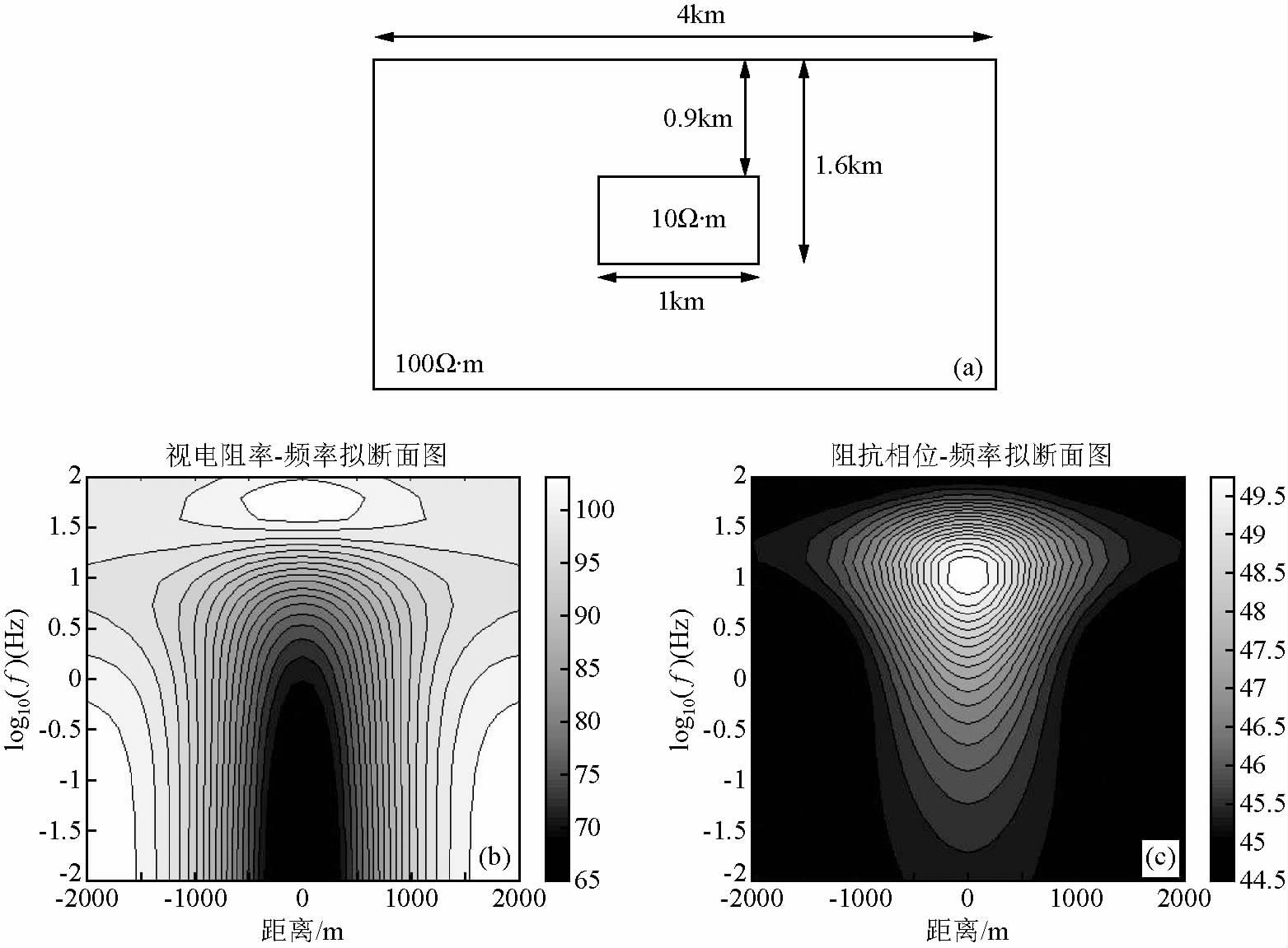
|
图 4 模型一有限元正演响应 (a)试验模型一;(b)TM模式视电阻率响应;(c)TM模式相位响应. Fig. 4 The finite elementforward response of the model1 |
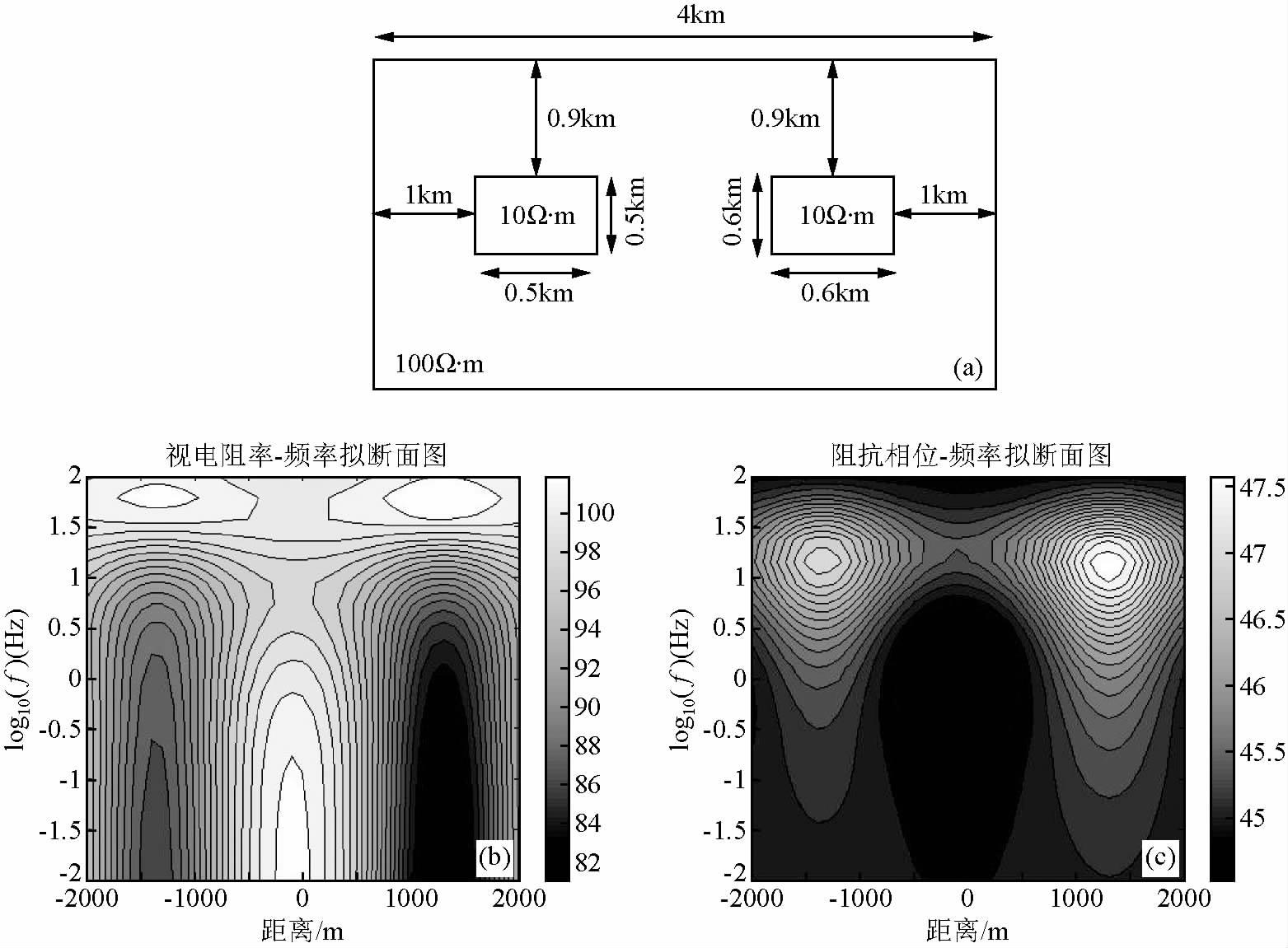
|
图 5 模型二有限元正演响应 (a)试验模型二;(b)TM模式视电阻率响应;(c)TM模式相位响应. Fig. 5 The finite elementforward response of the model2 |
有限元法是一种强有力的数值模拟方法,用有限元法对大地电磁二维问题进行正演,其原理清晰易懂,运算结果稳定可靠.本文在详细推导了大地电磁二维问题的正演过程后,给出了正确的形函数、单元刚度矩阵并将局部编码和整体编码的关系用图表的方式展现出来,完整地表现了整个正演的原理、方法和步骤.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Bi W, Liu Y. 2014. Two-dimensional magnetotelluric forward modeling by arbitrary quadrilateral finite element method[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 36(5): 521-528. |
| [2] | Chen L S, Wang G E. 1990. Magnetotelluric Sounding (in Chinese)[M]. Beijing: Geological Publishing House. |
| [3] | Chen X B. 1999. Direct iterative algorithm of the finite element[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 21(2): 165-171. |
| [4] | Chen X B, Hu W B. 2002. Direct iterative finite element (DIFE) algorithm and its application to electromagnetic response modeling of line current source[J]. Chinese Journal of Geophysics (in Chinese), 45(1): 119-130. |
| [5] | Chen X B, Zhang X, Hu W B. 2000. Application of finite-element direct iteration algorithm to MT 2-D forward computation[J]. OGP(in Chinese), 35(4):487-496. |
| [6] | Chen X B, Zhao G Z. 2004. An essential structure finite element (ESFE) algorithm and its application to MT 1D forward modeling of continuous medium[J]. Chinese Journal of Geophysics (in Chinese), 47(3): 535-541, doi: 10.3321/j.issn:0001-5733.2004.03.026. |
| [7] | Coggon J. 1971. Electromagnetic and electrical modeling by the finite element method[J]. Geophysics, 36(1): 132-155. |
| [8] | Courant R. 1943. Variational methods for the solution of problems of equilibrium and vibrations[J]. Bulletin of the American Mathematical Society, 49(1): 1-23. |
| [9] | Feng D S, Wang X. 2013. Magnetotelluric finite element method forward based on biquadratic interpolation and least squares regularization joint inversion[J]. The Chinese Journal of Nonferrous Metals (in Chinese), 23(9): 2524-2531. |
| [10] | Franke A, Brner R U, Spitzer K. 2004. 2D finite element modelling of plane-wave diffusive time-harmonic electromagnetic fields using adaptive unstructured grids[C].//Proceedings of the 17th Workshop on Electromagnetic Induction in the Earth. Hyderabad, India. |
| [11] | Liu J X, Jiang P F, Tong X Z, et al. 2009. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University (Science and Technology) (in Chinese), 40(2): 484-491. |
| [12] | Liu S C, He Z Y, Liu Z X. 2005. 2D FEM numerical simulation adapted to the fluctuant topography[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 27(2): 131-134. |
| [13] | Liu X J, Wang J L, Yu P. 2007. Secondary field-based two-dimensional magnetotelluric numerical modeling by finite element method[J]. Journal of Tongji University (Natural Science) (in Chinese), 35(8): 1113-1117. |
| [14] | Liu Y, Wang X B. 2010. FEM using adaptive topography in 2D MT forward modeling[J]. Seismology and Geology (in Chinese), 32(3): 382-391. |
| [15] | Pridmore D F, Hohmann G W, Ward S H, et al. 1981. An investigation of finite-element modeling for electrical and electromagnetic data in three dimensions[J]. Geophysics, 46(7), 1009-1024. |
| [16] | Rijo L. 1977. Modeling of electric and electromagnetic data[Ph. D. thesis]. Utah: University of Utah. |
| [17] | Rodi W L. 1976. A technique for improving the accuracy of finite element solutions for magnetotelluric data[J]. Geophysical Journal International, 44(2): 483-506. |
| [18] | Shi M J, Xu S Z, Liu B. 1997. Finite element method using quadratic element in MT forward modeling[J]. Acta Geophysica Sinica (in Chinese), 40(3): 421-430. |
| [19] | Wang X B, Li Y N, Gao Y C. 1999. Two dimensional topographic responses in magneto-telluric sounding and its correction methods[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 21(4): 327-332. |
| [20] | Wang X C, Shao M. 1997. Basic principle of finite element method and numerical method(in Chinese)[M]. Beijing: Tsinghua University Press. |
| [21] | Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements[J]. Geophysics, 51(11): 2131-2144. |
| [22] | Wannamaker P E, Stodt J A, Rijo L. 1987. A stable finite element solution for two-dimensional magnetotelluric modelling[J]. Geophysical Journal International, 88(1): 277-296. |
| [23] | Xu L H, Tong X Z, Liu J X, et al. 2009. Solution strategies for 2D and 3D magnetotelluric forward modeling based on the finite element method[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 31(5): 421-425. |
| [24] | Xu S Z. 1982. The second lecture Introduction to finite element method and its application in geophysical exploration[J]. Computing Technique for Geophysical and Geochemical Exploration(in Chinese), (Z1). |
| [25] | Xu S Z, Liu B. 1995. A numerical method for calculating MT field on a layered model with continuous change of conductivity in each layer[J]. Acta Geophysica Sinica (in Chinese), 38(2): 262-268. |
| [26] | 毕武, 刘云. 2014. 任意四边形剖分二维MT有限元正演模拟[J]. 物探化探计算技术, 36(5): 521-528. |
| [27] | 陈乐寿, 王光锷. 1990. 大地电磁测深法[M]. 北京: 地质出版社. |
| [28] | 陈小斌. 1999. 有限元直接迭代算法[J]. 物探化探计算技术, 21(2): 165-171. |
| [29] | 陈小斌, 胡文宝. 2002. 有限元直接迭代算法及其在线源频率域电磁响应计算中的应用[J]. 地球物理学报, 45(1): 119-130. |
| [30] | 陈小斌, 张翔, 胡文宝. 2000. 有限元直接迭代算法在MT二维正演计算中的应用[J]. 石油地球物理勘探, 35(4): 487-496. |
| [31] | 陈小斌, 赵国泽. 2004. 基本结构有限元算法及大地电磁测深一维连续介质正演[J]. 地球物理学报, 47(3): 535-541, doi: 10.3321/j.issn:0001-5733.2004.03.026. |
| [32] | 冯德山, 王珣. 2013. 大地电磁双二次插值FEM正演及最小二乘正则化联合反演[J]. 中国有色金属学报, 23(9): 2524-2531. |
| [33] | 柳建新, 蒋鹏飞, 童孝忠,等. 2009. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J]. 中南大学学报(自然科学版), 40(2): 484-491. |
| [34] | 刘树才, 何昭友, 刘志新. 2005. 适合地形起伏的二维有限单元数值模拟技术[J]. 物探化探计算技术, 27(2): 131-134. |
| [35] | 刘小军, 王家林, 于鹏. 2007. 基于二次场的二维大地电磁有限元法数值模拟[J]. 同济大学学报(自然科学版), 35(8): 1113-1117. |
| [36] | 刘云, 王绪本. 2010. 大地电磁二维自适应地形有限元正演模拟[J]. 地震地质, 32(3): 382-391. |
| [37] | 史明娟, 徐世浙, 刘斌. 1997. 大地电磁二次函数插值的有限元法正演模拟[J]. 地球物理学报, 40(3): 421-430. |
| [38] | 王绪本, 李永年, 高永才. 1999. 大地电磁测深二维地形影响及其校正方法研究[J]. 物探化探计算技术, 21(4): 327-332. |
| [39] | 王勖成, 邵敏. 1997. 有限单元法基本原理和数值方法[M]. 第2版. 北京: 清华大学出版社有限公司. |
| [40] | 徐凌华, 童孝忠, 柳建新,等. 2009. 基于有限单元法的二维/三维大地电磁正演模拟策略[J]. 物探化探计算技术, 31(5): 421-425. |
| [41] | 徐世浙. 1982. 第二讲 有限单元法及在物探中的应用简介[J]. 物化探电子计算技术, (Z1). |
| [42] | 徐世浙, 刘斌. 1995. 电导率分层连续变化的水平层的大地电磁正演[J]. 地球物理学报, 38(2): 262-268. |
 2016, Vol. 31
2016, Vol. 31


