2. 中国科学院地质与地球物理研究所 中国科学院页岩气与地质工程重点实验室, 北京 100029;
3. 山西省煤炭地质物探测绘院, 晋中 030600
2. Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of science, Beijing 100029, China;
3. shanxi coal geology geophysical surveying exploration institute, Jinzhong 030600, China
瞬变电磁法(Time domain electromagnetic methods,TEM)是利用不接地回线或接地电极向地下发送脉冲式一次电磁场,用线圈或接地电极观测由脉冲电磁场感应的地下涡流产生的二次电磁的空间和时间分布,从而解决有关地质问题的时间域电磁方法.瞬变电磁根据源的不同,可分为磁性源瞬变电磁和电性源瞬变电磁,磁性源瞬变电磁法一般在回线边长的1/3内观测,探测深度一般为n×10~n×100 m(考夫曼和凯勒,1987;朴华荣,1990;蒋邦远,1998;牛之链,2007;薛国强等,2007),而电性源瞬变电磁法探测深度为1~10 km,具有勘探深度大、垂向分辨率高、对高阻体探测灵敏的特点(薛国强等,2013,2014;王显祥等,2015;齐彦福等,2015).
电性源瞬变电磁法由前苏联在20世纪50年代提出,目前该方法在石油地球物理勘探中发挥着越来越重要的作用(Newman,1989;Stack et al.,1989;Stack,1992;陈明生,1999;Tang et al.,2011).长久以来,长偏移距法(Long Offset Transient electromagnetic,LOTEM)作为一种电性源瞬变电磁方法,所示在石油地球物理勘探中发挥着重要作用.其工作方式如图 1a,发射源长度一般为1~2 km,收发距2~20 km,一般测量Hz、Ex场.此外,David Wright在2002年提出了多通道瞬变电磁法(Multi-channel Transient Electromagnetic,MTEM)的概念,即利用伪随机电流(Pseudo-Random Binary Sequence,PRBS)向地下发射电磁信号,在发射源的轴向装置上测量Ex场变化,采用发射源和接收点同时移动的方式,观测装置如图 1b所示,利用反褶积提取大地脉冲响应或阶跃响应信号,该方法在油气资源的探测中,也取得了不错的效果(Wright,2001,2002;Wright,2003;Ziolkowski,2005;Ziolkowski,2007).
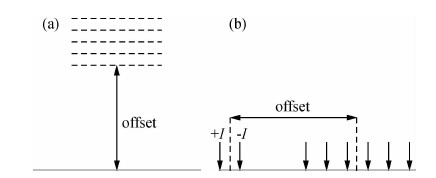 |
图 1 电性源瞬变电磁装置对比图 (a)赤道装置图; (b)轴向装置图. Fig. 1 Contrast diagram of device for ground source transient (a)Diagram of equatorial equipment; (b) Diagram of dipole device. |
LOTEM法和MTEM法既有相同之处也有不同之处,相同之处在于都采用电偶极子源发射,不同之处在于LOTEM法多采用赤道装置,采集Hz场,而MTEM法采用轴向装置,采集Ex场.电性源瞬变电磁有两种装置和两种分量(主要针对目前应用最多的Hz场和Ex场,其他分量暂不考虑),发射波形包括阶跃波和脉冲波.到底应选择何种装置,何种发射波行及哪种分量才能够取得对目标体的最近探测效果,是一个值得探讨的问题,为此本文对此进行了详细的讨论,试图找到一些规律性的东西.
1 数值模拟方法瞬变电磁场的求解方法有很多种,但大的分类主要有两种:从时间域直接解方程,或从频率域入手求解电磁场,再把频率域结果转到时间域.由于直接从时间域解方程比较复杂,现多从频率域出发求解电磁场.从频率域场到时间域场的转换方法也有很多,主要有:余弦变换(Newman et al.,1986)、G-S变换(Knight and Raiche,1982;Villinger,1985)、Guptasarma算法(Guptasarma,1982)、延迟谱算法等.Guptasarma算法计速度快、精度高、晚期响应稳定,但只适用于简单地电模型,适用性不强.延迟谱算法所需频率少,计算速度快,但是晚期响应不稳定,使用性也不是太强.综合考虑,余弦变换和G-S变换,无论从计算精度还是模型的适用性来说,都是较好的.本文采用的是G-S变换,现介绍其思想如下.
由拉普拉斯变换的定义可知,已知其频率函数,则其逆变换为(Knight and Raiche,1982):
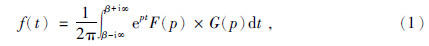
式中f(t)和F(P)分别为时间域和频率函数,G(p)为一次场源(阶跃电流或脉冲电流)的逆拉普拉斯变换.其中阶跃波的逆拉普拉斯变换为

脉冲波的逆拉普拉斯变换为

经过一系列的推导,并将(1)式离散化后可得:
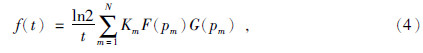
上式为G-S变换公式,其中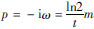 ,Km为G-S变换系数,为已知.
,Km为G-S变换系数,为已知.
为了验证程序的正确性,以均匀半空间为例进行说明,模型参数为:电阻率为1000,采用轴向装置,收发距为1000 m,发射源长度100 m,电流10 A.均匀半空间下,电偶极子沿x方向铺设,脉冲波与上阶跃波激发的Ex场表达式分别为(方文藻等,1993):
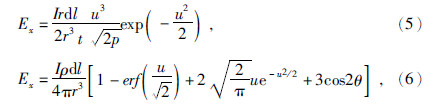
其中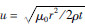 ,I为发射电流,dl为电偶极源长度,θ为与x轴夹角,ρ为电导率,r为收发距,erf为误差函数.G-S变换结果与利用(5)、(6)式求得的解析解对比结果如图 2a、b所示,分析此图可知:图 2a为利用G-S变换求取的脉冲响应与解析解对比图,除在10-7 s之前,G-S变换结果有震荡外,其与解析解吻合度较高;图 2b为利用G-S变换求取的阶跃响应与解析解对比图,从早期到晚期其与解析解几乎完全吻合.通过以上分析可知,G-S变换结果与解析解吻合度较高,证明了本文程序是可靠、正确的.
,I为发射电流,dl为电偶极源长度,θ为与x轴夹角,ρ为电导率,r为收发距,erf为误差函数.G-S变换结果与利用(5)、(6)式求得的解析解对比结果如图 2a、b所示,分析此图可知:图 2a为利用G-S变换求取的脉冲响应与解析解对比图,除在10-7 s之前,G-S变换结果有震荡外,其与解析解吻合度较高;图 2b为利用G-S变换求取的阶跃响应与解析解对比图,从早期到晚期其与解析解几乎完全吻合.通过以上分析可知,G-S变换结果与解析解吻合度较高,证明了本文程序是可靠、正确的.
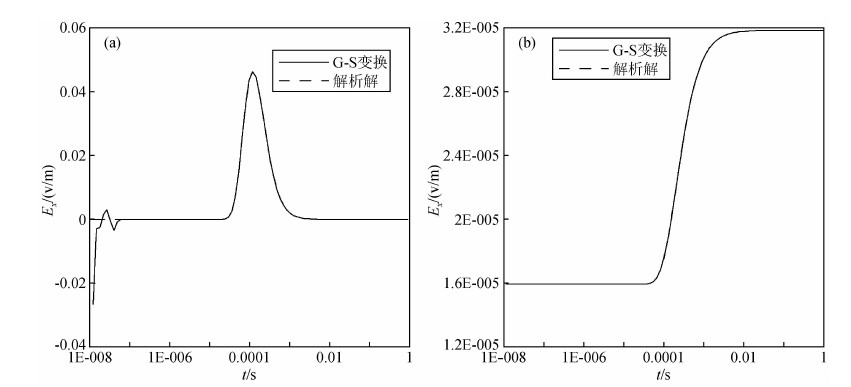 | 图 2 均匀半空间下G-S变换结果与解析解对比图 Fig. 2 Comparison diagram of results of G-S transform and cosine transform |
在电性源瞬变电磁测深中,虽然可以观测到Ex、Ey、Hx、Hy、Hz场等五个分量,但Ey、Hx、Hy对地层信息的分辨能力较差,主要观测水平电场Ex,和垂直磁场Hz.均匀半空间下,电偶极子源沿x方向铺设,脉冲波与上阶跃波激发的场表达式分别为(方文藻等,1993):
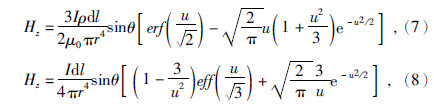
在均匀半空间下,通过分析(5)~(8)式可得出以下规律:Ex场只有在阶跃激励源下与θ角有关,且在赤道与轴向装置下场强都不会太弱;Hz场强度与θ有关,θ值越接近0°或180°时其值越小,θ值越接近90°或270°时其值越大,即Hz场强度在赤道装置下较强,在轴向装置下为零.考虑到当信号较弱时,采集到的数据信噪比难以保证,故在赤道装置下可以观测Ex、Hz场,而轴向装置下只能观测Ex场.
为比较Ex、Hz场对目标地质体的探测效果,特做三层地电结构模型,三层介质电阻率分别为1000 Ω·m、10000 Ω·m、1000 Ω·m,厚度分别为300 m、500 m.不同收发距下Hz场、Ex场全期视电阻率曲线如图 3所示,其中图 3a为不同收发距下Hz场全期视电阻率曲线,通过分析此图可知: Hz场视电阻率曲线受收发距影响较小,当收发距从1 m到10000 m变化时不同收发距下视电阻率曲线变换不大,通过分析不同收发距下视电阻率曲线可知,理论上在较小收发距下即可得到深部地电结构信息,视电阻率极大值约为1600 Ω·m.图 3b为不同收发距下Ex场全期视电阻率曲线,通过分析此图可知:场视电阻率曲线受收发距影响明显,当收发距为100 m时从早期到晚期视电阻率都为1000 Ω·m,表明只能反映第一层地电结构信息;随着收发距的增大视电阻率极值逐渐增大,表明视电阻率曲线中第二层地电结构信息的比重逐渐增大;当收发距增大到2000 m以后视电阻率极值开始变小,表明视电阻率曲线中第三层地电结构信息的比重逐渐增大;当收发距为10000 m时,视电阻率曲线从早期到晚期很好地反映了三层地电结构由浅到深信息的变化;通过以上分析可知当收发距较小时视电阻率曲线只能反映浅部地电结构信息,过大时则深部地电信息比重增大,为了得到某深度的地电结构信息需要合适的收发距,在最佳收发距下其视电阻率极大值约为2800 Ω·m,为场的1.75倍.
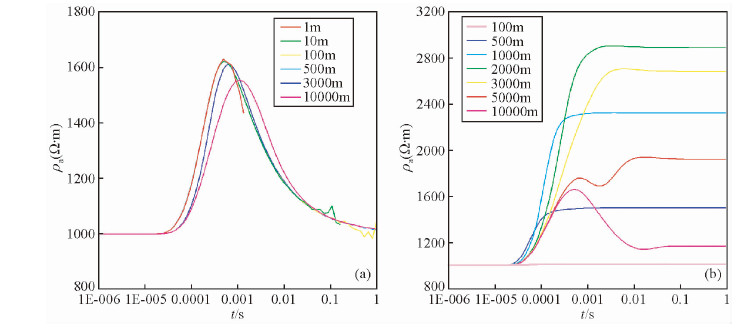 |
图 3 当中间层为高阻层时不同收发距阶跃激发的Hz、Ex场电阻率曲线对比图 (a)当中间层为高阻层时不同收发距下阶跃波激发的Hz场视电阻率曲线对比图; (b) 当中间层为高阻层时不同收发距下阶跃波激发的Ex场视电阻率曲线对比图. Fig. 3 Comparison diagram of apparent resistivity of step response Hz and Ex for different distances (a)Comparison diagram of apparent resistivity of Hz; (b) Comparison diagram of apparent resistivity of Ex. |
当把上面模型中的中间层电阻率变为100 Ω·m时,不同收发距下视电阻率曲线对比,如图 4所示.通过分析此图可知:Hz场视电阻率曲线同样受收发距影响较小,表明较小收发距下即可取得大深度地电结构信息,视电阻率极小值点略高于200 Ω·m;Ex场视电阻率曲线同样受收发距影响明显,不同收发距下视电阻率曲线差异较大,视电阻率极小值点略低于200 Ω·m.
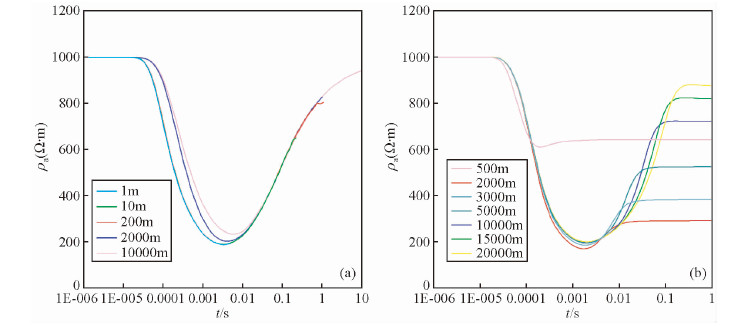 |
图 4 当中间层为低阻层时不同收发距下阶跃波激发的Hz、Ex场视电阻率对比图 (a) 当中间层为低阻层时不同收发距下阶跃波激发的Hz场视电阻率曲线对比图; (b) 当中间层为低阻层时不同收发距下阶跃波激发的 Ex场视电阻率曲线对比图. Fig. 4 Comparison diagram of apparent resistivity of step response Hz and Ex for different distances (a) Comparison diagram of apparent resistivity of step response Hz for different distances; (b) Comparison diagram of apparent resistivity of step response Ex for different distances. |
通过上文中1D数值模拟结果对比,可以发现Ex场无论对中间高阻层还是中间低阻层的探测效果都比Hz场好,特别是高阻层的探测上差异明显,对低阻层的识别二者差别并不是太大.当然Hz场较Ex场也具有以下优势:Hz场对收发距要求较小,在收发距为10 m时就能较好的反映本文所设计的三层地电信息,可见其对收发距要求之小,并且其视电阻率受收发距影响较小(当收发距变化时,电阻率几乎没什么大变化);受天然场干扰较小,对地层的分辨能力较强,薛国强在采集电性源瞬变电磁信号时,发现在五个分量中Hz受畸变影响最小,数据也最为光滑;Hz场不受静态效应的影响,Ex场可能受到静态效应的干扰,给数据的解释带来困难;测量时不需要接地,对接地困难的地区比较适用.本文综合以上分析认为,探测低阻体时选择Hz场可能较好,探测高阻体时Ex场可能较好.
3 观测装置的选择在电性源瞬变电磁测深中,LOTEM法多采用赤道装置进行观测,MTEM法多采用轴向装置采集数据,到底哪种装置最优,及两种观测装置各自有什么优势和劣势,本文将进行详细的探讨.
为了分析何种装置最优,本文对不同装置下Ex场探测效果进行了对比,如图 5所示.图 5a为电性源瞬变电磁阶跃波激发的Ex场不同装置、不同收发距下对第2节中的低阻层的模型响应视电阻率曲线对比图,通过分析此图不难发现:通过比较收发距同为500 m时的视电阻率曲线可以看出,在相同收发距下轴向装置探测深度较浅,赤道装置探测深度较大;通过大量计算比较可知,当收发距取1525 m时,赤道装置对中间低阻层探测效果最佳,而轴向装置下对中间低阻层探测效果最佳,最佳收发距为1825 m,比较同为最佳耦合收发距下的视电阻率曲线可知,轴向装置下视电阻率极小值点为192.05 Ω·m,赤道装置下视电阻率极小值点为163.69 Ω·m,赤道装置可以取得对中间低阻层较好勘探效果.
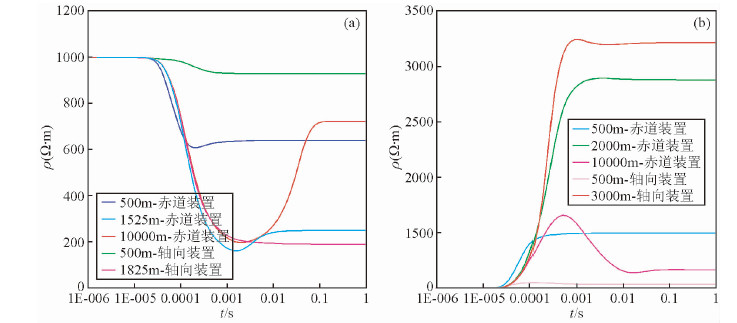 |
图 5 不同装置下阶跃波激发的Ex场探测效果对比图 (a)不同装置下跃波激发Ex场对低阻层探测效果对比图; (b)不同装置下阶跃波激发Ex场对高阻层探测效果对比图. Fig. 5 Comparison diagram of effects of step response Ex for different devices (a)Comparison diagram of effects of different devices for low resistivity layer; (b)Comparison diagram of effect for different devices for low resistivity layer. |
图 5b为电性源瞬变电磁阶跃波激发的场不同装置、不同收发距下对第2节中高阻层模型响应的视电阻率曲线对比图,通过此图不难看出:当收发距同为500 m时,轴向装置只能探测到第一层地电信息,而赤道装置不仅可以探测到第一层地电信息,在晚期还可以探测到第二层地电结构信息;通过计算可知,当收发距为2000 m时,赤道装置可以取得对中间高阻层的最佳耦合效果,轴向装置下则需要收发距为3000 m时取得对中间高阻层的最佳耦合效果,比较赤道装置与轴向装置最佳耦合收发距下视电阻率曲线可知,轴向装置视电阻率曲线明显高于赤道装置下视电阻率曲线,可以取得对高阻层的最佳勘探效果.
在实际工作中,是选择赤道装置还是轴向装置较为合适,可能要根据实际情况做出最合理的安排.本文仅把各自装置的优势罗列下来,请读者自行选择.赤道装置的优势:在探测相同深度的情况下,赤道装置收发距较小,信噪比自然较高;在均匀半空间下,Hz场在赤道装置下较强,轴向装置中强度较弱,不易观测;此外通过上文数值模拟可知,赤道装置下Ex场对低阻层的探测要好于轴向装置下Ex场.轴向装置的优势在于Ex场都能更好的刻画高阻异常,这也是MTEM法采用这种装置的原因.
4 发射源波形的选择为了探讨不同发射源波形对探测效果的影响,本文仍以第2节中的高阻层模型为例进行说明,为了更好的比较脉冲波与阶跃波对中间高阻层的探测能力,本文首先定义一个指数,即存在高阻层时的场与去掉高阻层时的均匀半空间场的比值,把这一比值暂且作为其对中间高阻层探测能力的指标.当收发距为3000 m时,利用不同发射波形轴向装置下场对中间高阻层探测效果如图 6所示,分析此图不难发现:对阶跃波而言,0.0001 s之前其比值为1,主要反映第一层地电结构信息,随着时间的推移其值逐渐增大,开始反映第二层地电结构信息,极大值点为4.699,极大值点后,其比值略有下降,其后就保持在3.211左右,表明其只能反映前两层地电结构;对于脉冲波,在早期和晚期脉其比值约为1,分别反映第一层和第三层地电结构信息,中段部分其比值远高于阶跃波比值,表明在这段时间内脉冲激发的场较阶跃波激发的场对高阻体的探测能力更强.
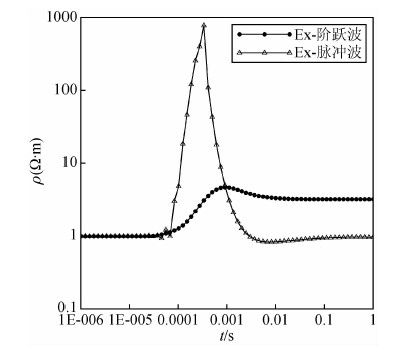 | 图 6 当收发距为3000 m时不同 激励源下Ex场比值曲线 Fig. 6 Effect drawing of detectability of Ex for high resistivity under 3000 m distance |
虽然脉冲波较阶跃波对异常体的探测更为灵敏,但其自身也存在着求取视电阻率难的问题,阶跃波下的场是关于电阻率的单调函数,其场值与电阻率存在一一对应关系,而脉冲波下的场并不是关于电阻率的单调函数,除极点外,一个场值与两个电阻率相对应,为了去求视电阻率需要以极点为界分为区间,在两个区间内分别求取视电阻率.当收发距为3000 m时,轴向装置下不同发射源视电阻率曲线如图 7所示.图 7b为阶跃函数激励下场视电阻率曲线,从早期到晚期很好的反映了地电结构由浅到深的变化.图 7a为脉冲函数激励下场视电阻率曲线,由上文分析可知,其视电阻率的求取需要分两个区间分别求取,再组合成一条完整的视电阻率曲线,在早期和晚期阶段视电阻率曲线能够很好的反映地电结构信息的变化,然而在过渡阶段存在着两条曲线不能很好衔接的问题.
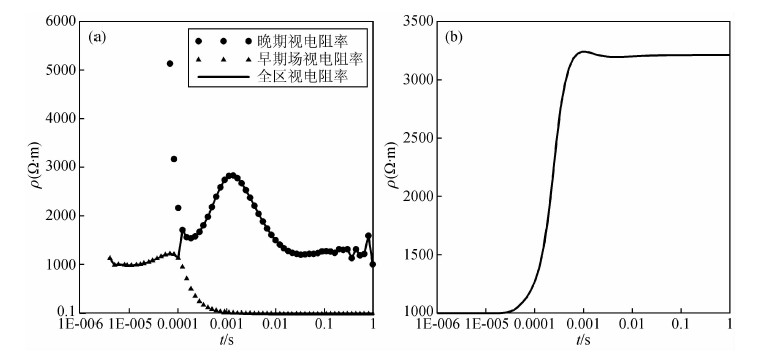 |
图 7 同一模型、不同激励源下Ex场视电阻率曲线对比图 (a)脉冲波激励下Ex长视电阻率曲线;(b)阶跃波激励下Ex场视电阻率曲线. Fig. 7 Comparison diagram of apparent resistivity curves of Hz for different sources (a) Diagram of apparent resistivity curves of Ex for step response; (b) Diagram of apparent resistivity curves of Ex under impulse response. |
总之,阶跃响应能够更好的刻画地电模型的整体面貌,而脉冲信号响应则可以更好的在整体面貌中刻画异常体信息.从数学角度讲,阶跃波可以通过脉冲波积分得到,而脉冲波又可以通过阶跃波微分得知,故脉冲响应对异常体响应更为灵敏,同时也易受噪声的干扰;阶跃响应对异常体响应可能更为迟钝一些,其受噪声的干扰可能也相对较小.总之,两种激励源是一种相辅相成的关系,最好的工作方式可能是两种信号的综合利用和解释,而不是选择其中一种信号.
5 结论5.1 电性源瞬变电磁激发的Hz场在小收发距下即可进行大深度探测,同时小收发距在一定程度上又保证了高信噪比,并且其无需接地即可进行测量;Ex场虽然需要在大收发距下进行大深度探测,但其对高阻体探测能力较场也更强.故本文认为,当对低阻体探测时选用Hz场可能较合适,高阻体探测时选用场可能较为适宜.
5.2 在选择何种装置最优时,通过数值模拟结果可知:在探测相同深度的情况下,赤道装置较轴向装置所需收发距较小,信噪比较高,并且在赤道装置下可观测Hz场,轴向装置下该场较弱;轴向装置的优势在于无论何种源激发的场都能更好的刻画高阻体异常,并且优势明显.
5.3 通过数值模拟结果可知:阶跃信号视电阻率求取方便,从早期到晚期能很好的反映地电结构由浅到深的变化;脉冲信号能够更好的刻画异常体的存在,但在过渡场阶段存在视电阻率畸变现象.总之,两种激励源是一种相辅相成的关系,最好的工作方式可能是两种信号的综合利用和解释,而不是选择其中一种信号.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Chen M S. 1999. Study on the transient electromagnetic (TEM) sounding with electric dipole. II. the solving process of tem field[J]. Coal Geology & Exploration (in Chinese), 27(2): 54-57. |
| [2] | Fang W Z, Li Y G, Li X. 1993. Theory of TEM Sounding (in Chinese)[M]. Xi'an: Press of North-West Industry University. |
| [3] | Guptasarma D. 1982. Computation of the time-domain response of a polarizable ground[J]. Geophysics, 47(11): 1574-1576. |
| [4] | Jiang B Y. 1998. Applied Near Zone Magnetic Source Transient Electromagnetic Exploration (in Chinese)[M]. Beijing: Geological Publishing House. |
| [5] | Kaufman A A, Keller G V. 1987. Frequency and Transient Soundings (in Chinese)[M]. Wang J M, trans. Beijing: Geological Publishing House. |
| [6] | Knight J H, Raiche A P. 1982. Transient electromagnetic calculations using the Gaver-Stehfest inverse Laplace transform method[J]. Geophysics (in Chinese), 47(1): 47-50. |
| [7] | Newman G A. 1989. Deep transient electromagnetic soundings with a grounded source over near-surface conductors[J]. Geophysical Journal International, 98(3): 587-601. |
| [8] | Newman G A, Hohmann G W, Anderson W L. 1986. Transient electromagnetic response of a three-dimensional body in a layered earth[J]. Geophysics, 51(8): 1608-1627. |
| [9] | Niu Z L. 2007. Theory of Tine-domain Electromagnetic Method (in Chinese)[M]. Changsha: Central South University Press. |
| [10] | Piao H R. 1990. Principle of Electromagnetic Sounding (in Chinese)[M]. Beijing: Geological Publishing Press. |
| [11] | Qi Y F, Yin C C, Wang R, et al. 2015. Multi-transient EM full-time forward modeling and inversion of m-sequences[J]. Chinese Journal Geophysics (in Chinese), 58(7): 2566-2577, doi: 10.6038/cjg20150731. |
| [12] | Stack K M. 1992. Exploration with Deep Transient Electromagnetics[M]. Amsterdam: Elsevier Science Publ. |
| [13] | Strack K M, Hanstein T, LeBrocq K, et al. 1989. Case histories of LOTEM surveys in hydrocarbon prospective areas[J]. First Break, 7(12): 467-477. |
| [14] | Tang X G, Hu W B, Yan L J. 2011. Topographic effects on long offset transient electromagnetic response[J]. Applied Geophysics, 8(4): 277-284. |
| [15] | Villinger H. 1985. Solving cylindrical geothermal problems using the Gaver-Stehfest inverse Laplace transform[J]. Geophysics, 50(10): 1581-1587. |
| [16] | Wang X X, Di Q Y, Tang J. 2015. The preliminary study of the ground source transient[J]. Progress in Geophysics (in Chinese), 30(2): 872-877, doi: 10.6038/pg20150253. |
| [17] | Weir G J. 1980. Transient electromagnetic fields about an infinitesimally long grounded horizontal electric dipole on the surface of a uniform half-space[J]. Geophysical Journal International, 61(1): 41-56. |
| [18] | Wright D A. 2003. Detection of hydrocarbons and their movement in a reservoir using time-lapse multi-transient electromagnetic (MTEM) data [Ph. D. thesis]. Edinburgh: University of Edinburgh. |
| [19] | Wright D A, Ziolkowski A, Hobbs B A. 2001. Hydrocarbon detection with a multi-channel transient electromagnetic survey[C].//71stAnnual International Meeting, SEG. Expanded Abstracts, 1435-1438. |
| [20] | Wright D, Ziolkowski A, Hobbs B. 2002. Hydrocarbon detection and monitoring with a multicomponent transient electromagnetic (MTEM) survey[J]. The Leading Edge, 21(9): 852-864. |
| [21] | Xue G Q, Chen W Y, Zhou N N, et al. 2014. Short-offset TEM technique with a grounded wire source for deep sounding[J]. Chinese Journal of Geophysics (in Chinese), 56(1): 255-261, doi: 10.6038/cjg20130126. |
| [22] | Xue G Q, Li X, Di Q Y. 2007. The progress of TEM in theory and application[J]. Progress in Geophysics (in Chinese), 22(4): 1195-1200, doi: 10.3969/j.issn.1004-2903.2007.04.026. |
| [23] | Xue G Q, Yan S, Chen W Y. 2014. Research prospect to grounded-wire TEM with short-offset[J]. Progress in Geophysics (in Chinese), 29(1): 177-181, doi: 10.6038/pg20140124. |
| [24] | Ziolkowski A. 2005. Detection of subsurface resistivity contrasts with application to location of fluids: US, 6914433[P]. |
| [25] | Ziolkowski A, Hobbs B A, Wright D. 2007. Multitransient electromagnetic demonstration survey in France[J]. Geophysics, 72(4), F197-F209. |
| [26] | 陈明生. 1999. 电偶源瞬变电磁测深研究(二)——瞬变电磁场的求解方法[J]. 煤田地质与勘探, 27(2): 54-57. |
| [27] | 方文藻, 李予国, 李貅. 1993. 瞬变电磁测深法原理[M]. 西安: 西北工业大学出版社. |
| [28] | 蒋邦远. 1998. 实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社. |
| [29] | 考夫曼A A,凯勒G V. 1987. 频率域和时间域电磁测深[M]. 王建谋, 译. 北京: 地质出版社. |
| [30] | 牛之琏. 2007. 时间域电磁法原理[M]. 长沙: 中南大学出版社. |
| [31] | 朴化荣. 1990. 电磁测深法原理[M]. 北京: 地质出版社. |
| [32] | 齐彦福, 殷长春, 王若,等. 2015. 多通道瞬变电磁m序列全时正演模拟与反演[J]. 地球物理学报, 58(7): 2566-2577, doi: 10.6038/cjg20150731. |
| [33] | 王显祥, 底青云, 唐静. 2015. 电性源瞬变电磁初探[J]. 地球物理学进展, 30(2): 872-877, doi: 10.6038/pg20150253. |
| [34] | 薛国强, 陈卫营, 周楠楠,等. 2013. 接地源瞬变电磁短偏移深部探测技术[J]. 地球物理学报, 56(1): 255-261, doi: 10.6038/cjg20130126. |
| [35] | 薛国强, 李貅, 底青云. 2007. 瞬变电磁法理论与应用研究进展[J]. 地球物理学进展, 22(4): 1195-1200, doi: 10.3969/j.issn.1004-2903.2007.04.026. |
| [36] | 薛国强, 闫述, 陈卫营. 2014. 接地源短偏移瞬变电磁法研究展望[J]. 地球物理学进展, 29(1): 177-181, doi: 10.6038/pg20140124. |
 2016, Vol. 31
2016, Vol. 31

