重磁勘探数据中的异常是由不同深度场源产生的异常的叠加.通常,深部异常体引起的重磁异常多呈低频特性;而浅部异常体引起的重磁异常变化则以中高频率为主.将不同尺度的重磁异常分离开是重磁资料解释中重要的一环,目前主要方法包括以下几种方法:最小二乘法(曾华霖,2005)、向上延拓法(曾华霖,2005)、带通滤波法(曾华霖,2005)、维纳滤波法(Pwalowski and Hansen,1990)、小波分析法(杨文采,2001)、优化滤波法(郭良辉等,2012)等.这些方法都可以在一定的使用范围下实现对重磁异常的有效分离.
Huang等(1998)等人提出了一种新的处理非线性、非稳态信号的方法:经验模态分解(Empirical Mode Decomposition,EMD),该方法的核心思想是对原始信号进行分解,从而得到一组有限个不同尺度的固有模态函数(Intrinic Mode Function,IMF).先分解出的IMF分量频率较高,随后频率会逐渐降低.Nunes等(2003)等人将该方法扩展为二维经验模态分解(Bidimensional Empirical Mode Decomposition,BEMD),并将其应用于图像处理领域.
Wu和Huang(2004)通过大量的实验研究发现白噪声在EMD算法下的统计特性:白噪声经EMD分解之后得到的每个IMF分量都满足正态分布;每个IMF的傅立叶频谱具有一致性,在半对数尺度坐标下覆盖同一个区域.而且Wu和Huang(2004)等人还有如下结论:IMF的能量密度与其对应的平均周期的乘积为一个常量.这些研究结果为BEMD去噪提供了理论基础.
二维经验模态分解方法作为一种新兴的图像处理方法,仍存在一些问题(葛光涛,2010).不少学者对BEMD算法提出过改进方案:为了改进包络面插值结果,Delaunay三角剖分法(张彦铎等,2013;秦绪佳等,2013)、双调和样条插值(陈建国等,2011)都被应用到BEMD算法中;针对BEMD分解过程中的边缘效应,黄大吉等(2003)等人提出用镜像法进行边界延拓,刘慧婷等(2004)等人提出基于多项式拟合的边界延拓方法.
在地球物理学中,经验模态分解已有许多应用,如地震信号处理(钱昌松等,2010)、大地电磁噪声压制(汤井田等,2008)、储层识别(胥德平等,2011)等.周文纳等(2010)等人将一维经验模态分解应用于重磁异常分离,并取得了较好的结果.陈建国等(2011)、曾琴琴和刘天佑(2011)进行了利用BEMD分解重磁异常的尝试.
在前人研究的基础上,本文对应用于位场分析的二位经验模态分解算法进行了研究:首先,针对重磁异常数据的特点,提出了一种适合位场分析的解决边缘效应的方法,然后对比了不同插值算法对包络面插值结果来选定最佳插值算法,而且还探究了不同筛分停止准则对分解结果的影响,最后,应用位场功率谱分析,使BEMD分解结果有了对应的深度概念.
1 二维经验模态分解基本原理二维经验模态分解(BEMD)的核心原理与Huang等(1998)提出的经验模态分解(EMD)原理相同,因此本文首先介绍EMD的分解原理.
EMD分解能够自适应的分解给定信号S(k)得到不同的窄带频率成分,各个成分被称作固有模态函数.EMD对信号S(k)的分解结果由多个固有模态函数imf(k)和一个残余模态res(k)(The Residual)组成,公式为
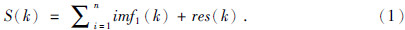
使用EMD分解一个给定信号S(k)时,必须满足以下两个条件(Huang et al.,1998):
(1)每个IMF具有的局部零点和极值点相同,同时上下包络关于时间轴局部对称.
(2)每个IMF相对于局部均值对称.
初始信号经过EMD分解之后得到的若干结果,按照分解出的先后顺序,频率从高到低分布.
Nunes等(2003)将一维经验模态分解算法中对一维线数据的处理扩展为二维面数据的处理,得到了二维经验模态分解的算法,对于一个给定的二维信号S(x,y),BEMD的分解过程如下:
首先寻找出原始信号S(x,y)的所有极大值点和极小值点,并对获得的极值进行插值拟合以获得上包络线U(x,y)与下包络线L(x,y),进而可以得到原始信号的平均包络线M1(x,y),即:
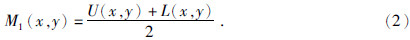
从S(x,y)中减去得到的平均包络线M1(x,y)即得到去掉低频的信号H11(x,y),即:
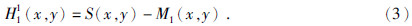
通常第一次的计算结果H11(x,y)并不满足上文的两个分解条件,因此需要重复以上过程,假定经过t次之后得到结果H1t(x,y)是满足条件的,则S(x,y)的一阶IMF C1(x,y)为
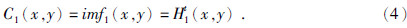
在实际情况中,通常无法满足两个分解条件,一般认为当H1t(k)的标准偏差SD足够小时,筛分结果就满足了理论条件(Huang et al.,1998),即:
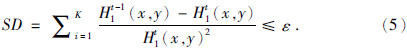
该公式即为筛选出单个固有模态的停止准则,根据以往经验,其中阈值ε的值一般取0.1到0.7之间.
分解得到第一个IMF之后,从原信号中减去一阶IMF C1(x,y)就得到去掉高频成分的残余模量R1(x,y),对R1(x,y)重复上述获得C1(x,y)的过程就可以得到第二个IMF分量.重复进行直至得到预设的第n阶IMF分量或者残余模量Rn(k)的极值小于三个为止.
根据上述的算法,我们可以得到BEMD的算法流程图,如图 1所示.
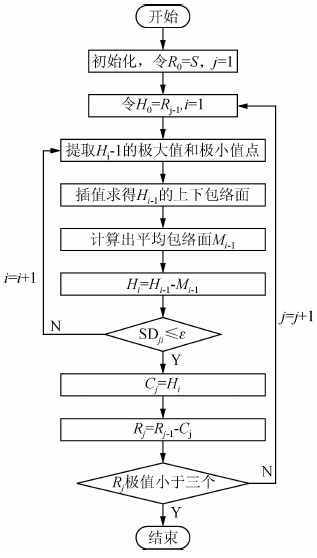 | 图 1 BEMD算法流程图 Fig. 1 The algorithm flowchart of BEMD |
在使用BEMD进行分解的过程中,存在边缘效应问题.在求取原始数据的平均包络面时,要通过对数据的极大值和极小值点进行插值拟合求取上下包络面,进而求出平均包络面.原始的算法对数据边缘不做任何处理,进行包络面插值时,由于数据的边缘不存在极值点,在进行样条插值时就会出现拟合误差,而且多次拟合结果的误差会逐渐积累,分解得到的IMF1就会有较大的误差,又因为继续分解得到的IMF2是在原始数据减去IMF1的基础上筛分得到的,所以,随着分解过程的继续,原始数据都会被初始的误差“污染”,导致分解结果失去意义.
针对物探数据的特点,本文提出了一种解决边缘效应的方法.在进行包络面插值时,将全部边缘数据点同时视为极大值点和极小值点,在这种情况下,建立包络面时插值算法带来的拟合过程和端点飞翼的现象能够被很好的抑制.而且原算法无法进行极值点过少的情况下的计算(Pei et al.,2012),采取此方法改进可以避免该情况.但是这种做法也破坏了原算法的最终停止准则,不过由于实际应用中的数据比较复杂,因此可以根据研究需要决定何时停止BEMD的分解过程,即需要将原始信号分解为几个模态就分解为几个模态.
2.2 包络面插值BEMD分解中的一个关键步骤是对数据的极大值和极小值点进行插值拟合得到上下包络面,进而求出平均包络面.所以包络面拟合是BEMD算法中及其重要的一个问题,插值方法的选择将直接影响BEMD的最终分解结果.Huang在原方法中提出采用三次样条插值来进行拟合的方法.虽然Huang提出的三次样条插值具有良好的光滑性,但是插值精度不高,而且极容易出现过冲和欠冲的现象,即使采用高次样条函数,令阶数提高到一定程度,精度也无法提高.
为了确定进行建立包络面的最佳插值算法,本文选取了三角剖分插值法、克里格插值法、径向基函数插值法、反距离加权插值法、三次样条插值法、移动平均插值法以及最小曲率插值法来进行试验,并使用以上方法对同一数据插值建立其上包络面.进行实验的数据如图 2a所示,该数据截取自某地实测重力数据所用数据,图中的蓝色点为数据的局部极大值点,极值点比较稀疏,是为了能够更好的测试插值算法的拟合能力.插值时使用的网格为150×150.图 2b-h展示了不同方法对该数据的上包络的拟合结果.
 |
图 2 试验数据及各插值方法形成的上包络面 (a)试验数据(蓝色点为极值点);(b)三角剖分插值结果;(c)克里格插值结果;(d)径向基函数插值结果;(e)反距离加权插值结果;(f)三次样条插值结果;(g)移动平均插值结果;(h)最小曲率插值结果. Fig. 2 Test data and the up envelope surface of various interpolation method |
对比上图中的各个结果可以看出:移动平均插值、三角剖分插值和克里格插值不能建立光滑的包络面;余下的插值算法虽然可以得到光滑的包络面,但是考虑到最小曲率插值法属于不精确插值,并未遍历全部极值点,因此建立的包络面不能将原始数据完全包络;而反距离插值法和拟合效果较差,会造成较大的计算误差;样条插值能取得较好的结果,但在细节部分径向基函数的精度更高.因此本文最终选用径向基函数插值法来作为BEMD的改进插值算法.
径向基函数的插值公式为
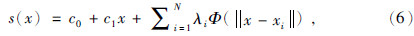
求解N+3元一次的线性方程组,可以得到径向基函数的组合系数λ1和系数c0、c2,进而可以通过代入各点的坐标值求得整个插值曲面.
3 算法实验3.1 对周期信号的分解结果为了测试改进后的BEMD算法的分解效果,我们使用改进的BEMD算法对一个由三个频率成分合成的周期信号(图 3a)进行分解,分解时选取的停止准则为ε=0.3.该周期信号的数学表达式如下,生成图 3a所示数据时网格为100×100,公式为
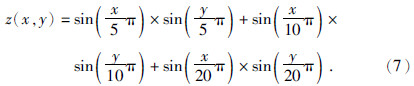
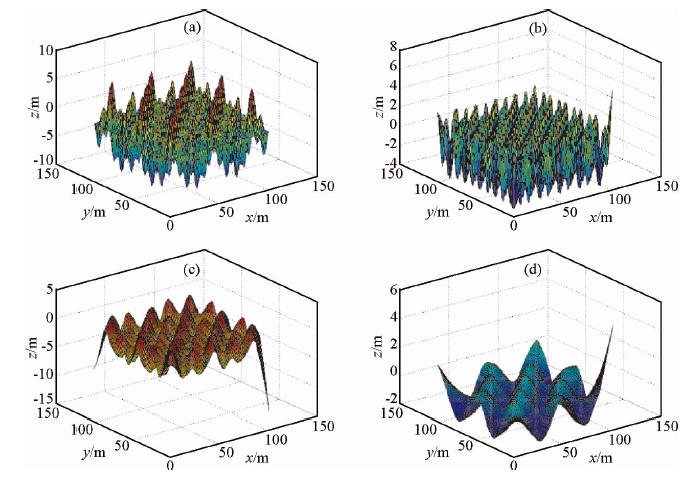 |
图 3 合成信号及三次样条BEMD算法分解结果对其分解结果 (a)合成信号;(b)IMF1;(c)IMF2;(d)RES. Fig. 3 Synthetic signal and the decomposition results of BEMD using cubic spline |
首先使用了三次样条作为插值算法的BEMD对该合成信号进行分解,共得到了2个IMF以及一个余量,如图 3b-d所示.
图 4是经过改进之后的BEMD的分解结果,通过对比改进后的分解结果与原算法的结果,可以发现,经过对算法的改进,很好的抑制了分解过程中的端点飞翼现象,基本消除了分解过程中边缘效应对分解结果的影响,比较成功的分离出了合成信号的3个组分.
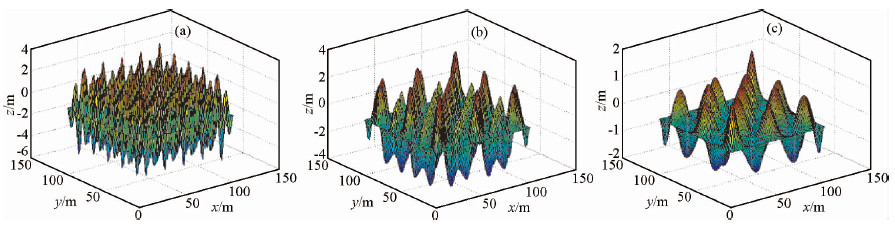 |
图 4 改进的BEMD算法分解结果 (a)IMF1;(b)IMF2;(c)RES. Fig. 4 Synthetic signal and the decomposition results of BEMD |
BEMD算法中的筛分停止准则实质上是判断分解结果是否为固有模态函数的依据,选择不同大小的筛分停止准则,分解得到的固有模态函数的频率成分与振幅也会不同.本文选取了0.5、0.3、0.1、0.01作为停止准则ε的值并分别进行了实验,实验用数据为上文的合成周期信号.得到的结果如图 5所示.为了更清晰的对比各分解结果,我们提取了不同停止准则下IMF2在Y=49(m)的二维剖面情况,如图 6所示.
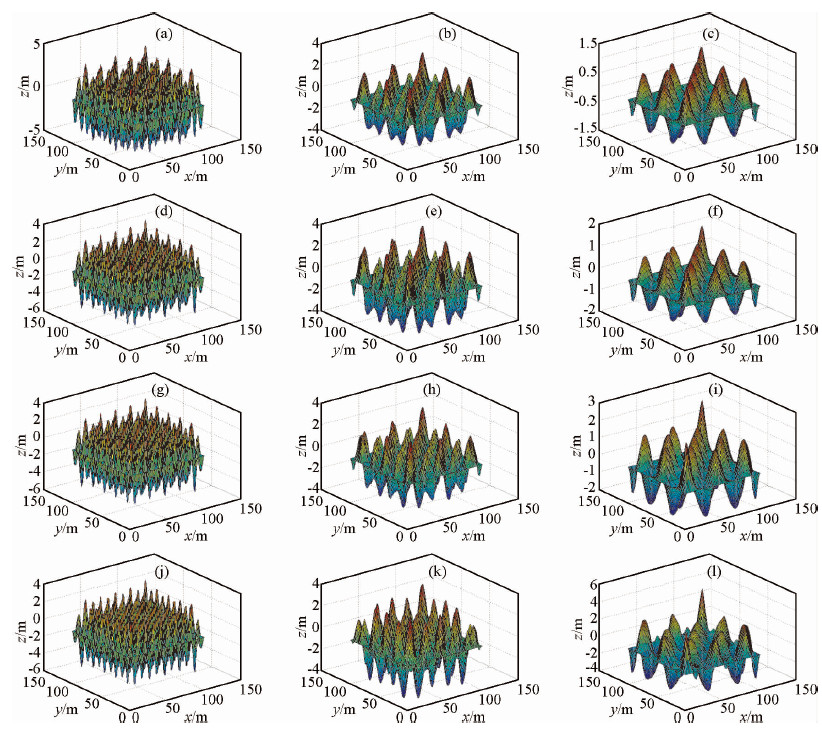 |
图 5 不同停止准则下分解周期信号结果 (a)IMF1;(b)IMF2;(c)RES;(d) IMF1;(e) IMF2;(f) RES; (g) IMF1;(h) IMF2;(i) RES;(j) IMF1;(k) IMF2;(l) RES. Fig. 5 Decomposition results of periodic signal with different stopping criteria |
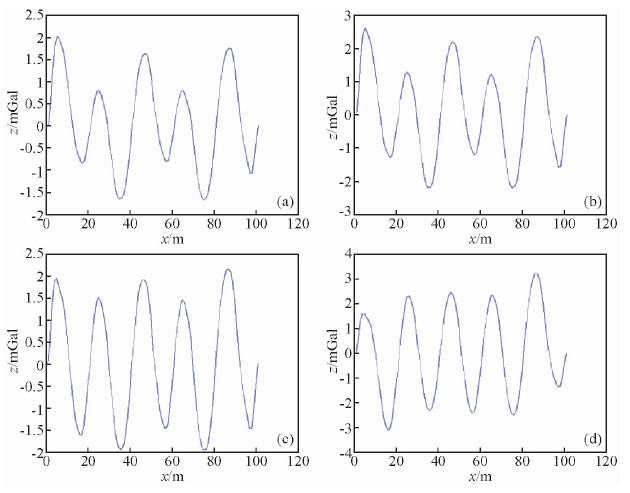 | 图 6 不同停止准则下IMF2在Y=49(m)的二维剖面 Fig. 6 Decomposition results IMF2 of periodic signal with different stopping criteria along profile Y=49(m) |
对比图 5中停止准则为0.5、0.3、0.1三种情况下分解得到的IMF2并结合图 6的剖面情况可以看出,随着ε值逐渐变小,分解出的同一个IMF中的频率成分逐渐变得单一而且低频成分逐渐减小;对比停止准则为0.5、0.3、0.1三种情况下分解得到的IMF3,可以知道IMF2中减少的低频组分主要进入了后一个IMF.但是如果ε值过小,则会造成多次拟合(ε=0.01时,分解一个IMF需要进行9次包络面拟合),过多次数的拟合会使原本并不突出的边缘效应变得严重,同时会极大的拖慢算法运行效率.综上,在使用BEMD算法时,针对研究对象,选取合理的停止准则,才能得到更好的分解结果.
4 算法应用4.1 理论模型分解结果实验使用的理论地质模型由三个深度不同的地质体组成,如图 7所示.地质体1为边长为400 km,埋深为35~55 km的正方形板状体,剩余密度为10 kg/m3;地质体2为边长为100 km,埋深为15~25 km的正方形板状体,剩余密度为5 kg/m3;地质体3为边长为100 km,埋深为10~20 km的正方形板状体,剩余密度为5 kg/m3.该模型正演获得的重力异常如8a所示.
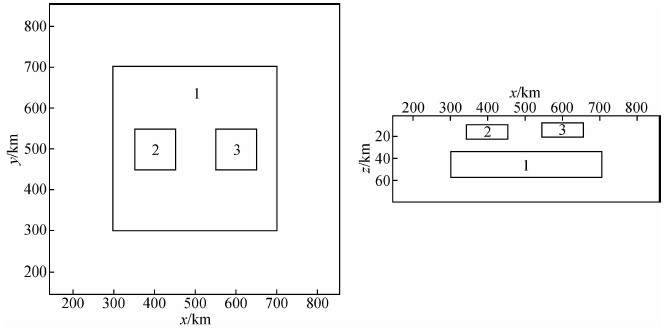 | 图 7 三维空间地质模型示意图 Fig. 7 Schematic diagram of geologic model in three-dimensional space |
用改进后的BEMD算法对该模型的重力异常进行分解,选取的停止准则为ε=0.3共分解得到三个IMF和一个余量RES(图 8b-e).
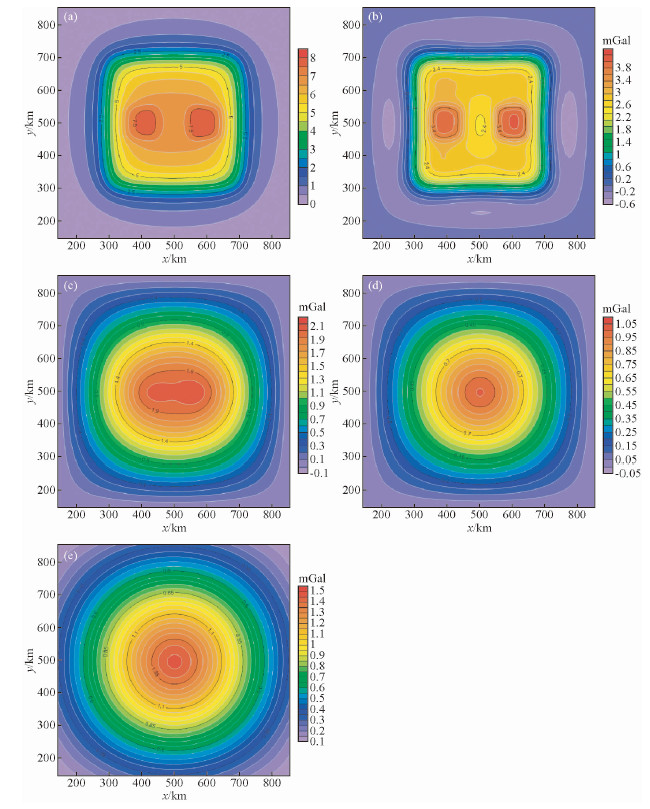 |
图 8 模型重力异常及BEMD多尺度分解 (a)模型重力异常;(b)IMF1;(c)IMF2;(d)IMF3;(e)RES. Fig. 8 Gravity anomaly of geologic model and multi-scale decomposition results with BEMD |
从图 8所示的分解结果来看IMF1主要凸显了近地表的两个异常体,IMF2仍旧反映地壳上部异常,但是与IMF1相比包含了更多的深部信息,而且反映出近地表地质中,地质体3的埋深更浅,IMF3、RES则不包含浅层信息,主要反映了moho面深度的板状异常.也就是说,使用BEMD算法对重力异常进行分解至三个IMF即可分离出深部异常.
4.2 实测数据分解结果本文选取长江中下游集矿区的实测数据来检验BEMD分解的有效性.长江中下游地区是我国东部成矿带,该地区矿种丰富、主要矿产的种类繁多、形成矿床的规模巨大、集中成群分布,占全国总量较重份额,素有“工业走廊”之称.长江中下游地质构造复杂,并经历了长期演化,区域构造具有多层次的构造网络的特点(董树文等,2010),主要断裂有郯庐断裂、江南断裂等(马杏垣,1989)(图 9).
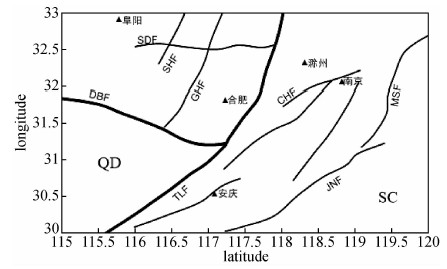 |
图 9 长江中下游地区基本构造格局(据马杏垣,1989) TLF—郯庐断裂;DBF—大别山北侧断裂;SDF—寿县-定远断裂;SHF—寿县-霍邱断裂;GHF—固镇-怀远断裂;CHF—滁河断裂;MSF—茅山断裂;JNF—江南断裂;QD—秦岭-大别地体;SC—华南地体. Fig. 9 Regional structure patterns of the middle and lower reaches of Yangtze river |
本文对长江中下游地区的卫星重力数据(郭良辉等,2012)(图 10a)进行了BEMD分解,试验后选取的停止准则为ε=0.5.共分解得到3个IMF以及一个RES(图 10b-e).
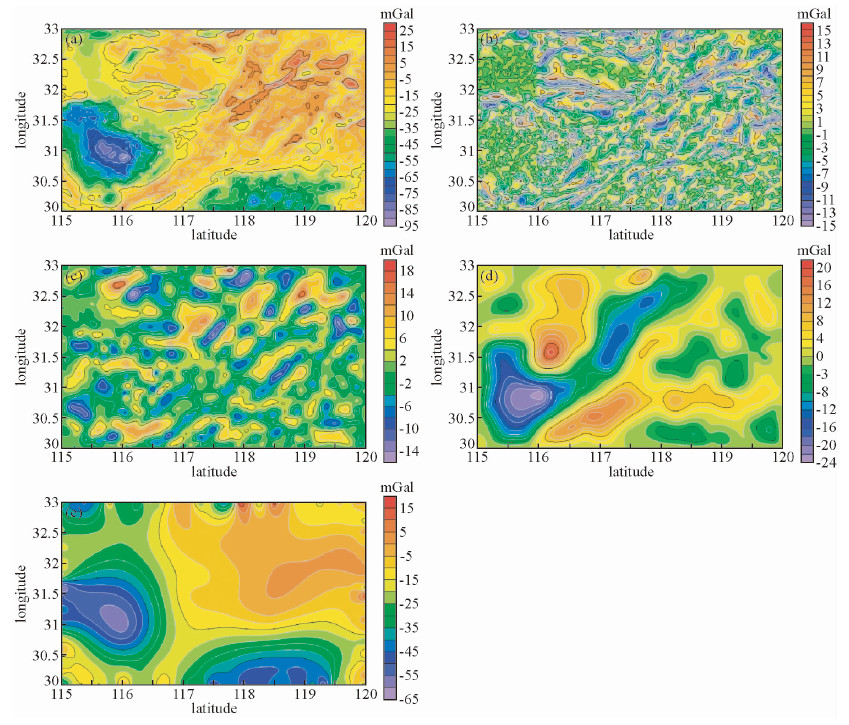 |
图 10 长江中下游地区布格重力异常及BEMD多尺度分解 (a)长江中下游地区卫星重力数据布格重力异常;(b)长江中下游地区IMF1;(c)长江中下游地区IMF2;(d)长江中下游地区IMF3;(e)长江中下游地区RES. Fig. 10 Bouguer gravity anomaly of the middle and lower reaches of Yangtze river and multi-scale decomposition results with BEMD |
BEMD的分解结果按照其分解出的顺序频率逐渐降低,因此先分解出的IMF可能是近地表的局部异常,而后分解出的IMF则是深部的区域异常.对长江中下游重力异常的BEMD分解结果进行分析后,本文认为IMF2、IMF3更可能反应长江中下游构造情况,所以,我们将IMF2、IMF3的结果相加重构,并将长江中下游的地质构造简图等比例的绘制在相加重构的结果图中,如图 11所示.几条大型断裂都与图中的重力梯度带比较契合,而且次级断裂也可以在图中反应出来,可以看出BEMD的分解结果在一定程度上反应了该地区的地质构造情况.
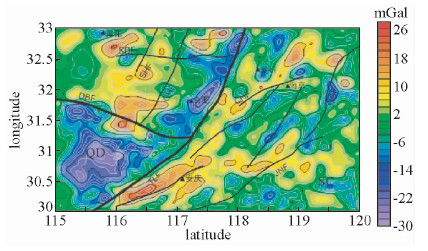 |
图 11 重构异常的构造解释 缩写含义与图 9相同 Fig. 11 The structural interpretation of reconstructed anomaly |
为了了解BEMD分解所得的IMF是否在统计意义上等效于分解来自不同深度场源的异常,我们求取了长江中下游重力异常各IMF分量的平均功率谱,在本文中平均功率谱指几个不同方向功率谱密度函数的平均.根据位场频谱理论,对数功率谱斜率与对应的场源深度成正比(杨文采等,1979),因此可以通过求得的平均功率谱的斜率来确定每个IMF的对应场源深度,使BEMD的分解结果有确定的物理含义.
图 12为长江中下游重力异常经BEMD分解的各个IMF对应的平均对数功率谱,可以看出,每个IMF的对应功率谱都有比较清晰的直线段,而且相较于低阶IMF,高阶IMF的直线斜率明显增加,这反映了IMF对应的场源深度在增加,其中IMF4平均功率谱的直线斜率最陡,表明IMF4反映了深度最大的重力场.
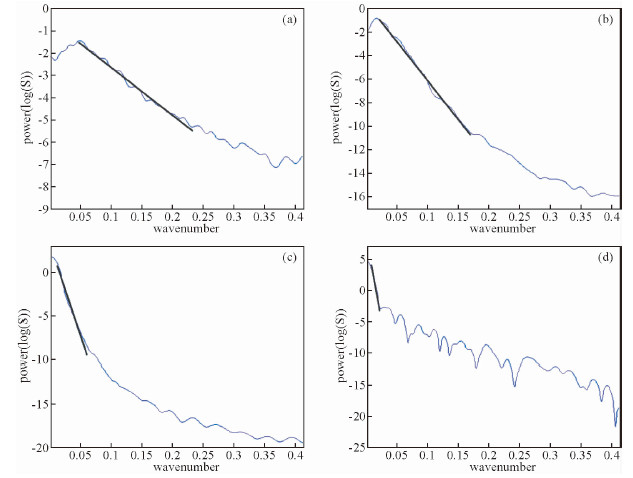 |
图 12 长江中下游地区IMF的平均对数功率谱 (a)IMF1;(b)IMF2;(c)IMF3;(d)RES.横坐标为波数,单位0.001428 km-1. Fig. 12 The IMFs’ average logarithmic power spectrum of the middle and lower reaches of Yangtze river |
据位场波数域理论(杨文采等,1979),可以通过功率谱中的直线段的斜率来求取IMF场源近似埋深.计算的结果是,IMF1的场源平均埋深为1.99 km,IMF2的场源平均埋深7.96 km,IMF3对应场源平均埋深为17.5 km,RES对应场源平均埋深27.86 km.由此可见,IMF1主要反映长江中下游近地表的密度异常;IMF2、IMF3反映上地壳的密度异常;RES可能反映莫霍面起伏引起的重力异常.
4.4 航磁数据去噪结果本文使用闽西南的原始航磁资料为例演示BEMD的去噪功能.如5-7a所见,原始的航磁数据包含很多由飞机飞行时颠簸或者工业电干扰而出现的高频噪声.
本文根据BEMD分解的滤波特性构造了如下低通滤波器:对于BEMD分解得到的若干个故有模量,去掉前面较高频率的IMF1后,由剩余的后几个固有模量重构原信号.
图 13b-f为原始数据经BEMD分解得到的IMF,选取的停止准则为0.7,图 14为去掉IMF1后其他所有IMF重构后的数据.观察图 14以及图 13a可以看到,BEMD去噪能够很好的去除了大部分高频噪声,且不会对原有地质信息造成过大影响.
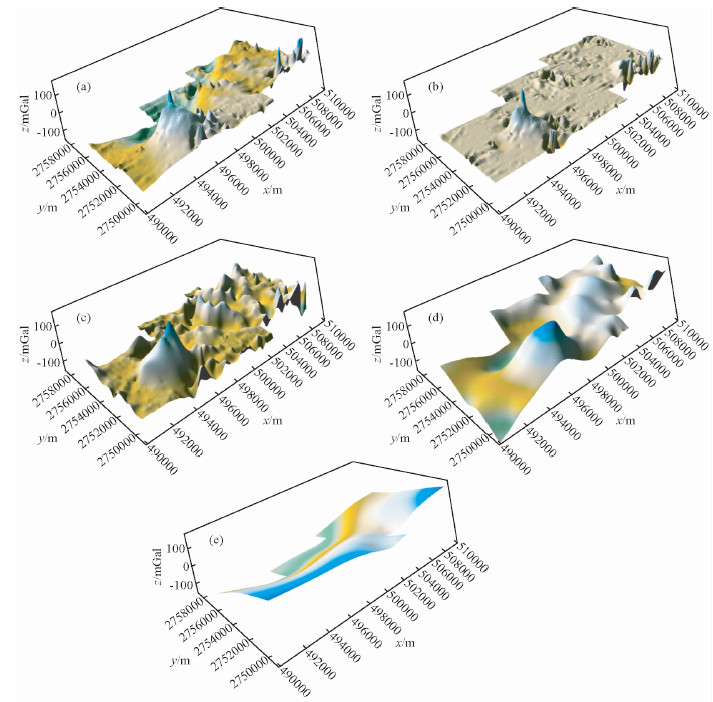 |
图 13 闽西南地区航磁数据及BEMD多尺度分解结果 (a)闽西南地区航磁数据;(b)固有模量1;(c)固有模量2;(d)固有模量3;(e)余量. Fig. 13 Aeromagnetics data of southwest Fujian and multi-scale decomposition results with BEMD |
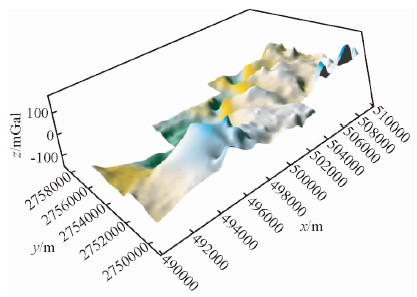 | 图 14 经BEMD去噪后航磁数据 Fig. 14 Aeromagnetics data after denoising using BEMD |
本文探究了如何对BEMD算法进行改进,并将改进后的BEMD应用于重磁异常数据处理,证实了BEMD对物探数据进行处理的有效性.本文研究得到如下结论:
(1)在进行包络面插值时,将全部边缘数据点同时视为极大值点和极小值点,可以有效抑制边缘效应.
(2)径向基函数相比其他插值算法更适合BEMD,有很好的包络面插值效果.
(3)BEMD算法可以有效地分解出不同深度的重力异常,而且其分解过程完全基于数据驱动,没有信息丢失.
(4)可以利用BEMD构造低通滤波器,能够有效地对原始重磁异常数据进行去噪.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | CHEN Jian-Guo, XIAO Fan, CHANG Tao 2011. Gravity and magnetic anomaly separation based on bidimensional empirical mode decomposition[J]. Earth Science-Journal of China University of Geosciences (in Chinese), 36(2): 327-335, doi: 10.3799/dgkx.2011.034. |
| [2] | DONG Shu-Wen, XIANG Huai-Shun, GAO Rui, et al. 2010. Deep structure and ore formation within Lujiang-Zongyang volcanic ore concentrated area in Middle to Lower Reaches of Yangtze River[J]. Acta Petrologica Sinica (in Chinese), 26(9): 2529-2542, doi: 1000-0569/2010/026(09)-2529-42. |
| [3] | GE Guang-Tao. 2010. Key problems of bidimensional empirical mode decomposition[C].//Proceedings of 2010 International Conference on Remote Sensing (ICRS 2010). Hangzhou: IEEE |
| [4] | GUO Liang-Hui, MENG Xiao-Hong, SHI Lei, et al. 2012. Preferential filtering method and its application to Bouguer gravity anomaly of Chinese continent[J]. Chinese Journal of Geophysics (in Chinese), 55(12): 4078-4088, doi: 10.6038/j.issn.0001-5733.2012.12.020. |
| [5] | Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A, 454(1971): 903-995. |
| [6] | HUANG Da-Ji, ZHAO Jin-Pin, SU Ji-Lan. 2003. Practical implementation of the Hilbert-Huang Transform algorithm[J]. Acta Oceanologica Sinica (in Chinese), 25(1): 1-11, doi: 10.3321/j.issn:0253-4193.2003.01.001. |
| [7] | LIU Hui-Ting, ZHANG Min, CHENG Jia-Xing. 2004. Dealing with the End Issue of EMD Based on Polynomial Fitting Algorithm[J]. Computer Engineering and Applications (in Chinese), 40(16): 84-86, 100, doi: 10.3321/j.issn:1002-8331.2004.16.028. |
| [8] | MA Xing-yuan. Lithospheric Dynamics Atlas of China (in Chinese)[M]. 1989. Beijing: China Cartographic Publishing House. |
| [9] | Nunes J C, Bouaoune Y, Delechelle E, et al. 2003. Image analysis by bidimensional empirical mode decomposition[J]. Image and Vision Computing, 21(12): 1019-1026, doi: 10.1016/S0262-8856(03)00094-5 |
| [10] | PEI Yao, WU Yan-Gang, JIA Da-Cheng. 2012. Gravity anomaly separation based on bidimensional empirical mode decomposition[J]. Research Journal of Applied Sciences, Engineering and Technology, 4(21): 4227-4236 |
| [11] | Pwalowski R S, Hansen R O. 1990. Gravity anomaly separation by Wiener filtering[J]. Geophysics, 1990, 55(5): 539-548, doi: 10.1190/1.1442865 |
| [12] | QIAN Chang-Song, LIU Dai-Zhi, LIU Zhi-Gang, et al. 2010. EMD based on recursive high-pass filter and its application on seismic signal analysis[J]. Chinese Journal of Geophysics (in Chinese), 53(5): 1215-1225, doi: 10.3969/j.issn.0001-5733.2010.05.024. |
| [13] | QIN Xu-Jia, FAN Ying-Lin, ZHENG Qin, et al. 2013. A fast bidimensional empirical mode decomposition algorithm[J]. Journal of Chinese Computer Systems (in Chinese), 34(9): 2182-2187, doi: 10.3969/j.issn1000-1220.2013.09.043. |
| [14] | TANG Jing-Tian, HUA Xi-Rui, CAO Zhe-Min, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics (in Chinese), 51(2): 603-610, doi: 10.3321/j.issn:0001-5733.2008.02.034. |
| [15] | Wu Z H, Huang N E. 2004. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society A-Mathematical, Physical and Engineering Sciences, 460(2046): 1597-1611, doi: 10.1098/rspa.2003.1221 |
| [16] | XU De-Ping, DENG Xing, GUO Ke, et al. 2011. Reservoir detection based on JADE and EMD[J]. Progress in Geophysics (in Chinese), 26(2): 572-578, doi: 10.3969/j.issn.1004-2903.2011 02.023. |
| [17] | YANG Wen-Cai, GUO Ai-Ying, XIE Yu-Qing, et al. 1979. Interpretation of gravity and magnetic anomalies in the frequency domain[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), (1): 1-16. |
| [18] | YANG Wen-Cai, SHI Zhi-Qun, HOU Zun-Ze, et al. 2001. Discrete wavelet transform for multiple decomposition of gravity anomalies[J]. Chinese Journal of Geophysics (in Chinese), 44(4): 534-541, doi: 10.3321/j.issn:0001-5733.2001.04.012. |
| [19] | ZENG Hua-Lin. 2005. Gravity field and gravity exploration (in Chinese)[M]. Beijing: Geological Publishing House. |
| [20] | ZHANG Yan-Duo, WANG Min-Min, LU Tong-Wei. 2013. Decomposition method of improved two-dimensional empirical mode[J]. Journal of Wuhan Institute of Technology (in Chinese), 35(4): 61-65, doi: 10.3969/j.issn.1674-2869.2013.04.014. |
| [21] | ZHOU Wen-Na, ZENG Zhao-Fa, DU Xiao-Juan, et al. 2010. Gravity anomaly separation based on empirical mode decomposition[J]. Global Geology (in Chinese), 29(3): 495-502, doi: 10.3969/j.issn.1004-5589.2010.03.019. |
| [22] | ZENG Qin-Qin, LIU Tian-You. 2011. EMD of gravity and magnetic anomalies and its application for iron deposit exploration in Zhangfushan, Eastern Hubei[J]. Progress in Geophysics (in Chinese), 26(4): 1409-1414, doi: 10.3969/j.issn.1004-2903.2011.04.036. |
| [23] | 陈建国, 肖凡, 常韬. 2011. 基于二维经验模态分解的重磁异常分离[J]. 地球科学-中国地质大学学报, 36(2): 327-335, doi: 10.3799/dgkx.2011.034. |
| [24] | 董树文, 项怀顺, 高锐,等. 2010. 长江中下游庐江-枞阳火山岩矿集区深部结构与成矿作用[J]. 岩石学报, 26(9): 2529-2542, doi: 1000-0569/2010/026(09)-2529-42. |
| [25] | 葛光涛. 2010. 二维经验模态分解的关键问题[C]. // 2010年国际遥感大会. 杭州: IEEE |
| [26] | 郭良辉, 孟小红, 石磊,等. 2012. 优化滤波方法及其在中国大陆布格重力异常数据处理中的应用[J]. 地球物理学报, 55(12): 4078-4088, doi: 10.6038/j.issn.0001-5733.2012.12.020. |
| [27] | 黄大吉, 赵进平, 苏纪兰. 2003. 希尔伯特-黄变换的端点延拓[J]. 海洋学报, 25(1): 1-11, doi: 10.3321/j.issn:0253-4193.2003.01.001. |
| [28] | 刘慧婷, 张旻, 程家兴. 2004. 基于多项式拟合算法的EMD端点问题的处理[J]. 计算机工程与应用, 40(16): 84-86, 100, doi: 10.3321/j.issn:1002-8331.2004.16.028. |
| [29] | 马杏垣. 1989.中国岩石圈动力学地图集[M]. 北京: 中国地图出版社. |
| [30] | 钱昌松, 刘代志, 刘志刚,等. 2010. 基于递归高通滤波的经验模态分解及其在地震信号分析中的应用[J]. 地球物理学报, 53(5): 1215-1225, doi: 10.3969/j.issn.0001-5733.2010.05.024. |
| [31] | 秦绪佳, 范颖琳, 郑琴,等. 2013. 一种快速的二维经验模式分解算法[J]. 小型微型计算机系统, 34(9): 2182-2187, doi: 10.3969/j.issn.1000-1220.2013.09.043. |
| [32] | 汤井田, 化希瑞, 曹哲民,等. 2008. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 51(2): 603-610, doi: 10.3321/j.issn:0001-5733.2008.02.034. |
| [33] | 胥德平, 邓兴, 郭科,等. 2011. 基于特征矩阵联合近似对角化和经验模态分解的储层识别[J]. 地球物理学进展, 26(2): 572-578, doi: 10.3969/j.issn.1004-2903.2011.02.023. |
| [34] | 杨文采, 郭爱缨, 谢玉清,等. 1979. 重磁异常在频率域的解释方法(上)[J]. 物化探电子计算技术, (1): 1-16. |
| [35] | 杨文采, 施志群, 侯遵泽,等. 2001. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 44(4): 534-541, doi: 10.3321/j.issn:0001-5733.2001.04.012. |
| [36] | 曾华霖. 2005. 重力场与重力勘探[M]. 北京: 地质出版社. |
| [37] | 曾琴琴, 刘天佑. 2011. 重、磁异常的经验模态分解及其在鄂东张福山铁矿勘探中的应用[J]. 地球物理学进展, 26(4):1409-1414, doi:10.3969/j.issn.1004-2903.2011.04.036. |
| [38] | 张彦铎,汪敏敏,鲁统伟. 2013. 改进的二维经验模式分解方法[J].武汉工程大学学报, 35(4):61-65, doi:10.3969/j.issn.1674-2869.2013.04.014. |
| [39] | 周文纳, 曾昭发, 杜晓娟,等. 2010. 基于经验模态分解的重力异常分离[J]. 世界地质, 29(3): 495-502, doi: 10.3969/j.issn.1004-5589.2010.03.019. |
 2016, Vol. 31
2016, Vol. 31


