地球物理学进展  2016, Vol. 31 Issue (2): 861-868   PDF    
引用本文
张学涛, 田坤, 黄建平. 2016. 黏弹性介质中瑞雷面波正演模拟及频散特征分析[J]. 地球物理学进展, 31(2): 861-868, doi: 10.6038/pg20160249  
ZHANG Xue-tao, TIAN Kun, HUANG Jian-ping. 2016. Forward modeling and dispersion properties analysis of Rayleigh surface wave in viscoelastic media. Progress in Geophysics , 31(2): 861-868, doi: 10.6038/pg20160249   
黏弹性介质中瑞雷面波正演模拟及频散特征分析
张学涛1, 田坤1 , 黄建平2    
1. 中国石化胜利油田分公司物探研究院, 东营 257022;
2. 中国石油大学(华东)地球科学与技术学院, 青岛 266580
收稿日期: 2015-10-05 修回日期: 2015-11-17.
基金项目: 国家自然科学基金(41274124)和胜利油田物探研究院院级项目(SOKYZC150285)联合资助.
作者简介: 张学涛,男,1982年生,山东乐陵人,主要从事地球物理技术的研究与应用.(E-mail:zhangxuetao397.slyt@sinopec.com)
通讯作者: 田坤,男,1986年生,山东齐河人,主要从事地球物理技术的研究与应用.(E-mail:tiankunwudi@163.com)
摘要: 正演模拟是瑞雷面波研究的一个主要方面,目前对于瑞雷面波的正演研究大多是基于均匀层状弹性介质条件下的瑞雷面波频散曲线方程,这只适用于层状模型,无法模拟全波场,而且不考虑实际介质的黏弹效应.本文采用交错网格高阶有限差分法对黏弹性介质中的瑞雷面波进行了高精度全波场模拟,并对频散特征进行了提取与分析.其中采用属于非线性最优化的Levenberg-Marquarat方法直接计算松弛时间来拟合常Q模型,并将应力镜像法与紧致差分格式相结合来准确实施自由表面条件,在其余边界处以非分裂的多轴卷积完全匹配层为吸收边界.然后利用相移法从地震记录中提取频散剖面并对几种典型模型的面波频散特征进行了对比分析.结果表明黏弹性对面波的频散特性有显著影响,面波勘探中有必要考虑黏弹性因素.
关键词: 黏弹性介质     瑞雷面波     频散特征     有限差分     正演模拟    
Forward modeling and dispersion properties analysis of Rayleigh surface wave in viscoelastic media
ZHANG Xue-tao1, TIAN Kun1 , HUANG Jian-ping2    
1. Geophysical Research Institute, Shengli oilfield Company, SINOPEC, Dongying 257022, China;
2. School of Geoscience of China University of Petroleum (huadong), Qingdao 266580, China
Abstract: Forward modeling plays an important role in research of Rayleigh wave. At present most forward modeling of Rayleigh wave is based on the dispersion equation which is derived from homogeneouslayered elastic media. So this is just suitable for lamellar model, and can not simulate full wavefield. In addition, the viscoelastic effects in real media are not considered in this case. This paper models high-accuracy full wavefield which includes Rayleigh wave in viscoelastic media with planar free surface by using the staggered-grid finite-difference method and extract and analyse the dispersion properties. In the simulation process the Levenberg-Marquarat algorithm which is belonged to nonlinear optimization method is adopted to directly compute the relaxation time to fitting the constant Q model.The stress imaging method and compact finite difference scheme are combined to implement the free surface conditions exactly. And for other boundaries the unsplit multi-axial convolutional perfectly matched layer is chosen to absorb waves. Then the dispersion profile is extracted from seismic record using phase shift method. And surface wave dispersion properties of several typical model are compared and analyzed.The results indicate that viscoelasticity can influence the surface wave dispersion markedly. So the viscoelastic factors should be considered in the surface wave exploration.
Key words: viscoelastic media     Rayleigh surface wave     dispersion properties     finite difference     forward modeling    
0 引 言

瑞雷面波勘探是近二十年来发展比较迅速的一种工程地球物理勘探方法，其主要思想是利用面波的频散特性反演浅层地质结构(林志平等，2015; 夏江海等，2015).正演的主要目的是从理论上认识瑞雷面波频散特征与介质特性的关系，奠定瑞雷面波勘探的基础.目前研究瑞雷面波频散特征的主要方法是基于瑞雷面波频散方程的解析方法，常被用来分析水平层状介质中瑞雷面波的理论频散特征.但是此法对实际介质中存在的其他类型的波不予考虑，在资料处理中无法体现其他波对结果的影响，而且不适用于地下异常体和横向速度变化等复杂模型(Haskell，1953; Park et al.，1998，1999; 凡友华等，2007; Luo et al.，2008; 潘冬明等，2010).有限差分法可以用来研究复杂情况下瑞雷面波的传播(张伟，2006； Xu et al.，2007; 周竹生等，2007; 张煜等，2015)，但是很多这方面的研究仅仅模拟了面波的传播现象，对于面波的频散特征没有进一步考虑.另外这些方法都没有考虑实际介质的黏弹效应.

实际地球介质更接近黏弹性介质，地震波在其中传播会发生频散和衰减.对于黏弹性介质中的波场正演，一些学者进行了比较多的研究，比如2004年Saenger和Bohlen(2004)研究了模拟黏弹性介质中波传播的旋转交错网格有限差分法；2002年Xia(Xia et al.，2002)等对层状介质中纵横波的Q值对面波衰减系数的影响进行了研究；2009年杨仁虎等(2009)提出了一种非均匀各向同性介质的黏弹性波简化方程并进行了数值模拟；赵海波等(2011)于2011年对标准线性体进行了高阶交错网格有限差分的VSP模拟；2012年严红勇等(2012)进行了黏弹TTI介质的旋转交错网格高阶有限差分数值模拟.但是这些研究都没有考虑瑞雷面波的传播特性.另外，有研究表明地下岩石的品质因子Q在地震频段内(5~100 Hz)基本不随频率变化，目前通常采用的黏弹模型在描述介质品质因子对频率的依赖关系方面存在不足.

获取高精度的瑞雷面波正演记录，是进一步研究面波频散特征的重要前提.本文基于广义标准线性固体，采用属于非线性最优化的Levenberg-Marquarat(L-M)方法求取松弛时间来拟合近似常Q模型；采用应力镜像法结合紧致差分格式来准确实施自由表面条件；在其余边界处将具有较好吸收效果的卷积完全匹配层(C-PML)和具有较高稳定性的多轴完全匹配层(M-PML)结合组成非分裂的多轴卷积完全匹配层(MC-PML)来吸收边界处的波场；然后使用相移法从地震记录中提取频散剖面并进行对比分析.从模拟记录提取的频散特征与理论频散特征进行比较，验证了本文正演模拟的精度和频散特征提取的有效性；弹性与黏弹性的比较说明了黏弹性对瑞雷面波频散特性的影响.

1 基本原理 1.1 黏弹性介质中的波动方程

根据波尔兹曼叠加原理，线性黏弹性介质的应力应变是卷积关系，可以表示为(Carcione et al.，1988)

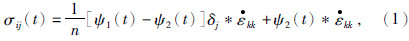
其中σ为应力，ε为应变，下标i，j取1，…，n，n表示空间维数，下标重复表示相加，t是时间，ψ1(t)和ψ2(t)是松弛函数，δij是单位冲激函数.

松弛函数求时间导数，然后进行傅里叶变换则得到频率域的复黏弹模量.对于广义标准线性固体来说，其松弛函数和复黏弹模量分别为

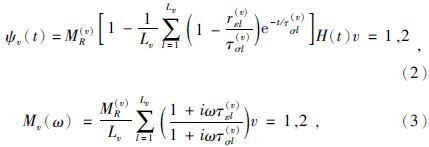
其中v取1或2分别对应胀缩或剪切运动，MR(v)是松弛模量，Lv是标准线性固体的个数，H(t)是单位阶跃函数，τεl(v)和τσl(v)是松弛时间，Mv(ω)是复黏弹模量.式(2)和(3)与大部分文献中的公式不相同，这是由于Liu等(1976)提出将单个标准线性体并联得到广义标准线性固体的时候公式中有一个小错误(Liu et al.，1976)，后来大部分文献在引用的时候仍然重复了这个错误，即使Moczo和Kristek(2005)提出正确的公式以后也没有改正.

对于运动平衡微分方程，黏弹性与弹性介质中的相同，再结合本构关系，并引入记忆变量消除卷积，可以得到基于广义标准线性固体的黏弹性介质的一阶速度-应力波动方程为(郭振波等，2014)：

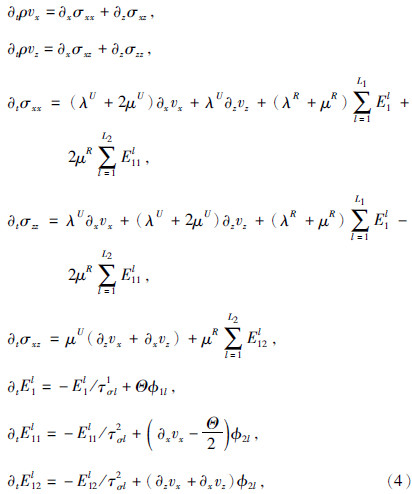
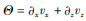其中表征胀缩场，λR和μR是松弛拉梅系数，λU=(λR+μR)MU1-μRMU2和μU=μRMU2是未松弛拉梅系数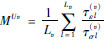，，v=1，2是t=0时刻松弛函数与松弛模量的比值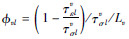，是t=0时刻的松弛函数时间导数的分量与松弛模量的比值，L1个记忆变量E1l对应于描述黏弹胀缩波的L1个标准线性体，L2个记忆变量E11l、E12l对应于描述剪切波的L2个标准线性体.

方程(4)可由有限差分法求解，本文采用时间二阶，空间四阶的高阶交错网格有限差分法进行计算.

1.2 常Q拟合

研究表明，地下岩石的品质因子在地震频带内(5~100 Hz)是近似常数，可以根据这一原则利用最小平方方法计算松弛时间从而实现常Q拟合.黏弹性介质中纵横波的品质因子分别为

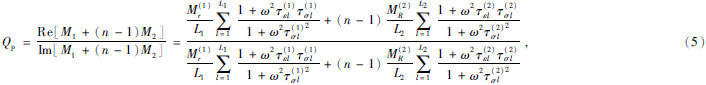
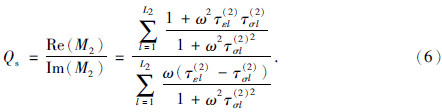
这里综合考虑纵横波，根据给定的常数品质因子，在指定频带内采样，直接由式(5)(6)联合建立方程组，并利用属于非线性最优化的Levenberg-Marquarat(L-M)方法(Tian et al.，2013)求解，从而实现常Q拟合.L-M算法是Gauss-Newton算法的一个变种，可以求解病态问题.方程组表示为

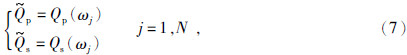
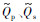其中分别是给定的纵横波品质因子，ωj是指定频带内的采样，N是采样数.

1.3 水平自由地表边界条件

对于在有限差分方法中实施自由表面条件，关键是如何在高阶情况下计算近地表应力和速度的z向导数.应力镜像法已经被证明是准确的，但是速度波场如何处理仍然有待研究.这里采用传统的交错网格高阶有限差分对内部格点进行计算，而对于近地表的应力z向导数采用应力镜像法，对于近地表的速度z向导数采用紧致交错差分格式，这样可以在高阶情况下不用地表以上的速度波场值.

二维黏弹性介质的自由表面条件为(Robertsson，1996)

或者可以等价为速度自由条件为

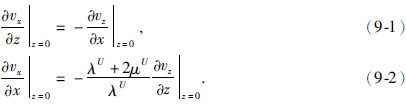
采用传统的交错网格分布系统，将自由地表放在vx和正应力所在的水平线上，因为关键是如何计算速度和应力的z向导数，所以只关注z向的分布.以四阶为例说明如何计算.对于应力可以使用应力镜像，公式为

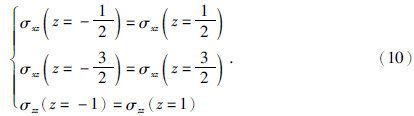
这样可以用传统交错差分格式计算出所需的应力z向导数，从而更新速度波场值.对于速度z向导数的计算可以采用紧致交错差分格式，紧致格式的一般形式为

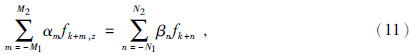
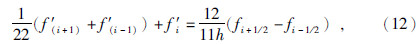
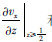其中αm和βm是差分系数，可由泰勒展开得到，fk+m，z是待求变量f位于格点k+m的z向导数值，fk+n是f位于格点k+n的函数值.紧致格式是一种空间隐式的差分格式，通过选择合适的形式并联立方程组求解，可以计算速度波场的z向导数而用不到地表以上的格点.这里选择四阶中心形式的交错紧致格式为(Boersma，2005)：

其中h是网格间距.四阶情况下和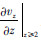属于内部格点的导数，可由传统交错差分法求出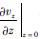，可由式(9-2)求出.若要更新应力所需要用交错紧致格式求的z向导数是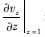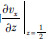，，由式(12)可以列出求解这两个导数的方程为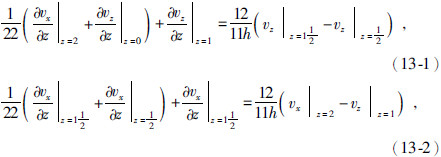

这样所有需要求的速度波场的导数都可以求出，从而更新应力.紧致格式具有精度高，模板宽度小等优点，而且可以不用地表以上的速度波场值，由此可以准确实施自由地表条件.扩展到高阶只需选择合适的高阶交错紧致格式即可，不过阶数越高待求导数值越多，所要求解的方程也就越多.

1.4 多轴卷积完全匹配层吸收边界

为了降低截断边界处引起的不期望数值反射，必须设置吸收边界条件吸收来自截断边界处的反射波.目前最有效的吸收边界条件是完全匹配层(PML)吸收边界条件，但是传统的PML也存在一定的缺陷，因此研究人员发展了改善吸收效果的基于不分裂的卷积完全匹配层(C-PML)和提高稳定性的基于分裂的多轴完全匹配层(M-PML).本文采用将二者结合的多轴卷积完全匹配层(MC-PML)，在保证稳定性的同时保持较好的吸收效果，并采用不分裂的形式，有效降低计算成本(田坤等，2014).

MC-PML就是将M-PML中多个方向同时引入衰减因子的思想借鉴到C-PML的实施过程之中，同时保留C-PML的复频移的坐标变换关系.具体实施过程就是对每一部分匹配层，均在几个正交方向上进行坐标变换，与匹配层垂直的方向为主方向，保留C-PML原来的坐标变换关系，其余方向通过稳定性因子引入的衰减系数进行坐标变换，并采用C-PML中的不分裂递推卷积方法计算变换后的空间偏导数.以二维情况下与x轴垂直的匹配层为例进行说明，在x和z两个方向上都进行空间坐标变换，公式为

对于与x轴垂直的匹配层，x轴方向为主方向，此方向上复拉伸函数为

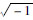其中κx、αx和dx(x) 为衰减系数，ω为角频率，i=，这与C-PML中一致.

z方向上复拉伸函数为

其中，dz(x)=p(z|x)×dx(x)，p(z|x)为常数稳定性因子.

以上是频率域坐标变换关系，在x方向变换回时域并采用以下公式进行变换后的计算(Martin and Komatitsch，2009)：

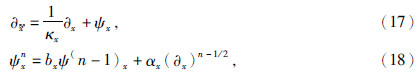
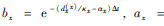
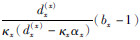其中ψx称为记忆变量，.z方向的变换和计算与式(17)(18)相同，只需令κ=1，α=0，并将dx(x)换为dz(x).

其余区域的匹配层与此类似，同理可得.这样对于每一部分的匹配层，都进行所有正交方向上的变换和计算.角上的情况与传统PML类似，进行简单的叠加处理.也就是说，MC-PML也可看作是对这几种PML的广义扩展，通过调整系数的取值，MC-PML可退化为C-PML或者M-PML或者传统的PML，当然在此处退化后都是不分裂的形式.

1.5 面波频散特征提取

采用以上方法进行计算，可以得到黏弹介质中全波场的记录，其中各种波型混合在一起，不太容易验证得到的记录是否正确，也无法有效分析瑞雷面波的频散特征.由于面波的相速度低于其他体波的相速度，因此可以在频率-相速度剖面上提取面波的频散特征.

目前有多种面波频散特征的提取方法，其中相移法是比较稳健有效的方法之一(秦臻等，2010).对于记录u(x，t)，进行时间傅里叶变换，则

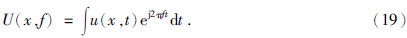
进一步做空间傅里叶变换，则

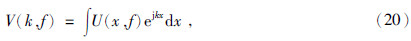
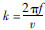其中波数与相速度有关系，则式(20)可表示为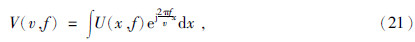

这样可按式(21)直接计算频率-相速度剖面.

2 模型试算与对比2.1 均匀半空间介质模型

模型尺寸为1000 m(宽)×500 m(深)，介质参数为：纵波速度VP=1200 m/s，横波速度VS=693 m/s，密度ρ=2.0 g/cm3，空间网格间距为Δx=Δz=2 m，时间步长为Δt=0.4 ms，震源位于模型左上角，为主频30 Hz的雷克子波.在上述参数条件下对弹性模型和品质因子分别为QP=50，QS=20与QP=21，QS=6的两个黏弹模型进行正演模拟，为方便在下面的论述中将两个黏弹模型称为大Q黏弹模型和小Q黏弹模型.图 1a、b、c分别是弹性模型、大Q黏弹模型和小Q黏弹模型的z分量单炮记录，由图中可以看出三种模型的炮记录都存在直达纵波和面波两个明显的同相轴，而且没有明显的边界反射，也没有不稳定现象发生，说明了本文的匹配层边界条件的有效性，波场也基本得到了正确地模拟.另外在这三个模型中瑞雷面波都没有出现明显的面波频散现象，说明在均匀介质中瑞雷面波不发生面波频散.从图中还可以看出黏弹性会对波场产生衰减和频散的影响.进一步利用相移法提取三个模型的频散剖面，如图 2所示.由图中可以看出，在弹性模型中由于没有面波频散所以频散曲线是一条水平直线，其对应的相速度与理论值638 m/s基本吻合，这也说明了本文正演模拟和频散特征提取的准确性和有效性.而在黏弹模型中，频散曲线有所变化，曲线变宽，分辨率降低，且走向倾斜，这是由于黏弹介质的固有频散造成的，Q越小，黏弹性越强，影响越严重，因此在面波勘探中有必要考虑黏弹性因素.

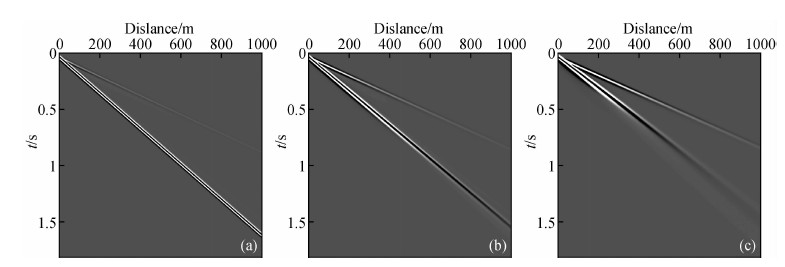图 1 均匀半空间模型的z分量单炮记录
(a)弹性模型；(b)大Q黏弹模型；(c)小Q黏弹模型. Fig. 1 Single-shot seismograms of z component in homogeneous half-space model
(a) Elastic model; (b) Viscoelastic model with larger Q; (c) Viscoelastic model with smaller Q.

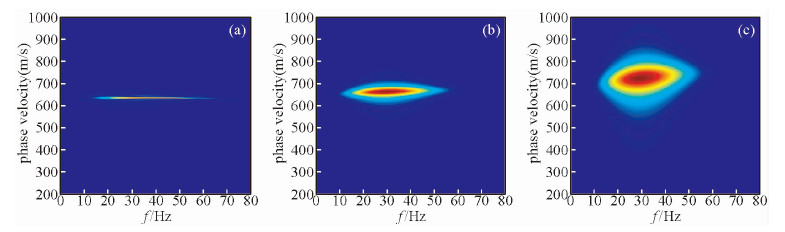图 2 均匀半空间模型的面波频散剖面
(a)弹性模型；(b)大Q黏弹模型；(c)小Q黏弹模型. Fig. 2 Surface wave dispersion profile of homogeneous half-space model
(a) Elastic model; (b) Viscoelastic model with larger Q; (c) Viscoelastic model with smaller Q.
2.2 两层介质模型

模型尺寸为500 m(宽)×100 m(深)，介质参数为：第一层纵波速度VP=800 m/s，横波速度VS=200 m/s，厚度10 m，第二层纵波速度VP=1200 m/s，横波速度VS=400 m/s，密度均匀ρ=2.0 g/cm3，空间网格间距为Δx=Δz=0.5 m，时间步长为Δt=0.1 ms，震源位于模型左上角，为主频30 Hz的雷克子波.在上述参数条件下对弹性模型、大Q黏弹模型和小Q黏弹模型进行正演模拟，大Q黏弹模型的品质因子为第一层QP=40和QS=20，第二层QP=50和QS=30，小Q黏弹模型的品质因子为第一层QP=10和QS=5，第二层QP=20和QS=10.模拟结果如图 3所示，其中(a)(b)(c)分别是弹性模型、大Q黏弹模型和小Q黏弹模型的z分量单炮记录.由图中可以看出，在这三种模型中瑞雷面波都发生了比较明显的面波频散，而且黏弹性会对波场尤其是面波频散产生影响，随着Q的减小，黏弹性的增强，面波的频散会变弱，分辨率降低，细节被模糊，这是由于黏弹介质的固有频散和衰减造成的.但是仅仅从记录上无法分析面波具体的频散特征，更无法验证频散特征是否正确合理，进一步利用相移法提取频散剖面，如图 4所示，其中(a)中的圆点表示弹性模型中面波的理论频散曲线(Hisada，1994).由图中可以看出，弹性模型中的频散剖面比较清晰，面波的频散特征得到了较好地模拟与刻画，而且频散曲线与理论值基本吻合，验证了本文正演模拟和提取的正确性.但是黏弹性会对频散特征造成比较严重的影响，在黏弹模型中基阶模式还比较清楚，而高阶模式就比较模糊，已基本分辨不出，而且总体来说Q越小，曲线越宽，细节越模糊，分辨率越低，这是由于黏弹介质的固有频散和衰减引起的.

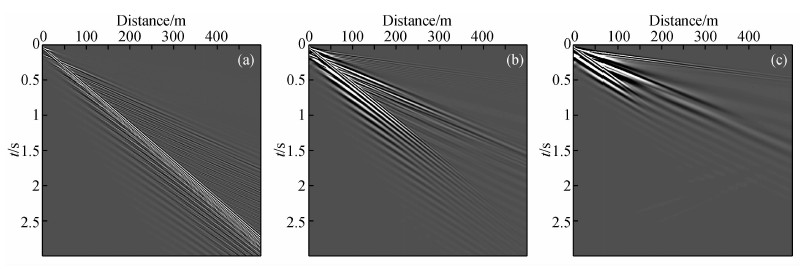图 3 两层介质模型的z分量单炮记录
(a)弹性模型；(b)大Q黏弹模型；(c)小Q黏弹模型. Fig. 3 Single-shot seismograms of z component in two-layer model
(a) elastic model; (b) viscoelastic model with larger Q; (c) viscoelastic model with smaller Q.

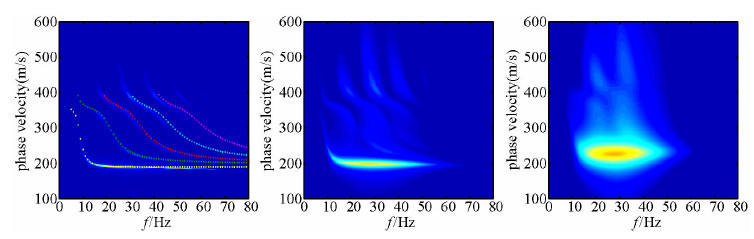图 4 两层介质模型的面波频散剖面
(a)弹性模型；(b)大Q黏弹模型；(c)小Q黏弹模型. Fig. 4 Surface wave dispersion profile of two-layer model
(a) Elastic model; (b) Viscoelastic model with larger Q; (c) Viscoelastic model with smaller Q.
2.3 三层软弱夹层介质模型

软弱夹层模型是面波勘探中的典型模型，模型尺寸为200 m(宽)×80 m(深)，介质参数为：第一层纵波速度VP=450 m/s，横波速度VS=150 m/s，密度ρ=1.9 g/cm3，厚度3 m，第二层纵波速度VP=300 m/s，横波速度VS=100 m/s，密度ρ=1.8 g/cm3，厚度2 m，第三层纵波速度VP=700 m/s，横波速度VS=225 m/s，密度ρ=2.0 g/cm3，空间网格间距为Δx=Δz=0.2 m，时间步长为Δt=0.1 ms，震源位于模型左上角，为主频30 Hz的雷克子波.在上述参数条件下对弹性模型、大Q黏弹模型和小Q黏弹模型进行正演模拟，大Q黏弹模型的品质因子为第一层QP=50和QS=30，第二层QP=40和QS=20，第三层QP=60和QS=40，小Q黏弹模型的品质因子为第一层QP=15和QS=8，第二层QP=10和QS=5，第三层QP=20和QS=12.模拟结果如图 5所示，其中(a)(b)(c)分别是弹性模型、大Q黏弹模型和小Q黏弹模型的z分量单炮记录.由图中也可以看出瑞雷面波发生了明显的面波频散，而黏弹性会对波场尤其是面波频散产生影响.进一步提取频散剖面，如图 6所示，其中(a)中的圆点表示弹性模型中的理论频散曲线.由图中可以看出，在弹性模型中频散特征可以较好地分辨，与理论曲线也基本吻合，但是在黏弹模型中频散特征受到比较严重的影响，尤其是高阶模式已经比较模糊甚至消失，基阶相对比较清楚不过分辨率有所降低且高频区域上翘，同样这是由于黏弹介质的固有频散和衰减造成的，而且Q越小影响越严重.

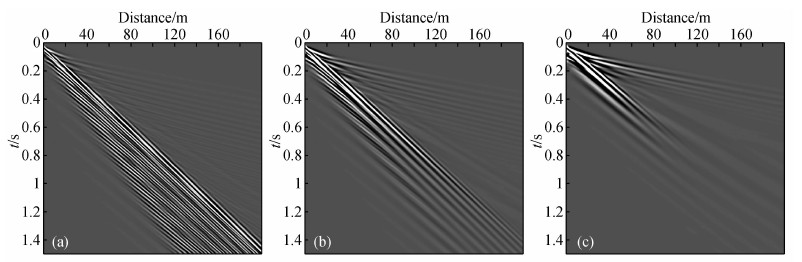图 5 三层软弱夹层介质模型的z分量单炮记录
(a)弹性模型；(b)大Q黏弹模型；(c)小Q黏弹模型. Fig. 5 Single-shot seismograms of z component in floppy interlayer model
(a) elastic model; (b) viscoelastic model with larger Q; (c) viscoelastic model with smaller Q.

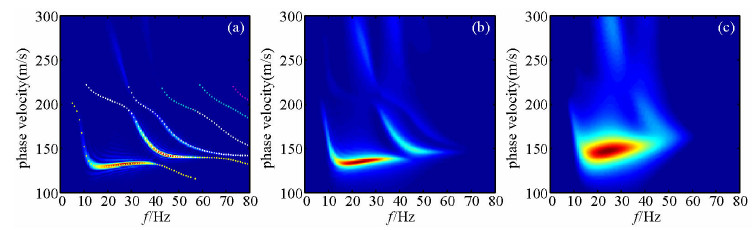图 6 三层软弱夹层介质模型的面波频散剖面
(a)弹性模型；(b)大Q黏弹模型；(c)小Q黏弹模型. Fig. 6 Surface wave dispersion profile of floppy interlayer model
(a) Elastic model; (b) Viscoelastic model with larger Q; (c) Viscoelastic model with smaller Q.
3 结论与讨论

3.1    本文基于广义标准线性固体，采用交错网格高阶有限差分法对水平自由表面的黏弹介质进行正演模拟.其中采用L-M方法直接计算松弛时间来拟合常Q模型，所得结果更精确，并将应力镜像法与紧致差分格式相结合来准确实施自由表面条件，在其余边界处以非分裂的多轴卷积完全匹配层为吸收边界.对几种典型模型进行了正演模拟并提取面波频散剖面，结果表明：(1)与弹性介质中理论频散曲线的对比说明本文方法的准确性与有效性；(2)对于弹性和黏弹性介质，在均匀模型中均观察不到明显的面波频散，而在两层模型和三层软弱夹层模型中瑞雷面波发生明显的面波频散现象；(3)黏弹性会对波场尤其是面波频散产生影响，因此在面波勘探中有必要考虑黏弹性因素.

3.2     本文方法能够准确模拟并提取复杂介质中的面波频散特征，而且能够直观地展示包括体波和面波在内的全波场，为面波勘探提供了有利工具.但是也存在一些问题，比如求取松弛时间时的L-M方法结果依赖初值，需经验获取，不过通过调节可以实现大范围品质因子采用一组初值.实现自由表面条件的紧致差分格式需要选择合适的形式，而且不同的形式需要重新计算系数，由于是空间隐式需要解方程组计算量也会稍微变大.下一步还可以将本文方法推广到更复杂的情况比如研究起伏地表或地下溶洞的影响等以及三维面波的正演模拟与频散特征提取.

致 谢    感谢审稿专家提出的修改意见和编辑部的大力支持！
参考文献
[1] Boersma B J. 2005. A staggered compact finite difference formulation for the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 208(2): 675-690.
[2] Carcione J M, Kosloff D, Kosloff R. 1988. Wave propagation simulation in a linear viscoelastic medium[J]. Geophysical Journal International, 95(3): 597-611.
[3] Fan Y H, Chen X F, Liu X F, et al. 2007. Approximate decomposition of the dispersion equation at high frequencies and the number of multimodes for Rayleigh waves[J]. Chinese Journal of Geophysics (in Chinese), 50(1): 233-239, doi: 10.3321/j.issn:0001-5733.2007.01.029.
[4] Guo Z B, Tian K, Li Z C, et al. 2014. Constructing nearly constant-Q viscoelastic model using the nonlinear optimization method[J]. Journal of China University of Petroleum, 38(2): 52-58.
[5] Haskell N A. 1953. The dispersion of surface waves on multilayered media[J]. Bull. Seism. Soc. Am., 43(1): 17-34.
[6] Hisada Y. 1994. An efficient method for computing Green's functions for a layered half-space with sources and receivers at close depths[J]. Bulletin of the Seismological Society of America, 84(5): 1456-1472.
[7] Lin C P, Lin C H, Wu P L, et al. 2015. Applications and challenges of near surface geophysics in geotechnical engineering[J]. Chinese Journal of Geophysics (in Chinese), 58(8): 2664-2680, doi: 10.6038/cjg20150806.
[8] Liu H P, Anderson D L, Kanamori H. 1976. Velocity dispersion due to anelasticity; implications for seismology and mantle composition[J]. Geophysical Journal International, 47(1): 41-58.
[9] Luo Y H, Xia J H, Miller R D, et al. 2008. Rayleigh-wave dispersive energy imaging using a high-resolution linear radon transform[J]. Pure and Applied Geophysics, 165(5): 903-922.
[10] Martin R, Komatitsch D. 2009. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation[J]. Geophysical Journal International, 179(1): 333-344.
[11] Moczo P, Kristek J. 2005. On the rheological models used for time-domain methods of seismic wave propagation[J]. Geophysical Research Letters, 32(1): L01306.
[12] Pan D M, Hu M S, Cui R F, et al. 2010. Dispersion analysis of Rayleigh surface waves and application based on Radon transform[J]. Chinese Journal of Geophysics (in Chinese), 53(11): 2760-2766, doi: 10.3969/j.issn.0001-5733.2010.11.025.
[13] Park C B, Miller R D, Xia J H. 1998. Imaging dispersion curves of surface waves on multi-channel record[C].//68th SEG Annual International Meeting. Expanded Abstracts,1377-1380.
[14] Park C B, Miller R D, Xia J H. 1999. Multichannel analysis of surface waves[J]. Geophysics, 64(3): 800-808.
[15] Qin Z, Zhang C, Zheng X D, et al. 2010. High precision finite difference Rayleigh wave simulation and frequency dispersion characteristics extraction[J]. Oil Geophysical Prospecting (in Chinese), 45(1): 40-46.
[16] Robertsson J O A. 1996. A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography[J]. Geophysics, 61(6): 1921-1934.
[17] Saenger E H, Bohlen T. 2004. Finite-difference modeling of viscoelastic and anisotropic wave propagationusing the rotated staggered grid[J]. Geophysics, 69(2): 583-591.
[18] Tian K, Huang J P, Li Z C, et al. 2013. Simulation of the planar free surface in the finite-difference modeling of half-space viscoelastic medium[C].//Proceedings of the 75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013. London: SPE.
[19] Tian K, Huang J P, Li Z C, et al. 2014. Multi-axial convolution perfectly matched layer absorption boundary condition[J]. Oil Geophysical Prospecting (in Chinese), 49(1): 143-152.
[20] Xia J H, Gao L L, Pan Y D, et al. 2015. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics (in Chinese), 58(8): 2591-2605, doi: 10.6038/cjg20150801.
[21] Xia J H, Miller R D, Park C B, et al. 2002. Determining Q of near-surface materials from Rayleigh waves[J]. Journal of Applied Geophysics, 51(2-4): 121-129.
[22] Xu Y X, Xia J H, Miller R D. 2007. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach[J]. Geophysics, 72(5): SM147-SM153.
[23] Yan H Y, Liu Y. 2012. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1354-1365, doi: 10.6038/j.issn.0001-5733.2012.04.031.
[24] Yang R H, Chang X, Liu Y K. 2009. Viscoelastic wave modeling in heterogeneous and isotropic media[J]. Chinese Journal of Geophysics (in Chinese), 52(9): 2321-2327, doi: 10.3969/j.issn.0001-5733.2009.09.016.
[25] Zhang W. 2006. Finite difference seismic wave modelling in 3D heterogeneous media with surface topography and its implementation in strong ground motion study (in Chinese)[Ph. D. thesis]. Beijing: Peking University.
[26] Zhang Y, Xu Y X, Xia J H, et al. 2015. Characteristics and application of surface wave propagation in fluid-filled porous media[J]. Chinese Journal of Geophysics (in Chinese), 58(8): 2759-2778, doi: 10.6038/cjg20150812.
[27] Zhao H B, Chen B J, Li K Z, et al. 2011. VSP record numerical modeling in viscoelastic media and its application in the study of Q-value estimation method[J]. Chinese Journal of Geophysics (in Chinese), 54(2): 329-335, doi: 10.3969/j.issn.0001-5733.2011.02.008.
[28] Zhou Z S, Liu X L, Xiong X Y. 2007. Finite-difference modelling of Rayleigh surface wave in elastic media[J]. Chinese Journal of Geophysics (in Chinese), 50(2): 567-573, doi: 10.3321/j.issn:0001-5733.2007.02.030.
[29] 凡友华, 陈晓非, 刘雪峰,等. 2007. Rayleigh波的频散方程高频近似分解和多模式激发数目[J]. 地球物理学报, 50(1): 233-239, doi: 10.3321/j.issn:0001-5733.2007.01.029.
[30] 郭振波, 田坤, 李振春,等. 2014. 利用非线性最优化方法构建近似常Q黏弹模型[J]. 中国石油大学学报(自然科学版), 38(2): 52-58.
[31] 林志平, 林俊宏, 吴柏林,等. 2015. 浅地表地球物理技术在岩土工程中的应用与挑战[J]. 地球物理学报, 58(8): 2664-2680, doi: 10.6038/cjg20150806.
[32] 潘冬明, 胡明顺, 崔若飞,等. 2010. 基于拉东变换的瑞雷面波频散分析与应用[J]. 地球物理学报, 53(11): 2760-2766, doi: 10.3969/j.issn.0001-5733.2010.11.025.
[33] 秦臻, 张才, 郑晓东,等. 2010. 高精度有限差分瑞雷面波模拟及频散特征提取[J]. 石油地球物理勘探, 45(1): 40-46.
[34] 田坤, 黄建平, 李振春,等. 2014. 多轴卷积完全匹配层吸收边界条件[J]. 石油地球物理勘探, 49(1): 143-152.
[35] 夏江海, 高玲利, 潘雨迪,等. 2015. 高频面波方法的若干新进展[J]. 地球物理学报, 58(8): 2591-2605, doi: 10.6038/cjg20150801.
[36] 严红勇, 刘洋. 2012. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 55(4): 1354-1365, doi: 10.6038/j.issn.0001-5733.2012.04.031.
[37] 杨仁虎, 常旭, 刘伊克. 2009. 基于非均匀各向同性介质的黏弹性波正演数值模拟[J]. 地球物理学报, 52(9): 2321-2327, doi: 10.3969/j.issn.0001-5733.2009.09.016.
[38] 张伟. 2006. 含起伏地形的三维非均匀介质中地震波传播的有限差分算法及其在强地面震动模拟中的应用[博士论文]. 北京: 北京大学.
[39] 张煜, 徐义贤, 夏江海,等. 2015. 含流体孔隙介质中面波的传播特性及应用[J]. 地球物理学报, 58(8): 2759-2778, doi: 10.6038/cjg20150812.
[40] 赵海波, 陈百军, 李奎周,等. 2011. 黏弹性介质VSP记录模拟及在估算Q值研究中应用[J]. 地球物理学报, 54(2): 329-335, doi: 10.3969/j.issn.0001-5733.2011.02.008.
[41] 周竹生, 刘喜亮, 熊孝雨. 2007. 弹性介质中瑞雷面波有限差分法正演模拟[J]. 地球物理学报, 50(2): 567-573, doi: 10.3321/j.issn:0001-5733.2007.02.030.