地球物理反演过程是一个将观测数据转换为地质-地球物理模型的过程,其首要解决的问题之一就是尽可能的减少地球物理场的多解性,从而得到一个可靠的地质模型(陈丽虹等,2002;敬荣中等,2003).然而,地球物理方法所采集到的数据集通常受到地表干扰或方法自身缺点的影响,使得反演结果难以全面的认识地下地质概况.直流电阻率法(Direct Current Resistivity,DC)在浅层勘探中具有较高的灵敏度,但是由于装置展布的限制和深部传导电流受到极大的削弱,因此很难获取到深部的有效信息(Max and Bjorn,1975;董浩斌和王传雷,2003;杨振威等,2012).大地电磁法(Magnetotelluric,MT)是一种广泛应用于地球物理勘探中的天然源电磁法,观测频率低,因此获取的浅部数据量少.同时,受到地形起伏和近地表横向电性分布不均匀,易产生静态效应,极易混淆真假异常,增加地质解释的难度(魏文博,2002;黄兆辉等,2006;程少华,2012).由此可见,单一地球物理方法的反演容易造成地下地质解释的模糊性.
在综合地球物理中同时运用多种地球物理数据进行同步、顺序、剥离、伸展等方式计算同一地质体的物性特征和几何展布称为联合反演,联合反演是综合地球物理工作中不可或缺的一种重要的定性和定量解释工具(祝靓谊,2003;陈洁等,2007).结合多种地球物理数据进行联合反演能够有效的减少模型解空间.这主要是由于:
(1)不同地球物理方法获得的解空间不尽相同.利用不同地球物理方法的优势,一种方法中的零空间可以通过联合反演在另一种方法中得到补充(Max and Bjorn,1975).
(2)不同地球物理方法测量的物性参数不尽相同.地下岩矿石包含了多种物理属性,通过在同一区域对不同物性参数的测量,从不同的侧面提高对该区域岩性及其范围的识别.
(3)不同地球物理方法所受的干扰因素不尽相同.某种方法部分受到强干扰的数据可以用另一种方法的数据经行校正,有时比单一方法采集更多数据更为有效(敬荣中等,2003).
自1975年Vozoff和Jupp首次提出进行MT和DC数据联合反演(Vozoff and Jupp,1975)以来,中外学者对联合反演从理论到应用都做了许多研究: Sasaki(1989)、Sharma(Sharma and Kaikkonen,1999; Sharma and Verma,2011)等对大地电磁和直流数据进行了联合反演研究.Zeyen和Pous(1993)进行了带有先验模型的磁法和重力联合反演研究.Hering等(1995)详细论述了DC与浅层地震的联合反演算法.Bosch等(2006)运用蒙特卡洛方法进行了三维重磁的联合反演研究.Moorkamp等(2011)提出了一种适用于地震、MT和重力的三维联合反演框架.国内学者对联合反演也做了许多贡献,于鹏等(2007)利用改进的全局寻优的快速模拟退火算法,实现了重力和地震资料的约束同步联合反演.万玲等(2013)提出地面磁共振MRS与瞬变电磁(TEM)联合反演方法,提高了解释结果的准确度.彭淼等(2013)研究了基于交叉梯度耦合约束的大地电磁与地震走时资料的三维联合反演算法.陈晓等(2010)采用非线性模拟退火方法实现了加入有效模型约束的大地电磁与地震的同步联合反演,使反演的解更实际更稳定.陈华根等(2012)在实际资料处理中应用了MT和重力的模拟退火联合反演并取得了较好的效果.刘彦等(2012)在对国内外大地电磁与地震数据联合反演的研究现状分析的基础上,总结了电震联合反演算法的类型.
回顾联合反演的发展历史,联合反演是综合地球物理定量解释的重要工具,是未来地球物理学的一个发展方向(杨辉等,2002).从总体上来说国内的联合反演主要集中在重磁电磁与地震方法的结合,而更具有合理性的基于相同物性基础的联合反演较为少见(于鹏等,2006).
基于联合反演在解决地球物理多解性中的重要意义,本文对直流电阻率(DC)和大地电磁(MT)进行联合反演,运用Tikhonov正则化思想建立反演目标函数,采用二阶最大平滑稳定因子、改进的“L-curve”法及非线性共轭梯度法实现了不同数据类型的电性二维联合反演.
1 DC与MT联合反演理论 1.1 反演目标函数的建立地球物理场受到场的等效性、观测数据的有限性、数据误差和场外干扰等多种因素影响,因此反演结果存在非稳定、多解的特点.正则化方法是减少多解性,提高反演结果稳定性的有效方法之一.
正则化目标函数(Tikhonov and Arsenin,1977)为
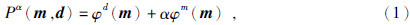
1)数据误差的设计;
2)模型误差的设计;
3)正则化因子的确定;
4)目标函数的最优化求解.
数据误差函数φd(m)指的是观测数据与模型正演数据的距离.为实现联合反演将DC和MT数据加入到同个观测数据集 d obs中,得到
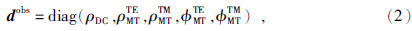
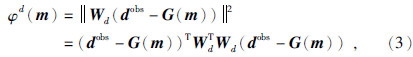
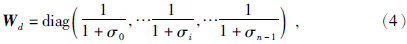
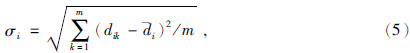
模型误差函数φm(m)也称稳定因子,其主要作用是限制反演模型的解空间,使反演结果更加符合实际地质条件.通常用反演模型与先验模型的差异来表示.稳定因子的种类很多,本文所采用的是具有平滑稳定突出模型主要特征的二阶最大平滑定因子.公式为
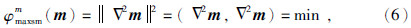
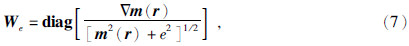
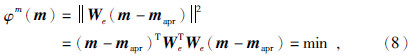
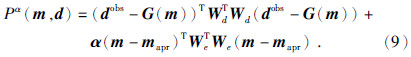
正则化因子α是数据误差φd(m)与模型误差φm(m)的平衡系数.当α取值较小时,反演目标函数更倾向于数据误差φd(m),这样将更加拟合观测数据,模型自由度加大;反之,当α取值较大时,反演目标函数中φm(m)将起主导作用,反演结果将更趋近于先验模型 m apr.因此,合理的选取正则化因子关系到反演的结果可靠性.本文采用基于点到直线距离的改进型“L-curve”法(李曼和林文东,2014),实现正则化因子的自动选取,提高正则化因子的求取效率及精度.
1.2 目标函数的最优化求解当目标函数构建完成之后,所需要解决的问题就是如何快速稳定的实现目标函数的求解.所有反演问题最终也都将转化为目标函数最优化求解问题.随着地球物理反演维数的增加,数据量的增大,如何快速、高效、稳定的获得高精度的反演结果,这将成为地球物理反演的重点和难点.本文在分析了前人多种优化方法的基础上,采用基于Polak和Ridiere改进的非线性共轭梯度法对反演目标函数进行最优化求解.
具体算法实现如下:
(1)设定初始模型 m 0,计算目标函数φ0=φ(m 0)及其梯度 ∇ φ0= ∇ φ(m 0).
(2)令初始搜索方向p0=- ∇ φ0,迭代次数初始化为k=0.
(3)当 ∇ φk≠0时,计算步长αk.同时,令 m k+1= m k+αk p k,计算 ∇ φk+1(m 0)和βk+1PR= ∇ φk+1T(∇ φk+1- ∇ φ)k/ ||∇ φk|| 2.
(4)更新迭代搜索方向 P k+1=- ∇ φk+1+βk+1PR P k,同时,令k=k+1.
(5)重复(1)-(4)过程直到满足φ(m k)≤χ,或达到最大迭代次数时,停止计算,求的最优模型参数.
需要注意的是,对于不精确的步长αk很难保证所得的 p k一定为下降方向.因此,采用以下强制条件进行约束,求得合理的αk.公式为
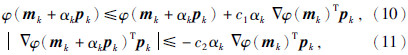
共轭梯度法以两次共轭方向的线性组合进行极小值搜索.只需计算目标函数及其梯度和存储有限的几个向量,不需要进行矩阵的分解等运算,提高了求解稳定性、保证计算高效性,所以它非常适用于大规模数据的反演目标函数的求解.
2 算例分析为验证联合反演算法的可行性,本文进行了两组模型对比分析.
模型1
如图 1所示,在背景电阻率为100 Ω·m的均匀地下半空间中有5个不同电性的目标体,其中,在浅部(25 m处)分布着三个大小相同,电阻率不同的目标体(M1、M2为10 Ω·m,M3为1000 Ω·m,大小均为20 m×10 m);在深部200 m处存在着两个边长为100 m×100 m的高阻和低阻目标体,电阻率分别是M4为1000 Ω·m,M5为10 Ω·m.地表网格间距为6.25 m,直流电测深的最小极距为12.5 m,采用二级装置观测;大地电磁的测量点距为24.5 m,观测频段范围为20~212 Hz.
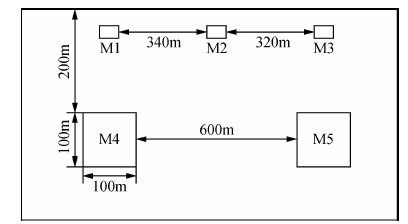 | 图 1 模型1示意图 Fig. 1 Schematic diagram of the model 1 |
由图 2分析得出,当采用DC单独反演时,对5个电性不同的目标体电阻率响应特征区别明显,浅层目标体的分辨率较高,而深部目标体不够收敛,且存在虚假异常.由图 3分析得出,MT对低阻体更加敏感,受到浅部低阻体影响,深部高阻体无法得到有效地识别;当浅部为高阻体时,MT反演对深部低阻体的识别影响较小.从图 4的反演结果可以看出,当采用DC和MT联合反演时,结合各自的特点能有效的约束目标体的范围,浅部异常刻画依然准确,深部异常范围收敛明显,中心位置更接近真实模型.
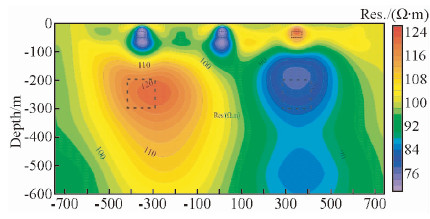 | 图 2 DC电阻率反演剖面图 Fig. 2 The DC resistivity inversion section |
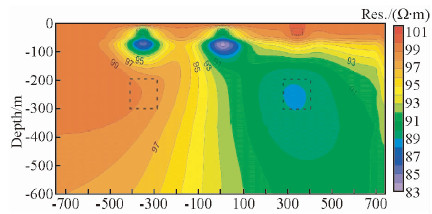 | 图 3 MT电阻率反演剖面图 Fig. 3 The MT resistivity inversion section |
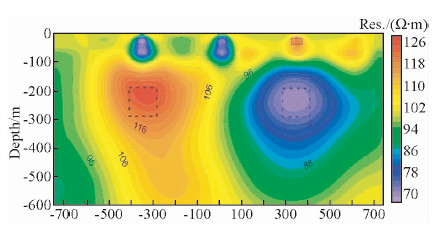 | 图 4 DC和MT联合反演电阻率剖面图 Fig. 4 DC and MT joint inversion of resistivity profile |
模型2
如图 5所示,在与模型1相同的背景条件下存在着6个不同的电性目标体,其中,在浅部25 m处分布着三个大小相同,电阻率不同的目标体(M1、M2为10 Ω·m,M3为1000 Ω·m,大小均为20 m×10 m);中深部150 m处分布着两个电阻率分别是:M4等于1000 Ω·m,M5等于10 Ω·m,大小均为200 m×100 m的高阻和低阻目标体;深部400 m存在着一个电阻率等于1000 Ω·m的M6,大小为400 m×200 m的高阻目标体.地表网格间距及采集参数如模型1.
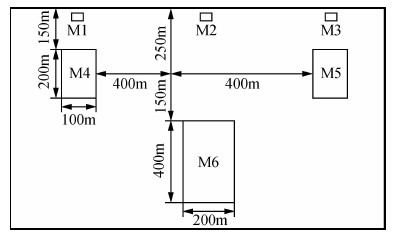 | 图 5 模型2示意图 Fig. 5 Schematic diagram of the model 2 |
从图 6可看出,DC单独反演时,由于反演深度加大,浅层分辨率较高,异常明显,位置准确,深部电性虽有所区分,异常的空间位置无法做出正确反映,只能识别出5各异常位置信息.从图 7可看出,MT单独反演时,对浅部反映不明显.可能受浅层电性不均匀的影响,中部及深部目标体空间展布失真严重,也未能得到有效圈闭,仅能部分反映目标体之间的电性关系,总体效果较差.从图 8的联合反演结果中可以看出,与MT单独反演相比,浅层目标体间电性区分明显,中部高阻异常也得到了部分体现,深部异常范围收敛明显,约束显著.
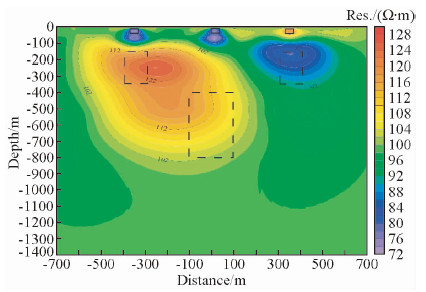 | 图 6 DC电阻率反演剖面图 Fig. 6 The DC resistivity inversion section |
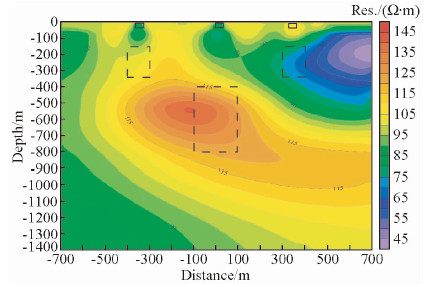 | 图 7 MT电阻率反演剖面图 Fig. 7 The MT resistivity inversion section |
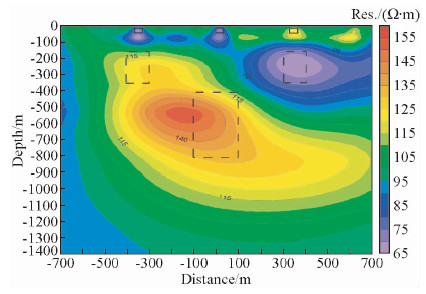 | 图 8 DC和MT联合反演电阻率剖面图 Fig. 8 DC and MT joint inversion of resistivity profile |
本文基于正则化思想实现了直流电阻率法(DC)和大地电磁法(MT)的联合反演.由算法特点及模型试算结果得出以下几点结论:
(1)DC和MT联合反演与单独的MT反演相比,利用DC勘探在浅层具有较高的分辨率,能有效的提高MT反演效果.
(2)非线性共轭梯度法以前后两次共轭方向的线性组合为搜索方向,不仅算法简单,收敛快速,而且避免了高次导数的计算使结果更加稳定.
(3)本研究实现了不同类型地球物理数据的融合,为其他地球物理方法的联合反演提供了参考.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Bosch M, Meza R, JimLénez R, et al. 2006. Joint gravity and magnetic inversion in 3D using Monte Carlo methods[J]. Geophysics, 71(4): G153-G156. |
| [2] | Chen H G, Li J X, Wu J S, et al. 2012. Study on simulated-annealing MT-gravity joint inversion[J]. Chinese Journal of Geophysics (in Chinese), 55(2): 663-670, doi: 10.6038/j.issn.0001-5733.2012.02.030. |
| [3] | Chen J, Wen N, Chen B Y. 2007. Joint inversion of gravity-magnetic- electrical-seismic combination survey: Progress and prospect[J]. Progress in Geophysics (in Chinese), 22(5): 1427-1438, doi: 10.3969/j.issn.1004-2903.2007.05.013. |
| [4] | Chen L H, Sun J G, Wu Y G, et al. 2002. Review of quasi-Linear approximation in geophysical inversion[J]. Progress in Geophysics (in Chinese), 17(3): 464-472, doi: 10.3969/j.issn.1004-2903.2002.03.016. |
| [5] | Chen X, Yu P, Zhang L L, et al. 2010. Regularized synchronous joint inversion of MT and seismic data[J]. Seismology and Geology (in Chinese), 32(3): 402-408. |
| [6] | Cheng S H. 2012. Contrastive analysis of different static shift correction methods in megnetotelluric (MT) (in Chinese) [Ph. D. thesis]. Xi'an: Chang'an University. |
| [7] | Dong H B, Wang C L. 2003. Development and application of 2D resistivity imaging surveys[J]. Earth Science Frontiers (in Chinese), 10(1): 171-176. |
| [8] | Hering A, Misiek R, Gyulai A, et al. 1995. A joint inversion algorithm to process geoelectric and sutface wave seismic data. Part I: Basic ideas[J]. Geophysical Prospecting, 43(2): 135-156. |
| [9] | Huang Z H, Di Q Y, Hou S L. 2006. CSAMT static correction and its application[J]. Progress in Geophysics (in Chinese), 21(4): 1290-1295, doi: 10.3969/j.issn.1004-2903.2006.04.038. |
| [10] | Jing R Z, Bao G S, Chen S Q. 2003. A review of the researches for geophysical combinative inversion[J]. Progress in Geophysics (in Chinese), 18(3): 535-540, doi: 10.3969/j.issn.1004-2903.2003.03.033. |
| [11] | Li M, Lin W D. 2014. The study of regularization inversion for 2.5 dimension DC resistivity based on minimum support stabilizing factor[J]. Journal of East China Institute of Technology (in Chinese), 37(3): 292-298. |
| [12] | Liu Y, Lv Q T, Meng G X, et al. 2012. Joint electromagnetic and seismic inversion survey: status and prospect[J]. Progress in Geophysics (in Chinese), 27(6): 2444-2451, doi: 10.6038/j.issn.1004-2903.2012.06.019. |
| [13] | Moorkamp M, Heincke B, Jegen M, et al. 2011. A framework for 3-D joint inversion of MT, gravity and seismic refraction data[J]. Geophysical Journal International, 184(1): 477-493, doi: 10.1111/j.1365-246X.2010.04856.x. |
| [14] | Peng M, Tan H D, Jiang M, et al. 2013. Three-dimensional joint inversion of magnetotelluric and seismic travel time data with cross-gradient constraints[J]. Chinese Journal of Geophysics (in Chinese), 56(8): 2728-2738, doi: 10.6038/cjg20130821. |
| [15] | Sasaki Y. 1989. Two-dimensional joint inversion of magnetotelluric and dipole-dipole resistivity data[J]. Geophysics, 54(2): 254-262. |
| [16] | Sharma S P, Kaikkonen P. 1999. Appraisal of equivalence and suppression problems in 1D EM and DC measurements using global optimization and joint inversion[J]. Geophysical Prospecting, 47(2): 219-249. |
| [17] | Sharma S P, Verma S K. 2011. Solutions of the inherent problem of the equivalence in direct current resistivity and electromagnetic methods through global optimization and joint inversion by successive refinement of model space[J]. Geophysical Prospecting, 59(4): 760-776, doi: 10.1111/j.1365-2478.2011.00952.x. |
| [18] | Tikhonov A N, Arsenin Y. 1977. Solution of Ill-Posed Problems[M]. Washington: Winston & Sons. |
| [19] | Vozoff K, Jupp D L B. 1975. Joint inversion of geophysical data[J]. Geophysical Journal of the Royal Astronomical Society, 42(3): 977-991. |
| [20] | Wan L, Lin T T, Lin J, et al. 2013. Joint inversion of MRS and TEM data based on adaptive genetic algorithm[J]. Chinese Journal of Geophysics (in Chinese), 56(11): 3728-3740, doi: 10.6038/cjg20131114. |
| [21] | Wei W B. 2002. New advance and prospect of magnetotelluric sounding (MT) in china[J]. Progress in Geophysics (in Chinese), 17(2): 245-254, doi: 10.3969/j.issn.1004-2903.2002.02.009. |
| [22] | Yang H, Dai S K, Song H B, et al. 2002. Overview of joint inversion of integrated geophysics[J]. Progress in Geophysics (in Chinese), 17(2): 262-271, doi: 10.3969/j.issn.1004-2903.2002.02.011. |
| [23] | Yang Z W, Yan J Y, Liu Y, et al. 2012. Research progresses of the high-density resistivity method[J]. Geology and Exploration, (in Chinese), 48(5): 969-978. |
| [24] | Yu P, Wang J L, Wu J S, et al. 2006. Review and discussions on geophysical joint inversion[J]. Progress in Exploration Geophysics (in Chinese), 29(2): 87-93, 134. |
| [25] | Yu P, Wang J L, Wu J S, et al. 2007. Comparative analysis of inversion methods of retrieving atmospheric profiles with GPS occultation measurements[J]. Chinese Journal of Geophysics (in Chinese), 50(2): 529-538, doi: 10.3321/j.issn:0001-5733.2007.02.026. |
| [26] | Zeyen H, Pous J. 1993. 3-D joint inversion of magnetic and gravimetric data with a priori information[J]. Geophysical Journal International, 112(2): 244-256. |
| [27] | Zhu J Y. 2003. Overview of integrated geophysics of oil & gas exploration[J]. Progress in Geophysics (in Chinese), 18(1): 19-23, doi: 10.3969/j.issn.1004-2903.2003.01.003. |
| [28] | 陈华根, 李嘉虓, 吴健生,等. 2012. MT-重力模拟退火联合反演研究[J]. 地球物理学报, 55(2): 663-670, doi: 10.6038/j.issn.0001-5733.2012.02.030. |
| [29] | 陈洁, 温宁, 陈邦彦. 2007. 重磁电震联合反演研究进展与展望[J]. 地球物理学进展, 22(5): 1427-1438, doi: 10.3969/j.issn.1004-2903.2007.05.013. |
| [30] | 陈丽虹, 孙建国, 吴燕冈,等. 2002. 地球物理反演的拟线性近似方法综述[J]. 地球物理学进展, 17(3): 464-472, doi: 10.3969/j.issn.1004-2903.2002.03.016. |
| [31] | 陈晓, 于鹏, 张罗磊,等. 2010. 大地电磁与地震正则化同步联合反演[J]. 地震地质, 32(3): 402-408. |
| [32] | 程少华. 2012. 大地电磁静态效应校正方法对比研究[硕士论文]. 西安: 长安大学. |
| [33] | 董浩斌, 王传雷. 2003. 高密度电法的发展与应用[J]. 地学前缘, 10(1): 171-176. |
| [34] | 黄兆辉, 底青云, 侯胜利. 2006. CSAMT的静态效应校正及应用[J]. 地球物理学进展, 21(4): 1290-1295, doi: 10.3969/j.issn.1004-2903.2006.04.038. |
| [35] | 敬荣中, 鲍光淑, 陈绍裘. 2003. 地球物理联合反演研究综述[J]. 地球物理学进展, 18(3): 535-540, doi: 10.3969/j.issn.1004-2903.2003.03.033. |
| [36] | 李曼, 林文东. 2014. 基于最小支持的2.5维直流电阻率正则化反演研究[J]. 东华理工大学学报(自然科学版), 37(3): 292-298. |
| [37] | 刘彦, 吕庆田, 孟贵祥,等. 2012. 大地电磁与地震联合反演研究现状与展望[J]. 地球物理学进展, 27(6): 2444-2451, doi: 10.6038/j.issn.1004-2903.2012.06.019. |
| [38] | 彭淼, 谭捍东, 姜枚,等. 2013. 基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演[J]. 地球物理学报, 56(8): 2728-2738, doi: 10.6038/cjg20130821. |
| [39] | 万玲, 林婷婷, 林君,等. 2013. 基于自适应遗传算法的MRS-TEM联合反演方法研究[J]. 地球物理学报, 56(11): 3728-3740, doi: 10.6038/cjg20131114. |
| [40] | 魏文博. 2002. 我国大地电磁测深新进展及瞻望[J]. 地球物理学进展, 17(2): 245-254, doi: 10.3969/j.issn.1004-2903.2002.02.009. |
| [41] | 杨辉, 戴世坤, 宋海斌,等. 2002. 综合地球物理联合反演综述[J]. 地球物理学进展, 17(2): 262-271, doi: 10.3969/j.issn.1004-2903.2002.02.011. |
| [42] | 杨振威, 严加永, 刘彦,等. 2012. 高密度电阻率法研究进展[J]. 地质与勘探, 48(5): 969-978. |
| [43] | 于鹏, 王家林, 吴健生,等. 2006. 地球物理联合反演的研究现状和分析[J]. 勘探地球物理进展, 29(2): 87-93, 134. |
| [44] | 于鹏, 王家林, 吴健生,等. 2007. 重力与地震资料的模拟退火约束联合反演[J]. 地球物理学报, 50(2): 529-538, doi: 10.3321/j.issn:0001-5733.2007.02.026. |
| [45] | 祝靓谊. 2003. 油气勘探综合地球物理研究方法综述[J]. 地球物理学进展, 18(1): 19-23, doi: 10.3969/j.issn.1004-2903.2003.01.003. |
 2016, Vol. 31
2016, Vol. 31


