2. 中国地质大学(武汉)“构造与油气资源”教育部重点实验室, 武汉 430074
2. Key Laboratory of Tectonics and Petroleum Resource of Ministry of Education, China University of Geosciences, Wuhan 430074, China
泾河油田长8段是典型的低孔特低渗储层(任大忠等,2014).各井区孔隙度相近,主要分布在4%~8%,渗透率差异较大,主要分布在0.1×10-3μm2~0.4×10-3 μm2.116块岩心样品的薄片分析结果显示,长8储层以细-中粒、中粒长石岩屑砂岩和岩屑长石砂岩为主.
该油田长8段储层孔隙度、渗透率、含油饱和度低,孔隙结构复杂、储层非均质性强,这些不利因素给测井评价工作带来了巨大挑战,解释结果误差大,与实际符合程度低(石玉江等,2010;刘堂晏等,2013;李雄炎等,2014).
究其原因,是在这种复杂的地质条件下,Archie公式适用性差,由此计算得出的含水饱和度不够准确,测井结果出现偏差.而Archie公式的可应用性取决于参数值的选取是否准确,其中胶结指数m和饱和度指数n的准确与否最为重要.
因此,通过37块岩心样品的岩电实验研究(赵发展等,2006;黄小刚等,2010),确定该区长8段的m、n值,并结合相关测试数据分析其与岩性、物性、孔喉结构的关系,归纳出针对性强的经验值或经验公式,进而提高测井解释符合率,为准确识别油水层提供可靠依据.
1 胶结指数m研究1.1 m值的影响因素胶结指数m受多种因素的影响(邓少贵等,2000;沈爱新等,2003;王黎等,2005;王秀娟等,2013;高华等,2014;宋延杰等,2014a),其中,粘土含量、物性特征、孔隙结构等因素的影响是显著的,以下主要讨论这几类因素对m值的影响.
1.1.1 粘土含量对m值影响Archie公式中的经验值m=2、a=1仅适用于不含粘土的纯砂岩,且起导电作用的是孔隙流体,岩石骨架不导电.实际上,粘土的存在从两个方面影响到岩石的导电性.一方面,粘土分散在孔隙和喉道中,造成储层的孔隙结构复杂,连通喉道迂曲甚至堵塞,储集和渗流能力变差,导电能力明显降低.另一方面,泥质的连续分布形成有别于连续分布流体的新导体,使导电性变好.李先鹏通过岩电实验研究认为,当粘土含量较低时,黏土的增加使孔隙结构复杂化,岩心导电能力降低,m值随粘土含量的增加而增大;随着粘土含量的上升,连续分布的粘土增多,其导电性能抵消了孔隙结构变差而导致的导电性变差,在某个范围内m值几乎不变;粘土含量的继续增加致使粘土导电成为主导,m值相应减小(李先鹏,2008).
粘土X衍射资料显示,泾河油田长8段储层含有的粘土矿物主要有伊蒙混层、绿泥石、高岭石、伊利石,各矿物占总粘土矿物的平均百分比依次为32.30%、21.15%、20.35%、26.20%.粘土矿物是储层重要的组成部分.对部分有粘土资料的岩心进行分析,在粘土含量小于25%时,长8段储层胶结指数m随粘土含量的增加而增加(图 1),存在较好的正相关性.
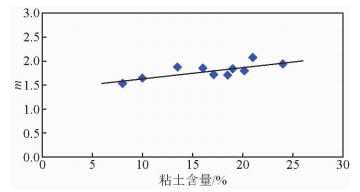 | 图 1 泾河长8段岩心样品粘土含量与胶结指数m关系图 Fig. 1 Relations of cementation exponent (m) and clay content of Chang 8 Member,Jinghe Oil Field,Ordos Basin |
孔隙度、渗透率是岩心物性的宏观参数,是衡量储层物性优劣的重要指标.综合分析长8段37块样品的物性、电性参数,发现胶结指数m与孔隙度Φ存在较好的正相关性(韩闯等,2013),这种相关性可以用对数方程表达,相关系数为0.724(图 2).但m值与渗透率并没有明显的相关特征(图 3),这可能与影响渗透率大小的因素(例如孔隙度、分选、层理、压实作用、胶结作用、溶蚀作用)较多有关,且这些影响因素对岩心电学性质影响效果不同.
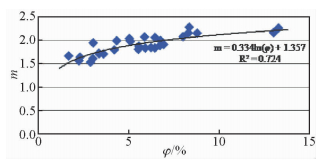 | 图 2 长8段孔隙度与m关系图 Fig. 2 Porosity parameters vs.m, Chang 8 Member |
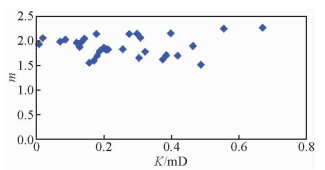 | 图 3 长8段渗透率与m关系图 Fig. 3 Permeability parameters vs.m, Chang 8 Member |
致密砂岩储层中孔隙空间主要由大小不等的孔隙和喉道组成,受颗粒大小、形状、分选、填积、压实、胶结、溶蚀等诸多因素的影响,孔隙结构千差万别,且有较强的非均质性.孔隙结构直接决定了流体的连通性以及流体的分布和运聚形式,储层的电学性质也与其密切相关(宋延杰等,2014b).因此,有必要研究孔隙结构对胶结指数m值的影响规律.
荆万学和陈永吉(1997)通过对Archie公式物理模型的研究和推导,提出m值是岩石骨架和孔隙网络混合引起孔隙空间曲折性增加的度量,孔隙曲折性越高,m值越大,假设能将孔隙流体与岩石骨架分离为各自连续的两部分,那么孔隙流体曲折度为1,m值为1.泾河油田长8段的实验结果很好的验证了这一理论推导(图 4),进汞迂曲度是孔隙连通长度与样品长度的比值,表示的是流体在孔隙空间流动路径的曲折程度.随着样品进汞迂曲度的增加,m值增大,二者呈现较好的正相关,说明随着孔隙结构的复杂程度增加,胶结指数m增大.
 | 图 4 长8段进汞迂曲度与m关系图 Fig. 4 Mercury penetration tortuosity vs. m, Chang 8 Member |
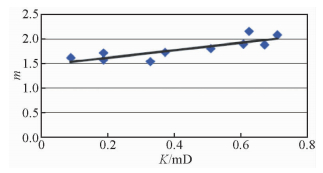
岩石的孔隙结构变化宏观表现为孔隙度和渗透率关系的不同,可以引入综合物性参数(K/Φ)1/2这一概念进行描述(图 5),综合物性参数减小表示孔隙结构更为复杂(王勇等,2006).研究结果显示,该层段储层的m值与综合物性参数呈负相关,随着孔隙结构变好,胶结指数m相应减小.这一结果与压汞资料的研究结果相一致,是对孔隙结构越复杂,胶结指数越大这一结论的验证和补充.
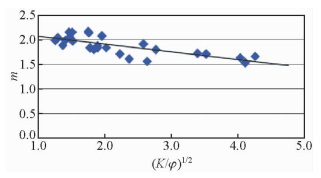 | 图 5 长8段综合物性参数与m关系图 Fig. 5 Comprehensive physical parameters ((K/Φ)1/2) vs.m, Chang 8 Member |
此外,在图 2中可以看出,该油田长8段m值大部分小于2,主要集中在1.5到2之间,这可能与该区储层中的溶蚀作用和微裂缝有关(樊云峰,2012)(图 6a~图 6d).溶蚀粒间孔和颗粒内孔使储层孔隙增大,孔隙流体的连通性增强,改善了导电网络的导电性能(黄跃,2014).微裂缝的影响也是如此,其连通孔隙的能力更强,有效的改善了储层性质.Archie公式理论模型的研究成果显示,裂缝储层的孔隙曲折度为1,m值等于1.就此可以推断,这一致密砂岩储层的储集空间和渗流通道并非仅有裂缝控制,孔隙在储集和渗流起到了相当的作用.
 | 图 6 (a)泾河36井,长8段,微裂缝;(b)泾河30井,长8段,微裂缝;(c)泾河60井,长8段,微裂缝沟通溶蚀孔;(d)泾河41井,长8段,粒内溶蚀孔 Fig. 6 (a)JH36 well,Chang 8 Member,Microfracture;(b)JH30 well,Chang 8 Member,Microfracture;(c)JH60 well,Chang 8 Member,Microfracture connect dissolution pores;(d)JH41 well,Chang 8 Member,intragranular dissolution pores |
确定测井参数的方法比较多,岩电实验是现今普遍使用的方法(冯春珍等,2007).常规砂岩的地层因素F和孔隙度Φ存在良好的幂函数关系(式1),可据此求取胶结指数m(张明禄和石玉江,2005;陈明君等,2014).
但对于致密砂岩而言,地层因素和孔隙度并不是简单的幂函数关系(图 7),图中所示的数据点有两种变化趋势.即以孔隙度8%为界限,当孔隙度大于这个值时地层因素和孔隙度呈现良好的幂函数关系,当孔隙度小于这个值时有左偏的趋势.如果不考虑致密砂岩的这一特点,直接对其进行拟合,a、m值就会偏离正常值.
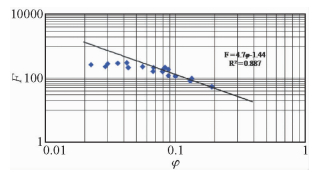 | 图 7 孔隙度与地层因素关系图 Fig. 7 The relationship between porosity and formation factor in Chang 8 Member |
为解决这一问题,首先对F、Φ同时取以10为底的对数,二者的关系可以表示二次函数表达式(式2),相关系数0.911,相关性较好.式中的a、b、c是拟合方程中的系数,可以直接获得,a、b和c的值分别为-0.867、-2.921、0.059.考虑到孔隙度等于1时,岩心可视为相同形状的地层水,地层因素为1.因此,公式中的c值为0,式(2)可以表达为式(3).公式为

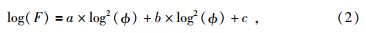
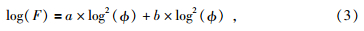

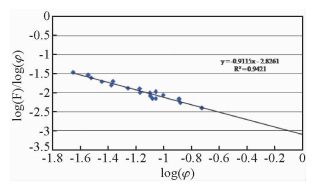 | 图 8 log(F)/log(φ)与log(φ)关系图 Fig. 8 The relationship between log(F)/log(φ) and log(φ) in Chang 8 Member |
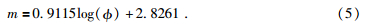
饱和度指数n的物理意义是对孔隙流体微观分布不均匀的校正(荆万学和陈永吉,1997).在不同的含水饱和度下,流体的分布情况不同,孔隙流体的微观非均质性越强,n值越大.孔隙流体的分布受多种因素的影响(罗少成等,2014),包括孔隙结构、地层水矿化度储层润湿性、油气充注强度等.其中,孔隙结构是重要的影响因素,孔隙结构直接决定了流体的连通性以及流体的分布,其复杂程度决定了流体分布非均质性的强弱.
孔隙结构的复杂程度可以用孔喉半径的分选性来度量.这里引入分选系数Sp进行定量分析(式6、式7),Sp表征了孔喉大小分布的均匀程度.在四个样品中,相对分选系数越大,n值越大.通过孔喉直径分布曲线(图 9a~图 9d)也可以直观的看出,随着孔喉直径的集中程度加强,孔隙结构相对变好,流体分布不均匀性减弱,n值减小(图 10).式中,Sp为分选系数,ψi是正态概率曲线汞饱和度为i时对应的喉道半径.公式为
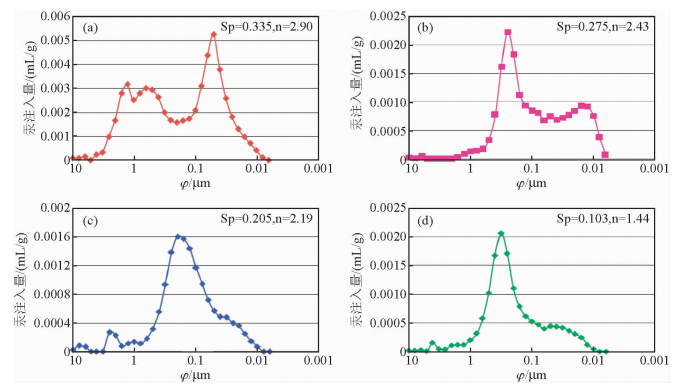 | 图 9 (a)JH 11样品孔喉直径分布;(b)JH 35样品孔喉直径分布;(c)JH 95样品孔喉直径分布;(d)JH 74样品孔喉直径分布 Fig. 9 (a)Pore-throat diameter distribution of sample JH11;(b)Pore-throat diameter distribution of sample JH35;(c)Pore-throat diameter distribution of sample JH95;(d)Pore-throat diameter distribution of sample JH74 |
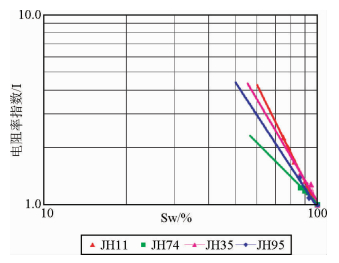 | 图 10 不同孔喉直径样品的电阻率指数和含水饱和度关系 Fig. 10 The relationship between saturation exponent (RI) and water saturation(Sw) of the different pore throat diameter samples |
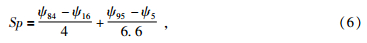

根据Archie公式对电阻率指数和含水饱和度关系的解释,在双对数坐标系下,含水饱和度和电阻率指数拟合所得直线,斜率的绝对值即为饱和度指数n(周改英和刘向君,2011;赵毅等,2013).岩电实验结果表明,饱和度指数n变化范围较大,从0.25到3.38不等.
将实验样品在不同饱和度下测试获得的电阻率指数的数据点投影在同一坐标系下(图 11),拟合结果显示,数据点相关性良好,相关系数为0.8869,获取饱和度指数n=2.266.该区长8段储层饱和度指数大于经验值2,根据上文分析结果,这种特征是该区长8段孔隙结构复杂,加剧了流体分布的不均匀性引起的.
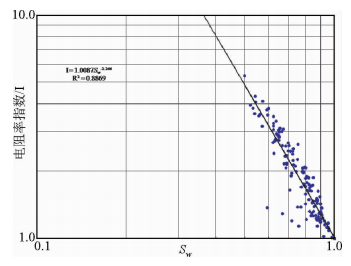 | 图 11 长8段含水饱和度与电阻率指数关系交会图 Fig. 11 The cross plot of the saturation exponent vs the water saturation in Chang 8 Member |
运用岩电实验获取的测井参数经验值和经验公式对泾河17井、泾河63井、泾河11井、早胜3井四口井进行验证性含水饱和度的测井解释工作,取得了较好的效果.泾河17井长8段1452~1456 m(图 12),运用实验获取参数计算所得的平均含水饱和度Sw1=56%,运用Archie公式的经验值m=2,n=2解释获得的平均含水饱和度Sw2=89%,试油结果显示,该层段日产油14.9吨,日产水0.8方,含水率5%.资料显示,该区长8段油层的含水饱和度上限为57%,应用实验参数获得的测井解释结果与实际符合程度高,解释效果较好.
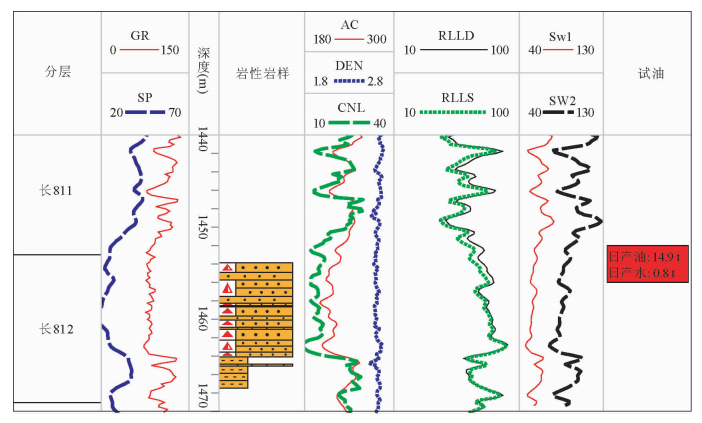 | 图 12 泾河17井测井解释成果 Fig. 12 The result of well logging interpretation for JH 17 well |
4.1 泾河油田长8段储层岩电性关系比较复杂.胶结指数m的大小受多种因素的控制,随粘土含量的升高,m值增大;m值与孔隙度有良好的正相关关系,且可以用对数函数表示,在实际测井解释中有重要的应用价值;研究发现孔隙结构越复杂,m值越大.
4.2 长8段储层的m值普遍小于2,主要集中在1.5到2.0之间,这可能与储层中发育的溶蚀孔隙和微裂缝对导电网络的改善作用有关.
4.3 饱和度指数n受孔隙结构的影响明显,随着孔隙结构复杂程度加深,孔隙流体分布的不均匀性加强,n值增大.
4.4 分析获取胶结指数m值与孔隙度的经验公式,结合测井数据可以连续计算m值.岩电测试结果显示,n的经验值为2.266.应用经验公式和经验值的解释结果与试油资料符合程度较高.
致 谢 中国地质大学(武汉)的严飞五、肖陈、贺敬聪对本文完成提出了宝贵意见,中石化华北分公司为实验提供了宝贵资料,在此一并表示感谢.| [1] | Chen M J, Kang Y L, You L J, et al. 2014. The response of electrical parameters of saturated tight sandstone to effective stress changes[J]. Progress in Geophysics (in Chinese), 29(3): 1128-1132, doi: 10.6038/pg20140316. |
| [2] | Deng S G, Bian R X, Fan Y R, et al. The effect of reservoir temperature on the parameters of Archie formula[J]. Well Logging Technology (in Chinese), 2000, 24(2): 88-91. |
| [3] | Fan Y F. 2012. Study on litho-electric property relation of Chang 61 reservoirs in Zhidan-Zibei oildom, the Ordos Basin (in Chinese)[MSc thesis]. Xi'an: Northwest University. |
| [4] | Feng C Z, Lin Z X, Cui L X. 2007. Determination of water saturation in reservoirs of low porosity and permeability[J]. World Well Logging Technology (in Chinese), 22(1): 27-30. |
| [5] | Gao H, Wu H S, He S L, et al. 2014. A research on the change of rock electricity parameters under high temperature and pressure in Ying-Qiong basin[J]. China Offshore Oil and Gas (in Chinese), 26(2): 30-34. |
| [6] | Han C, Fan S S, Chen W Z, et al. 2013. Rock Electrical Parameters Characteristics in Kuche Area[J]. Chinese Journal of Engineering Geophysics (in Chinese), 10(2): 210-215. |
| [7] | Huang X G, Huang X G, Bai W M. 2010. Progress of high temperature and high pressure experimental study on the electrical conductivity of the minerals and rocks[J]. Progress in Geophysics (in Chinese), 25(4): 1247-1258, doi: 10.3969/j.issn.1004-2903.2010.04.013. |
| [8] | Huang Y. 2014. Study on fluid evaluatuion of water-bearing tight gas reservior-in case of block Su54, sulige gas field (in Chinese)[MSc thesis]. Beijing: China University of Geosciences (Beijing). |
| [9] | Jing W X, Chen Y J. 1997. On the original physical model of Archie formula[J]. Well Logging Technology (in Chinese), 21(4): 289-291. |
| [10] | Li X P. 2008. Controlling factors and evaluation methods of cementation factor[J]. Lithologic Reservoirs (in Chinese), 20(4): 105-108. |
| [11] | Li X Y, Qin R B, Liu C C. 2014. Analyzing the effect of rock electrical parameters on the calculation of the reservoir saturation[J]. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 36(3): 68-74, doi: 10.11885/j.issn.1674-5086.2012.10.11.01. |
| [12] | Liu T Y, Tang T Z, Du H H, et al. 2013. Study of rock conductive mechanism based on pore structure[J]. Chinese Journal of Geophysics (in Chinese), 56(8): 2818-2826, doi: 10.6038/cjg20130830. |
| [13] | Luo S C, Cheng Z G, Zhou J Y, et al. 2014. Research on saturation index n of tight sandstone reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 36(4): 116-122, doi: 10.11885/j.issn.1674-5086.2013.10.10.01. |
| [14] | Ren D Z, Sun W, Wei H, et al. 2014. Diagenetic facies of Chang 81 sandstone reservoir in Huaqing Oilfield[J]. Geological Science and Technology Information (in Chinese), 33(2): 72-79. |
| [15] | Shen A X, Wang L, Chen S J. 2003. Low reservoir resistivity and litho-electric experiment of each parameter in Archie Equation[J]. Journal of Jianghan Petroleum Institute (in Chinese), 25(S1): 24-25. |
| [16] | Shi Y J, Zhang X L, Shen Y B, el al. 2010. Rock-logging relation of Chang 6 formation, southeast of Ordos Basin[J]. Progress in Geophysics (in Chinese), 25(5): 1716-1722, doi: 10.3969/j.issn.1004-2903.2010.05.027. |
| [17] | Song Y J, Jiang Y J, Song Y, et al. 2014a. Experimental on the influencing factors of m and n of low resistivity oil reservoirs in Southern Gulong Area[J]. Journal of Jilin University (Earth Science Edition )(in Chinese), 44(2): 704-714, doi: 10.13278/j.cnki.jjuese.201402307. |
| [18] | Song Y J, Zhang X, Song Y, et al. 2014b. On effective medium conductivity model based on non-efficient electrical pore for tight sandy conglomerate reservoirs[J]. Progress in Geophysics (in Chinese), 29(1): 209-216, doi: 10.6038/pg20140129. |
| [19] | Wang L, Sun B D, Shen A X, et al. 2005. On application of rock electricity parameters of Shaly sand reservoir with low-porosity and permeability, × field[J]. Well Logging Technology (in Chinese), 29(2): 91-94. |
| [20] | Wang X J, Wu S G, Wang J L, et al. 2013. Anomalous wireline logging data caused by gas hydrate dissociation in the Shenhu area, northern slope of South China Sea[J]. Chinese Journal of Geophysics (in Chinese), 56(8): 2799-2807, doi: 10.6038/cjg20130828. |
| [21] | Wang Y, Zhang C G, Li J F, et al. 2006. Study on influencing factors of lithological-electrical parameters[J]. Journal of Oil and Gas Technology (J. JPI) (in Chinese), 28(4): 75-77. |
| [22] | Zhang M L, Shi Y J. 2005. On archie's electrical parameters of sandstone reservoir with complicated pore structures[J]. Well Logging Technology (in Chinese), 29(5): 446-448. |
| [23] | Zhao F Z, Wang Y, Wang J Y, et al. 2006. Rock-electro parameters variant lithologic characters in Junggar and Tarim Basins[J]. Progress in Geophysics (in Chinese), 21(4): 1258-1265, doi: 10.3969/j.issn.1004-2903.2006.04.033. |
| [24] | Zhao Y, Zhu L H, Shi Z F, et al. 2013. Correction of lithological electrical parameters in low porosity and low permeability reservoir[J]. Complex Hydrocarbon Reservoirs (in Chinese), (4): 1-4, 23. |
| [25] | Zhou G Y, Liu X J. 2011. Experimental research of rock electrical parameters for tight sandstone[J]. Science & Technology Review (in Chinese), 29(18): 38-41. |
| [26] | 陈明君, 康毅力, 游利军,等. 2014. 饱和水致密砂岩电学参数对有效应力变化的响应[J]. 地球物理学进展, 29(3): 1128-1132, doi: 10.6038/pg20140316. |
| [27] | 邓少贵, 边瑞雪, 范宜仁,等. 2000. 储层温度对阿尔奇公式参数的影响[J]. 测井技术, 24(2): 88-91. |
| [28] | 樊云峰. 2012. 鄂尔多斯盆地志丹—子北油区长61储层岩电关系特征研究[硕士论文]. 西安: 西北大学. |
| [29] | 冯春珍, 林忠霞, 崔丽香. 2007. 低孔低渗储层含水饱和度的确定[J]. 国外测井技术, 22(1): 27-30. |
| [30] | 高华, 吴洪深, 何胜林,等. 2014. 莺琼盆地高温高压条件下岩电参数变化规律研究[J]. 中国海上油气, 26(2): 30-34. |
| [31] | 韩闯, 范姗姗, 陈伟中,等. 2013. 库车地区储层岩电性质研究[J]. 工程地球物理学报, 10(2): 210-215. |
| [32] | 黄小刚, 黄晓葛, 白武明. 2010. 高温高压下矿物岩石电导率的实验研究进展[J]. 地球物理学进展, 25(4): 1247-1258, doi: 10.3969/j.issn.1004-2903.2010.04.013. |
| [33] | 黄跃. 2014. 含水致密砂岩气藏气水层评价研究-以苏里格气田苏54区块为例[硕士论文]. 北京: 中国地质大学(北京). |
| [34] | 荆万学, 陈永吉. 1997. 浅探阿尔奇公式的物理学原型[J]. 测井技术, 21(4): 289-291. |
| [35] | 李先鹏. 2008. 胶结指数的控制因素及评价方法[J]. 岩性油气藏, 20(4): 105-108. |
| [36] | 李雄炎, 秦瑞宝, 刘春成. 2014. 岩电参数对储层饱和度计算精度的影响分析[J]. 西南石油大学学报(自然科学版), 36(3): 68-74, doi: 10.11885/j.issn.1674-5086.2012.10.11.01. |
| [37] | 刘堂晏, 汤天知, 杜环虹,等. 2013. 考虑储层孔隙结构的岩石导电机制研究[J]. 地球物理学报, 56(8): 2818-2826, doi: 10.6038/cjg20130830. |
| [38] | 罗少成, 成志刚, 周金昱,等. 2014. 致密砂岩储层饱和度指数n计算方法研究[J]. 西南石油大学学报(自然科学版), 36(4): 116-122, doi: 10.11885/j.issn.1674-5086.2013.10.10.01. |
| [39] | 任大忠, 孙卫, 魏虎,等. 2014. 华庆油田长81砂岩储层成岩相特征[J]. 地质科技情报, 33(2): 72-79. |
| [40] | 沈爱新, 王黎, 陈守军. 2003. 油层低电阻率及阿尔奇公式中各参数的岩电实验研究[J]. 江汉石油学院学报, 25(S1): 24-25. |
| [41] | 石玉江, 张小莉, 申贻博,等. 2010. 鄂尔多斯盆地东南部长6储层岩电关系特征[J]. 地球物理学进展, 25(5): 1716-1722, dio: 10.3969/j.issn.1004-2903.2010.05.027. |
| [42] | 宋延杰, 姜艳娇, 宋杨,等. 2014a. 古龙南地区低阻油层胶结指数和饱和度指数影响因素实验[J]. 吉林大学学报(地球科学版), 44(2): 704-714, doi: 10.13278/j.cnki.jjuese.201402307. |
| [43] | 宋延杰, 张啸, 宋杨,等. 2014b. 基于无效导电孔隙概念的致密砂砾岩有效介质导电模型[J]. 地球物理学进展, 29(1): 209-216, doi: 10.6038/pg20140129. |
| [44] | 王黎, 孙宝佃, 沈爱新,等. 2005. 某油田低孔隙度低渗透率泥质砂岩储层岩电实验及应用[J]. 测井技术, 29(2): 91-94. |
| [45] | 王秀娟, 吴时国, 王吉亮,等. 2013. 南海北部神狐海域天然气水合物分解的测井异常[J]. 地球物理学报, 56(8): 2799-2807, doi: 10.6038/cjg20130828. |
| [46] | 王勇, 章成广, 李进福,等. 2006. 岩电参数影响因素研究[J]. 石油天然气学报(江汉石油学院学报), 28(4): 75-77. |
| [47] | 张明禄, 石玉江. 2005. 复杂孔隙结构砂岩储层岩电参数研究[J]. 测井技术, 29(5): 446-448. |
| [48] | 赵发展, 王贇, 王界益,等. 2006. 准噶尔和塔里木盆地不同岩性岩电参数研究[J]. 地球物理学进展, 21(4): 1258-1265, doi: 10.3969/j.issn.1004-2903.2006.04.033. |
| [49] | 赵毅, 朱立华, 施振飞,等. 2013. 低孔低渗储层中岩电参数的修正[J]. 复杂油气藏, (4): 1-4, 23. |
| [50] | 周改英, 刘向君. 2011. 致密砂岩储层岩电参数实验研究[J]. 科技导报, 29(18): 38-41. |
 2016, Vol. 31
2016, Vol. 31


