2. 成都理工大学地球物理学院, 成都 610059
2. Geophysics School, Chengdu University of Technology, Chengdu 610059, China
测井解释过程中的岩性识别是储层测井评价的前提.目前,在复杂岩性识别任务中,支持向量机(SVM)(Vapnik,1995)应用广泛.其中,国外学者(Al-Anazi and Gates,2010)应用支持向量机预测非均质储层的渗透率及对岩相分类,表明支持向量机推广能力优于判别分析及神经网络.宋超等(2015)应用支持向量机识别砂岩中的流体类型,指出了支持向量机对石油勘探和开采的油水识别有一定的指导作用.韩学辉等(2013)、牟丹等(2015)、张尔华等(2011)应用支持向量机开展了储层岩性的测井识别,能够较好解决研究区域岩性识别问题.最小二乘支持向量机(LS-SVM)(顾燕萍等,2010)是支持向量机的变形算法,其在保证传统支持向量机的预测精度条件下有效克服了训练样本较大时训练时间长的缺点,本文采用LS-SVM进行岩性识别.支持向量机在实际应用中易受特征选择的影响,特征选取的好坏直接关系到预测效果的优劣.传统的特征优化方法,如PCA、ICA是一类线性变换法,在岩性识别(石宁等,2013;杨兆栓等,2015)、沉积微相定量识别(刘静等,2011)、无监督地震相分类(Coléou et al.,2003)都取得了明显的效果.然而,这些方法只有在原始数据集具有线性结构和满足高斯分布时才有较好的结果(胡昭华和宋耀良,2009),对于深层非均质岩性,测井响应特征之间表现为非线性关系,PCA等线性变换方法很大程度上会破坏数据的非线性结构,从而造成识别正确率降低(Hinton and Salakhutdinov,2006).为了弥补线性特征提取的缺陷,本文引入一类非线性特征提取方法-连续限制玻尔兹曼机(CRBM),它是一类包含可视层和一单隐层的对称限制扩散网络(RDN)(Chen and Murray,2002).CRBM具有强健的非线性高维数据模拟和非线性特征提取的能力(Chen and Murray,2003),目前已成功应用于指纹识别(Sahasrabudhe and Namboodiri,2013)、地球化学异常识别(Chen et al.,2014)、地震波形特征挖掘(Valentine and Trampert,2012)、地貌特征学习(Valentine et al.,2013)等领域.采用非线性函数作为激活函数,对原始特征进行非线性变换,可将原始特征之间隐含的高阶非线性关系解开得到区分性强的特征(Cottrell,2006;Hinton,2007;Tang and Murray,2007;Hu et al.,2009).
本文将CRBM与SVM结合起来应用于川西海相灰岩及白云岩的识别问题,识别正确率达到了81.9%.基于相同的支持向量机,CRBM提取特征识别正确率高于PCA提取特征.
1 CRBM原理1.1 CRBM结构CRBM是概率生成模型限制玻尔兹曼机(RBM)(Hinton,2002)的连续形式,见图 1,由一个可视层状态 {vj}(i=1…3)、偏置值v0和一个隐藏层状态{hj}(j=1…4)、偏置值h0及两层之间的权值{wij}连接构成.在训练过程中,可视层状态由原始特征代替,隐藏层状态是CRBM模型生成的新特征.RBM在建模二值图像数据、提取图像特征已表现出优越的能力,但是RBM在模拟连续数据效果却不尽人意(Chen and Murray,2002)
 | 图 1 3个可视单元及4个隐藏单元的CRBM网络结构图 Fig. 1 Diagram of an CRBM with three visible and four hidden units |
为了模拟连续数据,CRBM在可视层sigmoid函数中加入一个方差为σ2、均值为0的高斯单元,常数σ和Nj(0,1)共同产生了高斯输入分量nj=σNj(0,1),其概率分布为
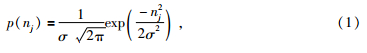


 ,方差为σ2的高斯分布.
1.2 CRBM无监督训练
,方差为σ2的高斯分布.
1.2 CRBM无监督训练
对称限制扩散网络(RDN)(Movellan,1998)属于专家乘积系统(PoE)(Marks and Movellan,2001;Murry,2001;Hinton,2002),因此可以采用PoE的最小化对比散度(MCD)权重更新算法来训练CRBM模型.MCD替代了Gibbs抽样的玻耳兹曼机的松弛搜索,大大减小了计算量.CRBM的权重更新及sigmoid函数的斜率控制项的更新公式为


 是单元j的一步采样状态,〈·〉为训练集上的期望值.
是单元j的一步采样状态,〈·〉为训练集上的期望值.
对(5)近似如下:


 进行多步采样.
1.3 CRBM监督微调
进行多步采样.
1.3 CRBM监督微调
一般认为CRBM按对比散度算法(MCD)训练权值后,权值已接近全局最优解,但为了使模型鲁棒性增强,需要对模型参数进行微调,本文中采用的微调方法是神经网络中的BP算法.首先,将CRBM结构展开,如图 2所示,输出目标数据设置为原输入数据.其次,利用模型输出与目标输出之间的误差对各权值的梯度调整所有权值,直至误差收敛.在模型的微调过程中,有三类参数需要调整:层之间的连接权值、每层的偏置值、斜率控制项.依据相关资料(Theodoridis and Koutroumbas,2010)求出连接权值、偏置值、斜率控制项的梯度值,以图 2三层神经网络为例,L=3,单个样本的目标函数值为
 | 图 2 CRBM微调模型结构 Fig. 2 The fine-tuning structure of CRBM |
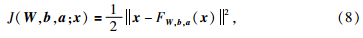

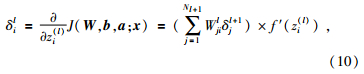







支持向量机(SVM)是Vapnik等人于20世纪90年代中期提出的一种基于统计学习理论的机器学习算法,它在解决小样本、非线性及高维模式识别中表现出许多特有优势,其本质为凸二次优化,能够保证获得全局最优解,即最优分类面,从理论上克服了神经网络无法避免的局部极值问题(张学工,2000).最小二乘支持向量机(LS-SVM)是Suykens设计的SVM变形算法(顾燕萍等,2010),该算法将SVM求解中的不等式约束变为等式约束,极大地提高了求解效率.LS-SVM求解思路如下
通过事先选择的非线性映射将输入向量映射到高维特征空间,从而在这个高维空间中构造最优决策函数.在构造最优决策函数时,利用了结构风险最小化原则.并巧妙地利用原空间的核函数取代了高维特征空间中的点积运算.
设样本为(xi,yj),i=1,…,m其中,xj∈Rn,yi∈R.假设一核函数为K,对所有x,z∈X满足条件为
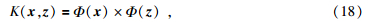
这里Φ是将输入空间X映射到一个新的空间F={Φ(x)x∈X}.根据泛函理论,只要一种核函数K满足Mercer条件,它对应着某一变换空间中的内积.因此,在最优分类面中采用适当的内积函数K就可以实现某一非线性变换后的线性分类,而计算复杂度没有增加.核函数主要有以下几种
(1)线性核函数

(2)多项式核函数

(3)径向基(RBF)核函数

(4)S型核函数
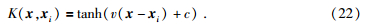
在高维空间中构造最优决策函数为



用Lagrange方法构建出目标优化函数为

由优化条件:



 | 图 3 DAG-SVM分类层次图 Fig. 3 The DAG-SVM classification hierarchy chart |
DAG-SVMs是由Piatt提出,主要是针对“一对一”SVMs存在的误分、拒分现象.这种方法的训练过程参见上图,是一种有向无环图.K个类别分类问题需要求解K(K-1)/2个支持向量机分类器.该有向无环图中含有K(K-1)/2个内部节点和K个叶子节点,每个节点对应一个二分类器.DAG-SVMs较“一对一”方法提高了测试速度,而且不存在误分、拒分区域.
3 基于CRBM特征提取的SVM岩性识别四川盆地目前发现的海相碳酸盐岩油气田的储层岩性主要是白云岩,原生沉积的灰岩一般比较致密,孔隙度和渗透率较低,很难成为具有工业价值的储层(曹俊兴等,2011),白云岩与灰岩的准确识别可以为该区域储层评价提供依据.白云岩储层通常是由灰岩经部分白云岩化形成的,空间上常与灰岩相伴,该研究区域碳酸盐岩埋藏深、灰岩及白云岩物性差异小,测井响应特征差异不明显,使得碳酸盐岩岩性识别难度较大.CRBM作为一类非线性特征提取方法,可将原始特征之间隐含的高阶非线性关系解开而得到区分性强的特征.本文以川西某地区CK1和XinS1井马鞍塘组-雷口坡组灰岩及白云岩作为研究对象,CK1井研究深度为5614.5~6910.5 m,共10072个采样点;XinS1井研究深度为5508~6241 m,共5140采样点.通过对录井及岩性剖面资料分析,选取CK1井及XinS1井共有且具有代表性的测井响应特征,分别为声波时差(AC)、密度(DEN)、自然伽马(GR)、深双侧向电阻率(RD),将这四条曲线作为CRBM特征提取的原始数据.工作流程如图 4.
 | 图 4 基于CRBM特征提取的SVM灰岩、白云岩识别流程 Fig. 4 The limestone and dolomite recognition process based on CRBM for feature extracting |
本文将CK1井研究层段数据作为训练样本,XinS1井研究层段数据作为测试样本.部分训练样本数据如表 1.
|
|
表 1 部分训练数据 Table 1 The part of the training data |
CRBM可视层及隐层的激活函数采用sigmoid函数,值域为[-1,1].因此,在进行模型训练之前需对原始数据进行归一化处理.公式为
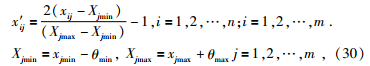
式中,xij,x′ij分别为归一化前后的第i个样本第j个特征值.为了使测试样本归一化在[-1,1]之间,分别将每个特征的最大值及最小值扩大及缩小一定数值,本文中设定θmin=θmax=0.01×(θjmax-θjmin),对于电阻率(RD),先对原数值进行对数变换后再用(30)式归一化.
3.3 基于CRBM-SVM岩性识别模型训练CRBM结构及学习参数的确定一直是个难点,为了使重构误差收敛,需对模型参数进行多次调整.本次实验取隐层单元个数为4,θL=-1,θH=1,可视层高斯分量标准差σ=0.05,权值学习率ηw=0.5、斜率控制项学习率ηa=0.2,隐藏层高斯分量标准差σ=0.02,权值学习率ηw=0.5、斜率控制项学习率ηc=0.1. CRBM模型经无监督训练及监督微调之后,训练数据的均方根重构误差随迭代次数变化见图 5a,可以看出,经5000次训练之后,训练数据重构误差基本趋于稳定,即模型趋于稳定.XinS1井研究层段重构数据AC-DEN交会图见图 5c,将图 5b与图 5c比较可知,CRBM重构效果明显.
 |
图 5 CRBM训练误差及XinS1井数据重构结果(数据经过归一化) (a)原始训练数据经CRBM训练的重构误差; (b) XinS1井测井响应AC-DEN交会图(蓝色:灰岩;红色:白云岩); (c) XinS1井测井响应经CRBM重构AC-DEN交会图(蓝色:灰岩;红色:白云岩). Fig. 5 The training error and XinS1 well reconstructed result by CRBM(Data Normalized) (a)The reconstruction error from raw data and; reconstruction data by CRBM; (b) The AC-DEN crossplot of XinS1 well log response (blue:limestone; red:dolomite); (c) The AC-DEN crossplot of XinS1 well log response reconstructed by CRBM(blue:limestone; red:dolomite). |
XinS1井原始数据经CRBM非线性特征提取后,特征1和特征3的交会图见图 6a,可以看出灰岩和白云岩主要分布区域是分开的,黄线框区域为灰岩,黑线框区域为白云岩.图 6b是XinS数据经PCA特征提取后提取到的主成分1、2的交会图,灰岩和白云岩区分不明显.
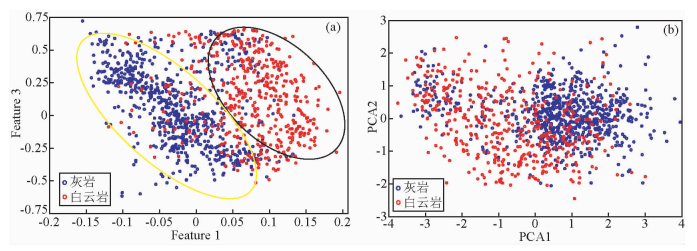 |
图 6 XinS1原始数据经CRBM学习特征及与PCA学习特征 (a)XinS1原始数据经CRBM学习特征(蓝色:灰岩;红色:白云岩); (b) XinS原始数据经PCA学习特征(蓝色:灰岩;红色:白云岩). Fig. 6 The CRBM learned features and the PCA learned features from XinS1 raw data (a) The CRBM learned features from XinS1 raw data(blue: limestone; red: dolomite); (b) The PCA learned features from XinS1 raw data(blue: limestone; red: dolomite). |
利用CK1井经CRBM提取到的特征1、3组合训练SVM.基于提取的特征基本属于线性可分,本文选用线性核函数(式19),采用交叉验证确定正规化参数c=5050.
3.4 应用效果及实例分析3.4节已经得到CRBM非线性特征提取模型及PCA线性特征提取模型,特征交会图显示灰岩、白云岩区分度CRBM模型优于PCA模型.为了得到定量的岩性识别结果,本文训练了三类SVM岩性识别模型,并在核函数选取一致的条件下比较了三类模型的岩性识别正确率.表 2给出了利用SVM识别XinS1井 目标层段灰岩及白云岩的正确率,原始数据经CRBM以及PCA特征提取之后识别正确率都比原始数据识别正确率高,PCA可以减少原始数据中的冗余信息,提取出相互独立的变量,提高识别正确率.而对于深层非均质岩性,CRBM可将原始特征之间隐含的高阶非线性关系解开而得到区分性强的特征,识别正确率进一步提高,平均识别率达到了81.9%,较原始数据提高5.3%、PCA特征提高3.2%.
|
|
表 2 岩性识别结果分析 Table 2 Lithology recognition result analysis |
图 7是XinS1井5508~5621 m岩性识别效果图,基于CRBM特征提取的SVM岩性识别结果与实际采样结果基本吻合.
 | 图 7 XinS1井某段实际岩心采样与CRBM-SVM岩性预测对比(深度范围:5508~5621 m) Fig. 7 The lithology comparison of actual core sampling and CRBM-SVM identification in a XinS1 section (Depth rang: 5508~5621 m) |
4.1 支持向量机是目前分辨能力最高的岩性识别方法,但针对诸如白云岩和灰岩等测井响应差别不明显的岩性识别问题,支持向量机很难寻找到最优分类面,识别正确率并不高.
4.2 特征优化可以提高支持向量机识别正确率,PCA是线性特征提取方法,CRBM是非线性特征提取方法.对于深层非均质岩性,测井响应特征之间表现为非线性关系,CRBM可将原始特征之间隐含的高阶非线性关系解开而得到区分性强的特征.
4.3 基于相同的支持向量机分类算法,CRBM非线性特征提取方法及PCA线性特征提取方法得到的特征识别正确率要高于原始测井响应.而且,CRBM提取特征识别正确率要高于PCA,平均识别率达到了81.9%.
致 谢 感谢导师曹俊兴教授的悉心指导,感谢审稿专家的宝贵修改意见和编辑部老师的帮助.| [1] | Al-Anazi A, Gates I D. 2010a. A support vector machine algorithm to classify lithofacies and model permeability in heterogeneous reservoirs[J]. Engineering Geology, 114(3-4): 267-277, doi: 10.1016/j.enggeo.2010.05.005. |
| [2] | Al-Anazi A, Gates I D. 2010b. On the capability of support vector machines to classify lithology from well logs[J]. Natural Resources Research, 19(2): 125-139, doi: 10.1007/s11053-010-9118-9. |
| [3] | Cao J X, Liu S G, Tian R F, et al. 2011. Seismic prediction of carbonate reservoirs in the deep of Longmenshan foreland basin[J]. Acta Petrologica Sinica (in Chinese), 27(8): 2423-2434. |
| [4] | Chen H, Murray A. 2002. A continuous restricted Boltzmann machine with a hardware-amenable learning algorithm[C].//Proceedings of 12th International Conference on Artificial Neural Networks (ICANN2002). Madrid, Spain: Springer-Verlag, 358-363, doi: 10.1007/3-540-46084-5_58. |
| [5] | Chen H, Murray A F. 2003. Continuous restricted Boltzmann machine with an implementable training algorithm[J]. IEE Proceedings of Vision, Image and Signal Processing, 150(3): 153-158, doi: 10.1049/ip-vis:20030362. |
| [6] | Chen Y L, Lu L J, Li X B. 2014. Application of continuous restricted Boltzmann machine to identify multivariate geochemical anomaly[J]. Journal of Geochemical Exploration, 140: 56-63, doi: 10.1016/j.gexplo.2014.02.013. |
| [7] | ColLéou T, Poupon M, Azbel K. 2003. Unsupervised seismic facies classification: a review and comparison of techniques and implementation[J]. The Leading Edge, 22(10): 942-953, doi: 10.1190/1.1623635. |
| [8] | Cottrell G W. 2006. New life for neural networks[J]. Science, 313(5786): 454-455, doi: 10.1126/science.1129813. |
| [9] | Gu Y P, Zhao W J, Wu Z S. 2010. Least squares support vector machine algorithm[J]. Journal of Tsinghua University (Science & Technology) (in Chinese), 50(7): 1063-1067, 1071. |
| [10] | Han X H, Zhi L F, Liu R, et al. 2013. A lithologic identification method in Es4 reservoir of Guangli oilfield with Least square support vector machine[J]. Progress in Geophysics (in Chinese), 28(4): 1886-1892, doi: 10.6038/pg20130430. |
| [11] | Hinton G E. 2002. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 14(8): 1711-1800, doi: 10.1162/089976602760128018. |
| [12] | Hinton G E. 2007. Learning multiple layers of representation[J]. Trends in Cognitive Sciences, 11(10): 428-434, doi: 10.1016/j.tics.2007.09.004. |
| [13] | Hinton G E, Salakhutdinov R R. 2006. Reducing the dimensionality of data with neural networks[J]. Science, 313(5786): 504-507, doi: 10.1126/science.1127647. |
| [14] | Hu Z H, Fan X, Song Y L, et al. 2009. Joint trajectory tracking and recognition based on bi-directional nonlinear learning[J]. Image and Vision Computing, 27(9): 1302-1312, doi: 10.1016/j.imavis.2008.11.011. |
| [15] | Hu Z H, Song Y L. 2009. Dimensionality reduction and reconstruction of data based on Autoencoder network[J]. Journal of Electronics & Information Technology (in Chinese), 31(5): 1189-1192. |
| [16] | Liu J, Li Z C, Wang Z, et al. 2011. Quantitative identification of microfacies based on ICA, PCA and SVM[J]. Well Logging Technology (in Chinese), 35(3): 262-265, doi: 10.3969/j.issn.1004-1338.2011.03.015. |
| [17] | Li H. 2012. Statistics Learning Method (in Chinese)[M]. Beijing: Tsinghua University Press, 219-224. |
| [18] | Marks T K, Movellan J R. 2001. Diffusion networks, products of experts, and factor analysis[R]. UCSD MPLab Technical Report, 2: 481-485. |
| [19] | Movellan J R. 1998. A learning theorem for networks at detailed stochastic equilibrium[J]. Neural Computation, 10(5): 1157-1178, doi: 10.1162/089976698300017395. |
| [20] | Mou D, Wang Z W, Huang Y L, et al. 2015. Lithological identification of volcanic rocks from SVM well logging data: Case study in the eastern depression of Liaohe Basin[J]. Chinese Journal of Geophysics (in Chinese), 58(5): 1785-1793, doi: 10.6038/cjg20150528. |
| [21] | Murry A F. 2001. Novelty detection using products of simple experts-a potential architecture for embedded systems[J]. Neural Networks, 14(9): 1257-1264, doi: 10.1016/s0893-6080(01)00097-1. |
| [22] | Sahasrabudhe M, Namboodiri A M. 2013. Learning fingerprint orientation fields using continuous restricted Boltzmann machines[C].//Proceedings of the 2013 2nd IAPR Asian Conference on Pattern Recognition. Naha: IEEE, 351-355, doi: 10.1109/ACPR.2013.37. |
| [23] | Shi N, Li H Q, Luo W P. 2013. Lithology identification of reservoir containing anhydrite based on independent component analysis and Naive Bayes algorithm[J]. Journal of Xi'an Shiyou University (Natural Science Edition) (in Chinese), 28(5): 39-42, doi: 10.3969/j.issn.1673-064X.2013.05.007. |
| [24] | Song C, Guo Z Q, Lu Q, et al. 2015. Fluid type identification of sandstone based on support vector machine[J]. Progress in Geophysics (in Chinese), 30(2): 616-620, doi: 10.6038/pg20150218. |
| [25] | Tang T B, Murray A F. 2007. Adaptive sensor modelling and classification using a continuous restricted Boltzmann machine (CRBM)[J]. Neurocomputing, 70(7-9): 1198-1206, doi: 10.1016/j.neucom.2006.11.014. |
| [26] | Theodoridis S, Koutroumbas K. 2010. Pattern Recognition (fourth edition) (in Chinese)[M]. Li J J, Wang A X, Wang J, Trans. Beijing: Publishing House of Electronics Industry, 110-119. |
| [27] | Valentine A P, Kalnins L M, Trampert J. 2013. Discovery and analysis of topographic features using learning algorithms: A seamount case study[J]. Research Letters, 40(12): 3048-3054, Geophysical doi: 10.1002/grl.50615. |
| [28] | Valentine A P, Trampert J. 2012. Data space reduction, quality assessment and searching of seismograms: autoencoder networks for waveform data[J]. Geophysical Journal International, 189(2): 1183-1202, doi: 10.1111/j.1365-246x.2012.05429.x. |
| [29] | Vapnik V N. 1995. The Nature of Statistical Learning Theory[M]. New York, NY, USA: Springer-Verlag, 111-289. |
| [30] | Wang G C, Carr T R, Ju Y W, et al. 2014. Identifying organic-rich Marcellus shale lithofacies by support vector machine classifier in the Appalachian basin[J]. Computers & Geosciences, 64: 52-60. |
| [31] | Yang Z S, Lin C S, Yin H, et al. 2015. Application of principal component analysis in carbonate lithology identification of the Ordovician Yingshan Formation in Tazhong area[J]. Natural Gas Geoscience (in Chinese), 26(1): 54-59, doi: 10.11764/j.issn.1672-1926.2015.01.0054. |
| [32] | Zhang E H, Guan X W, Zhang Y G. 2011. Support vector machine in volcanic reservoir forecast; East slope in Xujiaweizi depression[J]. Chinese Journal of Geophysics (in Chinese), 54(2): 428-432, doi: 10.3969/j.issn.0001-5733.2011.02.020. |
| [33] | Zhang X G. 2000. Introduction to statistical learning theory and support vector machines[J]. Acta Automatica Sinica (in Chinese), 26(1): 32-42. |
| [34] | Zhao X L, Wang G W, Zhou Z L, et al. 2015. A review of lithology interpretation methods using geophysical well logs[J]. Progress in Geophysics (in Chinese), 30(3): 1278-1287, doi: 10.6038/pg20150338. |
| [35] | 曹俊兴, 刘树根, 田仁飞,等. 2011. 龙门山前陆盆地深层海相碳酸盐岩储层地震预测研究[J]. 岩石学报, 27(8): 2423-2434. |
| [36] | 顾燕萍, 赵文杰, 吴占松. 2010. 最小二乘支持向量机的算法研究[J]. 清华大学学报(自然科学版), 50(7): 1063-1067, 1071. |
| [37] | 韩学辉, 支乐菲, 刘荣,等. 2013. 应用最小二乘支持向量机识别广利油田沙四段储层岩性[J]. 地球物理学进展, 28(4): 1886-1892, doi: 10.6038/pg20130430. |
| [38] | 胡昭华, 宋耀良. 2009. 基于Autoencoder网络的数据降维和重构[J]. 电子与信息学报, 31(5): 1189-1192. |
| [39] | 李航. 2012. 统计学习方法[M]. 北京: 清华大学出版社, 219-224. |
| [40] | 刘静, 李正从, 王智,等. 2011. 基于ICA、PCA、与SVM方法的沉积微相定量识别[J]. 测井技术, 35(3): 262-265, doi: 10. 3969/j.issn.1004-1338.2011.03.015. |
| [41] | 牟丹, 王祝文, 黄玉龙,等. 2015. 基于SVM测井数据的火山岩岩性识别—以辽河盆地东部坳陷为例[J]. 地球物理学报, 58(5): 1785-1793, doi: 10.6038/cjg20150528. |
| [42] | 石宁, 李洪奇, 罗伟平. 2013. 利用独立成分分析和朴素贝叶斯算法识别含硬石膏储层的岩性[J]. 西安石油大学学报(自然科学 版),28(5):39-42,doi:10.3969/j.issn.1673-064X.2013.05.007. |
| [43] | 宋超, 郭智奇, 鹿琪,等. 2015. 基于支持向量机法识别砂岩中流体类型[J]. 地球物理学进展, 30(2): 616-620, doi: 10.6038/pg20150218. |
| [44] | Theodoridis S, Koutroumbas K. 2010. 模式识别(第四版)[M]. 李晶皎, 王爱侠, 王骄, 译. 北京: 电子工业出版社, 110-119. |
| [45] | 杨兆栓, 林畅松, 尹宏,等. 2015. 主成分分析在塔中地区奥陶系鹰山组碳酸盐岩岩性识别中的应用[J]. 天然气地球科学, 26(1): 54-59, doi: 10.11764/j.issn.1672-1926.2015.01.0054. |
| [46] | 张尔华, 关晓巍, 张元高. 2011. 支持向量机模型在火山岩储层预测中的应用—以徐家围子断陷徐东斜坡带为例[J]. 地球物理学报,54(2):428-432,doi:10.3969/j.issn.0001-5733.2011.02.020. |
| [47] | 张学工. 2000. 关于统计学习理论与支持向量机[J]. 自动化学报, 26(1): 32-42. |
| [48] | 赵显令, 王贵文, 周正龙,等. 2015. 地球物理测井岩性解释方法综述[J]. 地球物理学进展, 30(3): 1278-1287, doi: 10.6038/pg20150338. |
 2016, Vol. 31
2016, Vol. 31


