2. 吉林大学地球探测科学与技术学院, 长春 130026
2. College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China
导数换算在位场数据处理中占据着重要的地位,它不仅有助于异常的分区和解释,还参与到了许多位场数据处理和反演方法之中,如:重力归一化总梯度(Zeng et al.,2002;张凤旭等,2005)、欧拉反褶积(Thompson,1982; Reid et al.,1990;Stavrev and Reid,2010).然而,导数转换因子是高通滤波,对干扰的放大作用导致计算结果稳定性较差,学者们往往是通过附加低通滤波器来解决这一问题(侯重初,1981;姚长利等,1997),并普遍认为采用向上延拓一定高度的方法压制导数换算中的高频成分最为方便和实用(王万银等,2010;张季生等,2011),但这种做法虽然提高了计算稳定性,但对中、低频成分的消弱导致计算分辨率随之降低.近些年,由于迭代法在解决位场计算中不稳定问题时有着较好的应用效果而受到了普遍重视(李宏伟,2012),但事实上迭代法也并不能从根本上解决计算精度和不稳定性之间的矛盾问题(姚长利等,2012;王彦国,2013).不过在迭代法计算稳定性较强的信号压制区内①(王彦国,2013),若能通过某种数学手段来提高有效异常的转换能力,势必可以从一定程度上解决上述矛盾问题.基于此,本文提出了一种新的位场数据处理方法—基于迭代差分的视导数,同时将其应用到了位场边界识别方法之中,并通过模型试验和实例应用验证了方法的有效性.
①信号压制区是指迭代次数较少时计算结果的集合。在该区域内,迭代法具有较强稳定性,但是异常转换程度较差;详述见王彦国博士论文。
1 位场视导数的基本原理 1.1 导数的波数域迭代法在波数域中,位场导数的波谱可以表示为

首先构造一个φder与相关的低通滤波算子ϕ:
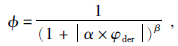
利用滤波因子ϕ将转换因子φder初始改造为

将理论转换因子φder与初始改造值φder(1)的差值利用滤波因子ϕ进行修正,修正结果φder(2)为φder的二次改造值,即有:
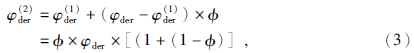
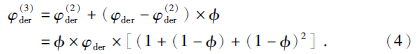
按如上的迭代补偿模式,则第n次改造值与n-1改造值的关系可表示为
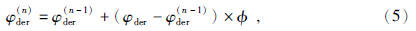
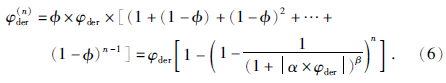
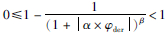 ,所以当迭代次数趋于无穷时,φder(n)的极限存在:
,所以当迭代次数趋于无穷时,φder(n)的极限存在: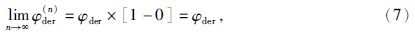
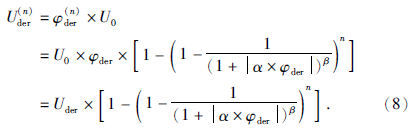
由(8)式可以看出,采用迭代法得到的波谱Uder(n)等价于在理论导数波谱Uder中加入了一个与迭代次数n相关的低通滤波器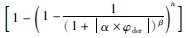 ,即波数域的迭代法事实上同样是一种滤波算法.
,即波数域的迭代法事实上同样是一种滤波算法.
在迭代法的信号压制区,初始迭代次数为n(很小,可取n=1)的导数为uder(n)=F-1[Uder(n)],迭代次数间隔为Δn的导数值为uder(n+Δn)=F-1[Uder(n+Δn)],则迭代差分一次的结果Ader(1nd)可表示为

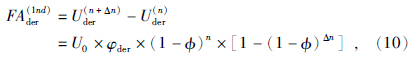
令φ(1nd)=(1-ϕn)×[1-(1-ϕ)Δn],则将公式(10)改写为

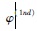 的最大值,则迭代差分一次的
的最大值,则迭代差分一次的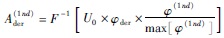 ,其滤波算子Afder(1nd)=
,其滤波算子Afder(1nd)=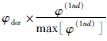 是相当于在导数算子φder上乘以一个新的滤波算子,因此Ader(1nd)与理论导数的异常特征具有一定的相似性,故称Ader(1nd)是位场异常u的迭代差分一次视导数.
是相当于在导数算子φder上乘以一个新的滤波算子,因此Ader(1nd)与理论导数的异常特征具有一定的相似性,故称Ader(1nd)是位场异常u的迭代差分一次视导数.
令迭代次数间隔为2Δn的导数为uder(n+2Δn)=F-1[Uder(n+2Δn)],则迭代差分二次结果Ader(2nd)为
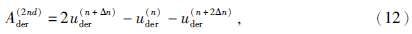
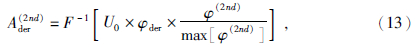
仿照上述流程,则迭代差分m次的视导数为
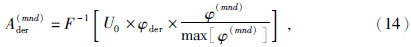
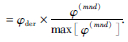 1.3 视导数的滤波特性
1.3 视导数的滤波特性
在位场波数域数据处理中,滤波算子的选择往往决定着计算的稳定性、目标地质体异常的转换程度及异常的分辨能力.因此,讨论常规导数和视导数的滤波特性则具备重要意义.
从图 1中可以看出:(1)常规导数算子对高频成分起到了显著的放大作用,势必因原始异常中的噪声干扰导致结果稳定性较差;(2)不同迭代差分次数及不同迭代次数间隔情况下的迭代差分视导数算子滤波响应特征相似,均呈现为带通滤波器,对中频成分起到了放大作用,对高频成分起到了压制作用;(3)迭代差分视导数相对于常规导数来说,其滤波算子对低频成分的压制能力更显著;(4)当迭代次数间隔Δn不变时,随着迭代差分次数m的增加,视导数滤波算子的频带变窄,且主峰向低频移动,并对高频成分的压制能力增强;(5)当迭代差分次数m不变时,随着迭代间隔Δn的增加,滤波算子的主峰向高频移动.
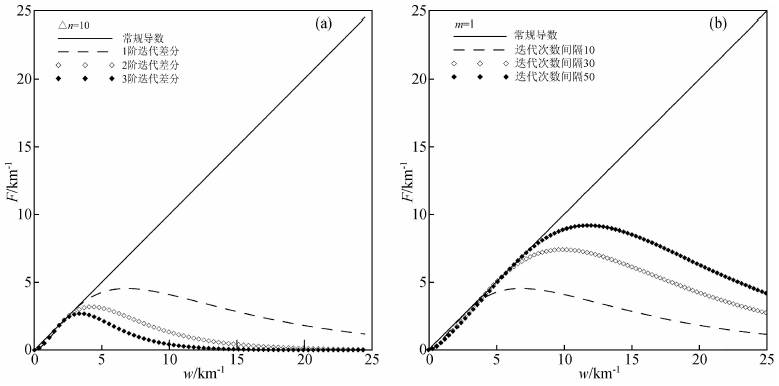 |
图 1 视导数滤波响应特性 (a) 迭代差分次数的影响; (b) 迭代次数间隔的影响. Fig. 1 Filtering characteristic of apparent derivative (a) Effected by iterative difference times; (b) Effected by intervals of iterative times. |
由上可以推出,视导数为带通滤波器,仅对中频成分起到放大作用,较高的迭代差分次数和较小的迭代次数间隔,会使视导数具有较强的计算稳定性.在理论上,迭代初始次数n、迭代次数间隔Δn及迭代差分次数m的选择具有随意性,但为确保计算结果的稳定性及异常的分辨能力,建议选取迭代初始次数n=1,迭代间隔Δn≤100与迭代差分次数m满足1≤m≤3.
1.4 模型检验为对视导数进行验证,这里设计了一个组合模型,在此基础上还进行了算法稳定性试验,并与常规导数结果进行了对比分析,模型体密度均设为1.0 g/cm3,模型示意图见图 2b.图 2可以看出,由于地质体异常的叠加,重力异常(图 2a)无法有效反映出浅部地质体的异常信息.为了提高异常横向分辨率,往往需要对原异常进行导数转换.
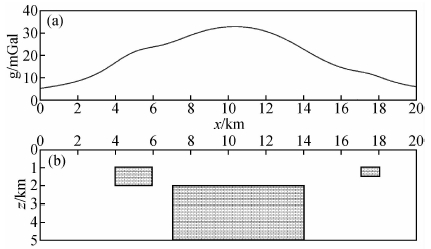 | 图 2 模型示意图(b)及理论重力异常(a) Fig. 2 The sketch map of model (b) and forward gravity anomaly (a) |
图 3是常规导数和视导数对理论重力异常及添加噪声异常的处理结果.可以看出,常规垂向一阶导数(图 3Aa)提高了异常分辨率,对三个地质体均有反映,常规水平一阶导数模可以通过极大值反映出地质体B1左、B3右和B2边界,但对B1右、B3左边界却是以极小值展现;同时由于噪声影响,常规导数(图 3Ba)已无法显示出地质体的有用信息.不同迭代差分次数的视导数对理论重力异常的处理结果(图 3Ab-d)基本完全相同,其垂向一阶视导数(相对常规导数而言)更加显著地提高了异常的分辨率,其水平一阶视导数模通过极大值基本可以识别出场源的所有边界;当原异常含有噪声时,视导数(图 3Bb-d)显然具备更强的计算稳定性,且随着迭代差分次数的增加,计算结果的稳定性也随之增强.
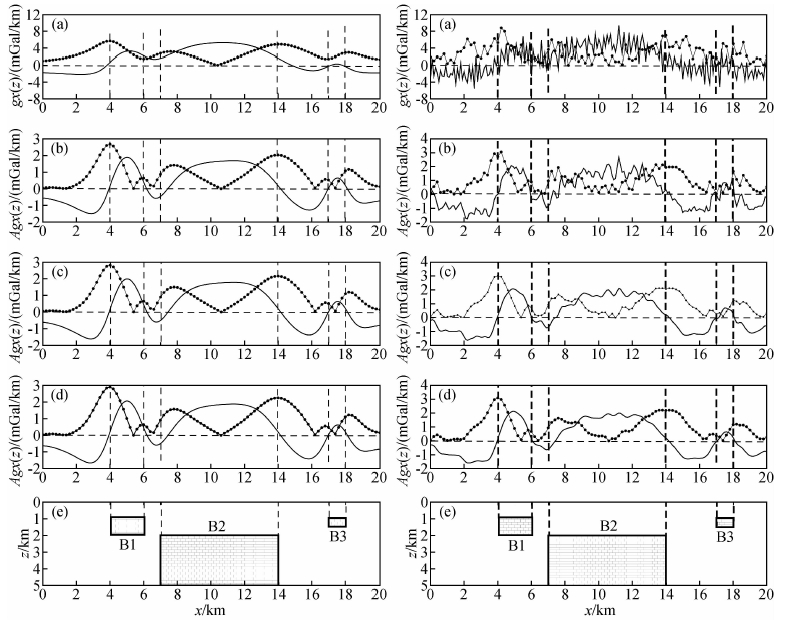 |
图 3 (A)、(B)分别是理论重力异常、含1%噪声重力异常的常规导数和迭代差分不同次数视导数 (Δn=10,点线为水平一阶导数模,实线为垂向一阶导数) (a) 常规导数;(b) 迭代差分1次视导数;(c) 迭代差分2次视导数;(d) 迭代差分3次视导数. Fig. 3 (A), (B) The results of conventional derivatives and apparent derivatives with different iterative differential of forward gravity anomaly and anomaly including 1% random noise, respectively (Δn=10, dotted lines are the horizontal derivatives and solid lines are the vertical derivatives) (a) Conventional derivatives; (b), (c), (d) apparent derivatives with m=1, m=2 and m=3, respectively. |
上述分析表明,相对于常规导数而言,本文提出的视导数不仅具有更强的计算稳定性,而且具有更高的异常分辨能力.
2 位场边界识别方法的简易改造为了说明视导数可以代替常规导数参与到一些位场数据处理方法之中,在此将视导数应用到了场源边界识别中,在此之前,先对常用的边界识别方法进行简易改造,使之可以更清晰地反映场源边界.
2.1 改进的归一化水平总梯度Cordell(1979)发现水平总梯度的极大值与地质体边界有着较好的对应关系,其表达式为
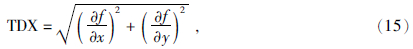
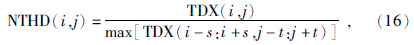

2005年,Wijns等(2005)提出了Theta map的边界识别方法,其形式为
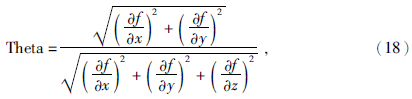
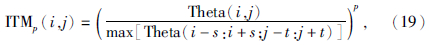
2008年,Cooper和Cowan(2008)另辟蹊径,利用导数标准差的归一化形式进行了场源边界的识别,其归一化形式为
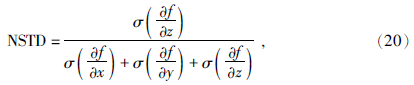
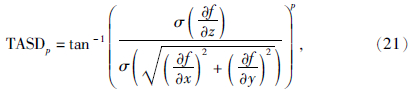
为了试验视导数在边界识别中应用的可行性,建立了有5个地质体组成的模型,各个模型体的平面展布及几何参数见图 4a及表 1,模型体的剩余密度均为1.0 g/cm3,图 4b及图 4c分别是模型体产生的理论重力异常及添加1%噪声的重力异常.分别利用基于常规导数和视导数(模型中选取迭代差分次数m=3,迭代间隔Δn=10)的上述边界识别方法对图 4b及图 4c进行相应处理,处理结果见图 5~7.
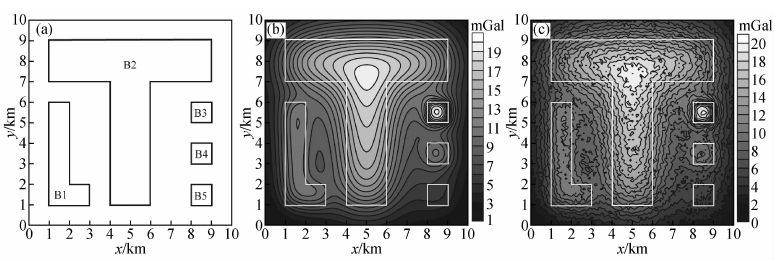 | 图 4 组合模型(a)产生的重力异常(b)及添加1%噪声的异常(c) Fig. 4 (a) Combined model; (b) Forward gravity anomaly; (c) adding 1% random noise to forward anomaly |
| 表 1 模型参数 Table 1 The model parameters |
 |
图 5 基于常规导数和视导数的水平总梯度及其改进水平总梯度结果 (a) 、(b) 和 (c) 分别是图 4b常规导数下的TDX、NTHD和ITDX3;(d)、(e) 和 (f) 分别是图 4b视导数的TDX、NTHD和ITDX3; (g)、(h)和(i)分别图 4c常规导数下的TDX、NTHD和ITDX3;(j)、(k)和(l)分别图 4c 视导数下的TDX、NTHD和ITDX3. Fig. 5 The total horizontal derivative and its improved versions with conventional and apparent derivative (a),(b),(c) are TDX,NTHD,ITDX3 based on conventional derivative of the data in Fig. 4b,respectively; (d),(e),(f) are TDX,NTHD,ITDX3 based on apparent derivative of the data in Fig. 4b,respectively; (g),(h),(i) are TDX,NTHD,ITDX3 based on conventional derivative of the data in Fig. 4c,respectively; (j),(k),(l) are TDX,NTHD,ITDX3 based on apparent derivative of the data in Fig. 4c,respectively. |
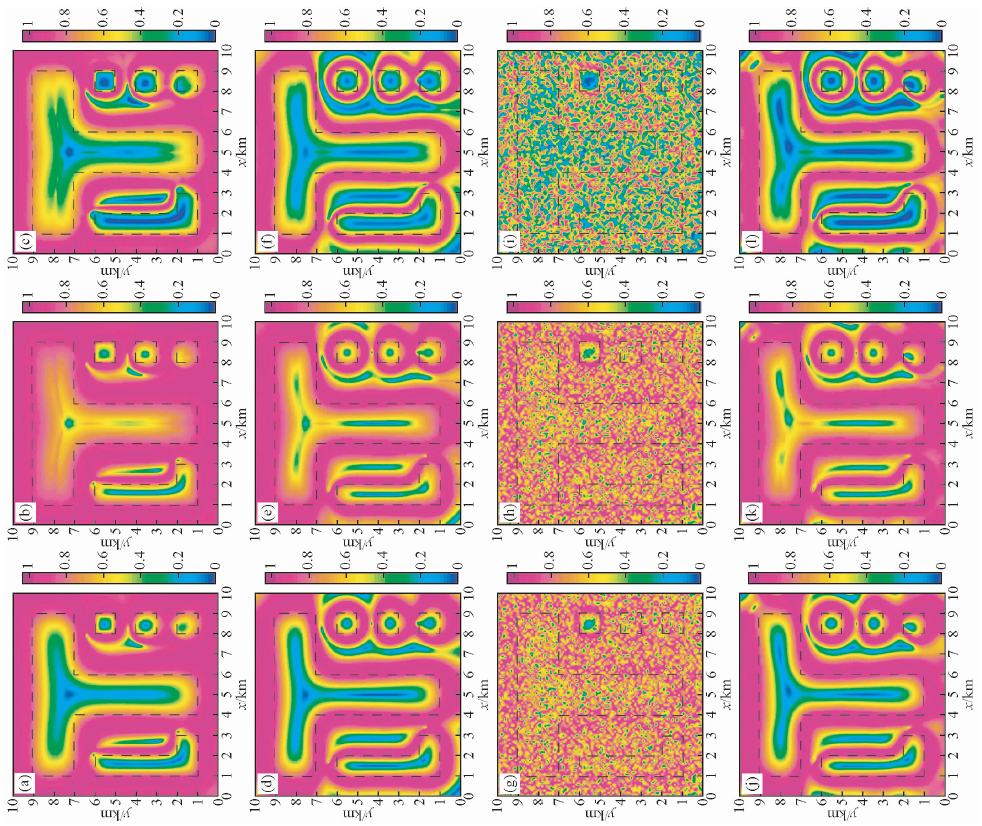 |
图 6 基于常规导数和视导数的Theta map及改进Theta map的边界识别结果 (a)、(b)、(c)分别是图 4b常规导数的Theta map、ITM1、ITM3;(d)、(e)、(f)分别是图 4b视导数的Theta map、ITM1、ITM3;(g)、(h)、(i)分别是图 4c常规导数的Theta map、ITM1、ITM3;(j)、(k)、(l)分别是图 4c视导数的Theta map、ITM1、ITM3. Fig. 6 Theta map and its improved versions with conventional and apparent derivative (a),(b),(c) are Theta map,ITM1 and ITM3 based on conventional derivative of the data in Fig. 4b,respectively; (d),(e),(f) are Theta map,ITM1 and ITM3 based on apparent derivative of the data in Fig. 4b,respectively; (g),(h),(i) are Theta map,ITM1 and ITM3 based on conventional derivative of the data in Fig. 4c,respectively; (j),(k),(l) are Theta map,ITM1 and ITM3 based on apparent derivative of the data in Fig. 4c,respectively. |
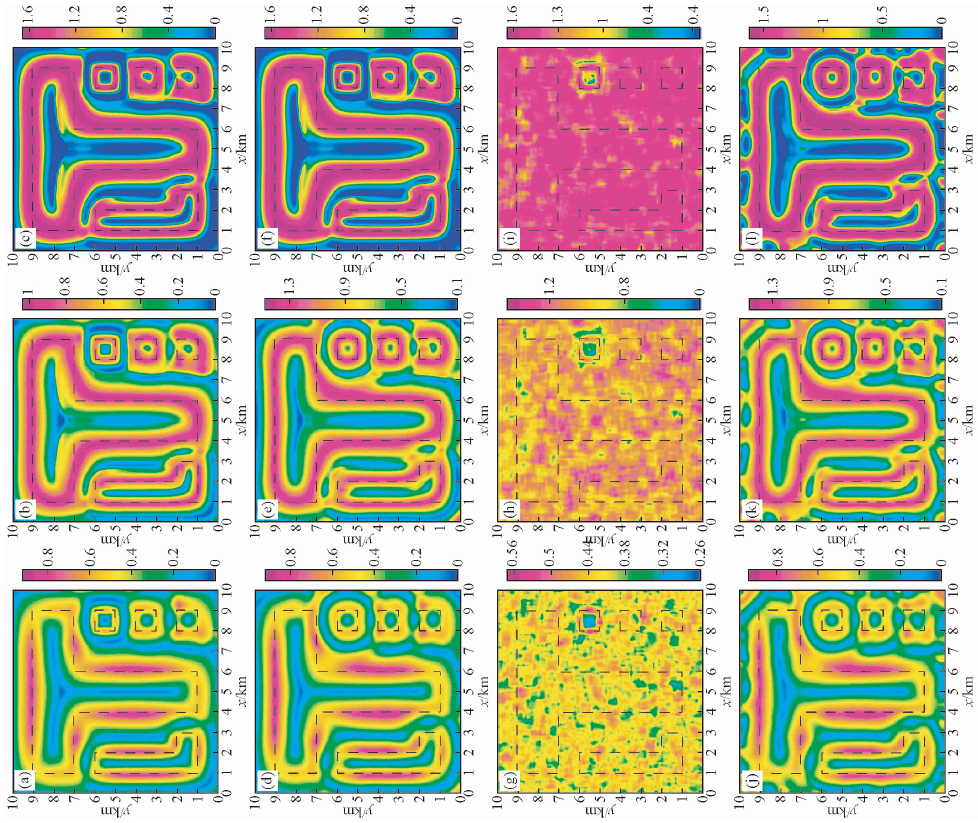 |
图 7 基于常规导数和视导数的归一化标准差及改进归一化标准差的边界识别结果 (a)、(b)、(c)分别是图 4b常规导数的NSTD、TASD1、TASD2;(d)、(e)、(f)分别是图 4b视导数的NSTD、TASD1、TASD2; (g)、(h)、(i)分别是图 4c常规导数的NSTD、TASD1、TASD2;(j)、(k)、(l)分别是图 4c视导数的NSTD、TASD1、TASD2. Fig. 7 NSTD and its improved versions with conventional and apparent derivative (m=3,Δn=10) (a),(b),(c) are NSTD,TASD1、TASD2 based on conventional derivative of the data Fig. 4b,respectively; (d),(e),(f) are NSTD,TASD1、TASD2 based on apparent derivative of the data Fig. 4b,respectively; (g),(h),(i) are NSTD,TASD1、TASD2 based on conventional derivative of the data Fig. 4c,respectively; (j),(k),(l) are NSTD,TASD1、TASD2 based on apparent derivative of the data Fig. 4c,respectively. |
从图 5中可以看出,在原异常中未含有噪声时(图 4b),水平总梯度(图 5a)清晰地反映出了埋深最浅地质体B3的边界,还可以模糊地识别出规模最大的地质体B2的边界,地质体B1和B4的边界也有所反映,但识别的边界存在明显的缺失,而在地质体B5上基本无信息反映;归一化水平总梯度(图 5b)较好地识别出了不同深度、不同规模地质体的边界,但识别边界的异常特征较为发散;改进的归一化水平总梯度(图 5c)更加精细地反映出了地质体的边界,但识别出的边界也存在一定的缺失(尤其地质体B5左上边界).而基于视导数的TDX(图 5d)、NTHD(图 5e)和ITDX3(图 5f)分别相对于5a、5b和5c来说,展示出了更多的边界信息,这表明了基于视导数的边界识别方法具有更高的分辨率.当原异常中含有噪声时,基于常规导数的TDX(图 5g)仅能模糊地识别出地质体B3的边界,而NTHD(图 5h)、ITDX3(图 5i)受随机干扰影响严重,已无法有效的识别出地质体的边界;基于视导数的TDX(图 5j)、NTDX(图 5k)及ITDX3(图 5l)除了测区边部存在波动外,仍可清晰地识别出地质体的边界.
从图 6可以看出,基于常规导数的Theta map(图 6a)虽然较好地平衡了不同深度地质体的边界异常,但边界异常特征过于发散,展示的边界异常位置与真实地质体边界存在较大偏差;ITM1(图 6b)与Theta map的异常特征相似,同样反映边界的异常特征过于发散;ITM3(图 6c)提高了原方法的边界异常收敛性,但反映边界的异常位置与真实边界偏差仍较大;基于视导数的Theta map(图 6d)、ITM1(图 6e)和ITM3(图 6f)不仅清晰地反映出了地质体的边界,且异常极大值圈闭更加接近于场源边界;当原始异常含有随机干扰时,常规导数的Theta map(图 6g)、ITM1(图 6h)和ITM3(图 6i)均受高频干扰影响严重,基本上都无法识别出地质体的边界;而基于视导数的Theta map(图 6j)、ITM1(图 6k)和ITM3(图 6l)仍可清晰地识别出所有地质体边界.
图 7可以看出,基于常规导数的NSTD(图 7a)可以较好地平衡不同深度地质体边界的异常特征,但识别边界的极值圈闭连续性较差;而TASD1(图 7b)和TASD2(图 7c)显著地提高了原方法的边界识别能力,除地质体B5上边界外,该方法清晰地识别出了地质体的其他边界;基于视导数的NSTD(图 7d)的异常特征与图 7a基本相同,而基于视导数的TASD1(图 7e)和TASD2(图 7f)可以清晰地显示出场源的所有边界;当原异常中含有噪声时,基于常规导数的NSTD(图 7g)、TASD1(图 7h)和TASD2(图 7i)除地质体B3边界有模糊显示外,其他场源边界均无信息反映,而基于视导数的NSTD(图 7k)、TASD1(图 7j)和TASD2(图 7l)同样除边部数据存在波动外,对地质体边界仍有着清晰的展示.
上述实验结果表明,改进的边界识别方法虽然无法提高原方法的计算稳定性,但可以提高原方法对边界的精细识别能力;而基于视导数的边界识别方法不仅具有更强的计算稳定性,还可以检测出更多的边界信息,这也再次说明了视导数相对于常规导数具有强稳定性和高分辨率的优势.
4 实例应用为了验证视导数在实际资料中的应用效果,选取了黑龙江虎林盆地布格重力异常进行试算.虎林盆地位于那丹哈达岭燕山褶皱带和吉黑华力西褶皱带的交接处,南至兴凯湖,北接完达山,西至勃利盆地、宝清地体,东临锡霍特山脉(图 8),该盆地是在构造复杂的环境中形成的中新生代坳陷带,其内部次级构造发育,是大庆油田外围东带油气勘探的重点地区之一(曹成润等,2001;林泽付等,2004;张凤旭等,2010).
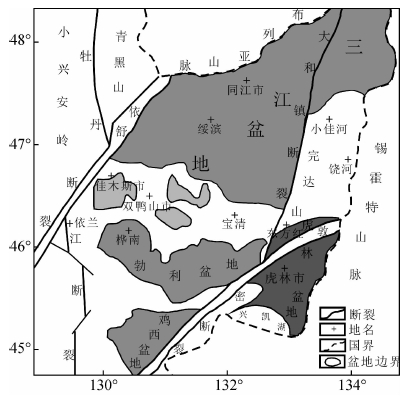 | 图 8 虎林盆地区域位置图(张渝金,2010) Fig. 8 Regional-position map of Hulin Basin(From Zhang Yujin,2010) |
虎林盆地重力异常(图 9a)等值线分布较为复杂,反映断层平面展布的重力场标志不仅表现为大、小型重力异常梯级带特征,而且表现为封闭等值线突然变宽或变窄以及等值线扭曲等非梯级带特征.该地区的重力异常已被多种边界方法处理过(张凤旭等,2007;Jiang and Gao,2012; 刘银萍等,2012;王彦国等,2012,2013),这里将主要的已知断裂构造的水平位置在布格重力异常图用黑色虚线标出.
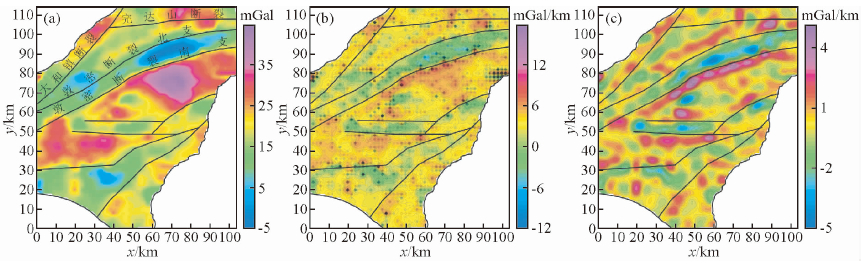 | 图 9 虎林盆地重力异常;(b)常规垂向一阶导数;(c)迭代差分3次垂向一阶视导数(Δn=10) Fig. 9 (a)Bouguer gravity anomaly of Hulin Basin;(b)Conventional vertical derivative;(c)Apparent vertical derivative based on iterative differential(m=3,Δn=10) |
首先,对原始异常利用常规垂向一阶导数和垂向一阶视导数进行处理,结果分别见图 9b和图 9c.可以看出,资料的数字化带来的珠状圈闭异常在原异常(图 9a)中没有显示,但在常规垂向导数(图 9b)有着明显的反映,同时,常规导数在整体上表现出的异常特征与原始异常基本相似,并没有显著地提高异常的分辨率;而垂向视导数(图 9c)不仅具有较强的计算稳定性,同时清晰地展示出了异常间的相互关系,显著地提高了原异常的分辨能力.
接下来,利用基于常规导数和视导数的上述边界识别方法对重力数据进行处理,结果见图 10. 基于常规导数的NTHD(图 10a)同样展示出了明显的串珠状异常,且识别边界的响应特征连续性较差,不利于边界的精确定位;基于常规导数的Theta map(图 10b)虽然反映地质体边界的极值圈闭连续性较好,但反映地质体边界的异常特征较宽泛,不利于场源边界的精细检测;基于常规导数的NSTD(图 10c)基本上消除了导数中的珠状特征,但反映边界的异常圈闭连续性欠佳.基于视导数的ITDX3(图 10d)、ITM3(图 10e)及TASD2(图 10f)不仅具有较强的抗干扰能力,而且较强地刻画出了不同地质体的界限,并与已知断裂有着较好的对应关系,同时还反映出了更多的边界细节信息,尤其TASD2(图 10f)刻画的边界信息尤为丰富.需要指出的是,完达山断裂是完达山地体与虎林盆地的重要界限(曹成润等,2001),但该断裂在重力图(图 9a)中反映并不明显,常规边界识别方法(图 10a~c)未能有效识别,且一直未被前人提出的边界识别方法所检测(张凤旭等,2007;Jiang and Gao,2012; 刘银萍等,2012;王彦国等,2012,2013),而基于视导数的TASD2(图 10f)可清晰地展示出该断裂的存在;不仅如此,在敦密断裂南支南侧,基于视导数的边界检测方法还检测出一条明显的东北走向断裂带(图 10d~f虚线所示),推断可能是敦密断裂的另一分支.
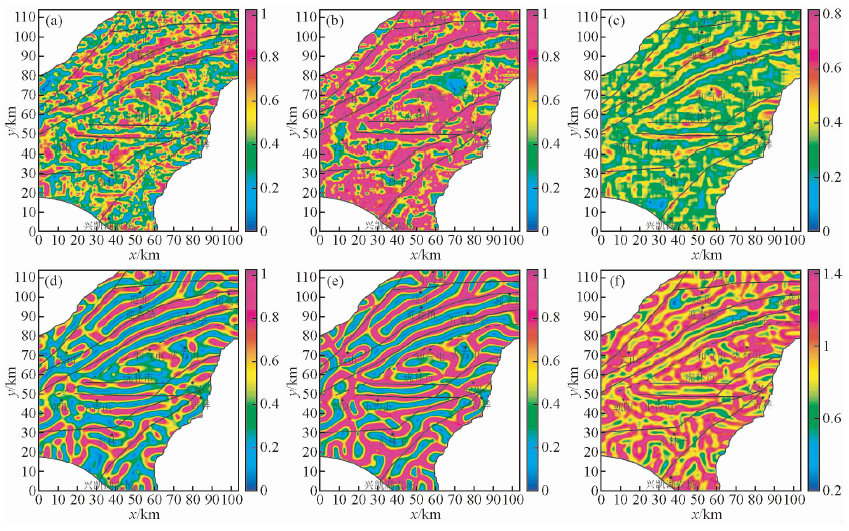 |
图 10 基于常规导数和迭代差分3次视导数(Δn=10)的边界识别结果 (a)、(b)、(c)分别是基于常规导数的NTHD、Theta map和NSTD;(d)、(e)、(f)分别是基于视导数的ITDX、ITM和TASD. Fig. 10 Results of edge detection based on conventional and apparent derivative(m=3, Δn=10) (a), (b), (c)are NTHD,Theta map, NSTD based on conventional derivative of the data in Fig. 9a, respectively;(d), (e), (f)are ITDX3,ITM3, TASD2 based on apparent derivative of Fig. 9a, p=3, respectively. |
上述结果表明,视导数不仅提高了常规导数的稳定性,而且还可以提高异常的分辨能力,同时基于视导数的边界识别方法可以提供更多、更清晰的边界细节信息,这充分地说明了视导数的实用性及优越性.
5 结 论5.1 针对常规导数存在计算精度和不稳定性之间的问题,本文提出了位场导数转换的新方法——基于迭代差分的视导数,其带通滤波特性表明了方法在理论上具备强稳定性,模型试验和实际算例表明视导数具有高分辨率和强抗干扰的能力.
5.2 文中还对常用的三种边界识别方法进行了简易改造,试验证实了改造后的边界检测方法所反映的场源边界异常更加精细地收敛于实际地质体边界位置.同时,试验还表明,基于视导数的边界识别方法具有更稳定的计算结果和更强的边界识别能力.在实例应用中,基于视导数的边界识别方法不仅获得了区域断裂构造的水平位置,还显示了更丰富的边界细节特征.
5.3 本文提出的视导数是一种非常灵活、有效的位场数据处理方法,该方法相对常规导数具有较强的抗噪能力和较高的异常分辨能力,因此具有良好的应用前景.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Cao C R, Liu Z H, Wang D P. 2001. The structure features and the movement regularity of fault blocks in Hulin basin, east Heilongjiang Province[J]. Journal of Changchun University of Science and Technology (in Chinese), 31(4): 340-344. |
| [2] | Cordell L. 1979. Gravimetric expression of graben faulting in Santa Fe country and the espanola basin, New Mexico[A]. //Ingersoll R V, Woodward L A, James H L, eds. New Mexico: New Mexico Geological Society. Guidebook: 30th Field Conference. Santa Fe Country: New Mexico Geological Society, 59-64. |
| [3] | Cooper G R J, Cowan D R. 2008. Edge enhancement of potential-field data using normalized statistics[J]. Geophysics, 73(3): H1-H4. |
| [4] | Hou Z C. 1981. Filtering of smooth compensation[J]. Oil Prospecting for Petroleum (in Chinese), (2): 22-29. |
| [5] | Jiang F Y, Gao L K. 2012. Edge enhancement of gravity anomalies and gravity gradient tensors using an improved small sub-domain filtering method[J]. Applied Geophysics, 9(2): 119-130. |
| [6] | Li H W. 2012. Research on iteration method using in potential field transformations and its filter characteristic (in Chinese)[Ph. D. thesis]. Beijing: China University of Geosciences, 47-56. |
| [7] | Lin Z F, Xue J, Yang S, et al. 2004. Characteristics of gravity-magnetic anomaly and their geological interpretation on map-area of Hulin City in Heilongjiang Province[J]. Global Geology (in Chinese), 23(4): 397-401. |
| [8] | Liu Y P, Wang Z W, Du X J, et al. 2012. Boundary detection method and its application in Hulin Basin[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 42(S3): 271-278. |
| [9] | Ma G Q, Li L L. 2012. Edge detection in potential fields with the normalized total horizontal derivative[J]. Computers & Geosciences, 41: 83-87. |
| [10] | Ma G Q, Huang D N, Yu P, et al. 2012. Application of improved balancing filters to edge identification of potential field data[J]. Chinese Journal of Geophysics (in Chinese), 55(12): 4288-4295, doi: 10.6038/j.issn.0001-5733.2012.12.040. |
| [11] | Reid A B, Allsop J M, Granser H, et al. 1990. Magnetic interpretation in three dimensions using Euler deconvolution[J]. Geophysics, 55(1): 80-91. |
| [12] | Stavrev P, Reid A. 2010. Euler deconvolution of gravity anomalies from thick contact/fault structures with extended negative structural index[J]. Geophysics, 75(6): 151-158. |
| [13] | Tai Z H, Zhang F X, Liu G X, et al. 2014. Potential field edge detection based on difference derivative with cosine of pseudo total gradient[J]. Oil Geophysical Prospecting (in Chinese), 49(4): 807-814. |
| [14] | Thompson D T. 1982. EULDPH—A new technique for making computer assisted depth estimates from magnetic data[J]. Geophysics, 47(1): 31-37. |
| [15] | Wang W Y, Qiu Z Y, Yang Y, et al. 2010. Some advances in the edge recognition of the potential field[J]. Progress in Geophysics (in Chinese), 25(1): 196-210, doi: 10.3969/j.issn.1004-2903.2010.01.027. |
| [16] | Wang Y G, Wang Z W, Zhang F X, et al. 2012. Edge detection of potential field based on normalized vertical gradient of mean square error ratio[J]. Journal of China University of Petroleum (in Chinese), 36(2): 86-90, 96. |
| [17] | Wang Y G, Zhang F X, Wang Z W, et al. 2013. Edge Detection of potential field using normalized differential[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 43(2): 592-602. |
| [18] | Wang Y G. 2013. Study and application of high-precision methods in potential-field data processing (in Chinese)[Ph. D. thesis]. Changchun: Jilin University, 20-31. |
| [19] | Wijns C, Perez C, Kowalczyk P. 2005. Theta map: edge detection in magnetic data[J]. Geophysics, 70(4): L39-L43. |
| [20] | Yao C L, Guan Z N, Huang W N. 1997. Resampled grouping method for potential field transformation[J]. Oil Geophysical Prospecting (in Chinese), 32(5): 696-702. |
| [21] | Yao C L, Li H W, Zhen Y M, et al. 2012. Research on iteration method using in potential field transformations[J]. Chinese Journal of Geophysics (in Chinese), 55(6): 2062-2078, doi: 10.6038/j.issn.0001-5733.2012.06.028. |
| [22] | Zeng H L, Meng X H, Yao C L, et al. 2002. Detection of reservoirs from normalized full gradient of gravity anomalies and its application to Shengli oil field, east China[J]. Geophysics, 67(4): 1138-1147. |
| [23] | Zhang F X, Meng L S, Lin Z F, et al. 2004. Study on gravity anomaly, basin structure and gas-oil potential of the Hulin basin in Heilongjiang Province[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 34(4): 555-559. |
| [24] | Zhang F X, Meng L S, Zhang F Q, et al. 2005. Calculating normalized full gradient of gravity anomaly using Hilbert transform[J]. Chinese Journal of Geophysics (in Chinese), 48(3): 704-709, doi: 10.3321/j.issn:0001-5733.2005.03.031. |
| [25] | Zhang F X, Zhang F Q, Liu C, et al. 2007. A technique for elaborate explanation of faulted structures: three-directional small subdomain filtering[J]. Chinese Journal of Geophysics (in Chinese), 50(5): 1543-1550, doi: 10.3321/j.issn:0001-5733.2007.05.031. |
| [26] | Zhang F X, Zhang X Z, Zhang F Q, et al. 2010. Study on geology and geophysics on structural units of Hulin Basin in Heilongjiang Province[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 40(5): 1170-1176. |
| [27] | Zhang J S, Gao R, Li Q S, et al. 2011. A combined Euler and analytic signal method for an inversion calculation of potential data[J]. Chinese Journal of Geophysics (in Chinese), 54(6): 1634-1641, doi: 10.3969/j.issn.0001-5733.2011.06.023. |
| [28] | Zhang Y J. 2010. Analysis of petroleum geological conditions in the Qihulin River depression of Hulin Basin (in Chinese)[MSc thesis]. Changchun: Jilin University, 4-7. |
| [29] | 曹成润, 刘正宏, 王东坡. 2001. 黑龙江省东部虎林盆地断块构造特征及其运动学规律[J]. 长春科技大学学报, 31(4): 340-344. |
| [30] | 侯重初. 1981. 补偿圆滑滤波方法[J]. 石油物探, (2): 22-29. |
| [31] | 李宏伟. 2012. 位场转换计算中迭代法与其滤波特性的综合分析与研究[博士论文]. 北京: 中国地质大学(北京), 47-56. |
| [32] | 林泽付, 薛进, 杨恕等. 2004. 黑龙江省虎林市幅重磁场特征及其地质解释[J]. 世界地质, 23(4): 397-401. |
| [33] | 刘银萍, 王祝文, 杜晓娟,等. 2012. 边界识别技术及其在虎林盆地中的应用[J]. 吉林大学学报(地球科学版), 2012, 42 (S3): 271-278. |
| [34] | 马国庆, 黄大年, 于平,等. 2012. 改进的均衡滤波器在位场数据边界识别中的应用[J]. 地球物理学报, 55(12): 4288-4295, doi: 10.6038/j.issn.0001-5733.2012.12.040. |
| [35] | 邰振华, 张凤旭, 刘国兴,等. 2014. 基于差分求导的伪总梯度余弦值法的位场边界检测[J]. 石油地球物理勘探, 49(4): 807-814. |
| [36] | 王万银, 邱之云, 杨永等. 2010. 位场边缘识别方法研究进展[J]. 地球物理学进展, 25(1): 196-210, doi: 10.3969/j.issn.1004-2903.2010.01.027. |
| [37] | 王彦国, 王祝文, 张凤旭,等. 2012. 基于均方差比归一化垂向梯度法的位场边界检测[J]. 中国石油大学学报(自然科学版), 36(2): 86-90, 96. |
| [38] | 王彦国. 2013. 位场数据处理的高精度方法研究及应用[博士论文]. 长春: 吉林大学, 20-31. |
| [39] | 王彦国, 张凤旭, 王祝文,等. 2013. 位场归一化差分法的边界检测技术[J]. 吉林大学学报(地球科学版), 43(2): 592-602. |
| [40] | 姚长利, 管志宁, 黄卫宁. 1997. 位场转换的抽样分组法[J]. 石油地球物理勘探, 32(5): 696-702. |
| [41] | 姚长利, 李宏伟, 郑元满,等. 2012. 重磁位场转换计算中迭代法的综合分析与研究[J]. 地球物理学报, 55(6): 2062-2078, doi: 10.6038/j.issn.0001-5733.2012.06.028. |
| [42] | 张凤旭, 孟令顺, 林泽富,等. 2004. 黑龙江省虎林盆地重力异常、基底构造及油气远景区研究[J]. 吉林大学学报(地球科学版), 34(4): 555-559. |
| [43] | 张凤旭, 孟令顺, 张凤琴,等. 2005. 利用Hilbert变换计算重力归一化总梯度[J]. 地球物理学报, 48(3): 704-709, doi: 10.3321/j.issn:0001-5733.2005.03.031. |
| [44] | 张凤旭, 张凤琴, 刘财,等. 2007. 断裂构造精细解释技术—三方向小子域滤波[J]. 地球物理学报, 50(5): 1543-1550, doi: 10.3321/j.issn:0001-5733.2007.05.031. |
| [45] | 张凤旭, 张兴洲, 张凤琴,等. 2010. 黑龙江省虎林盆地单元结构的地质—地球物理研究[J]. 吉林大学学报(地球科学版), 40(5): 1170-1176. |
| [46] | 张季生, 高锐, 李秋生,等. 2011. 欧拉反褶积与解析信号相结合的位场反演方法[J]. 地球物理学报, 54(6): 1634-1641, doi: 10.3969/j.issn.0001-5733.2011.06.023. |
| [47] | 张渝金. 2010. 虎林盆地七虎林河坳陷油气地质条件分析[硕士论文]. 长春: 吉林大学, 4-7. |
 2016, Vol. 31
2016, Vol. 31

