2. 国家能源页岩油研发中心, 北京 100083;
3. 中国石化页岩油气勘探开发重点实验室, 北京 100083;
4. 中国石化石油勘探开发研究院, 北京 100083;
5. 胜利油田鲁胜石油开发有限责任公司, 东营 257077
2. National Energy R & D Center of Shale Oil, Beijing 100083, China;
3. SinoPEC Key Laboratory of Shale Oil/Gas Exploration and Production Technology, Beijing 100083, China;
4. SinoPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China;
5. Lusheng Petroleum Development Co., Ltd, Dongying 257077, China
几乎所有油气藏都会在某种程度上受到天然裂缝的影响.地下发育的裂缝往往是油气存储的重要场所,而裂缝作为一种普遍现象广泛地存在于各类岩石地层中.在碳酸盐岩储层中,天然裂缝有助于形成次生孔隙,并强化了储集空间的连通性.在大多数非常规储层,包括煤层气、页岩气、基岩和火山岩储层中,天然裂缝是主要的产能影响因素.
裂缝的形成受多种因素控制,其物理属性复杂,横向、纵向变化大,表现出很强的各向异性.因此利用各向异性的地震响应检测裂缝是当前地球物理学家们研究热点,其理论研究的基础是等效介质模型.等效理论模型通过一定的假设条件把实际的裂缝储层理想化,建立地震响应与裂缝性质的关系.根据岩石组分、孔隙和颗粒结构、流体饱和程度等,量化储层岩石的弹性和非弹性特征.传统的裂缝各向异性等效介质理论(Schoenberg,1980; Hudson,1980,1981)没有考虑频率对弹性参数的影响,导致这些模型缺乏对裂缝尺寸的敏感度.比如,均匀各向同性介质背景中发育少数定向排列的大裂缝而得到的弹性参数可以等效为相同介质背景中发育多个定向排列的小裂缝的情况.因此,一些学者提出了考虑地震波诱导流体流动机制的等效模型(Thomsen,1995;Hudson et al.,1996;Pointer et al.,2000;van der Kolk et al.,2001)并开展了流体识别(吴小羊,2010;印兴耀等,2013),但这些模型并不能很好的解释整个频率范围内地震各向异性频变特征.Chapman(2001,2003)提出了考虑了裂缝及孔隙间流体流动情况的动态等效岩石物理模型,可以很好的解释实验室测量岩石样本(Sothcott et al.,2000)速度随频率与饱和度的变化规律,并将各向异性的频变特征拓展到全频率范围.
AVAZ(amplitude versus offset and azimuth)分析即研究地震子波经界面反射后振幅随入射角和方位角的变化,可定量研究HTI(horizontal transverse isotropic)介质的裂缝性质.然而,基于AVAZ特征的反演裂缝性质的研究受到长波长假设条件下静态等效介质模型的限制,一般只能反演裂缝密度和裂缝方向(朱培民等,2001;张广智等,2011;刘财等,2013).近年来,随着考虑了流动机制的裂缝性孔隙介质模型的发展(杨顶辉,2002;郭智奇等,2007;魏修成,2008;王者江,2008;张显文等,2009;杜启振等,2009),频变AVAZ特征被证明对更多的裂缝性质具有敏感性(刘喜武等,2015). Ali和Jakobsen(2013)利用频变AVAZ信息反演裂缝走向、裂缝密度、裂缝开度和裂缝半径,并估计渗透率;兰慧田(2014)利用频变AVO反演裂缝密度、裂缝半径和孔隙度.本文以Rüger近似公式和Chapman等效理论为基础,开展频变AVAZ响应特征分析;基于地震频变AVAZ响应和地质、测井得到的裂缝性质先验信息,提出了将贝叶斯理论和遗传算法与结合运用反演裂缝密度、裂缝走向、裂缝长度和流体充填类型的频变AVAZ反演新方法.该方法可以利用统计的方法分别展示裂缝参数的概率分布情况,减少反演结果对先验信息的依赖性.
1 频变AVAZ响应特征分析1.1 Chapman等效理论Chapman提出的动态岩石物理模型是基于喷射流机制,考虑了地震波引起的定向排列的裂缝、随机排列的微裂隙和背景等径孔隙间的流体流动,得到具有频率依赖性的弹性参数,可以更合理的解释地震波的散射或吸收引起的地震响应衰减与频散.其中,微裂隙和孔隙的半径与岩石颗粒尺寸相同,而裂缝的半径远大于颗粒尺寸且小于地震波波长.微裂隙之间、孔隙之间以及微裂隙与孔隙之间可相互连通,每条裂缝可以与多个微裂隙或孔隙连通,但裂缝之间互不连通,每条微裂隙、每个孔隙最多与一条裂缝连通.Chapman模型定义的有效刚度张量为
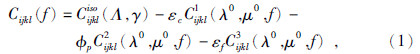

Λ和γ没有明确的物理意义,定义为
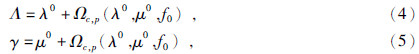
另外,该理论指出,当裂缝性孔隙岩石中的球形孔隙的孔隙度远大于微裂隙孔隙度且研究频段低于微观喷射流动频率fm时,式(1)中与微裂隙项可以被忽略,以便于计算,同时这也符合大多数裂缝性储层的野外地震勘探情况.
1.2 频变各向异性和频变AVAZ特征Rüger(1997,1998)推导出了弱各向异性HTI介质的纵波反射系数近似公式为
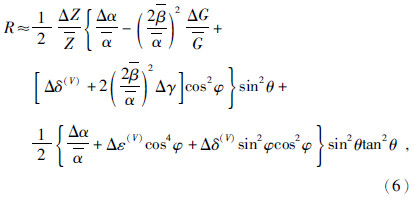
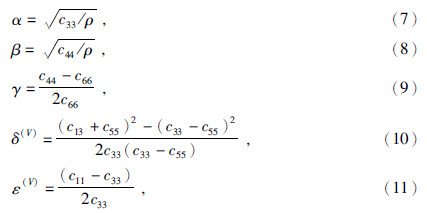
假设两层模型,上层为均匀各向同性介质,下层为HTI介质.孔隙度φp为0.1,微裂隙密度为0,裂缝密度为0.1,裂缝长度为1 m,其他主要参数如表 1所示.HTI介质的各向异性如图 1所示,γ不受频率和流体类型的影响.流体类型为气态时,δ(V)和ε(V)频变最大且频变发生在地震频带范围内;流体类型为油时,δ(V)和ε(V)频变最小且频变发生在频率极低的情况;流体类型为盐水时,δ(V)和ε(V)频变主要发生在30 Hz以内.当流体类型为气态时,δ(V)和ε(V)的值接近,当流体类型为液态时δ(V)远小于ε(V)且接近于0.
|
|
表 1 两层模型的主要参数 Table 1 Two-layer model’s main parameters |
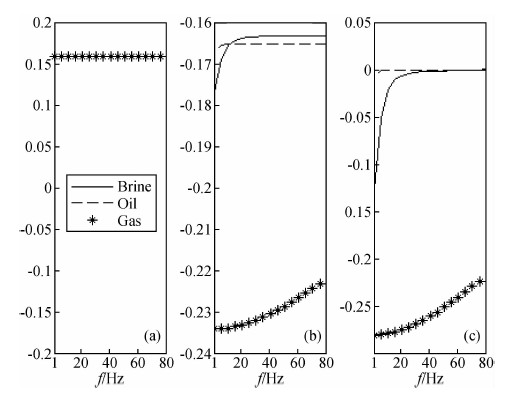 | 图 1 随频率变化的各向异性参数 (a)γ;(b)δ(V);(c)ε(V) Fig. 1 Anisotropic parameters with respect to frequency. (a)γ;(b)δ(V); (c) ε(V) |
无论流体为油、盐水还是气时,随着频率的增加,AVAZ响应特征变化越来越大;随着入射角的增大,反射系数随频率的变化特征也呈现越来越大的趋势;检波点在垂直裂缝走向时反射系数受频率的影响低于检波点沿着裂缝走向时反射系数受频率的影响(图 2-图 4).尽管岩石骨架相同,但是不同流体受频率的影响不同:流体为气体时反射系数受频率影响最大,流体为油时反射系数受频率影响最小,即随着流体的粘滞系数的增大,反射系数受频率的影响减小.将模型中裂缝长度分别变为0.5 m和2 m,得到含盐水时的频变AVAZ响应特征(图 5和图 6).对比图 3、图 5和图 6,随着裂缝长度的减小,AVAZ响应受到频率的影响越大.因此,流体类型和裂缝长度是对频变AVAZ响应特征敏感的裂缝参数.即使不考虑频率的影响,裂缝密度和裂缝走向均是AVAZ响应的敏感参数(Liu et al.,2012),在此不再赘述.综上所述,频变AVAZ响应特征可以用于反演对其敏感的裂缝性质即裂缝密度、裂缝走向、裂缝长度和流体类型.
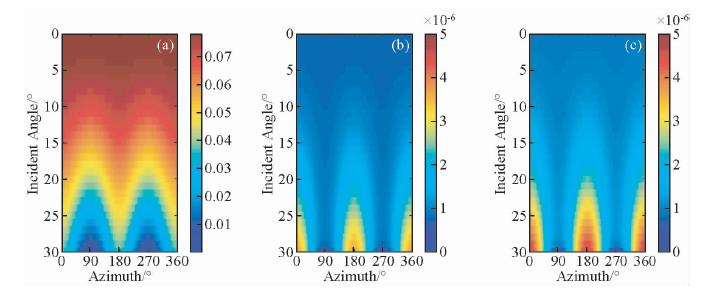 |
图 2 流体为油时频变AVAZ响应 (a)频率为10 Hz时AVAZ响应; (b)频率为20 Hz和10 Hz时AVAZ响应差值; (c)频率为40 Hz和10 Hz时AVAZ响应差值. Fig. 2 Frequency-dependent AVAZ response when fractures filled with oil (a) AVAZ response when frequency is 10 Hz. (b) The differences of AVAZ response when frequencies are 20 Hz and 10 Hz. (c) Same as (b) but when frequencies are 40 Hz and 10 Hz. |
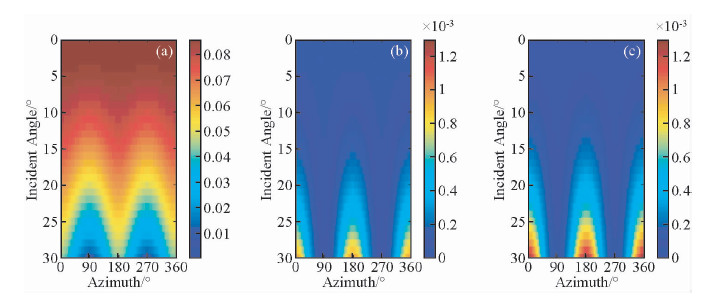 |
图 3 流体为盐水时频变AVAZ响应 (a)频率为10 Hz时AVAZ响应;(b)频率为20 Hz和10 Hz时AVAZ响应差值; (c)频率为40 Hz和10 Hz时AVAZ响应差值. Fig. 3 Frequency-dependent AVAZ response when fractures filled with brine (a)AVAZ response when frequency is 10 Hz; (b) The differences of AVAZ response when frequencies are 20 Hz and 10 Hz; (c) Same as (b) but when frequencies are 40 Hz and 10 Hz. |
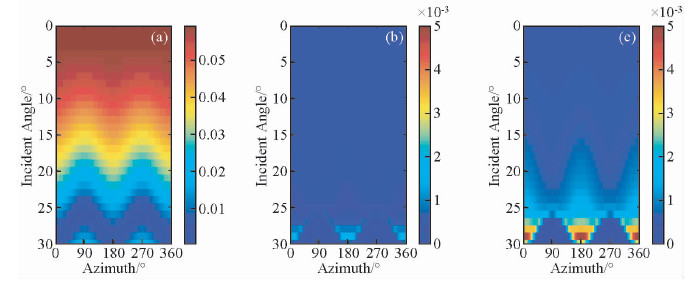 |
图 4 流体为气体时频变AVAZ响应 (a)频率为10 Hz时AVAZ响应; (b)频率为20 Hz和10 Hz时AVAZ响应差值; (c)频率为30 Hz和10 Hz时AVAZ响应差值; (d)频率为40 Hz和10 Hz时AVAZ响应差值. Fig. 4 Frequency-dependent AVAZ response when fractures filled with gas (a)AVAZ response when frequency is 10 Hz; (b) The differences of AVAZ response when frequencies are 20 Hz and 10 Hz; (c) Same as (b) but when frequencies are 40 Hz and 10 Hz. |
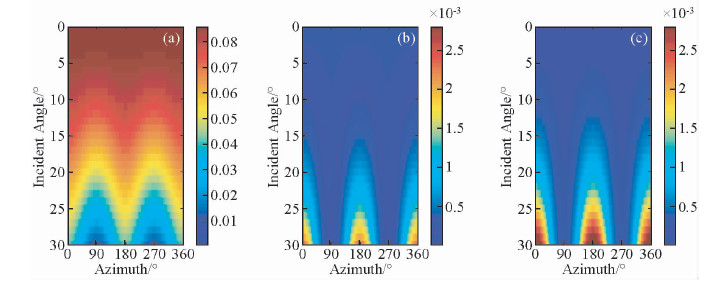 |
图 5 流体为盐水且裂缝长度为0.5 m时频变AVAZ响应 (a)频率为10 Hz时AVAZ响应; (b)频率为20 Hz和10 Hz时AVAZ响应差值; (c)频率为30 Hz和10 Hz时AVAZ响应差值; (d)频率为40 Hz和10 Hz时AVAZ响应差值. Fig. 5 Frequency-dependent AVAZ response when fractures filled with brine and fracture length is 0.5 m (a)AVAZ response when frequency is 10 Hz; (b) The differences of AVAZ response when frequencies are 20 Hz and 10 Hz; (c) Same as (b) but when frequencies are 40 Hz and 10 Hz. |
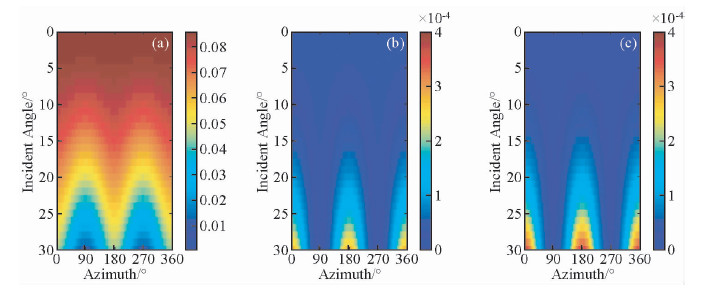 |
图 6 流体为盐水且裂缝长度为2 m时频变AVAZ响应 (a)频率为10 Hz时AVAZ响应; (b)频率为20 Hz和10 Hz时AVAZ响应差值; (c)频率为40 Hz和10 Hz时AVAZ响应差值. Fig. 6 Frequency-dependent AVAZ response when fracture filled with brine and fracture length is 2 m (a)AVAZ response when frequency is 10 Hz; (b) The differences of AVAZ response when frequencies are 20 Hz and 10 Hz; (c) Same as (b) but when frequencies are 40 Hz and 10 Hz. |
贝叶斯定理是一种可以用于计算条件概率分布的概率学理论.最大的特点是将未知参数的看做随机变量,从而有了参数的分布,并给出区间估计.数学上,贝叶斯理论可以表示为
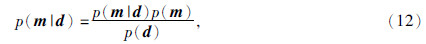


这个方程表明贝叶斯理论主要取决于构建或者模拟问题的先验分布.因此,必须选择合理的先验概率分布,才能获得可靠的反演结果.基于贝叶斯理论可以将多学科信息进行融合.
2.2 裂缝性质反演方法及模型测试对于裂缝预测问题,根据通过地震观测信息可获得模型参数的似然函数,地质和测井等手段得到的参数信息作为先验分布. 然而,由于裂缝的复杂性,地质和测井等信息与地震信息可能会出现不一致的情况,因此,为了控制基于贝叶斯理论的多参数反演结果对先验信息的依赖程度,本文提出了贝叶斯理论与遗传算法混合运用的反演流程.
首先,根据遗传算法结果构建裂缝参数似然函数.Chapman理论和Rüger近似的频变纵波反射系数函数为R(θ,φ,f;e,l,t,o).其中,f是频率,e是裂缝密度,l是裂缝长度,t是流体类型,o是构建Chapman模型时涉及的其他参数且在本文反演过程中作为已知参数.假设观测数据Rijk是在一系列离散的入射角θi,方位角φj和频fk率情况下的合成数据.定义某一测线的方位角为φ,根据观测系统信息可计算其他测线与该测线方位角的差为ηj,即其他测线方位角为φj=φ+ηj.建立的目标函数为
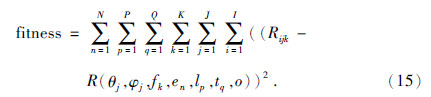
基于如图 3所示的合成频变AVAZ响应和公式(15)构建目标函数并定义方位角为30°的测线为待求方位测线,运用遗传算法求解可以得到一组方位角,裂缝密度,裂缝长度和流体类型.如图 7所示,条带的分布是遗传算法最后一代种群数,遗传算法结果与模型参数设置吻合.若将其中一个未知裂缝参数看做随机变量m,则数据噪声和一些理论误差n为
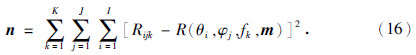
将随机变量m与其数据噪声和理论误差n结合高斯分布,并适当调整方差,可以得到该参数的似然函数概率分布(图 7).
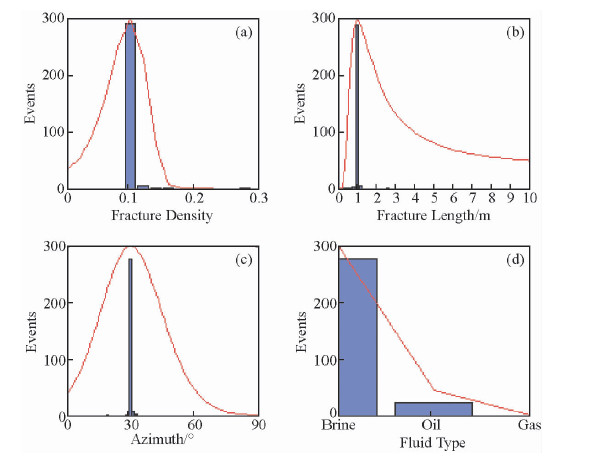 | 图 7 遗传算法裂缝性质反演结果(条带)及其似然函数概率分布(曲线) Fig. 7 The solution of fracture properties using GA (bar) and their scaled likelihood function (red line) |
其次,加入先验信息获得后验概率分布.加入如表 2所示的与合成数据的模型一致的先验信息,并令先验信息服从高斯分布,如图 8所示,结合先验信息和似然函数后得到的归一化后验概率分布.统计结果展示了在各个模型参数空间上的分布概率.
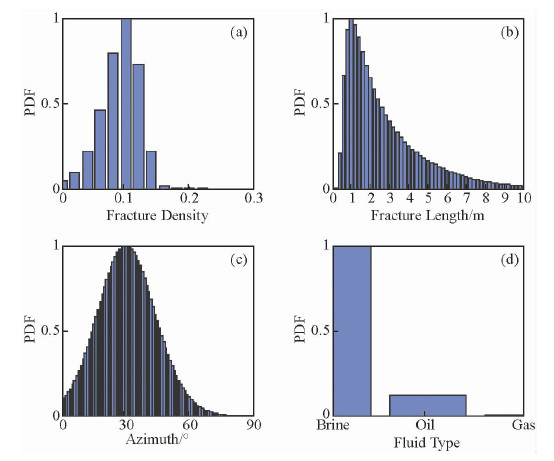 | 图 8 先验信息与合成数据的模型一致时裂缝性质后验概率分布 Fig. 8 The normalized posterior distribution with the prior information identified the model for synthetic data |
最后,进行先验信息的影响分析.为了分析根据地质、测井信息得到的先验信息对反演结果的影响,加入如表 2所示的先验信息,该先验信息与合成地震数据的模型不一致且差别较大(表 2),此时反演结果即后验概率是地震频变AVAZ反演结果与先验信息的一个综合响应(图 9).若减小先验裂缝参数的方差,裂缝性质后验概率分布受先验信息影响比较大,参数概率分布最大值比较接近先验裂缝参数值(图 10);若增大先验裂缝参数的方差,裂缝性质后验概率分布受似然函数即地震信息影响比较大,参数概率分布最大值比较接近合成地震数据的模型参数值(图 11).总之,可以通过调节先验裂缝参数的方差来均衡地震数据及地质、测井数据的信息采用量.
|
|
表 2 先验信息 Table 2 Prior information |
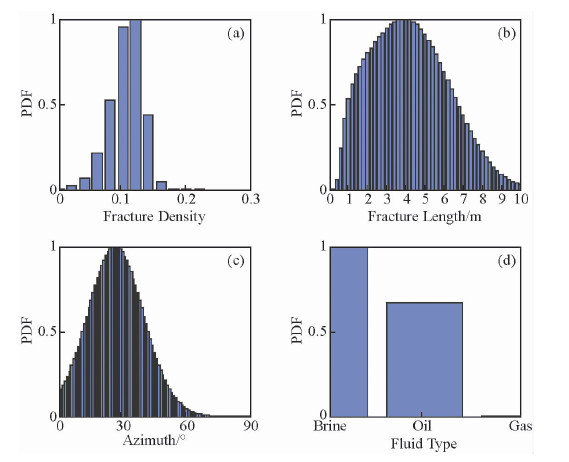 | 图 9 先验信息与合成数据的模型不一致时裂缝性质后验概率分布 Fig. 9 The normalized posterior distribution with the prior information differed with the model for synthetic data |
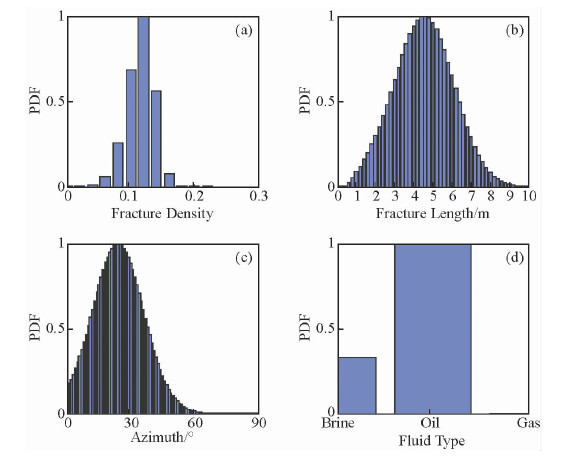 | 图 10 减小方差时裂缝性质后验概率分布(先验信息与合成数据模型不一致) Fig. 10 The normalized posterior distributions of fracture properties with a decreased standard deviation. (The prior information differed with the model for synthetic data) |
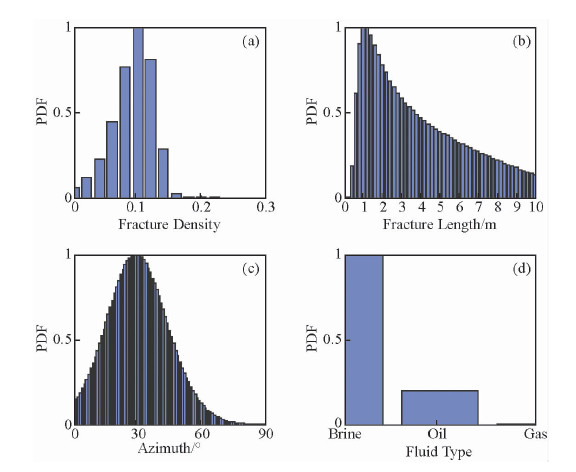 | 图 11 先验信息与合成数据模型不一致且增大方差时裂缝性质后验概率分布 Fig. 11 The normalized posterior distributions of fracture properties with an increased standard deviation. (The prior information differed with the model for synthetic data) |
本文分析了HTI介质频变AVAZ响应特征并提出了一种反演裂缝性质的新方法,可以同时反演裂缝密度、裂缝长度、裂缝方位和流体类型.通过对合成数据的分析和反演得到了以下认识:
(1)HTI介质受裂缝性质影响较大的各向异性参数不随频率发生变化;受流体性质影响较大的各向异性参数和随频率发生变化.
(2)AVAZ响应随频率变化特征随着流体粘滞性减小而增大.频变AVAZ响应对裂缝流体为气体和盐水的情况敏感性较好,对流体为油的情况敏感性较差.
(3)AVAZ响应随频率变化特征随着裂缝长度的减小而增大.
(4)本文提出贝叶斯理论与遗传算法的结合反演方法,可以减少反演结果对先验信息的依赖性并且有效的均衡地震数据及地质、测井数据的信息采用量.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Ali A, Jakobsen M. 2014. Anisotropic permeability in fractured reservoirs from frequency-dependent seismic amplitude versus angle and azimuth data [J]. Geophysical prospecting, 62(2):293-314. |
| [2] | Chapman M. 2001. Modelling the wide-band laboratory response of rock samples to fluid pressure changes [Ph. D. thesis]. Edinburgh: University of Edinburgh . |
| [3] | Chapman M. 2003. Frequency-dependent anisotropy due to mesoscale fractures in the presence of equant porosity [J]. Geophysical Prospecting,51(5):369-379. |
| [4] | Du Q, Kong L, Han S. 2009. Wavefield propagation characteristics in the fracture-induced anisotropic double-porosity medium [J](in Chinese). Chinese Journal of Geophysics, 52(4): 1049-1058. |
| [5] | Guo Z, Liu C, Yang B et al. 2007. Seismic wave fields modeling and feature in viscoelastic anisotropic media [J] (in Chinese). Progress in Geophysics.22(3): 804-810. |
| [6] | Hudson J A. 1980. Overall properties of a cracked solid [J]. Mathematical Proceedings of the Cambridge Philosophical Society, 88: 371-384. |
| [7] | Hudson J A. 1981. Wave speeds and attenuation of elastic waves in material containing cracks [J]. Geophysical Journal of the Royal Astronomical Society, 64(1):133-150. |
| [8] | Hudson J A, Liu E, Crampin S. 1996. The mechanical properties of materials with interconnected cracks and pores [J]. Geophysical Journal International ,124(1):105-112. |
| [9] | Lan H. 2014. Wave Field Modeling in Fractured Porous Media and Frequency-dependent AVO Reservoir Parameters [Ph. D. thesis](in Chinese). Changchun:Jilin University. |
| [10] | Li C, Yin X, Zhang G,et al. 2015. Prestack AVA inversion for pore fluid modulus based on the Bayesian theory[J] (in Chinese). Geophysical Prospecting for Petroleum,54(4):467-476. |
| [11] | Liu C, Liu Y, Feng X, et al. 2012. Constructing the convex quadratic function for the evaluation of crack density of HTI media using P- and converted waves [J] (in Chinese). Journal of Geophysics and Engineering, 9 (6) :729-735. |
| [12] | Liu C, Liu Y, Feng X, et al. 2013. Invert crack density of HTI media by using SVD based on PP-wave AVA data from crossing seismic survey lines [J] (in Chinese).Journal of Jilin University(Earth Science Edition),43(5):1655-1662. |
| [13] | Liu X, Dong N, Liu Y, et al. 2015. Progress on frequency-dependent AVAZ inversion for characterization of fractured porous media [J] (in Chinese). Geophysical Prospecting for Petroleum, 54(2):210-217. |
| [14] | Pointer T, Liu E, Hudson J A. 2000. Seismic wave propagation in cracked porous media [J]. Geophysical Journal International, 142(1): 199-231. |
| [15] | Rüger A. 1997. P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry [J]. Geophysics, 62(3) :713-722. |
| [16] | Rüger A. 1998 Variation of P-wave reflectivity with offset and azimuth in anisotropic media [J]. Geophysics,63(3):935-947. |
| [17] | Schoenberg M. 1980. Elastic wave behavior across linear slip interfaces [J]. Journal of the Acoustical Society of America, 68: 1516-1521. |
| [18] | Sothcott J, McCann C, O’Hara S G. 2000. The influence of two different pore fluids on the acoustic properties of reservoir sandstones at sonic and ultrasonic frequencies [A]. 70th SEG Meeting, Calgary, Canada, Expanded Abstracts[C], 1883-1886. |
| [19] | Thomsen L. 1995. Elastic anisotropy due to aligned cracks in porous rock [J]. Geophysical Prospecting, 1995, 43(3), 805-829. |
| [20] | Van der Kolk C M, Guest W S, Potters J H H M. 2001. The 3D shear experiment over the Natih field in Oman: the effect of fracture filling fluids on shear propagation [J]. Geophysical Prospecting, 49(2), 179-197. |
| [21] | Wang L, Gu H, Li Z et al.2014. The prestack Bayesian inversion prediction study of Ordovician fractured-vuggy carbonate reservoir in Tazhong area[J] (in Chinese).Geophysical Prospecting for Petroleum. 53(6):270-276. |
| [22] | Wang Z. 2008. A study of numerical simulation and propagation characteristics for 3D two phase orthotropic medium based on the BISQ mechanism[D] (in Chinese).Jilin: Jilin University. |
| [23] | Wei X, Lu M, Ba J et al. 2008. Dispersion and attenuation of elastic waves in a viscous fluid-saturated anisotropic porous solid[J] (in Chinese). Chinese Journal of Geophysics,2008,51(1):213-220. |
| [24] | Wu X. 2010. Frequency dependent AVO inversion using spectral decomposition techniques[D] (in Chinese). Wuhan: China University of Geosciences. |
| [25] | Yang D.2002. Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media[J]. (in Chinese).Chinese Journal of Geophysics,45(4):575-583. |
| [26] | Yin X, Li C,Zhang S. 2013. Seismic fluid discrimination based on two-phase theory[J]. (in Chinese).Journal of China University of Petroleum (Edition of Natural Sciences),2013,37(5):38-43. |
| [27] | Zhang G, Chen H, Yin X et al. 2012. Method of fracture elastic parameter inversion based on anisotropic AVO [J](in Chinese). Journal of Jilin University (Earth Science Edition)42(3):845-851. |
| [28] | Zhang X,Wang D, Wang Z et al. 2010. The study on azimuth characteristics of attenuation and dispersion in 3D two-phase orthotropic crack medium based on BISQ mechanism[J] (in Chinese). Chinese Journal of Geophysics. 53(10):2452-2459. |
| [29] | Zhu P, Wang J, YuW et al.2001. Inverting reservoir fracture density using P-wave AVO data. [J](in Chinese). Geophysical Prospecting for Petroleum. 40(2):1-12. |
| [30] | 杜启振,孔丽云,韩世春. 2009. 裂缝诱导各向异性双孔隙介质波场传播特征[J]. 地球物理学报, 52(4): 1049-1058. |
| [31] | 兰慧田.2014. 裂缝孔隙介质波场模拟与频变AVO储层参数反演[D].长春:吉林大学. |
| [32] | 郭智奇,刘 财,杨宝俊,等. 2007. 粘弹各向异性介质中地震波场模拟与特征[J] . 地球物理学进展,22(3): 804-810. |
| [33] | 李超,印兴耀,张广智,等. 2015. 基于贝叶斯理论的孔隙流体模量叠前AVA反演[J]. 石油物探,54(4):467-476. |
| [34] | 刘喜武,董宁,刘宇巍. 2015. 裂缝性孔隙介质频变AVAZ反演方法研究进展[J]. 石油物探,54(2):210-217. |
| [35] | 刘财,刘宇巍,冯晅,等. 2013. 基于方位相交的纵波AVA数据运用SVD反演HIT介质裂缝密度[J]. 吉林大学学报(地球科学版),43(5):1655-1662. |
| [36] | 杨顶辉.2002.双相各向异性介质中弹性波方程的有限元解法及波场模拟[J]. 地球物理学报,45(4):575-583. |
| [37] | 印兴耀,李超,张世鑫. 2013. 基于双相介质的地震流体识别[J].中国石油大学学报(自然科学版),37(5):38-43. |
| [38] | 王丽萍,顾汉明,李宗杰. 2014. 塔中奥陶系碳酸盐岩缝洞型储层贝叶斯叠前反演预测研究[J].石油物探,53(6):270-276. |
| [39] | 王者江.2008.基于BISQ机制的三维双相正交介质正演模拟及传播特性研究[D].吉林:吉林大学. |
| [40] | 魏修成.2008.含黏滞流体各向异性孔隙介质中弹性波的频散和衰减[J].地球物理学报,51(1):213-220. |
| [41] | 吴小羊. 2010. 基于频谱分析技术的频散AVO反演研究[D]. 武汉:中国地质大学. |
| [42] | 张广智,陈怀震,印兴耀,等. 2012. 基于各向异性AVO的裂缝弹性参数叠前反演方法[J]. 吉林大学学报:地球科学学报,42(3):845-851. |
| [43] | 张显文,王德利,王者江,等.2010. 基于BISQ机制三维双相正交裂隙各向异性介质衰减及频散方位特性研究[J]. 地球物理学报,53(10): 2452-2459. |
| [44] | 朱培民,王家映,於文辉,等. 2001. 用纵波AVO数据反演储层裂隙密度参数[J]. 石油物探, 40(2):1-12. |
 2016, Vol. 31
2016, Vol. 31

