2. 青岛海洋地质研究所, 青岛 266071
2. Qingdao Institute of Marine Geology, Qingdao 266071, China
地震子波用途广泛,是地震资料反褶积、地震正演和反演等的必要环节.通过合成地震记录,地震子波把测井资料和地震资料联系在一起,以确定地质层位;通过研究地震子波的振幅、能量及相关性等特征,预测油气藏(高建虎和雍学善,2004).地震子波估计一直是地震数据处理重要研究课题之一.现今国内外地震子波估计方法主要基于地震记录褶积模型,分为确定性和统计性两大类方法(杨培杰和印兴耀,2008; 高少武等,2009).确定性子波估计方法先利用测井资料求得反射系数序列,之后结合井旁地震记录由褶积模型求取地震子波(Walden and White,1984; Bunch and White,1985).冯晅等(2002)采用分时窗方法提取子波,提高了合成地震记录与地震剖面的吻合度和分辨率;Buland和Omre(2003)提出一种基于地震和测井资料的贝叶斯子波估计方法,采用非线性的蒙特卡罗算法求解,可在叠后或叠前角道集上提取子波;许升辉和马劲风(2003)受速度分析中多道相关思想的启发,提出了多井条件下子波提取方法;袁三一和陈小宏(2008)应用粒子群优化算法提取子波,在数值模拟算例中取得不错的效果;Passos等(2014)发展了贝叶斯框架下的反演方法,利用叠后地震资料估计子波和噪声水平并进行声阻抗反演.这类方法的优点是无需对反射系数的分布做某种假设,利用测井资料可以得到较为精确的子波,缺点是不能适用于没有测井资料的情况,也难以刻画子波的空间变化.统计性子波估计方法是先对地震资料和地下的反射系数的分布作一定的假设,再通过统计计算求取子波(周兴元,1983; Lazear,1993; 陈健等,2013).李大卫等(2005)提出了基于双谱和三谱混合的子波提取方法;Lu(2005)利用地震道的二阶统计量和三阶矩估计非最小相位子波,不需要反射系数为零均值独立同分布的非高斯序列假设;Lü和Wang(2007)通过高阶统计量方法获得初始子波,结合迭代线性反演方法逐步收敛估计子波;Misra和Sacchi(2007)采用非线性算法结合全通算子估计非最小相位子波;Van der Baan(2008)将常相位旋转方法推广到处理非平稳信号中,利用最大峰度进行相位估计,进而获得时变子波;戴永寿等(2008)应用自回归滑动平均模型对地震子波进行参数化建模,并提出利用线性和非线性相结合的参数估计方式进行参数估计;Edgar和Van der Baan(2011)研究了三种统计性子波估计方法的可靠性,认为统计性方法在研究频率与相位的依赖关系、时变子波等方面比确定性方法更有优势,可以为确定性方法提供质量控制和进行子波外推.这类方法的优点是不需要测井资料,缺点是对地下的信息掌握不足而导致求取的子波精度相对不高.
近几年,子波估计方法在原有理论基础上不断完善和发展(戴永寿等,2011; 张栋等,2012),时变子波的研究也逐步深入(高静怀等,2009; 张漫漫等,2014; 王蓉蓉等,2015),虽然方法众多,但是不同方法的比较研究相对较少.本文对三种典型的子波估计方法,即确定性的最小平方法及统计性的复赛谱法和双谱法进行了对比研究.最小平方法是利用测井信息提取井旁道子波;复赛谱法是通过在复赛谱域对子波和反射系数序列进行分离,从而求得子波;双谱法是在双谱域分别对子波振幅和相位进行重构来获取子波.这三种方法利用的已知信息、假设条件和方法原理皆不尽相同.本文通过理论分析、理论模型和实测资料实验,讨论和比较了各方法的优缺点及适用性等,以期为不同情况下选择合适的地震子波估计方法提供参考.
1 子波提取方法1.1 最小平方法及改进 1.1.1 最小平方法原理地震子波估计的最小平方法属于一种确定性方法.根据已有的声波测井和密度测井等资料,求取地层反射系数序列r(t),再由井旁地震道求取地震子波.
若所求的地震子波为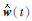 ,则地震道为
,则地震道为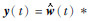 r(t).根据最小平方原理,该道与实际井旁地震道x(t)之间的误差能量达到最小.误差能量可表示为
r(t).根据最小平方原理,该道与实际井旁地震道x(t)之间的误差能量达到最小.误差能量可表示为
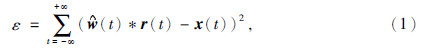
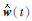 的偏导数等于0,整理得
的偏导数等于0,整理得 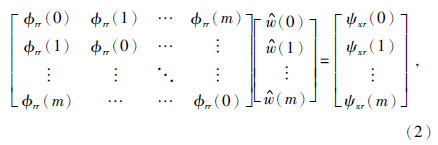

直接解方程(3),在估计的地震子波的旁瓣上会出现一些起伏变化.为此,程乾生(1993)采用自相关函数的白噪化处理方法,将方程中出现的自相关函数Φ变为 ,公式为
,公式为
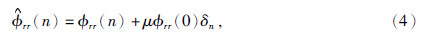
其中μ为白噪因子,要求μ>0,一般取在0~0.2之间.
设地震记录x(t)的开始时间为t1,结束时间为t2,子波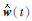 )的开始时间-p,结束时间为q.考虑到截断误差和直流分量的影响(梁光河,1998; 张广智等,2005),在提取t1到t2时间段的地震子波时,使用t1-q至t2+p时间段内的反射系数序列.同时加入约束
)的开始时间-p,结束时间为q.考虑到截断误差和直流分量的影响(梁光河,1998; 张广智等,2005),在提取t1到t2时间段的地震子波时,使用t1-q至t2+p时间段内的反射系数序列.同时加入约束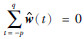 ,推导出优化最小平方子波公式为
,推导出优化最小平方子波公式为


当地震记录存在噪声时,用优化最小平方法提取的子波幅值抖动较剧烈,两端更为明显,Yue等(2014)假设地震信号服从非高斯α稳定分布,应用分数低阶矩理论提高求解的稳定性,李月等(2010)通过核函数主分量对数据进行降维,改善矩阵求解时易出现的病态问题.我们通过加窗的方法削弱这种影响,公式为

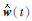 为由上述方法估计的子波,h(t)为窗函数.
为由上述方法估计的子波,h(t)为窗函数.
经反复试验,在信噪比较低的情况下,h(t)可采用钟形函数,公式为
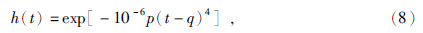
子波提取的另一种方法是基于同态反褶积(Ulrych,1971)的方法,它是在复赛谱域中分离子波,是一种统计性地震子波提取方法.这种方法能将地震道的褶积形式变换成线性和的形式,不需要子波为最小相位的假设.
在时间域内,若用s(t)表示地震记录序列,w(t)和r(t)分别表示子波和反射系数序列,根据褶积模型:

傅里叶变换到频率域为

两边取对数得:
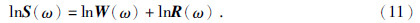
反傅里叶变换到时间域为

经上述变换得到时间序列的复赛谱.由于子波复赛谱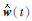 的能量主要集中在t=0附近,反射系数复赛谱
的能量主要集中在t=0附近,反射系数复赛谱 )为原点处最小的周期性单边右序列,因此可通过低通滤波实现
)为原点处最小的周期性单边右序列,因此可通过低通滤波实现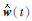 和
和 的分离.得到子波的近似复赛谱序列
的分离.得到子波的近似复赛谱序列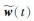 ,将其变换到频率域得lnW(ω),取指数得W(ω),再反变换到时间域得地震子波w(t).分离
,将其变换到频率域得lnW(ω),取指数得W(ω),再反变换到时间域得地震子波w(t).分离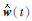 和
和 的低通滤波器的时间特性为
的低通滤波器的时间特性为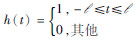 ,
, 为滤波门限,
为滤波门限, 选取越准确分离效果越好.
选取越准确分离效果越好.
对实际地震资料用复赛谱估计子波时,上述低通滤波器门限往往难以确定,而且,很多情况下子波和反射系数在复赛谱域并不能完全分开,存在一定的交集,这时利用单道提取子波的效果并不理想.因此,在单道复赛谱法的基础上发展了指数加权、多道复赛谱序列平均法等(周兴元,1983).一般认为不同地震道对应的反射系数序列的时间位置不同,对多道复赛谱序列叠加后求平均,反射系数的平均复赛谱会趋向于零,而地震子波的平均复赛谱保持不变,从而分离出地震子波的平均复赛谱,进而估计出地震子波.当地层界面水平时,不同地震道的反射系数序列不变,反射系数的平均复赛谱将不趋向于零,这时,可以采用时窗随机化处理方法,强迫反射系数序列变化(徐伯勋和姜成栋,1991).传统的复赛谱法要求较为苛刻,反射系数序列愈是最小相位化,效果愈好.基于平均思想的改进方法则放宽了这一限制条件,使该方法应用范围更广,Herrera和Van der Baan(2012)联合短时窗叠加和对数谱平均方法提取子波,取得了不错的效果.
1.3 双谱法双谱定义为信号的三阶累积量的二维傅里叶变换,若用X(ω)表示某个信号的傅里叶变换,则该信号双谱可以表示为

双谱幅值为

双谱相位为

假设地层反射系数序列为零均值独立同分布的非高斯随机序列,噪声为高斯白噪声或色噪声,则地震子波的双谱与地震记录的双谱成正比,提取地震子波就是利用地震记录双谱的振幅|Bx(ω1,ω2)|和相位φx(ω1,ω2)分别估计子波的振幅X(ω)和相位φ(ω),即子波振幅和相位的重构,其结果至多相差一比例常数.
子波相位重构采取最小长度法,令ω1=2mπ/N,ω2=2nπ/N,N为采样点数,由双谱对称性,令m=1,2,…,N/4,n=m,m+1,…,N/2-m.φx(ω1,ω2)是φ(m)的线性组合,可写成矩阵形式为

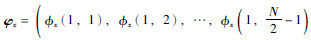 ,
,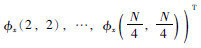 为N2/16维列向量,Φ=
为N2/16维列向量,Φ= 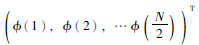 为N/2维列向量,G=
为N/2维列向量,G= 为
为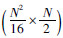 阶矩阵.
阶矩阵.
解方程(16),求得

根据对称性得:
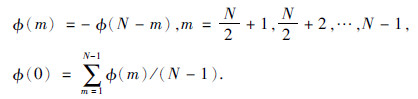
子波振幅|X(ω)|重构可以采取类似的算法,其他算法(谢桂生等,2000; 唐斌和尹成,2001; 李亚峻等,2007)可供参考,Yu等(2011)将保角变换应用到双谱法提取子波中,提高了相位重构的精度.频率域子波表示为W(ω)=|X(ω)|exp[iφ(ω)],通过傅里叶反变换,得到时间域地震子波.通过相邻多道地震记录分别估计子波后求平均,可获得双谱法平均子波.
2 合成数据实验及分析2.1 基于非稀疏反射系数序列的合成地震数据合成数据如图 1所示,考虑到实际地震子波一般为混合相位,为便于对比,本文模型实验统一采用混合相位雷克子波,其表达式为

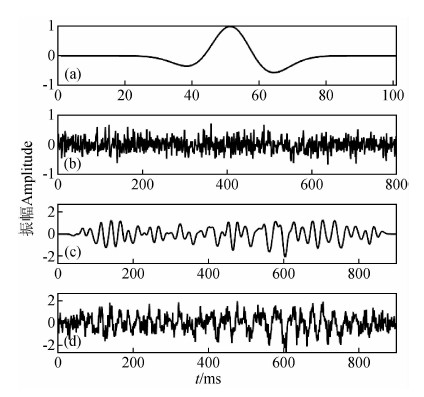 |
图 1 合成地震数据1 (a) 理论子波;(b) 随机反射系数序列; (c) 合成地震记录;(d) 加噪地震记录. Fig. 1 Synthetic seismic data 1 (a) Theoretical wavelet; (b) Random reflection coefficient series; (c) Synthetic seismogram; (d) Synthetic seismogram with noises. |
利用图 1c中未加噪合成地震记录和(b)中的反射系数,使用最小平方法估计了优化子波,以及仅利用未加噪合成地震记录使用复赛谱法和双谱法估计子波,与理论子波对比,结果如图 2所示.由于准确知道反射系数序列,确定性方法比统计性方法估计的子波更精确.但是在反射系数未知的情况下,统计性方法就可以发挥对先验数据依赖性较小的优势,实现对地震子波的估计.对于复赛谱法,利用图 1中的理论子波,构造五组随机反射系数序列,将合成的五道地震记录在复赛谱域内求平均后再估计子波,所得多道平均子波比单道估计子波的效果更好.
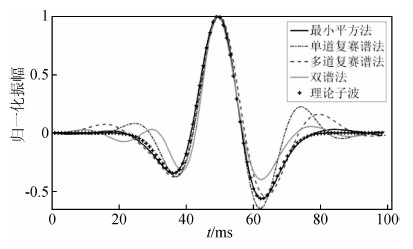 | 图 2 对无噪数据1不同方法估计子波的对比 Fig. 2 Different kinds of wavelets estimated using non-noise data in Fig. 1 |
图 3是图 2所示的三种不同方法估计子波的频谱,表 1是这些频谱的振幅值和主频.估计子波的频谱与理论子波频谱的对比也表明,在反射系数为非稀疏随机分布的条件下,最小平方法效果优于复赛谱法,复赛谱法效果优于双谱法.
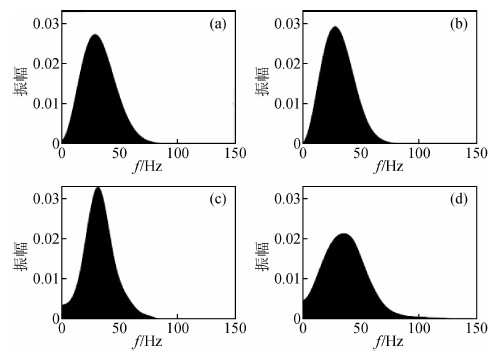 |
图 3 提取子波的频谱对比 (a) 理论子波;(b) 最小平方法子波; (c) 复赛谱法子波;(d) 双谱法子波. Fig. 3 Spectrum comparison of wavelets estimated using different methods (a)Theoretical wavelet; (b) Wavelet estimated by the least square method; (c) Wavelet estimated by the cepstrum; (d) Wavelet estimated by the bispectrum. |
|
|
表 1 提取子波主频和对应振幅表 Table 1 Main frequency and the amplitude of the wavelets estimated using different methods |
实际地层的反射系数序列往往具有非高斯分布的稀疏脉冲特征(彭更新等,2013; 王万里等,2014; 刘畅和张琴,2014),为此,设计反射系数为零均值服从柯西分布的非高斯序列,幅值较大的反射系数相对稀疏,如图 4a所示,该反射系数序列与图 1a的理论子波进行褶积后合成的单道地震记录如图 4b所示.对该地震数据,用三种子波估计方法得到的子波如图 5所示,图 6和表 2是估计的子波频谱.结果表明,三种方法估计的子波与理论子波的变化趋势一致,其中,最小平方法子波与理论子波相似度最高,双谱法子波比复赛谱法子波稍好.复赛谱法估计子波在波谷处幅值与理论子波的差别最大.因此,在反射系数为零均值独立同分布的非高斯序列的条件下,最佳提取方法依次为:最小平方法效果优于双谱法,而双谱法效果优于复赛谱法.
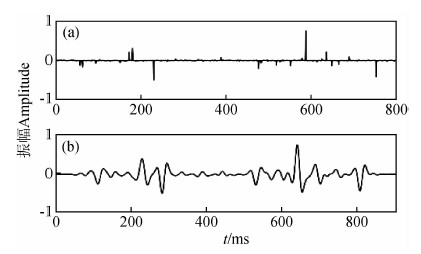 |
图 4 合成地震数据2 (a) 反射系数序列;(b) 合成地震记录. Fig. 4 Synthetic seismic data 2 (a) Reflection coefficient series; (b) Synthetic seismogram. |
 | 图 5 对无噪数据2三种方法估计子波的对比 Fig. 5 Wavelets estimated using the three methods from synthetic data without noises in Fig. 4 |
 |
图 6 提取子波的频谱对比 (a) 理论子波;(b) 最小平方法子波; (c) 复赛谱法子波;(d) 双谱法子波. Fig. 6 Spectrum comparison of wavelets estimated using the three methods (a) Theoretical wavelet; (b) Wavelet estimated by the least square method; (c) Wavelet estimated by the cepstrum; (d) Wavelet estimated by the bispectrum. |
|
|
表 2 提取子波主频和对应振幅表 Table 2 Main frequency and the amplitude of wavelets estimated using the three methods |
信噪比(SNR)是衡量地震资料质量的重要参数(刘洋和李承楚,1997),往往信噪比越高,数据的可信度就越高.实测地震数据不可避免含有噪声,这就要求地震子波估计方法要具有一定的容噪能力.
虽然优化最小平方法在无噪情况下可以对地震子波进行精确的估计,但是对于低信噪比资料,效果并不理想,幅值抖动严重.我们通过对最小平方法结果进行加窗平滑处理,较好地解决了这一问题.如图 7所示是对图 1d所示的SNR=2 dB的加噪地震记录,利用最小平方法估计的子波,然后使用(9)式的窗函数(p=1,q=51)和五点平滑进行加窗圆滑处理的结果,加窗平滑后的子波与理论子波吻合度很高.
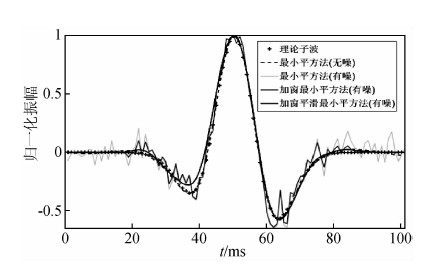 | 图 7 加噪数据最小平方法改进前后效果对比 Fig. 7 Comparison of wavelets using the least square method and its modified version, respectively, from the data with noises |
为了对比上述三种子波估计方法的抗噪性,对图 1c和图 4b所示的合成地震记录分别加入了20 dB、7 dB、2 dB的高斯白噪声,见图 8.对这些含噪地震记录,用三种子波估计方法估计的地震子波分别如图 9所示.可以看出,当SNR等于20 dB时,三种方法估计的子波均与理论子波吻合较好.当SNR降为7 dB时,加窗最小平方法提取效果依然不错;双谱法和复赛谱法效果差一些.当SNR继续减小至2 dB,加窗最小平方子波形态并没有发生太大变化,显示出了此方法的稳健性;而双谱法和复赛谱法估计的子波的精确度有所降低,但仍与理论子波的变化趋势一致.可见,三种子波估计方法均具有一定的抗噪能力,且加窗最小平方法的抗噪性优于双谱法,双谱法的抗噪性优于复赛谱法.值得一提的是,当噪声为高斯色噪声时,三种方法也可以取得不错的效果,反映了这些方法的稳定性.
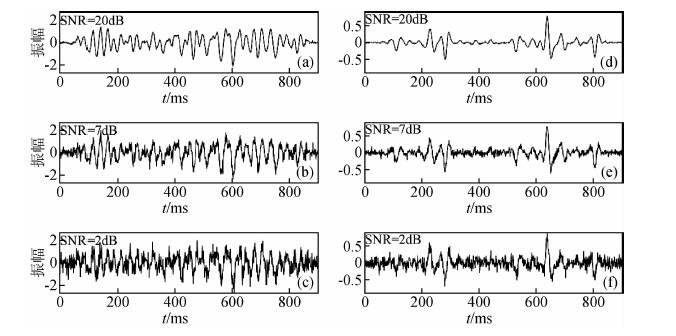 |
图 8 不同信噪比地震数据 合成地震数据1 (a) SNR=20 dB,(b) SNR=7 dB,(c) SNR=2 dB; 合成地震数据2 (d) SNR=20 dB,(e) SNR=7 dB,(f) SNR=2 dB. Fig. 8 Synthetic seismic data with different Signal to Noise Ratio Seismic data 1 with (a) SNR=20 dB, (b) SNR=7 dB, (c) SNR=2 dB; Seismic data 2 with (d) SNR=20 dB, (e) SNR=7 dB, (f) SNR=2 dB. |
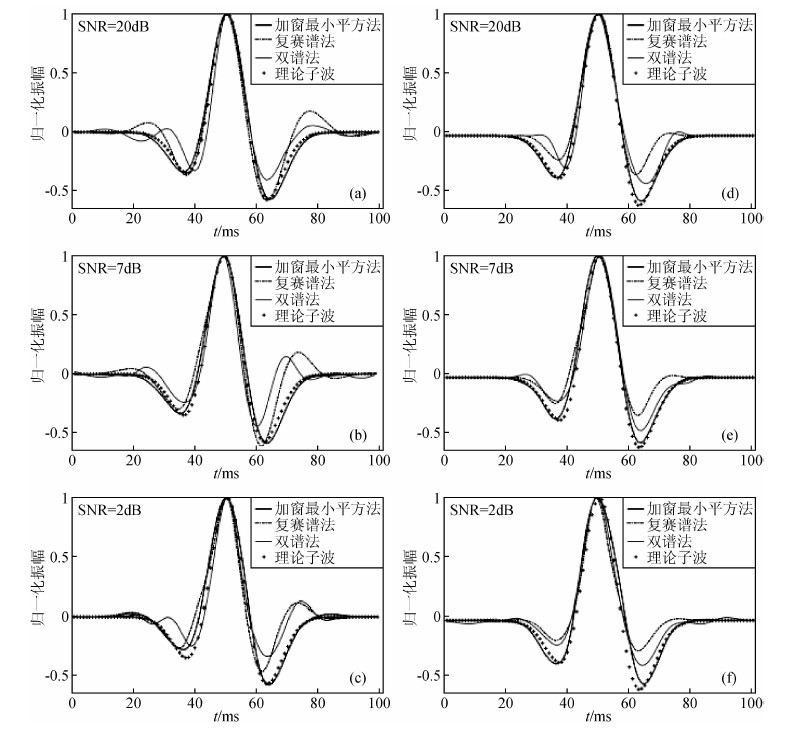 |
图 9 三种方法对不同信噪比地震数据估计的子波 合成地震数据1 (a) SNR=20 dB,(b) SNR=7 dB,(c) SNR=2 dB. 合成地震数据2 (d) SNR=20 dB,(e) SNR=7 dB,(f) SNR=2 dB. Fig. 9 Wavelets estimated using above three methods from the synthetic seismic data with different SNR Synthetic seismic data 1 with (a) SNR=20 dB, (b) SNR=7 dB, (c) SNR=2 dB. Synthetic seismic data 2 with (d) SNR=20 dB, (e) SNR=7 dB, (f) SNR=2 dB. |
为了检验不同子波估计方法对实际资料的应用效果,用上述三种方法对南海某地区实际地震资料进行了处理.图 10a和图 10b分别为邻近地震测线的声波速度测井曲线和密度测井曲线,图 10c是利用测井数据经预处理、时深转换等步骤求得的反射系数序列.
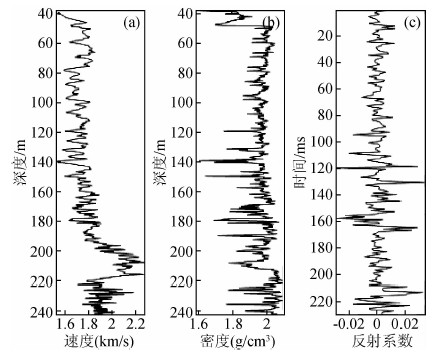 |
图 10 速度、密度测井曲线及求取反射系数 (a)速度测井;(b)密度测井;(c)反射系数. Fig. 10 Velocity logging curve, density logging curve and calculated reflection coefficients (a) Velocity log; (b) Density log; (c) Reflection coefficient. |
分别用三种方法提取子波,即利用声波和密度测井资料计算沿井的反射系数序列,结合井旁地震道提取最小平方子波;利用井旁附近多道求取复赛谱序列平均子波和双谱平均子波,实际提取子波对比如图 11所示.然后,分别利用三种估计子波对原始地震剖面进行了反褶积处理.图 12a是原地震剖面,图 12b是复赛谱法子波反褶积剖面,图 12c是双谱法子波反褶积剖面,图 12d是最小平方法子波反褶积剖面.可以看出,利用三种子波的反褶积处理对剖面均有所改善,其中,复赛谱法子波反褶积的效果不十分明显;双谱法子波反褶积相对较好,而最小平方子波反褶积的效果最好,同相轴更加清晰,构造细节更加可辨.在图 12d中两条黑色曲线之间的条带内,沿条带下边界附近地震波剖面振幅与其上下振幅差距明显,极性为负,且与海底界面大致平行,推判为似海底反射(bottom simulating reflector,BSR).声波测井资料表明BSR之上为高速层,实际钻探发现此处有天然气水合物分布.使用估计的子波进行了反褶积处理,提高了地震剖面的分辨率,更细地反映了该带的含水合物沉积层特征.
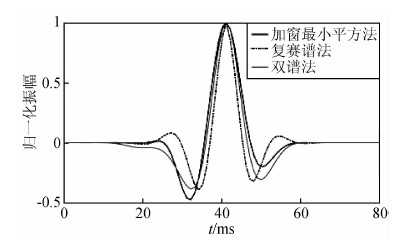 | 图 11 实际资料提取子波 Fig. 11 Estimated wavelets from the field data |
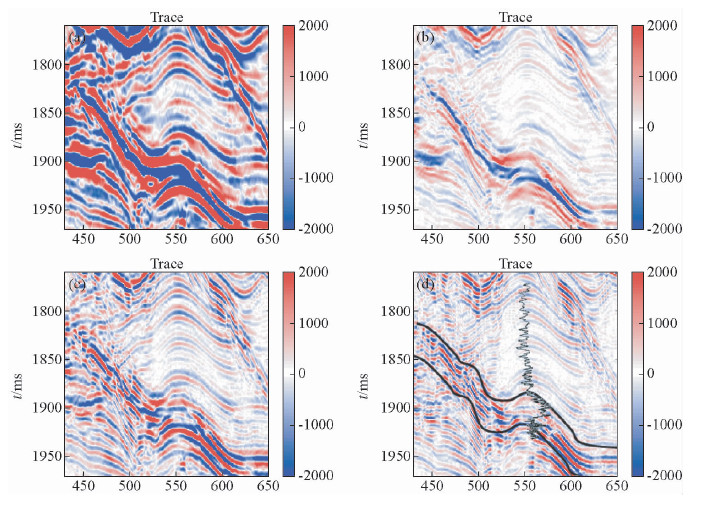 |
图 12 地震剖面与反褶积结果的对比 (a)原始地震剖面;(b)复赛谱子波反褶积;(c)双谱子波反褶积;(d)最小平方子波反褶积. Fig. 12 Seismic section and its deconvolution results using different wavelets (a) Raw seismic data; (b) Using cepstrum wavelet; (c) Using bispectrum wavelet; (d) Using least square wavelet. |
前述估计子波方法的原理不尽相同,所需先验信息、假设条件、技术步骤、抗噪性和适用性等方面也各有其特点,具有各自的优势和不足,具体总结于表 3.综合它们的特点及合成资料和实测资料的测试结果,得到下列结论:
|
|
表 3 三种估计子波方法性能比较 Table 3 Performance comparison of three kinds of estimated wavelets |
(1)对有测井资料地区的地震资料,采用优化最小平方法估计子波的效果较好,在处理实际资料时,采用加窗平滑的改进算法提高了此法的抗噪性和稳定性.
(2)在反射系数为非稀疏随机分布的条件下,加窗最小平方法效果优于复赛谱法,复赛谱法效果优于双谱法.在反射系数为零均值独立同分布的非高斯序列的条件下,加窗最小平方法效果优于双谱法,双谱法效果优于复赛谱法.
(3)对于白噪声或有色噪声地震数据,加窗最小平方法、复赛谱法和双谱法均有一定的抗噪能力.总体上,加窗最小平方法优于双谱法,双谱法优于复赛谱法.采用分时窗平均或多道平均,复赛谱法或双谱法的效果有所改善.
(4)加窗最小平方法是确定性子波提取方法,相比于双谱法和复赛谱法等统计性提取方法需要测井资料等已知信息.在测井资料可靠的前提下,确定性方法的效果较好;当测井资料的误差较大时,可以用统计性子波估计方法作为辅助和佐证.在没有测井资料时,需根据工区和地震资料的特点,选择合适的统计性子波估计方法,或使用不同方法估计子波,通过比较应用子波的后续处理效果,择优使用适当的子波.
致 谢 感谢审稿专家提出的宝贵意见和编辑部老师的耐心指导帮助.| [1] | Buland A, Omre H. 2003. Bayesian wavelet estimation from seismic and well data[J]. Geophysics, 68(6): 2000-2009. |
| [2] | Bunch A W H, White R E. 1985. Least-squares filters without transient errors: An examination of the errors in least-squares filter design[J]. Geophysical Prospecting, 33(5): 657-673. |
| [3] | Chen J, D Y S, Zhang Y N, et al. 2013. Evaluation approaches for wavelet pickup based on high-order statistics[J]. OGP(in Chinese), 48(3):497-503. |
| [4] | Cheng Q S. 1993. Mathematical Principles of Digital Signal Processing (in Chinese) [M]. Beijing: Petroleum Industry Press, 516-521. |
| [5] | Dai Y S, Peng X, Niu H. 2011. Research on high precision seismic wavelet estimation based on information feedback[J]. Progress in Geophysics (in Chinese), 26(3): 1004-1009. |
| [6] | Dai Y S, Wang J L, Wang W W, et al. 2008. Seismic wavelet extraction via cumulant-based ARMA model approach with linear and nonlinear combination[J]. Chinese Journal Geophysics(in Chinese), 51(6): 1851-1859. |
| [7] | Edgar J A, Van der Baan M. 2011. How reliable is statistical wavelet estimation?[J]. Geophysics, 76(4): 59-68. |
| [8] | Feng X, Liu C, Yang B J, et al. 2002.The extractive method of seismic wavelet in different time window and the application in synthetic seismogram[J]. Progress in Geophysics (in Chinese), 17(1): 71-77. |
| [9] | Gao J H, Wang L L, Zhao W. 2009. Enhancing resolution of seismic traces based on the changing wavelet model of the seismogram[J]. Chinese Journal of Geophysics(in Chinese),52(5):1289-1300. |
| [10] | Gao J H, Yong X S. 2004. Applying the wavelet to detect hydrocarbon [J]. Natural Gas Geoscience (in Chinese),15(1): 47-50. |
| [11] | Gao S W,Zhao B,He Z H, et al. 2009. Research progress of seismic wavelet extraction[J]. Progress in Geophysics (in Chinese), 24(4): 1384-1391. |
| [12] | Herrera R H, Van der Baan M. 2012. Short-time homomorphic wavelet estimation[J]. Journal of Geophysics and Engineering, 9(6): 674-686. |
| [13] | Hu Q Y. 1984. A possible way for homomorphic deconvolution [J]. Geophysical Prospecting for Petroleum (in Chinese), 23(2): 109-111. |
| [14] | Lazear G D. 1993. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 58(7): 1042-1051. |
| [15] | Li Y J, Li Y, Gao Y. 2007. A method of extracting seismic wavelet based on bispectrum amplitude and phase reconstruction[J]. Progress in Geophysics (in Chinese), 22(3): 947-952. |
| [16] | Li D W, Yin C, Xiong X J, et al. 2005. A hybrid high-order spectrum method for seismic wavelet estimation and processing [J]. Progress in Geophysics (in Chinese), 20(1): 29-33. |
| [17] | Li Y, Ma H T, Lin H B, et al. 2010. The research of principal-component Wiener filtering method based on kernel function[J]. Chinese Journal of Geophysics(in Chinese),53(5):1226-1233. |
| [18] | Liang G H. 1998. On the methods of seismic wavelet extraction[J]. Geophysical Prospecting for Petroleum (in Chinese), 37(1): 31-39. |
| [19] | Liu C, Zhang Q. 2014. Sparse-spike deconvolution promoting frequency dependent seismic stratigraphic analysis and an application[J]. Progress in Geophysics (in Chinese), 29(2): 780-785. |
| [20] | Liu Y, Li C C. 1997. Some methods for estimating the signal noise ratio of seismic data[J]. OGP (in Chinese), 32(2): 257-262. |
| [21] | Lu W K. 2005. Non-minimum-phase wavelet estimation using second-and third-order moments[J]. Geophysical prospecting, 53(1): 149-158. |
| [22] | Lü X L, Wang Y H. 2007. Mixed-phase wavelet estimation by iterative linear inversion of high-order statistics[J]. Journal of Geophysics and Engineering, 4(2): 184-193. |
| [23] | Misra S, Sacchi M D. 2007. Non-minimum phase wavelet estimation by non-linear optimization of all-pass operators[J]. Geophysical Prospecting, 55(2): 223-234. |
| [24] | Passos de Figueiredo L, Santos M, Roisenberg M, et al. 2014. Bayesian Framework to Wavelet Estimation and Linearized Acoustic Inversion[J]. Geoscience and Remote Sensing Letters, IEEE, 11(12): 2130-2134. |
| [25] | Peng G X, Wang W L, Chen M, et al. 2013. Analysis on statistical characteristics of reflection coefficient and its application in high resolution seismic data processing[J]. Journal of Oil and Gas Technology (in Chinese), 35(4): 55-58. |
| [26] | Tang B, Yi C. 2001. Non-minimum phase seismic wavelet reconstruction based on higher order statistics[J]. Chinese Journal of Geophysics (in Chinese), 44(3): 404-410. |
| [27] | Ulrych T J. 1971. Application of homomorphic deconvolution to seismology [J]. Geophysics, 36(4): 650-660. |
| [28] | Van der Baan M. 2008. Time-varying wavelet estimation and deconvolution by kurtosis maximization[J]. Geophysics, 73(2): 11-18. |
| [29] | Walden A T, White R E. 1984. On errors of fit and accuracy in matching synthetic seismograms and seismic trace[J]. Geophysical Prospecting, 32(5): 871-891. |
| [30] | Wang R R, Dai Y S, Zhang Y N, et al. 2015. Time-varying wavelet extraction methods in non-stationary seismogram[J]. Progress in Geophysics (in Chinese), 30(2): 700-708. |
| [31] | Wang W L, Yang W Y, Wei X J, et al. 2014. Stochastic sparse spike nonlinear deconvolution. Progress in Geophysics (in Chinese), 29(4): 1780-1784, doi: 10. 6038/pg20140439. |
| [32] | Xie G S, Shi Y M, Wei Y. 2000. Wavelet estimation based on bispectrum[J]. Journal of Southwest Petroleum Institute (in Chinese), 22(3): 25-33. |
| [33] | Xu B X, Jiang C D, 1991. An improvement on wavelet extraction using homomorphic filtering[J]. Geophysical Prospecting for Petroleum (in Chinese), 30(3): 22-37. |
| [34] | Xu S H, Ma J F. 2003. Wavelet extraction method of wave impedance inverse with multi-well restrictions[J]. Progress in Geophysics (in Chinese), 18(4): 623-627. |
| [35] | Yang P J, Yin X Y. 2008. Summary of seismic wavelet pick-up[J]. OGP (in Chinese), 43(1): 123-128. |
| [36] | Yu Y C, Wang S X, Yuan S Y, et al. 2011. Phase estimation in bispectral domain based on conformal mapping and applications in seismic wavelet estimation[J]. Applied Geophysics, 8(1): 36-47. |
| [37] | Yuan S Y, Chen X H. 2008. A new method for seismic wavelet extraction and interval velocity inversion[J]. Progress in Geophysics (in Chinese), 23(1): 198-205. |
| [38] | Yue B, Peng Z, Zhang Q. 2014. Seismic Wavelet Estimation Using Covariation Approach[J]. Geoscience and Remote Sensing, IEEE Transactions on, 52(12): 7495-7503. |
| [39] | Zhang D, Xu L L, Jia J M, et al. 2012. Wavelet extraction from microseismogram logs and wavelet application[J] OGP (in Chinese), 47(4): 519-523. |
| [40] | Zhang G Z, Liu H, Yin X Y. 2005. Method for fine picking up seismic wavelet at up-hole trace[J]. OGP(in Chinese), 40(2):158-162. |
| [41] | Zhang M M, Dai Y S, Zhang Y N, et al. 2014. Time-variant seismic wavelet estimation method based on spectral modeling in time-frequency domain[J]. Geophysical Prospecting for Petroleum(in Chinese), 53(6):675-682. |
| [42] | Zhou X Y. 1983. The estimation of seismic wavelet by homomorphic theory[J]. OGP (in Chinese), 18(6): 510-521. |
| [43] | 陈健,戴永寿,张亚南,等. 2013. 基于高阶统计量的地震子波提取方法评价[J]. 石油地球物理勘探, 48(3):497-503. |
| [44] | 程乾生. 1993. 信号数字处理的数学原理[M]. 北京:石油工业出版社, 516-521. |
| [45] | 戴永寿,彭星,牛慧. 2011. 一种基于信息反馈的高精度地震子波提取方法[J]. 地球物理学进展,26(3):1004-1009. |
| [46] | 戴永寿,王俊岭,王伟伟,等. 2008. 基于高阶累积量ARMA模型线性非线性结合的地震子波提取方法研究.地球物理学报,51(6):1851-1859. |
| [47] | 冯晅,刘财,杨宝俊,等. 2002. 分时窗提取地震子波及在合成地震记录中的应用[J]. 地球物理学进展,17(1):71-77. |
| [48] | 高静怀,汪玲玲,赵伟. 2009. 基于反射地震记录变子波模型提高地震记录分辨率[J]. 地球物理学报,52(5):1289-1300. |
| [49] | 高建虎,雍学善. 2004. 利用地震子波进行油气检测[J]. 天然气地球科学, 15(1):47-50. |
| [50] | 高少武,赵波,贺振华,等. 2009. 地震子波提取方法研究进展[J]. 地球物理学进展,24(4):1384-1391. |
| [51] | 胡启宇. 1984. 同态反褶积的一种可能途径[J]. 石油物探,23(2):109-111. |
| [52] | 李月,马海涛,林红波,等. 2010. 基于核函数主分量的维纳滤波方法研究[J]. 地球物理学报,53(5):1226-1233. |
| [53] | 梁光河. 1998. 地震子波提取方法研究[J]. 石油物探,37(1):31-39. |
| [54] | 李大卫,尹成,熊晓军,等. 2005. 高阶谱混合方法地震子波估计及处理[J].地球物理学进展,20(1):29-33. |
| [55] | 刘畅,张琴. 2014. 基于稀疏脉冲反褶积的分频地震层序分析方法及应用[J]. 地球物理学进展,29(2):780-785. |
| [56] | 刘洋,李承楚. 1997. 地震资料信噪比估计的几种方法[J]. 石油地球物理勘探, 32(2):257-262. |
| [57] | 李亚峻,李月,高颖. 2007. 基于双谱幅值和相位重构的地震子波提取[J].地球物理学进展, 22(3):947-952. |
| [58] | 彭更新,王万里,陈猛,等. 2013. 反射系数统计特征分析及其在高分辨率地震资料处理中的应用. 石油天然气学报,35(4):55-58. |
| [59] | 唐斌,尹成. 2001. 基于高阶统计的非最小相位地震子波恢复[J]. 地球物理学报, 44(3):404-410. |
| [60] | 王蓉蓉,戴永寿,张亚南,等. 2015. 非平稳地震记录中时变子波提取方法研究[J]. 地球物理学进展,30(2):700-708. |
| [61] | 王万里,杨午阳,魏新建,等. 2014. 随机稀疏脉冲非线性反褶积. 地球物理学进展,29(4):1780-1784, doi: 10. 6038/pg20140439. |
| [62] | 谢桂生,石玉梅,魏野. 2000. 双谱地震子波估计[J]. 西南石油学院学报,22(3):25-33. |
| [63] | 徐伯勋,姜成栋. 1991. 应用同态滤波提取子波的改进方法[J]. 石油物探,30(3):22-37. |
| [64] | 许升辉,马劲风. 2003. 波阻抗反演中多井条件下的子波提取方法[J]. 地球物理学进展,18(4):623-627. |
| [65] | 杨培杰,印兴耀. 2008. 地震子波提取方法综述[J]. 石油地球物理勘探,43(1):123-128. |
| [66] | 袁三一,陈小宏. 2008. 一种新的地震子波提取与层速度反演方法[J]. 地球物理学进展,23(1):198-205. |
| [67] | 张栋,徐雷良,贾静敏,等. 2012. 微地震测井记录子波提取方法及应用[J]. 石油地球物理勘探,47(4):519-523. |
| [68] | 张广智, 刘洪, 印兴耀. 2005. 井旁道地震子波精细提取方法[J]. 石油地球物理勘探, 40(2):158-162. |
| [69] | 张漫漫,戴永寿,张亚南,等. 2014. 基于时频域谱模拟的时变子波估计方法[J]. 石油物探,53(6):675-682. |
| [70] | 周兴元. 1983. 应用同态理论估算地震子波[J]. 石油地球物理勘探,18(6):510-521. |
 2016, Vol. 31
2016, Vol. 31


