Through petrophysical experiments analysis of core rock data from eight oilfields of three basin, it has been confirmed that formation factor and porosity of tight sandstone show a piecewise linear relationship in double logarithmic coordinates. The significant inflection point appears when porosity is approximately equal to 10%, according to that, the Archie parameters with versatility could be fitted when porosity is less than 10%. Mercury injection experimental data in Honghe oilfield shows that core pore throat distributions present significant differences when the core porosity is less than 10% and when it is more than 10%. Therefore, the pore is divided into large-diameter pore part and small-diameter pore part, each part of which is supposed to have a different proportion of “macro conductive pore” and is defined as “pseudo macro conductive porosity” variables. The combined measurements data of core electricity and mercury injection experiments indicate that the pseudo macro conductive porosity and formation factor display a good single linear relationship in double logarithmic coordinates. Thus we establish the improved Archie formula, the expression and parameters of which keep unified under different porosity conditions. This formula behaves better application effect in formation factor calculation.
The calculation effect is examined and improved by core electricity experiments data of tight sandstone samples in the Silurian formation of Honghe oilfield and Tarim oilfield. It could be able to conclude that the formation factor calculated by the improved Archie formula and experimentally measured formation factor are in good agreement, conforming the reliability of the formula.
致密砂岩泛指物性条件以“常压下孔隙度小于10%、空气渗透率小于1×10-3 μm2”为主的一类砂岩.近年来,致密砂岩油气藏在油气勘探开发中的地位越来越重要(李闽等,2009;朱如凯等,2009;李卓等,2013;宋连腾等,2015;赖锦等,2015).针对致密砂岩的岩石物理实验研究表明,其孔隙度-电阻率关系呈现明显的“非阿尔奇”现象(双对数坐标下地层因素与孔隙度不再是简单的线性关系),测井资料定量解释中最常用的阿尔奇公式是否适用于致密砂岩因此存在争议.国内外学者对致密砂岩孔隙度-电阻率关系及地层因素计算方法进行了研究,取得了相应的成果:毛志强等(1997)、张明禄和石玉江(2005)、郑庆林等(2006)、伍泽云等(2009)分析了不同盆地致密砂岩油气区孔隙度-电阻率关系,依据孔隙度分段拟合阿尔奇公式参数,或用二次函数建立孔隙度与地层因素关系,来提高地层因素计算精度.也有多名学者提出了新的计算模型:如李霞等(2012)将致密砂岩电阻视为自由水和微孔隙水两部分电阻的并联,提出了考虑孔隙结构的双孔隙饱和度计算模型; Li等(2010)通过模型分析与岩心实验,建立了包含孔隙度、渗透率、平均孔喉半径的致密砂岩地层因素计算模型.综合来看,新的计算模型考虑因素较多,形式较阿尔奇公式复杂,在实际测井资料处理解释应用中有一定的局限性.
本文在多个致密砂岩油田岩电实验数据分析的基础上,以鄂尔多斯盆地南部红河油田致密砂岩为主要研究对象,探索致密砂岩孔隙度与电阻率的关系,进而确立致密砂岩地层因素计算新方法.
1 致密砂岩孔隙度-电阻率关系1942年,美国测井工程师Archie(1942)发表了关于砂岩电阻率的定律(即阿尔奇公式),其中关于地层因素与孔隙度关系部分可理解为:在双对数坐标下,“纯净”砂岩地层因素与孔隙度呈线性关系为

G.E.Archie的研究成果主要基于取自美国海湾地区的岩心样本孔隙度、电阻率测量结果,岩样孔隙度范围介于10%~40%.近年来,大量针对致密砂岩的岩电实验数据表明:在双对数坐标下,致密砂岩地层因素与孔隙度不再是单一线性关系,而是呈现分段线性,约以孔隙度10%为分界(李秋实等,2002;陈杰,2005;杨雪,2008;么丽娜,2012;樊云峰,2012).图 1为依据鄂尔多斯盆地、松辽盆地、塔里木盆地等3个盆地的8个油气田共282块致密砂岩岩样的地层因素和孔隙度测量结果绘制的交会图,图中岩样的孔隙度范围为2%~20%,其中孔隙度小于10%的岩样200块,由图可知:当孔隙度大于10%时,数据点分布在经典阿尔奇线(a=1、m=2)附近;当孔隙度小于10%时,数据点明显偏离经典阿尔奇线,孔隙度越小,偏离越远,从整体趋势上看,地层因素与孔隙度呈现比经典阿尔奇线斜率更小的线性关系,且数据点集中在趋势线附近,即当孔隙度小于10%时,对数坐标下地层因素随孔隙度的线性变化关系也非常明确.依据孔隙度小于10%的数据拟合阿尔奇公式参数a、m,得a=7.06,m=0.950,即阿尔奇公式在孔隙度小于10%时,有

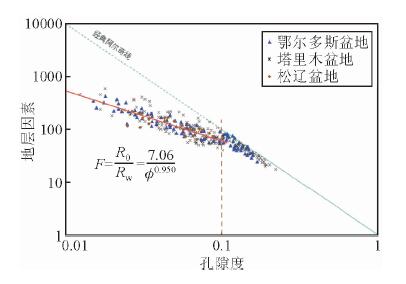 |
图 1 三个盆地致密砂岩孔隙度-地层因素关系 Fig. 1 The relationship between porosity and formation factor of tight sandstone in three basins1 |
致密砂岩地层因素与孔隙度关系在孔隙度约10%处存在明显的拐点,这是一个难以理解的现象.前人大量的研究工作表明,孔隙结构是除孔隙度之外另一个影响岩石导电性的重要因素(刘忠华等,2013;孔强夫等,2015).为了探寻孔隙度大于10%和孔隙度小于10%时砂岩孔隙结构的差异,对鄂尔多斯盆地南部红河油田43块致密砂岩岩样进行岩电-压汞联测实验.这些岩样孔隙度介于2.7%~13.7%之间,其孔隙度-地层因素关系与前述的多个油田致密砂岩数据总结的孔电关系基本吻合(如图 2).依据岩样的压汞实验数据绘制孔径分布图,如图 3所示,孔隙度小于10%的岩样孔喉半径基本小于0.3 μm,而孔隙度大于10%的岩样孔喉半径以大于0.3 μm为主.将孔隙按照其孔径分布划分为两种组分:孔喉半径大于0.3 μm的孔隙为大孔径孔隙,孔喉半径小于0.3 μm的孔隙为小孔径孔隙,对应的孔隙度分别为大孔径孔隙度(记为Φx)和小孔径孔隙度(记为Φn).由地层因素与孔隙度的分段线性关系和不同孔隙度条件下岩样的孔径分布差异可推测:大孔径孔隙与小孔径孔隙对岩样导电性影响有明显差异.因此提出一个合理的假设:孔隙中存在部分对岩电导电性无贡献或贡献微弱的“死”孔隙(张超谟等,2009;章海宁和张超谟,2011),小孔径孔隙中“死”孔隙比例与大孔径孔隙不同.由该假设可得,对岩石导电性起主导作用的是“死”孔隙之外的孔隙,将之命名为“宏导电孔隙”,其对应的孔隙度为“宏导电孔隙度”(记为Φs),设大孔径孔隙中宏导电孔隙比例为cx,小孔径孔隙中宏导电孔隙比例cn,则有

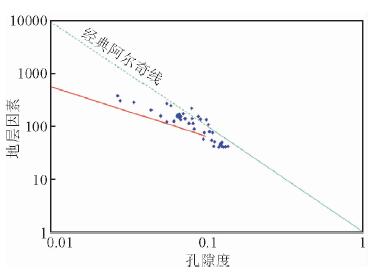 |
图 2 红河油田致密砂岩孔隙度-地层因素交会图 Fig. 2 Porosity and formation factor crossplot of tight sandstone in Honghe oilfield |
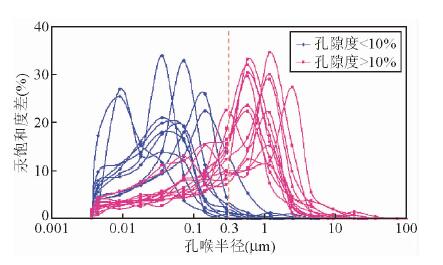 |
图 3 红河油田致密砂岩孔喉半径分布图(部分) Fig. 3 Pore throat diameters distribution of tight sandstone in Honghe oilfield (partial) |
基于上述假设,参考阿尔奇公式形式,提出地层因素计算新公式为

将式(3)代入式(4),可将新公式写为

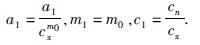
式(5)中,岩样导电因素F可由岩电实验得到,Φx、Φn可由压汞实验数据结合孔隙度测量结果计算得到.利用红河油田致密砂岩岩电-压汞联测实验数据拟合新公式参数,得:a1=5.23,m1=0.867,c1=0.280.
令

则式(5)可表示为

式(7)参考阿尔奇公式形式建立,将其命名为“阿尔奇公式改进式”(后文简称“改进式”).显然,改进式中Φps与前文所述宏导电孔隙度并不等同,但两者之间有一定的比例关系,因此将定义为“伪宏导电孔隙度”.基于岩电-压汞联测实验数据绘制伪宏导电孔隙度-地层因素交会图(图 4),与图 1、图 2相比,伪宏导电孔隙度与地层因素呈现为良好的单一线性关系,即、取固定值足以描述地层因素与伪宏导电孔隙度之间的关系,这意味着:在岩样所属的孔隙度范围内(2%~13.7%),式(7)的形式和参数均可保持统一.
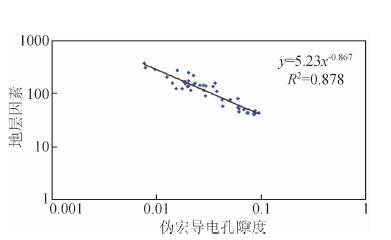 |
图 4 红河油田伪宏导电孔隙度与地层因素交会图 Fig. 4 Pseudo macro conductive porosity and formation factor crossplot in Honghe oilfield |
对红河油田43块岩电-压汞联测实验数据利用改进式计算地层因素,结合实验得到的岩样地层因素绘制交会图,如图 5,数据点(红色点)均分布45°线附近,显示计算地层因素与实验地层因素吻合较好,与直接由实验地层因素、孔隙度拟合阿尔奇公式参数进而计算的地层因素相比,改进式对应的数据点大多数更集中在45°线附近,表现出良好的计算效果.
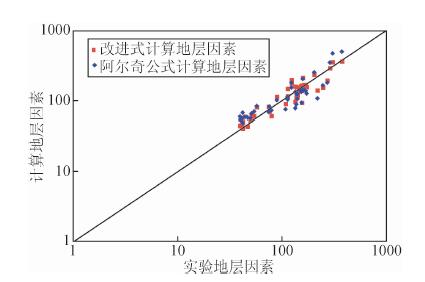 |
图 5 计算地层因素与实验地层因素交会图 Fig. 5 Calculated and experimental formation factors crossplot |
采用同样的方法对塔里木盆地志留系致密砂岩油区26块岩样压汞-岩电联测实验数据进行处理.该区岩样孔隙度范围2.0%~15.0%,实验测量孔隙度与地层因素交会图如图 6a,其孔隙度-地层因素关系与图 1所示孔隙度-地层因素关系一致,即当孔隙度大于10%时,孔隙度-地层因素数据点分布在经典阿尔奇线附近;而当孔隙度小于10%时,地层因素与孔隙度呈现比经典阿尔奇线斜率更小的线性关系.利用压汞数据得到各岩样的大孔径孔隙度、小孔径孔隙度,结合实验测量地层因素,拟合式(5)中参数值得a1=4.31,m1=1.21,c1=0.247,利用改进式计算地层因素,与实验地层因素吻合较好,如图 6b,显示了改进式在不同油田的应用前景.
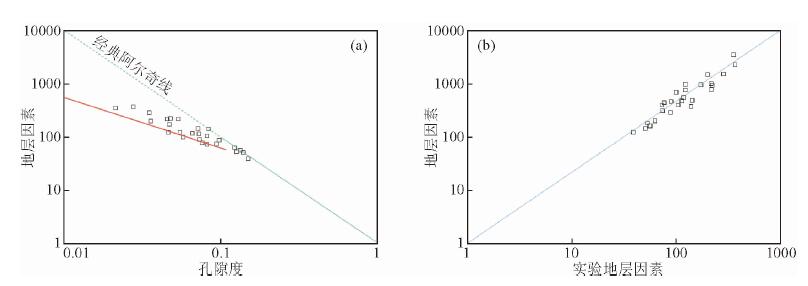 |
图 6 塔里木盆地志留系岩电实验数据检验改进式计算效果(26块岩样)
Fig. 6 The improved Archie formula is confirmed by core electricity experiment data of Tarim oilfield (from 26core samples) (a) Porosity and formation factor crossplot;(b) Calculated and experimental formation factors crossplot. |
在实际测井资料处理解释中,大孔径孔隙度Φx、小孔径孔隙度Φn较难得到,为了便于实际应用,可基于压汞实验数据建立了伪宏导电孔隙度与岩石孔隙度Φ的关系,以红河油田为例,伪宏导电孔隙度与岩石孔隙度关系如图 7,由此可得到利用孔隙度计算伪宏导电孔隙度的计算公式:以孔隙度8.5%为界,当孔隙度大于8.5%时,公式为

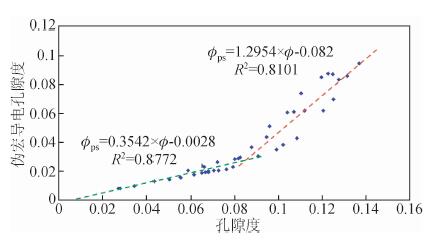 |
图 7 伪宏导电孔隙度与孔隙度关系 Fig. 7 The relationship between pseudo macro conductive porosity and rock porosity |
当孔隙度小于8.5%时,公式为
测井资料可以较准确地计算地层孔隙度,进而根据式(8)、式(9)计算得到伪宏导电孔隙度Φps,再结合改进式即可计算得到地层因素.
对红河油田其他72块致密砂岩岩心样品进行岩电实验检验改进式应用效果:测量岩样孔隙度(孔隙度范围2.0%~16.9%)与地层因素,利用式(8)、式(9)计算伪宏导电孔隙度Φps,绘制Φps与实验测量地层因素F交会图,如图 8a,Φps与F在双对数坐标下同样呈现单一线性关系,进一步说明了改进式所代表的地层因素与伪宏导电孔隙度关系的稳定性.将计算的Φps利用改进式计算地层因素,绘制计算地层因素与实验测量地层因素交会图,如图 8b,数据点绝大部分集中分布在45°线周围,表明改进式计算结果较为可靠.
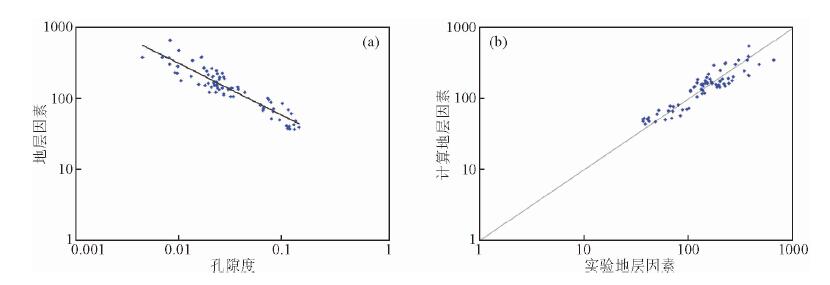 |
图 8 红河油田岩电实验数据检验改进式计算效果(72块岩样) (a)伪宏导电孔隙度与地层因素交会图; (b)实验地层因素与计算地层因素交会图. Fig. 8 The improved Archie formula is confirmed by core electricity experiment data of Honghe oilfield (from 72 core samples) (a) Pseudo macro conductive porosity and formation factor crossplot;(b) Calculated and experimental formation factors crossplot. |
| [1] | Archie G E. 1942. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Transactions of the AIME, 146(1): 54-62. |
| [2] | CHEN Jie. 2005. Research on pore structures in tight sand by using resistivity logging data (in Chinese)[MSc thesis]. Chengdu: Southwest Petroleum University. |
| [3] | FAN Yun-Feng. 2012. Study on litho-electric property relation of Chang 6-1 reservoirs in Zhidan-Zibei oildom, the Ordos basin (in Chinese)[MSc thesis]. Xi’an: Northwest University. |
| [4] | KONG Qiang-Fu, ZHOU Can-Can, Zhang Yan, et al. 2015. Numerical simulation methods of rock electrical properties based on digital cores: a review[J]. Progress in Geophysics (in Chinese), 30(2): 718-724, doi: 10.6038/pg20150232 |
| [5] | LAI Jin, WANG Gui-Wen, MENG Chen-Qing, et al. 2015. Pore structure characteristics and formation mechanisms analysis of tight gas sandstones[J]. Progress in Geophysics (in Chinese), 30(1): 217-227, doi: 10.6038/pg20150133. |
| [6] | LI Chang-Xi, TANG Liang-Min, HU Fa-Long, et al. 2010. On the electrical property of low porosity and low permeability sandstone reservoirs with well-developed secondary pore space[C]. // Proceedings of the SPWLA 51th Annual Logging Symposium. Perth, Australia: Society of Petrophysicists and Well-Log Analysts, BBBB1-BBBB9. |
| [7] | LI Min, XIAO Wen-Lian, GUO Xiao, et al. 2009. Laboratory study of the effective pressure law for permeability in Ta-Ba-Miao low-permeability sandstones[J]. Chinese Journal of Geophysics (in Chinese), 52(12): 3166-3174, doi: 10.3969/j.issn.0001-5733.2009.12.027. |
| [8] | LI Qiu-Shi, ZHOU Rong-An, ZHANG Jin-Gong, et al. 2002. Relations between Archie’s formula and reservoir pore structure[J]. Oil & Gas Geology (in Chinese), 23(4): 364-367. |
| [9] | LI Xia, ZHAO Wen-Zhi, ZHOU Can-Can, et al. 2012. Dual-porosity saturation model of low-porosity and low-permeability clastic reservoirs[J]. Petroleum Exploration and Development (in Chinese), 39(1): 82-91. |
| [10] | LI Zhuo, JIANG Zhen-Xue, PANG Xiong-Qi, et al. 2013. Genetic types of the tight sandstone gas reservoirs in the Kuqa depression, Tarim basin, NW China[J]. Earth Science-Journal of China University of Geosciences (in Chinese), 38(1): 156-164. |
| [11] | LIU Zhong-Hua, WU Shu-Qin, DU Bao-Hui, et al. 2013. Experimental study on the relationship between reservoir permeability and its formation resistivity factor[J]. Chinese Journal of Geophysics (in Chinese), 56(6): 2088-2097, doi: 10.6038/cjg20130629. |
| [12] | MAO Zhi-Qiang, TAN Ting-Dong, LIN Chun-Zeng, et al. 1997. The laboratory studies on pore structure and electrical properties of core samples fully-saturated with brine water[J]. Acta Petrolei Sinica (in Chinese), 18(3): 51-55. |
| [13] | SONG Lian-Teng, WANG Yun, LIU Zhong-Hua et al. 2015. Elastic anisotropy characteristics of tight sands under different confining pressures and fluid saturation states[J]. Chinese Journal of Geophysics (in Chinese), 58(9): 3401-3411, doi: 10.6038/cjg20150932. |
| [14] | WU Ze-Yun, WANG Xiao-Guang, WANG Hao. 2009. Improvement on the method to determine Archie parameters a and m in low porosity and low permeability reservoirs[J]. Journal of Oil and Gas Technology (in Chinese), 31(3): 76-78, 121. |
| [15] | YANG Xue. 2008. Determination of water saturation model on low porosity and low permeability reservoir and its application in Songnan area (in Chinese)[MSc thesis]. Changchun: Jilin University. |
| [16] | YAO Li-Na. 2012. Study on original oil saturation for low porosity and permeability sand reservoirs in Daqing placanticline (in Chinese)[MSc thesis]. Daqing: Northeast Petroleum University. |
| [17] | ZHANG Chao-Mo, ZHANG Zhan-Song, LI Jun, et al. 2009. Study on electrical conduction mechanism and water saturation equation based on gulf effect[J]. Journal of Oil and Gas Technology (in Chinese), 31(6): 86-89, 95. |
| [18] | ZHANG Hai-Ning, ZHANG Chao-Mo. 2011. The water saturation equation of eliminating background electric conduction for the complicated porosity structure formation[J]. Well Logging Technology (in Chinese), 35(1): 41-44. |
| [19] | ZHANG Ming-Lu, SHI Yu-Jiang. 2005. On Archie’s electrical parameters of sandstone reservoir with complicated pore structures[J]. Well Logging Technology (in Chinese), 29(5): 446-448. |
| [20] | ZHENG Qing-Lin, WANG Yu-Sen, ZHAO Yu. 2006. Improvement of Archie water-saturation model for the low porosity formation[J]. Well Logging Technology (in Chinese), 30(1): 57-59. |
| [21] | ZHU Ru-Kai, ZOU Cai-Neng, ZHANG Nai, et al. 2008. Diagenetic fluids evolution and genetic mechanism of tight sandstone gas reservoirs in Upper Triassic Xujiahe Formation in Sichuan Basin, China[J]. Science in China Series D: Earth Sciences, 51(9):1340-1353. |
| [22] | 陈杰. 2005. 基于电阻率测井资料研究致密砂岩孔隙结构特征[硕士论文]. 成都: 西南石油学院. |
| [23] | 樊云峰. 2012. 鄂尔多斯盆地志丹-子北油区长6-1储层岩电关系特征研究[硕士论文]. 西安: 西北大学. |
| [24] | 孔强夫, 周灿灿, 张艳,等. 2015. 基于数字岩心岩石电性数值模拟方法综述[J]. 地球物理学进展, 30(2): 718-724, doi:10.6038/pg20150232. |
| [25] | 赖锦, 王贵文, 孟辰卿,等. 2015. 致密砂岩气储层孔隙结构特征及其成因机理分析[J]. 地球物理学进展, 30(1): 217-227, doi: 10.6038/pg20150133. |
| [26] | 李闽, 肖文联, 郭肖,等. 2009. 塔巴庙低渗致密砂岩渗透率有效应力定律实验研究[J]. 地球物理学报, 52(12): 3166-3174, doi: 10.3969/j.issn.0001-5733.2009.12.027. |
| [27] | 李秋实, 周荣安, 张金功,等. 2002. 阿尔奇公式与储层孔隙结构的关系[J]. 石油与天然气地质, 23(4): 364-367. |
| [28] | 李霞, 赵文智, 周灿灿,等. 2012. 低孔低渗碎屑岩储集层双孔隙饱和度模型[J]. 石油勘探与开发, 39(1): 82-91. |
| [29] | 李卓, 姜振学, 庞雄奇,等. 2013. 塔里木盆地库车坳陷致密砂岩气藏成因类型[J]. 地球科学—中国地质大学学报, 38(1): 156-164. |
| [30] | 刘忠华, 吴淑琴, 杜宝会,等. 2013. 储层渗透性与地层因素关系的实验研究与分析[J]. 地球物理学报, 56(6): 2088-2097, doi: 10.6038/cjg20130629. |
| [31] | 毛志强, 谭廷栋, 林纯增,等. 1997. 完全含水多孔岩石电学性质及其孔隙结构实验研究[J]. 石油学报, 18(3): 51-55. |
| [32] | 宋连腾, 王赟, 刘忠华,等. 2015. 不同围压和流体饱和状态下致密砂岩弹性各向异性特征[J]. 地球物理学报, 58(9): 3401-3411, doi: 10.6038/cjg20150932. |
| [33] | 伍泽云, 王晓光, 王浩. 2009. 低孔低渗储层中确定Archie参数m与a的改进方法[J]. 石油天然气学报(江汉石油学院学报), 31(3): 76-78, 121. |
| [34] | 杨雪. 2008. 低孔低渗储层含水饱和度模型的确定及在松南地区的应用[硕士论文]. 长春: 吉林大学. |
| [35] | 么丽娜. 2012. 大庆长垣低孔渗砂岩储层原始含油饱和度模型研究[硕士论文]. 大庆: 东北石油大学. |
| [36] | 张超谟, 张占松, 李军,等. 2009. 基于港湾效应的导电机理与饱和度方程研究[J]. 石油天然气学报(江汉石油学院学报), 31(6): 86-89, 95. |
| [37] | 章海宁, 张超谟. 2011. 适用复杂孔隙结构地层消除背景导电饱和度模型[J]. 测井技术, 35(1): 41-44. |
| [38] | 张明禄, 石玉江. 2005. 复杂孔隙结构砂岩储层岩电参数研究[J]. 测井技术, 29(5): 446-448. |
| [39] | 郑庆林, 王钰森, 赵雨. 2006. 低孔隙度条件下阿尔奇含水饱和度解释模型改进[J]. 测井技术, 30(1): 57-59. |
| [40] | 朱如凯, 邹才能, 张鼐,等. 2009. 致密砂岩气藏储层成岩流体演化与致密成因机理—以四川盆地上三叠统须家河组为例[J]. 中国科学 D辑: 地球科学, 39(3): 327-339. |
 2016, Vol. 31
2016, Vol. 31

