地球物理学进展  2016, Vol. 31 Issue (2): 637-642   PDF    
引用本文
张晓鹏, 李世维, 靳平. 2016. 负电阻反馈式地震计的自标定技术[J]. 地球物理学进展, 31(2): 637-642, doi: 10.6038/pg20160217  
ZHANG Xiao-peng, LI Shi-wei, JIN Ping. 2016. Self-calibration technique for negative impedance feedback seismometers. Progress in Geophysics, 31(2): 637-642, doi: 10.6038/pg20160217   
负电阻反馈式地震计的自标定技术
张晓鹏, 李世维, 靳平    
西北核技术研究所, 西安 710024
收稿日期: 2015-04-25 修回日期: 2015-11-21.
作者简介: 张晓鹏,男,1988年生,硕士,现主要从事地震传感器研制工作.(E-mail:zhangxiaopeng@nint.ac.cn)
摘要: 针对负电阻反馈式地震计缺乏标定线圈无法进行现场标定的问题,研制了一种可内置于地震计内部的相对标定系统,该系统在信号线圈内接入阶跃电流,通过电磁感应对摆体施加阶跃加速度激励,测量仪器的暂态响应输出求解得到地震计的传递特性.文章首先推导和建立了自标定模型,设计和制作标定电路,采用L-M法求解地震计的传递函数,分别对三台样机进行了自标定和振动台标定实验.实验表明两种标定方法的结果较为一致,相对误差在5%以内,证明了这种自标定技术的有效性,实现了该类型地震传感器的灵活标定.
关键词: 负电阻反馈式地震计     单线圈     自标定     L-M法    
Self-calibration technique for negative impedance feedback seismometers
ZHANG Xiao-peng, LI Shi-wei, JIN Ping    
Northwest Institute of Nuclear Technology, Xi'an 710024, China
Abstract: The calibration of the sensor's transfer function is important to test the performance of a seismometer. Since the miniaturized negative impedance feedback seismometers lack the calibration coils, it's hard to calibrate the sensor without a shake table. Considering this problem, a self-calibration technique based on the step transient response is described. The calibration circuit, which can be integrated into the sensors system is designed and manufactured. A theory based on the L-M algorithm is developed that can obtain the transfer function from the transient output. The method is confirmed by comparing this single coil method to the shake table method. And these results were within 5.0 % error with each other, which makes the calibration work of this kind of seismometer easy and efficient.
Key words: negative impedance feedback seismometer     single coil     self-calibration     L-M method    
0 引 言

根据激励方式不同，地震计的标定方法可分为绝对标定法和相对标定法(Wielandt，2002).绝对标定法对仪器整体施加运动激励，如振动台标定和倾斜标定；相对标定法对摆体施加已知的力激励，如阶跃标定和随机信号标定(Havskov and Alguacil，2005).目前，国内已经有少数单位建成了性能指标世界领先的标准振动装置(韩冬和何闻，2008；于梅等，2011)，这种振动台标定的方法精度较高，但需要依托相关实验设备和环境，不适用于地震计的现场标定.近些年来中国地震局的科研人员对地震计的台站相对标定技术进行了深入研究(李海亮，2000；周云耀，2004)，并对装备于“国家数字地震台网”的CTS-1、JCZ-1和BBVS-60等宽频带地震计进行了自标定(蔡亚先和吕永清，2005；林湛，2008；周云耀等，2008)，该标定技术依托地震计内部的标定线圈对摆体施加力激励，无需额外的振动台等设备和实验环境，具有较高的灵活性，适用于固定地震台站的现场标定.近年来随着大范围流动地震观测应用如军事地球物理探测(刘光鼎和刘代志，2003；刘代志等，2006)、主动震源探测和高精度地震勘探(王洪体，2009；赵春蕾等，2013)的兴起，地震计的便携性变得越发重要，一种重量和体积均较小的负电阻反馈式地震计(张晓鹏等，2014)被广泛用于这类流动地震观测应用，然而由于该类型地震计对小型化有较高要求，其机械结构中除换能线圈外无法再加入额外的标定线圈，导致依托标定线圈的自标定技术无法适用于该类地震计的现场标定，在一定程度上制约了流动地震观测应用的发展，需要对该类型地震计的自标定技术展开研究.

考虑到负电阻反馈式地震计是一种单一线圈的电磁换能式地震计，由于物探领域常用的地震检波器也采用类似的结构，所以可以将检波器的标定方法用于负电阻反馈式地震计.对于检波器的标定技术，除了采用振动台或本底噪声测试等标定手段外(Pavlis and Vernon，1994)，美国学者Rogers曾提出了“Weight-Release”单线圈标定方法(1995)，该方法在信号线圈内接入标准电流源，该电流在磁场中产生电磁力将摆体“托举”至一定位置，断开电流源，测量检波器暂态响应来求取检波器的系统参数.由于负电阻反馈式地震计具有类似的换能结构，可基于“Weight-Release”原理完成仪器的相对标定，但要实现地震计在野外的灵活标定，仍然需要解决“Weight-Release”方法数据利用率低、记录不完整和集成度差的问题，并基于该类型地震计特有的检测和反馈电路，推导建立标定模型，求解地震计的传递函数.

1 检波器的“Weight-Release”标定

图 1为“Weight-Release”方法的标定模型，该模型包括接入阻尼电阻Rd的检波器、电流源、数据采集器和单刀双掷开关.首先将单刀双掷开关接通左边的电流源，待系统稳定后，标定电流流过线圈电阻Rcoil，该电流在磁场的作用下所产生的电磁力同弹簧弹力平衡，摆体停留在偏离中心位置的某处.当单刀双掷开关接通右边数据采集器时，电流源同时断开，电磁力消失，摆体从之前的平衡位置释放，释放的过程等效于对摆体施加了一个与电磁力方向相反的阶跃加速度.通过计算这一电磁力的大小求取该阶跃加速度的值，并根据理论响应和实验的测量结果求解出检波器的传递函数.

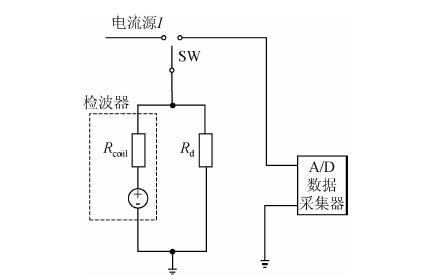图 1 检波器的“Weight-Release”标定模型 Fig. 1 “Weight-Release”calibration model for geophones

该方法虽然适用于电磁式地震检波器，但是若直接应用于负电阻反馈式地震计的标定，将会存在如下问题：

(1)数据利用率较低，只测量了单刀双掷开关与电流源断开并接入数据采集器时的暂态响应，但单刀双掷开关在接入电流源时的暂态响应将无法测得，导致实验的数据利用率较低.

(2)记录不完整，在实际测量中，开关断开电流源后并接入数据采集器这一操作需经历一段时间，数据采集器无法记录该段时间内的暂态响应，造成数据的丢失.

(3)集成度较低，该标定方法需要标准电流源、单刀双掷开关和数据采集器，并搭建相应的标定电路，导致这种标定形式不易集成在传感器的内部.

2 负电阻反馈式地震计的自标定2.1 标定模型

图 2为负电阻反馈式地震计的自标定模型，虚线部分为地震计的原理图(滤波输出部分未画出)，Rg和R3构成负反馈分压网络，负反馈系数γn=Rg/R3，R1、R5和R2构成正反馈分压网络，正反馈系数γp=(R1+R5)/R2，地震计的传递函数可表示为

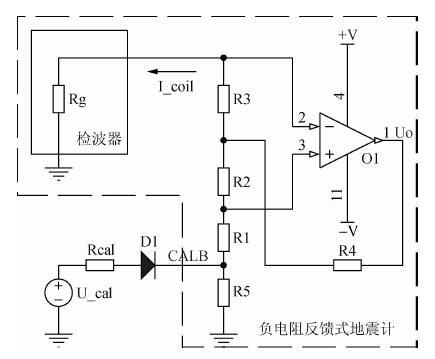图 2 负电阻反馈式地震计自标定模型 Fig. 2 Self-calibration model for the negative impedance feedback seismometer

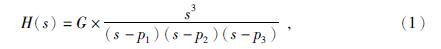
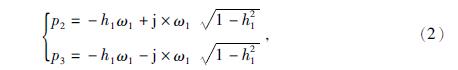
G为地震计的灵敏度，s为复频率，p1为负实极点， p2和p3为一对共轭极点，公式为

其中h1为阻尼系数，ω1为谐振圆频率.

根据“Weight-Release”标定思想，负电阻反馈式地震计需要在检波器线圈内接入标定电流，考虑前置放大器中正反馈支路和负反馈支路的电路结构，如图 2所示，可在正反馈支路电阻R1处经标定电阻Rcal接入标定电压ucal(t)，负反馈支路的检波器线圈流过标定电流icoil(t)，稳压二极管D1单向导通，隔离标定信号和前置放大器.

由于检波器线圈为绕向相反的两个线圈串联而成，其线圈电感可大部分抵消，整个线圈的剩余电感较小(10 mH左右)，并且地震信号频率较低(80 Hz以内)，所以这部分感抗的取值较小(小于5Ω)，对标定电流的幅度和相位的影响较小，那么ucal(t)为阶跃电压时，可认为icoil(t)为阶跃电流，为了便于求解，将ucal(t)和icoil(t)写为复频率形式Ucal(s)和Icoil(s).经过分析可知，自标定模块经地震计的输出信号Estep(s)不仅包含摆体对阶跃加速度的响应输出Ecal_coil(s)，还包含Ucal(s)经前置放大器和地震计电路的输出Ecal_Uc(s)，下面将分别求解.

(1)线圈中的标定电流Icoil(s).令Ucal(s)为幅值Vcc的阶跃电压信号，可认为Icoil(s)为幅值I0的阶跃电流信号，为了不改变前置放大器的输出特性，使满足R5<<R1且R5<<Rcal，所以有R5//Rcal≈R5，根据运算放大器特性求解Icoil(s)：

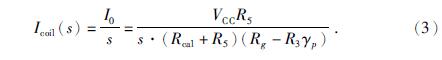
(2)加速度响应输出Ecal_coil(s).机电常数为G0的线圈在磁场的作用下对质量为m的摆体施加的电磁力为G0×Icoil(s)，根据牛顿第二定理，此时摆体受到大小为G0×Icoil(s)/m的加速度激励，地震计的关于加速度的传递函数为H(s)/s，所以可求得地震计系统在该加速度的作用下的输出信号Ecal_coil(s)为

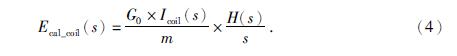
(3)Ucal(s)经前置放大器的输出Ecal_Uc(s).分析前置放大器电路，Ucal(s)经前置放大器输出电压为

经滤波放大电路的输出为

地震计关于标定模块的输出为

结合式(4)和式(6)，求解拉式逆变换，得到Estep(s)的时间域波形为

其中，k1、k2和k3为幅值系数，公式为

u(t)为单位阶跃函数，ωd为有阻频率，公式为

2.2 标定电流取值

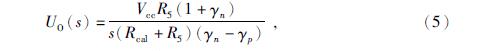
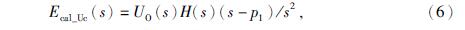
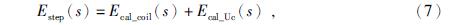
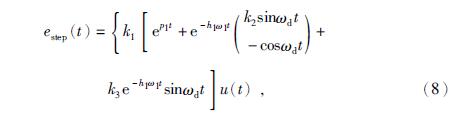
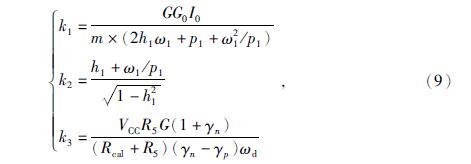
由于地震计的本底噪声会对自标定的输出信号的测量带来影响，所以应确保estep(t)具有较高的信噪比，这要求质量块在系统的线性范围内尽可能的偏离平衡位置，针对灵敏度较高的地震传感器，还应确保最大输出电压低于数据采集器的最大测量电压.一种较为合理的摆体位移z的取值依据为质量块的最大位移的一半(Rodgers，1992)，那么设弹簧弹性系数为k，摆体受力平衡，电磁力G0×I0和弹簧弹力k×z大小相等，可求取标定电流的大小I0，如式(11)所示，结合式(3)，可确定标定电阻Rcal的取值，使得标定信号在线性范围内具有较高的信噪比.式(11)为

2.3 自标定系统的电路设计

负电阻反馈式地震计的自标定系统最主要的部分为电压源ucal，其不仅能产生阶跃电压，还应具有小巧、简洁和易集成等特点.本文采用TL555型定时器芯片实现这一功能，该芯片可输出宽度可控的方波电压信号，其标定模块的电路原理图如图 3所示.当使能端TRIG接地时，可输出幅值等于Vcc的单个方波信号，方波的上升沿和下降沿可对地震计分别提供了方向相反的阶跃加速度激励.

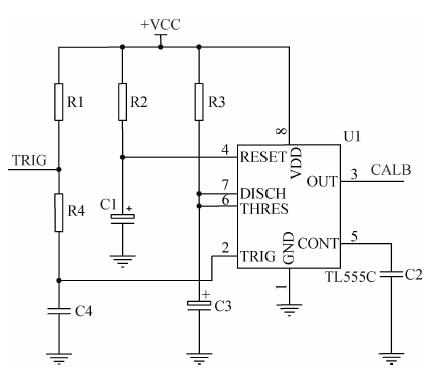图 3 自标定模块的电路原理图 Fig. 3 Circuit schematic design of the self-calibration module

根据TL555的工作原理，TRIG接地时，芯片②脚的电压由Vcc变为0 V，内置的比较器状态翻转，输出端CALB由0 V变为Vcc，此时电路进入暂稳态，Vcc通过电阻R3开始对电容C3充电，极板电压按指数规律上升，当其上升到2Vcc/3时，比较器的状态再次翻转，CALB由高电平变为0 V，暂稳态结束.根据电容充放电的规律，方波电压的宽度为

根据式(8)可知，地震计的阶跃输出主要为时间常数衰减的脉冲，为保证两次激励输出之间干扰较小，方波宽度应尽可能大于输出信号恢复到稳态的时间，考虑到本底噪声的干扰和测量的精度，在实际的标定模块设计中，可取t0>3/(h1ω1).

3 基于L-M法由标定数据求解地震计传递函数

经实验测量，地震计关于标定系统的实际输出d(t)如图 4所示，标定模型的理论输出如式(8)所示，由理论模型我们可以对实际输出波形进行拟合，求解出地震计的传递函数.下面将给出这一问题的基本描述，并采用改进的采非线性最小二乘法进行求解.

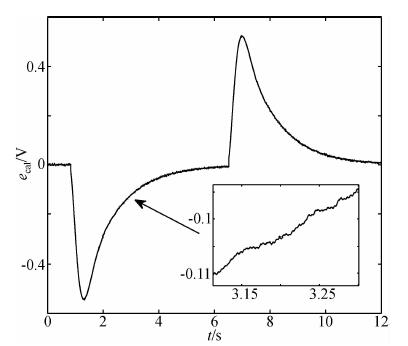图 4 自标实验地震计的实测波形 Fig. 4 Output data of the seismometer driven by the self-calibration system

(1)非线性最优化问题

根据式(8)，标定模块的输出信号为状态参量X=[k1 k2 k3 ω1 h1 p1]T的非线性函数，若t1，t2…tm时刻的理论波为向量E(X)=[estep(t1)estep(t2)estep(tm)]T，测量得到相应时刻所记录到地震计的实际输出d(t)的离散波形为向量D=[d(t1)d(t2)… d(tm)]T，第i个时刻的误差函数为f(X)=estep(ti)-d(ti)，一组测量点的误差向量可写为

求取误差向量的平方和，构造误差函数为

所以求取地震计传递的问题可转化为求使F(X)取极小值的状态参量X的最优化问题.然而F(X)是X的非线性函数，常规的线性最优化方法已经不再使用，一般可采用最速下降法、共轭梯度法、非线性最小二乘法等方法进行求解.根据式(15)，针对F(X)这种平方和形式的误差函数，一般采用非线性最小二乘方法较为快速和有效.该方法首先对误差函数进行线性化，采用迭代方法求解一系列线性最小二乘问题，从而逼近问题的真实解，下面将介绍求解方法.

(2)Levenberg-Marquardt法求解

设X(k)是第k次迭代的结果，在点X(k)处将f(X)采用一阶Taylor展开的方法将其线性化，求解该线性最小二乘问题得到第k+1次迭代结果X(k+1)为

d(k)为X(k)处的Gauss-Newton(高斯-牛顿，简称G-N)下降方向

其中Ak为f(X)关于X的雅克比矩阵，各元素为

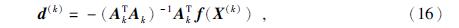
在实际求解中，当矩阵Ak奇异或者接近奇异时，(AkTAk)-1将无法求解或误差较大，此时G-N方向的更新步长可能过长，造成迭代不收敛的情况发生.为解决这一问题，Levenberg-Marquardt法(简称L-M法)将下降方向改进为

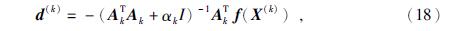
参数αk的取值决定了迭代的下降速度，迭代过程中可选取合适的αk，实现稳定而快速的收敛.当误差函数F(X)小于事先规定的阈值时，可认为迭代收敛，得到状态解X.X中直接给出了阻尼系数h1和实极点 p1的估计值，并且可算出传感器的谐振频率f1和灵敏度G.

4 实验结果和分析

图 4为实验测量到的自标定系统经负电阻反馈式地震计输出波形，可以看出地震计的输出为趋势相同、极性相反的对称脉冲信号，分别对应于方波电压的上升沿和下降沿，由波形的细节部分还可以发现信号中还包含有本底噪声，这将对最终的处理结果带来一定误差.

实验中分别对三台负电阻反馈式地震计样机制作了自标的模块，每台样机分别进行了5次标定实验，将负脉冲反向，求取10个脉冲的平均值作为实测信号d(t)，经L-M法求解系统参数.其中一台样机的理论模型(点划线)和实测波形(实线)的拟合结果如图 5所示，可以看到两条曲线基本符合，证明了L-M法的有效性.

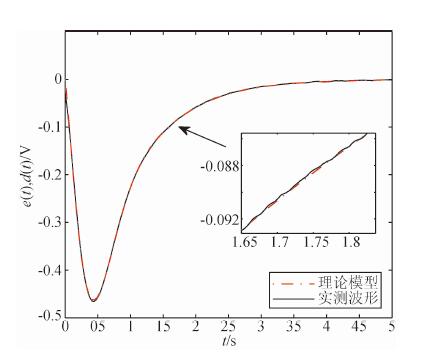图 5 理论模型与实测波形的拟合结果 Fig. 5 Fit between computed model and output data method

为了衡量自标定系统的性能，三台地震计样机还在中国计量科学研究院的低频振动台进行了标定实验，在该标定实验中选取了0.1~120 Hz内的15个频率，并采用频率域拟合的Levy方法(1959)求解出了地震计的传递函数(图 6).

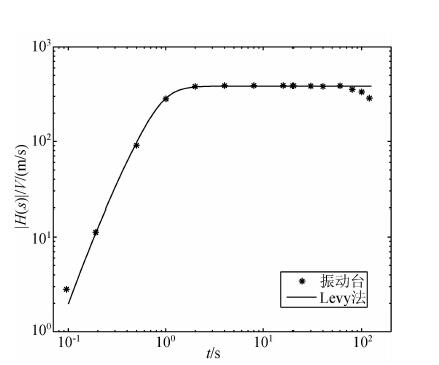图 6 振动台标定和Levy法的拟合结果 Fig. 6 Fit between shake table calibration and Levy method

表 1为两种标定方法的实验结果，以振动台的结果为标准值，衡量自标定实验的相对误差.根据实验结果可知：

表 1 三台样机的振动台标定值和自标定值的对比 Table 1 Three prototype of the shaking table set value is compared with self calibration value

(1)自标定的实验结果与振动台标定的实验结果符合较好，传递函数各参量的相对误差基本小于5%，具有较好的精度，可满足负电阻反馈式地震计的现场标定需求.

(2)地震计灵敏度G反应了信号的幅值特性，可利用的信息较为丰富，所以自标定系统对G的测量较为精确.

(3)谐振频率f1主要决定了波形的上升时间和脉冲宽度，由于信号在极大值附近具有较高的信噪比，所以自标定系统对f1的测量误差较小.

(4)自标定系统对阻尼系数h1和极点p1的测量误差相对较大，是因为p1和h1主要决定通频带之外(f1以下)的传递函数形状，该频带内的系统灵敏度急剧下降，信噪比较低，给自标定结果带来一定误差.

5 结 论

本文主要针对负电阻反馈式地震计缺乏标定线圈无法实现现场标定的问题，基于“Weight-Release”标定思想，提出了一种可内置于地震计的自标定系统，主要工作可概括为：

(1)基于该类型地震计的原理和结构，建立了自标定系统的模型，推导了标定输出的理论表达式，给出了标定电流的取值依据.

(2)基于TL555芯片，设计和制作了标定电路模块，该模块可输出幅值一定的方波电压信号，电路简洁紧凑，易于集成在地震计系统内部.

(3)给出了由理论模型和实测波形求解系统参数的问题描述，并采用改进的非线性最小二乘L-M法进行求解.

(4)对三台实验样机进行了自标定实验，实验结果与振动台的测试结果符合较好，证明了这种自标定技术及处理算法对负电阻反馈式地震计的有效性.

总的来说，本文所提出的自标定系统具有集成度高、记录完整和使用便捷等优点，解决了单一线圈型地震计较难进行现场标定的问题，为大范围流动地震观测等应用提供了技术基础.接下来还需要在波形预处理、最优化算法等方面开展研究，提升结果的精度.

致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持！

参考文献
[1] Cai Y X, Lü Y Q. 2005. In-situ calibration of JCZ-1 ultra broadband seismometer and CTS-1 very broadband seismometer at seismostation[J]. Journal of Geodesy and Geodynamics (in Chinese), 25(4): 117-122, doi: 10.3969/j.issn.1671-5942.2005.04.026.
[2] Han D, He W. 2008. Design of foundation for standard vibration systems with ultra-low-frequency[J]. Journal of Vibration and Shock (in Chinese), 27(9): 20-22, 50, doi: 10.3969/j.issn.1000-3835.2008.09.005.
[3] Havskov J, Alguacil G. 2005. Instrumentation in earthquake seismology[M]. Berlin: Springer.
[4] Levy E C. 1959. Complex-curve fitting[J]. IRE Transactions on Automatic Control, AC-4(1): 37-43.
[5] Li H L. 2000. The accurate measurement of seismometer thansfer function (in Chinese)[Ph. D. thesis]. Beijing: Institute for Geophysics, China Earthquake Administration.
[6] Lin Z. 2008. Calibration of the seismometer at the seismic station (in Chinese) [MSc thesis]. Beijing: Institute of Earthquake Science China Earthquake Administration.
[7] Liu D Z, Huang S Q, Qian C S. 2006. Developing military geophysics, making contribution for national safety——review on the inaugural meeting and the first symposium of geophysical special committee for national safety and military[J]. Progress in Geophysics (in Chinese), 21(1): 248-250,doi: 10.3969/j.issn.1004-2903.2006.01.037.
[8] Liu G D, Liu D Z. 2003. On military geophysics[J]. Progress in Geophysics (in Chinese), 18(4): 576-582, doi: 10.3969/j.issn.1004-2903.2003.04.001.
[9] Lü Y Q. Cai Y X, Zhou Y Y, et al. 2002. Precise fast determination of cycle and damping coefficient of wideband seismograph by MATLAB tool[J]. Journal of Geodesy and Geodynamics (in Chinese), 22(2): 116-120.
[10] Pavlis G L, Vernon F L. 1994. Calibration of seismometers using ground noise[J]. Bulletin of the Seismological Society of America, 84(4): 1243-1255.
[11] Rodgers P W. 1992. Frequency limits for seismometers as determined from signal-to-noise ratios. Part 1. The electromagnetic seismometer[J]. Bulletin of Seismological Society of America, 82(2): 1071-1098.
[12] Rodgers P W, Martin A J, Robertson M C, et al. 1995. Signal-coil calibration of electromagnetic seismometers[J]. Bulletin of the Seismological Society of America, 85(3): 845-850.
[13] Wang H T, Zhuang C T, Xue B, et al. 2009. Precisely and actively seismic monitoring[J]. Chinese Journal of Geophysics (in Chinese), 52(7): 1808-1815, doi: 10.3969/j.issn.0001-5733.2009.07.015.
[14] Wielandt E. 2002. Seismic sensors and their calibration[A]. //Bormanm P ed. New Manual of Seismological Observatory Practice (NMSOP)[M]. Potsdam: GeoForschungsZentrum.
[15] Yu M, Liu A D, Ma M D, et al. 2011. Magnitude and phase measurement technology for ultra-low frequency vibration using laser interferometry[J]. Journal of Vibration and Shock (in Chinese), 30(11): 130-134,doi: 10.3969/j.issn.1000-3835.2011.11.026.
[16] Zhang X P, Li S W, Wang T D, et al. 2014. An improved short period geophone-based seismometer[J]. Progress in Geophysics (in Chinese), 29(5): 2466-2471, doi: 10.6038/pg20140572.
[17] Zhao C L, Lu C, Hao T Y, et al. 2013. A study of the high-precision modular lightweight small vibrator[J]. Chinese Journal of Geophysics (in Chinese), 56(11): 3690-3698, doi: 10.6038/cjg20131110.
[18] Zheng X F, Ouyang B, Zhang D N, et al. 2009. Technical system construction of data backup centre for China seismograph network and the data support to researches on the Wenchuan earthquake[J]. Chinese Journal of Geophysics (in Chinese), 52(5): 1412-1417, doi: 10.3969/j.issn.0001-5733.2009.05.031.
[19] Zhou Y Y. 2004. Research and application on precise calibration techniques for ultra-broadband & very-broadband seismometers (in Chinese)[Ph. D. thesis]. Institute for Geophysics, China Earthquake Administration.
[20] Zhou Y Y, Wu T, Wang D. 2008. Precise test methods of 2nd order transfer function for Ultra broadband and very broadband seismometer[J]. Geomatics and Information Science of Wuhan University (in Chinese), 33(7): 730-734.
[21] 蔡亚先, 吕永清. 2005. 超宽频带与甚宽频带地震计的台站现场标定[J]. 大地测量与地球动力学, 25(4): 117-122, doi:10.3969/j.issn.1671-5942.2005.04.026.
[22] 李海亮. 2000. 地震计传递函数精确测定研究[博士论文]. 北京: 中国地震局地球物理研究所.
[23] 韩冬, 何闻. 2008. 超低频标准振动系统基础设计技术[J]. 振动与冲击, 27(9): 20-22, 50, doi: 10.3969/j.issn.1000-3835.2008.09.005.
[24] 刘代志, 黄世奇, 钱昌松. 2006. 发展军事地球物理, 为国家安全作贡献——国家安全与军事地球物理专业委员会成立大会暨首届学术研讨会综述[J]. 地球物理学进展, 21(1): 248-250, doi: 10.3969/j.issn.1004-2903.2006.01.037.
[25] 刘光鼎, 刘代志. 2003. 试论军事地球物理学[J]. 地球物理学进展, 18(4): 576-582, doi: 10.3969/j.issn.1004-2903.2003.04.001.
[26] 吕永清, 蔡亚先, 周云耀,等. 2002. 用MATLAB工具精确快速测定宽频带地震计的周期与阻尼系数[J]. 大地测量与地球动力学, 22(2): 116-120.
[27] 王洪体, 庄灿涛, 薛兵,等. 2009. 精密主动地震监测[J]. 地球物理学报, 52(7): 1808-1815, doi: 10.3969/j.issn.0001-5733.2009.07.015.
[28] 于梅, 刘爱东, 马明德,等. 2011. 超低频激光干涉法振动幅相特性测量技术的研究[J]. 振动与冲击, 30(11): 130-134, doi: 10.3969/j.issn.1000-3835.2011.11.026.
[29] 张晓鹏, 李世维, 王同东,等. 2014. 基于检波器的短周期地震计的改进[J]. 地球物理学进展, 29(5): 2466-2471, doi: 10.6038/pg20140572.
[30] 赵春蕾, 卢川, 郝天珧,等. 2013. 高精度组合式轻便小型可控震源的研究[J]. 地球物理学报, 56(11): 3690-3698, doi: 10.6038/cjg20131110.
[31] 郑秀芬, 欧阳飚, 张东宁,等. 2009. “国家数字测震台网数据备份中心”技术系统建设及其对汶川大地震研究的数据支撑[J]. 地球物理学报, 52(5): 1412-1417, doi: 10.3969/j.issn.0001-5733.2009.05.031.
[32] 赵春蕾, 卢川, 郝天珧,等. 2013. 高精度组合式轻便小型可控震源的研究[J]. 地球物理学报, 56(11): 3690-3698, doi: 10.6038/cjg20131110.
[33] 周云耀, 吴涛, 王墩. 2008. 甚宽频带地震计二阶传递函数的精确测定方法研究[J]. 武汉大学学报·信息科学版, 33(7): 730-734.