2. 国家卫星海洋应用中心, 北京 100081;
3. 山东科技大学测绘科学与工程学院, 青岛 266590
2. National Satellite Ocean Application Service, Beijing 100081, China;
3. College of Geodesy and Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
HY-2A卫星于2011 年8 月16 日在太原卫星发射中心成功发射,是我国第一颗海洋动力环境卫星,至今仍在轨运行.雷达高度计是HY-2A卫星搭载的主载荷之一,能够全天候获取海面高度、浪高、风速等多种海洋动力环境参数,直接为灾害性海况预警预报提供实测数据,并为海洋防灾减灾、海洋资源开发、海洋环境保护及海洋科学研究等提供支撑服务(蒋兴伟等,2014).
HY-2A临时地球物理数据集IGDR(Interim Geophysical Data Record)从2011年10月1日开始分发,目前已发布了数年的IGDR数据,并在一些领域取得了实际应用,如Chen与Lillibridge等人利用HY-2A单轨数据监测到了2012年飓风桑迪经过美国近海时的规模和风暴潮的近岸特征,提高了海洋灾害预警与评估的时效性和准确性(Chen et al,2014; Lillibridge et al,2014),另外法国Centre national d’études spatiales/ Collecte Localisation Satellites(CNES/CLS)对HY-2A波形数据S-IGDR重处理后,已将HY-2A测高数据融合到多任务测高数据处理系统Ssalto/Duacs V15.1(Picot et al,2013).但相对国际上其他测高卫星TOPEX/Poseidon(T/P)、Jason-1&2等在海洋各领域的广泛应用(暴景阳等,2000; 常晓涛等,2006; Niedzielski et al,2008;郭金运等,2010; Sandwell et al,2014),我国HY-2A测高数据的应用仍较少,其数据的科学价值未能有效体现,这与卫星数据的质量检核和误差定标的滞后有一定关系(杨磊等,2014).通常卫星高度计的测量误差可通过绝对定标得到,但这需要专门的定标场地和持续的维护费用,现在全球仅有四处较为成熟的卫星测高定标场(Watson et al,2011),而我国的测高卫星海上定标场仍在规划建设中.除绝对定标外,不同卫星间的交叉定标与评估也是国内外学者主要采用的一种数据质量和精度评估方式(Ablain et al,2010),其优点是可以对全球数据分析,而不存在绝对定标场的地域限制,通过对星间数据的交叉对比分析,可探测系统异常和地域性误差特征,评估系统性能和测量精度,为数据的改进和应用提供定量依据.
在卫星发射后,国内学者对HY-2A测高数据也做了少量的质量评估和定标研究,如Jiang等对HY-2A初期的多传感器数据分析表明其海面高度SSH、有效波高SWH观测符合设计技术指标要求(Jiang et al,2012),Jia等计算HY-2A第22周期的SSH交叉点不符值为-2 cm±8.6 cm(Jia et al,2014),Cheng等将HY-2A第49周期数据在极地海域的SSH与Saral/AltiKa和CryoSat-2比较,发现HY-2A观测的SSH偏高约10 cm(Cheng and Andersen,2014).上述学者研究的主要不足是数据量偏少(单周期或者单轨迹),所分析的参数不全面,不足以支持HY-2A长期观测数据的质量评估和精度分析.本文以Jason-2同时期观测的GDR数据为参考,利用最新公布的HY-2A一年多观测数据对其完整性和有效性进行分析,评估其数据质量和系统特征,对HY-2A的主要参数后向散射系数、有效波高、海况偏差、湿延迟、电离层延迟等进行了评价分析;计算HY-2A观测的一年多海面高异常时间序列漂移量,分析其时变特征;计算HY-2A海面高的交叉点不符值,并分析其空间分布特征.本文研究结果可为HY-2A IGDR数据的应用提供依据,并为GDR数据的生产提供参考.
1 HY-2A高度计数据和数据处理HY-2A卫星采用太阳同步轨道,卫星轨迹最高可至南北纬80.69°,可覆盖全球开阔海域以及部分北极海域.卫星前期采用周期为14 天的重复轨道,后期计划采用周期为168 天的回归轨道(赵罡等,2012),至今卫星已运行3年多,但仍沿用周期14天的轨道.HY-2A雷达高度计是一个发射频率为13.58 GHz±160 MHz和5.25 GHz±160 MHz的双频雷达高度计,采用脉冲有限工作方式测量海面高度、有效波高和海面风速等海洋要素(许可等,2013).另外卫星搭载了星载校正微波辐射计用于反演雷达脉冲的大气湿延迟改正,并搭载双频全球定位系统GPS、多普勒地球轨道和无线电定位系统DORIS和激光反射棱镜阵列SLR用于精密定轨(蒋兴伟等,2014).
HY-2A雷达高度计数据由国家卫星海洋应用中心对外发布,目前对外发布的数据只有IGDR,申请者获授权后可下载使用.本文使用HY-2A第51至80周期的同一版IGDR数据(由于第51周期之前的数据版本与之后不同,因此没有采用),时间跨度从2013年8月31日至2014年10月25日,由于时间跨度超1年,因而可探测仪器参数或地球物理参数的季节性变化.本文利用Jason-2第190至231周期同期观测GDR数据(时间范围2013年8月29日至2014年10月19日)作为对比数据,以分析高度计主要参数的星间差异.
Jason-2和HY-2A的海面高SSH和海面高异常SLA采用公式(1)和(2)计算(Fu and Cazenave 2001),公式为
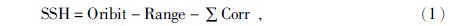

式中Orbit表示卫星轨道高度,Range表示高度计测距值;∑Corr表示仪器改正和地球物理改正项之和,地球物理改正包括大气干延迟、大气湿延迟、电离层延迟、海潮、极潮、地球固体潮与高频振荡改正,由于Jason-2的仪器改正已经加入到距离观测值(CNES 2011),而HY-2A测距值中未加入仪器改正,因此HY-2A还需要加入仪器内部延迟改正和天线质心距离改正.计算HY-2A和Jason-2海面高和海面高异常所用的主要改正项来源见表 1.虽然HY-2A采用的海潮模型和Jason-2不同,但研究表明模型在近海区域有较明显的影响,在开阔海域影响很小(CLS 2013),本文在分析SSH交叉点和SLA趋势时对海深做了约束(海深大于1000 m),因此模型差异的影响可以忽略.
|
|
表 1 计算HY-2A 与Jason-2 SSH采用的主要地球物理改正 Table 1 Main geophysical corrections applied to SSH for HY-2A and Jason-2 |
理论上HY-2A一个周期有386个轨迹,但实际上由于卫星测量模式的调整或其他原因(地面接收站问题或数据传输异常,也可能是由于地面控制等)(Zaouche et al,2010),HY-2A IGDR数据存在整轨迹缺失的现象.图 1a为HY-2A每周期的轨迹缺失情况,第51至68周期的轨迹缺失现象较轻,但69周期后轨迹缺失较显著,其中第69周期缺失超过120个轨迹,缺失比例占到总轨迹数的31%,第69周期的观测数据分布如图 2b所示,与图 2a显示的理论轨迹空间分布相比其观测密度稀疏了很多.如图 1b所示,Jason-2也存在较轻的轨迹缺失现象,研究表明导致Jason-2轨迹缺失的原因是卫星调整为安全模式(CLS 2013).
 | 图 1 HY-2A与Jason-2轨迹缺失个数以及比例 Fig. 1 Missing pass number and percentage of HY-2A and Jason-2 |
 | 图 2 HY-2A 理论轨迹全球分布(a)和第69周期轨迹分布(b) Fig. 2 Theoretical distribution of HY-2A ground tracks (a) and real ground pass distribution of HY-2A circle 69 (b) |
另外利用实际沿轨观测数据数量和理论沿轨数据量可确定HY-2A雷达高度计数据完整性,即数据的缺失数量及比例,进一步可反映卫星雷达高度计在轨运行状况.图 3a是HY-2A 陆地和海洋观测数据每周期的缺失比例,可见陆地数据的缺失比例要高于海洋,这是因为测高系统设计的回波跟踪器适用于海洋高斯反射面,而陆地表面由于起伏不规则,不是高斯分布面,对回波信号的跟踪处理带来较大影响.图 3a表明HY-2A在海洋的数据缺失比例在68周期前约为10%,但由于整轨的缺失导致第69周期后的数据缺失比例偏高且不规则.为排除轨迹缺失对统计的影响,图 3b表示HY-2A在有观测轨迹情况下的数据缺失比例,统计表明其陆地观测数据缺失比平均值为39%,介于Jason-2(11.51%)和Jason-1(54.48%)之间;其海洋观测数据缺失比平均值为8%,比Jason-2(0.03%)和Jason-1(2%)偏高,海洋数据缺失的最主要原因可能是沿海陆地、海冰或较差海况的影响.
 | 图 3 HY-2A观测数据缺失比例(a),不考虑缺失轨迹的HY-2A观测数据缺失比例(b) Fig. 3 Percentage of HY-2A missing measurements over ocean and landcomputed with (a) and without (b) the missing passes |
计算SSH和SLA时,需按一定的编辑条件对测高数据进行数据编辑,可将不符合条件的观测数据滤除(Watson et al,2003).数据的编辑比例即不符合约束条件被滤除的数据比例,能够反映卫星测高数据的质量,编辑比例越低,表明其可用性越好.
对高度计、辐射计和相关地球物理参数参照表 2给定的阈值进行约束,得到的HY-2A和Jason-2的数据编辑比例见图 4,图 4a表明HY-2A 第76周期后的数据编辑比例为100%,对各约束参数的单独分析发现这是由于干、湿延迟模型和极潮模型无效造成的.图 4表明HY-2A和Jason-2在浅海和高纬度地区的数据编辑占了较高比重,对海深(大于1000 m)和纬度范围(南北纬60°之间)约束后,HY-2A和Jason-2的编辑比例都明显下降,约束前后的Jason-2的编辑比例均值分别为13.5%±3.7%和2.9%±1.5%,约束前后的HY-2A编辑均值为52%±29%和44%±34%.
 | 图 4 HY-2A (a)与Jason-2 (b) 的海洋数据编辑比例 Fig. 4 Percentage of edited measurements for HY-2A (a) and Jason-2 (b) over ocean |
|
|
表 2 卫星高度计和辐射计主要数据编辑阈值. Table 2 Main editing thresholds values for satellite altimeter and microwave radiometer. |
为评估HY-2A IGDR数据产品的质量和精度,对主要观测参数和地球物理改正分别分析,并与同期观测的Jason-2 GDR数据进行对比,探测星间系统差异和系统漂移.由于HY-2A和Jason-2都以Ku波段作为高度计的主要测量频率,而将C波段作为辅助,因此本文主要分析Ku波段的参数.在统计分析前,首先对高度计参数进行数据编辑,因HY-2A第76周期后的干延迟模型和极潮模型均无效(测高数据自身的问题),又因干延迟和模型和极潮模型相对稳定,该约束对数据编辑的影响小,故为了提高有效数据观测量,在统计分析HY-2A参数时不对这2项参数约束.另外为使HY-2A数据空间分布与Jason-2一致,对HY-2A约束在南北纬66.15°内.
3.1 后向散射系数后向散射系数(sigma0)可通过波形重定计算,和雷达回波能量的最大振幅相关,是雷达高度计的主要观测参数之一.图 5表明Jason-2观测的sigma0总体上表现稳定,没有出现异常值和趋势变化,但HY-2A出现多次跳变和漂移情况,其中在第62和63周期出现断层式下降,到第64周期再回正常水平,随后第64至69周期再次表现出下降趋势,第69周期后再回到正常.排除HY-2A的第62、63异常值,对HY-2A和Jason-2同期sigma0进行统计,表明二者的差异均值为-0.10 dB±0.26 dB.另外选择HY-2A第60(正常)和第63周期(异常)为例,分析其与Jason-2同期sigma0的差值空间分布特征,结果如图 6所示二者差值未表现出显著的地域相关分布,但与Jason-2比较HY-2A第63周期存在约-2 dB的系统差异.
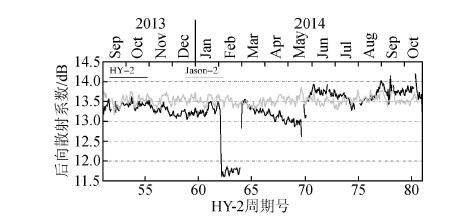 | 图 5 HY-2A和Jason-2 Ku波段后向散射系数日均值时间序列 Fig. 5 Temporal evolution of the daily mean of backscatter coefficient for HY-2A and Jason-2 |
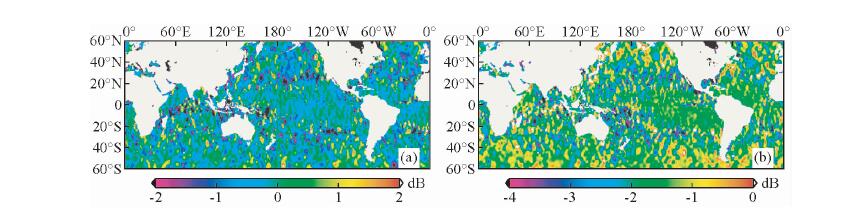 | 图 6 HY-2A第60周期与Jason-2第203周期sigma0差值空间分布(a),HY-2A第63周期与Jason-2 第207周期sigma0差值空间分布(b) Fig. 6 Distribution of Sigma0 differences between HY-2A circle 60 and Jason-2 circle 203 (a) and between HY-2A circle 63 and Jason-2 circle 207 (b) |
有效波高(SWH)是从雷达回波前缘坡度计算而来,近似等于一段时间内或者给定海域内最高海浪的三分之一高度.虽然sigma0存在较为显著的异常和漂移变化,但图 7表明HY-2A和同期Jason-2观测的有效波高SWH具有很好的一致性,二者相关系数为0.84,星间SWH日均值差异均值为-3.8 cm±7.1 cm,表明HY-2A反演SWH的精度较高.
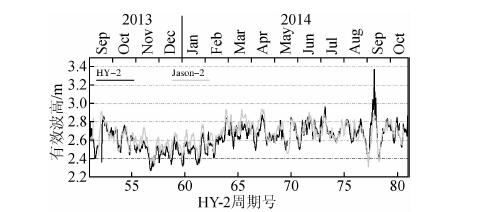 | 图 7 HY-2A与Jason-2有效波高SWH日均值时间序列 Fig. 7 Temporal evolution of the daily mean of significant wave height for HY-2A and Jason-2 |
由于海面对雷达回波反射的贡献并不平均,而是波谷对回波的贡献大于波峰,因此平均反射面将偏离平均海面而趋近波谷,从而使卫星的测距值偏大,另外由于星载高度计算法假设海面高的概率密度是对称的,而实际情况是倾斜的,同时还存在着高度计的波形跟踪误差,这三者合称为海况偏差(SSB).目前最精确的SSB可采用SWH相关的经验模型计算,通常2 m的SWH对应着约10 cm±2 cm的SSB,它是目前测高中的最主要误差源(Tran et al,2010).图 8 为HY-2A和Jason-2 SSB时间序列,统计表明星间差值均值为-3.3 cm±0.3 cm,相关系数为0.82,与星间SWH的相关系数0.84很接近,但因SSB是计算海面高和海面高异常的改正参数,该参数的星间系统差异将对测高精度产生直接影响.
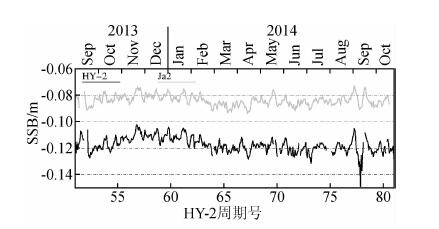 | 图 8 HY-2A与Jason-2 SSB时间序列 Fig. 8 Temporal evolution of the daily mean of SSB for HY-2A and Jason-2 |
雷达脉冲在穿越大气层时受大气的衰减作用,导致传播速率变化,因此必须对高度计测距进行大气延迟改正.大气延迟分为干延迟和湿延迟,其中干延迟分量接近常数,而湿延迟则变化显著,通常采用星载微波辐射计观测亮度温度进行反演,另一种方法是采用气象模型内插(如欧洲中尺度气象模型ECMWF),当辐射计观测数据出现异常时可采用模型值代替.HY-2A和Jason-2高度计湿延迟均有微波辐射计实测值和模型值.
首先分析HY-2A星载校正微波辐射计观测数据和模型插值的湿延迟改正的有效性情况,结果如图 9a所示,研究发现辐射计和模型的无效数据分布较明显,总体上模型值在第65周期之前表现良好,大部分周期不存在无效数据,但第66至68周期湿延迟模型出现显著的无效数据情况,并且2014年8月8日后(第75周期)模型值全部变为无效数据,如图 9b所示,整轨数据的无效数据比例变为100%,而微波辐射计观测的湿延迟改正无效数据比例基本小于10%,但如图 9c,HY-2A第51周期至80周期持续存在辐射计湿延迟在单个轨迹全部无效的情况.
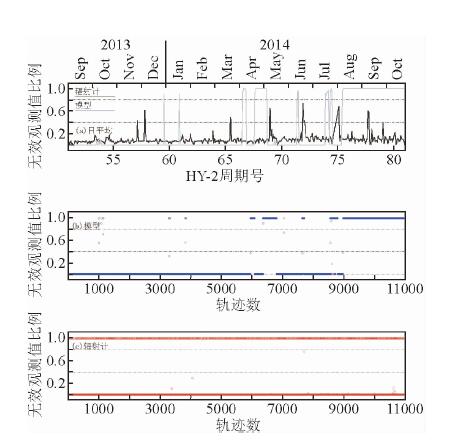 | 图 9 按天统计的HY-2A 辐射计和模型值湿延迟日均值无效比例(a),按轨迹统计的HY-2A 模型值无效比例(b)和辐射计无效比例(c) Fig. 9 Percentage of the daily mean of the invalid wet troposphere delay derived from model and microwave radiometer (a) for HY-2A,and the invalid proportion of model (b) and microwave radiometer (c) |
剔除无效数据后的湿延迟日均值时间序列如图 10所示,其中(a)为HY-2A的辐射计、模型值及其差值的时间序列,统计表明辐射计与模型值差值均值为-24±15 mm,并且HY-2A辐射计湿延迟存在显著的阶梯式漂移现象;(b)表示Jason-2的辐射计和模型值湿延迟时间序列,统计表明辐射计湿延迟和模型值差异均值为5±0.5 mm,具有系统性特征且差异较小;(c)表示Jason-2和HY-2A的辐射计湿延迟差异,统计表明星间差值为-17±15 mm.HY-2A IGDR数据中的辐射计湿延迟改正异常可能和辐射计自身的漂移有关,需要在日后的数据生产过程中考虑辐射计漂移的影响.
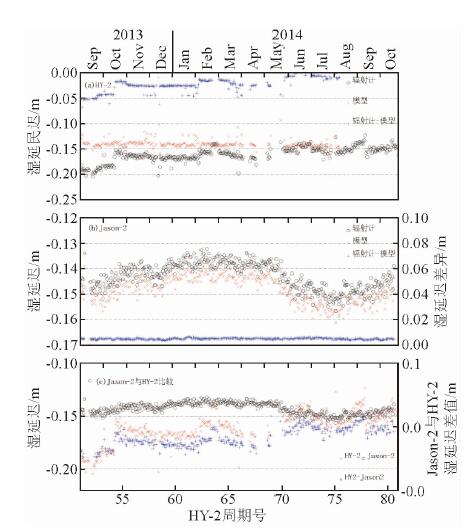 | 图 10 HY-2A (a)和Jason-2 (b)湿延迟日均值时间序列和星间比较(c) Fig. 10 Temporal evolution of the daily mean of wet troposphere delay for HY-2A (a), Jason-2 (b) and the comparison between HY-2A and Jason-2 (c) |
雷达脉冲在传播过程中还受地球电离层自由电子的影响,自由电子密度越大则脉冲传播速度越低.由于电离层延迟和脉冲频率的平方成反比,因此通常用双频观测方式估计电离层延迟.HY-2A和Jason-2高度计都采用Ku和C双波段来估计电离层延迟,同时还提供电离层延迟的GIM(Global Ionosphere Maps)模型值,以备双频电离层延迟失效或者非海洋反射面测高采用.分别对HY-2A和Jason-2的双频电离层延迟和模型值差异进行了对比分析,如图 11a所示HY-2A电离层延迟的模型值时间序列未呈现出时变特征,而是非常平稳,统计表明其与HY-2A双频电离层延迟的相关系数仅为9.7%,差值均值为-25±9 mm,说明其中一个值存在显著误差;图 11b是Jason-2的双频电离层延迟和模型值比较,分析表明二者的相关系数为99.7%,差异均值为6±2 mm,数据质量较好;如图 11c表示Jason-2和HY-2A的双频电离层延迟改正比较,统计表明二者相关系数为91.7%,差值均值为-14.8±6.7 mm,表明HY-2A的双频电离层延迟改正时变趋势和Jason-2较符合.
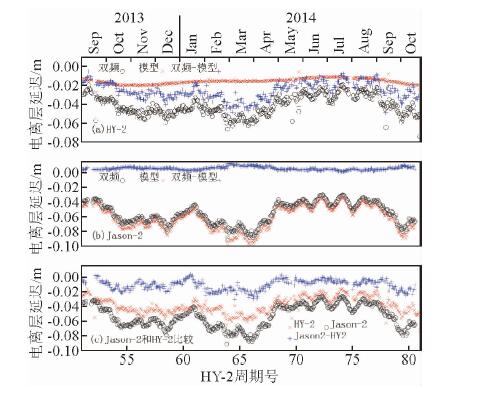 | 图 11 HY-2A(a)和Jason-2(b)电离层延迟双频观测值与模型值的时间序列,Jason-2和HY-2A的 电离层延迟改正的双频观测值比较(c) Fig. 11 Temporal evolution of the daily mean of ionosphere delay for HY-2A (a), Jason-2 (b) and the comparison between HY-2A and Jason-2 (c) |
理论上电离层延迟改正的模型值和双频观测值之间的关系应如Jason-2具有较高的相关系数,存在一定的系统性差异而非随机性差异,但HY-2A电离层延迟的模型值和实测值具有较小的相关系数,另外统计表明HY-2A与Jason-2电离层延迟的模型值差异为-46±15 mm,也显著偏大,故HY-2A的电离层模型值存在计算错误.
4 海面高与海面高异常 4.1 海面高异常分析海面高异常SLA是海面高SSH减去平均海面高MSS(为平均动态海面高MDT和大地水准面高之和)的结果,SLA长时间序列可以用于监测高度计长期的稳定性,探测SSH观测异常趋势和相关误差等.图 12为HY-2A和Jason-2同期观测的SLA全球日均值时间序列,与Jason-2比较可发现HY-2A存在明显的漂移,分析得到2014年6月之前HY-2A SLA的漂移速率是-60.9 cm/y,每天存在约-1.7 mm 的漂移,2014年6月之后速率变慢为0.2 cm/y.而Jason-2的SLA变化趋势为0.18 cm/y,为上升趋势,或与海面高季节性变化有关.初步分析表明HY-2A观测的SLA漂移和地面数据处理过程中未加USO(Ultra Stable Oscillator)改正有关,采用地面应答器标定的HY-2A USO漂移速率达到-53.3 cm/y(中科院空间中心观测提供).USO已成为SLA漂移的关键因素,但辐射计湿延迟改正漂移等也对SLA漂移有一定影响.
 | 图 12 HY-2A和Jason-2 SLA 同期观测时间序列比较 Fig. 12 Temporal evolution of the daily mean of SLA for HY-2A and Jason-2 |
交叉点不符值是分析高度计测高数据质量的一种常用方法,卫星的升轨和降轨在不同时间飞过同一地点形成的交汇点称为交叉点,交叉点处海面高观测值差异为交叉点不符值(Wessel 2010).为减小海面高的时变影响,规定交叉点前后轨迹经过时间最大间隔为3天,另外为减小浅海与海冰的影响,约束海深大于1000 m,纬度在南北纬50°间.图 13为HY-2A和Jason-2的各周期海面高交叉点不符值标准差的时间序列,总体上HY-2A和Jason-2每周期的交叉点不符值标准差都较稳定,未出现明显的漂移现象,HY-2A交叉点不符值标准差均值为6.52 cm,Jason-2交叉点不符值标准差均值为5.35 cm,二者差异约为1.2 cm,此差异可能和HY-2A的飘移有关.
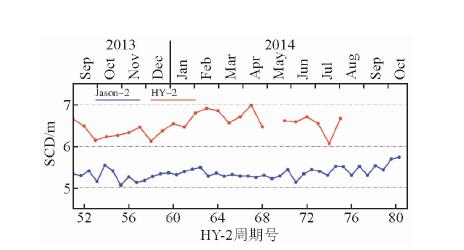 | 图 13 HY-2A和Jason-2海面高交叉点不符值标准差时间序列 Fig. 13 Temporal evolution of standard deviation of SSH differences at crossovers for HY-2A and Jason-2 |
图 14表示HY-2A和Jason-2星内与星间的交叉点海面高不符值空间分布,(a)表示Jason-2第190周期至231周期的交叉点海面高不符值空间分布,(b)表示HY-2A第51周期至75周期的星内交叉点不符值空间分布.图 14表明HY-2A和Jason-2各自的交叉点海面高不符值均未表现出显著的地域分布特征,即不符值分布较均衡,(b)图显示HY-2A在中国南海和澳大利亚东北部海域的异常与HY-2A数据在该海域的有效数据不足而引起的网格插值误差有关.
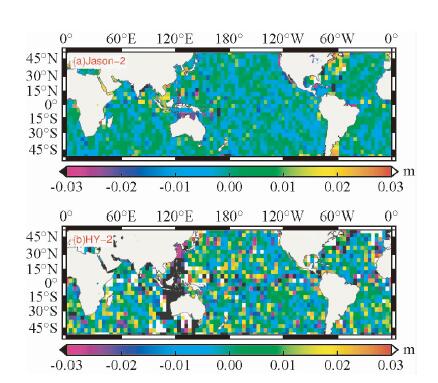 | 图 14 HY-2A与Jason-2的交叉点不符值空间分布 Fig. 14 Spatial distribution of the SSH difference at crossovers for HY-2A and Jason-2 |
| [1] | Ablain M, Philipps S, Picot N, et al. 2010. Jason-2 Global Statistical Assessment and Cross-Calibration with Jason-1. Marine Geodesy 33(sup1): 162-185. |
| [2] | BAO J Y, CHAO D B, LI J C. 2000. Tidal Harmonic Analysis near Crossovers of TOPEX/POSEIDON Ground Track in South China Sea [J]. ACT A GEODAET ICA et CARTOGRAPHICA SINICA (in Chinese), 29(1): 17-23. |
| [3] | Cartwright D E,Edden A C. 1973. Corrected Tables of Tidal Harmonics. Geophysical journal international 33(3): 253-264. |
| [4] | Chang X T, Li J C, Guo J Y, et al. 2006. A mult-i leading edge and mult-i threshold waveform retracker. Chinese J. Geophys (in Chinese), 49(6) : 1629- 1634. |
| [5] | Chen N, Han G, Yang J, et al. 2014. Hurricane Sandy storm surges observed by HY-2A satellite altimetry and tide gauges. Journal of Geophysical Research: Oceans 119(7): 4542-4548. |
| [6] | Cheng Y,Andersen O B. 2014. HY-2A satellite altimetric data evaluation in the Arctic ocean. Geoscience and Remote Sensing Symposium (IGARSS), 2014 IEEE International, IEEE. |
| [7] | CLS. 2013. Jason-2 GDR Quality Assessment Report Cycle 174. Edition 01.0. |
| [8] | CLS. 2013. Jason-2 reprocessing impact on ocean data(cycle 001 to 145). Issue: 2rev 1. |
| [9] | CNES. 2011. Jason-2 Products Handbook. Issue: 1 rev 8. |
| [10] | Fu L-L,Cazenave A, Eds. (2001). Satellite altimetry and earth sciences: a handbook of techniques and applications. California, Academic Press. |
| [11] | Guo J Y, Chang X T, Huang J W, et al. 2010. Oceanic surface geostrophic velocities determined with satellite altimetric crossover method. Chinese J. Geophys (in Chinese), 53(11): 2582-2589. |
| [12] | Jia Y, Lin M,Zhang Y. 2014. Current status of the HY-2A satellite radar altimeter and its prospect. Geoscience and Remote Sensing Symposium (IGARSS), 2014 IEEE International, IEEE. |
| [13] | Jiang X, Lin M, Liu J, et al. 2012. The HY-2 satellite and its preliminary assessment. International Journal of Digital Earth 5(3): 266-281. |
| [14] | Jiang X W, Lin M S, Zhang Y G. 2014. An overview of HY-2 satellite ground application system. Engineering Sciences (in Chinese), 16(6): 4-12. |
| [15] | Lillibridge J, Lin M,Shum C K. 2014. Hurricane Sandy storm surge measured by satellite altimetry. Oceanography 26(2): 8-9. |
| [16] | Niedzielski T,Kosek W. 2008. Forecasting sea level anomalies from TOPEX/Poseidon and Jason-1 satellite altimetry. Journal of Geodesy 83(5): 469-476. |
| [17] | Picot N, Lachiver J,Lambin J. 2013. Towards an Operational Use of HY-2A in Ssalto/Duacs: Evaluation of the Altimeter Performances Using NSOAS S-IGDR Data. Ocean Surface Topography Science Team Conference (OSTST), Boulder, USA. |
| [18] | Sandwell D T, MLüller R D, Smith W H F, et al. 2014. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 346(6205): 65-67. |
| [19] | Tran N, Labroue S, Philipps S, et al. 2010. Overview and Update of the Sea State Bias Corrections for the Jason-2, Jason-1 and TOPEX Missions. Marine Geodesy 33(sup1): 348-362. |
| [20] | Wahr J M. 1985. Deformation induced by polar motion. Journal of Geophysical Research: Solid Earth 90(B11): 9363-9368. |
| [21] | Watson C, Coleman R, White N, et al. 2003. Absolute Calibration of TOPEX/Poseidon and Jason-1 Using GPS Buoys in Bass Strait, Australia Special Issue: Jason-1 Calibration/Validation. Marine Geodesy 26(3-4): 285-304. |
| [22] | Watson C, White N, Church J, et al. 2011. Absolute Calibration in Bass Strait, Australia: TOPEX, Jason-1 and OSTM/Jason-2. Marine Geodesy 34(3-4): 242-260. |
| [23] | Wessel P. 2010. Tools for analyzing intersecting tracks: The x2sys package. Computers & Geosciences 36(3): 348-354. |
| [24] | Xu K, Liu H G, Jiang J S. 2013. HY-2A radar altimeter design and in flight results. Engineering Sciences (in Chinese), 15(7): 25-32. |
| [25] | Yang L, Zhou X H, Peng H L, et al. 2014. Global assessment and cross-calibration of Saral/AltiKa based on Jason-2 altimeter. Advances in marine science (in Chinese), 32(4): 482-490. |
| [26] | Zaouche G, Perbos J, Lafon T, et al. 2010. OSTM/Jason-2: Assessment of the System Performances (Ocean Surface Topography Mission: OSTM). Marine Geodesy 33(sup1): 26-52. |
| [27] | Zhao G, Zhou X H, Wu B. 2012. Precise orbit determination of Haiyang-2 using satellite laser ranging. Chin Sci Bull (in Chinese), 57(36): 3475-3483. |
| [28] | 暴景阳, 晁定波,李建成. 2000. 南中国海TOPEX/POSEIDON轨迹交叉点测高数据的潮汐调和分析. 测绘学报 29(1): 17-23. |
| [29] | 常晓涛, 李建成, 郭金运,等. 2006. 一种多前缘多阈值的波形重构算法. 地球物理学报 49(6): 1629-1634. |
| [30] | 郭金运, 常晓涛, 黄金维,等. 2010. 基于卫星测高交叉点的海洋表面地转流速度. 地球物理学报 53(11): 2582-2589. |
| [31] | 蒋兴伟, 林明森,张有广. 2014. HY-2 卫星地面应用系统综述. 中国工程科学 16(6): 4-12. |
| [32] | 许可, 刘和光,姜景山. 2013. HY-2A 卫星雷达高度计设计及其在轨工作结果. 中国工程科学 15(7): 25-32. |
| [33] | 杨磊, 周兴华, 彭海龙,等. 2014. 基于Jason-2的Saral/AltiKa高度计全球统计评估与交叉定标. 海洋科学进展 32(4): 482-490. |
| [34] | 赵罡, 周旭华,吴斌. 2012. 海洋二号卫星 SLR 精密定轨. 科学通报 57(36): 3475-3483. |
 2016, Vol. 31
2016, Vol. 31

