地球物理学进展  2016, Vol. 31 Issue (2): 622-628   PDF    
引用本文
熊德永, 钟振, 刘高福. 高分辨率卫星重力和激光测高数据的月球岩石圈有效弹性厚度估计的分析及应用[J]. 地球物理学进展, 2016, 31(2): 622-628, doi: 10.6038/pg20160215  
XIONG De-yong, ZHONG Zhen, LIU Gao-fu. Analysis and application in the estimation of the lunar effective elastic thickness based on the high-resolution gravity and topography data. Progress in Geophysics, 2016, 31(2): 622-628, doi: 10.6038/pg20160215   
高分辨率卫星重力和激光测高数据的月球岩石圈有效弹性厚度估计的分析及应用
熊德永1, 钟振2,3 , 刘高福1    
1. 贵州师范学院物理与电子科学学院, 贵阳 550018;
2. 贵州师范大学物理与电子科学学院, 贵阳 550001;
3. 中科院国家天文台-贵州师范大学天文研究与教育中心, 贵阳 550001
收稿日期: 2015-06-19 修回日期: 2015-12-11 .
基金项目: 国家自然科学基金(41404021、11364007)、贵州省科学技术基金(黔科合J字[2014]2128)和贵州省教育厅自然科学研究项目(黔教合人才团队字[2014]38、黔教科合KY[2014]217)联合资助.
作者简介: 熊德永,男,1975年生,硕士,副教授,主要从事行星物理方法及应用研究.(E-mail:dyongxiong@163.com)
通讯作者: 钟振,男,博士,副教授,主要从事月球岩石圈弹性厚度和月球内结构研究.(E-mail:zhenzhongmail@163.com)
摘要：应用高分辨率GRAIL重力场模型和LOLA激光测高数据,利用两者间重力/地形导纳的统计关系反演月球岩石圈的结构特征是当前的重要手段.在研究区域物理性质各向同性的前提下,可将不同载荷模型引起的岩石圈挠曲量的球谐系数,表示成观测地形球谐系数的函数关系,结合非线性反演算法,可将不同参数的模型导纳谱与观测值进行最优拟合.结果表明导纳方法求解的高地地形平均月壳密度较接近高地地形的平均值2550 kg/m3.载荷比有正有负,表明内部载荷与表面载荷可能同相也有可能反相,也反映了月球岩石圈较复杂的结构特征.在各向同性的前提下,少部分区域的拟合残差接近其期望值1,可反演出参数的最优解.大部分区域较难反演出最优值,表明月球岩石圈的物理性质大部分并不均一,在各向异性的前提下,在空间域内使用数值计算方法有望对大部分区域的弹性厚度进行最优估计.
关键词： 重力场     地形     导纳     挠曲模型     弹性厚度    
Analysis and application in the estimation of the lunar effective elastic thickness based on the high-resolution gravity and topography data
XIONG De-yong1, ZHONG Zhen2,3 , LIU Gao-fu1    
1. School of Physics and Electronic Science, Guizhou Normal College, Guiyang 550018, China;
2. School of Physics and Electronic Science, Guizhou Normal University, Guiyang 550001, China;
3. NAOC-GZNU Center for Astronomy research and education, Guizhou Normal University, Guiyang 550001, China
Abstract: The high-resolution gravity fields model from GRAIL (Gravity Recovery and Interior Laboratory) mission and topography from LOLA (Lunar Orbiter Laser Altimeter) are available. This makes it possible to explore the lunar lithosphere structure by using the gravity/topography admittance. With the selenophysical isotropy hypothesis of the studied area, functions of spherical harmonic expansion coefficients between lithosphere deflection resulted from various loadings and topography observed are likely deduced. With the help of nonlinear inversion algorithm, the best solution of various parameters can be frequently estimated by fitting the modeled admittance and observed. Results indicate that the mean crustal density over highland sections gets close to the mean value 2550 kg/m3. The load ratios may be positive or negative, which shows a complex lithospheric structure. A positive load ratio generally suggests argument in phase between surface and subsurface load, A negative one contrarily means out of phase. The expectation of fitting residual error closing to one in a few areas implies that not all of the zones have a best isotropic solution. This indicates that most parts of the lithosphere may be anisotropic, thus failing in the best solution's inversion. A numeric calculation in the best estimation of elastic thickness is inevitable spatially employed for most part of anisotropic areas.
Key words: gravity fields     topography     admittance     deflection model     elastic thickness    
0 引 言

岩石圈形变演化主要受其力学强度的影响，力学强度则由有效弹性厚度来量化(Burov and Diament，1995).有效弹性厚度的大小反映了岩石圈在载荷作用下抵抗形变的能力，是研究区域内部热状态的有力工具，对研究行星表面热流分布具有重要意义.岩石圈有效弹性厚度的计算主要依据岩石圈挠曲模型，即岩石圈在垂向载荷和水平作用力的加载下发生挠曲，通过观测因岩石圈挠曲产生的重力异常与地形之间的统计关系——重力/地形导纳，进而给出岩石圈的区域分布.受观测手段的限制，当前月球岩石圈有限弹性厚度的估计主要通过卫星重力和激光测高数据进行(Huang and Wieczorek，2012；Zhong et al.，2014).受月球自转和公转同步的影响，早期探月卫星轨道跟踪数据在月球背面无直接观测量，解算的重力场模型有效阶次较低，在月球背面甚至不足15阶次，不适合作背面区域的有效弹性厚度估计.日本曾使用四程多普勒跟踪模式一度提升月球重力场模型的有效阶次，但模型全球有效阶次仍然低于70阶次，不利于计算众多小尺度地形地貌区域的弹性厚度(Matsumoto et al.，2010).最新超高分辨率月球重力场模型GL0420A、GL0660B、GRGM660PRIM、GL0990C和GL0990D来自GRAIL(Gravity Recovery and Interior Laboratory)任务，与早期模型相比，模型改正精度在2~10阶次达2个量级，高阶次甚至高达4个量级，可满足小尺度区域导纳研究的需求(Zuber et al.，2013；Lemoine et al.，2013；Konopliv et al.，2013，2014).

应用重力/地形导纳研究行星物理特征比较普遍，最早可追溯到1997年Simons等(1997)人应用该方法对金星幔动力学过程进行约束，随后McGovern等(2002)应用该方法对火星岩石圈主要物理参数如火星行星壳厚度、弹性厚度和载荷加载时的热流密度进行了估计.在月球科学中导纳方法的应用也比较多.Arkani-Hamed(1998)曾利用Clementine卫星重力和激光测高数据求解了部分质量瘤盆地的月壳厚度，Crosby和McKenzie(2005)则利用该方法估计了近月面古月壳的弹性厚度，李斐等(2009)则在频率域内估计了月球正面主要月海区的月壳厚度，杜劲松等(2010)研究了月球表层及月壳物质密度分布特征，钟振等(2013)对常见重力场模型在局部导纳和相关性分析中的适定性进行了分析.随着重力场模型有效阶次的增加，Huang和Wieczorek(2012)利用SGM100h和LOLA(Lunar Orbiter Laser Altimeter)激光测高数据间的导纳关系，给出了大部分典型区域的月壳密度和孔隙度分布，随后，又利用GRAIL重力场模型和LOLA激光测高数据高分辨率、可分辨小尺度重力异常和地形地貌的特点，对正面盾形火山区的弹性厚度进行了估计(Huang et al.，2014).由于月球岩石圈的相关约束较少，利用重力/地形导纳估计物理参数是一个多参数反演问题，为了搜索全局最优解，并提升效率，Zhong等(2014)引入了非线性粒子群算法，可在短时间内搜索到待估参数的全局最优解.

应用重力/地形导纳反演月球物理参数理论上较成熟，超高分辨率的GRAIL重力场模型和LOLA的激光测高数据，使得研究小尺度地形地貌区的弹性厚度成为可能.本文首先对载荷模型及其组合进行分析，构建了载荷同相和反相情况下不同参数的模型导纳谱.利用载荷模型、重力场模型GL0990D和LOLA(Smith et al.，2010)测高数据，结合非线性粒子群算法，对月球岩石圈小尺度地形地貌区域的弹性厚度进行了估计.

1 模型与方法1.1 局部导纳和局部相关函数

假设g和h分别表示月球的表面地形和重力，空间角Ω范围内的重力和地形可进行球谐展开为(Wieczorek and Simons， 2005，2007)：

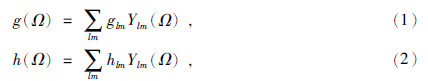
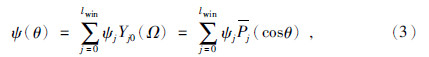
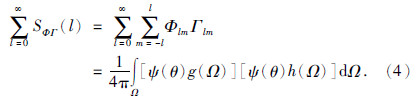
其中glm和hlm分别表示重力和地形的l阶m次球谐展开系数.为了求得研究区域的局部导纳和相关函数，需对全球重力和地形进行局部化处理.本文应用轴对称窗口对重力场模型和地形模型进行局部化处理，进而求得研究区域的局部重力和局部地形.若研究区域的空间角径为θ，轴对称窗口为ψ(θ)，可将该窗口展开成最大阶数成lwin的带谐函数为

进一步可得局部重力ψ(θ)g(θ)与局部地形ψ(θ)h(θ)的交叉功率谱为

同理，可分别求得局部重力和局部地形的功率谱SΦΦ(l)和SΓΓ(l)，进而求得局部导纳函数z(l)和局部相关函数γ(l)(Wieczorek and Simons，2005，2007)为

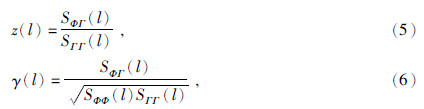
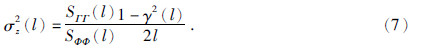
由于局部重力与局部地形相关程度会对局部导纳函数产生影响，有必要对局部导纳函数的方差进行估计，局部导纳函数的方差估计为

1.2 表面载荷和内部载荷

月球岩石圈在整个地质时间尺度内，受重力作用朝着内部应力减小的方向演化，逐渐趋于均衡稳定(Reindler and Arkani-Hameda，2003).受作用于岩石圈表面地形和内部异常密度的影响，岩石圈表现出一定的区域补偿特征.通常将作用于月球表面的地形看成表面载荷，而岩石圈内部异常密度主要来自内部壳-幔界面，一般将该密度异常看成内部载荷.由于岩石圈的厚度相对月球半径较小，考虑月球曲率的影响，月球岩石圈常看成薄弹性球层(Zhong et al .，2000).若假设表面地形载荷加载后的地形高ht向上为正，相应的岩石圈挠曲大小wt向下为正，研究区域的物理性质是各向同性，即不考虑物理参数的横向差异，可得两者l阶m次球谐展开系数ht，lm和wt，lm间的关系(钟振等，2014，2015)为

其中

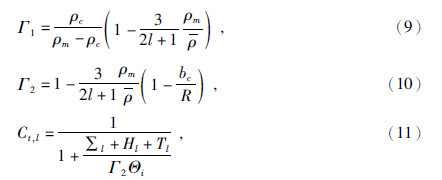
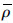这里Ct，l表示表面载荷的补偿系数，ρc和ρm分别表示平均月壳密度和月幔密度，表示月球的平均密度.若g表示参考表面半径为R处的重力加速度，D表示弹性刚度，Te表示岩石圈的弹性厚度，ν表示泊松比率，E为杨氏模量，则有无量纲参数σ=D/[gR4(ρm-ρc)]和τ=ETe/[gR2(ρm-ρc)].若n=l(l+1)-2，有∑l=σ(n3+2n2)、Hl=-4σl(l+1)、Θl=(n+1-ν)、Tl=nτ.相关参数的取值如表 1所示.

表 1 模型计算参数 Table 1 Nominal Parameter Values

McGovern等(2002)和Huang等(2014)(Huang and Wieczorek 2012，)将内部载荷看成具有一定密度异常的起伏界面，并认为内部载荷起始于壳-幔界面，此时，内部载荷深度zb等于月壳厚度bc，即zb=bc.若该密度异常界面的密度差为ρm-ρc，假设密度异常界面加载后的起伏大小wb向上为正，相应的岩石圈挠曲大小hb向下为正，并考虑研究区域的物理性质各向同性，可得两者l阶m次球谐展开系数wb，lm和hb，lm之间的关系为(钟振等，2014，2015)：

其中

这里Cb，l表示内部载荷的补偿系数，相关参数与表面载荷模型相同.

1.3 载荷组合

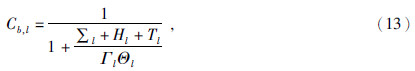
假设表面载荷的初始地形高为hi，内部载荷的初始起伏大小为wi，表面实际观测地形为h，根据文献(Turcotte et al.，1981；McGovern et al.，2002；Huang et al.，2002，2014)，若研究区域物理性质各向同性，可得三者的球谐展开系数hi，lm、wi，lm、hlm为

为了实现表面载荷与内部载荷的组合，Forsyth等(1985)引入了载荷比率f，若研究区域为各向同性，则有如下关系为

其中ρb表示内部载荷的剩余密度，在本文中ρb =ρm-ρc.

若假设：

其中：αt=1+Ct，lΓ1/Γ2和αb=1+Cb，lΓ2/Γ1.根据文献(Turcotte et al.，1981)，若表面自由空气重力异常仅由表面地形和壳-幔界面产生，由公式(5)和(8-18)可得模型导纳谱为

其中：

由式(19)可得不同参数下的模型导纳谱.根据文献(Wieczorek et al.，2013)，取月幔密度ρm=3200 kg/m3，平均月壳密度bc=2550 kg/m3，平均月壳厚度bc=35 km，其他参数如表 1所示，可得不同弹性厚度和载荷比的模型导纳谱，如图 1所示.图 1表明在载荷比f较小的情况下，模型导纳谱位于均衡补偿(纯实线，Te=0 km)和未补偿模型(纯虚线，Te=200 km)之间，除低阶项外，导纳值随球谐阶次单调递增，这种情况表示表面载荷对重力异常的贡献占优势.在载荷比f较大的情况下，此时导纳谱随球谐阶数不再单调变化，并在75阶附近出现凹陷.由公式(17)可知，内部载荷占优势，表明自由空气重力异常受内部载荷的影响较大.尽管如此，高阶项的导纳值接近均衡补偿和未补偿模型.

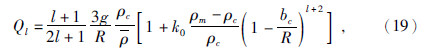
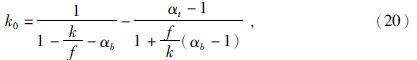
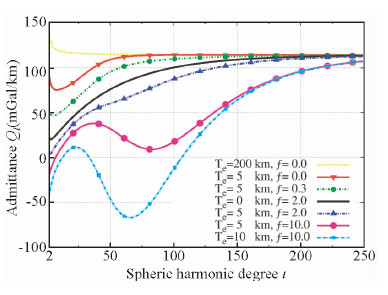图 1 不同弹性厚度Te和载荷比f的模型导纳谱 Fig. 1 Modeled admittance of various elastic thicknesses Te and load ratios f
1.4 界面起伏及重力异常

McKenzie等(2002)和Belleguic等(2005)将表面载荷与内部密度载荷看成具有一定密度大小的起伏界面，本文采用类似方法，可得界面起伏产生的重力异常Δg为

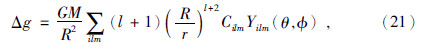
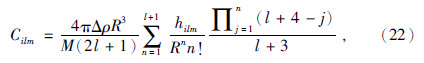
其中重力异常的球谐展开系数Cilm为(Wieczorek and Phillips，1998)

公式(19)相当于公式(22)在n=1阶的近似结果，一般n=5就可精确计算位系数.

McGovern等(2002)和Huang和Wieczorek(2012)认为内部载荷主要由壳-幔界面隆起所致，本文采用类似假设，可得表 2所示的各界面层起伏、密度差及相应的参考半径.表面总重力异常的球谐展开系数为

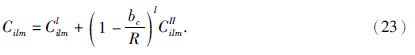
表 2 计算重力异常的参考界面 Table 2 Interfaces for gravity anomaly calculation
1.5 目标函数

对于给定的模型参数如载荷比f、平均月壳密度ρc、平均月壳厚度bc和弹性厚度Te，由式(8-23)，可得对应模型的重力异常，再由(5)式即可求出模型导纳谱zmod(l).利用(5)式对观测重力和地形进行局部导纳处理，可求得观测导纳谱zobs(l).利用文献(Zhong et al.，2014)的非线性粒子群算法可对不同物理参数的模型导纳谱和观测导纳谱进行最优拟合，进而求得物理参数的最优解.Beuthe等(2012)和Grott和Wieczorek(2012)对模型参数反演时，目标函数选择卡方估计函数(chi-squared function)，其形式为

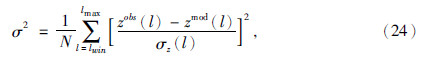
其中N=lmax-lmin+1-p，即参与卡方估计的球谐阶数，p为待求参数个数，在本文中p=4，lmax为重力场模型的最大有效展开阶次，σz(l)为(7)式观测导纳的方差估计.(24)式卡方估计函数的期望值为1，即E(σ2)=1.

2 结果与分析

文献(Forsyth，1985)表明当内部载荷与表面载荷非同相和反相时，导纳值和相关值可能为复数，为了简化运算，本文仅考虑内部载荷与表面载荷同相和反相的情况.如果重力和地形在频率域内线性相关，那么相关值(6)式在理论上应为1或-1.但由于重力场模型可能存在未考虑的重力信息或由于噪声的影响，使得该相关值一般不等于±1，因此，大多数研究选择相关系数大于0.95的区域进行分析(Huang et al.，2012)，本文选择的研究区域大部分能满足该条件.考虑到重力/地形导纳分析时，弹性球层模型的均衡响应仅在中低阶范围内有效(Turcotte et al.，1981)，选择重力场模型和地形模型的前200阶次进行导纳分析已经足够.考虑到质量瘤盆地大尺度重力异常的影响，本文选择(3)式的轴对称窗口的空间角径为5°，这样可以最大限度地减小大尺度重力异常的影响.该角径对应的频谱带宽为52阶次，导纳谱的有效范围为52≤l≤148.本文选择单窗口(single taper)进行谱分析，为了使重力和地形限定在研究范围内，空间集中度设为99%，这样可以保证研究区域以外的功率接近于0(Wieczorek and Simons，2005，2007).另外，进行导纳分析时，为了同时对多参数进行反演，本文采用了文献(Zhong et al.，2014)的非线性粒子群算法，该算法可在短时间内迅速地搜索到待求参数的全局最优解，效率较高.

图 2表示中心坐标为(20°S，165°W)，角径θ=5°区域的观测相关谱(虚线)、观测导纳谱(误差棒)和模型导纳谱(实线).相关谱在60阶后的值接近1，但在60阶前的值明显小于1，甚至低于0.75，对应的观测导纳值也呈现较大的误差，这种现象主要由公式(3)加窗截断所致.拟合残差除140阶后的高阶项略有差异外，整体拟合最优，表 3序1给出了反演参数的统计结果.图 3表示观测重力异常(a)及观测重力异常与模型重力异常的差值(b)，研究区域以白色圆圈标注.图 3b表明研究区域观测重力异常与反演最优参数求得的模型重力异常的差值较小，因此，反演参数具有一定的合理性.

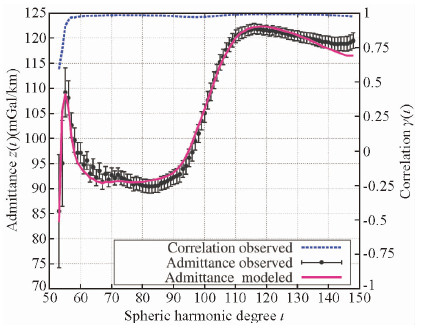图 2 观测相关谱(虚线)、观测导纳谱(误差棒)和模型导纳谱(实线) Fig. 2 Correlation spectra observed (dotted line),admittance spectra observed (error bar) and admittance spectra modeled (solid line)

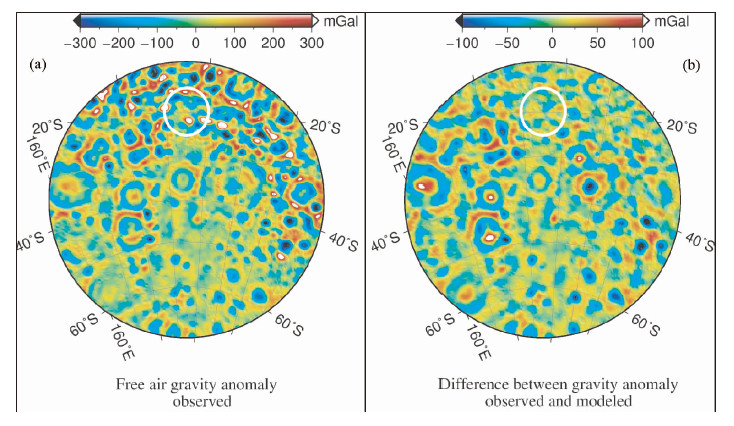图 3 研究区域(白色圆圈所示)的自由空气重力异常(a)及观测重力异常与模型重力异常的差值(b) Fig. 3 (a) Free air gravity anomaly and difference between gravity anomaly observed and modeled (b) of the studied area figured with white circles

表 3 部分区域的最优反演参数统计 Table 3 Summary of the best inversion parameters of several zones

为了探究不同物理参数之间的变化关系，图 4给出了拟合残差随载荷比、平均月壳厚度、平均月壳密度和弹性厚度的变化关系.图 4a表明拟合残差最小值(图中黑色和粉色区域)对应的月壳厚度范围在[30，32]之间，对应的弹性厚度在[20，35]之间，表 3序1表明该区域的最优月壳厚度为31 km，最优弹性厚度为21 km，很显然最优值在最小拟合残差的范围内.图 4b表明最小拟合残差对应的载荷比在[0.5，0.57]之间，最优弹性厚度在[20，40]之间，表 3序1表明该区域的最优载荷比为0.54，在最优载荷比的范围内.图 4c表明最优月壳密度的范围为[2490，2530]，表 3序1表明该区域的最优值为2507 kg/m3，完全在最小拟合残差的范围内，并与文献(Wieczorek et al.，2013)使用GL0420a求的高地平均密度2550 kg/m3接近.这可能是由于该研究区域位于月球背面，在高地和SPA撞击盆地交界处，因此，求解的平均月壳密度接近高地地形的平均值2550 kg/m3.图 4d表示最小拟合残差随平均月壳密度和平均月壳厚度的变化关系，两者的最优解范围均包括它们的最优值，这说明参数估计具有一定的合理性.

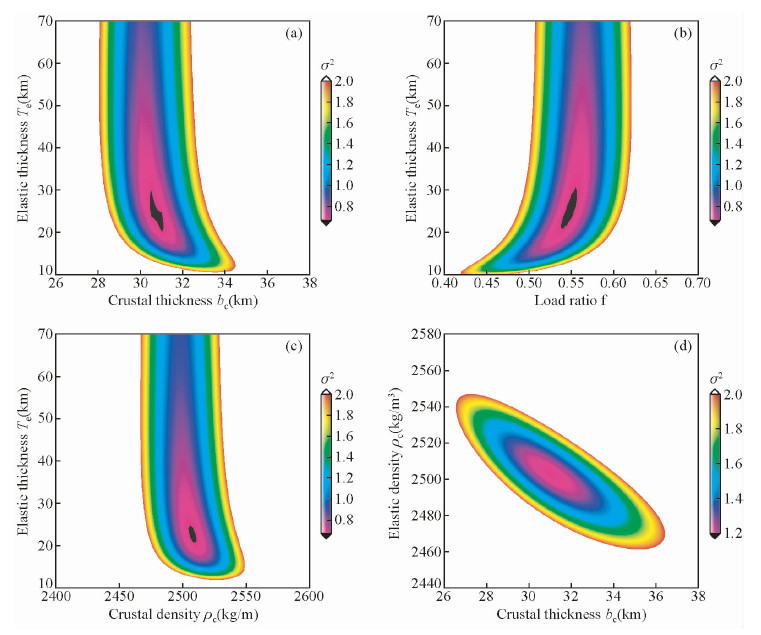图 4 拟合残差随不同参数的变化关系 Fig. 4 The fitting residual error distribution for various parameters

表 3给出了其他区域的反演结果，有的区域载荷比为负数，而有的区域为正，这说明月表底部结构较为复杂.正的载荷比说明内部载荷与表面载荷同相，负的载荷比表示内部载荷与表面载荷反相.根据公式(24)，拟合残差的期望值应为1，表 3未列出拟合残差超过2.0的统计结果.表 3中6个区域的平均月壳密度值在2500 kg/m3左右，其中序号2和序号4两个区域位于月球正面，但它们的纬度为45°S，这两个区域恰好是月球正面南半球的高地型区域，因此，其密度值接近Wieczorek等(2013)给出的高地地形平均月壳密度2550 kg/m3也就不难理解.另外，对比表 3所有区域的反演结果，很显然序号1和序号5两个区域的拟合残差较小，其他区域的拟合残差稍大.由于本文计算结果是在研究区域各向同性的条件下求得的，这说明这两个区域的弹性厚度横向分布比较均匀，而其他区域更趋向于各向异性.

3 结 论

应用卫星重力和激光测高数据研究月球岩石圈结构是比较重要的手段，当前高分辨率GRAIL重力场模型和LOLA激光测高数据使得应用重力/地形导纳反演相关物理参数成为可能.在研究区域物理性质各向同性的前提下，对载荷进行组合，求得岩石圈挠曲量的球谐系数与观测地形球谐系数间的函数关系，进而在球谐域内求得不同参数情况下的模型导纳谱，将模型导纳谱与观测导纳谱进行拟合，并结合非线性反演算法，可计算出待估参数的最优值.结果表明大部分高地地形的平均月壳密度值比较接近2550 kg/m3，载荷比有正有负，表明月球岩石圈的结构比较复杂.在各向同性的前提下，少部分区域的拟合残差接近其期望值1.表明仅有少部分区域各向同性，大部分区域的物理性质可能并不均一，后期研究工作应该在各向异性的条件对岩石圈结构进行研究.由于各向异性，岩石圈挠曲大小与观测地形无法表示成简单的球谐系数间的关系，因此，在空间域内使用数值方法有望对大部分区域的弹性厚度进行最优估计.

致 谢 本文所用重力场模型和地形模型取自NASA PDS Geosciences Node Data中心，球谐分析使用了SHTOOLS2.8，球面投影采用了The Generic Mapping Tools(GMT)软件.

参考文献
[1] Arkani-Hamed J. 1998. The lunar mascons revisited[J]. J. Geophy. Res., 103(E2): 3709-3739.
[2] Belleguic V, LognonnLé P, Wieczorek M. 2005. Constraints on the Martian lithosphere from gravity and topography data[J]. J. Geophy. Res., 110(E11), doi: 10.1029/2005JE002437.
[3] Beuthe M, Le Maistre S, Rosenblatt P, et al. 2012. Density and lithospheric thickness of the Tharsis Province from MEX MaRS and MRO gravity data[J]. J. Geophys. Res., 117(E4): E04002.
[4] Burov E B, Diament M. 1995. The effective elastic thickness (Te) of continental lithosphere: What does it really mean?[J] J. Geopys. Res., 100(B3): 3905-3927.
[5] Crosby A, McKenzie D. 2005. Measurements of the elastic thickness under ancient lunar terrain[J]. Icarus, 173(1): 100-107.
[6] Du J S, Chen C, Liang Q, et al. 2010. The characteristics of rock-density distributions on the surface and in the crust of the Moon[J]. Chinese Journal of Geophysics (in Chinese), 53(9): 2059-2067, doi: 10.3969/j.issn.0001-5733.2010.09.006.
[7] Forsyth D W. 1985. Subsurface loading and estimates of the flexural rigidity of continental lithosphere[J]. J. Geophy. Res., 90(B14): 12623-12632.
[8] Grott M, Wieczorek M A. 2012. Density and lithospheric structure at Tyrrhena Patera, Mars, from gravity and topography data[J]. Icarus, 221(1): 43-52.
[9] Huang Q, Wieczorek M A. 2012. Density and porosity of the lunar crust from gravity and topography[J]. J. Geophy. Res., 117(E5), doi: 10.1029/2012JE004062.
[10] Huang Q, Xiao Z Y, Xiao L. 2014. Subsurface structures of large volcanic complexes on the nearside of the Moon: A view from GRAIL gravity[J]. Icarus, 243, 48-57.
[11] Konopliv A S, Park R S, Yuan D N, et al. 2013. The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL Primary Mission[J]. J. Geophy. Res., 118(7): 1415-1434.
[12] Konopliv A S, Park R S, Yuan D N, et al. 2014. High resolution lunar gravity fields from the GRAIL primary and extended Missions[J]. Geophy. Res. Lett., 41(5): 1452-1458.
[13] Lemoine F G, Goossens S, Sabaka T J, et al. 2013. High-degree gravity models from GRAIL primary mission data[J]. J. Geophy. Res., 118(8): 1676-1698.
[14] Li F, Ke B G, Wang W R, et al. 2009. Estimation of the ancient lunar crust thickness from the admittance[J]. Chinese Journal of Geophysics (in Chinese), 52(8): 2001-2007, doi: 10.3969/j.issn.0001-5733.2009.08.007.
[15] Matsumoto K, Goossens S, Ishihara Y, et al. 2010. An improved lunar gravity field model from SELENE and historical tracking data: Revealing the farside gravity features[J]. J. Geophysics. Res., 115(E6), doi: 10.1029/2009JE003499.
[16] McGovern P J, Solomon S C, Smith D E, et al. 2002. Localized gravity/topography admittance and correlation spectra on Mars: Implications for regional and global evolution[J]. J. Geophy. Res., 107(E12): 5136.
[17] McKenzie D, Barnett D N, Yuan D N. 2002. The relationship between Martian gravity and topography[J]. Earth Planet. Sc. Lett., 195(1-2): 1-16.
[18] Reindler L, Arkani-Hameda J. 2003. The Strength of the Lunar Lithosphere[J]. Icarus, 162(2): 233-241.
[19] Simons M, Solomon S C, Hager B H. 1997. Localization of gravity and topography: constraints on the tectonics and mantle dynamics of Venus[J]. Geophy. J. Int., 131(1): 24-44.
[20] Smith D E, Zuber M T, Neumann G A, et al. 2010. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA)[J]. Geophys. Res. Lett., 37(18), doi: 10.1029/2010GL043751.
[21] Turcotte D L, Willemann R J, Haxby W F, et al. 1981. Role of membrane stresses in the support of planetary topography[J]. J. Geophys. Res., 86(B5): 3951-3959.
[22] Wieczorek M A, Phillips R J. 1998. Potential anomalies on a sphere: Applications to the thickness of the lunar crust[J]. J. Geophys. Res., 103(E1): 1715-1724.
[23] Wieczorek M A, Simons F J. 2005. Localized spectral analysis on the sphere[J]. Geophy. J. Int., 162(3): 655-675.
[24] Wieczorek M A, Simons F J. 2007. Minimum-Variance multitaper spectral estimation on the sphere[J]. J. Fourier Anal. Appl., 13(6): 665-692.
[25] Wieczorek M A, Neumann G A, Nimmo F, et al. 2013. The crust of the Moon as seen by GRAIL[J]. Science, 339(6120): 671-675.
[26] Zhong S J, Parmentier E M, Zuber M T. 2000. A dynamic origin for the global asymmetry of lunar mare basalts[J]. Earth Planet. Sci. Lett., 177(3-4): 131-140.
[27] Zhong Z, Li F, Yan J G, et al. 2013. Localized gravity/topography admittance and correlation analysis of recent lunar gravity field models[J]. Chinese Journal of Geophysics (in Chinese), 56(3): 783-791, doi: 10.6038/cjg20130307.
[28] Zhong Z, Li F, Yan J G, et al. 2014. Lunar geophysical parameters inversion based on gravity/topography admittance and particle swarm optimization[J]. Advances. in Space Research, 54(4): 770-779.
[29] Zhong Z, Li F, Yan J G, et al. 2014. Application of Gravity/Topography Admittance to the Inversion of Lunar Geophysical Parameters Considering the Lithosphere as a Thin Elastic Spherical Shell [J]. Geomatics and Information Science of Wuhan University, 39(12): 1487-1492.
[30] Zhong Z, Yan J G, Pang L J. 2015. Geophysical parameters inversion for Apollo crater based on recent high-resolution lunar gravity field and topography data (in Chinese) [J]. Sci Sin-Phys Mech Astron, 45(2):029601-9.
[31] Zuber M T, Smith D E, Watkins M M, et al. 2013. Gravity Field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) Mission[J]. Science, 339(6120): 668-671.
[32] 杜劲松, 陈超, 梁青,等. 2010. 月球表层及月壳物质密度分布特征[J]. 地球物理学报, 53(9): 2059-2067, doi: 10.3969/j.issn.0001-5733.2010.09.006.
[33] 李斐, 柯宝贵, 王文睿,等. 2009. 利用重力地形导纳估计月壳厚度[J]. 地球物理学报, 52(8): 2001-2007, doi: 10.3969/j.issn.0001-5733.2009.08.007.
[34] 钟振, 李斐, 鄢建国,等. 2013. 新近月球重力场模型与地形模型的局部导纳和相关性分析[J]. 地球物理学报, 56(3): 783-791, doi: 10.6038/cjg20130307.
[35] 钟振, 李斐, 鄢建国,等. 2014. 利用重力/地形导纳和岩石圈单一薄层模型的月球物理参数反演[J]. 武汉大学学报·信息科学版, 39(12): 1487-1492.
[36] 钟振, 鄢建国, 庞礼军. 2015. 基于高分辨率卫星重力和地形数据的月球Apollo撞击坑物理参数反演[J]. 中国科学: 物理学、力学、天文学, 45(2): 82-90.