目前计算理论地震图经常使用的滑动速度函数主要有Haskell函数、钟形函数、指数函数、三角形函数等(Anderson and Richards,1975).Hisada从理论上提出了一个不等边三角形形状的断层滑动速度函数,该滑动速度函数具有迅速上升,相对缓慢地下降的特点(Hisada,2001).以上这些滑动时间函数或滑动速度函数的共同特点都是理论研究的结果,是否符合实际尚需进一步的验证.
目前主要有两种方法从实际地震资料中提取震源滑动时间函数,第一种是矩张量反演方法.这种方法通过波形资料反演得到描述震源的矩张量随时间的变化(倪江川等,1991),用矩张量反演方法无须对震源时间滑动函数做任何假设就可以同时得到震源的矩张量和震源滑动时间函数,但反演的结果取决于人们对地震波传播介质的认识水平.另一种方法是通过波形反演直接求出震源滑动时间函数.这种方法又可以进一步分为两种方法:一种是理论格林函数方法,另一种是经验格林函数方法.理论格林函数方法指格林函数是根据弹性动力学原理,通过假定的传播介质模型计算得到的;而经验格林函数方法中的格林函数是由发生在同一地震断层上的较小地震的地震记录得到的.虽然用理论格林函数能够估算出震源滑动时间函数(Dreger,1994a),但这样得到的震源滑动时间函数与人们对震源以及对地震波传播介质的认识水平有关.经验格林函数法把小震记录作为格林函数,自动地考虑到了传播介质对地震波的影响,也一定程度上考虑了震源对地震波的影响,这正是经验格林函数方法的突出优点,正是因为如此,这种方法被许多研究者用以研究震源破裂过程和震源的复杂性(Dreger,1994b).但是由于经验格林函数法要求在同一台站记录到来自同一地点的、震源机制相同的较大地震和较小地震的记录,这一过于苛刻的要求限制了经验格林函数方法的应用范围,所以,虽然人们在用经验格林函数方法反演震源滑动时间函数方面做了一些工作(周家玉等,1993),但由于地震资料的匮乏,其工作成果是有限的.
利用波形反演还可以得到地震的震源机制随时间和空间变化(许力生和陈运泰,1996;王卫民等,2008;张勇等,2009;李圣强等,2013; 周辉等,2013).但反演的结果仅仅是众多可能结果之一,不同研究者由于选取的资料不同等因素导致对同一事件反演的结果会有所不同,有的差异会比较大.
由于滑动时间函数或滑动速度函数要么是通过理论研究获得的,要么虽然是由地震记录计算得到的,但由于人们对震源和地震波传播介质认识的局限性,导致目前应用的滑动时间函数或滑动速度函数距离真实的地震过程有一定的距离.有必要对断层的滑动速度进行深入研究.
1 用多普勒效应计算断层滑动速度函数多普勒效应是当波源和接收器之间发生相对运动时,接收器接收到的波的频率与发出的波的频率不同的现象.日常生活中交通工具行驶速度的测定就是利用了多普勒效应,用该效应计算断层的滑动速度在理论上应该不存在问题.地震断层作为波源滑动时,其发出的频率与接收到的频率是不同的.断层的滑动速度计算公式为
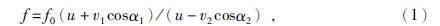
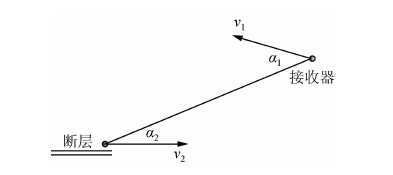 | 图 1 公式(1)示意图 Fig. 1 Sketch map of formula one |
在三分量的地震记录中,是接收器在某一水平方向的运动速率,是断层在同一方向的滑动速率,在计算中取波速率,并用适当的时间窗提取波(欧阳行艳等,2009).由于波速率远远大于接收器运动的速率,公式(1)变为

当断层可以看做点源时,如果已知两个台站接收到的同一v波频率、v波的传播速率u、断层上的波源和接收器连线与断层上的波源运动方向之间的夹角A就能计算出断层在某水平方向的滑动速率v2如图 2.
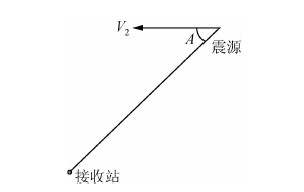 | 图 2 公式(2)的示意图 Fig. 2 Sketch map of formula two |
下面进一步说明公式(2)中接收器接收到的地震波频率f确定方法:
如公式(3),震源在一点引起地震动的傅立叶谱可以看作由震源过程、传播效应和场地效应共同决定的(Boore,2003).Oi(f)是第i次地震在台站记录的傅立叶谱,可以是位移、速度、也可以是加速度谱;Si(f)是震源谱,它是频率的函数;Gi(f)是场地效应;Pi(f)是路径效应,它是频率、震源距和波速的函数.从以上的分析可以看出地震动的傅立叶谱是频率的函数,此处的频率应该理解为是断层发出的频率固有频率.对于基岩台站,Gi(f)为常数.对于距离很近的基岩台站,地震记录的傅立叶谱幅值唯一地取决于断层发出的频率f0,某一个频率地震波如果在一个基岩台站引起的地震动傅立叶幅值谱为极值,那么它在附近的另一个基岩台站引起的地震动傅立叶幅值谱也一定为极值,两者的区别在于由于多普勒效应使得两台站接收到的频率不同.于是,我们可以根据基岩台站傅立叶幅值谱的极值点所对应的接收到的不同频率带入公式(2),就可以计算出地震断层的滑动速度分量.在实际计算中,我们采用基岩场地,公式(3)为

如果断层是单侧滑动,计算得到的断层滑动速度总是沿同一方向的;如果是双侧滑动,计算得到的断层滑动速度是两个相反方向,所以用多普勒效应还可以判断出断层是单侧滑动还是双侧滑动.
因为短时傅立叶变换具有时间定位功能,理论上可以借助短时傅里叶变换确定我们计算得到的断层滑动速度发生的时刻.比如,我们对地震记录每间隔1 s进行短时傅立叶变换,再根据计算到的频率等信息,由公式(2)可以计算出断层在第一个变化时段的速度,我们把它看作第一秒末断层的滑动速度,同样的办法,我们可以计算出断层在各个时刻的滑动速度,最后可以得出断层滑动速度随时间的变化曲线,即,滑动速度函数.对滑动速度函数进行积分计算就可以得到滑动时间函数.但由于采用短时傅里叶变换的数据量过少,用傅里叶变换计算得到的频率准确度不高,会严重影响计算结果,所以上述方法没有可行性.
在实际用多普勒效应计算断层滑动速度时,我们把全部地震记录做傅里叶变换,根据傅里叶幅值强度特征找出同一频率地震波引起的地震动,再根据多普勒效应计算断层的滑动速度.
仅用傅里叶变换无法确定用多普勒效应计算得到的断层滑动速度发生的时刻,但可以用断层的上升时间和滑动位错作为约束条件计算出断层滑动速度函数.断层滑动速度随时间的变化曲线下所包含的面积就是断层滑动的位错,我们把断层的滑动时间约束在上升时间内,改变断层滑动速度发生的时间,最后使得速度曲线下包含的面积接近断层滑动位错时,就是我们要求得断层滑动速度函数.计算过程中我们要求断层滑动速度函数下包含的面积与断层滑动位错的相对误差不超过5%,我们称这种拟合方法为最小误差法.
最小误差法的步骤如下:
(1)用多普勒效应计算断层滑动速度.
(2)用反演或经验关系计算断层滑动位错和上升时间.
(3)以断层上升时间为约束,随机排列断层滑动速度,得到断层速度-时间曲线.
(4)计算断层滑动速度-时间曲线下包围的面积,与断层滑动速度的位错比较,计算相对误差.
(5)如果相对误差大于5%,则重复步骤(3)、(4)和(5),直到相对误差小于等于5%.这时得到的断层滑动速度-时间曲线表示的函数就是滑动速度函数.
2 用多普勒效应计算汶川余震断层滑动速度汶川大地震发生后,中国地震局工程力学研究所迅速建立起大量的临时地震记录台,记录到了MS=6.0余震.我们将根据此次地震两个基岩场地的记录计算该次地震断层的滑动速度.根据有关经验关系(李启成,2010),表 1中列出了汶川地震余震(MS=6.0)参数.
|
|
表 1 汶川地震余震(MS=6.0)参数 Table 1 Aftershock parameters(MS=6.0) of Wenchuan earthquake |
图 3是两个基岩台站记录到的E-W方向58.86~59.2 Hz的傅里叶幅值随频率的变化.图中1点、2点、3点、4点和5点分别对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度为-45.6 m/s、-29.5 m/s、-39.3 m/s、-40.6 m/s、-36.7 m/s.
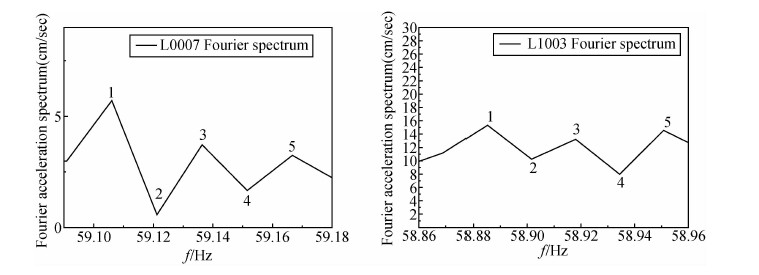 | 图 3 两基岩台记录到58.86~59.2 Hz的傅里叶幅值随频率变化 Fig. 3 Relationship between Fourier amplitudes and frequencies from 58.86~59.2 Hz at two bed rock sites |
图 4是两个基岩台站记录到的50.5~50.7 Hz的傅里叶幅值随频率的变化.图中1点和2点分别对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度为-5.8 m/s和13.6 m/s.
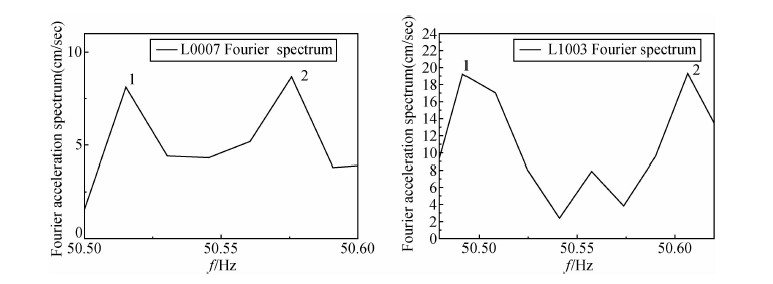 | 图 4 两基岩台记录到50.5~50.7 Hz的傅里叶幅值随频率变化 Fig. 4 Relationship between Fourier amplitudes and frequencies from 50.5~50.7 Hz at two bed rock sites |
图 5是两个基岩台站记录到的50.99~51.2 Hz的傅里叶幅值随频率的变化.图中1~3点对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度分别为31.7 m/s,34.3 m/s,32.1 m/s.
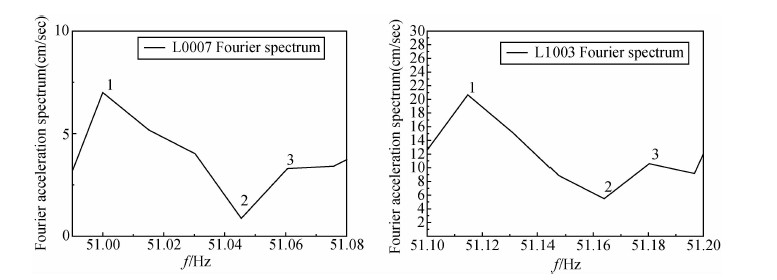 | 图 5 两基岩台记录到50.99~51.2 Hz的傅里叶幅值随频率变化 Fig. 5 Relationship between Fourier amplitudes and frequencies from 50.99~51.2 Hz at two bed rock sites |
图 6是两个基岩台站记录到的52~52.3 Hz的傅里叶幅值随频率的变化.图中1~2点对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度分别为25.4 m/s,-30.9 m/s.
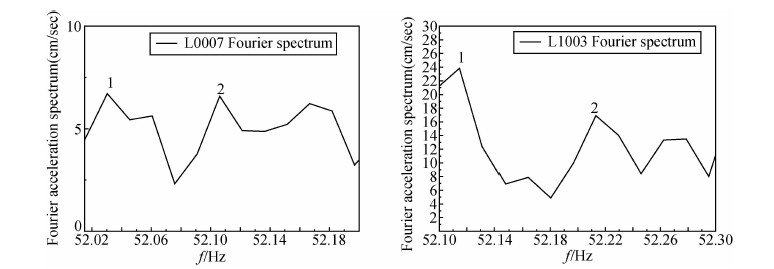 | 图 6 两基岩台记录到52~52.3 Hz的傅里叶幅值随频率变化 Fig. 6 Relationship between Fourier amplitudes and frequencies from 52~52.3 Hz at two bed rock sites |
图 7是两个基岩台站记录到的53.08~53.2 Hz的傅里叶幅值随频率的变化.图中1~2点对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度分别为8.3 m/s,0.8 m/s.
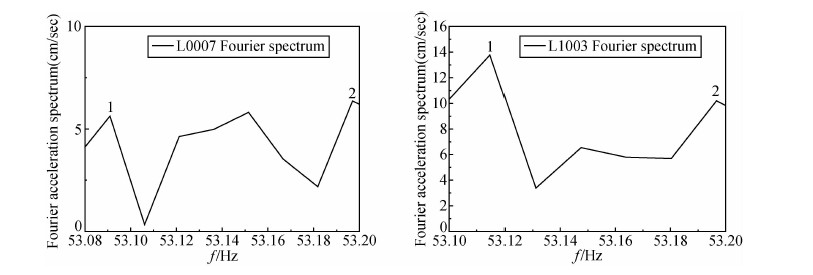 | 图 7 两基岩台记录到53.08~53.2 Hz的傅里叶幅值随频率变化 Fig. 7 Relationship between Fourier amplitudes and frequencies from 53.08~53.2 Hz at two bed rock sites |
图 8是两个基岩台站记录到的54~55.2 Hz的傅里叶幅值随频率的变化.图中1点、2点、3点和4点对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度分别为-29.3 m/s、-27.4 m/s、-28.7 m/s、-25.1 m/s.
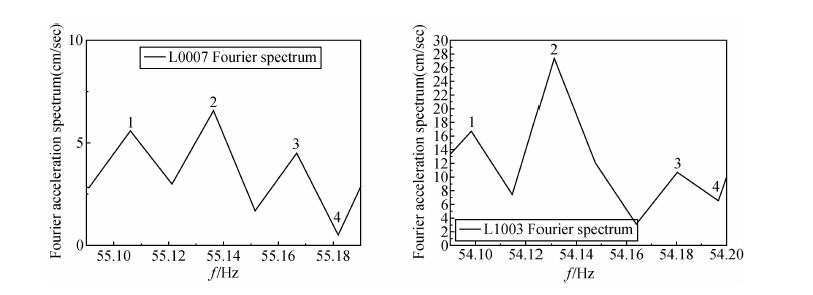 | 图 8 两基岩台记录到54~55.2 Hz的傅里叶幅值随频率变化 Fig. 8 Relationship between Fourier amplitudes and frequencies from 54~55.2 Hz at two bed rock sites |
图 9是两个基岩台站记录到的55.9~56.2 Hz的傅里叶幅值随频率的变化.图中1点、2点、3点和4点对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度分别为7.9 m/s、5.2 m/s、-5.3 m/s、-4.1 m/s.
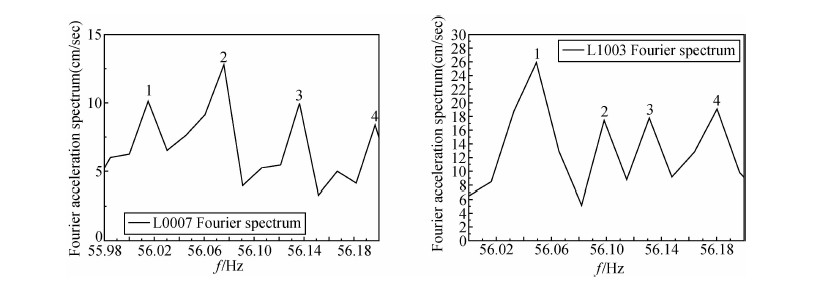 | 图 9 两基岩台记录到55.9~56.2 Hz的傅里叶幅值随频率变化 Fig. 9 Relationship between Fourier amplitudes and frequencies from 55.9~56.2 Hz at two bed rock sites |
图 10是两个基岩台站记录到的57.1~57.3 Hz的傅里叶幅值随频率的变化.图中1~4点对应的频率是由同一频率的地震波产生的,据此我们计算得到地震断层的滑动速度分别为17.4 m/s,19.0 m/s,24.1 m/s,25.9 m/s.
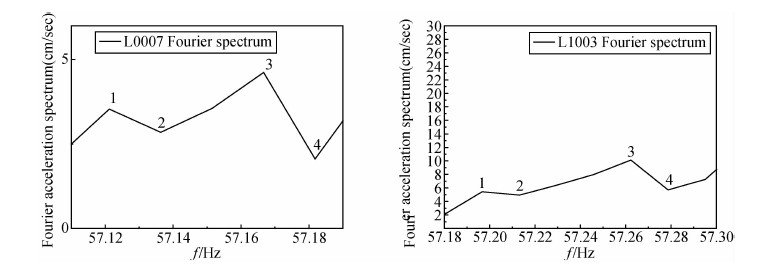 | 图 10 两基岩台记录到57.1~57.3 Hz的傅里叶幅值随频率变化 Fig. 10 Relationship between Fourier amplitudes and frequencies from 57.1~57.3 Hz at two bed rock sites |
根据上述断层滑动速度的计算结果,以断层的位错和上升时间为约束条件,用最小误差法估计了地震断层东西方向和南北方向滑动速度.图 11是断层向东方向的滑动速度函数,图 12是断层向西方向滑动的速度函数.图 13~14分别是断层向南和北方向的滑动速度函数,考虑到篇幅,没有给出图 13~14的计算过程.
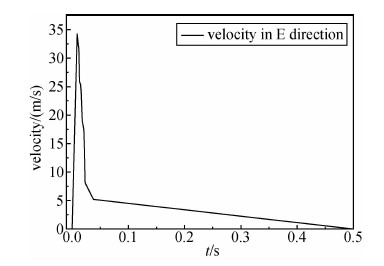 | 图 11 断层向东方向的滑动速度函数 Fig. 11 Sliding velocity function of fault in the direction of east |
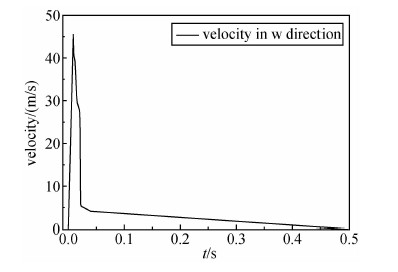 | 图 12 断层向西方向的滑动速度函数 Fig. 12 Sliding velocity function of fault in the direction of west |
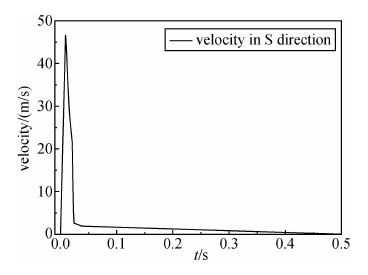 | 图 13 断层向南方向的滑动速度函数 Fig. 13 Sliding velocity function of fault in the direction of south |
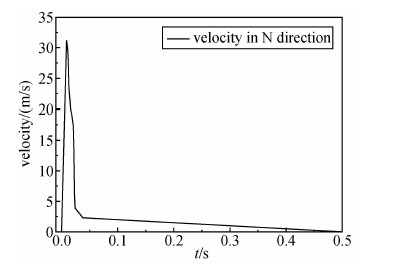 | 图 14 断层向北方向的滑动速度函数 Fig. 14 Sliding velocity function of fault in the direction of north |
岩石破裂实验表明,压机的刚度对岩样的失稳过程有重要影响.用压机对岩样加压时,压机和岩样同时开始变形.当压机的压力增加到某数值时,岩样开始破坏.由岩样的破坏,使得压机的形变得以恢复.由于要恢复原来的形状,储存在压机中的应变能力得以释放,从而加速了岩样的破坏,造成了爆炸式的失稳破坏.用多普勒效应计算得到地震断层滑动速度具有迅速上升的特点与岩石破裂实验结果是吻合的.
岩石破裂实验还表明,岩样的稳定性不仅仅取决于岩样的性质和其本身的应力水平,还取决于压机的性质,即取决于岩样和压机刚度的相对大小.压机刚度越小,岩样刚度越大,岩样越容易失稳.这说明地震的发生,不仅仅取决于震源介质刚度,还取决于围岩刚度.地震往往发生在震源有较大刚度,而围岩具有相对小刚度的地壳的介质中.正是由于围岩的刚度相对较小,使得断层的滑动速度具有相对缓慢下降的特点.
4 讨论与结论4.1 目前计算理论地震图经常使用的震源滑动速度函数主要有Haskell函数、钟形函数、指数函数、三角形函数等.Hisada提出了断层滑动速度函数,该速度函数具有迅速上升,相对缓慢地下降的特点.我们用多普勒效应计算结果证实了Hisada的推断.
4.2 断层滑动速度迅速上升,相对缓慢下降的计算结果符合断层断裂的物理过程.当断层周围应变能量积聚到一定程度时,断层错动,此时能量迅速释放,所以其滑动速度迅速增加.以后由于不再受到大应变能的驱动,同时由于受到周围岩体的阻碍使得其滑动速度迅速降低,但速度下降的加速度没有上升的加速度大.
4.3 目前可以通过矩张量反演方法和波形反演从实际地震资料中提取震源滑动速度函数,其中波形反演又分为理论格林函数方法和经验格林函数方法.一般认为用矩张量反演和理论格林函数方法得到的震源滑动速度函数与人们对地震波传播介质的认识水平有关,由于地壳介质的不可入性,同时由于利用波形反演的结果仅仅是众多可能结果之一,使得用上述方法计算得到的地震断层滑动速度函数的准确性有值得商榷的地方.
4.4 经验格林函数法把小震记录作为格林函数,自动地考虑到了传播介质对地震波的影响,也一定程度上考虑了震源对地震波的影响,普遍认为用经验格林函数方法得到的断层滑动速度函数与目前人们对地震波传播介质的认识水平无关.但同时也认为由于经验格林函数法要求在同一台站记录到来自同一地点的、震源机制相同的较大地震和较小地震的记录,这一过于苛刻的要求限制了经验格林函数方法的应用范围.
4.5 大地震发生后,震源介质的物理参数会发生很大的变化,此时在相同的地点发生小震的震源机制与大地震的震源机制已经发生了较大变化,所以即使在同一台站记录到来自同一地点的较大地震和较小地震的震源机制也不会相同.有理由认为,用经验格林函数方法计算得到断层滑动速度函数与人们对震源机制的认识水平有关.而用多普勒效应计算得到的断层滑动速度函数与地壳介质和震源机制无关,应该是一种有前途的计算地震断层滑动速度的方法.
4.6 当我们计算地震断层沿东西方向滑动时,既得到了向西方向的滑动,也得到了向东方向的滑动;当计算地震断层沿南北方向滑动时,既得到了向南方向的滑动,也得到了向北方向的滑动,说明此次地震断层是双向滑动.
致 谢 感谢审稿老师和编辑老师的辛勤工作.| [1] | Anderson J G, Richards P G. 1975. Comparison of strong ground motion from several dislocation models[J]. Geophysical Journal of the Royal Astronomical Society, 42(2): 347-373. |
| [2] | Boore D M. 2003. Simulation of ground motion using the stochastic method[J]. Pure Appl. Geophys., 160(3-4): 635-676. |
| [3] | Dreger D S. 1994a. Empirical Green’s function study of the January 17, 1994 Northridge, California earthquake[J]. Geophys. Res. Lett., 21(24): 2633-2636. |
| [4] | Dreger D S. 1994b. Investigation of the rupture process of the 28 June 1992 Landers earthquake utilizing TERRAscope[J]. Bull. Seismol. Soc. Am., 84(3): 713-724. |
| [5] | Hisada Y. 2001. A theoretical omega-square model considering the spatial variation in slip and rupture velocity. Part 2: Case for a two-dimensional source model[J]. Bull. Seismol. Soc. Am., 91(4): 651-666. |
| [6] | Li Q C. 2010. Research on ground motion simulation with empirical Green’s function method (in Chinese)[Ph. D. thesis]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. |
| [7] | Li S Q, Chen Q F, Zhao L, et al. 2013. Anomalous focal mechanism of the May 2011 Mw 5.7 deep earthquake in northeastern China: regional waveform inversion and possible mechanism[J]. Chinese J. Geophys. (in Chinese), 56(9): 2959-2970, doi: 10.6038/cjg20130910. |
| [8] | Ni J C, Chen Y T, Wang M, et al. 1991. Moment tensor inversion of some aftershocks of the April 18, 1985, Luquan, Yunnan, China, earthquake[J]. Acta Seismologica Sinica (in Chinese), 13(4): 412-419. |
| [9] | Ouyang X Y, Zhang W B, Zhang Y B. 2009. Estimation on site effect from different techniques using aftershocks of Chi-Chi earthquake[J]. Journal of the Graduate School of the Chinese Academy of Sciences (in Chinese), 26(3): 373-382. |
| [10] | Wang W M, Zhao L F, Li J, et al. 2008. Rupture process of the MS 8.0 Wenchuan earthquake of Sichuan, China[J]. Chinese Journal of Geophysics (in Chinese), 51(5): 1403-1410, doi: 10.3321/j.issn:0001-5733.2008.05.013. |
| [11] | Xu L S, Chen Y T. 1996. Source time function extraction of Gonghe earthquake using Green function method from long period digital waveform data[J]. Acta Seismologica Sinica (in Chinese), 8(2): 156-169. |
| [12] | Zhang Y, Xu L S, Chen Y T. 2009. Spatio-temporal variation of the source mechanism of the 2008 great Wenchuan earthquake[J]. Chinese Journal of Geophysics (in Chinese), 52(2): 379-389. |
| [13] | Zhou H, Feng G C, Li Z W, et al. 2013. The fault slip distribution of the Myanmar Mw 6.8 inferred from InSAR measurements[J]. Chinese Journal of Geophysics (in Chinese), 56(9): 3011-3021, doi: 10.6038/cjg20130914. |
| [14] | Zhou J Y, Chen Y T, Ni J C, et al. 1993. To determine the source time function of small earthquakes by the empirical Green function[J]. Acta Seismologica Sinica (in Chinese), 15(1): 22-31. |
| [15] | 李启成. 2010. 经验格林函数方法模拟地震[博士论文]. 哈尔滨: 中国地震局工程力学研究所. |
| [16] | 李圣强, 陈棋福, 赵里,等. 2013. 2011年5月中国东北Mw 5.7深震的非同寻常震源机制: 区域波形反演与成因探讨[J]. 地球物理学报, 56(9): 2959-2970, doi: 10.6038/cjg20130910. |
| [17] | 倪江川, 陈运泰, 王鸣,等. 1991. 云南禄劝地震部分余震的矩张量反演[J]. 地震学报, 13(4): 412-419. |
| [18] | 欧阳行艳, 章文波, 张有兵. 2009. 利用集集地震余震记录分析场地地震动反应[J]. 中国科学院研究生院学报, 26(3): 373-382. |
| [19] | 王卫民, 赵连锋, 李娟,等. 2008. 四川汶川8.0级地震震源过程[J]. 地球物理学报, 51(5): 1403-1410, doi:10.3321/j.issn:0001-5733.2008.05.013. |
| [20] | 许力生, 陈运泰. 1996. 用经验格林函数方法从长周期数字波形资料中提取共和地震的震源时间函数[J]. 地震学报, 18(2): 156-169. |
| [21] | 张勇, 许力生, 陈运泰. 2009. 2008年汶川大地震震源机制的时空变化[J]. 地球物理学报, 52(2): 379-389. |
| [22] | 周辉, 冯光财, 李志伟,等. 2013. 利用InSAR资料反演缅甸Mw 6.8地震断层滑动分布[J]. 地球物理学报, 56(9): 3011-3021, doi: 10.6038/cjg20130914. |
| [23] | 周家玉, 陈运泰, 倪江川,等. 1993. 用经验格林函数确定中小地震的震源时间函数[J]. 地震学报, 15(1): 22-31. |
 2016, Vol. 31
2016, Vol. 31

