2. 中国煤炭科工西安研究院, 西安 710077
2. China Coal Research Institute, Xi'an Science and Industry Group, Xi'an 710077, China
钻定向水平井中,随钻方位伽马测井是地质导向中最常用的方法之一(吴华强等,2005;裴素安,2006).方位伽马测井是以常规自然伽马测井为基础,将多个伽马探测器晶体设计在仪器的不同方向上,从而使探测到的伽马测井资料具有方位特性(杜志强等,2008).方位伽马测井的应用除了传统自然伽马测井具有的识别岩性,计算泥质含量(张景廉等,2000;李建红和周伦先,2008)之外,由于其具有方向性,因而可以进行实时监测钻井轨迹和计算钻头距层界面的距离,以及利用方位伽马测井资料成像显示,进行直观储层评价(Weller et al.,2005).
钻井技术是一项由地质部门、物探部门测绘部门等多个部门协同工作的过程,钻前地质部门对区域构造做大体划分和定性,再由物探部门、测绘部门对地下的构造层位走向倾角做细致描绘,因此可以根据获得的地下资料建立模型,进行方位伽马测井的正演模拟计算.
对于方位伽马测井技术,国外技术相对发展较快(Efnik et al.,1999;Neville et al.,2007;Pitcher et al.,2009),国内相对国外来说发展缓慢,目前国内对方位伽马的研究处于研发阶段(袁超等,2014).对于伽马测井正演研究多用蒙特卡罗方法进行模拟(Mendoza et al.,2006;Yin et al.,2008;袁超,2012;袁超等,2014).然而蒙特卡罗方法模拟计算量大、速度慢,该方法在测井仪器的优化设计和测井响应因素分析上却具有很大优势(吴文圣和黄隆基,2004;王珺和董延亮,2004).为使得地层模型满足经常模型实时更新的需求,邵才瑞等(2013)提出了自然伽马测井快速正演模型,推导出了伽马探头在地层不同位置时,探测到地层放射性值的响应方程.而该方法模拟常规自然伽马测井仪,并利用探测器探测到地层的自然伽马值的大小来确定仪器所在地下的位置,虽然该方法克服了蒙特卡罗方法的缺点,但由于该方法要准确探测到来自层界面的放射性计数,才能准确确定仪器所在位置与层界面的关系,因此该方法在应用上具有一定的局限性.且对于具有多探测器的方位伽马测井正演来说,算法仍显复杂.
本文在方位伽马测井原理及传统自然伽马测井的优势的基础上,结合实际生产中具有的条件和需求,提出一种方位伽马测井的快速正演算法.并利用正演模拟获得的曲线,定量计算沿钻进方向上钻头到界面的距离,包括在钻进方向上钻头到层界面的距离及钻头到界面的垂直距离,同时考虑了仪器直径,提高计算距离过程中的精度.
1 随钻方位伽马测井快速正演算法 1.1 正演地层数学模型方位伽马仪器上下探测器,在仪器的两侧呈180°方向排列,之间的垂直距离为仪器直径,两个探测器距钻头的距离相等(图 1).
 | 图 1 方位伽马测井仪器上下探测器位置示意图 Fig. 1 Diagram of detectors position in azimuth gamma logging instrument |
地层垂直剖面上地层与水平面有一夹角,为地层视倾角.地层沿钻进方向上倾,视倾角为正;下倾,视倾角为负;地层水平视倾角为0°;设置目的层为低放射性层,上、下围岩为高放射性层;目的层顶界面与底界面平行,仪器与目的层顶、底界面有一角度;图 2所示为所建正演模型示意图.利用该模型正演上下伽马测井曲线,并计算沿钻进方向上钻头到界面的距离和钻头到界面的垂直距离.
 | 图 2 正演地层数学模型 Fig. 2 Forward model of stratum a_dip—视地层倾角,°;Dis—探测器到界面距离;a_dip—视地层倾角,°;d—探测器到界面距离;L—探测器到钻头的距离;γ—仪器倾角(仪器与水平面夹角);α—仪器与界面夹角; a_L—沿钻进方向上钻头到界面的距离; c_L—钻头到界面的垂直距离,h-目的层厚度,m. |
模型满足:
(1)目的层为均匀低放射性层,其上下围岩为均匀高放射性层,且上下围岩所具有的放射性相等,放射性设为当量强度;
(2)上、下围岩无限厚;
(3)井眼无扩径,忽略泥饼影响;
(4)仪器测量时,保持上伽马探测器在上,下伽马探测器在下.
本文利用此模型,模拟仪器在不同位置时上伽马下伽马探测器探测到地层的放射性计数.
1.2 方位伽马正演理论 1.2.1 上下伽马测井曲线正演探测器计数原则:探测范围看做地层垂直剖面上以探测器为圆心,探测深度为半径的圆.围岩、目的层按各自在二维圆中所占面积比提供相应比例的放射性计数.也可以按三维空间球内所占体积比例进行计数,这样更符合实际情况,但值得说明的是,由于方位伽马曲线本身的特性,在计算钻头到界面距离的应用中,我们不必强调探测器计数的具体值,只需知道上下方位伽马的变化趋势(有无幅度差),无论三维球体或是二维圆面,探测器探测到界面时,都不影响上下曲线出现幅度差.应用时,用的也正是上下伽马曲线的幅度差来计算钻头到界面距离.为了减小计算复杂性,这里建立穿过一个层界面的二维圆模型(图 3).
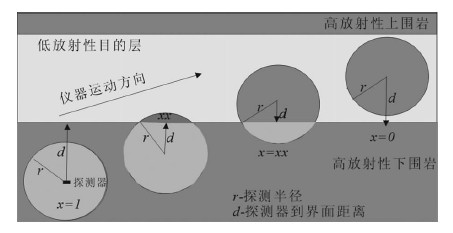 | 图 3 探测器计数原理图 Fig. 3 Diagram of counting principle |
图中四个圆分别表示探测器距离界面不同距离时,地层提供探测器放射性计数示意图,快速正演模拟上下方位伽马计数率的理论公式(1)~(3):
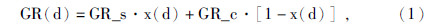
根据图 3模型,x是探测器到界面的距离的函数,其计算方法如下:
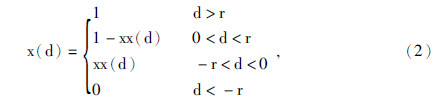
其中,
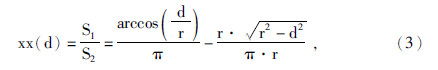
式中,r为探测器的探测深度,m; xx(d)为较小弓形面积占整个圆面积比(公式推导的中间变量); 1为较小弓形面积; 2为圆的面积.
在正演模拟上下伽马计数时,需要确定探测器到界面的四个距离:仪器上探测器到顶界面距离d_uu、上探测器到底界面的距离d_ud、仪器下探测器到顶界面的距离d_du、下探测器到底界面的距离d_dd(图 4).将各距离带入到公式(1)~(3),得到上伽马测井曲线和下伽马测井曲线的正演公式为
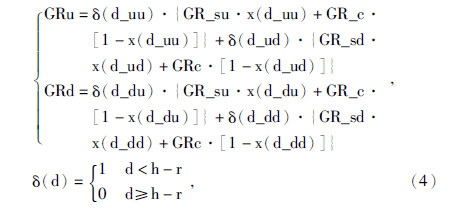
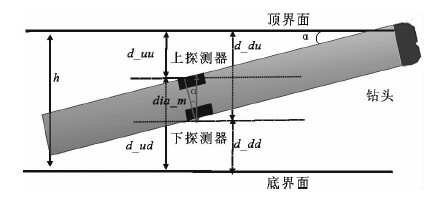 | 图 4 探测器到界面的距离关系图 Fig. 4 Diagram of the relationship among the distances |
图 5为仪器以2°倾角从放射性为50API的下部围岩进入放射性为20API的目的层,以同样的倾斜角度从目的层进入到放射性为80API的上部围岩,这个过程的上下伽马正演曲线.
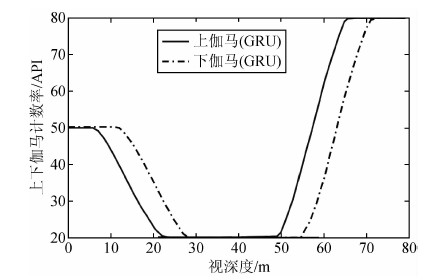 | 图 5 正演上下伽马测井曲线 Fig. 5 Upper and lower azimuth gamma curves |
1.2.2 沿钻进方向钻头到界面距离及垂直距离
利用仪器的上下伽马探测器到上下层界面的距离,来正演仪器在各测点处在钻进方向上钻头距上下界面距离和钻头到界面的垂向距离为

探测器到界面的四个距离分别带入到式5中,得到4组正演的沿钻进方向钻头到界面的距离和钻头到界面的垂直距离.
1.3 正演模拟曲线利用以上几何关系推倒数学公式,并模拟了仪器从目的层进入到上围岩、又从上围岩穿过顶界面、底界面进入下围岩的过程的上下伽马曲线(图 6).
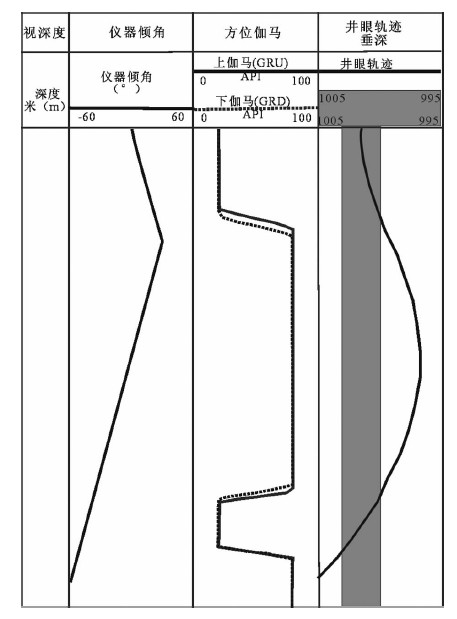 | 图 6 上下方位伽马正演模拟曲线 Fig. 6 Upper and lower azimuth gamma forward simulation curve |
所建模型中基本参数设置:
地层视倾角a_dip=0°;仪器的初始位置设为:上探测器距上界面初始距离d_uu=1.5 m;仪器探测深度d=0.3 m;采样深度间隔S_dep=0.3 m;仪器直径dia_m=0.13 m;目的层厚度h=3 m;探测器到钻头距离L=1 m;仪器钻进过程起始位置仪器角度γ由0度现增加到30°,再减小到-60°(仪器水平偏向顶界面γ为正、偏向底界面γ为负).
图中第一道为视深度道,模拟了视深度从0~36 m的上下伽马测井曲线.第二道为仪器倾角数据,设为均匀变化.第三道为正演上下伽马测井曲线结果.红色实线为上伽马曲线,蓝色虚线为下伽马测井曲线.第四道为井眼轨迹与地层的位置关系,深色为目的层,两边浅色为高放射性围岩,绿色实线为井眼轨迹,此处模拟地下垂深为995 m到1005 m层段处井眼轨迹.
从曲线中可以看到:当层界面位于在伽马探测器的探测范围之内,上下伽马曲线就开始出现幅度差.图中共三次出现了幅度差.
第一段幅差,该段伽马计数表示仪器由低放射性目的层从上界面钻入上部高放射性层,由于上伽马探测器先探测到层界面,故上伽马计数先增大,下伽马曲线随后增大.当探测器逐渐远离界面时,上伽马先停止增加而后下伽马计数也停止增加;当上下伽马探测器完全进入上部高放射性层时,上下伽马曲线重合.
第二次出现幅差段,该段伽马计数表示仪器由上方高放射性层(高放射性围岩)从上界面钻入低放射性目的层,由于该过程中下伽马探测器先探测到层界面,故下伽马计数先减小,上伽马曲线随后减小.当探测器逐渐进入低放射性目的层远离界面时,下伽马先停止减小保持不变,而后上伽马计数也停止减小;当上下伽马探测器完全进入低放射性层时,上下伽马曲线再次完全重合.
第三次出现幅差段,该段伽马计数表示仪器探测器由中间低放射性层由下界面钻入下部高放射性围岩,由于该过程中下伽马探测器先探测到层界面,故下伽马计数先增大,上伽马曲线随后增大.当探测器逐渐进入高放射性目的层远离界面时,下伽马先停止减小保持不变,而后上伽马计数也停止减小;当上下伽马探测器完全进入下部高放射性层时,上下伽马曲线又一次完全重合.
该模拟结果符合理论推导,并分别模拟了仪器从目的层的顶界面穿出高放射性围岩、从高放射性层从目的层顶界面穿入目的层、以及由目的层的地界面穿出到高放射性围岩中这三个过程.为利用方位伽马数据计算钻头的目的层顶底界面提供合理的模拟数据.
2 定量动态监测2.1 仪器钻进状态判断原理通过以上正演分析,可以得到探测器在不同层界面的不同位置时,上下伽马曲线呈现出不同的形态,可以看到,在高低放射性层放射性均匀且保持不变的情况下,上下伽马曲线除重合段之外,所呈现的幅差形态与探测器的位置是一一对应的,不存在多解性.由此,本文只利用上下方位伽马曲线的不同组合形态来确定仪器所处地层中的位置,也就是反演过程.
以本文所建模型为例:
1)当上伽马曲线值大于下伽马曲线值,同时上伽马先变化,则说明仪器开始从低放射性目的层由上界面钻入高放射性层(图 7a);
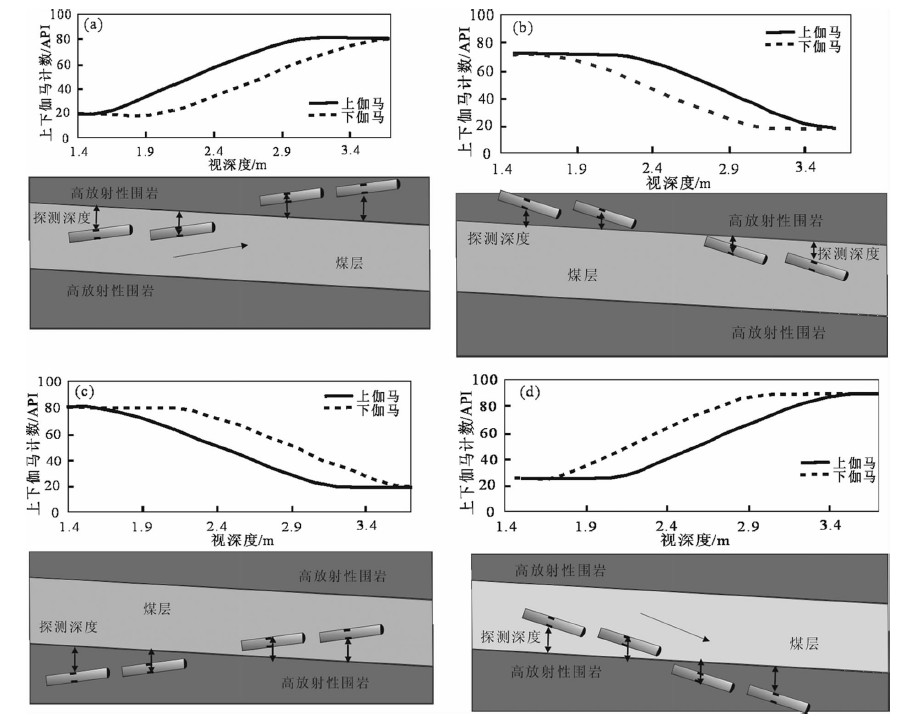 | 图 7 上下方位伽马曲线与仪器所处位置对应图 Fig. 7 Graphs of the location of instrument and the upper and lower azimuth gamma curves |
2)当上伽马曲线大于下伽马曲线值,同时下伽马先变化,则说明此时仪器开始从高放射性层由上界面进入到低放射性目的层(图 7b);
3)当上伽马曲线值小于下伽马曲线值,同时上伽马先变化,则说明仪器开始从下部高放射性层由下界面钻入低放射性目的层(图 7c);
4)当上伽马曲线小于下伽马曲线值,同时下伽马先变化,则说明此时仪器开始从低放射性目的层由下界面钻入到下部高放射性层(图 7d).
2.2 定量计算钻头到层界面距离利用方位伽马测井曲线反演钻头到界面的距离,目的层厚度、真倾角可根据地震地质等资料确定出来,探测器直径、探测深度、钻头到探测器距离等为仪器参数,上下方位伽马曲线利用的是正演曲线数据,井斜数据、方位数据可通过仪器的测斜部分得到测井资料,以上数据或参数在计算过程中为已知量.
当上下伽马曲线出现幅度差,即可计算每个测点探测器到层界面的距离,由于仪器直径与探测器探测深度相差不大,在计算钻头到界面的距离时不能忽略,应该分别利用上下探测器到界面的距离来计算钻头到界面沿钻进方向上的距离和垂直距离.以图 7a图为例,根据上下伽马曲线出现的幅度差利用式(6)计算探测器到界面的距离,在利用式(7)反演计算沿钻进方向上钻头到界面距离及钻头到界面的垂直距离.反演过程图 8所示:
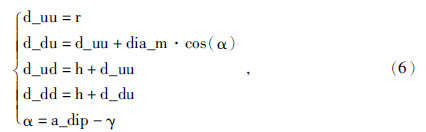
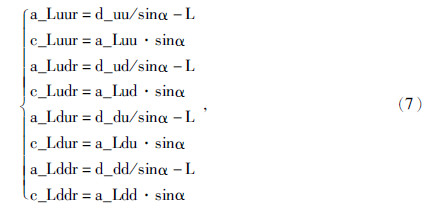
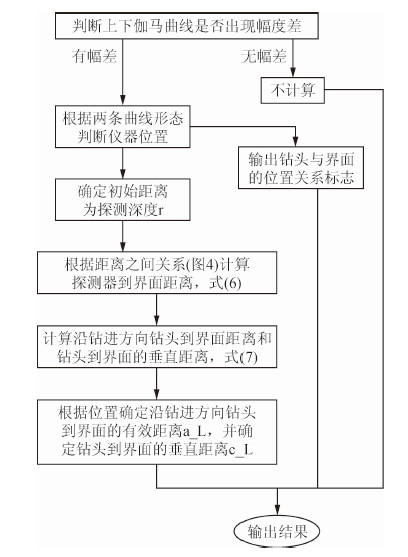 | 图 8 计算过程图 Fig. 8 Diagram of the process of calculation |
 | 图 9 沿钻进方向钻头到界面的距离示意图 Fig. 9 Diagram of the distances of from bit to the interface along the drilling direction 图中,a_Luu—钻头顶部距顶界面距离,m;a_Ldu—钻头底部距顶界面距离,m;a_Lud—钻头顶部距底界面距离,m;a_Ldd—钻头底部距底界面距离,m. |
正演计算直接利用探测器到界面的距离,结合几何关系计算得到;反演计算钻头到界面的距离,利用正演的上下伽马测井曲线出现的幅度差,来判断仪器所处位置,反推探测器到界面距离,从而计算钻头到界面的距离.
利用以上正演反演模型公式进行正反演结果对比,对比结果图 10所示.图为目的层厚度为3 m,反演计算的沿钻进方向上钻头到层界面距离与正演结果对比图.
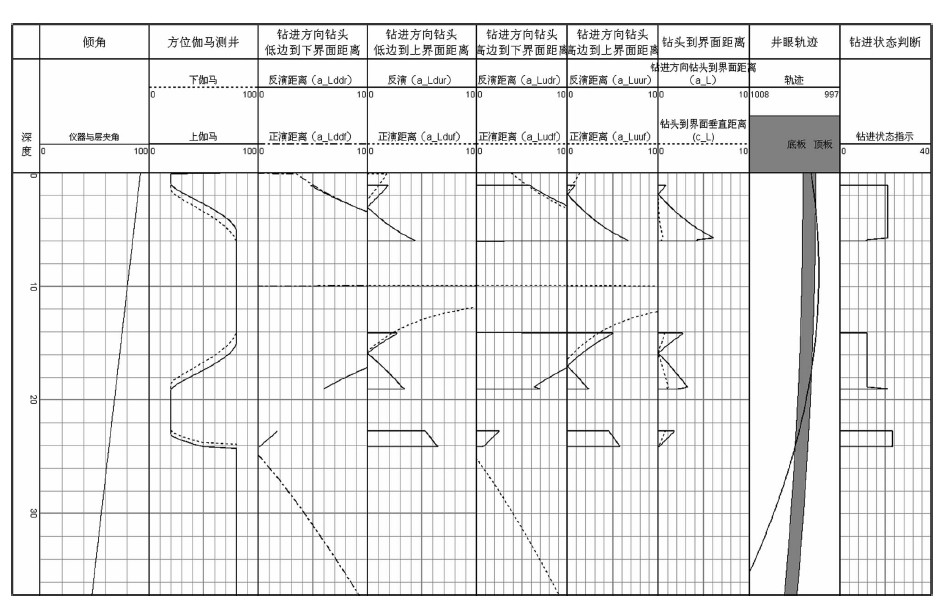 | 图 10 方位伽马计算钻头到层界面距离正反演对比图 Fig. 10 Comparison chart of inversion and forward distance from bit to layer interface calculated with azimuth gamma |
第1道为深度道,是深度范围在0~30 m;
第2道为仪器倾角,规定仪器水平为0°,偏向顶界面为正,偏向底界面为负;图中可以看出,仪器倾角从10°变化到-40°;
第3道为利用正演理论获得的上下方位伽马曲线;模拟了仪器从目的层进入上围岩,从上围岩穿过目的层到下围岩中,这个过程的上下伽马测井曲线;
第4道虚线为正演计算的沿钻进方向上钻头下部到下界面的距离a_Lddf,实线表示反演计算的沿钻进方向上钻头下部到下界面的距离a_Lddr;
第5道虚线为正演计算的沿钻进方向上钻头顶部到上界面的距离a_Luuf,实线表示反演计算的沿钻进方向上钻头顶部到界面的距离a_Luur;
第6道虚线为正演计算的沿钻进方向上钻头下部到上界面的距离a_Lduf,实线表示反演计算的沿钻进方向上钻头底部到上界面的距离a_Ldur;
第7道虚线为正演计算的沿钻进方向上钻头顶部到下界面的距离a_Ludf,实线表示反演计算的沿钻进方向上钻头顶部到下界面的距离a_Ludr;
第8道为计算的钻头到界面的有效的垂直距离;
第9道为从四个距离中根据上下伽马测井曲线形态确定的沿钻进方向上钻头到界面的有效距离,即具有导向作用的距离(图 9中具有导向作用的距离为a_Ldd);
第10道为井眼轨迹与层界面关系,本模型中模拟的是具有一定倾角的层为正演的数据结果.
最后一道为仪器钻进状态指示道,四条虚线表示四种状态的指示基线,分别用来表示仪器从顶界面穿入目的层、从目的层进入到顶部围岩层、从目的层进入下部围岩层、从下部围岩层进入目的层;深色实线为反演的钻头状态的指示标记,仪器处于什么状态,实线就会与相应的基线重合,图中红色虚线标注在上下伽马测井曲线出现幅差处,可以清楚的看出指示线的状态有三段,分别表示了从目的层进入到顶部围岩层、从顶界面穿入目的层、从目的层进入下部围岩层这三个状态.
从对比图中可以看到,基于以上反演算法利用正演上下伽马测井曲线计算的钻头到层界面的各个距离与正演计算的距离虽并非完全相等,但基本一致.
3 结 论3.1 本文正演模型能够模拟方位伽马测井上下伽马探测器在地层的不同位置时,不同计数情况,模拟结果与理论值相符.同时,该正演模拟方法在不影响应用情况下采用二维圆模拟上下伽马测井曲线,具有计算量小,计算复杂性低的特点.
3.2 上下伽马曲线出现幅差段的不同形态,与钻头与界面的位置关系一一对应的,不存在多解性,可利用上下伽马曲线幅差和变化趋势能够判断钻头与目的层界面的位置关系,在随钻过程中可根据伽马曲线形态及时判断钻头与目的层界面位置关系,及时调整钻进方向,可为方位伽马应用于地质导向进一步提供理论支持.
3.3 在定量计算钻头到层界面的距离时,考虑了仪器直径,因而先判断钻头与界面位置关系,再定量计算沿钻进方向上钻头距上下界面的距离.
3.4 本文中提出的正演和反演模型在计算钻头到层界面的距离上、随钻过程中对井眼轨迹的形态动态监测上适用,并具有一定优势.在方位成像上并不适用,即本文正演模型不适用于成像研究中.
3.5 本文模型理论属初步研究,仅限于二维情况,复杂地层模型有待于进一步研究.
致 谢 感谢中煤科工集团西安研究院物探研发中心研究人员对本研究的大力支持,以及对本文提出的宝贵意见,在此一并表示感谢.| [1] | Du Z Q, Hao Y L, Zhang G L, et al. 2008. The application of the azimuth gamma logging while drilling for the Geosteering in the horizontal wells in Jidong oilfield[J]. Mud Logging Engineering (in Chinese), 19(1): 18-21, doi: 10.3969/j.issn.1672-9803.2008.01.004. |
| [2] | Efnik M S, Hamawi M, Shamri A A, et al. 1999. Using new advances in LWD technology for geosteering and geologic modeling[C]. // SPE/IADC Middle East Drilling Technology Conference. Abu Dhabi: Society of Petroleum Engineers, 1-9. |
| [3] | Li J H, Zhou L X. 2008. Response features of gamma ray log and its application in glutenite of Dongying depression[J]. Journal of Oil and Gas Technology (in Chinese), 30(1): 88-91, doi: 10.3969/j.issn.1000-9752.2008.01.020. |
| [4] | Mendoza A, Ellis D V, Rasmus J C. 2006. Why the LWD and wireline gamma ray measurements may read different values in the same well[C]. // International Oil Conference And Exhibition. Cancun, Maxico: International Oil Conference and Exhibition. |
| [5] | Neville T J, Weller G, Faivre O, et al. 2007. A new-generation LWD tool with colocated sensors opens new opportunities for formation evaluation[J]. SPE Reservoir Evaluation & Engineering, 10(2): 132-139. |
| [6] | Pei S A. 2006. Application of Geosteering drilling technique in Jidong oilfield[J]. Natural Gas Exploration and Development (in Chinese), 29(04): 57-59, doi: 10.3969/j.issn.1673-3177.2006.04.016. |
| [7] | Pitcher J L, Schafer D B, Botterell P. 2009. A new azimuthal gamma at bit imaging tool for geosteering thin reservoirs[C]. // SPE/IADC Drilling Conference and Exhibition. Amsterdam: Society of Petroleum Engineers, 1-8. |
| [8] | Shao C R, Cao X J, Chen G X, et al. 2013. A fast forward algorithm for LWD gamma-ray response and its Geosteering application[J]. Chinese Journal of Geophysics (in Chinese), 56(11): 3932-3942, doi: 10.6038/cjg20131135. |
| [9] | Wang J, Dong Y L. 2004. Influence of mud cake on multidetector density logging[J]. Natural Gas Industry (in Chinese), 24(8): 30-31, 38, doi: 10.3321/j.issn:1000-0976.2004.08.010. |
| [10] | Weller G, Galvin S D, El-Halawani T. 2005. A new integrated LWD platform delivers improved drilling efficiency, well placement, and formation evaluation services[C]. // Offshore Europe. Aberdeen: Society of Petroleum Engineers, 1-11. |
| [11] | Wu H Q, Zhou Y Q, Xu Y W, et al. 2005. The application of MWD GAMMA survey technology in geo-steering drilling[J]. Fault-block Oil & Gas Field (in Chinese), 12(2): 71-72, doi: 10.3969/j.issn.1005-8907.2005.02.024. |
| [12] | Wu W S, Huang L J. 2004. Monte Carlo Simulation of three-detector density logging[J]. Chinese Journal of Geophysics (in Chinese), 47(1): 164-170, doi: 10.3321/j.issn:0001-5733.2004.01.025. |
| [13] | Yin H Z, Zhou J J, Guo P J. 2008. A hybrid solution for fast 3d gamma ray tool modeling in high angle and horizontal wells[C]. // 49th Annual Logging Symposium. Austin, Texas: Society of Petroleum Engineers. |
| [14] | Yuan C. 2012. Fundamental study on LWD azimuthal gamma ray well logging (in Chinese) [Ph. M. thesis]. Qingdao: China University of Petroleum. |
| [15] | Yuan C, Zhou C C, Li C L, et al. 2014. Quantitative prediction of the distance from drilling bit to boundary surface in geosteering based on azimuthal gamma Ray Logging[C]. // SPWLA 55th Annual Logging Symposium. Abu Dhabi: Society of Petroleum Engineers. |
| [16] | Yuan C, Zhou C C. Zhang F, et al. 2014. Optimization of diameter of detector for azimuthal gamma logging while drilling[J] China Petroleum Machinery (in Chinese), 42(3): 1-4, doi: 10.3969/j.issn.1001-4578.2014.03.001. |
| [17] | Zhang J L, Liu Q X, Liang X W, et al. 2000. Discussion on the application of natural gamma spectrometry log to reservoir prediction[J]. Oil Geophysical Prospecting (in Chinese), 35(3): 395-400. |
| [18] | 杜志强, 郝以岭, 张国龙等. 2008. 方位伽马随钻测井在冀东油田水平井地质导向中的应用[J]. 录井工程, 19(1): 18-21, doi: 10.3969/j.issn.1672-9803.2008.01.004. |
| [19] | 李建红, 周伦先. 2008. 东营凹陷砂砾岩自然伽马测井响应特征研究及应用[J]. 石油天然气学报, 30(1): 88-91, doi: 10.3969/j.issn.1000-9752.2008.01.020. |
| [20] | 裴素安. 2006. 地质导向技术在冀东油田的应用[J]. 天然气开发, 29(4): 57-59, doi: 10.3969/j.issn.1673-3177.2006.04.016. |
| [21] | 邵才瑞, 曹先军, 陈国兴等. 2013. 随钻伽马测井快速正演算法及地质导向应用[J]. 地球物理学报, 56(11): 3932-3942, doi: 10.6038/cjg20131135. |
| [22] | 王珺, 董延亮. 2004. 多探测器密度测井泥饼影响的研究[J]. 天然气工业, 24(8): 30-31, 38, doi: 10.3321/j.issn:1000-0976.2004.08.010. |
| [23] | 吴华强, 周艳琴, 许永伟等. 2005. MWD GAMMA 测量技术在地质导向钻井中的应用[J]. 断块油气田, 12(2): 71-72, doi: 10.3969/j.issn.1005-8907.2005.02.024. |
| [24] | 吴文圣, 黄隆基. 2004. 三探测器密度测井的Monte Carlo模拟[J]. 地球物理学报, 47(1): 164-170, doi: 10.3321/j.issn:0001-5733.2004.01.025. |
| [25] | 袁超. 2012. 随钻方位伽马测井方法基础研究[硕士论文]. 青岛: 中国石油大学. |
| [26] | 袁超, 周灿灿, 张锋等. 2014. 随钻方位伽马测井探测器直径优化设计[J]. 石油机械, 42(3): 1-4, doi: 10.3969/j.issn.1001-4578.2014.03.001. |
| [27] | 张景廉, 刘全新, 梁秀文等. 2000. 有关自然伽马能谱测井在储层预测中的应用讨论[J]. 石油地球物理勘探, 35(3): 395-400. |
 2016, Vol. 31
2016, Vol. 31

