2. 吉林大学地球信息探测仪器教育部重点实验室, 长春 130061
2. Key Laboratory of Geo-Exploration and Instrumentation of Education Ministry, Jilin University, Changchun 130061, China
地震层析成像是利用地震数据对地下物质属性进行反演,并逐层剖析以对其内部结构进行成像的技术.地震层析成像能够以图像的形式,直观清晰地显示地球内部的精细结构和局部不均匀性,因而被广泛应用于内部地球物理和地球动力学、能源勘探开发、工程和灾害地质、金属矿勘探等领域(杨文采,1993).正演数值模拟计算是层析成像的关键性步骤,正演计算的精度和计算速度,直接关系到成像的分辨率和可靠程度(雷栋和胡祥云,2006).地震层析成像中用于波场数值模拟的方法分为两类,即波动方程数值模拟和射线追踪数值模拟.波动方程包含了丰富的波场信息,模拟结果较为准确,为研究地震波的传播机理和复杂地层的解释提供了更多的佐证(李信富等,2007).然而,该方法易引起干扰波,计算速度慢,对计算机要求较高,且假定地表为水平面,与野外实际地震勘探情况不符(张岭和刘劲松,2005;雷栋和胡祥云,2006;熊晓军等,2006).射线追踪方法概念明确,能够直观反映地震波的几何传播路径,计算速度快,能够灵活处理起伏地表情况,作为探究地下介质分布和地层中地震波传播问题的有效手段,已在地震正演问题中得到广泛应用,尤其在层析成像、叠前深度偏移等领域占据重要地位.
所谓射线追踪指给定震源点和检波点位置及波在介质中传播的速度模型,求从震源点到检波点的射线轨迹及其走时(波传播的时间)的方法.射线追踪方法众多,从计算走时和射线路径的运动学追踪到计算振幅信息的动力学追踪,各种方法层见叠出(Julian and Gubbins,1977;张钋等,2000a;李飞等,2013).经典方法是基于初值问题的试射法和基于边值问题的弯曲法.试射法是最早提出的一种射线追踪方法,该方法基于Snell定律,通过不断修改震源点处射线的出射方向,找到能够到达检波点的合适的入射角,从而确定射线路径,该方法比较适用于水平地层或者具有相同走向的倾斜界面地层的射线追踪.弯曲法基于Fermat最小走时原理,通过扰动一条连接震源和接收点的初始路径,不断迭代修改射线路径与各地层界面的交点坐标,直到满足走时最小准则,相对于试射法计算效率有所提高.
经典射线追踪方法为计算地震走时和描述射线路径提供了最原始的方法,但是在处理介质中较强速度变化以及求取多值走时中的全局最小走时方面均存在困难.试射法的主要问题在于:出射角的微小变化可能给射线路径带来巨大扰动,存在着射线不能到达接收点的可能性,且不能追踪阴影区中的射线路径.对于弯曲法,每次只能追踪一条射线,追踪效率不高,对于两点距离较远的情况效率更低,此外路径的走时可能只是局部最小,不能保证全局最小(杨兰锁等,2006;和锐等,2007).
鉴于传统方法在以上方面的不足,并随着研究的深入,出现了大量不同于传统方法的新型算法.这些方法的主要特点是直接从惠更斯原理或Fermat原理出发,采用等价的波前描述地震波场的特征(刘洪等,1995;刘玉等,2014).本文对其中已广泛应用的有限差分法、走时插值法、最短路径法及波前构建法在算法基本原理、运算精度及效率、算法优越性、存在的主要问题及相应改进算法等方面进行了研究讨论,分析了各方法的研究现状,最后对射线追踪法的发展趋势进行了展望.
1 有限差分法利用有限差分方法近似程函方程是由Vidale(1988)基于扩张波前的思想提出的一种地震波走时计算方法.随后,该方法被扩展至三维并应用于地震射线追踪(Vidale,1990).与经典算法不同,有限差分射线追踪方法属于向前——向后方法的一种,计算过程分为两个部分.首先将介质模型离散化为矩形网格,从震源点所在的网格单元开始,利用已知节点的初至走时,通过求解程函方程获取网格中其他节点初至走时,并逐步扩展直至完成所有网格节点上的走时计算.然后依据平面波理论,从接收点出发沿着走时数据的最大梯度方向返回到震源点,以获得最小走时路径.
1.1 有限差分法优越性及局限性利用有限差分近似求解程函方程的方法,从波前到所有节点的最小走时算一遍即可求出,因而计算初至波走时的效率高,并且不存在盲区问题.然而,Vidale算法只考虑按照矩形差分扩展方式,用内圈网格点上的走时求取与其相邻的外圈网格点上的走时并逐层向外推进,而忽略了初至能量有可能迂回传播的情况,致使该算法不能得到真正的全局最小走时波前(杨兰锁等,2006;李文杰等,2008).此外,当介质中速度差较大的情况下,该方法有可能得不到正确结果.
1.2 针对地震波向源传播问题及算法局部稳定性的改进针对地震波向源传播的问题,Qin等(1992)提出一种波前扩展有限差分算法,该算法使用真正的波前传播理论来模拟波前扩展,尽量使差分网格点的走时计算次序符合波前扩展因果关系,每次差分计算都从波前面上的最小走时节点开始,从而克服了矩形波前差分计算扩展方式因果稳定性差的缺点.但是该方法需要耗费大量时间进行全局极值的查找,计算效率不高.
由于Qin直接沿用了Vidale算法的差分格式,因而在对某些局部速度变化剧烈的介质模型进行计算时,仍可能出现负数开平方的问题,算法的局部稳定性没有得到彻底解决.为改善算法的局部稳定性,国外学者Podvin和Lecomte(1991)提出了一种体波、首波、散射波相结合的走时算法,该算法同样按照扩展方阵的方式求取走时,但对每一个网格点的走时计算的可能性进行细分,系统的比较来自各个方向的透射波、衍射波和首波,达到了局部算法稳定的目的.在国内,张霖斌等(1993)也做了类似研究,并将局部算法与扫描算法相结合,提出一种有限差分的改进算法,在计算精度上有所提升.Sun等(2007)在前人工作的基础上,提出了多种走时计算方案相结合的改进措施,使算法的局部稳定性问题得到了有效解决.李文杰等(2008)在前人研究的基础上,提出了改进的运用程函方程计算走时的方法,该方法仅利用已知的两点初至走时求取相邻第三点的初至时间,并将扩展波阵面法与多种局部算法综合应用,使得算法更加稳健.
与Vidale所采用的差分格式相比较,迎风差分格式具有无条件稳定性(Sethian and Popovici,1999),能够满足复杂地形地区地震波走时计算在不规则边界处需采用稳定的局部走时算法的要求.孙章庆等(2012a)对应用于正方形网格模型的迎风差分格式进行了改进,提出了阶梯网格迎风差分法,对于复杂地形、近地表及地下复杂介质等复杂地形条件下的走时计算具有很好的适应性和稳定性.孙章庆等(2012b)利用迎风差分格式的思想控制算法稳定性,结合适用于不等距网格计算的不等距差分格式,建立了一种局部走时计算公式,有效解决了三维起伏地表条件下的地震波走时计算问题且具有较高的计算精度.
1.3 对有限差分算法运算效率的改善有限差分算法总是将波前面上的最小走时节点作为差分计算的扩展点,因此需要对波前面上节点的走时进行排序,以查找波前面上的最小走时点.这样的步骤加大了算法的复杂程度,当波前面上点数较多时,会影响整个算法的计算效率.
研究针对性强的、高效的波前最小走时点查找方法是提高算法效率的途径之一.Sethian和Popovici(1999)利用迎风差分格式对局部程函方程进行求解,应用窄带技术进行走时波前重建,采用堆选排技术保存走时数据,提出了一种快速推进方法.对于走时数据的处理,总是将最小走时存放于堆顶部,大大节约了极小值查找的时间,有效减少了计算量并提升了计算效率.杨昊等(2007)将波前点的存储和查找问题概括为优先队列问题,提出了更加符合波前点传播规律的列队式存储方法,并在Vidale算法不稳定点处使用体波、首波、散射波相结合的走时算法,在兼顾算法稳定性的同时有效提高了运算效率.杨昊等(2010)分析了波前扩展有限差分射线追踪方法向前处理部分地震波走时算法的具体特点,以原始二叉树堆排序方法为基础,优化了波前面上新节点插入和最小走时节点移除的算法流程,有效提高了波前面上最小走时点的查找速度.
为避免极小走时节点排序和查询等操作,国外学者Van Trier和Symes(1991)将程函方程化为守恒型程函方程,用迎风法对变换后的方程进行直接求解,进而求出地震波场的最小走时.该算法无需进行排序和从相对极小点开始计算,易于向量化.其主要局限性在于:守恒通量函数在介质速度梯度较大的情况下可能变为虚数,导致计算终止;此外,需要频繁地将走时数据由极坐标网格转换到直角坐标网格,这在一定程度上增加了计算量.在国内,朱金明和王丽燕(1992)将求解守恒型程函方程的思路应用于直角坐标系中,避免了不同坐标系下走时的转换,然而该方法仅限于研究单一方向传播的波,且为保证差分格式的稳定性和相容性,需要对计算网格进行特殊处理,因而优越性不大.
有限差分法克服了经典射线追踪方法不能进行阴影区射线追踪的不足,因其一次计算即可求得波前到所有节点的最小走时,计算效率较高.经过国内外学者的不断研究,提出了利用真正的波前传播理论模拟波前扩展和多种走时计算与局部算法相结合等方法,有效改善了原始算法的稳定性,通过对守恒型程函方程的研究及波前最小走时点查找方式的改进,进一步提高了算法计算效率.
2 走时插值法Asakawa和Kawanaka(1993)针对井孔间的初至波射线追踪问题提出了二维走时线性走时插值法(Linear Travel-time Interpolation Method,简称LTI算法).该方法以线性走时假设为前提.首先将模型划分为规则的网格单元,并在单元边界上插入n个节点,随后分向前、向后处理两部分进行.在向前处理中,根据走时线性变化的假定以及走时最小原理,计算整个空间离散节点的时间场分布;在向后处理中,利用最小走时计算结果,从接收点开始根据走时插值公式反向追踪射线路径直至激发点,得到具有最小走时的初至射线路径.
2.1 LTI算法研究及优缺点分析在LTI原始算法的基础上,张建中等(2003)以Asakawa提出的适用于正方形单元的走时插值射线追踪方法为基础,发展了适于任意多边形单元和任意点激发任意点接收的较通用的地震走时插值方法.孙章庆等(2009)为适应复杂地表条件下地震波走时计算的要求,运用线性插值与窄带技术,提出了一种走时计算的新方法.该方法利用窄带技术模拟初至波前的传播过程,在局部采用线性插值计算走时,并采用三角网和矩形网相结合的方法剖分速度模型以逼近起伏地表,具有较高的计算精度.黄翼坚等(2010)借鉴了LTI算法计算节点走时的思想,分析了初至波走时LTI算法的计算结果中包含非直达波走时的原因,通过在更新节点走时的过程中,舍去由低速层传向高速层而后又返回该低速层的射线的走时的方法,实现了对射线方向的约束,提出了直达波走时线性插值计算的方法.
线性走时插值的方法克服了基于网格模型的射线追踪方法在射线折射角不能随入射角连续变化方面的问题.因其计算速度快、精度高、易于实现等优点而被广泛应用于各种类型的初至波走时计算和射线追踪.虽然LTI算法在计算走时和追踪射线路径时比其他常规方法更为准确,但也存在两点不足:走时线性假定会产生误差,导致路径不够精确;当存在射线逆向传播时,LTI算法无法求得具有最小走时的路径(刘玲君等,2014).
2.2 针对走时线性假设及射线逆向传播问题的改进2.2.1 多种非线性插值方法的研究针对走时线性假设影响算法精度的问题,国内学者对多种非线性插值方法进行了大量研究.二维条件下,聂建新和杨慧珠(2003)对LTI算法进行误差分析后认为:线性插值式在远场可以较精确的逼近走时真实值,而在近场线性插值的误差较大.根据上述分析结果提出了走时二次/线性联合插值法,即在震源的进场采用二次插值计算走时,在远场仍用LTI算法.该算法继承原算法优点的同时改善了近场走时的计算精度,降低了累积误差,进而提高了全场(尤其是远场)走时的计算精度.张赛民等(2007)提出了基于走时的抛物线插值射线追踪算法,使用网格边界上的三个节点计算走时,利用了更多的走时信息,计算结果更加接近真实值.彭直兴和沈忠民(2008)给出了一种基于双线性插值计算三维地震波走时的方法,并推导了相应的计算公式.在三维情况下,梅胜全等(2010)对双线性走时插值算法进行了改进,运用判定条件与简化插值计算公式进行快速计算,减少了插值次数,降低了运算量,在保证计算精度的同时明显提升了效率.李培明等(2013)在此基础上引入了动态网格变密度剖分方法,在近场采用加密网格剖分,在远场采用常规网格剖分,以提高近场走时计算精度、减少近场走时误差的累积效应.Zhang等(2011)采用将4个网格顶点分为三组计算分别求取3点插值极小值的折中算法,解决了三维条件下走时插值法求解极小值方程成为超越方程,所造成的不能解析求解的问题.张东等(2013)根据地震初至波路径垂直于波前面的原理,提出基于B样条插值的走时场梯度反向射线追踪方法.该方法通过三次B样条插值得到空间连续的走时场,从而解决了传统三维射线追踪算法由于受到计算区域网格离散化限制所导致的射线路径出现不应有的弯折和射线合并现象.
2.2.2 对射线逆向传播问题的改进LTI算法虽然基于最小走时的Fermat原理,但原始算法在向前处理过程中只按列或行扫描来计算节点走时而没有考虑到地震波逆向传播的情况,使得向后处理过程追踪到的不是最小走时路径,从而降低了射线追踪的精度.为此,张东等(2009)考虑了地震波从各个方向传来的可能性,通过增加计算方向并重复计算,真正得到节点的最小走时,改善了射线精度;由于采用了标记,重复计算时每次插值只考虑走时有变化的边,因而在提高射线追踪精度的同时,也保证了计算效率,该算法能够追踪到逆向传播的射线路径,并且获得精确的节点走时,这将有助于提高反演或层析成像的精度.卢江波(2014)在前人研究的基础上,改进了扩张-收缩扫描算法中逐列扫描的具体计算方法,结合逐列扫描过程中进行交叉扫描的思想,在保留原扩张-收缩算法优点的同时,减少了迭代次数,模型网格划分数较多时,改进算法在计算效率方面的优势尤为突出.叶佩和李庆春(2013)提出在向前处理过程中采用全方位循环的方法考虑来自各个方向的射线,并在网格边界插入次生节点,改进后算法较传统LTI算法对复杂模型具有更强的适应能力,计算精度及计算效率均大幅提升.
线性走时插值射线追踪法是一种具有全局搜索能力且计算效率相对较高的射线追踪方法.该方法算法简单,计算局部走时效率高,能追踪直达波、折射波和透射波的射线路径,适用于速度突变情况,具备解决复杂地表射线追踪问题的潜力.鉴于走时插值算法的突出优点,国内学者对该算法进行了广泛研究,主要集中在以下方面:提出了各种走时非线性假设算法,降低了利用走时线性假设所造成的误差,提高了算法精度;针对射线逆向传播的问题,考虑各个方向地震波的可能性,提出增加计算方向等解决方案,使得算法逐渐完善.对算法今后的研究需要进一步解决射线追踪步长受制于网格尺寸的问题,避免在向后处理中射线路径出现不应有的曲折、兼并等现象.
3 最短路径法最短路径射线追踪方法的算法基础是费马最小走时原理和图论中的最小路径理论.该方法将所要追踪的介质模型离散为一系列规则的矩形单元,并在单元边界上设置若干节点,将各节点通过射线段连接起来,在整个空间形成一个网络图.从震源点出发到接收点的射线路径可以通过网络中节点之间的连线来近似.借鉴网格理论中的最短路径算法可同时求出从震源点传至所有节点的最小走时及射线路径.
3.1 最短路径算法优缺点分析最短路径算法是一种稳健的地震波射线追踪方法,可用于复杂地表条件各向异性介质中初至射线路径的模拟计算(赵后越和张美根,2014),适用于二维、三维地震层析成像.这种方法不受经典射线理论的限制,不存在盲区,可以灵活有效地同时计算介质内所有初至路径和时间,计算一条路径花费的时间和计算所有路径花费的时间相同,尤其适用于共炮点道集(桑运云等,2013).但最短路径方法也存在以下方面的不足.该方法利用节点之间的连线近似地震射线路径,使得波前只能从一个节点到达另一个节点,单元边界上射线的出射角不能随入射角连续变化,射线路径存在不满足斯奈尔定律的可能,且走时的计算误差随着波的传播不断累积,走时计算精度并不优于经典算法,射线路径精度甚至低于传统算法.最短路径法的另一个问题是不能处理低变速区容易出现的射线路径多值现象,使得最终的走时和路径位置出现较大偏差.虽然加大网格剖分密度以及增加子波出射方向可以较好地逼近实际波传播路径,但这需要大量的计算时间和计算机贮存空间,三维网格计算中问题尤为突出.
3.2 射线路径修正方法及对多值现象的改进针对最短路径法存在的不足,国内外学者对其改进算法进行了研究:在国外,Fischer和Lee(1993)利用Snell定律修正追踪得到的锯齿状射线路径,以减小走时误差,并在射线多值点处增加直射线追踪,很好地改善了追踪结果.Klimes和Kvasnicha(1994)对算法的误差来源进行了详细分析,以此优化了子波源的出射方向.Moser等(1992)提出一种混合射线追踪算法,把最短路径法得到的射线路径作为初值,再利用弯曲法对射线路径进行改善.Van Avendonk等(2001)对该混合算法进行研究后,得出混合算法以相对较低的运算成本获得精确射线走时需要满足两个前提.首先,利用最短路径法获取的射线路径必须尽量接近真实解,以便为射线弯曲法提供正确的可行解;其次,在路径没有收敛到稳定解之前迭代过程不能终止,否则射线路径虽然得到改善但仍然接近于初始路径,且走时将大于真实值.前者指出最短路径解需满足较高精度要求,后者要求为射线弯曲提供充足迭代时间.
在国内,张美根等(2006b)基于最短路径算法原理,提出一种以界面离散点为二次源的全局最小走时射线追踪方法,该方法只将子波源点设置在物性分界面上,在均匀块体内或层内地震波以直线传播,子波出射方向数远多于传统最短路方法,在均匀块体内以精确直射线追踪,基本上消除了多值现象和锯齿状射线路径.魏亦文和周竹生(2008)分析了当方向数较多,相邻节点的空间分布规律,利用质因数分解法建立了最短路径射线追踪节点自动搜索函数,解决了在网格密度和有效半径很大的情况下,最短路径追踪节点搜索的难题.王辉和常旭(2000)将计算机图形学中的Bresenham画线算法引入局部走时计算中,从而提高了走时和射线路径的计算精度,并在最小走时节点的查询操作中采用快速排序算法与插入排序算法的结合替代以往常用的堆排序算法,加快了算法的计算速度.张建中等(2003)为克服最短路径射线追踪方法中路径只能从一个节点到达另一个节点的限制,提出了动态网络最短路径射线追踪方法,并应用走时线性插值法和费马原理进行插值,提高了射线追踪的精度.桑运云等(2013)在此基础上,考虑到很多情况下走时的变化是非线性的,推导了抛物走时插值公式,由此提出了基于抛物走时插值的最短路径射线追踪方法.卞爱飞和於文辉(2006)将最短路径法和弯曲法相结合,利用该混合方法克服了射线之字形扭曲的缺陷,提高了追踪结果的精度,在网格稀疏的情况下效果尤其明显.鲁彬等(2009)提出利用经修正的迭代法优化由网络最短路径算法得到的射线路径,与传统方法比较,利用较稀疏的网格节点设置即可达到同等精度要求,减小了所需计算机存储空间并大大提高计算效率,适用于任意复杂介质的初至波的正演数值计算.
3.3 对最短路径法算法精度及运算效率的改善利用最短路径法进行射线追踪,速度模型的离散方式、出射射线的分布形式,以及最小走时节点的排序方式等均会对算法精度及运算效率造成影响.
3.3.1 速度模型节点设置及出射射线分布速度模型的节点设置方式有两种:方式一如图 1a所示,节点设置在单元角点,在各个节点设定波速值,每个节点均可与相邻节点相连接.在二维情况下震源点与子波源点间有16个出射方向,三维条件下,射线出射方向达到26个.这种设置能够为绘制走时和速度等值线图提供方便,更重要的是可以引入速度界面,进行反射波的射线追踪(Moser,1991);方式二是在单元的边界上设置规则节点(不包括单元角点),单元内波速设定为常数,节点间不允许穿过单元边界进行连接.这种模型使两个节点之间的走时计算简单而快速,保证了射线追踪在一个单元内的精确性.在该方式中,节点设置有按照等间距分布和等角度分布(震源与边界节点之间的夹角相等)两种选择(如图 1b所示,设d为网格单元间距,实心圆点为等间距分布节点,其中,a1=a3=0.25d,a2=0.5d;空心圆点为等角度分布节点,其中,b1=b3=0.29289d,b2=0.41421d,α=22.5°).对于折射波的计算,后者要比前者减少50%的误差(Zhang and Toksöz,1998;张美根等,2006a).
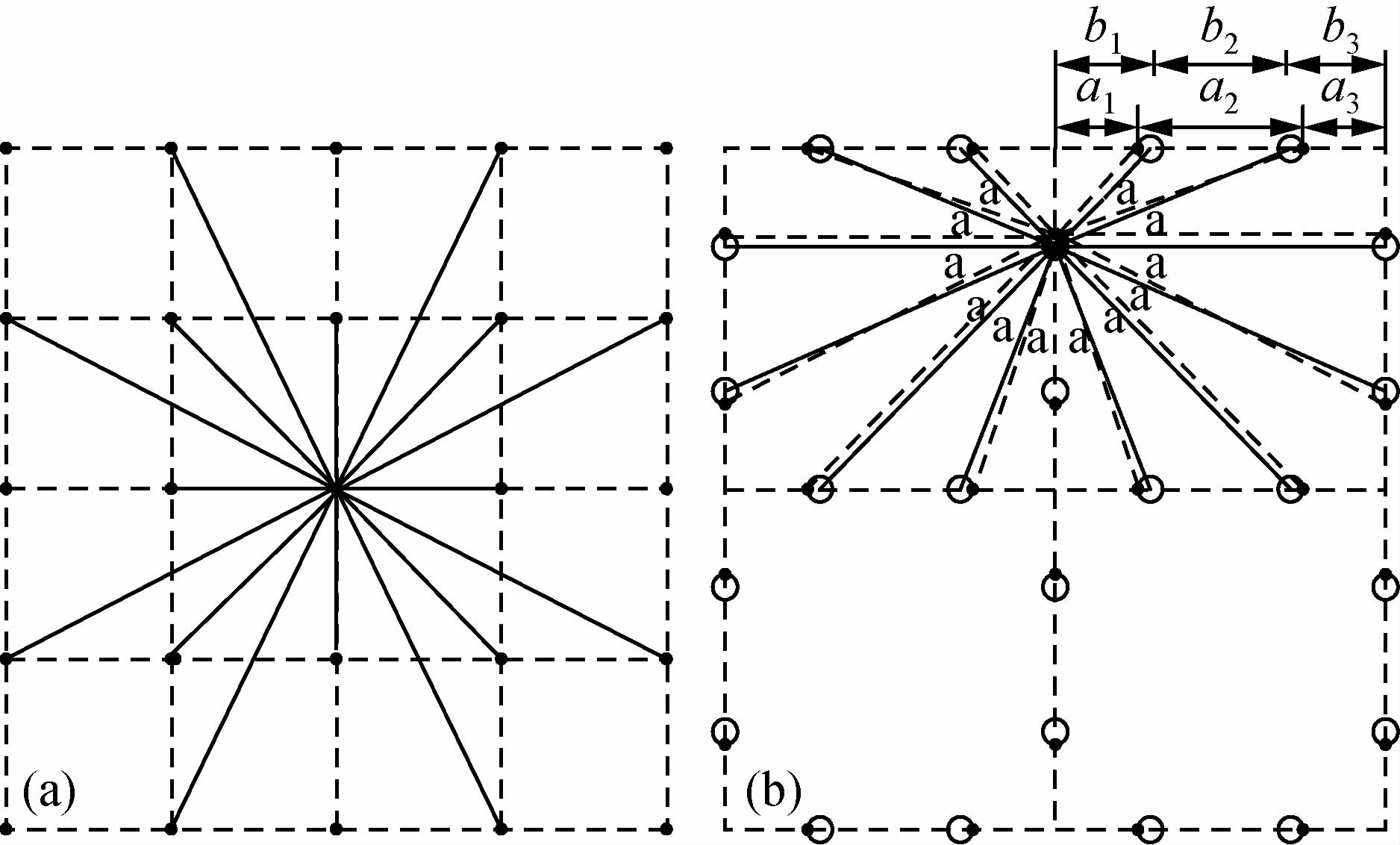 |
图 1 速度模型节点设置方式及射线分布 (a) 节点分布在单元角点,节点上设置波速值;(b) 单元边界设置规则节点,单元内速度均匀. Fig. 1 Nodes and rays distribution (a) Nodes distributed at the grid corner, setting the velocity values on nodes; (b) Regular nodes set on the grid boundary, velocity in the grid is uniform. |
在最短路径算法中,完成离散节点走时计算后,需要进行最小走时节点的选取和删除、更新以及添加,这些操作是最短路径射线追踪中最为耗时的步骤.提高这些操作的效率也成为提高整个算法效率的关键.在国外,Moser(1991)对几种常用的排序方法进行了分析,认为堆排序的处理速度是最快的一种,且在此后的研究和应用中人们也大多采用了这种方法.对多种排序算法进行对比分析后,Ford和Topp(1996)认为,对于无序数列,快速排序算法的平均性能最佳,而对于正序数列,插入排序算法所耗时间可以减到量级,为提高最小走时节点的搜索速度,可综合使用快速排序算法和插入算法.国内学者张美根等(2006a)采用链表实现的桶排序方法管理波前点,并利用斯奈尔定律和来自邻近节点的波动走时信息来限定子波的有效传播方向,排除了大量不必要的子波传播方向,从而使计算速度提高到传统方法的几倍至十几倍.
最短路径射线追踪方法不受射线理论的约束,不需做向前向后处理,能够同时得到震源点到接收点的射线路径及全局最小走时,算法实现不受波速模型的复杂性与空间维度的影响,具有灵活、高效、实用性强的特点.国内外学者通过算法综合、算法引入以及修正射线路径等方法,克服了最短路径射线追踪方法存在的不足,改善了计算效率及运算精度,减少了所需的计算机贮存空间.今后,最短路径法的研究重点还应放在排序算法、计算单元的优化以及计算单元的方向数与模型的节点数之间的最佳匹配问题等方面.
4 波前构建法为了提高射线场发出的整个射线簇的计算效率.Vinje等(1993)基于水平地表条件提出了波前构建法.在该方法中,震源向各个方向发出的射线上具有相同走时的各点构成了该时刻的波前,对一系列波前面上的点按照某一时间步长重复使用局部射线追踪算法,从而得到扩展的波前,如此递推,直到射线将整个区域覆盖.对扩展波前使用局部射线追踪的方法可以同时提供与射线相关的振幅参数及射线走时,具备计算多值走时的潜力,因而被认为是实现Kirchhoff型偏移和反偏移的重要途径.
4.1 波前构建法优越性及存在的问题波前构建法不再局限于传统射线追踪方法只能进行单条射线路径的追踪计算,而是从整个波场中的射线簇出发,求解以时间为自变量的射线方程来计算波前的传播,实现了对成千上万条射线路径及其走时和振幅的同时计算,从而保证了很高的计算效率;此外,对每一个根据时间步长计算得到的波前进行分析,以插值标准为依据,在不满足射线密度要求的区域进行插值,克服了传统射线追踪方法射线覆盖不足的缺陷.波前构建法虽具备上述优点,却在计算机实现上存在一定困难.主要问题表现为两个方面:波前传播计算中非网格节点速度及其导数的插值问题;波前构建法计算所得到的非规则网格节点走时及振幅向规则矩形网格转换的问题.
4.2 对算法精度及运算效率的改善利用波前构建法解决射线追踪问题时,对速度模型进行光滑处理是首要步骤.首先,光滑处理满足了运动学射线追踪对于速度模型具有2阶连续导数的要求,保证了射线追踪的可行性;其次,避免了在速度分界面处应用Snell定律,能够提高射线追踪的计算速度.但对于速度模型的光滑处理,必须兼顾速度模型在波数域内的空间分布、计算速度、计算精度以及光滑次数之间的关系(韩复兴等,2011).常用于光滑处理的方法有两种,分别为改变输入节点值的方法(如采用模型的渐进曲线及卷积类算法)以及在输入节点间采用插值曲线来减小速度梯度的方法.
模型的光滑处理完成后,需要对波前进行初始化,确定初始波前位置及初始射线几何属性所采取的计算方法关系到整个算法的稳定性、精确性及运算效率.通常的做法是假设震源附近是速度分布均匀的介质,在二维条件下,可将初始化区域设为单位圆,在包含震源点在内的单位圆内,以初始发射角及角度间隔进行波前初始化(韩复兴等,2007).然而在三维情况下,这种方法容易造成计算的不稳定以及竖直方向上对球形波前面的过度采样(如图 2a、b所示),造成不必要的运算时间消耗.针对该问题,Lee和Gibson(2007)提出利用立方球面网格确定初始波前的方法,如图 2c、d所示,在以震源点为体心的正方体的每条棱上设置N个节点,在每个面上构成规则网格,震源的初始射线方向对应于正方体体心到各网格节点的矢量方向.采用立方球网格的方法,射线在各个方向上的密度几乎是相同的,不存在过度采样的问题,该方法能够使计算更加稳定,波前网格上的计算更加精准.
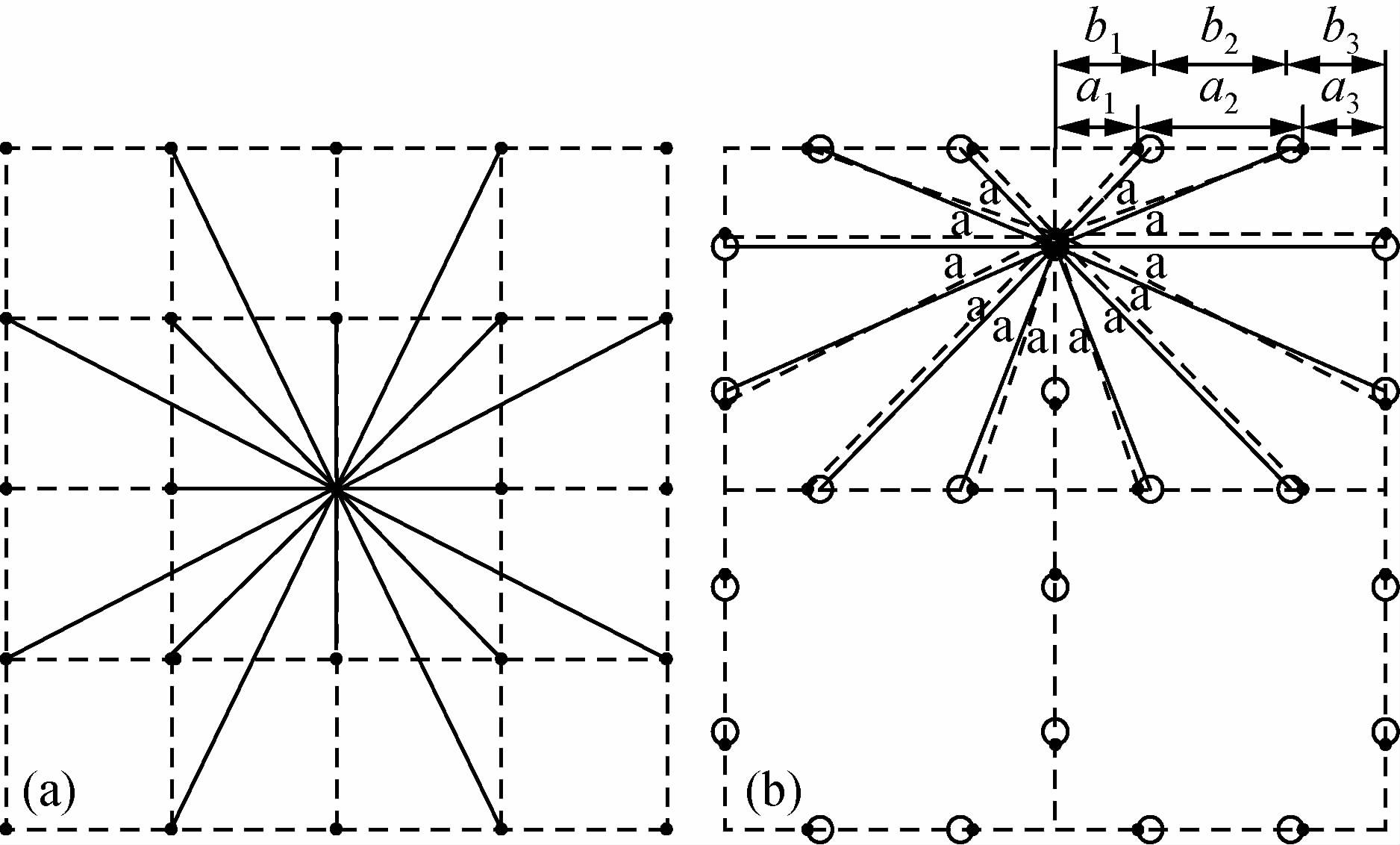 |
图 2 波前初始方法对比图 (a) 初始发射角度示意图,r(ψ,Φ,τ)为初始射线矢量;(b) 各向同性均匀介质中的初始射线法波前面网格图,射线从震源点经网格交点出射,在球面波前的两极射线密度较高;(c) 立方球面网格射线坐标示意图,r(xc,yc,τ)为射线方向矢量;(d) 各向同性均匀介质中立方球面波前网格图,射线从震源点经网格交点出射,射线密度较(b)图更加均匀(Lee and Gibson,2007). Fig. 2 The comparison for wave-front initialization method (a) Illustration of the takeoff-angle coordinates, r(ψ,Φ,τ) represents the takeoff-angle vector; (b) Example of a takeoff-angle wave-front mesh in a homogeneous, isotropic medium, a ray will be traced through each intersection point in the mesh, there is a very ray density near the poles; (c) Illustration of the cube-sphere mesh coordinates, r(xc,yc,τ) represents the ray orientation vector; (d) Example of a cube-sphere wave-front mesh in a homogeneous, isotropic medium, a ray will be traced through each intersection point in the mesh, ray density uniform compared to the takeoff-angle method(Lee and Gibson,2007). |
在初始波前给定的条件下,经典运动学射线方程组转化为常微分方程组,利用数值计算的方法获得其数值解的过程即为波前传播计算.在算法形成之初,Vinje等(1993,1996)先后采用二阶及四阶泰勒展开的方法求解常微分方程.二阶泰勒展开的方法只能满足二阶近似,精度不高,而四阶泰勒展开虽能满足精度要求,但由于需要计算大量高阶导数,计算效率受到一定影响.综合考虑算法对计算精度和速度的影响,Ettrich和Gajewski(1996)采用4阶的龙格一库塔(Runge-Kutta)法来求解射线追踪方程组.该算法采用低阶导数的线性组合逼近高阶导数,避免了高阶导数的求解,使计算精度达到,因而得到了普遍应用.由于波前随着时间不断传播和扩散,射线逐渐分散,波前两个相邻节点之间的距离不断扩大,为保证射线在研究区域的覆盖率须按照插值标准进行新射线的插值(韩复兴等,2011).
利用Runge-Kutta法以时间为步长进行波前传播计算,需要知道模型中对应于每一个时间步长处点的速度及其导数的值,因此,需要选择一种有效的插值算法对模型中任意点的速度及其导数值进行计算,计算结果的准确性直接关系到射线路径以及走时的精确性.韩复兴等(2011)对几种常用的插值算法进行了对比分析得出,使用二维三次卷积插值,不但能够提高射线路径的准确度及射线追踪的效率,并且可以为下一步做偏移成像提供精确的数据.为克服波前构建法射线追踪在波前路径计算实现方面存在的困难,韩复兴等(2007)提出一种基于C++语言的实现方法,避免了由于射线插值和网格变换所造成的数据重排和标记等问题,简化了计算.
利用波前构建法进行射线追踪得到的数据分布在波前不规则的四边形上,而在层析成像、偏移成像等领域通常采用规则网格数据.因此,将波前构建法应用于层析成像或偏移成像过程,必须进行不规则波前四边形网格数据向规则网格数据的转化.针对该问题,Vinje等(1993)采用在波前面上插入虚拟震源的方法,从虚拟震源点向需要计算的规则网格节点进行射线追踪,以获得规则网格节点数据.然而,虚拟震源点到规则网格节点之间的距离计算会造成大量的时间消耗,严重影响算法运算效率.Ettrich和Gajewski(1996)在前人研究的基础上,提出了利用矢量叉乘结果对规则网格节点与波前不规则四边形的相对位置进行判断,并采用距离权重插值及走时外推的方法计算规则网格节点处的属性的算法,在准确性及运算效率方面都有很大程度的提高.
4.3 多值射线路径追踪及三维复杂结构下的研究地震波传播过程中,当遇到低速异常体或弯曲界面时,波前将会出现自相缠绕的现象,造成检波器不仅能够记录到初至波还能记录到后续波.后续波的传播路径不遵循费马最小走时原理,因而能够穿过低速异常区或对弯曲界面采样,携带了低速异常区或弯曲界面的宝贵信息,对复杂速度结构及速度界面的重建至关重要.波前构建法可适用于复杂反射界面的处理,能够同时考虑射线路径走时以及与多路径问题相关的振幅参数,在多值走时方面已有应用.张钋等(2000b)基于波前构建的思路,将波前构建法推广到三维,针对三维复杂地质模型中的多值走时情况,提出一种在相空间拉格朗日流形上的波场重建及格林函数的高效计算方法.王庆林和白超英(2013)则在相空间方法基础上,对波前构建法进行了改进,其中包括反射界面处理过程中采用连续波前映射法和射线追踪过程中采用检波器精确定位算法等.
为实现三维复杂构造条件下走时和射线路径的准确快速计算,孙小东等(2007)利用了四面体网格化模型对复杂模型做精细描述方面的优势,将其与波前构建法结合,在处理三维射线追踪方面得到了满意的效果.李波涛等(2009)利用三角形网格剖分可以对波前面进行精细描述且无需大量网格数目的优势,将其与三维波前重建法射线追踪技术结合应用,实现了射线路径和走时的准确快速计算.该方法在三维复杂构造成像方面有独特优势,目前在实际的Kirchhoff偏移中已经有相关应用.
波前构建法提高了射线在研究区的覆盖率,可以同时计算路径走时及振幅参数,具备计算多值走时的潜力,而且不受观测系统的限制,能够适应较为复杂的速度模型.自该算法提出以来,得到众多学者的广泛研究,并在三维复杂地质模型的射线追踪及各项异性介质的数值模拟和速度分析中得到应用.对于波前构建法而言,需要深入研究的问题主要是以下三个方面:模型光滑处理对于地震波走时、射线路径以及振幅信息带来的影响;在模型界面处应用斯奈尔定律,以实现反射波和透射波同时计算的问题;处理复杂模型运算时遇到的焦散问题.
5 总结和展望地震波射线追踪方法是一种快速有效的波场模拟方法,在研究地下介质速度分布和地层中地震波传播问题等方面得到了广泛应用.随着层析成像,叠前偏移成像等技术在工程、能源和矿产等资源勘探领域的深入应用研究,射线追踪方法也将具有更大的发展空间.以上分别对有限差分法、走时插值法、最短路径法及波前扩展法在算法原理、算法不足、改进方法、计算精度及运算效率等方面进行了讨论,下面对射线追踪方法的未来发展方向进行分析.
(1)引入动力学参数
射线追踪的理论基础是:在无限高频近似条件下,地震波场的主要能量沿射线轨迹传播.事实上,地震波的频率是有限的.将动力学参数——波的频率引入到射线追踪中,将会减小当波穿过的异常体大小和菲涅尔带相当时,将波的传播路径近似为射线给走时计算带来的误差.把射线和波场联系起来,能够充分发挥波场信息全面和几何射线计算简便的优点.
(2)多次波射线路径追踪
多次波同一次反射波一样,包含着地下界面的信息,在复杂地下构造情况下,利用多次波甚至能够获得更好的成像效果.在以往的地震勘探中,多次波通常被视为干扰波.但随着地震勘探向精细化描述方向研究的深入,多次波射线追踪、多次波成像问题得到了越来越多的重视.目前,射线追踪已由过去简单的单一震相(如:初至波、反射波或折射波)发展到多次(反射、折射、及转换)波的射线追踪.二维及三维层状介质中多次波的射线追踪已经实现,对于块状模型的多次波追踪具有一定难度,需进一步进行算法探究.
(3)多值射线路径追踪
由地震波速的连续(或不连续)变化,或速度界面的不规则起伏变化所导致的两点间射线路径不止一条的现象(即多值射线路径问题)更符合地震记录波形的复杂性,并随着勘探难度和深度的增加得到了更多的讨论和重视.现有用于解决多值路径问题的算法,均采用向前—向后的处理办法,先完成走时场的计算,然后获得相应射线路径,效率不高.对可同时计算走时场和相应射线路径的算法的开发,能够提高多值射线追踪的有效性及实用性.
(4)适用于复杂地质模型的射线追踪方法研究
对复杂地质模型描述方法及高效求取射线路径、射线走时算法的探究,符合地震勘探目标区域逐渐由简单地表条件向复杂地表区域转移的趋势.随着我国能源需求量的不断增大及油气勘探的逐步深入,西部沙漠、山地、高原及丘陵地区的地震勘探工作已然展开.将地质模型描述由传统规则网格发展到非规则网格和规则网格混合,以及发展考虑起伏地表和地震各项异性的射线追踪方法,对复杂地质勘探区域地震正演模拟、走时层析成像、偏移成像等正反演研究具有重要理论意义和实际应用价值.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Asakawa E, Kawanaka T. 1993. Seismic ray tracing using linear travel-time interpolation[J]. Geophysical Prospecting, 41(1):99-111, doi:10.1111/j.1365-2478.1993.tb00567.x. |
| [2] | Bian A F, Yu W H. 2006. 3-D shortest path method of ray tracing and its improvement[J]. Natural Gas Industry(in Chinese), 26(5):43-45. |
| [3] | Ettrich N, Gajewski D. 1996. Wave front construction in smooth media for pre-stack depth migration[J]. Pure and Applied Geophysics, 148(3-4):481-502. |
| [4] | Fischer R, Lees J M. 1993. Shortest path ray tracing with sparse graphs[J]. Geophysics, 58(7):987-996. |
| [5] | Ford W, Topp W. 1996. Data Structures with C++[M]. Englewood Cliffs, New Jersey:Prentice Hall, Inc. |
| [6] | Han F X, Sun J G, Sun Z Q. 2011. Research status of the wave-front construction method[J]. Progress in Geophysics(in Chinese), 26(3):1045-1051, doi:10.3969/j.issn.1004-2903.201103033. |
| [7] | Han F X, Sun J G, Yang H. 2007. Ray tracing by implementing C+ + language-based wavefront construction approach[J]. Oil Geophysical Prospecting(in Chinese), 42(4):474-481. |
| [8] | Han F X, Sun J G, Yang H. 2008. Ray-tracing of wavefront construction by Bicubic convolution interpolation[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 38(2):336-340. |
| [9] | He R, Yang J S, Zhang Y. 2007. A review on the technology of seismic tomography[J]. CT Theory and Applications(in Chinese), 16(1):35-48. |
| [10] | Huang L J, Li Y M, Wu R S. 1992. The wave-front ray tracing method for image reconstruction[J]. Acta Geophysica Sinica(in Chinese), 35(2):223-233. |
| [11] | Huang Y J, Zhu G M, Guo M. 2010. Direct wave travel time linear interpolation algorithm[J]. Oil Geophysical Prospecting(in Chinese), 45(2):225-229. |
| [12] | Julian B R, Gubbins D. 1977. Three-dimensional seismic ray tracing[J]. Journal of Geophysics, 43(1):95-113. |
| [13] | Klimes L, Kvasnicha M. 1994. 3-D network ray tracing[J]. Geophysical Journal International, 116(3):726-738. |
| [14] | Lee K L, Gibson R L. 2007. An improved mesh generation scheme for the wave-front construction method[J]. Geophysics, 72(1):T1-T8, doi:10.1190/1.2399366. |
| [15] | Lei D, Hu X Y. 2006. Review of Seismic Tomography Methods[J]. Journal of Seismological Research(in Chinese), 29(4):418-426. |
| [16] | Leidenfrost A, Ettrich N, Gajewski D, et al. 1999. Comparison of six different methods for calculating traveltimes[J]. Geophysical Prospecting, 47(3):269-297, doi:10.1046/j1365-2478.1999.00124.x. |
| [17] | Li B T, Yang C C, Chen Y H, et al. 2009. 3-D wavefront construction method ray tracing based on triangular grids layout on wavefront[J]. Progress in Geophysics(in Chinese), 24(2):507-512, doi:10.3969/j.issn.1004-2903.200902019. |
| [18] | Li F, Xu T, Wu Z B, et al. 2013. Segmentally iterative ray tracing in 3-D heterogeneous geological models[J]. Chinese Journal of Geophysics(in Chinese), 56(10):3514-3522, doi:10.6038/cig20131026. |
| [19] | Li P M, Mei S Q, Ma Q P. 2013. An improved bilinear interpolation travel-time ray-tracing method[J]. Oil Geophysical Prospecting(in Chinese), 48(4):553-558. |
| [20] | Li Q, Bai C Y. 2012. Review on seismic wave-front and ray tracing in complex media[J]. Progress in Geophysical(in Chinese), 27(1):92-104, doi:10.6038/j.issn.1004-2903.201201011. |
| [21] | Li W J, Wei X C, Ning J R, et al. 2008. A method using improved eikonal equation to compute travel time[J]. Oil Geophysical Prospecting(in Chinese), 43(5):589-594. |
| [22] | Li X F, Li X F, Zhang M G. 2007. Review of seismic wave numerical modeling methods[J]. Journal of Disaster Prevention and Mitigation Engineering(in Chinese), 27(2):241-248. |
| [23] | Liu H, Meng F L, Li Y M. 1995. The interface grid method for seeking global minimum travel-time and the correspondent raypath[J]. Acta Geophysica Sinica(in Chinese), 38(6):823-832. |
| [24] | Liu L J, Xie Z H, Yang C. 2014. Ray tracing algorithm based on boundary linear travel-time interpolation[J]. Journal of South China University of Technology(Natural Science Edition)(in Chinese), 42(5):23-28, 35, doi:10.3969/j.issn.1000-565X.201405004. |
| [25] | Liu Y, Wang X M, Hu X Y. 2014. Analysis of seismic reflection tomography[J]. Chinese Journal of Engineering Geophysics(in Chinese), 11(2):208-217, doi:10.3969/j.issn.1672-7940.201402014. |
| [26] | Lu B, Zhou L F, Kong X W, et al. 2009. A method of shortest path raytracing by iterative optimization[J]. Progress in Geophysics(in Chinese), 24(4):1420-1425, doi:10.3969/j.issn.1004-2903.200904033. |
| [27] | Lu J B, Fang Z. 2014. Improvement of ray tracing algorithm based on linear traveltime interpolation[J]. Journal of Hunan University(Natural Sciences)(in Chinese), 41(1):39-44. |
| [28] | Mei S Q, Deng F, Zhong B S, et al. 2010. The 3D ray tracing method base on the improved bilinear traveltime interpolation[J]. Computing Techniques for Geophysical and Geochemical Exploration(in Chinese), 32(2):152-157. |
| [29] | Moser T J. 1991. Shortest path calculation of seismic rays[J]. Geophysics, 56(1):59-67. |
| [30] | Moser T J, van Eck T, Nolet G. 1992. Hypocenter determination in strongly heterogeneous earth models using the shortest path method[J]. Journal of Geophysical Research, 97(B5):6563-6572, doi:10.1029/91JB03176. |
| [31] | Nie J X, Yang H Z. 2003. Quadratic/linear travel time interpolation of seismic ray-tracing[J]. Journal of Tsinghua University(Science and Technology)(in Chinese), 43(11):1495-1498. |
| [32] | Peng Z X, Shen Z M. 2008. Computation of three-dimensional seismic travel-time based on bilinear interpolation[J]. Journal of Southwest Petroleum University(Science & Technology Edition)(in Chinese), 30(5):85-87, 92, doi:10.3863/j.issn.1000-2634. 200805018. |
| [33] | Podvin P, Lecomte I. 1991. Finite difference computation of traveltimes in very contrasted velocity models:a massively parallel approach and its associated tools[J]. Geophysical Journal International, 105(1):271-284. |
| [34] | Qin F H, Luo Y, Olsen Kim B, et al. 1992. Finite-difference solution of the eikonal equation along expanding wavefronts[J]. Geophysics, 57(3):478-487. |
| [35] | Sang Y Y, Li Z C, Zhang K. 2013. Shortest path ray tracing based on parabolic travel-time interpolation[J]. Oil Geophysical Prospecting(in Chinese), 48(3):403-409. |
| [36] | Sethian J A, Popovici A M. 1999. 3-D traveltime computation using the fast marching method[J]. Geophysics, 64(2):516-523. |
| [37] | Sun J G, Yang H, Han F X. 2007. A finite-difference scheme for solving the eikonal equation with varying grid spacing[C].//77th SEG Technical Program Expanded Abstracts. San Antonio:SEG, 2120-2124. |
| [38] | Sun Z Q, Sun J G, Han F X. 2009. Traveltimes computation using linear interpolation and narrow band technique under complex topographical conditions[J]. Chinese Journal of Geophysics(in Chinese), 52(11):2846-2853, doi:10.3969/j.issn.0001-5733.200911019. |
| [39] | Sun Z Q, Sun J G, Han F X. 2012a. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3-D undulating surface condition[J]. Chinese Journal of Geophysics(in Chinese), 55(7):2441-2449, doi:10.6038/j. issn.0001-5733.201207028. |
| [40] | Sun Z Q, Sun J G, Han F X. 2012b. The comparison of three schemes for computing seismic wave traveltimes in complex topographical conditions[J]. Chinese Journal of Geophysics(in Chinese), 55(2):560-568, doi:10.6038/j.issn.0001-5733.201202018. |
| [41] | Tang X P, Bai C Y, Liu K H. 2011. Multivalued and multiple reflected ray tracing with extreme value based on the multistage modified shortest-path method[J]. Progress in Geophysics(in Chinese), 26(6):2064-2074, doi:10.3969/j.issn.1004-2903.201106022. |
| [42] | Van Avendonk H J A, Harding A J, Orcutt J A, et al. 2001. Hybrid shortest path and ray bending method for traveltime and ray path calculations[J]. Geophysics, 66(2):648-653. |
| [43] | Van Trier J, Symes W W. 1991. Upwind finite-difference calculation of travel-times[J]. Geophysics, 56(6):812-821. |
| [44] | Vidale J E. 1988. Finite-difference calculations of travel times[J]. Bulletin of Seismological Society of America, 78(6):2062-2076. |
| [45] | Vidale J E. 1990. Finite-difference calculation of travel-times in three dimensions[J]. Geophysics, 55(5):521-526. |
| [46] | Vinje V, Iversen E, Gjøystadal H. 1993. Traveltime and amplitude estimation using wavefront construction[J]. Geophysics, 58(8):1157-1166, doi:10.1190/1.1443499. |
| [47] | Vinje V, Iversen E, Åstebøl K, et al. 1996. Estimation of multivalued arrivals in 3D models using wavefront construction-Part I[J]. Geophysical Prospecting, 44(5):819-842. |
| [48] | Wang H, Chang X. 2000. 3-D Ray tracing method based on graphic structure[J]. Chinese Journal of Geophysics(in Chinese), 43(4):534-541. |
| [49] | Wang Q L, Bai C Y. 2013. Multi-valued ray tracing based on a modified wavefront construction method in phase space[J]. Oil Geophysical Prospecting(in Chinese), 48(1):15-21. |
| [50] | Wei Y W, Zhou Z S. 2008. A node auto-finding function based on decomposition of the prime-factor number in shortest path ray tracing[J]. Computing Techniques for Geophysical and Geochemical Exploration(in Chinese), 30(3):191-196. |
| [51] | Xiong X J, He Z H, Huang D J. 2006. Study on numerical simulation method of the seismic wave field with complex surface conditions[J]. Journal of Xi'an Shiyou University(Natural Science Edition)(in Chinese), 21(6):5-7. |
| [52] | Yang H, Sun J G, Han F X. 2007. An C++ language program implement of traveltime calculation of expending wavefronts finite-difference method[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 37(3):615-619. |
| [53] | Yang H, Sun J G, Han F X, et al. 2010. Fast algorithm of the expanding wavefronts finite-difference traveltime calculation based on the three branch tree structure heap sorts[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 40(1):188-194. |
| [54] | Yang L S, Wang S Y, Liu C, et al. 2006. Ray tomography static correction[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 36(S2):49-54. |
| [55] | Ye P, Li Q C. 2013. Improvements of linear traveltime interpolation ray tracing for the accuracy and efficiency[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 43(1):291-298. |
| [56] | Zhang D, Xie B L, Yang Y, et al. 2009. A ray tracing method based on improved linear travel time interpolation[J]. Chinese Journal of Geophysics(in Chinese), 52(1):200-205. |
| [57] | Zhang D, Zhang T T, Qiao Y F, et al. 2013. A 3-D ray tracing method based on B-spline travel time interpolation[J]. Oil Geophysical Prospecting(in Chinese), 48(4):559-566. |
| [58] | Zhang J, Toksoz N M. 1998. Nonlinear refraction traveltime tomography[J]. Geophysics, 63(5):1726-1737, doi:10.1190/1.444468. |
| [59] | Zhang J Z, Chen S J, Yu D X. 2003. Improvement of shortest path ray tracing method[J]. Progress in Geophysics(in Chinese), 18(1):146-150, doi:10.3321/j.issn:0001-5733.2004.05.023. |
| [60] | Zhang J Z, Chen S J. 2003. Numerical modeling of seismic first break in complex media[J]. Chinese Journal of Computational Physics(in Chinese), 20(5):429-433. |
| [61] | Zhang J Z, Chen S J, Xu C W. 2004. A method of shortest path ray-tracing with dynamic networks[J]. Chinese Journal of Geophysics(in Chinese), 47(5):899-904, doi:10.3321/j.issn:0001-5733.2004.05.023. |
| [62] | Zhang L, Liu J S. 2005. Advance and development in seismic tomography-highlights of AGU 2004 fall meeting[J]. Progress in Geophysics(in Chinese), 20(3):600-610, doi:10.3969/j.issn.1004-2903.2005.03.004. |
| [63] | Zhang L B, Liu Y X, Zhao Z F, et al. 1993. Finite-difference ray tracing[J]. Oil Geophysical Prospecting(in Chinese), 28(6):673-677, 684. |
| [64] | Zhang M G, Cheng B J, Li X F, et al. 2006a. A fast algorithm of shortest path ray tracing[J]. Chinese Journal of Geophysics(in Chinese), 49(5):1467-1474, doi:10.3321/j.issn:0001-5733.2006.05.026. |
| [65] | Zhang M G, Jia Y G, Wang M Y, et al. 2006b. A global minimum travel time ray tracing algorithm of wave-front expanding with interface points as secondary sources[J]. Chinese Journal of Geophysics(in Chinese), 49(4):1169-1175, doi:10.3321/j.issn:0001-5733.2006.04.032. |
| [66] | Zhang P, Liu H, Li Y M. 2000a. The situation and progress of ray tracing method research[J]. Progress in Geophysics(in Chinese), 15(1):36-45, doi:10.3969/j.issn.1004-2903.2000.01.002. |
| [67] | Zhang P, Yang C C, Li Y M. 2000b. 3-D multi-valued seismic wavefield reconstruction and Green's function computation[J]. Chinese Journal of Geophysics(in Chinese), 43(2):241-250, doi:10.3321/j.issn:0001-5733.2000.02.012. |
| [68] | Zhang S M, Zhou Z S, Chen L J, et al. 2007. Seismic ray tracing method of applying parabolic interpolation to travel time[J]. Progress in Geophysics(in Chinese), 22(1):43-48, doi:10.3969/j.issn.1004-2903.2007.01.005. |
| [69] | Zhao H Y, Zhang M G. 2014. Tracing seismic shortest path rays in anisotropic medium with rolling surface[J]. Chinese Journal of Geophysics(in Chinese), 57(9):2910-2917, doi:10. 6038/jcg20140916. |
| [70] | Zhu J M, Wang L Y. 1992. Finite difference calculation of seismic travel times[J]. Acta Geophysica Sinica(in Chinese), 35(1):86-92. |
| [71] | 卞爱飞, 於文辉. 2006. 三维最短路径法射线追踪及改进[J]. 天然气工业, 26(5):43-45. |
| [72] | 韩复兴, 孙建国, 杨昊. 2007. 基于C++语言实现波前构建射线追踪[J]. 石油地球物理勘探, 42(4):474-481. |
| [73] | 韩复兴, 孙建国, 杨昊. 2008. 基于二维三次卷积插值算法的波前构建射线追踪[J]. 吉林大学学报(地球科学版), 38(2):336-340. |
| [74] | 韩复兴, 孙建国, 孙章庆. 2011. 波前构建法研究现状[J]. 地球物理学进展, 26(3):1045-1051, doi:10.3969/j.issn.1004-2903.201103033. |
| [75] | 和锐, 杨建思, 张翼. 2007. 地震层析成像方法综述[J]. CT理论与应用研究, 16(1):35-48. |
| [76] | 黄联捷, 李幼铭, 吴如山. 1992. 用于图像重建的波前法射线追踪[J]. 地球物理学报, 35(2):223-233. |
| [77] | 黄翼坚, 朱光明, 敦敏. 2010. 直达波走时线性插值算法[J]. 石油地球物理勘探, 45(2):225-229. |
| [78] | 雷栋, 胡祥云. 2006. 地震层析成像方法综述[J]. 地震研究, 29(4):418-426. |
| [79] | 李波涛, 杨长春, 陈雨红,等. 2009. 基于波前面三角形网格剖分的波前重建法三维射线追踪[J]. 地球物理学进展, 24(2):507-512, doi:10.3969/j.issn.1004-2903.200902019. |
| [80] | 李飞, 徐涛, 武振波,等. 2013. 三维非均匀地质模型中的逐段迭代射线追踪[J]. 地球物理学报, 56(10):3514-3522, doi:10.6038/cig20131026. |
| [81] | 李培明, 梅胜全, 马青坡. 2013. 一种改进的双线性插值射线追踪方法[J]. 石油地球物理勘探, 48(4):553-558. |
| [82] | 李强, 白超英. 2012. 复杂介质中地震波前及射线追踪综述[J]. 地球物理学进展, 27(1):92-104, doi:10.6038/j.issn.1004-2903.201201011. |
| [83] | 李文杰, 魏修成, 宁俊瑞,等. 2008. 一种改进的利用程函方程计算走时的方法[J]. 石油地球物理勘探, 43(5):589-594. |
| [84] | 李信富, 李小凡, 张美根. 2007. 地震波数值模拟方法研究综述[J]. 防灾减灾工程学报, 27(2):241-248. |
| [85] | 刘洪, 孟凡林, 李幼铭. 1995. 计算最小走时和射线路径的界面网全局方法[J]. 地球物理学报, 38(6):823-832. |
| [86] | 刘玲君, 谢中华, 杨萃. 2014. 基于边界线性走时插值的射线追踪算法[J]. 华南理工大学学报(自然科学版), 42(5):23-28, 35, doi:10.3969/j.issn.1000-565X.201405004. |
| [87] | 刘玉, 王贤敏, 胡祥玉. 2014. 反射地震层析成像的现状分析[J]. 工程地球物理学报, 11(2):208-217, doi:10.3969/j.issn.1672-7940.201402014. |
| [88] | 鲁彬, 周立发, 孔省吾,等. 2009. 迭代优化的网络最短路径射线追踪方法研究[J]. 地球物理学进展, 24(4):1420-1425, doi:10.3969/j.issn.1004-2903.200904033. |
| [89] | 卢江波, 方志. 2014. 线性走时插值射线追踪算法的改进[J]. 湖南大学学报(自然科学版), 41(1):39-44. |
| [90] | 梅胜全, 邓飞, 钟本善,等. 2010. 基于改进的双线性走时插值的三维射线追踪[J]. 物探化探计算技术, 32(2):152-157. |
| [91] | 聂建新, 杨慧珠. 2003. 地震波走时二次/线性联合插值法[J]. 清华大学学报(自然科学版), 43(11):1495-1498. |
| [92] | 彭直兴, 沈忠民. 2008. 基于双线性插值的三维地震波走时计算[J]. 西南石油大学学报(自然科学版), 30(5):85-87, 92, doi:10.3863/j.issn.1000-2634.200805018. |
| [93] | 桑运云, 李振春, 张凯. 2013. 抛物走时插值最短路径射线追踪[J]. 石油地球物理勘探, 48(3):403-409. |
| [94] | 孙小东, 李振春, 栗宝鹃,等. 2007. 波前构建法三维射线追踪[J]. 天然气工业, 27(增刊A):75-277. |
| [95] | 孙章庆, 孙建国, 韩复兴. 2009. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算[J]. 地球物理学报, 52(11):2846-2853, doi:10.3969/j.issn.0001-5733.200911019. |
| [96] | 孙章庆, 孙建国, 韩复兴. 2012a. 三维起伏地表条件下地震波走时计算的不等距迎风差分法[J]. 地球物理学报, 55(7):2441-2449, doi:10.6038/j.issn.0001-5733.201207028. |
| [97] | 孙章庆, 孙建国, 韩复兴. 2012b. 针对复杂地形的三种地震波走时算法及对比[J]. 地球物理学报, 55(2):560-568, doi:10.6038/j.issn.0001-5733.201202018. |
| [98] | 唐小平, 白超英, 刘宽厚. 2011. 分区多步最短路径极值法多值多次反射波追踪[J]. 地球物理学进展, 26(6):2064-2074, doi:10.3969/j.issn.1004-2903.201106022. |
| [99] | 王辉, 常旭. 2000. 基于图形结构的三维射线追踪方法[J]. 地球物理学报, 43(4):534-541. |
| [100] | 王庆林, 白超英. 2013. 相空间波前构造法地震多值射线追踪的改进[J]. 石油地球物理勘探, 48(1):15-21. |
| [101] | 魏亦文, 周竹生. 2008. 一种基于质因数分解法的最短路径射线追踪节点自动搜索函数[J]. 物探化探计算技术, 30(3):191-196. |
| [102] | 熊晓军, 贺振华, 黄德济. 2006. 复杂地表条件下的地震波场模拟方法研究[J]. 西安石油大学学报(自然科学版), 21(6):5-7. |
| [103] | 杨兰锁, 王世煜, 刘财,等. 2006. 射线层析静校正[J]. 吉林大学学报(地球科学版), 36(S2):49-54. |
| [104] | 杨文采. 1993. 应用地震层析成像[M]. 北京:地质出版社. |
| [105] | 杨昊, 孙建国, 韩复兴. 2007. 波前扩展有限差分地震波走时算法的C++语言描述[J]. 吉林大学学报(地球科学版), 37(3):615-619. |
| [106] | 杨昊, 孙建国, 韩复兴,等. 2010. 基于完全三叉树堆排序的波前扩展有限差分地震波走时快速算法[J]. 吉林大学学报(地球科学版), 40(1):188-194. |
| [107] | 叶佩, 李庆春. 2013. 走时线性插值射线追踪提高计算精度和效率 的改进方法[J]. 吉林大学学报(地球科学版), 43(1):291-298. |
| [108] | 张东, 谢宝莲, 杨艳,等. 2009. 一种改进的线性走时插值射线追踪算法[J]. 地球物理学报, 52(1):200-205. |
| [109] | 张东, 张婷婷, 乔友锋,等. 2013. 三维走时场B样条插值射线追踪方法[J]. 石油地球物理勘探, 48(4):559-566. |
| [110] | 张建中, 陈世军. 2003. 复杂介质地震初至波数值模拟[J]. 计算物理, 20(5):429-433. |
| [111] | 张建中, 陈世军, 余大祥. 2003. 最短路径射线追踪方法及其改进[J]. 地球物理学进展, 18(1):146-150, doi:10.3321/j.issn:0001-5733.2004.05.023. |
| [112] | 张建中, 陈世军, 徐初伟. 2004. 动态网络最短路径射线追踪[J]. 地球物理学报, 47(5):899-904, doi:10.3321/j.issn:0001-5733.2004.05.023. |
| [113] | 张岭, 刘劲松. 2005. 从AGU2004秋季年会看地震层析成像的进展[J]. 地球物理学进展, 20(3):600-610, doi:10.3969/j.issn.1004-2903.2005.03.004. |
| [114] | 张霖斌, 刘迎曦, 赵振峰,等. 1993. 有限差分法射线追踪[J]. 石油地球物理勘探, 28(6):673-677, 684. |
| [115] | 张美根, 程冰洁, 李小凡,等. 2006a. 一种最短路径射线追踪的快速算法[J]. 地球物理学报, 49(5):1467-1474, doi:10.3321/j.issn:0001-5733.2006.05.026. |
| [116] | 张美根, 贾豫葛, 王妙月,等. 2006b. 界面二次源波前扩展法全局最小走时射线追踪技术[J]. 地球物理学报, 49(4):1169-1175, doi:10.3321/j.issn:0001-5733.2006.04.032. |
| [117] | 张赛民, 周竹生, 陈灵君,等. 2007. 对走时进行抛物型插值的地震射线追踪方法[J]. 地球物理学进展, 22(1):43-48, doi:10.3969/j.issn.1004-2903.2007.01.005. |
| [118] | 张钋, 刘洪, 李幼铭. 2000a. 射线追踪方法的发展现状[J]. 地球物理学进展, 15(1):36-45, doi:10.3969/j.issn.1004-2903.2000.01.002. |
| [119] | 张钋, 杨长春, 李幼铭. 2000b. 三维多值走时地震波场重建及格林函数计算[J]. 地球物理学报, 45(2):241-250, doi:10.3321/j.issn:0001-5733.2000.02.012. |
| [120] | 赵后越, 张美根. 2014. 起伏地表条件下各向异性地震波最短路径射线追踪[J]. 地球物理学报, 57(9):2910-2917, doi:10.6038/cjg20140916. |
| [121] | 朱金明, 王丽燕. 1992. 地震波走时的有限差分法计算[J]. 地球物理学报, 35(1):86-92. |
 2016, Vol. 31
2016, Vol. 31

