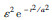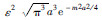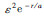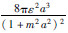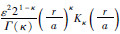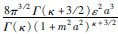随着地震勘探方法的不断发展,传统的反射波勘探技术正面临着巨大的挑战,尤其当地下的构造异常复杂且存在着孔、洞、缝等小尺度的非均匀构造时,常规的反射波理论及均匀层状介质模型受到了限制.因此,针对非均匀介质的散射波理论更具有普适性.
地震波散射理论包含的内容很多.广义上,地震波散射可看作是地下任意的三维非均匀介质产生的波场变化,狭义上通常将小尺度非均匀性引起的地震波走时及振幅差异定义为地震波的散射.研究也表明,实际的地球介质存在着普遍的横向非均匀性,这种非均匀性的范围可划分为8个尺度级,吴如山等曾对此作了详细的描述(吴如山等,1989).不同尺度的非均匀体引起的波场变化也不同.在矿产勘探领域,非均匀性的存在表明地下蕴藏着更多的地质现象及油气资源.为此,国内外学者曾深入地研究了地震波的散射理论及各种技术方法.到目前为止,地震波散射的研究成果比较成熟,其理论已经被广泛的应用到地球物理勘探的各个方面,如尾波模拟、短周期地震波的散射衰减研究、散射场模拟、层析成像、地震波反演等.
尽管上述理论及方法的巨大进步,散射波的应用仍需进一步的发展与推进.当前,许多学者都对散射波进行了广泛的研究,其中,国外对散射波的研究已十分全面,代表性的学者主要包括Wu Rushan及Haro Sato等.他们在散射理论方面的研究仍处于国际领先水平.在国内,人们对散射波的研究仍十分有限,主要集中于散射波的正演模拟及成像方法的研究,代表性的学者包括李小凡、沈鸿雁、刘学伟及奚先等.其中,李小凡对地震波非弱散射理论及地震散射层析成像的研究做出了突出贡献,其研究成果在国际上也具有重要意义.后者则主要集中于散射波在金属矿地震勘探中的应用与研究,包括散射波方法在二维地震资料中的采集、处理及解释.
本文详细地总结了地震波的单次、弱散射及多次、强散射理论,并讨论了散射波场的数值模拟及其在各领域的应用表现.通过研究可发现当前各项技术存在的不足及其适用范围,从而对未来的研究提供进一步的指导.
1 地震波的散射理论根据地球介质中背景介质及扰动介质的物性差异大小,可以将非均匀介质产生的散射划分为弱散射和强散射;根据散射体的分布情况,可以将散射划分为单次散射和多次散射,它反映了散射体分布的疏密程度.当散射体分布较稀疏,密度较小时,仅考虑局部散射体的散射,即单次散射.反之,需要考虑邻近的散射体之间相互影响而引起的多次散射.在实际的研究中,为了便于理论推导,人们总是先考虑简单的单次、弱散射效应,随后再考虑复杂的多次、强散射效应,为此,本文分别从这两个方面进行了总结.
1.1 单次、弱散射理论
当介质的非均匀性较弱时,即扰动介质的密度、速度等弹性参数远小于背景介质的相应参数,在这种情况下可以采用微扰理论,对散射场的积分方程运用Born或Rytov近似等进行处理.Born近似研究的是地震波的振幅信息,它的适用条件是: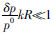 ,其中,
,其中,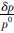 是非均匀介质的平均参数微扰,k是波场的波数,R是非均匀体的尺度(如球半径);Rytov近似研究的则是地震波的相位信息.在弱散射的情况下,Rytov近似可简化为Born近似.因此,两种近似方法在弱散射介质中具有相同的适用区域.对于单次散射,通常假设散射波只包含散射源的一次效应,二次及多次散射效应则忽略不计.单次散射近似的适用条件是:
是非均匀介质的平均参数微扰,k是波场的波数,R是非均匀体的尺度(如球半径);Rytov近似研究的则是地震波的相位信息.在弱散射的情况下,Rytov近似可简化为Born近似.因此,两种近似方法在弱散射介质中具有相同的适用区域.对于单次散射,通常假设散射波只包含散射源的一次效应,二次及多次散射效应则忽略不计.单次散射近似的适用条件是: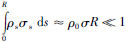 ,该方程是对穿过体积Δ3x的路径作积分,R是Δ3x的线性尺度,ρs是散射体的密度,ρ0是其平均值,σs是散射体的散射截面,σ是其在Δ3x内的平均值.只有当散射体分布较稀疏时,单次散射理论才成立.由于在弱散射情况下,大部分的散射能量仅经历过散射源的一次散射,因此,在某些范围内,单次散射近似可认为是Born近似.在实际应用中,单次散射理论也常用来模拟非均匀介质的弱散射.
,该方程是对穿过体积Δ3x的路径作积分,R是Δ3x的线性尺度,ρs是散射体的密度,ρ0是其平均值,σs是散射体的散射截面,σ是其在Δ3x内的平均值.只有当散射体分布较稀疏时,单次散射理论才成立.由于在弱散射情况下,大部分的散射能量仅经历过散射源的一次散射,因此,在某些范围内,单次散射近似可认为是Born近似.在实际应用中,单次散射理论也常用来模拟非均匀介质的弱散射.
早期人们对散射理论的研究主要是借助标量波理论,该理论最早由Chernov(1960)引入,这一工作有力地推动了地震波散射理论的建立与发展.后来,标量波入射下的随机介质理论已成功地解释了地震学中的很多现象.其主要成就可概括为三个方面:通过对地震台阵中纵波记录的振幅和相位的研究,推算出岩石圈中非均匀体的均方根速度扰动为2%~4%,相关长度为10~20 km(Aki,1973; Capon,1974; Berteusen et al.,1975);模拟尾波的激发及其包络衰减,认为尾波是小尺度非均匀介质引起的散射S波(Aki et al.,1969; Chouet,1975; Sato,1977);研究非均匀性引起的散射衰减及其与固有衰减的关系(Aki,1980; Wu,1982).但标量波理论只适应于某些特定的情况,仅当介质参数满足关系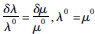 时,该理论才成立.此外,随着横波源及三分量检波器的引入,标量波理论在处理固体介质中波函数的矢量性时受到限制,在处理大角度散射时也存在问题.
时,该理论才成立.此外,随着横波源及三分量检波器的引入,标量波理论在处理固体介质中波函数的矢量性时受到限制,在处理大角度散射时也存在问题.
要克服上述的不足,需采用弹性波散射理论.在弹性波散射中,球形、圆柱形等简单的散射体产生的散射是研究复杂的任意形状介质引起的弹性波散射的基础.Sezawa最先对此进行了研究,他引入了特殊函数并推导了纵波入射下的圆柱、椭圆柱及球体的散射.Wolf(1945),Nagase(1957),Knopoff(1959)也先后研究了单个球体的散射.Knopoff等于1964年又研究了随机非均匀介质中的弹性波散射,推导了高斯型随机介质中散射波的均方振幅.此后,很多学者都推导了不同的复杂介质情况下的弹性波散射的理论公式,并给出了它们在地球物理中的应用(Hudson,1968; Cleary,1972; Wu and Aki,1985; Sato and Fehler,1998).总的来说,早期的研究主要是针对横向长度较小的非均匀介质,但实际介质的横向长度通常较大(大于野外测量距离).为此,Ellison利用Born近似推导了标量波入射至大横向长度的随机介质中的一阶近似解,但全弹性波入射时的近似解却是若久未得.Li利用等效原理推出横向无界的连续散射介质中的弹性波解,并由此建立大横向尺度介质的全弹性波解.该理论是单次弱散射情况下的更一般的理论,它适用于横向小尺度及大尺度散射介质,同时也适用于标量波及弹性波入射时的散射问题(Li,1993).
1.2 多次、强散射理论对于地下高度复杂的非均匀介质,单次、弱散射理论是不精确的,需要考虑介质的多次、强散射效应.解析理论(多次散射理论)和传递理论是求解多次散射问题的两种不同方法.解析理论考虑了波动方程,求出了散射及吸收介质中各类统计量的微分或积分方程,如方差和相关函数.该理论经过了数学上的严格推导,也考虑了散射体间的多次散射和相互干涉.但各方程的精确解通常很难获得,求得的各种有效解大多是仅在某些参数范围内适用的近似解.传递理论研究的是波场能量在介质中的传递,并不涉及波动方程.该理论虽然缺少数学上的严谨性,却简单直观,考虑了介质的散射和吸收效应,同时也考虑了波场的相互干涉.此外,推导的各公式主要利用了能量的叠加,而不是场的叠加,这主要是因为假定了散射场之间互不相关.
解析理论的早期研究包括Ryde(1931)、Ryde和Cooper(1939)、Foldy(1945)、Snyder和Scott(1949)以及Lax(1951)等人的工作.Twersky(1977)扩展了这些研究,深入分析了各种不同类型的双相关函数所代表的多重散射,并引入了由刚性球组成的气态粒子标量方程,通过Virial展开和对双相关函数采用P-YA近似的方法改善了“空洞修正积分”.McQuarrie提出了自洽理论,该理论可以解决随机分布的非均匀介质在弹性波入射时所产生的多重散射.Varadan等(1987)借助于T矩阵法,推导了横向各向同性圆柱状散射体的多重散射理论.随后,Varadan和Ma等(1989)利用该理论讨论了随机介质中弹性波的散射及衰减问题.
传递理论直接考虑处理非均匀介质中的能量传递,其考虑的变量为能量、密度和流量,因假定散射场的主要部分不相干,所以人们更关心的是能量的叠加而非场的叠加.目前,研究多重散射能量传递的方法主要有三种:第一种是采用漫射理论,当散射很强,以至于所有的能量都可以看作是散射引起的,根据能量守恒定理可推出相应的扩散方程.可以看出,这种方法是一种极端的情况,适用于散射体密集分布的强散射,但该理论有很多假设条件,其中最重要的是假设散射衰减很强,吸收衰减很弱.Wesley(1965)、Aki和Chouet(1975)等都曾利用该理论分析了地震记录中的尾波.第二种是不同阶多重散射的叠加,即将到达观测点的各种散射波叠加,这种积分法的原理非常直观易懂,但仅适合于很简单的模型.在这一方面,Kopnichev(1977)研究了二维、三维介质中的双重散射和三重散射;Gao(1983)考虑了三维介质中的二至七重散射的效应.第三种是利用辐射传输理论,采用一种相对复杂的传输方程,但该方法更有潜力适用于复杂的实际情况.目前,合成多次散射的大多数方法都是基于辐射传输理论.Wu(1985)、Wu和Aki(1988)最早将该理论引用到地震学领域.后来,尚铁梁和高铁龙(1988)根据震源的脉冲辐射原理,推导了二维无限空间内各向同性多次散射过程中的动态积分方程.Li和Hudson推导了弹性波在横向大尺度非均匀连续介质中的能量传输公式,并由此建立了适用于强散射和弱散射、转换波散射及一般散射的弹性动力学能量传输理论(Li and Hudson,1996; 李小凡,2002).在2002年,Sato和Nishino利用辐射传输理论模拟了多次Rayleigh散射.关于该理论的详细推导及最新研究进展,Margerin和Sato在其著作中给出了全面的介绍(Margerin,2004; Sato,2012).
对于强散射问题,除了上述的辐射传输理论外,其他的理论方法还有很多.这些方法在处理强散射问题时都有所成效,但所有方法均建立在某些近似的基础上,仅适用于一些特殊的情况.如弹性波抛物线近似,该近似假设散射波的主要能量分布在入射波传播方向的附近,并忽略了介质的背向散射.因此,它适用于弹性参数在一个波长内变化较小的介质,多用来研究弹性波的小角强散射,Candel(1979)、Husdon(1980,1981)、Corones(1982)、Wales和McCoy(1983)等都曾研究了弹性波的抛物线近似理论.Fisk和McCartor(1991),Fisk、Charrette和McCartor(1992),De Hoop(2000),Wu(2003)发展了弹性波的各类相屏法,该理论既适用于强散射又适用于弱散射情况,但该近似也忽略了背向散射,仅考虑前向散射,需满足条件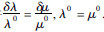 .此外,基于二阶Neumann级数近似,Herman(1994)研究了二维非均匀介质中声波的多次散射问题;Wu(1996)研究了多次散射中的各类薄板近似;Huang(1999)等提出了推广的局部Born近似及Rytov近似.这些近似方法在实际应用中受到了很多限制.因此,如何建立一个全面的、包含弱散射及强散射的全波散射理论,是目前各国学者研究的重点,制约这一问题的关键在于如何得到一个适用于任意散射介质的Green函数.2001年,Li应用摄动理论推导了任意非均匀介质中的Green函数,求出了相应的全波解(Li,2001).尽管该理论仅适用于标量波散射情况,却为任意非均匀介质的全波散射理论的建立奠定了基础.
.此外,基于二阶Neumann级数近似,Herman(1994)研究了二维非均匀介质中声波的多次散射问题;Wu(1996)研究了多次散射中的各类薄板近似;Huang(1999)等提出了推广的局部Born近似及Rytov近似.这些近似方法在实际应用中受到了很多限制.因此,如何建立一个全面的、包含弱散射及强散射的全波散射理论,是目前各国学者研究的重点,制约这一问题的关键在于如何得到一个适用于任意散射介质的Green函数.2001年,Li应用摄动理论推导了任意非均匀介质中的Green函数,求出了相应的全波解(Li,2001).尽管该理论仅适用于标量波散射情况,却为任意非均匀介质的全波散射理论的建立奠定了基础.
散射波场的数值模拟方法可分为确定性方法和统计性方法两大类.前者是通过数值计算对阶地及沉积盆地等特殊的速度结构进行数值模拟;后者是建立在研究介质统计特性的基础上,将速度或地形作为随机变量来处理,而不是研究介质中每一个散射体的确定位置.目前,广泛采用的数值模拟方法主要是有限差分法、有限元法、体积分方程法和FK域积分法等.
有限差分法已广泛应用于散射波的正演模拟.这种方法简单易行,无需对速度变化的尺度作任何限制,可以简略地分析散射场的分布和波场运移特征.但是有限差分法也有着不可回避的缺陷,模拟得到波场中包含了非散射场的信息,散射波能量很小,其细节信息被一次场所淹没.另外,该方法还受计算机内存以及计算精度的限制.秦雪霏利用六阶有限差分法模拟了含凹形坑介质的波场,同时设计了自适应Alpha-Trimmed滤波器对多次散射波场进行提取(秦雪霏,2007).Gunnar等将高阶有限差分法格式应用到轴对称介质的弹性SH波方程中,并用其分析了整个地幔的散射特征(Gunnar et al.,2008).Shunsuke(2014)采用2D和3D有限差方法模拟了日本千叶西北地区地下20~40 km的低速层中的散射波场,并证明大洋地壳及低速层中分布的局部强的小尺度非均匀性是引起高频S波(1~8 Hz)包络扩展及峰值延迟的主要原因,推算出该区非均匀体的自相关长度为1~2 km,均方根速度扰动为0.07~0.09.
与有限差分法相比,FK域积分法模拟的波场中不包含一次场,常见的直达波不会出现在剖面中,并且该算法的精度比有限差分法高.但它的计算效率低,在计算点数相同时,其计算量比显示有限差分法要大很多.吴如山(1993)曾利用相屏法计算出一次场,然后借助该方法计算出散射场.黄雪继(2003)对其方法进行了改进,在求解波动方程时,采用相移法计算出一次波场,再用FK域积分法模拟散射场.刘铁华(2010)先利用高阶有限差分方法计算出总场,然后通过FK域积分法计算散射场,并改进了散射场的空间能量衰减,大大提高了计算效率及计算精度.
散射波场的数值模拟方法还有很多,这些方法的原理不尽相同,但它们都设法提高数值模拟的精度和效率,使其适用于复杂介质的散射场模拟.在实际的研究过程中,应根据模拟的精度及需求选取合适的模拟方法.这些方法包括:Eaton采用Kirchhoff积分法研究了分布在均匀介质中的各类矿体产生的散射场(Eaton et al.,2000).孙明采用Gauss射线束法模拟了直立板状构造的散射场(孙明等,2001).Xie(2001)、Hobbs(2003)研究了复弹性波相位屏法,模拟了3D非均匀介质及围岩介质为随机介质时所产生的散射波场.孙建国首次将拟解析近似方法应用到声波散射数值模拟中,并给出了相应积分方程的拟解析近似解及其迭代表达式(孙建国,2006).与传统的数值计算方法相比,这种方法在计算散射场的数值解时可直接进行积分,无需求解方程组.Cakir(2009)利用多层快速多级子算法模拟了2.5D远震P波的多次散射波场,该算法可以提高计算速度.Chen等(2012,2013)分别采用边界元法及联合边界元法和有限差分法的混合方法模拟了二维含裂缝非均匀介质的SH波散射波场,极大地提高了计算速度.
2.2 随机介质的散射场模拟由于地下介质的复杂性,确定性的模拟方法或是难以应用,或是不切实际.在这种情况下,随机方法发挥着重要作用,其主要研究内容包括:随机介质模型的构建、散射场的正演模拟及波场特征分析.其中,随机介质模型是由无数的非均匀介质组成的大集合,集合中的每一个元素依一定的概率存在,且在具体结构上存在着差别,但却具有共同的统计特性.声波测井资料是构造随机介质模型的基础.随机介质的波场模拟大多采用有限差分方法,模拟得到的散射场的强弱与随机介质的模型特征及地震波的频率和波长有关.当地震波的频率较高,或地震波长接近于非均匀体的尺度时,散射现象越明显.目前,随机介质的大部分研究主要集中在模型构建方面,得到的随机介质可以用来反映地下不同的非均匀体分布情况,关于其波场特征的研究还没有深入展开.
关于随机介质,国内外的很多学者进行了研究,主要的几种随机介质模型如表 1所示.此外,Holliger(1992)还构造了具有各向异性自相关函数的随机介质,这种描述方法考虑到了小尺度非均匀体的方向,对于实际的沉积地层,垂直方向的相关距离通常也要比水平方向的短.Thomas等(2001)模拟了三维黏弹性随机介质的波场,并讨论了地震波在其中的散射衰减.奚先和姚姚(2001-2005)构建了单尺度、平稳随机介质和多尺度、非平稳随机介质模型,并分析了不同模型下的波场特征.李红星(2009)在随机介质中引入双相介质,建立了双相各向异性随机介质,并采用伪谱法分析了其波场特征.Xie(2013)模拟了三维随机介质的散射波场,并对散射波场进行了复合域分析(时空域和慢度-频率域).
|
|
表 1 常见的几种随机介质模型 Table 1 Common random medium model |
图 2是构造的具有椭圆自相关函数的指数型随机介质,其自相关函数的表达式为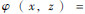
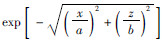 ,a和b分别代表介质在横向和纵向上的自相关长度.这种模型描述的随机介质可表示地质体在纵横向上的不同尺度,可以看出,随着a的增大,介质在横向上的成层性越明显,当a趋近于无穷大时,得到的模型可看作是常见的薄互层模型.
,a和b分别代表介质在横向和纵向上的自相关长度.这种模型描述的随机介质可表示地质体在纵横向上的不同尺度,可以看出,随着a的增大,介质在横向上的成层性越明显,当a趋近于无穷大时,得到的模型可看作是常见的薄互层模型.
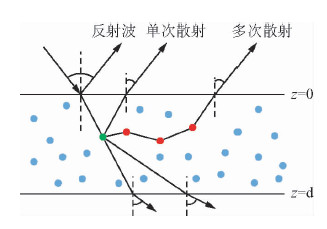 | 图 1 单次散射与多次散射示意图 Fig. 1 Schematic diagram of singal and multiple scattering |
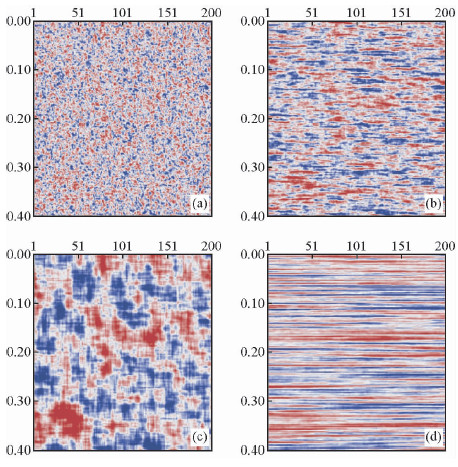 |
图 2 不同尺度的随机介质模型 (a) a=b=1; (b) a=10,b=1;(c) a=b=10; (d) a=∞,b=1. Fig. 2 Stochastic medium model with different scales (a) a=b=1; (b) a=10,b=1;(c) a=b=10; (d) a=∞,b=1. |
裂缝的柔量、大小、空间分布及填充流体等参数都会对地震波场产生很大的影响.当地震波长远小于裂缝间距,裂缝会引起很强的散射,反之,散射场较弱,可采用各向异性介质的理论进行研究.其次,当地震波长远小于裂缝的尺度,也会产生很强的散射,反之,它对波场的影响较小.描述裂缝介质的模型包括两种,一种是等效介质理论,该理论假定相邻裂缝间的空间距离远小于地震波长,然后通过静态应变分析求得裂缝介质的等效弹性参数模型,从而得到岩石的地震响应特征.另一种是位移不连续模型,该模型适用于相邻裂缝间的空间距离接近于或大于地震波长的情况,每一个裂缝两侧的应力连续,但位移是不连续的.在位移不连续模型中,裂缝介质对地震波传播的影响可看作是波传播的边界条件.
通过对裂缝介质的波场模拟可有效地分析裂缝参数对散射波场的影响.广泛使用的数值模拟方法包括有限差分法和伪谱法.与有限差分法相比,伪谱法可很好地解决数值频散问题,改善计算速度和精度.但在模型较复杂时,其效果较差,也会产生边界反射.Vlastos等(2003)就利用伪谱法模拟了裂缝介质产生的散射波场,并分析了裂缝的分布对多次散射的影响.刘恩儒等(2006)建立了裂缝的等效介质模型,通过有限差分方法模拟并分析了不同裂缝尺度及其尺度分布对散射场的影响.Chi等(2006)采用旋转交错网格有限差分法模拟了交错裂缝组产生的散射波场,分析不同的裂缝间距和柔量产生的散射模式.裂缝产生的散射波场具有方位特性,这一特点可用来分析裂缝的方向.朱铁源(2008)研究了裂缝黏弹性介质对地震波传播的影响.文中通过等效介质模型描述离散裂缝体,二维交错网格高阶有限差分方法模拟波场,对比分析了倾斜裂缝模型、含水含气裂缝模型、多组交叉裂缝模型及不同密度裂缝模型对波场的影响.结果表明,当裂缝层底部存在反射界面时,产生的散射波会严重干扰底部反射,散射波的能量与填充流体、裂缝密度和倾角有着密切的联系.在裂缝的倾角较大、裂缝间距大于纵波波长的1/4及含气体的裂缝中产生的散射能量比较强(朱铁源,2008).雷蕾(2010)采用变网格有限差分算法模拟了孔洞及裂缝非均匀介质的地震散射波场,发现当裂缝间距与地震波长满足关系a/λs>0.5,裂缝散射波的波形图中出现尾波.
2.4 散射波场特征研究散射波场的特征分析对地下散射体的有效识别及反演具有重要的指导意义.国内外的很多学者已开展了相关的研究,其总体思路是:根据波的传播理论建立非均匀介质的波场函数,通过物理模拟或数值模拟获得散射体的波场记录,然后考虑散射体的尺度、分布密度、形状、散射角、波阻抗及波场能量等对散射场的影响.但是大部分的研究主要采用定性的方式,讨论了特定模型中散射波场与散射体各参数的相对关系.对于散射波特征与非均匀地质体之间的定量关系仍需日后的深入研究.
早在1985年,Wu和Aki采用等效源法及微扰法推导出瑞雷散射的波场函数,通过散射图形指出了弹性波散射的几个重要特征,并将地下的扰动介质划分为速度微扰及阻抗微扰.后来,很多学者在模拟非均匀介质的波场后,都定性地分析了散射波场与散射体之间的关系.其中,比较突出的研究包括:张丽琴(2004)对散射波场进行高阶统计分析,其结论为有效地检测和识别碳酸盐岩非均匀储集体奠定了基础.李灿苹等(2009)提取了散射波场的振幅属性,定性地研究了振幅与非均匀体尺度的关系;同时,利用相干技术研究了非均匀体的尺度对散射波场的影响.刘铁华(2012)研究了散射波的振幅及能量与散射体的纵横向尺度、扰动量的定量关系,给出的经验公式可用于获得散射波的动力学特征.
图 3、图 4是建立的点散射体及随机介质模型,所有模型中上层介质的厚度均为150 m,纵波速度均为2000 m/s(随机介质中为纵波速度的平均值),点散射体的波速为1000 m/s.从模拟的波场中可以看出,对于简单的点散射模型而言,其同相轴类似于双曲线,满足点散射波的时距曲线;对于随机介质而言,当模型的横向尺度较大时,产生的散射波的能量较强,对反射波的有效识别产生干扰作用,当模型的纵向尺度也变大时,散射波会使反射波的同相轴扭曲变形,且纵向尺度越大,其形变就越显著.关于纵横向尺度对波场能量及反射波波形改变的定量关系有待于精确的理论分析及大量的模型试算.
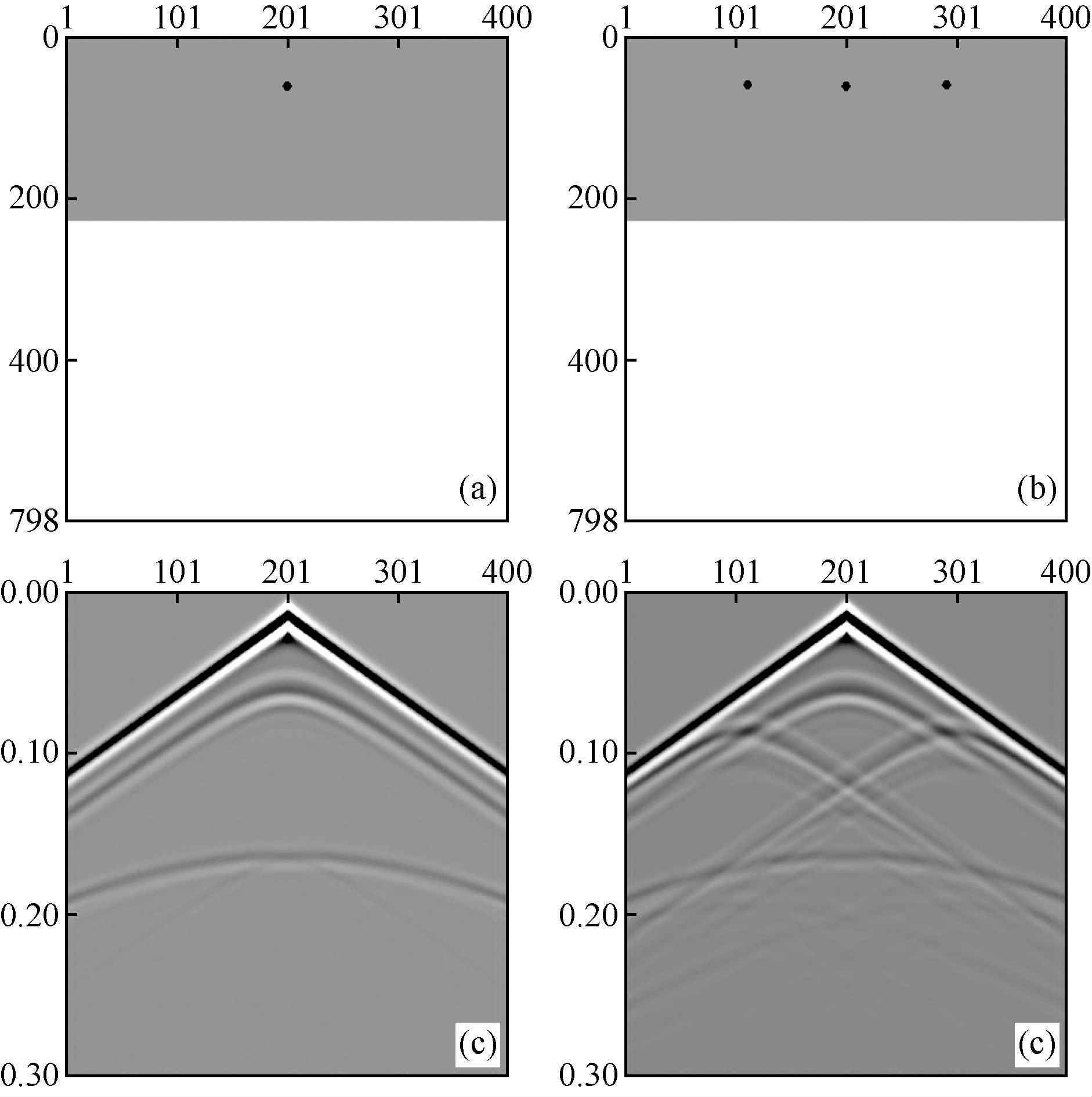 |
图 3 点散射体模型及其波场记录 (a)单点散射体模型;(b) 多点散射体模型;(c)、(d)为(a)、(b)模型的波场记录. Fig. 3 Model of point scatterer and the seismic record (a) Singal-point scatterer; (b) Multi-point scatterer; (c) and (d) is the seismic record of(a) and (b). |
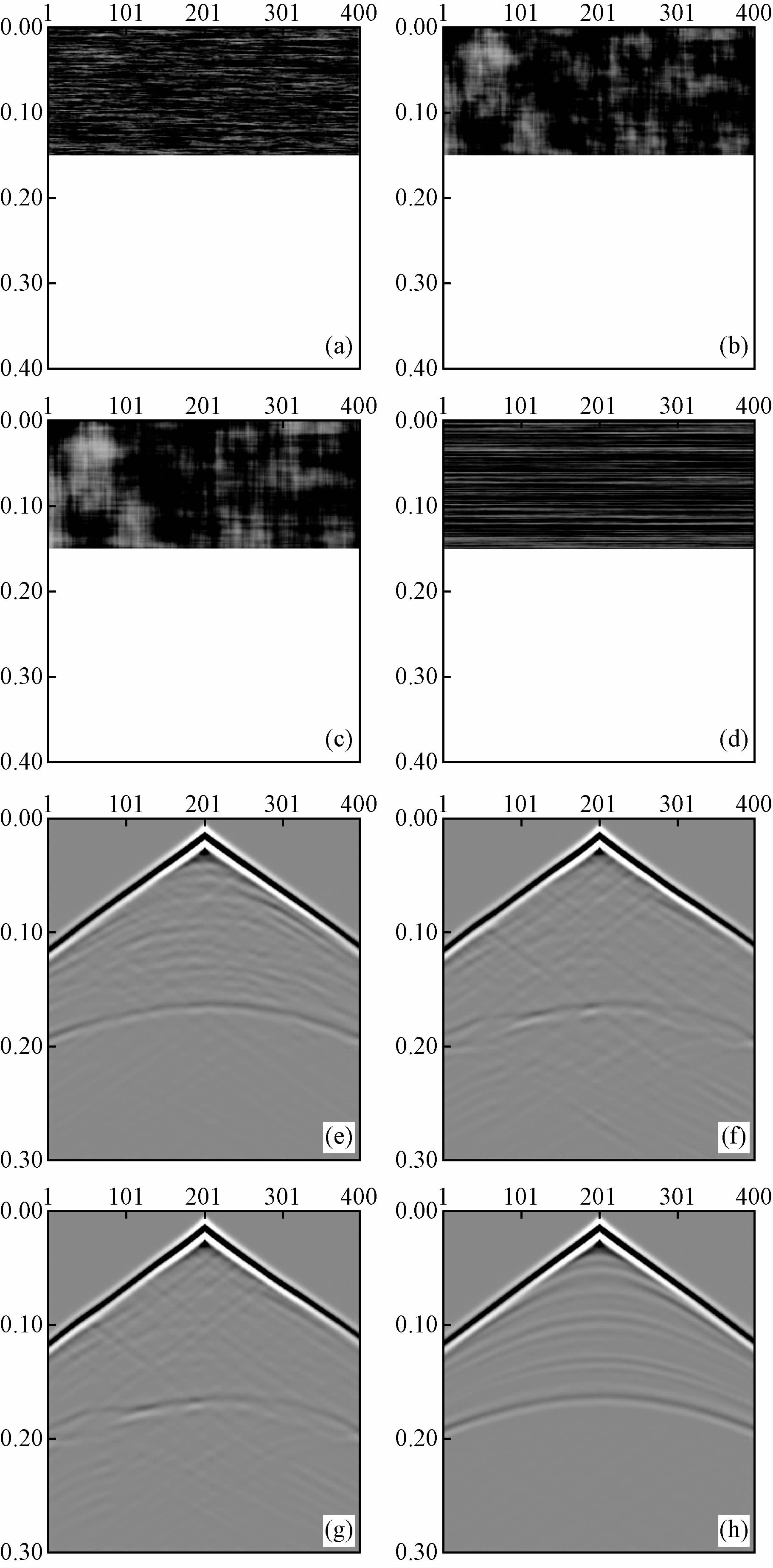 |
图 4 不同尺度的随机介质模型及其波场记录 (a) a=50,b=1; (b) a=b=50; (c) a=b=100; (d) a=∞,b=1;(e)~(h)是(a)~(b)模型中相应的波场记录. Fig. 4 Stochastic medium model and the seismic record at different scales (a) a=50,b=1; (b) a=b=50; (c) a=b=100; (d) a=∞,b=1;(e)~(h) is the seismic record of(a)~(b). |
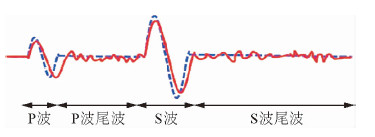 | 图 5 地震记录的P波和S波尾波(蓝色虚线代表均匀介质,红色实线代表非均匀介质)(Sato,1982) Fig. 5 P wave and S wave coda in seismic record (The dashed line represents the homogeneous medium, the solid line represents the inhomogeneous media) (Sato,1982) |
地震记录中的尾波是地震波散射的最显著现象,主要是指跟随在主波型(如P波、S波和面波)后的不规则波至(吴如山等,1989),如图 2所示,它表明岩石层中存在着随机非均匀弹性构造.尾波理论的研究主要包括尾波激发、尾波包络线衰减及尾波Q值等方面,其分析结果已广泛地应用于地震预报和地震工程领域,如尾波振幅的强弱可用来估算地震矩,尾波延续时间的长短可用来测定震级的大小,尾波激发的测量结果反应了岩石的非均匀性.
关于尾波的数学模型,前人已做过很多研究.早期,Aki和Sato(1969)提出在弱散射模式下,S尾波是随机分布的非均匀体引起的背向散射,并建立了单次背向散射模型.Kopnichev(1975)、Sato(1977)还研究了不同情况下的单次散射模型.Sato(1982、1994、1995)给出了单次各向异性及多次各向异性散射模型.Wesley(1965)、Kopnichev(1977)、Gao(1983)、Hoshiba(1991)等研究了适用于强散射的扩散模型及多次散射模型.另一个关于尾波包络的模型是Frankel和Wennerberg(1987)提出的能通量模型.目前,这些数学模型在实际中的应用已十分广泛,但每个模型考虑的内容有所不同,如单散射模型认为尾波包络衰减是吸收系数和散射系数之和,能通量模型则认为尾波包络衰减主要由吸收系数造成.关于尾波的最好的数学模型仍需要对理论模型作进一步研究以及大量的实验验证.
通过尾波的数学模型计算尾波包络,然后利用包络反演可确定全球范围内的总散射系数g0、尾波衰减系数Qc-1、固有衰减Qi-1及散射衰减Qsc-1等参数,进而确定岩石圈内非均匀体的分布情况及介质的固有吸收和散射衰减特征.Nishigami(2000)通过尾波包络反演分析方法研究了加利福尼亚中部的圣安地列斯断裂系统中散射体的分布情况.Saito等(2002)研究了三维Von Karman型随机介质模型,应用Markov近似方法模拟了外行球面标量波的均方根包络扩展,定量估算出日本东北部区域的随机非均匀介质参数,求得了该区Von Karman型随机介质的功率谱密度函数.Lee等(2003)基于辐射传输理论,采用Monte Carlo方法模拟了ScS波包络,估算出中亚地区上、下地幔的S波总散射系数.Jin和Aki(2005)求出了1~2、2~4、4~8、8~16、16~32 Hz频带范围内高空间分辨率的尾波Q值,发现低频带内的低尾波Q值与俯冲作用和板内地震有关;高频带内的低尾波Q值与第四纪火山活动有关.Takahashi等(2007,2009)将随机射线方法推广至Von Karman型三维随机介质,并计算了包络峰值延迟时间,构建了峰值延迟时间与随机介质谱密度函数的特征参数之间的定量关系,随后利用包络峰值延迟时间反演得到了日本东北地区的速度扰动随深度的变化图.Nakahara(2010)提出了利用极大似然法估算尾波Q值的新方法,并发现高频地震包络服从Nakagami-m分布,将m参数引入地震学中有利于根据地震包络的扰动研究小尺度速度扰动的统计特征.
3.1.2 尾波包络合成从上述的研究可以看出,包络合成是分析确定各项参数的前提与基础,该方面研究的最新进展主要包括如下几项:Sato(2007)基于Markov近似模拟了具有Gaussian型自相关函数的三维随机介质中球面矢量波入射时的尾波包络,发现S波的包络扩展现象比P波更明显.随后,Sato(2008)又研究了上述情况下具有各向异性Gaussian型自相关函数的三维随机介质中的尾波包络.Sato的研究假定入射波为球面波,但该假设无法解释剪切位错源激发时非球面波入射产生的尾波包络的方向性.为此,Sato和Korn(2007)模拟了二维随机介质中柱面矢量波入射时的尾波包络,证明了剪切位错源入射时产生的矢量波包络具有方向性.Sawazaki等将上述理论扩展至三维随机介质模型(Sawazaki et al.,2011).Emoto在2010、2012及2013年模拟了三维随机介质自由表面上产生的矢量波包络、具有各向异性Gaussian型自相关函数的二维层状随机介质的矢量波尾波包络及二维层状随机介质中柱面波产生的尾波包络.可以看出,目前关于尾波包络的研究均是基于Markov近似方法,但该方法仅考虑了地震波的前向散射,综合考虑后向散射对地震包络的影响是未来研究的重点,这需要结合Markov近似及辐射传输理论.
3.1.3 尾波干涉研究近年来关于尾波干涉理论的应用研究也十分广泛.由于多次散射形成的尾波是对介质的多次采样,因此相对于直达波,尾波包含的介质信息更为丰富.该理论最早由Snieder等在2002年提出,它利用了尾波的振幅及相位信息,通过对介质变化前后的尾波波形进行互相关计算来获取走时扰动.尾波干涉法已广泛应用于测量介质中波速的相对变化、散射体及震源的位置等方面.Snieder和Hagerty(2004)、Gret(2005)等利用尾波干涉法检测了介质波速的微小变化.后来,Snieder详细地总结了尾波干涉的一般理论与实际应用(Snieder,2006).Tonegawa(2009)提出远震S波尾波的干涉方法可以用来提取体波,如直达P波、S波及反射波.Zhou等(2010)将该方法用于时移VSP监测,分析了CO2注入前后地震波速度的变化.Khatiwada(2012)进行了类似的研究,将该方法应用于层状玄武岩油气藏.肖震(2014)利用尾波干涉法研究了汶川地震的余震定位,并分析了该方法的可行性与稳定性,相对于其他震源定位方法,尾波干涉法对输入数据要求比较低,适用于台阵较少且对地下的速度结构认识不清的情况.但也存在着诸多不足,如它要求两次地震事件的相距时间及距离都不能太长(肖震,2014).目前,尾波干涉法的研究尚处于起步阶段,其理论及应用潜力仍需要进一步的完善.
3.2 散射衰减非均匀体的散射使接受到的地震波有效信号的能量减小,这种衰减定义为散射衰减.它主要是由于散射使波的能量偏离了原始的传播方向,在时空域上重新分配造成的.因此,散射衰减并不会使波场的总能量减少,散射损失的能量可以再次被散射到传播方向,晚一点被接受,最终形成尾波.早期,人们根据Born近似对各种小尺度非均匀弹性构造产生的散射进行了相当程度的研究(Miles,1960; Knopoff和Hudson,1964; Wu和Aki,1985a),如果非均匀程度比较弱,该近似对非均匀体形状不作任何要求.运用统计方法处理散射问题的平均波公式(KKaral和eller,1964; Frisch,1968; Howe,1971; Sato,1979)也是一种有效的方法,这种方法对弱非均匀情形下的散射衰减结算结果与Born近似结果类似.但在高于1Hz的频率范围内,这两种方法计算的QS-1和QP-1值随频率的增加而增加,这与实际的衰减测量结果之间存在着差异.为此,Wu和Sato采用不同的方法对上述的理论进行了修正.其中,Wu的方法是在散射衰减计算过程中,忽略了前向散射波的能量(Wu,1982);Sato则校正了相位(或走时)起伏造成的影响,提出了走时校正的Born近似(Sato,1982).关于散射衰减的另一个问题是尾波的散射衰减,由于尾波没有相干性,尾波衰减主要是关于能量的散射损失.由上一节的讨论可知,尾波的数学模型不同,其衰减及Q值的计算就有所差异.
很多学者致力于研究固有衰减及散射衰减的关系,并设法分离这两种不同机制的衰减作用.关于该方面的理论研究主要集中在20世纪90年代.Wu(1985)采用辐射传输理论构建了多次散射模型,估算了固有衰减和散射衰减的相对值.Zeng(1991)将Wu的方法扩展至尾波包络模型.Fehler(1992)在上述研究的基础上,提出了多延迟时窗分析法(MLTWA),该方法在三个或多个时窗内将波的能量沿距离积分,进而估算出各衰减系数.Wennerberg(1993)提出了利用直达S波及尾波Q值估算固有衰减和散射衰减的Q值.目前,这些方法已广泛应用于研究各地区的衰减性质,如Giampiccolo(2004、2006)、Bianco等(2005)、Sahin等(2007)、Baruah等(2010)、Edoardo等(2011)、Mahood等(2011)、Prudencio等(2013)、Padhy等(2013)都利用上述的方法计算了全球不同地区的固有衰减和散射衰减的Q值.
3.3 近地表散射3.3.1 近地表散射机制近地表对体波和面波的影响很大,它会使入射波散射、散焦、聚焦并耦合不同的波型,如纵波和横波、体波和面波,既可以诱发尾波又可以改变直达波的波形和能量,同时还将体波转换成波导和共振波型等,最终使有效波场变得异常复杂(吴如山,1989).根据非均匀构造的类型,置于不规则地层中的点源引起的散射波可分为面波散射、体波-面波散射和面波-体波散射等.Lev and er系统地总结了1990年前人们对近地表地震波散射的研究,从不规则地形的体波散射、不规则表层的体波散射以及不规则波导和穿过不规则地形的面波传播三个方面进行了评述.由于近地表散射会使记录的波场变得复杂并掩盖弱的反射信号,因此很多研究者通过各种数值模拟方法,讨论了近地表散射机制,如不规则地形、浅层非均匀体的散射等,为散射噪声的衰减提供了理论依据.曹军(2004)通过计算半圆柱形峡谷模型和具有不同陡度的高斯型峡谷模型的地震波散射,比较了三种用于模拟不规则界面模型中地震波散射问题的半解析方法——Aki-Larner方法、Bouchon-Campillo方法和全局广义反射透射矩阵方法,分析了各种方法的有效性.Christina(2005)在分析了有限差分法、有限元法及各种高频渐近方法在计算近地表散射场的缺陷后,提出了一种通过求解频域积分方程的方法,发现近地表的散射体使接收到的P波延迟,同时产生大量的散射Rayleigh波,随着散射体的增大,这种干扰也变得更加复杂,使有效信号的连续性变差.刘宁(2007)详细地推导了三维频率域内起伏地表模型的散射积分方程,并采用拟解析近似的方法求解积分方程.此外,Appelo(2009)、Lan(2011)、Wen(2012)、Almuhaidib(2011,2014)等都对有限差分法做了不同的改进,使其适应于复杂的不规则地层及近地表散射体的波场模拟,并分析了其中的散射机制.总的说来,不规则表层、非均匀近地表结构、浅层点散射体等都会产生复杂的散射波,严重地污染了底层的有效反射信号.
3.3.2 近地表散射噪声衰减在近地表散射噪声的衰减方面,杨旭明(2002)采用微扰理论,假定近地表点源产生的地震波场由入射波场和散射波场组成,通过采用散射波场正演及炮集记录反演的方法消除了散射噪声.郭向宇(2002)提出了一种消除近地表散射波的叠后方法,它是对叠后记录进行偏移成像获得散射场,然后通过中值滤波方法将其衰减.Campman(2005)基于近地表散射的积分方程,估算了研究区域的表面阻抗函数,利用该函数模拟了散射面波,并将其从总波场中减去.吴希光(2012)通过对各地区炮记录的分析及西部地区特殊地质模型的现场考察,提出表层散射是复杂地区地震资料低信噪比的根本原因,并从野外资料采集的角度提出了压制表层干扰的技术方法.Yanchak(2013)提出了两种模拟散射面波的方法,一种是基于面波分析、模拟及反演的方法,另一种是基于模型驱动的干涉方法,从总波场中减去模拟的散射面波即可实现去噪的目的.徐基祥(2014)采用地震干涉法分离近地表散射,该方法不需要事先求取近地表结构的速度,且适应于任意复杂的起伏构造和不均匀近地表模型.总之,散射噪声的衰减是一项庞大的综合体系,不仅要考虑各种复杂的处理技术,还要考虑采集过程中的各项因素,使散射噪声的影响达到最小.此外,相对于传统的多域多道滤波方法,分析散射波的性质,模拟预测出实际的散射波模型,然后从地震数据中消除散射波的方法则更具优势.这种方法对反射波的影响最小,使反射振幅及相位具有更好的保真度,有利于后续的处理.但该方法依赖于对散射波场的正确认识及精确模拟,这就需要其他相关理论和技术的研究与进步.
4 结论与展望4.1 本文从散射波的理论研究、数值模拟及应用的角度全面的总结了散射波的研究历史以及当前关于散射波的最新进展,可以看出地震波散射理论是研究波在介质中传播的更一般的理论,它可以解决更复杂的地质问题.在散射波的理论研究方面,其总的趋势可概括为从考虑简单的二维、各向同性、层状非均匀介质到三维、各向异性、含近地表及不规则界面的复杂介质,从研究层内球、圆柱等单个散射体到多个具有任意形状的散射体及随机介质;从特殊的考虑标量波的单次散射到一般的弹性波散射;从简单的弱散射模式到复杂的多次散射及强散射模式.此外,当前关于强散射问题的处理都是建立在一定的近似条件下,其精确解尚未得到.因此,建立一个精确的、综合考虑强散射及弱散射的弹性波理论体系是未来散射波理论研究的重点,这也是长期困扰人们的世界性难题.
4.2 虽然散射波的理论研究已有了较大的发展,但如何将这些复杂的理论应用到地震勘探中也是一项急需解决的问题.很多地球物理学家已将散射波引入到实际的勘探领域,但大部分研究与应用仍是基于弱散射的假设,关于多次散射以及强散射理论的应用则很少涉及.对于地下高度复杂的强非均匀介质,弱散射假设必然存在着很多限制.其次,人们对地震散射波层析成像的研究已十分广泛,但这些研究都是利用反射波的处理方法对散射波成像,并没有实现真正意义上的散射波成像.但散射波成像技术在医学等其他领域的应用研究已十分成熟,如何将其他学科的成就过渡到地震勘探领域也是日后研究的一个重要方向.另外,随着地震勘探逐步向复杂地表及精细化方向发展,基于散射理论的近地表散射噪声压制、非均匀介质速度分析及复杂构造成像等必将成为未来研究的重点及热点.对于复杂近地表产生的多种波动信息,除了采用有效的方法压制散射噪声,充分地利用这些信息以获取近地表的结构也是十分重要的.同样,对地震资料中尾波的利用也是不容忽视的关键问题,从而使采集的资料真正做到物尽其用.
4.3 总的来说,对散射波的地震采集及相应的处理方法仅在金属矿勘探领域涉及到,但也处于起步阶段.在石油勘探领域,反射波勘探技术仍是当前的主流技术,关于散射波的地震勘探技术仍需要未来的不断研究与广泛推广.
致 谢 感谢审稿专家对文章提出的宝贵意见,感谢编辑对文章的修改完善!| [1] | Çakir Ö. 2009. Forward modelling the multiply scattered 2.5-D teleseismic P waves accelerated by the multilevel fast multipole method[J]. Geophys. J. Int., 176(2):505-517. |
| [2] | Campman X H, van Wijk K, Scales J A, et al. 2005. Imaging and suppressing near-receiver scattered surface waves[J]. Geophysics, 70(2):V21-V29. |
| [3] | Cao J, Gai Z X, Zhang J, et al. 2004. A comparative study on seismic wave methods for multi-layered media with irregular interfaces:irregular topography problem[J]. Chinese J. Geophys.(in Chinese), 47(3):495-503, doi:10.3321/j.issn:0001-5733.2004.03.020. |
| [4] | Chen T R, Fehler M, Fang X D, et al. 2012. SH wave scattering from 2-D fractures using boundary element method with linear slip boundary condition[J]. Geophys. J. Int., 188(1):371-380. |
| [5] | Chen T R, Li J L, Toksöz N. 2013. Simulating shear wave propagation in two-dimensional fractured heterogeneous media by coupling boundary element and finite difference methods[J]. Geophys. J. Int., 194(3):1810-1822. |
| [6] | Eaton D W, Clarke G. 2000. A Kirchhoff integral method to model 3-D elastic-wave scattering[C].//SEG 70th Annual Meeting, Soc. Expl. Geophys., Expanded Abstracts, 1-4. |
| [7] | Emoto K, Sato H, Nishimura T. 2010. Synthesis of vector wave envelopes on the free surface of a random medium for the vertical incidence of a plane wavelet based on the Markov approximation[J]. J. Geophys. Res., 115(B8):B08306. |
| [8] | Emoto K, Sato H, Nishimura T. 2012. Synthesis and applicable condition of vector wave envelopes in layered random elastic media with anisotropic autocorrelation function based on the Markov approximation[J]. Geophys. J. Int., 188(1):325-335. |
| [9] | Emoto K, Sato H, Nishimura T. 2013. Envelope synthesis of a cylindrical outgoing wavelet in layered random elastic media based on the Markov approximation[J]. Geophys. J. Int., 194(2):899-910. |
| [10] | Guo X Y, Ling Y, Wei X C. 2002. Post-stack attenuation of near-surface scattered wave[J]. Oil Geophysical Prospecting(in Chinese), 37(3):201-208. |
| [11] | Han J J, Han L G, Gong X B, et al. 2010. Attenuation of near-surface scattering noise based on wave theory[J]. Global Geology(in Chinese), 29(2):310-313, 322. |
| [12] | Huang X J. 2003. The forward modeling of seismic wave scattering field with phase shift method(in Chinese)[D]. Beijing:China University of Geoscience(Beijing). |
| [13] | Jahnke G, Thorne M S, Cochard A, et al. 2008. Global SH-wave propagation using a parallel axisymmetric spherical finite-difference scheme:application to whole mantle scattering[J]. Geophys. J. Int., 173(3):815-826. |
| [14] | Jin A S, Aki K. 2005. High-resolution maps of Coda Q in Japan and their interpretation by the brittle-ductile interaction hypothesis[J]. Earth, Planets and Space, 57(5):403-409. |
| [15] | Lee W S, Sato H, Lee K. 2003. Estimation of S-wave scattering coefficient in the mantle from envelope characteristics before and after the ScS arrival[J]. Geophysical Research Letters, 30(24), doi:10.1029/2003GL018413. |
| [16] | Lei L. 2010. Seismic scattered wave field forward modeling for the inhomogeneous media(in Chinese)[Master thesis]. Qingdao:China University of Petroleum(East China). |
| [17] | Li C P, Liu X W. 2009. Study on amplitude attributes of seismic wave in random-uniform medium model[J]. Geophysical Prospecting for Petroleum(in Chinese), 48(5):1318-1324. |
| [18] | Li H X, Tao C H. 2009. Features analysis of seismic wave field in two-phase anisotropic random medium with the pseudo-spectral method[J]. Acta Physica Sinica(in Chinese), 58(4):2836-2842. |
| [19] | Li X F. 2001. Scattering of seismic waves in arbitrarily heterogeneous and acoustic media:a general solution and simulations[J]. Geophysical Research Letters, 28(15):3003-3006. |
| [20] | Li X F. 2002. Theory of full elastic scattering of seismic waves for heterogeneous media of large extent-Ⅱ. Theory of elastic waves of multiple scattering[J]. Acta Mechanica Sinica(in Chinese), 34(5):743-755. |
| [21] | Liu E R, Yue J H, Liu Y. 2006. Finite difference simulation of seismic wave propagation in 2-D solids with spatial distribution of discrete fractures[J]. Chinese Journal of Geophysics(in Chinese), 49(1):180-188, doi:10.3321/j.issn:0001-5733.2006.01.024. |
| [22] | Liu N, Sun J G. 2007. The integral method for numerical modeling of acoustic scattering on irregular topography[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 37(supplement):61-65. |
| [23] | Liu T H. High precision numerical modeling and dynamic characteristic analysis of seismic scattering wave[J]. Chinese Journal of Geophysics(in Chinese), 55(4):1318-1324, doi:10.6038/j.issn.0001-5733.2012.04.027. |
| [24] | Liu T H. 2010. High precision numerical modeling of seismic scattering wave[J]. Chinese Journal of Engineering Geophysics(in Chinese), 7(6):699-703. |
| [25] | Margerin L. 2005. Introduction to radiative transfer of seismic waves[A]. Levander A, Nolet G eds. Seismic Earth:Array Analysis of Broadband Seismograms[M]. Washington:American Geophysical Union. |
| [26] | McQuarrie D A. 1976. Statistical Mechanics[M]. New York:Harper and Row. |
| [27] | Nakahara H, Carcole E. 2010. Maximum-likelihood method for estimating coda Q and the Nakagami-m parameter[J]. Bulletin of the Seismological Society of America, 100(6):3174-3182. |
| [28] | Nishigami K. 2000. Deep crustal heterogeneity along and around the San Andreas fault system in central California and its relation to the segmentation[J]. J. Geophys. Res., 105(B4):7983-7998. |
| [29] | Qin X F. 2007. The characters analysis about the multiply scatter of seismic wave(in Chinese)[Master thesis]. Changchun:Ji'lin University. |
| [30] | Riyanti C D, Herman G C. 2005. Three-dimensional elastic scattering by near-surface heterogeneities[J]. Geophys. J. Int., 160(2):609-620. |
| [31] | Saito T, Sato H, Ohtake M. 2002. Envelope broadening of spherically outgoing waves in three-dimensional random media having power law spectra[J]. J. Geophys. Res., 107(B5):ESE 3-1-ESE 3-15. |
| [32] | Sato H. 2007. Synthesis of vector wave envelopes in three-dimensional random elastic media characterized by a Gaussian autocorrelation function based on the Markov approximation:Spherical wave case[J]. J. Geophys. Res., 112(B1), doi:10.1029/2006JB004437. |
| [33] | Sato H. 2008. Synthesis of vector-wave envelopes in 3-D random media characterized by a nonisotropic Gaussian ACF based on the Markov approximation[J]. J. Geophys. Res., 113(B8), doi:10.1029/2007JB005524. |
| [34] | Sato H, Fehler M C. 2012. Seismic Wave Propagation and Scattering in the Heterogeneous Earth[M]. Berlin Heidelberg:Springer-Verlag. |
| [35] | Sato H, Korn M. 2007. Envelope syntheses of cylindrical vector-waves in 2-D random elastic media based on the Markov approximation[J]. Earth, Planets and Space, 59(4):209-219. |
| [36] | Sawazaki K, Sato H, Nishimura T. 2011. Envelope synthesis of short-period seismograms in 3-D random media for a point shear dislocation source based on the forward scattering approximation:Application to small strike-slip earthquakes in southwestern Japan[J]. J. Geophys. Res., 116(B8), doi:10.1029/2010JB008182. |
| [37] | Snieder R. 2006. The theory of coda wave interferometry[J]. Pure Appl. Geophys., 163(2-3):455-473. |
| [38] | Sun J G. 2006. Two new schemes for numerical modeling of acoustic scattering[J]. Journal of Jilin University(Earth Science Edition)(in Chinese), 36(5):863-868. |
| [39] | Sun M, Lin J. 2001. Study of seismic scattering wave field numerical model for metallic ore exploration[J]. Geology and Prospecting(in Chinese), 37(4):68-70. |
| [40] | Takahashi T, Sato H, Nishimura T. 2008. Recursive formula for the peak delay time with travel distance in Von Kármán type non-uniform random media on the basis of the Markov approximation[J]. Geophys. J. Int., 173(2):534-545. |
| [41] | Takahashi T, Sato H, Nishimura T, et al. 2009. Tomographic inversion of the peak delay times to reveal random velocity fluctuations in the lithosphere:method and application to northeastern Japan[J]. Geophys. J. Int., 178(3):1437-1455. |
| [42] | Thomas Bohlen. 2001. Parallel finite-difference modeling of seismic wave scattering in 3-D elastic random media[C].//SEG Annual Meeting, Soc. Expl. Geophys., Expanded Abstracts, 1147-1150. |
| [43] | Tonegawa T, Nishida K, Watanabe T, et al. 2009. Seismic interferometry of teleseicmic S-wave coda for retrieval of body waves:an application to the Philippine Sea slab underneath the Japanese Islands[J]. Geophys. J. Int., 178(3):1574-1586. |
| [44] | Xi X, Yao Y. 2001. 2-D random media and wave equation forward modeling[J]. Oil Geophysical Prospecting(in Chinese), 36(5):546-552. |
| [45] | Xi X, Yao Y. 2002. Simulations of random medium model and intermixed random medium[J]. Earth Science-Journal of China University of Geosciences(in Chinese), 27(1):67-71. |
| [46] | Xi X, Yao Y. 2005. Non-stationary random medium model[J]. Oil Geophysical Prospecting(in Chinese), 40(1):71-75. |
| [47] | Xiao Z, Zheng Y, Xiong X. 2014. Application of coda wave interferometry method in relative location of the Wenchuan earthquake sequence[J]. Earthquake(in Chinese), 34(2):1-11. |
| [48] | Xie X B. 2013. Seismic wave scattering in 3D random media:a finite-difference simulation and slowness domain analysis[C].//SEG Annual Meeting, Soc. Expl. Geophys., Expanded Abstracts, 3428-3432. |
| [49] | Xu J X. 2014. Separating the near-surface seismic scattered wave using seismic interferometry method[J]. Chinese J. Geophys.(in Chinese), 57(6):1910-1923, doi:10.6038/cjg20140622. |
| [50] | Yanchak D, Monk D, Zarkhidze A V, et al. 2013. Solutions for scattered surface-wave attenuation in the Western Desert of Egypt[C].//EAGE 75th Annual Meeting, Soc. Expl. Geophys., Expanded Abstracts, 1-5. |
| [51] | Yang X M, Wang X X, Wang K B, et al. 2002. Forward and inverse method for near surface seismic scattered noises[J]. Geophysical Prospecting for Petroleum(in Chinese), 41(3):312-316, 320. |
| [52] | Yao Y, Xi X. 2004. Regionalized multi-scale random medium model and its wavefield analysis[J]. Geophysical Prospecting for Petroleum(in Chinese), 43(1):1-7. |
| [53] | Zhang L Q, Zhan Q, Zhu P M, et al. 2004. High-order statistic analysis of seismic dispersed wavefield[J]. Oil Geophysical Prospecting(in Chinese), 39(1):45-49. |
| [54] | Zhou R M, Huang L J, Rutledge J T, et al. 2010. Coda-wave interferometry analysis of time-lapse VSP data for monitoring geological carbon sequestration[J]. International Journal of Greenhouse Gas Control, 4(4):679-686. |
| [55] | Zhu T Y. 2008. Simulation of seismic wave propagation in fractured-anisotropic and viscoelastic media(in Chinese)[Master thesis]. Beijing:Graduate School of Chinese Academy of Sciences. |
| [56] | 曹军, 盖增喜, 张坚,等. 2004. 用于不规则界面多层介质的地震波方法比较研究:不规则地形问题[J]. 地球物理学报, 47(3):495-503, doi:10.3321/j.issn:0001-5733.2004.03.020. |
| [57] | 郭向宇, 凌云, 魏修成. 2002. 近地表散射波的叠后衰减[J]. 石油地球物理勘探, 37(3):201-208. |
| [58] | 韩佳君, 韩立国, 巩向博,等. 2010. 基于波动理论的近地表散射噪声衰减[J]. 世界地质, 29(2):310-313, 322. |
| [59] | 黄雪继. 2003. 地震波散射场相位移法波动方程正演模拟[D]. 北京:中国地质大学(北京). |
| [60] | 雷蕾. 2010. 非均匀介质地震波散射波场正演模拟方法研究[硕士论文]. 青岛:中国石油大学(华东). |
| [61] | 李灿苹, 刘学伟. 2009. 随机-均匀介质地震波振幅属性研究[J]. 石油物探, 48(5):465-469. |
| [62] | 李红星, 陶春辉. 2009. 双相各向异性随机介质伪谱法地震波场特征分析[J]. 物理学报, 58(4):2836-2842. |
| [63] | 李小凡. 2002. 大延伸非均匀介质中地震波全弹性散射理论Ⅱ-弹性波多次散射理论[J]. 力学学报, 34(5):743-755. |
| [64] | 刘恩儒, 岳建华, 刘彦. 2006. 具有离散裂缝空间分布的二维固体中地震波传播的有限差分模拟[J]. 地球物理学报, 49(1):180-188, doi:10.3321/j.issn:0001-5733.2006.01.024. |
| [65] | 刘宁, 孙建国. 2007. 起伏地表条件下的声波散射数值模拟的积分方程法[J]. 吉林大学学报(地球科学版), 37(增刊):61-65. |
| [66] | 刘铁华. 2010. 高精度地震散射波数值模拟[J]. 工程地球物理学报, 7(6):699-703. |
| [67] | 刘铁华. 2012. 地震散射波的高精度数值模拟与振幅分析[J]. 地球物理学报, 55(4):1318-1324, doi:10.6038/j.issn.0001-5733.2012.04.027. |
| [68] | 秦雪霏. 2007. 地震波多次散射波场属性分析[硕士论文]. 长春:吉林大学. |
| [69] | 孙建国. 2006. 声波散射数值模拟的两种新方案[J]. 吉林大学学报(地球科学版), 36(5):863-868. |
| [70] | 孙明, 林君. 2001. 金属矿地震散射波场的数值模拟研究[J]. 地质与勘探, 37(4):68-70. |
| [71] | 肖震, 郑勇, 熊熊. 2014. 尾波干涉法在汶川地震余震定位中的应用[J]. 地震, 34(2):1-11. |
| [72] | 徐基祥. 2014. 地震干涉测量法近地表散射波分离技术[J]. 地球物理学报, 57(6):1910-1923, doi:10.6038/cjg20140622. |
| [73] | 杨旭明, 周熙襄, 王克斌, 等. 2002. 近地表地震散射噪声的正反演方法[J]. 石油物探, 41(3):312-316, 320. |
| [74] | 姚姚, 奚先. 2004. 区域多尺度随机介质模型及其波场分析[J]. 石油物探, 43(1):1-7. |
| [75] | 张丽琴, 詹麒, 朱培民,等. 2004. 地震散射波场的高阶统计分析[J]. 石油地球物理物探, 39(1):45-49. |
| [76] | 朱铁源. 2008. 离散裂缝诱导各向异性黏弹性地震波模拟与特征分析[硕士论文]. 北京:中国科学院研究生院. |
| [77] | 奚先, 姚姚. 2001. 二维随机介质及波动方程正演模拟[J]. 石油地球物理勘探, 36(5):546-552. |
| [78] | 奚先, 姚姚. 2002. 随机介质模型的模拟与混合型随机介质[J]. 地球科学-中国地质大学学报, 27(1):67-71. |
| [79] | 奚先, 姚姚. 2005. 非平稳随机介质模型[J]. 石油地球物理勘探, 40(1):71-75. |
 2016, Vol. 31
2016, Vol. 31