多尺度地震资料综合研究和应用可以更好地实现油藏特征描述,井间地震技术凭借高精度和高分辨率的特点在多尺度地震资料联合应用中起着重要作用(曹丹平等,2010).因其独特的工作环境,井间震源与地面地震震源相比具有不同的特性.除去激发有效波,其激发的部分能量也会沿着井轴方向在钻井液中传播,由于井壁与钻井液的大波阻抗差使得这部分能量一直在钻井液中来回激荡,形成井间地震中的管波.实际井间地震资料中管波为很强的干扰波(刘合等,1998;曹辉,2002).目前消除管波影响的方法有两种:一种是数据采集中使用特殊设备压制管波的产生和接收,另一种是数据处理中根据管波与有效波的差异去除管波.为压制管波产生而设计的井间定向震源(如OYO公司研制的井下轨道式可控震源)几乎不产生管波,其资料可直接进行后续处理,在生产中得到广泛应用.但井间定向震源辐射能量的方向性导致炮记录同相轴连续性差(图 1)(毛中华,2004;何惺华,2006,2008),影响井间地震反射波偏移成像效果.因此,研究井间定向震源能量辐射机理以及波场特征,以及在偏移成像中能量补偿的方法具有很大的研究价值.
 | 图 1 实际定向震源炮记录 Fig. 1 Record of directional source in cross-hole seismic |
1953年Heelan第一次阐述了有限长度圆柱形震源(数值模拟中将其设置为壁上受到对称的横向应力和切向应力的“等效空腔”)产生的辐射能量的理论研究结果(Heelan,1953).1981年Michael Fehler第一次给出了井间声波震源的辐射花样,他指出井中声波测井工具产生的P波和S波的振幅与井轴和传播方向之间的夹角有关,知道这个角度关系,或者辐射花样,对于正确测量波场在两井之间传播时产生的衰减是很有必要的(Fehler and Pearson,1981).1993年刘银斌等人对充液井中不同类型的震源(点涨缩源、径向应力源、切向应力源)激发的弹性波低频远场辐射花样进行了研究和模拟(刘银斌等,1993).2006年何惺华通过研究理论模型的井间合成记录,指出可控震源与检波器的能量方向特性是大入射角反射能量强的主要原因(何惺华,2006).2008年何惺华提出震源能量方向性的改善有利于井间可控震源的推广与应用,并介绍了震源能量辐射花样(何惺华,2008).
井间定向震源的能量辐射花样近似于花生状.激发井所在的平面上,垂直于井轴方向(水平方向)的辐射能量最强,随着与水平方向的夹角(锐角)的增加,辐射能量逐渐减小,大于30°后迅速衰减至零(图 2).通常用辐射能量曲线揭示辐射能量A与最大能量A0及辐射角θ之间的关系,常见的辐射能量曲线有两种:A=A0cosθ和A=A0 .很显然,大于45°后,第二种曲线的能量为零,与实际地震资料的方向特性更加贴近(何惺华,2006,2008;孔庆丰,2006).
.很显然,大于45°后,第二种曲线的能量为零,与实际地震资料的方向特性更加贴近(何惺华,2006,2008;孔庆丰,2006).
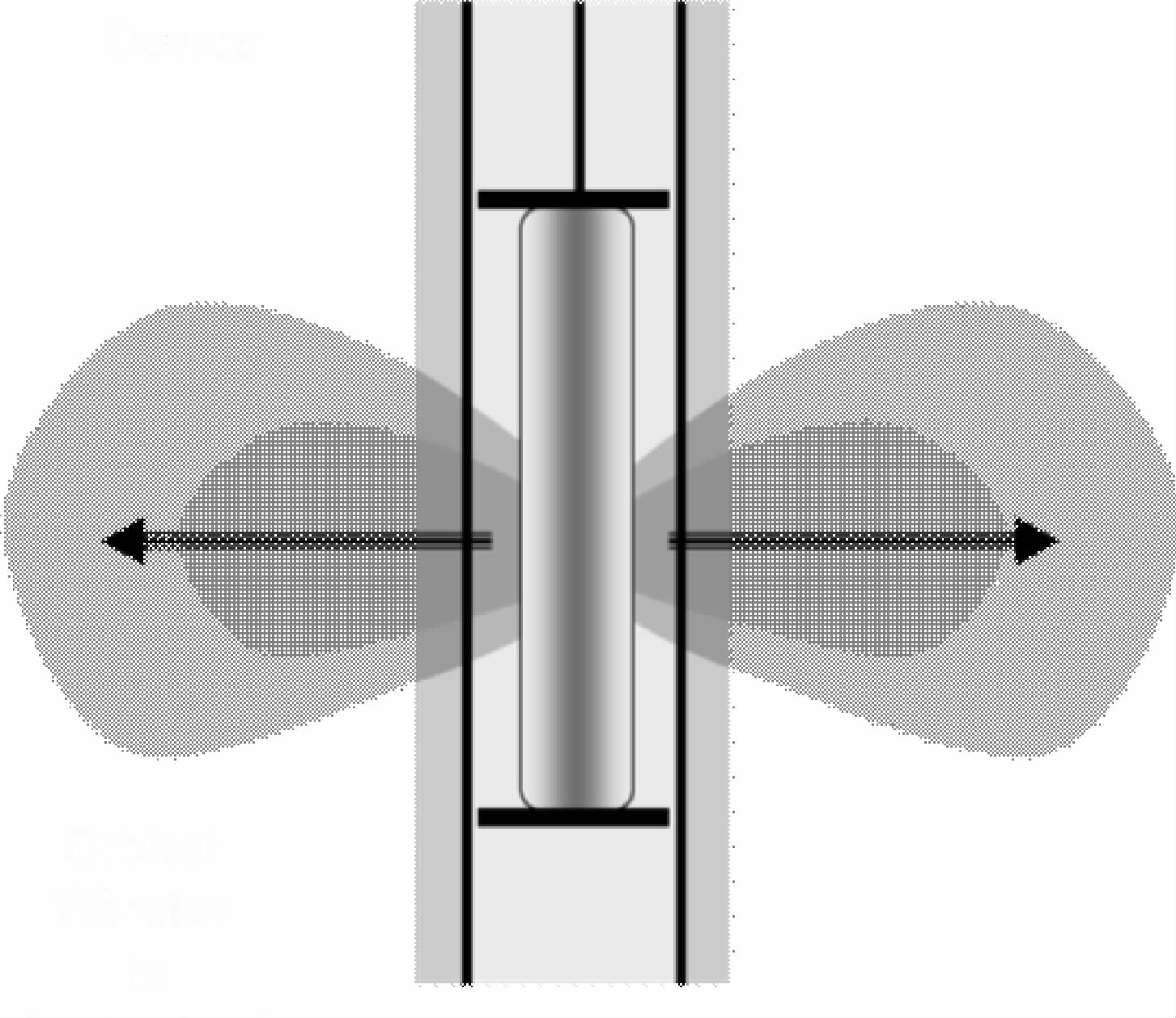 | 图 2 震源能量辐射花样(何惺华,2006) Fig. 2 Energy radiation pattern of source |
目前,模拟井间定向震源的方法主要有两种:吸收衰减层法和圆形震源阵列法.吸收衰减层法假设震源周围为具有衰减特性的海绵层,地震波在其中的传播满足黏弹性介质波动方程.在不同的方向上采用不同的渐变衰减因子,使地震波离开震源一定距离后具有方向性.圆形震源阵列法则用震源附近一定范围内的质点振动来模拟理论定向震源的方向性.根据定向震源的辐射特性写出近源质点的振动方程解析式,在波动方程有限差分模拟中直接给出震源附近圆形区域内质点的波场值,引起其他质点的振动,具有一定的方向性.
为了灵活地模拟实际井间地震采集中定向震源能量的方向性,将两种定向震源模拟方法结合在一起.首先,利用有限差分法离散声波方程模拟对比点源和无方向性圆形震源阵列的接收波场,验证圆形震源阵列模拟井间定向震源的合理性;其次,确定了模拟定向震源的圆形震源阵列半径;然后,定性分析了井间距、方向性参数对接收波场能量分布的影响.数值模拟发现圆形震源阵列模拟的地震波场具有一定方向性,但与实际地震记录的方向性相比较弱.最后联合采用圆形震源阵列与吸收衰减层法进行正演模拟,地震波场方向性得到了明显改善.实际速度场正演模拟展示了反射波能量分布特征与震源方向特性的密切关系.
1 方法原理1.1 圆形震源阵列法将围绕震源位置(x0,z0)的圆形区域内的网格点划为近源区.圆形区域的半径记为阵列半径,即圆形区域内各方向上包含的网格点数的最大值.圆形震源阵列法在近源区各网格点给定随方向变化而改变的初始振动函数,通过时间空间上的波场外推来模拟震源辐射能量的方向性.近源区内网格点的初始振动由震源辐射能量曲线确定的方向性参数a(θ)和地震波从震源传播到该网格点的时间τ(x,z)(杜世通,2004;姜弢等和,2004,2006,2008;汪仁富等,2011;刘福烈等,2013)共同确定(孔庆丰,2015).设网格点位置坐标为(x,z),则其振动函数为
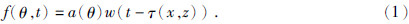
方向性参数采用 ,近源区网格点的方向性参数和延迟时间为
,近源区网格点的方向性参数和延迟时间为
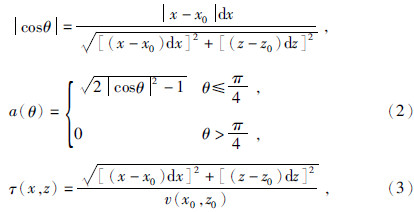
吸收衰减法是在震源附近一定区域内设置海绵层,对不同方向的地震波进行不同程度的吸收衰减.借鉴完全匹配层吸收边界条件的思想(王守东,2003;王永刚等,2007;左莹,2009;智敏等,2013),将吸收衰减层法引入到声波波动方程.首先引入中间变量p,将二维声波方程降阶为二维一阶双曲型声波波动方程为

然后分解波场,令p=px+pz,加入衰减因子αi,得到
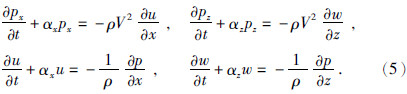
将正演模型分为三个区域:近源衰减区、正常波场延拓区和边界吸收区.近源衰减区内,x方向不做衰减,只对z方向衰减,即αx=0.αz随震源—网格点连线与水平方向间的夹角的改变而改变,若改变衰减系数αz的表达形式,震源的方向性将随之改变.一般可取 ,其中,α0是常值,其大小决定能量衰减的程度,L是井间距,h为纵向衰减范围,即震源吸收层厚度,其与子波长度有关,为近源衰减区内网格点到震源的距离,且n≤h.波场延拓区不做衰减,ax、az均设置为0.边界吸收区内,ax、az的设置参照Collino(2001)提出的纵波PML吸收衰减因子(图 3).
,其中,α0是常值,其大小决定能量衰减的程度,L是井间距,h为纵向衰减范围,即震源吸收层厚度,其与子波长度有关,为近源衰减区内网格点到震源的距离,且n≤h.波场延拓区不做衰减,ax、az均设置为0.边界吸收区内,ax、az的设置参照Collino(2001)提出的纵波PML吸收衰减因子(图 3).
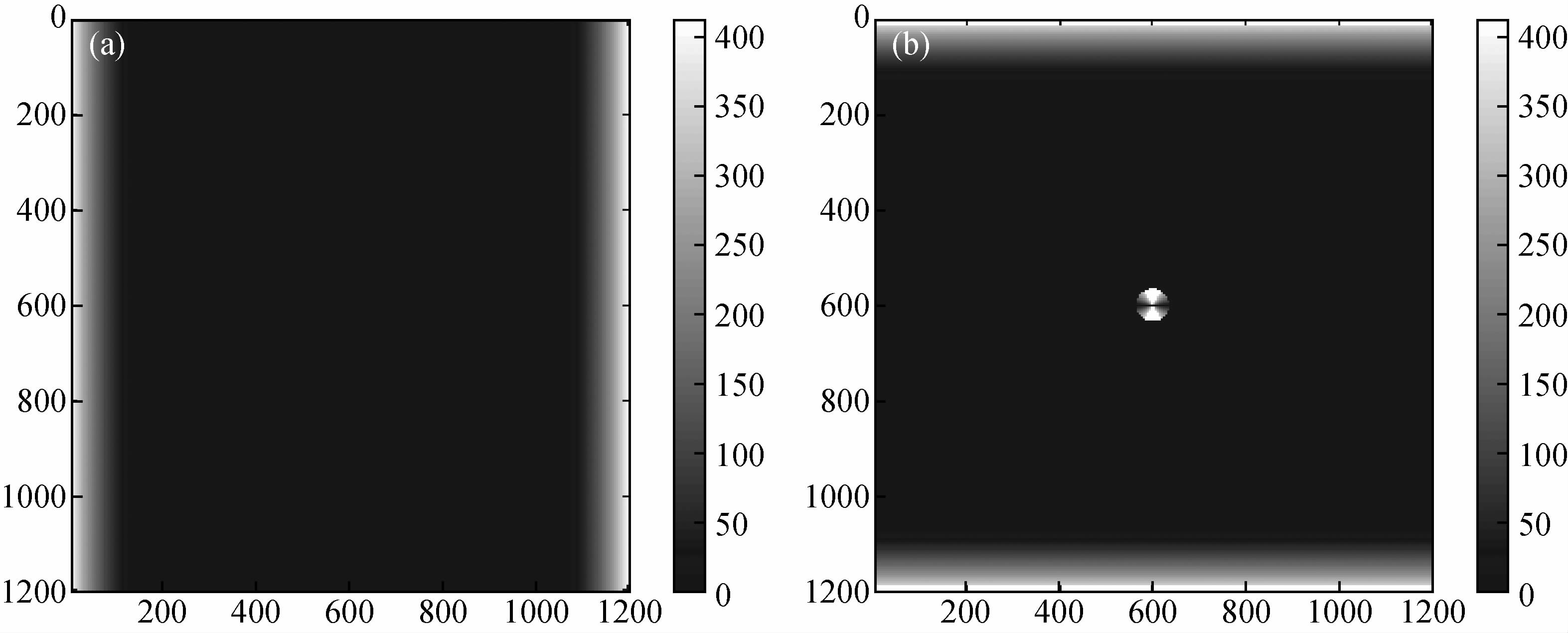 | 图 3 衰减吸收系数分布图 Fig. 3 The map of attenuation coefficient |
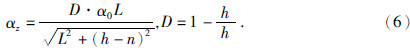
 | 图 4 改进的衰减吸收系数分布图 Fig. 4 The map of improved attenuation coefficient |
基于上述原理,利用有限差分法求解二维声波方程,编制相应的应用程序.首先对均匀介质进行模拟分析,验证模拟数据与理论能量分布的一致性.在证实方法可行后,对层状介质进行了模拟,分析方向性与反射波能量的关系.最后对胜利油田某实际井间地质剖面进行模拟分析,所产生的井间地震记录与实际井间地震剖面的能量分布相吻合.
值得注意的是采用的PML吸收边界(王春燕,2007)对边界地震道能量有一定影响.此外模拟中采用了如下的有限差分稳定性条件为(吴国忱和梁锴,2005;潘海滨和孙萍,2009):
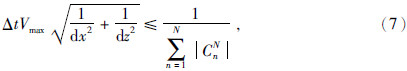
为了验证用圆形震源阵列代替点源的合理性,设计均匀无限介质模型,分别用点源和无方向性圆形阵列震源进行地震波激发,检测两种方法是否是一致的.模型大小为1000 m×1000 m,速度为3000 m/s,网格间距为1 m,边界吸收区厚度为150 m.震源点位置为(500 m,500 m),第一个检波点埋深为200 m,检波点间距为3 m,共设置201个检波点(图 5).震源采用120 Hz的雷克子波.时间步长为0.2 ms,总的记录时间为160 ms.
 | 图 5 观测系统简图 Fig. 5 Geometry |
首先讨论阵列半径对无方向性圆形震源阵列与点源拟合程度的影响.由于炮记录受球面扩散影响,能量分布随检波器而变化.对炮记录进行球面扩散补偿,计算各检波点接收到的能量并将各检波点位置换算成角度,从而得到图 6所示的能量随角度变化的曲线,其中阵列半径为0时的圆形震源阵列为点源.可见各方向上能量基本一致,且阵列半径越大,对点源的拟合程度越差,阵列半径为4时与点源的能量分布吻合程度最高,阵列半径为8时与点源的能量分布相差较大(图 6),因此,圆形震源阵列半径大小应接近4.
 | 图 6 阵列半径对接收波场能量分布的影响 Fig. 6 The impact of the array radius on wave field energy distribution |
进一步分析井间距对无方向性震源接收波场的能量分布特征的影响.对不同井间距的炮记录进行球面扩散补偿,计算各检波点接收到的能量并将各检波点位置换算成角度,从而得到图 7所示的不同井间距下能量随方向的变化曲线.可以看到各角度的能量基本一致,不具有方向性.由此可知震源的方向性是引起井间地震记录中能量方向性变化的主要原因.
 | 图 7 井间距对接收波场能量分布的影响 Fig. 7 The impact of the well spacing on wave field energy distribution |
同样采用均匀模型,用不同半径的方向性震源激发地震波.表 1为圆形震源阵列的半径及方向性参数.对模拟得到的炮集资料进行归一化,然后进行球面扩散补偿,再提取直达波的能量和角度,得到图 8所示的直达波能量随方向分布曲线,可以看出阵列半径越大接收波场的方向性越接近理论方向性(图 8),但当角度大于40°时,能量分布相差较大.
|
|
表 1 正演模拟参数 Table 1 Forward modeling parameter |
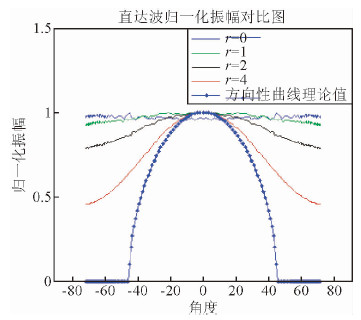 | 图 8 阵列半径对定向震源波场能量分布的影响 Fig. 8 The impact of the array radius on the directional source’s wave field energy distribution |
考虑到介质不可能是大规模均匀的,阵列半径不能太大,不妨设模拟中阵列半径为4.用不同方向性震源进行模拟,表 2为方向震源参数.模拟的井间地震数据经归一化和球面扩散补偿后,对比能量分布(图 9)发现,具有不同方向性的定向震源产生的波场能量具有不同的方向性,震源方向性越强,产生的直达波方向性越强.
|
|
表 2 方向震源参数 Table 2 Directional source parameter |
 | 图 9 方向性参数对直达波能量分布的影响 Fig. 9 The impact of the directional parameter on direct wave energy distribution |
进一步分析井间距对定向震源接收波场的能量分布特征的影响.对不同井间距(表 3)的炮记录进行球面扩散补偿,计算各检波点接收到的能量并将各检波点位置换算成角度,从而得到图 10所示的不同井间距下能量随方向的变化曲线,可以发现井间距不同时,相同方向性定向震源的接收波场入射角范围不同,能量分布特征也不相同.井间距较小时,能量分布特征相近,随井间距不断增加,直达波的方向性逐渐减弱.
|
|
表 3 方向震源参数 Table 3 Directional source parameter |
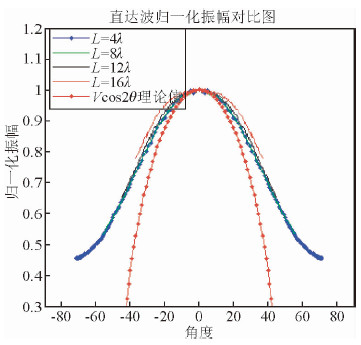 | 图 10 井间距对直达波能量分布的影响 Fig. 10 The impact of the well spacing on direct wave energy distribution |
实际地震资料处理中多使用反射波成像,因此进一步分析定向震源对接收波场中反射波能量分布的影响是十分必要的.在双层介质中模拟井间定向震源激发的波场,模型大小为1000 m×1000 m,界面埋深为600 m,第一层介质速度为2500 m/s,第二层介质速度为3000 m/s,网格间距为1 m,PML边界吸收区厚度为150 m.震源点位置为(500 m,500 m),第一个检波点埋深为300 m,检波点间距为2 m,共设置201个检波点.震源采用120 Hz的雷克子波.时间步长为0.2 ms,总的传播时间为240 ms.分别讨论井间距和有方向性圆形震源阵列的方向性参数对接收波场中反射波能量分布特征的影响(表 4、表 5).
|
|
表 4 不同井间距模拟参数 Table 4 Simulation parameters of different well spacing |
|
|
表 5 震源方向性参数 Table 5 Source directivity parameter |
对不同井间距炮记录进行去直达波、归一化、球面扩散补偿等处理,将检波点位置转换为角度,得到图 11反射波能量分布曲线,对比处理结果发现,随井间距的增加,震源入射角范围不同,反射波所具有的方向性也不相同.
 | 图 11 井间距对反射波能量分布的影响 Fig. 11 The impact of the well spaceing on reflected wave energy distribution |
对不同方向性震源激发的炮记录进行去直达波、归一化、球面扩散补偿等处理,将检波点位置转换为角度,得到图 12反射波能量分布曲线,对比发现,不同方向性参数震源产生的接收波场方向性不同,震源的方向性越强则接收波场中反射波能量分布的方向性越强.
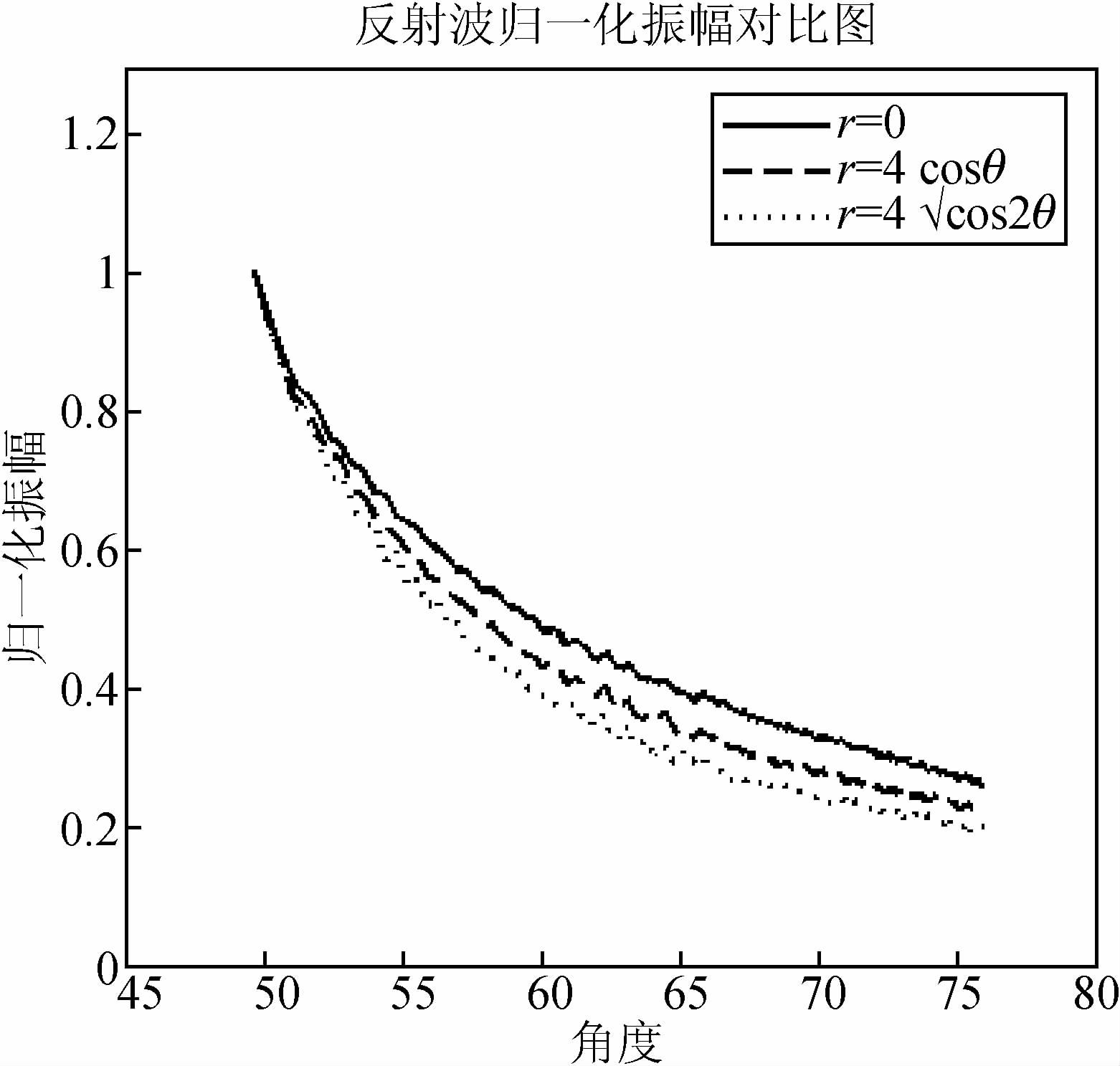 | 图 12 方向性参数对反射波能量分布的影响 Fig. 12 The impact of the directional parameter on reflected wave energy distribution |
对比有、无方向性震源激发的炮记录发现模拟波场中直达波具有较强的方向性,但与实际资料相比,反射波能量方向性较弱(图 13).
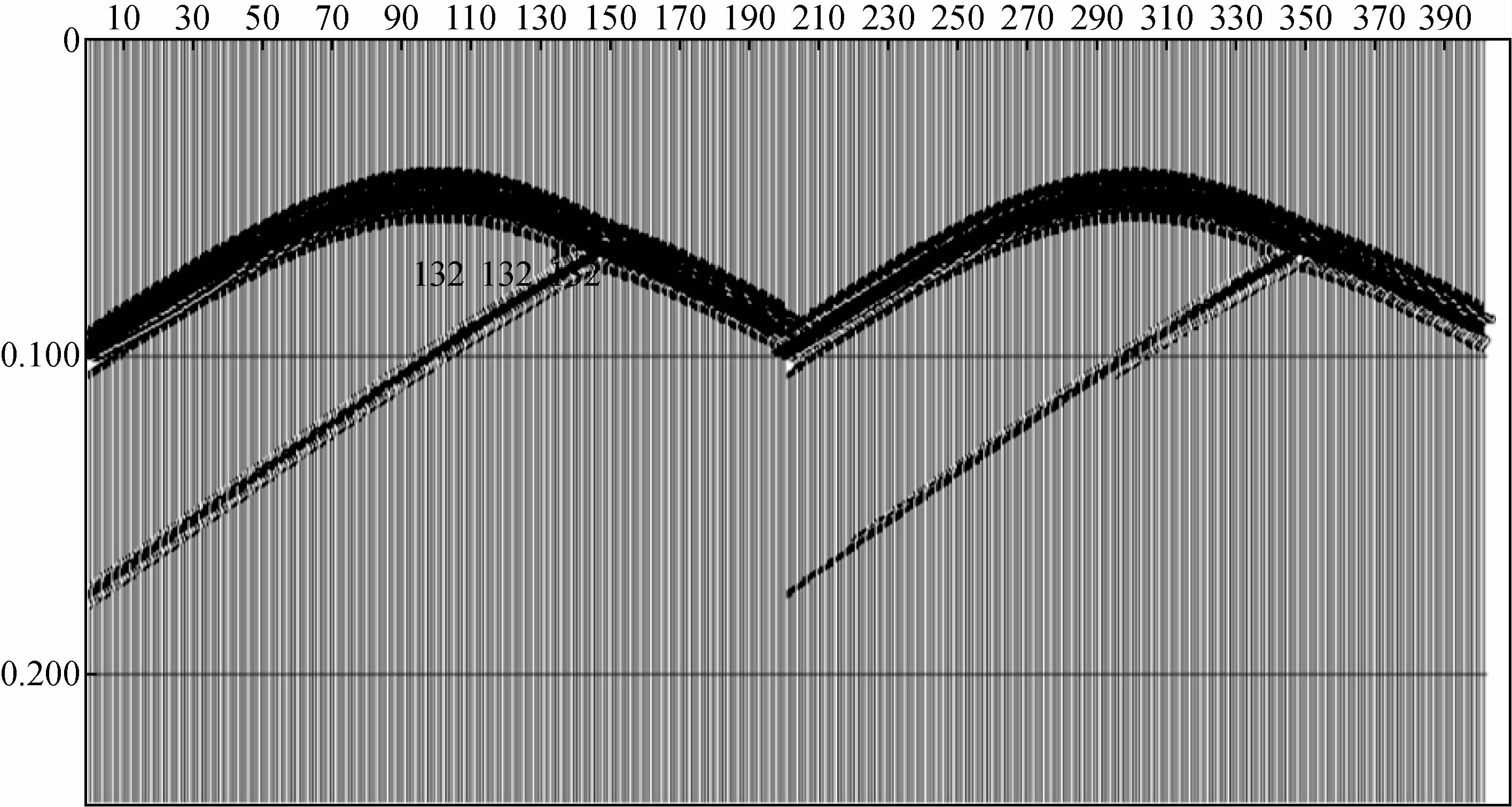 | 图 13 有方向性圆形震源阵列激和无方向性圆形震源阵列激发的炮记录 Fig. 13 Record of non-directional circle array and directional circle array |
联合使用圆形震源阵列法和改进的吸收衰减层法模拟震源的方向特性.同样采用双层介质,模型大小为1000 m×1000 m,界面埋深为600 m,第一层介质速度为2500 m/s,第二层介质速度为3000 m/s,网格间距为1 m,PML边界吸收区厚度为150 m.震源点位置为(500 m,500 m),井间距为100 m,第一个检波点埋深为300 m,检波点间距为2 m,共设置201个检波点.震源采用120 Hz的雷克子波,最大波长为25 m.时间步长为0.2 ms,总的传播时间为240 ms.近源衰减区半径为25 m,纵向衰减系数αz=α0Dsinθ,D=1- ,其中α0=300,h=25 m,n为近源区内网格点到震源点位置的距离.分析得到的正演模拟波场(图 14)发现,相对只有圆形震源阵列方法,联合模拟的直达波能量衰减更快,反射波的能量随偏移距(角度)的增加衰减速度变快.
,其中α0=300,h=25 m,n为近源区内网格点到震源点位置的距离.分析得到的正演模拟波场(图 14)发现,相对只有圆形震源阵列方法,联合模拟的直达波能量衰减更快,反射波的能量随偏移距(角度)的增加衰减速度变快.
 | 图 14 无方向性圆形震源阵列和联合模拟震源激发的炮记录 Fig. 14 Record of modeling by non-directional circle array and by directional circle array and attention layer |
联合两种方法对某实际速度场(图 15)进行正演模拟.速度场大小为371 m×1801 m,网格间距为1m.震源点位置为(150 m,1400 m),井间距为100 m,第一个检波点埋深为900 m,检波点间距为3 m,共设置301个检波点.震源采用120 Hz的雷克子波.时间步长为0.2 ms,总的传播时间为0.4 s.圆形震源阵列半径为4 m,方向性参数为 ,近源衰减层半径为25 m,近源衰减层纵向衰减系数αz=α0Dsinθ,D=1-
,近源衰减层半径为25 m,近源衰减层纵向衰减系数αz=α0Dsinθ,D=1- ,其中α0=300,h=25 m,n为近源区内网格点到震源点位置的距离.
,其中α0=300,h=25 m,n为近源区内网格点到震源点位置的距离.
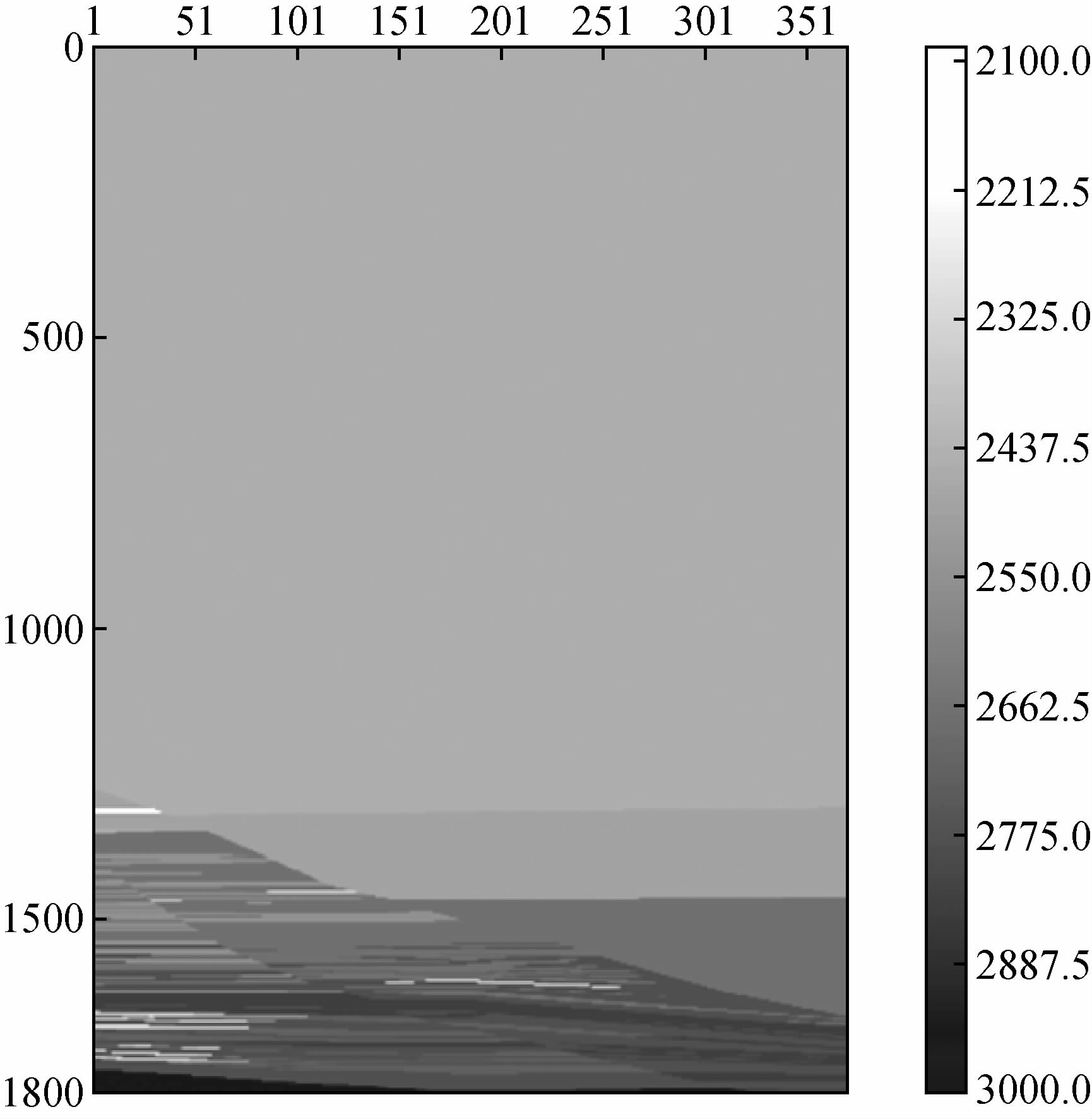 | 图 15 实际速度场 Fig. 15 Factual Velocity |
 | 图 16 圆形震源阵列法和联合模拟结果对比 Fig. 16 Contrast results modeling by circle array with by both two methods |
对比有、无方向性震源激发的炮记录发现模拟定向震源激发的波场具有较强的方向性.反射波能量还受界面倾角和几何扩散等影响,如何提取实际接收波场中受定向震源影响的方向特性并进行能量补偿有待深入研究.
3 结论方向性震源在介质中激发的地震波具有一定的方向性.通过对圆形震源阵列法和吸收衰减层法的数值模拟分析,以及与实际资料的对比,可知圆形震源阵列法模拟井间定向震源是合理的,并初步确定了模拟定向震源的圆形震源阵列的最佳半径为4.通过井间距、方向性参数对接收波场能量分布的影响分析可知角度震源方向性的主要参量.由于圆形震源阵列法半径有限,制约了正演的方向性差异,引入改进的吸收衰减层法,联合两种方法进行模拟,可以较好地调节接收波场的方向性.在此仅仅考虑的是均匀介质和水平界面,在实际速度场模拟中界面倾角等可能对能量分布特征也有很大的影响,这是进一步研究方向性震源能量辐射特性的一个方向.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Berraki M, Baroni A. 2004. Numerical modeling of a buried directional seismic source[C].//SEG Int'l Exposition and 74th Annual Meeting. Denver, Colorado:SEG. |
| [2] | Cao D P, Yin X Y, Liang K. 2010. Characteristics analysis of multi-scale seismic data based on forward modeling of one-way waves[J]. Progress in Geophysics(in Chinese), 25(4):1306-1312, doi:10.3969/j.issn.1004-2903.2010.04.019. |
| [3] | Cao H. 2002. Current status of crosswell seismic technology[J]. Progress in Exploration Geophysics(in Chinese), 25(6):6-10. |
| [4] | Chen K Y. 2010. Study on perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum(in Chinese), 49(5):472-477. |
| [5] | Du S T. 2004. The finite unit method of cross-hole seismic observations modeling and migration[J]. Petroleum Geophysics(in Chinese), 2(4):78-82. |
| [6] | Fehler M, Pearson C F. 1981. Acoustic Radiation Patterns for Borehole Sources[M]. Los Alamos:Los Alamos National Laboratory. |
| [7] | Heelan P A. 1953. Radiation from a cylindrical source of finite length[J]. Geophysics, 18(3):685-696. |
| [8] | He X H. 2005. Reflection analysis for cross-well seismic[J]. Petroleum Geophysics(in Chinese), 3(4):1-8. |
| [9] | He X H. 2006. Reflection analysis for cross-well seismic[J]. Geophysical Prospecting for Petroleum(in Chinese), 45(5):520-526. |
| [10] | He X H. 2008. Cross-well Seismic(in Chinese)[M]. Beijing:Petroleum Industry Press. |
| [11] | Jiang T. 2006. Study on seismic beam-forming method based on phased-array vibrator system(in Chinese)[Ph. D. thesis]. Changchun:Jilin University. |
| [12] | Jiang T, Lin J, Chen Z B, et al. 2004. Seismic beam-forming in phased array of vibroseis[J]. Journal of Jilin University(Information Science Edition)(in Chinese), 22(3):181-184. |
| [13] | Jiang T, Lin J, Chen Z B, et al. 2006. High signal-to-noise ratio detection of horizontal layer underground medium with phased-array vibroseis[J]. Chinese Journal of Scientific Instrument(in Chinese), 27(11):1369-1372. |
| [14] | Jiang T, Lin J, Yang D, et al. 2008. Analysis of directional seismic signal based on phased-array vibrator system[J]. Chinese Journal of Geophysics(in Chinese), 51(5):1551-1556, doi:10.3321/j.issn:0001-5733.2008.05.030. |
| [15] | Kong Q F. 2006. Numerical modeling of crosswell seismic wave-field and its application[J]. Progress in Exploration Geophysics(in Chinese), 29(5):333-336. |
| [16] | Kong Q F. 2015. The numerical modeling of directional source in crosshole seismic[J]. Progress in Geophysics(in Chinese), 30(1):274-278, doi:10.6038/pg20150139. |
| [17] | Liu F L, Xu F, Li Z Y, et al. 2013. Source pattern parameters theoretical analysis[J]. Oil Geophysical Prospecting(in Chinese), 48(1):1-7. |
| [18] | Liu H, Wang Y P, Sui J, et al. 1998. Crosswell Seismic Technology Abroad(in Chinese)[M]. Beijing:Petroleum Industry Press. |
| [19] | Liu Y B, Li Y M, Wu R S, et al. 1993a. Radiative energies from downhole Source and array source[J]. Oil Geophysical Prospecting(in Chinese), 28(4):389-395 |
| [20] | Liu Y B, Li Y M, Wu R S, et al. 1993b. Far-field radiation pattern of downhole source and array source[J]. Oil Geophysical Prospecting(in Chinese), 28(4):379-388 |
| [21] | Mao Z H. 2004. Cross-hole seismic equipments in Shengli Oilfield[J]. Equipment for Geophysical Prospecting(in Chinese), 14(3):154-157. |
| [22] | Pan H B, Sun P. 2009. Frequency dispersion analysis and correction strategy of staggered-grid seismic wave modeling[J]. Marine Geology Letters(in Chinese), 25(6):36-41. |
| [23] | Pan H B, Wang C B, Chen K Y. 2009. Diversity and unitarity of knott equation expression forms at elastic interface[J]. Computer Applications of Petroleum(in Chinese),(3):12-15, 19. |
| [24] | Wang C Y. 2007. The calculation of the seismis wave-field with high-order staggered-grid finite-difference scheme(in Chinese)[Ph. M. thesis]. Chengdu:Chengdu University of Technology. |
| [25] | Wang R F, Xu F, Liu F L, et al. 2011. Quantitative analysis of source array effectiveness based on wave equation[J]. Oil Geophysical Prospecting(in Chinese), 46(4):538-544. |
| [26] | Wu G C, Liang K. 2005. Quasi P-wave forward modeling in frequency-space domain in VTI media[J]. Oil Geophysical Prospecting(in Chinese), 40(5):536-544. |
| [27] | 曹丹平, 印兴耀, 梁锴. 2010. 基于单程波正演模拟的多尺度地震资料特征分析[J]. 地球物理学进展, 25(4):1306-1312, doi:10.3969/j.issn.1004-2903.2010.04.019. |
| [28] | 曹辉. 2002. 井间地震技术发展现状[J]. 勘探地球物理进展, 25(6):6-10. |
| [29] | 陈可洋. 2010. 完全匹配层吸收边界条件研究[J]. 石油物探, 49(5):472-477. |
| [30] | 杜世通. 2004. 井间地震观测数据模拟和偏移的有限单元法[J]. 油气地球物理, 2(4):78-82. |
| [31] | 何惺华. 2005. 井间地震中的反射波分析[J]. 油气地球物理, 3(4):1-8 |
| [32] | 何惺华. 2006. 对井间地震反射波的分析[J]. 石油物探, 45(5):520-526. |
| [33] | 何惺华. 2008. 井间地震[M]. 北京:石油工业出版社. |
| [34] | 姜弢. 2006. 基于相控震源的地震波定向方法研究[博士论文]. 长春:吉林大学. |
| [35] | 姜弢, 林君, 陈祖斌,等. 2004. 相控震源地震波定向技术[J]. 吉林大学学报(信息科学版), 22(3):181-184. |
| [36] | 姜弢, 林君, 陈祖斌,等. 2006. 相控震源对水平层状地下介质的高信噪比检测[J]. 仪器仪表学报, 27(11):1369-1372. |
| [37] | 姜弢, 林君, 杨冬,等. 2008. 相控震源定向地震波信号分析[J]. 地球物理学报, 51(5):1551-1556, doi:10.3321/j.issn:0001-5733.2008.05.030. |
| [38] | 孔庆丰. 2006. 井间地震波场数值模拟技术研究与应用[J]. 勘探地球物理进展, 29(5):333-336. |
| [39] | 孔庆丰. 2015. 井间地震方向性震源模拟方法[J]. 地球物理学进展, 30(1):274-278, doi:10.6038/pg20150139. |
| [40] | 刘福烈, 徐峰, 李志勇,等. 2013. 组合激发参数理论分析[J]. 石油地球物理勘探, 48(1):1-7. |
| [41] | 刘合, 王玉普, 隋军,等. 1998. 国外井间地震技术[M]. 北京:石油工业出版社. |
| [42] | 刘银斌, 李幼铭, 吴如山,等. 1993a.井下震源和阵列震源的辐射能量[J]. 石油地球物理勘探, 28(4):389-395 |
| [43] | 刘银斌, 李幼铭, 吴如山,等. 1993b.井下震源和阵列震源的远场辐射花样[J]. 石油地球物理勘探, 28(4):379-388 |
| [44] | 毛中华. 2004. 胜利油田井间地震装备技术[J]. 物探装备, 14(3):154-157. |
| [45] | 潘海滨, 孙萍. 2009. 交错网格波场数值模拟频散分析与校正策略[J]. 海洋地质动态, 25(6):36-41. |
| [46] | 潘海滨, 王成彪, 陈开远. 2009. 弹性界面Knott方程表达形式的差异性和统一性[J]. 石油工业计算机应用,(3):12-15, 19. |
| [47] | 王春燕. 2007. 高阶交错网格有限差分地震波场计算[硕士论文]. 成都:成都理工大学. |
| [48] | 汪仁富, 徐峰, 刘福烈,等. 2011. 波动方程震源组合模拟定量研究[J]. 石油地球物理勘探, 46(4):538-544. |
| [49] | 吴国忱, 梁锴. 2005. VTI介质频率-空间域准P波正演模拟[J]. 地球物理学进展, 40(5):536-544. |
| [50] | 智敏, 张广忠, 杨光明,等. 2013. 一阶声波方程高阶交错网格有限差分数值模拟方法[J]. 黑龙江科技信息,(34):84-85. |
| [51] | 左莹. 2009. 基于高阶交错网格的有限差分地震波场数值模拟[硕士论文]. 西安:长安大学. |
 2016, Vol. 31
2016, Vol. 31

