2. 国土资源部应用地球物理综合解释理论开放实验室-波动理论与成像技术实验室, 长春 130026
2. Laboratory for Integrated Geophysical Interpretation Theory of Ministry for Land and Resources, Changchun 130026, China
自从地震勘探技术诞生以来,其观测数据的存储技术主要经历了五个阶段的发展(罗福龙,2006).①光纸存储技术;②模拟磁带存储技术;③数字开盘磁带存储技术;④盒式磁带存储技术;⑤磁盘存储技术.同样的,其记录格式也在不断完善.SEG(美国地球物理学家协会)发布了多种不同的记 录格式,1975年SEG发布了SEG-Y rev 0数据交换格式(Barry et al.,1975).由于其定义类型单一,使用读、写较方便,常用于野外采集、室内数据传递与处理,已成为各个石油公司内部与相互之间数据交换的标准,在地球物理界应用广泛(郑秀芬等,2009;孙章庆等,2009,2012;张东良等,2011).目前的最新版本是2002年发布的SEG-Y rev 1地震数据记录格式(Norris and Faichney,2002).
现代微机的功能强大,许多地震数据的处理与解释直接在微机中进行.由于知识产权保护的原因,商业软件的源代码不能被普通用户阅读并自由使用.而随着地震数据处理方法的不断发展,用户对地震数据自由存取的需求逐步提高.通常地震数据是以IBM工作站格式存储的,由于微机和工作站的CPU架构不同,微机不能直接进行读取和利用.因此,地震数据经常在工作站与微机间进行转化(Bl and ,1993; Kahan,1997).不同CPU架构的计算机平台有各自统一的浮点数格式(IBM,1967,1974; IEEE,1985,2008),这就涉及到不同浮点数格式之间的相互转化(符茂松,2011;詹泽东等,2011).
虽然有一些在不同系统环境下应用各类编程语言对SEG-Y格式进行的解析与转化,但是依然存在不少问题.一是他们仅针对SEG-Y格式中的小部分问题进行具体介绍,并没有给出完整的转化方法;二是许多编程语言的可移植性较低,对于用户需要在多种操作系统间进行处理与操作的需求不能满足.为了解决上述存在的问题,本文通过分析SEG-Y格式各部分的结构,同时利用C语言的位操作能力,结合C代码的可移植性,将SEG-Y格式文件进行转化,从而达到在不同CPU架构的计算机中自由读取地震数据进行处理与解释的目的.
1 SEG-Y格式基本结构SEG-Y rev 1数据交换格式的标准磁盘格式如表 1中所示.与1975的SEG-Y rev 0标准相比,扩展的3200字节文本文件头是新标准在结构上做的最大改变.一个SEG-Y文件按存储顺序包含1个3200字节EBCDIC编码的文本文件头C卡;1个400字节的二进制头文件;0个或多个扩展的文本文件头;最后是所有炮的道记录,每一道由1个240字节的道头和道样点值组成.
|
|
表 1 SEG-Y rev 1标准磁盘文件格式 Table 1 SEG-Y rev 1 standard disk file format |
为了对SEG-Y格式进行转化,首先需要一定的计算机基础和C语言编程基础.下面介绍预备知识和SEG-Y文件的各部分转化方法.
2.1 字节序的概念字节序便是多字节数据在内存中的寄存次序.对于单一的字节,大部分CPU的处理方式通常是相同的.但对于多字节数据,在不同架构的CPU上的存放方式有三种:小端序(Little-Endian)、大端序(Big-Endian)和混合序(Middle-endian).其中小端序和大端序是应用最为普遍的两种存放方式.
小端序(Little-Endian)就是低字节排放在内存的低地址端,高字节存在高地址端.而大端序(Big-Endian)正好相反.例如在一个32位计算机中,整形数通常占4个字节.故对于十六进制整形数0x12345678,在不同字节序的系统中,存储形式如图 1所示:
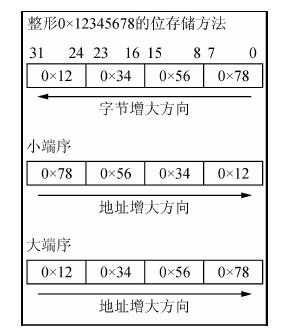 |
图 1 十六进制整形0x12345678在小、
大端序中的表示方法 Fig. 1 Hexadecimal integer 0x12345678 representing method in little or big endian |
可以通过下面的代码来判断CPU是属于哪种字节序:void JudgeEndian(){
short int a = 0x1234;
char b = *(char *)& a; }
当b==0x12时,则CPU是大端序;当b==0x34时,CPU是小端序.通常的微机CPU都是小端序,SUN工作站是大端序.在SEG-Y rev 1标准中规定所有二进制值都采用大端序进行存储.本文叙述的是将SEG-Y文件转换为微机可以处理的数据.即通过位序交换来转化大小端模式,达到读取、修改和存储数据的目的.
2.2 文本文件头的转化3200字节文本文件头是采用EBCDIC格式编码,记录了系统的硬件信息.EBCDIC卷头包含了40条,每条以大写字母C开头共80字节的记录卡.这类记录可使使用者讯速找到有效信息,增添文本可读性.但是,EBCDIC格式编码并不能在微机中直接显示,需要将文本转换为ASCII编码才能被使用者阅读.
转化代码
static unsigned char a2e[256] = {0,1,2,3,55,45,46,47,22,5,37,11,12,13,14,15,16,17,18,19,60,61,50,38,24,25,63,39,28,29,30,31,64,79,127,123,91,108,80,125,77,93,92,78,107,96,75,97,240,241,242,243,244,245,246,247,248,249,122,94,76,126,110,111,124,193,194,195,196,197,198,199,200,201,209,210,211,212,213,214,215,216,217,226,227,228,229,230,231,232,233,74,224,90,95,109,121,129,130,131,132,133,134,135,136,137,145,146,147,148,149,150,151,152,153,162,163,164,165,166,167,168,169,192,106,208,161,7,32,33,34,35,36,21,6,23,40,41,42,43,44,9,10,27,48,49,26,51,52,53,54,8,56,57,58,59,4,20,62,225,65,66,67,68,69,70,71,72,73,81,82,83,84,85,86,87,88,89,98,99,100,101,102,103,104,105,112,113,114,115,116,117,118,119,120,128,138,139,140,141,142,143,144,154,155,156,157,158,159,160,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,202,203,204,205,206,207,218,219,220,221,222,223,234,235,236,237,238,239,250,251,252,253,254,255 }; static unsigned char e2a[256] = {0,1,2,3,156,9,134,127,151,141,142,11,12,13,14,15,16,17,18,19,157,133,8,135,24,25,146,143,28,29,30,31,128,129,130,131,132,10,23,27,136,137,138,139,140,5,6,7,144,145,22,147,148,149,150,4,152,153,154,155,20,21,158,26,32,160,161,162,163,164,165,166,167,168,91,46,60,40,43,33,38,169,170,171,172,173,174,175,176,177,93,36,42,41,59,94,45,47,178,179,180,181,182,183,184,185,124,44,37,95,62,63,186,187,188,189,190,191,192,193,194,96,58,35,64,39,61,34,195,97,98,99,100,101,102,103,104,105,196,197,198,199,200,201,202,106,107,108,109,110,111,112,113,114,203,204,205,206,207,208,209,126,115,116,117,118,119,120,121,122,210,211,212,213,214,215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,123,65,66,67,68,69,70,71,72,73,232,233,234,235,236,237,125,74,75,76,77,78,79,80,81,82,238,239,240,241,242,243,92,159,83,84,85,86,87,88,89,90,244,245,246,247,248,249,48,49,50,51,52,53,54,55,56,57,250,251,252,253,254,255 }; unsigned char A2E(const unsigned char c){return a2e[c];
} unsigned char E2A(const unsigned char c){return e2a[c];
}在此调用自定义函数E2A(char string)和A2E(char string)来完成EBCDIC编码与ASCII编码之间的相互转换.
2.3 二进制文件头的转化在400字节二进制文件头中包含了描述全部数据信息的2字节或4字节的整形参数数值.例如像采样点数、采样间隔、道长和格式码等重要信息均记录在此.由于在SEG-Y数据格式中,数据按大端序排列,故读取整形数值时需先进行位交换,变为微机的小端序,然后再进行读取.其转换方法如下:
对于2字节位换序
short swap2byte(short value){ short svalue; svalue =((value & 0xff00)>> 8)|((value & 0x00ff)<< 8); return svalue; }对于4字节位换序
int swap4byte(int value){ int svalue;svalue =((value & 0xff000000)>> 24)|((value & 0x00ff0000)>> 8)|
((value & 0x0000ff00)<< 8)|((value & 0x000000ff)<< 24);
return svalue; }转换完位序之后,将转换后的值直接赋给整形变量即可.在标准的400字节二进制文件头中,前12字节包含了3个4字节的整形数值,后面的388字节包含了194个2字节的整形数值.故我们可以定义如下结构体变量来任意存储和改写二进制文件头:
struct s400 { int a1[3]; short a2[194]; }s400_1;通过位序交换操作后,将数据存入结构体变量s400_1中,就完成了二进制文件头的转化与存储.用户可根据自己的需要,来设定所有变量的值.
2.4 道头的转化道头中以2字节或4字节的两位互补整形数据共240字节来存储道属性信息,其中前180字节的内容,新SEG-Y标准与老标准是一致的,例如线号、道号、CDP号和物理坐标等.而对于后80个字节,新标准为了便于处理的需要对每个字节都分配了固定的内容,最后8个字节为了可选信息而未定义.相比于400字节二进制文件头,在新标准下的240字节道头中2字节或4字节整形数据的分布排列是较为分散的.其具体分布如表 2所示:
|
|
表 2 道头中2字节或4字节整形数据的分布排列情况 Table 2 Distribution situations for 2 or 4 bytes integer data in trace head |
根据表 2我们可以定义如下的结构体变量来对240字节道头中的可用信息进行任意存储和改写:
struct trace_head { int a1[7]; short a2[4]; int a3[8]; short a4[2]; int a5[4]; short a6[46]; int a7[5]; short a8[2]; int a9[1]; short a10[8]; int a11[1]; short a12[2]; int a13[2]; }th240_1;通过定义并赋值结构体变量,完成了二进制文件头的转化与存储.用户可根据自己的需要,来设定所有变量的值.
3 道数据转化在SEG-Y格式中,地震数据以规定的格式码表示的数据类型记录在文件内.格式码记录在400字节二进制文件头第25和26两个字节中,即变量s400_1.a2[6]中记录的内容.其中格式码1代表IBM单精度浮点数,5代表IEEE 单精度浮点数.IEEE格式即微机上float型单精度浮点数.地震数据绝大多数都是使用IBM单精度浮点数作为数据记录格式.为了达到在微机上读取地震数据的目的,下文将重点介绍32位IBM浮点数与IEEE浮点数之间相互转换的算法和转换精度分析.
3.1 浮点数的概念浮点数在计算机中用于近似表示任意某个实数.浮点数的这类表示形式的概念来源于十进制的科学计数法.其表达式可以表示为
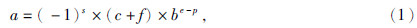
32位IBM浮点数和IEEE浮点数在小端序中的结构如表 3所示:
|
|
表 3 32位IBM浮点数和IEEE浮点数在内存中的存储形式 Table 3 Storage schema for 32 bit IBM floating point and IEEE floating point in memory |
其中,S(sign)代表符号位;E(exponent)代表指数位;F(fraction)代表小数位.
另外,32位IBM浮点数和IEEE浮点数均有五个特定的概念,分别是+0,-0,正无穷大,负无穷大和非数字.在计算机中用特殊表示来表达这些特定概念,具体形式如表 4所示:
|
|
表 4 32位IBM浮点数和IEEE浮点数特定概念的表示 Table 4 Expression of specific concept for 32 bit IBM floating point and IEEE floating point |
由于在计算机中只能用某一固定的位数来表示浮点数,故浮点数能表示的范围是有限的.只能表示整个实数轴中的三个部分,即某个很大的接近于负无穷的负数到很接近于0的负数、0、某个很接近于0的正数到很大的接近于正无穷的正数.这说明在计算机中两个浮点数之间只有有限个浮点数,相邻的两个浮点数之间的差可能是巨大的,因此浮点数都有精度限制.例如32位IEEE浮点数,其小数部分只有23位,第24位及其后都会被舍去.于是可近似认为其相对误差为2-23≈1.192×10-7,即浮点型变量能保证的有效数字是6~7位,后面的数字是无意义的.而32位IBM浮点数以16为基,能表示的数的动态范围更大,小数部分虽然有24位二进制位,但只能保证21位的有效位,所以表示精度与IEEE浮点数相比较低.两种浮点数各部分的表示范围如表 5所示.浮点数仅是对实数的近似表示,并不能完全刻画实数.
|
|
表 5 32位IBM浮点数和IEEE浮点数各部分的表示范围 Table 5 Expression region for each part of 32 bit IBM floating point and IEEE floating point |
对于一般的地震数据,记录格式通常为32位IBM浮点数.为了能够在微机上处理地震数据,需要进行浮点数格式转化,即将32位IBM浮点数转化为IEEE浮点数.具体方法是先转化字节序,然后再进行数据格式的转化.
3.2.1 32位IBM浮点数转化为IEEE浮点数由(1)式可知,32位IBM浮点数可以表示为

32位IEEE浮点数为
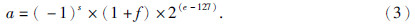
由(2)和(3)式的关系可知,经过简单的数学变换得到两种浮点数格式之间指数的相互转化关系为

EIBM表示IBM浮点数的指数部分;EIEEE表示IEEE浮点数的指数部分.由表 5知浮点数指数的表示范围不同,在相互转化时要考虑指数部分是否会溢出的问题.对于EIBM,由于0≤EIBM≤127,-130≤(4EIBM-130)≤378与EIEEE的表示范围0≤EIEEE≤254相比,IBM浮点数的表示范围大于IEEE浮点数.只有当0≤(4EIBM-130)≤254时,即32≤EIBM≤96时,才能正确的将IBM浮点数转化为IEEE浮点数.故当EIBM<32时,令转化后的IEEE浮点数结果为0;当EIBM>96时,令转化后结果为无穷大.若IBM浮点数为非数字,则转化后的IEEE浮点数也为非数字.
当IBM浮点数转化为IEEE浮点数后,经过变换变为类似科学计数法的标准格式,IEEE浮点数指数部分的值将变为  ,可能的变化值P的取值为0,1,2,3,公式为
,可能的变化值P的取值为0,1,2,3,公式为

指数的变化是由于在转化为标准格式时向左移动小数位的过程中最末位自动补零造成的,这种舍入误差不可避免.
本文通过两种算法来实现这种转化.算法1是计算出32位IBM浮点数各部分值直接带入(2)式中计算十进制浮点数值,然后存入float型变量中完成转化;算法2是由(5)式计算出EIEEE,然后应用(6)式的P值即IEEE浮点数指数与小数部分的关系得到  ,最后利用位操作组合IEEE浮点数各部分值来获得转化后的浮点数值.下面给出具体算法.
,最后利用位操作组合IEEE浮点数各部分值来获得转化后的浮点数值.下面给出具体算法.
算法1
float ibm2float(int x){ int sign,expo,mantissa,res; float result,mant; if(x){sign = x>>31 & 0x01; //计算IBM浮点数的符号s
expo = x>>24 & 0x7f; //计算IBM浮点数的指数e
mantissa = x & 0x00ffffff; //计算IBM浮点数的小数部分f
if(expo == 127 &&(mantissa & 0x00800000)&& !(mantissa & 0x007fffff)){//判断非数字
res=(sign<<31)| 0x7f800001;
memcpy(&result,&res,sizeof(float));
return result;
}
if(expo > 96){ //判断无穷大值
res =(sign<<31)| 0x7f800000;
memcpy(&result,&res,sizeof(float));
}
else if(expo < 32)result = 0; //判断0值
else {
expo = expo-64; //得到指数偏移后的指数e-64
mant =(float)(mantissa)/ pow(2,24); //转化为十进制小数0.f
result =(1-2*sign)* mant * pow(16,expo); //带入(2)式中得到十进制数值
}
return result; //返回结果 } result = x; //当x=0时,返回0值 return result; }算法2
float ibm2float(int x){ int sign,expo,mantissa,res; float result; if(x != 0){sign = x>>31 & 0x01; //计算IBM浮点数的符号s
expo = x>>24 & 0x7f; //计算IBM浮点数的指数e
mantissa = x & 0x00ffffff; //计算IBM浮点数的小数部分f
expo =(expo<<2)- 130; //转换为IEEE的指数部分
if(expo == 378 &&(mantissa & 0x00800000)&& !(mantissa & 0x007fffff)){ //判断非数字
res=(sign<<31)| 0x7f800001;
memcpy(&result,&res,sizeof(float));
return result;
}
if(expo > 254){ //判断无穷大值
res =(sign<<31)| 0x7f800000;
memcpy(&result,&res,sizeof(float));
} else if(expo < 0)result = 0; //判断0值 else {while(!(mantissa & 0x00800000)){expo--;mantissa <<= 1;} //调整指数与小数部分
res =(sign<<31)|(expo<<23)|(0x007fffff & mantissa);
memcpy(&result,&res,sizeof(float)); //将无穷大值内存拷贝给result变量
}return result; //返回结果
} result = 0; //当x=0时,返回0值 return result; }无论是算法1还是算法2,其转化结果是相同的.我们选取了一些十进制数进行由32位IBM浮点数向IEEE浮点数的转化实例.其结果如表 6所示:
|
|
表 6 IBM浮点数转化为IEEE浮点数的转化实例 Table 6 Conversion experiments for IBM floating point converts to IEEE floating point |
从表 6中可以看出,十进制数20.5可以无精度损失和溢出危险的完全转化为IEEE浮点数,这得益于给出的十进制数与IBM浮点数之间的转化没有误差且要转化的十进制数也没有超过两种浮点数的表示范围.对于-20.5同样成立,只是符号不同.但是,当转化20.4时,十进制数与IBM浮点数存在转化误差,IBM浮点数只能用20.399 993 9来近似的表示20.4.IBM浮点数转化为IEEE浮点数与将20.4直接转化为IEEE浮点数仅最后三位不同.这是因为P=3即IBM浮点数转化为IEEE浮点数后变为标准格式的过程中,小数位向左移动3位最末位自动补零造成的.对于0x1FFFFFFF(指数e=31)和0x64FFFFFF(指数e=100)来说,都超过了IEEE浮点数的表示范围,所以分别被赋值为0和0x7F7FFFFF(即正无穷大).通过以上的浮点数格式转化对比可知,程序转化正确有效.
3.2.2 32位IEEE浮点数转化为IBM浮点数上文的处理已经将地震数据由IBM浮点数转化为IEEE浮点数,数据经过处理后仍想输出保存为SEG-Y记录格式,这时便需要进行从IEEE浮点数到IBM浮点数的转化过程.

转化算法同样有两种.算法3是利用十进制浮点数直接计算出IBM浮点数各部分的值,然后进行位操作组合得到的各部分值,从而获得转化后的IBM浮点数值;算法4是由(5)式可推得(7)式得到两种浮点数格式之间指数的相互转化关系,根据已知的IEEE浮点数先计算出EIEEE,然后将(6)式带入(4)式中,调整IEEE浮点数中指数与小数部分的关系得到(4)式中右边项的值,从而求出EIBM,最后进行位操作组合IBM浮点数各部分值来获得转化后的IBM浮点数值.下面给出具体算法.
算法3
int float2ibm(float x){ int sign,expo,mantissa; float x1; int result; result = *(int *)&x; sign=result >> 31 & 0x01; //计算IEEE浮点数的符号s expo = result >> 23 & 0xff; //计算IEEE浮点数的指数e mantissa = 0x007fffff & result; //计算IEEE浮点数的小数部分f if(expo == 255 && mantissa){//判断非数字
result =(sign<<31)| 0x7f800000;
return result;
} else if(expo == 255 && !mantissa){//判断无穷大值
result =(sign<<31)| 0x7f000000;
return result;
} x = x*(1-2*sign); //负数与正数计算相同,故取绝对值 x1 = x; expo = 0; if(x1 > 0){if(x1 > 1){
expo++;
while(x1/16 > 1){expo++; x1/=16;}
}
else while(x1*16 < 1){expo--; x1*=16;}
} else {result = 0; return result;} mantissa =(int)(x * pow(16,-expo)* pow(2,24)); //计算IBM浮点数的小数部分f expo = expo+64; //计算IBM浮点数的指数e result =(sign<<31)|(expo<<24)| mantissa; //组合IBM浮点数各部分到result变量中 return result; }算法4
int float2ibm(float x){ int sign,expo,mantissa; int result; result = *(int *)&x; sign = result >> 31 & 0x01; //计算IEEE浮点数的符号s expo = result >> 23 & 0xff; //计算IEEE浮点数的指数e mantissa = 0x007fffff & result; //计算IEEE浮点数的小数部分f if(expo == 255 && mantissa){//判断非数字
result =(sign<<31)| 0x7f800000;
return result;
} else if(expo == 255 && !mantissa){//判断无穷大值result =(sign<<31)| 0x7f000000;
return result;
} if(result){mantissa = mantissa | 0x00800000; //计算IEEE浮点数的小数部分f补上1变为1.f
expo -= 126; //结合(6)式得到(4)式中
while(expo & 0x3){ expo++; mantissa>>=1; } //调整指数与小数部分
expo=(expo>>2)+ 64; //计算IBM浮点数的指数e
result =(sign << 31)|(expo << 24)| mantissa; //组合IBM浮点数各部分到result变量中
} return result; }无论是算法3还是算法4,其转化结果是相同的.我们选取了一些十进制数进行由32位IEEE浮点数向IBM浮点数的转化实例.其结果如表 7所示:
|
|
表 7 IEEE浮点数转化为IBM浮点数的转化实例 Table 7 Conversion experiments for IEEE floating point converts to IBM floating point |
由于IBM浮点数的表示范围要大于IEEE浮点数的表示范围,所以IEEE浮点数均可以在有限精度损失的情况下转化为IBM浮点数.从表 7可以看出,±20.5可以无精度损失和溢出危险的完全转化为IBM浮点数,这得益于给出的十进制数与IEEE浮点数之间的转化没有误差且要转化的十进制数也没有超过两种浮点数的表示范围.但是,当转化20.4时,十进制数与IEEE浮点数存在转化误差,IEEE浮点数只能用20.399 999 6来近似的表示20.4.转化时需要舍掉的位数P=3.所以IEEE浮点数小数部分在转化的过程中向右移动小数位最后3位将被舍掉,进一步造成转化误差.因此转化后的IBM浮点数的十进制值变为了20.399 993 9,精度再次降低.通过以上的浮点数格式转化对比可知,程序转化正确有效.
两种浮点数格式的互相转化,由于表示范围和精度的不同导致并不能实现完全转化,只是最大限度的近似.以上介绍的两种浮点数格式互相转化的算法在完成常规浮点数转化的同时考虑了所有特殊情况下的转化问题,具有一般性.
为了对比上文介绍的四个算法的计算效率.在主频为2.33 GHz,内存是2 GB的双核计算机上,基于VC++ 6.0编译器环境,对648道每道6 001个采样点共计3 888 648个点的地震数据进行了转化测试.各个算法的CPU耗时如表 8所示:
|
|
表 8 四个算法的CPU耗时对比 Table 8 Compare the cost of CPU time for four algorithms |
由表 8可知,无论哪种转化方向,算法2和4的计算效率始终优于算法1和3.这是由于位操作的计算速度远远高于乘、除法在程序中的计算速度.算法1和3的优点是易于理解与编程,但是计算效率较差.算法2和4的优点是计算效率高,但相对而言不易理解.对于大量地震数据的读取等计算,算法2和4相比于算法1和3将节省大量的计算时间.
4 结 论本文系统介绍了SEG-Y地震数据格式的结构.给出了SEG-Y格式中EBCDIC编码的3200字节文本文件头与ASCII编码之间的转化方法.分析了400字节二进制文件头和240字节道头字中长短整形数据结构分布并定义了相应的结构体变量,实现了文件头与道头的自由读取、改写与存储.研究了记录地震数据的两种浮点数格式——32位IBM浮点数和IEEE浮点数,并分别给出了两种它们之间互相转化的算法以及转化实例与精度分析.在完成转化的同时考虑了所有特殊情况下的转化问题,具有一般性.通过对SEG-Y结构数据编码进行分析,编写了基于C语言的程序代码,实现了对SEG-Y文件的自由读取、改写与存储.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Barry K M, Cavers D A, Kneale C W. 1975. Recommended standards for digital tape formats[J]. Geophysics, 40(2):344-352. |
| [2] | Bland H C. 1993. Rationalizing varying seismic data formats[R]. Calgary:CREWES. |
| [3] | Cohen D. 1981. On holy wars and a plea for peace[J]. Computer, 14(10):48-54. |
| [4] | Fu M S. 2011. Bytes expressions and conversion between 32 bits IEEE and IBM floating point numbers[J]. Chinese Journal of Engineering Geophysics(in Chinese), 8(6):759-766, doi:10.3969/j.issn.1672-7940.2011.06.022. |
| [5] | IBM Corporation. 1967. GA27-2719-0 IBM system/360 principles of operation[S]. New York:IBM Corporation. |
| [6] | IBM Corporation. 1974. GA22-7000-4 IBM system/370 principles of operation[S]. New York:IBM Corporation. |
| [7] | IEEE. 1985. ANSI/IEEE Std 754-1985 IEEE standard for binary floating-point arithmetic[S]. New York:IEEE. |
| [8] | IEEE. 1987. ANSI/IEEE Std 854-1987 IEEE standard for radix-Independent floating-point arithmetic[S]. New York:IEEE. |
| [9] | IEEE. 2008. ANSI/IEEE Std 754-2008 IEEE standard for floating-point arithmetic[S]. New York:IEEE. |
| [10] | Kahan W. 1997. IEEE standard 754 for binary floating-point arithmetic[R]. California:Computer Science University of California Berkeley CA 94720-1776. |
| [11] | Luo F L. 2006. Overview of seismic data storage technology[J]. Petroleum Instruments(in Chinese), 20(3):1-5. |
| [12] | Norris M W, Faichney A K. 2002. SEG Y rev 1 data exchange format[S]. Tulsa, Oklahoma:SEG Technical Standards Committee. |
| [13] | Sun Z Q, Sun J G, Han F X. 2009. Traveltimes computation using linear interpolation and narrow band technique under complex topographical conditions[J]. Chinese Journal of Geophysics(in Chinese), 52(11):2846-2853, doi:10.3969/j.issn.0001-5733.2009.11.019. |
| [14] | Sun Z Q, Sun J G, Han F X. 2012. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3D undulating surface condition[J]. Chinese Journal of Geophysics(in Chinese), 55(7):2441-2449, doi:10.6038/j.issn.0001-5733.2012.07.028. |
| [15] | Zhan Z D, Xu D P, Wu H Y, et al. 2011. Deep analysis about accuracy problem for segy format conversion of seismic data[J]. Geophysical & Geochemical Exploration(in Chinese), 35(6):851-854. |
| [16] | Zhang D L, Sun J G, Sun Z Q. 2011. Finite-difference DC electrical field modeling on 2D and 2.5D undulate topography[J]. Chinese Journal of Geophysics(in Chinese), 54(1):234-244, doi:10.3969/j.issn.0001-5733.2011.01.025. |
| [17] | Zheng X F, Ouyang B, Zhang D N, et al. 2009. Technical system construction of Data Backup Centre for China Seismograph Network and the data support to researches on the Wenchuan earthquake[J]. Chinese Journal of Geophysics(in Chinese), 52(5):1412-1417, doi:10.3969/j.issn.0001-5733.2009.05.031. |
| [18] | 符茂松. 2011. 32位IEEE和IBM浮点数结构及其转换方法[J]. 工程地球物理学报, 8(6):759-766, doi:10.3969/j.issn.1672-7940.2011.06.022. |
| [19] | 罗福龙. 2006. 地震数据存储技术综述[J]. 石油仪器, 20(3):1-5. |
| [20] | 孙章庆, 孙建国, 韩复兴. 2009. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算[J]. 地球物理学报, 52(11):2846-2853, doi:10.3969/j.issn.0001-5733.2009.11.019. |
| [21] | 孙章庆, 孙建国, 韩复兴. 2012. 三维起伏地表条件下地震波走时计算的不等距迎风差分法[J]. 地球物理学报, 55(7):2441-2449, doi:10.6038/j.issn.0001-5733.2012.07.028. |
| [22] | 詹泽东, 胥德平, 吴海洋等. 2011. 深入解析SEGY格式地震数据转化的精度问题[J]. 物探与化探, 35(6):851-854. |
| [23] | 张东良, 孙建国, 孙章庆. 2011. 2维和2.5维起伏地表直流电法有限差分数值模拟[J]. 地球物理学报, 54(1):234-244, doi:10.3969/j.issn.0001-5733.2011.01.025. |
| [24] | 郑秀芬, 欧阳飚, 张东宁等. 2009. "国家数字测震台网数据备份中心"技术系统建设及其对汶川大地震研究的数据支撑[J]. 地球物理学报, 52(5):1412-1417, doi:10.3969/j.issn.0001-5733.2009.05.031. |
 2016, Vol. 31
2016, Vol. 31


