2. 胜利油田物探研究院, 东营 257022
2. Geophysical Research Institute of Shengli Oil-field Branch, Dongying 257022, China
全波形反演(FWI)作为一种较为重要的速度建模方法,近年来一直是地球物理工作者研究的热点.目前,制约全波形反演方法生产实用化的因素较多,例如:计算稳定性、反演收敛情况、迭代计算效率等.针对上述问题,国内外研究人员开展了大量的研究,其中编码方式是一种较为流行的策略.下面,本文将重点从全波形反演方法、编码算子以及二者的结合等方面介绍国内、外研究进展.
首先,关于全波形反演方法的国内、外研究进展.按照在不同域中求解方程可分为时间域、频率域、拉普拉斯域及混合域全波形反演方法.20世纪80年代,Tarantola提出基于广义最小二乘时间域全波形反演(Tarantola 1984,1986),随后Bunks等提出时间域多尺度反演,通过对资料的处理将问题分解为不同的空间尺度,增加了求解稳定性,降低非线性程度(Bunks et al.,1995).20世纪90年代,Pratt提出声波及弹性波频率域全波形反演方法(Pratt 1990,1999).随后,Shin等利用拉普拉斯域对频率不敏感的特性发展了拉普拉斯域的全波形反演(Shin et al.,2008;2009).为克服拉普拉斯域全波形反演较难获取速度场高频信息的不足,Kim等将拉普拉斯域与频率域结合提出了拉普拉斯频率域的全波形反演方法,可以同时反演模型的低、高频成分以及地震子波(Kim et al.,2013).Youngseo Kim等提出时间域正演、拉普拉斯域反演的FWI,将该方法用于SEG/EAGE 3D盐丘模型试算和3D宽方位角实际勘探数据,数值示例表明,该混合FWI可建立高精度地下速度模型,提高逆时偏移成像效果(Kim et al.,2013).
目前,这些FWI方法在理论上较为完善,针对理论模型的试算也较为准确,但在实际资料处理,尤其陆上采集资料处理方面,还处于试处理和探索阶段,离大规模生产应用还有一定的距离.
其次,关于编码思想在国内外的研究进展.主要从编码方式、编码位置、编码实施策略等方面介绍.第一、编码方式.目前常见的编码方式包括:相位编码(Romero et al.,2000)、振幅及极性编码(Godwin and Sava,2011)、时域编码(黄建平等,2015)、频率域分频编码(Yunsong Huan et al.,2012;黄建平等,2015);第二、编码位置.可以在震源编码(Krebs et al.,2009),可以在接收点编码,Ali Almomin(2012)提出一种接收点、震源二者同时编码的方法,证实了该方法优于震源编码、接收点编码;第三、编码实施策略.编码策略包括:动态编码、静态编码、混合编码.静态编码是使用上一次编码得到的数据进行迭代,动态编码是每一次使用不同编码得到新的数据进行迭代,混合编码是同时有静态编码和动态编码.Romero等(2000)系统比较了静态编码和动态编码两种编码策略,在计算内存、计算效率、迭代收敛速度方面的差异.Morton和Ober(1998)提出一种动态的获取最佳偏移次数和信噪比的经验关系.Daiwei等(2012;2013)以及黄建平等(2015)发展了基于不同编码策略的最小二乘偏移方法,极大的提高了偏移效率并压制了串扰噪声.
最后,关于编码策略与全波形反演结合的国内外研究进展。Krebs等(2009)提出了联合编码震源全波形反演(ESSFWI),对混叠数据在每次迭代时更改编码函数,就编码长度、随机噪声、初始模型等方面做了对比研究.Routh等(2011)将编码FWI用于海洋拖缆数据,提高了大型3D模型的计算效率.Ben-Hadj-Ali等(2011)指出编码技术可以为3D声波FWI提供详尽的参数化表征,使其易拓展到3D弹性波FWI.
编码FWI极大提高了计算效率,并在一定程度上减少了串扰噪声,但是在求解非线性地震波形反演问题时容易陷入局部极小值,出现“锯齿”的反演不稳定现象.基于此,本文尝试引入抛物拟合法求取迭代最优步长,并发展了一种基于优化步长的编码FWI方法,在实现方法的基础上,通过简单的洼陷模型及国际标准的Marmousi模型验证方法的正确性和适应性,并通过与传统FWI及传统编码的FWI对比,探讨本文方法在迭代稳定性、收敛速度等方面的优势.
1 方法原理 1.1 最优化求取方式本文引入抛物线拟合方法来估算迭代步长(Vigh et al.,2009),通过优化步长以减少反演迭代次数,可以较为显著的提高计算效率.步长估算过程如图 1所示.
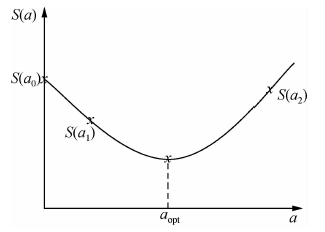 | 图 1 抛物线拟合法步长搜索Fig. 1 Step search by parabolic fitting |
优化步长求取的步骤为:找到两个步长a1、a2,使其对应的目标函数满足条件和S(a1)<S(a2),其中a0=0,由三个步长所对应的点拟合一条抛物线,抛物线极小点处对应的步长aopt,即为最终估计步长.
1.2 最优化步长FWI方法以二维声波方程为例,利用全波形反演获取地震波速度场,一般将全波形反演问题定义为求解目标函数取得极小值,即:
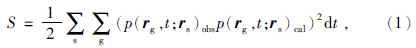

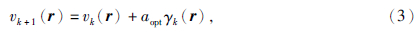
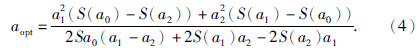
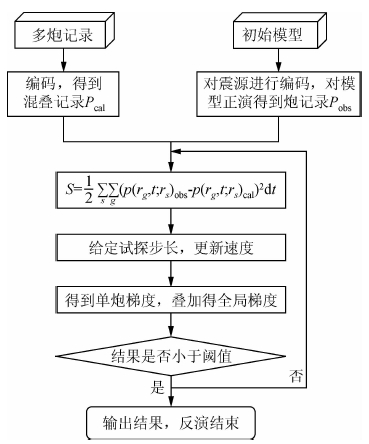 | 图 2 基于最优化步长的混叠数据编码全波形反演流程Fig. 2 Process of aliasing data encoded fwi Based on optimal step length |
编码全波形反演实现流程图如下:首先,基于地质与地球物理观测数据建立真实速度模型,进行正演得到多炮记录,对炮集进行编码获取编码后的混叠数据.对震源进行编码,对初始速度模型进行正演得到炮记录.构建一个合适的目标泛函,首先对每一炮计算每一时刻的正传波场,计算检波点位置的波场残差,将波场残差反传播到模型空间,得到反传播数据,求取反传波场与正传波场在时间上的二阶导数在时间上的内积,得到单炮的梯度.叠加所有炮求取的梯度值,得到模型空间的全局梯度,给定一个全局的试探步长(如将速度更新量控制在背景速度的1%),以此更新速度得到一个伪更新速度模型,直到迭代至合适的速度场.
2 模型试算在编程实现基于混叠数据优化步长的FWI方法基础上,本文通过简单的洼陷模型及国际标准的Marmousi模型来验证方法的正确性和实用性,并通过与混叠数据的FWI方法及混叠数据固定步长的FWI方法对比,验证本文方法在迭代稳定性、收敛速度等方面的优势.为了方便表述,本文分别用F1、F2、F3代表混叠数据不编码FWI方法,混叠数据固定步长编码FWI方法,混叠数据优化步长编码FWI方法.
2.1 洼陷模型计算结果模型参数:所设计模型为简单的三层结构,速度值分别为3500 m/s,4000m/s,4500 m/s,如图 3a所示;速度网格大小201×201,纵横向间距均为8 m.观测系统:地表放炮,炮数49炮,炮间距32 m,第一炮的位置在第32 m 处,接收方式为全接收.计算参数:利用主频为25 Hz的零相位雷克子波激发,时间采样率0.5 ms,采样点数为2001,最大迭代次数为49次.将真实速度场进行10点平滑得到初始速度模型如图 3b所示.
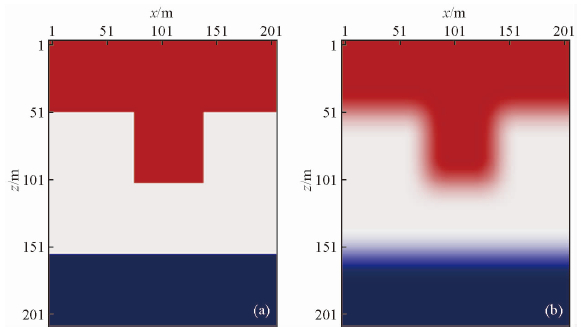 | 图 3 洼陷模型速度场 (a)真实速度模型; (b)初始速度模型.Fig. 3 Sag model velocity field (a) Real velocity model; (b) Initial velocity model. |
基于本文的优化算法进行模型试算,得到了不同迭代次数下对应的全波形反演结果如图 4所示,基于最优化步长编码的FWI方法反演结果与真实的速度场较为接近,洼陷位置及形态都得到了很好恢复.
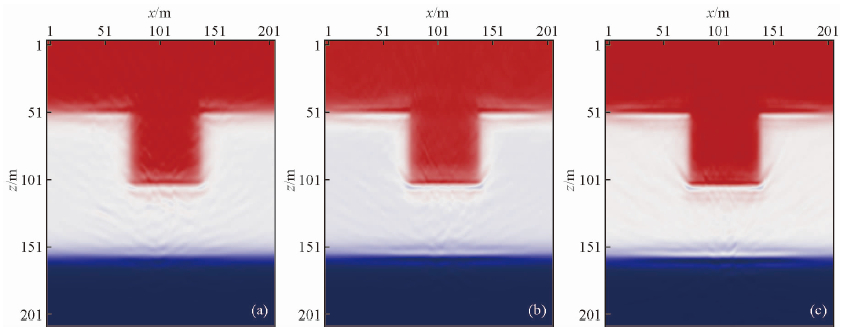 | 图 4 速度场示意图 (a)(b)(c)分别为F3第5、25、49次迭代后的速度场.Fig. 4 Sag model velocity field (a) (b) (c) respectively show the velocity field of F3 after 5、25、49 iteration. |
为了进一步分析反演结果的正确性,本文基于反演得到的速度模型4c,进行了地震波正演模拟,并与基于真实速度模型3a采用相同计算参数正演得到的炮记录进行对比,炮记录如图 5及单道速度如图 6所示.首先,由图 5单炮记录对比结果可知:基于反演速度模型模拟的地震波记录与真实速度场模拟记录主要震相,在到达时刻、振幅能量等方面都较为接近,验证了本文方法反演得到的速度模型的正确性.其次,从图 6中给出的第30、100、180道速度场对比可知:F1、F2、F3都能较好的反演得到地下的主要界面,且速度值较为准确,且F3方法得到的结果在一定程度上要优于F1和F2方法,尤其是界面位置处速度值的恢复.
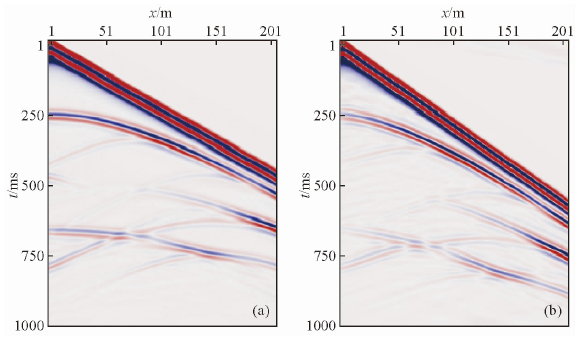 | 图 5 炮记录示意图 (a)真实速度模型正演结果; (b)迭代49次速度模型正演结果.Fig. 5 Sag model shot record (a)Real velocity model shot record;(b)After 49 iteration velocity model shot record. |
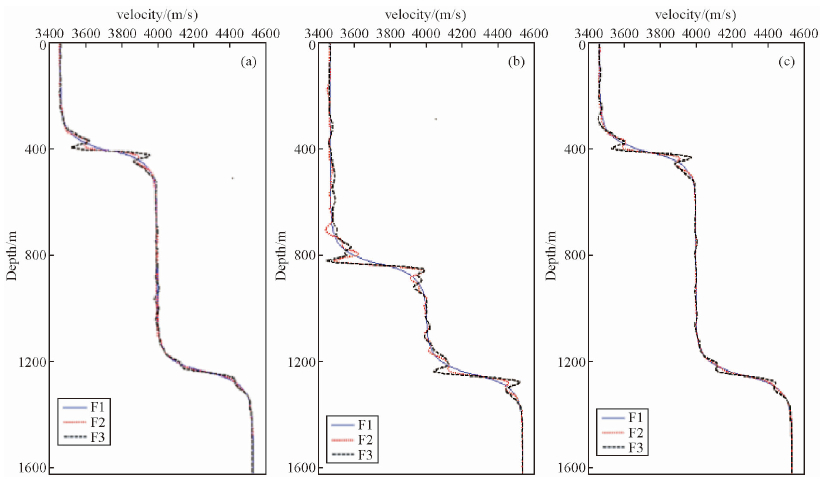 | 图 6 单道速度对比示意图 (a)(b)(c)分别为第30、100、180道速度场.Fig. 6 Single trace velocity contrast diagram (a) (b) (c) respectively show 30、100、180 trace velocity. |
基于混叠数据的三种反演方法的对比分析及讨论:基于F1及F2方法不同迭代次数对应的反演结果如图 7所示.从箭头指示地方看,F1方法反演得到的速度场中仍然存在明显的串扰噪声,F2方法速度场串扰噪声明显减少,且随着迭代次数的增加,反演得到的速度场更接近真实速度场.
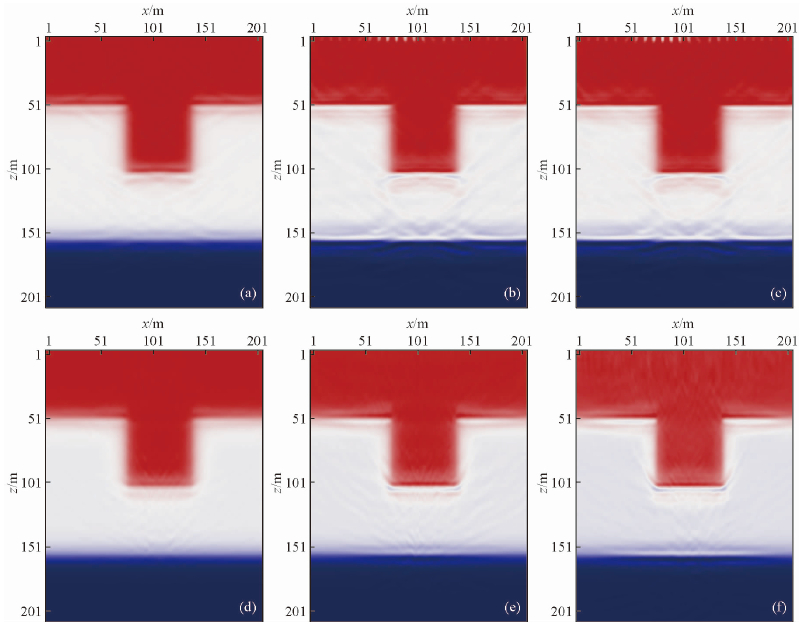 | 图 7 速度场示意图 (a)(b)(c)分别为F1第5、25、49次迭代后的速度场; (d)(e)(f)分别为F2第5、25、49次迭代后的速度场.Fig. 7 Sag model velocity field (a)(b)(c)respectively show the velocity field of F1 after 5、25、49 iteration; (d)(e)(f)respectively show the velocity field of F2 after 5、25、49 iteration. |
进一步,本文给出了三种方法对应的残差随着迭代次数的变化关系图,如图 8所示.
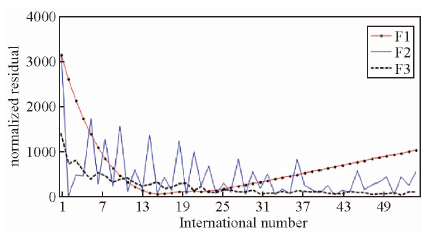 | 图 8 基于混叠数据的三种FWI算法的残差随迭代次数变化图Fig. 8 Residual versus iteration number |
由图 8中可以看出,F1残差值(红色线)随着迭代次数的增加,残差先快速降低,当迭代次数大于15后,残差逐渐增大.原因可能是由于本文基于的是混叠数据,炮记录中除了炮内的有效信息外,还存在较强的临炮干扰及串扰噪声,反演迭代到一定次数会由于虚假波形信息的影响增大而不收敛.F2残差值(蓝色实线)整体上呈收敛趋势,但会出现“锯齿”形状的分布特征.可能是因为求解非线性地震波形反演问题时,存在很多局部极值,这会阻碍全局极小值的求解,而且步长的选取采用的是固定步长而非最优步长.F3残差值(黑色虚线)收敛趋势优于F2,其中较小的波动情况,可能是局部极小值造成的,而且使用了极性编码,每炮的编码序列不同,都会对误差函数的值造成一定影响.总体来说:本文发展的基于优化步长的混叠数据编码FWI方法,在迭代稳定性、收敛速度等方面优于传统FWI及传统编码的FWI方法.
2.2 Marmousi模型计算结果在测试方法正确性基础上,本文进一步利用国际标准Marmousi模型来验证方法对复杂模型的适用性.
Marmousi模型的示意图如图 9a所示,从图 9a中可以看到:Marmousi模型具有背斜、大倾角断裂的复杂构造,速度变化剧烈,可以很好的验证速度建模和成像方法的优劣.速度网格大小249×250,纵横向间距均为8 m.水平坐标范围0~1992 m.地表放炮,共放49炮,炮间距32 m,第一炮的位置在第32 m处,接收方式为全接收,利用主频为25 Hz的零相位雷克子波激发,时间采样率0.5 ms,采样点数为3200,最大迭代次数为200次.将真实速度场进行10点平滑得到初始速度模型如图 9b所示,初始速度场与真实速度场大体趋势(低频部分)较为一致,但许多细节高频部分已经不再相似.
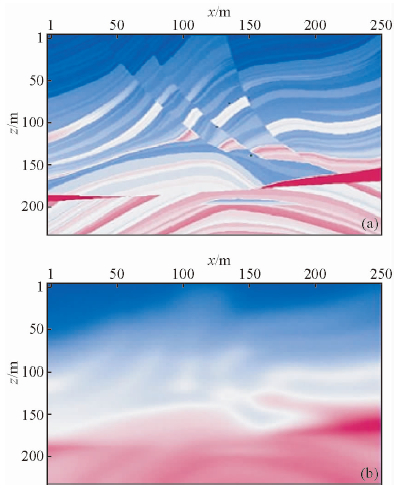 | 图 9 Marmousi 模型速度场 (a)真实速度模型; (b)初始速度模型.Fig. 9 Marmousi model velocity field model |
图 10是最优步长极性编码FWI第10、50、100、200次迭代更新后的速度场,无明显串扰噪声,断层和背斜形态反演结果较为更加清晰,反演速度场逐渐收敛到真实值.
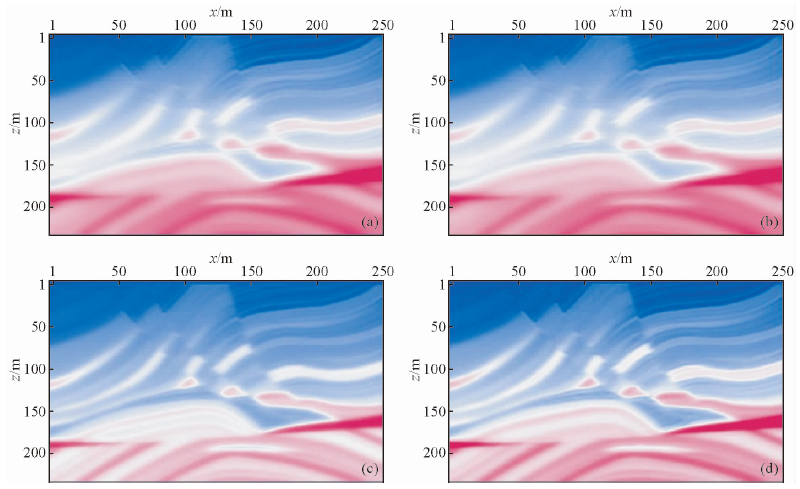 | 图 10 Marmousi模型最优步长极性编码FWI速度场
(a)第10次迭代; (b)第50次迭代; (c)第100次迭代; (d)第200次迭代.Fig. 10 Optimum step length coding FWI velocity field model of Marmousi model |
图 11为Marmousi模型残差随迭代次数变化的示意图中,由于编码会对收敛造成影响,最优步长混叠数据编码FWI方法误差函数曲线总体趋势较好,随着迭代次数增加呈现稳定的下降趋势,虽然在迭代一定次数后反演收敛到局部较小值的情况,这是由于输入数据为混叠数据,数据本身存在明显的串扰噪声和邻炮干扰.
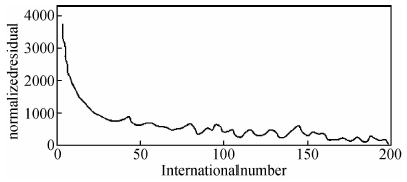 | 图 11 Marmousi模型残差随迭代次数变化示意图Fig. 11 Residual versus iteration number of Marmousi model |
3.1 本文通过引入抛物法求取反演步长,实现了一种基于优化步长的编码FWI方法,通过洼陷和Marmousi模型的试算及对比分析,得到以下几点认识:
(1)通过洼陷模型试算,证明基于最优步长编码FWI方法的有效性,通过Marmousi模型试算,证明方法一定的适用性.
(2)对两个模型的数值实现可知,全波形反演可以建立高精度速度模型,相位编码的方式可以消除相干项,减少串扰噪声,提高成像结果的信噪比.
(3)不编码的混叠数据存在串扰噪声,误差函数不收敛,常规编码FWI使串扰噪声减少,误差函数收敛,但存在“锯齿”现象,最优步长FWI误差函数曲线平滑,收敛效果好,最优步长编码FWI在编码函数的影响下,误差函数曲线收敛趋势好,优于传统编码FWI.
3.2 虽然本文的方法在一定程度上改善了FWI反演稳定性和收敛速度的问题,但是还存在一些不足:求解非线性地震波形反演问题时,会遇到许多局部极值,这会阻碍全局极小值的求解.多尺度反演是近几年提出的一个能加快收敛速度、克服局部极小值影响、搜索全局最小极值点的反演策略.在下一步研究过程中,希望可以将多尺度反演与编码结合,提高反演的精度和稳定性.
致 谢 感谢国家重点基础研究发展计划(973)(2014CB239006,2011CB202402),国家自然科学基金(41104069,41274124),中石化课题(KJWX-2014-05),中央高校科研业务费专项基金(R1401005A)联合资助.
| [1] | Ben-Hadj-Ali H, Operto S, Virieux J. 2011. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources. Geophysics, 76(4):R109-R124. |
| [2] | Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion[J]. Geophysics, 60(5):1457-1473. |
| [3] | Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion[J]. Chinese Journal of Geophysics(in Chinese), 56(10):3445-3460, doi:10.6038/cjg10131020. |
| [4] | Etienne V, Chaljub E, Virieux J, et al. 2010. An hp-adaptive discontinuous Galerkin finite-element method for 3-D elastic wave modelling[J]. Geophysical Journal International, 183(2):941-962. |
| [5] | Godwin J, Sava P. 2011. A comparison of shot-encoding schemes for wave-equation migration[C].//SEG Technical Program Expanded Abstracts 2011. Expanded Abstracts, 32-36. |
| [6] | Ha W, Shin C. 2012. Laplace-domain full-waveform inversion of seismic data lacking low-frequency information[J]. Geophysics, 77(5):R199-R206. |
| [7] | Hu G H. 2012. Three-dimensional acoustic full waveform inversion:method, algorithm and application to Val-hall petroleum field[Ph. D. thesis]. Grenoble:Universite de Josph Fourier. |
| [8] | Huang J P, Li C, Li Q Y, et al. 2015. Least-squares reverse time migration with static plane-wave encoding[J]. Chinese Journal of Geophysics(in Chinese), 58(6):2046-2056, doi:10.6038/cjg20150619. |
| [9] | Krebs J R, Anderson J E, Hinkley D, et al. 2009. Fast full-wavefield seismic inversion using encoded sources. Geopohysics, 74(6):WCC177-WCC188. |
| [10] | Kim Y, Shin C, Calandra H, et al. 2013a. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion[J]. Geophysics, 78(4):R151-R166. |
| [11] | Kim Y, Shin C, Calandra H, et al. 2013b. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion[J]. Geophysics, 78(4):R151-R166. |
| [12] | Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method[J]. Geophysics, 47(10):1402-1412. |
| [13] | Kosloff D D, Reshef M, Loewenthal D. 1984. Elastic wave calculations by the Fourier method[J]. Bulletin of the Seismological Society of America, 74(3):875-891. |
| [14] | Levander A R. 1988. Fourth-order finite-difference P-SV seismogram[J]. Geophysics, 53(11):1425-1436. |
| [15] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 49(5):533-549. |
| [16] | Niu B H, Sun C Y. 2004. Developing theory of propagation of seismic waves-medium model and propagation of seismic waves[J]. Progress in Geophysics(in Chinese), 19(2):255-263 doi:10.3969/j.issn.1004-2903.2004.02.008. |
| [17] | Operto S, Virieux J, Amestoy P, et al. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver:a feasibility study[J]. Geophysics, 72(5):SM195-SM211. |
| [18] | Pratt R G. 1990. Frequency-domain elastic wave modeling by finite differences; a tool for crosshole seismic imaging[J]. Geophysics, 55(5):626-632. |
| [19] | Pratt R G. 1999. Seismic waveform inversion in the frequency domain, part 1:theory and verification in a physical scale model[J]. Geophysics, 64(3):888-901. |
| [20] | Romero L A, Ghiglia D C, Ober C C, et al. 2000. Phase encoding of shot records in prestack migration[J]. Geophysics, 65(2):426-436. |
| [21] | Routh P, Krebs J, Lazaratos S, et al. 2011. Encoded simultaneous source full-wavefield inversion for spectrally shaped marine streamer data[C]// SEG Technical Program Expanded Abstracts.Expanded Abstracts, 2433-2438. |
| [22] | Schuster G T, Wang X, Huang Y, et al. 2011. Theory of multisource crosstalk reduction by phase-encoded statics. Geophys. J. Int., 184(3):1289-1303. |
| [23] | Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J]. Geophysics, 69(1):231-248. |
| [24] | Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 51(10):1893-1903. |
| [25] | Vigh D, Starr E W, Kapoor J. 2009. Developing Earth models with full waveform inversion[J]. The Leading Edge, 28(4):432-435. |
| [26] | Virieux J, Operto S, Ben-Hadj-Ali H, et al. 2009. Seismic wave modeling for seismic imaging[J]. The Leading Edge, 28(5):538-544. |
| [27] | Wei Z F, Gao H W, Zhang J F. 2014. Time-domain full waveform inversion based on an irregular-grid acoustic modeling method[J]. Chinese Journal of Geophysics(in Chinese), 57(2):586-594, doi:10.6038/cjg20140222. |
| [28] | Yang W Y, Wang X W, Yong X S, et al. 2013. The review of seismic Full waveform inversion method[J]. Progress in Geophysics(in Chinese), 28(2):766-776, doi:10.6038/pg20130225. |
| [29] | 董良国, 迟本鑫, 陶纪霞,等. 2013. 声波全波形反演目标函数性态[J]. 地球物理学报, 56(10):3445-3460, doi:10.6038/cjg10131020. |
| [30] | 黄建平, 李闯, 李庆洋,等. 2015. 一种基于平面波静态编码的最小二乘逆时偏移方法[J]. 地球物理学报, 58(6):2046-2056, doi:10.6038/cjg20150619. |
| [31] | 牛滨华, 孙春岩. 2004. 地震波理论研究进展-介质模型与地震波传播[J]. 地球物理学进展, 19(2):255-263 doi:10.3969/j.issn.1004-2903.2004.02.008. |
| [32] | 任浩然. 2011. 声介质地震波反演成像方法研究[博士论文]. 上海:同济大学. |
| [33] | 王华忠, 王雄文, 王喜文. 2012. 地震波反演的基本问题分析[J]. 岩性油气藏, 24(6):1-9. |
| [34] | 魏哲枫, 高红伟, 张剑锋. 2014. 基于非规则网格声波正演的时间域全波形反演[J]. 地球物理学报, 57(2):586-594, doi:10.6038/cjg20140222. |
| [35] | 杨午阳, 王西文, 雍学善,等. 2013. 地震全波形反演方法研究综述[J]. 地球物理学进展, 28(2):766-776, doi:10.6038/pg20130225. |
| [36] | 杨勤勇, 胡光辉, 王立歆. 2014. 全波形反演研究现状及发展趋势[J]. 石油物探, 53(1):77-83. |
 2016, Vol. 31
2016, Vol. 31


