2. 国防科学技术大学机电工程与自动化学院, 长沙 410073
2. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China
谱方法是解决位场(徐世浙,2007;徐世浙和余海龙,2007;王万银等,2009;刘金钊等,2013;张恩会等,2015)、电磁场(魏宝君和Liu,2007;叶红霞等,2010;张建国等,2013)、波场(刘洪等,2006;卢回忆等,2010)等地球物理场的高效数值模拟和大规模数据处理(如延拓、求导)等问题的一种重要方法,快速傅里叶变换(FFT)算法的出现进一步提升了谱方法的重要性.FFT算法本质上是一种实现离散傅里叶变换的计算方法.1965年Cooley和Tukey(1965)提出了便于计算机实现的FFT算法,极大提高了离散傅里叶变换的计算效率.FFT算法利用算子eiωx的周期特性,采用分解-迭代的策略,先将数据按照维数分解,再利用低维数变换迭代求解高维数变换,以此降低冗余计算量,实现高效计算(Press et al.,1997).在Cooley-Tukey FFT算法提出之后,许多学者又提出了新的FFT算法(Rader,1968;Winograd,1976,1978;Chu and Burrus,1982;Duhamel and Hollmann,1984).对FFT算法的发展史的了解,可参考文献(Cooley et al.,1967;Heideman et al.,1984;Duhamel and Vetterli,1990).根据采样点个数,FFT算法可分为基于2n、3n、2nK(n和K为正整数)的算法,以及基于质数分解的算法,其中效率最高的是基于2n的FFT算法,也是目前常用的FFT算法.结合不同种类的FFT算法,能够实现任意采样点数的离散傅里叶变换.在这种意义上,本文将上述算法统称为任意采样点数FFT算法.随着计算机性能的提高,任意采样点数FFT算法的效率得到极大提高,并且出现了诸如FFTW(Frigo and Johnson,2005)和FFTPACK(Swarztrauber,1982)等成熟的软件包,集成了不同种类的FFT算法,供科研人员使用,尤其是前者,能够自动根据采样点个数,调用效率相对高的某种FFT算法,国内学者已对该软件包进行了深入分析(郭红等,2011).
利用任意采样点数FFT算法,能够快速计算得到“离散谱”.为解决位场、电磁场、波场等地球物理场的数值模拟和数据处理问题,使用任意采样点数FFT算法得到“离散谱”的同时,还需要知道其所对应的离散频率.只有正确计算出一一对应的离散频率和离散谱,才能正确求解地球物理问题.目前对任意采样点数情况下离散频率的计算问题研究甚少.本文从离散傅里叶变换作为傅里叶变换的一种数值逼近的观点出发(柴玉璞,1997;叶其孝和沈永欢,2006),通过推导和分析任意采样点数情况下离散傅里叶变换数学表达式,给出离散频率计算公式,明确揭示出离散频率和离散谱的对应关系,为正确使用任意采样点数FFT算法奠定理论基础.
1 离散频率计算方法以二维离散傅里叶变换为例,采用地球物理领域中常用的傅里叶变换对形式(Blakely,1996)
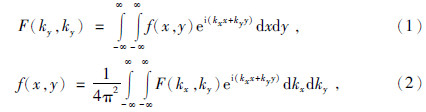
式中,f(x,y)表示某种地球物理场,F(kx,ky)为其频谱.
考虑实际观测情况,假设观测数据是在有限范围内,观测点距和线距分别为Δx和Δy,观测点数和线数分别为M和N.观测数据表示为f(xm,yn),其中离散坐标为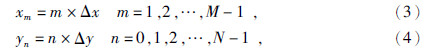
采用数值积分方法,通过如下过程对式(1)进行离散化:
第一步:以观测数据为中心,以Δx和Δy为边长,构成M×N个矩形网格,用网格上的积分逼近式的右侧积分,可得
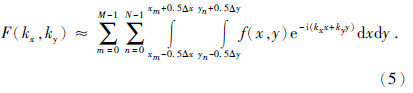
第二步:将每个网格积分区域上的函数f(x,y)视为常值f(xm,yn),可得
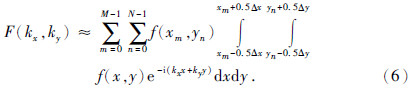
第三步:将每个网格积分区域上的函数e-i(kxx+kyy)视为常值e-i(kxxm+kyyn),可得
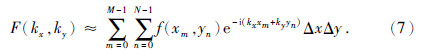
上述三步是将傅里叶变换中空间域坐标进行离散化过程,为了计算离散谱F(kx,ky),还需要对频率坐标进行离散化,这就涉及到如何确定离散频率问题.从数学上讲,由式(7)可以估算任意频率点上F(kx,ky)的值.蔡宗熹(2002)认为,离散频率的选取具有一定的人为约定性,也就是离散频率的取值不是唯一的.通过分析傅里叶级数与傅里叶变换之间的关系,下面给出一种任意采样点情况下离散频率的取值方法.
对于二维位场观测数据,定义两个方向上的基本波长为

对应基本波长,定义基频为

根据基本波长和基频的定义,可得如下关系

在周期函数的傅里叶级数展开式中,级数中每项的频率为基频的整数倍.与之对比,选取基频Δkx、Δky的整数倍作为离散频率,即

为了进一步确定p和q,利用采样定理对p和q的取值范围进行约束.将地球物理场视为空间坐标的连续函数,由采样定理可知,当采样间隔给定时,采样信号能够分辨出的原始连续信号中的最大频率,必须小于或者等于截止频率.由数字信号处理理论可知,当采样间隔Δx和Δy确定后,两个方向上的截止频率分别为

所以,离散频率需满足丨kxp丨≤kxmax,丨kyp丨≤kymax.
满足约束条件,给出如下p和q的取值方法:
当采样点数M和N为偶数时,p和q的取值为
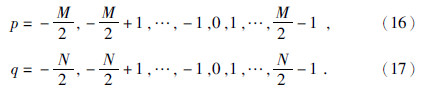

式(16)和式(17)给出的采样点数M和N为偶数时离散频率的计算方法,是目前文献中常用的(蔡宗熹,2002;管志宁,2005;曾华霖,2005),而式(18)和式(19)给出的M和N为奇数时离散频率的计算方法,在目前文献中很少见到.从上文分析可知,式(16)~式(19)给出的离散频率计算方法,从物理上讲是合理的,因为它们满足采样定理.下文将从数学上阐述按照式(16)~式(19)选取离散频率的含义.
根据离散频率,对式(7)进一步离散化,可得

此式是计算观测数据离散谱近似计算公式,不论M和N是奇数还是偶数,式(20)都适用.按照离散傅里叶变换作为一种傅里叶变换近似的观点,本文也称式(20)为离散傅里叶变换.为了从数学上说明式(16)~式(19)给出的离散频率取值的优势,需要按照式(20)的推导方法,得到离散傅里叶反变换的计算公式,推导过程从略.当M和N奇偶性不同时,p和q的取值不同,离散傅里叶反变换表达式略有不同.
当M和N为偶数时,离散傅里叶反变换表达式为
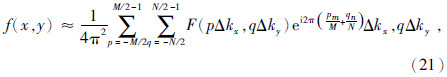
当M和N为奇数时,离散傅里叶反变换表达式为

当M为偶数,N为奇数时,离散傅里叶反变换表达式为

其中,空间域离散坐标xm,yn的取值与式(3)和式(4)相同.
在纯数学上,离散傅里叶变换和离散傅里叶变换常采用的公式为(柴玉璞,1997;叶其孝和沈永欢,2006)
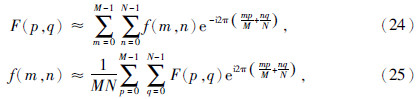
式(24)与式(25)都是等式关系,它们构成严格意义上的正反变换,即将式(24)代入式(25),或者将式(25)代入式(24),得到恒等式.显然,数学意义上的离散傅里叶变换式(24)与本文推导的离散傅里叶变换式(20),既有联系又有区别.从形式上看,式(24)是等式关系,而式(20)是近似关系,且式(24)和式(20)右侧计算式相差一个常数.而从上文推导可以看出,式(20)具有明确物理含义,它是计算某种地球物理场离散谱的近似公式,而式(24)只是一种纯数学变换.对于离散傅里叶反变换式(25)和本文给出的反变换式(21)、式(22)、式(23),存在同样的区别.需要特别指出一点,式(24)和式(25)中的量“p,q”,不具有物理意义上频率的含义,而本文推导的变换式中的量“kxp,kyq”,具有频率的含义.
若将式(20),式(21),式(22)和式(23)写成等式关系,附录A中证明,式(20)分别与式(21)、式(22),式(23)构成严格意义上的正反变换.从这种角度讲,根据式(16)~式(19)进行离散频率取值,便具有重要的数学意义:它保证了本文推导的离散傅里叶变换和反变换是严格数学意义上的正反变换,而这样一来就可以使用相同的某种FFT算法,实现具有物理意义的傅里叶变换和反变换的高效数值计算.又由于式(24)与式(20)之间,以及式(25)与式(21)、式(22)、式(23)之间只相差一个常数,易知,目前的FFT算法完全可以用于式(20)、式(21)、式(22)、式(23)的高效计算.
综上所述,本文给出的离散频率取值方式具有明确的物理意义和数学含义.前文已指出,离散频率的取值不是唯一的.柴玉璞(1997)提出了一套用于分析和提高傅里叶变换数值计算精度的偏移抽样理论,其中给出了新的离散傅里叶变换和反变换公式,离散频率选取的不是基频的整数倍,而是在整数倍基础上进行“偏移”.仔细分析本文推导式(20)的过程,可以发现,在第三步中,网格区域积分为
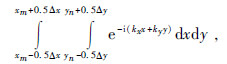
存在解析解.利用解析解代替文中所用的近似公式,是否可以提高傅里叶变换数值计算精度,值得进一步研究.
2 模型检验关于位场、电磁场和波场等地球物理场的许多问题,如正演模拟、延拓、求导等,都可以用空间域卷积来描述.由傅里叶卷积定理可知,空间域卷积对应于频率域乘积.将问题转换到频率域,能够提高计算效率.本部分以重力场向上延拓问题为例,使用理论模型数据,通过对向上延拓结果分析,检验本文给出的离散频率计算公式的正确性,同时展示任意采样点数FFT算法的效率.
如图 1所示,重力场向上延拓问题在空间域可以成如下卷积为
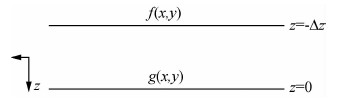 | 图 1 重力场向上延拓示意图 Fig. 1 Illustration of upward continuation of gravity field |

对应式(26),重力场向上延拓频率域表达式为
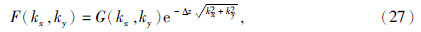
其中,F(kx,ky)和G(kx,ky)分别为f(x,y)和g(x,y)的傅里叶变换,Δz>0为延拓高度,z轴方向垂直向下为正.
数学上说,重力场向上延拓就是根据g(x,y)计算f(x,y).对于实际问题而言,实测数据为离散数据g(xm,yn),频率域重力场向上延拓数值计算流程如图 2所示.
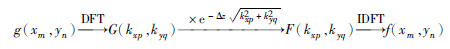 | 图 2 频率域重力场向上延拓数值计算流程图中,DFT表示离散傅里叶变换,IDFT表示离散傅里叶反变换. Fig. 2 Numerical computing process for upward continuation of gravity field in frequency domain |
由图 2给出的数值计算流程可以看出,延拓算子离散值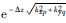 的计算是与离散频率相关的.如果离散频率取值不当,导致
的计算是与离散频率相关的.如果离散频率取值不当,导致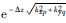 计算不准确,最终将不能得到正确的延拓结果.利用谱方法在频率域求解地球物理场问题,都会遇到计算某种频率域算子的离散值的问题,此时正确给出离散频率是至关重要的.
计算不准确,最终将不能得到正确的延拓结果.利用谱方法在频率域求解地球物理场问题,都会遇到计算某种频率域算子的离散值的问题,此时正确给出离散频率是至关重要的.
本文利用球体重力场垂直分量理论公式,计算由5个球体组合模型产生的理论重力数据.采样点数取为M=N=1117,采样点距为Δx=Δy=20 m,向上延拓高度为Δz=200 m.z=0 m和z=-200 m高度面的理论重力数据如图 3和图 4所示.利用Matlab编制频率域延拓算法程序,调用fft2函数实现FFT算法,由于采样点数为奇数,采用本文给出的式(14)、式(15)、式(18)和式(19)计算离散频率.在CPU主频为3.40 GHz,内存为16 GB的计算机上,程序运行时间约为0.2秒.简单分析可知,1117本身为质数,fft2内部调用了基于质数分解的FFT算法,可见基于质数分解的FFT算法效率很高.目前多种类型FFT算法组合,能够实现对任意采样点数的数据进行快速离散傅里叶变换.
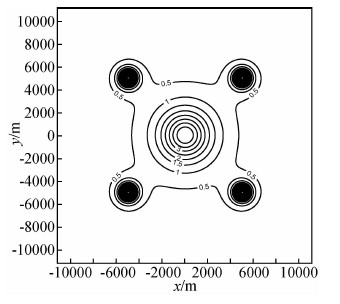 | 图 3 重力数据理论值(z=0 m) Fig. 3 Theoretical gravity data (z=0 m) |
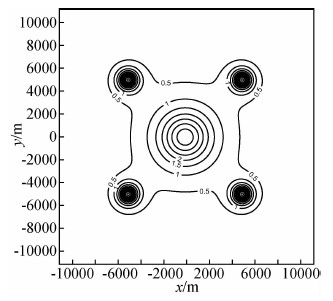 | 图 4 重力数据理论值(z=-200 m) Fig. 4 Theoretical gravity data (z=-200 m) |
可能是习惯于使用基于的FFT算法,在国内外一些地球物理文献中(Blakely,1996;蔡宗熹,2002;管志宁,2005;曾华霖,2005),强调在使用FFT算法前,需将采样数据插值为形式.若按照这样做法,本文给出的算例中采样数据需要由插值成,即,这样做不仅降低了计算效率,还会引入误差.由本文结论可知,插值成形式是不必要的.
延拓结果如图 5所示.将图 5与图 4所示理论值对比可知,两者在形态上基本一致.理论值与延拓结果作差并取绝对值,得到延拓误差.延拓误差和z=-200 m高度面的理论重力数据统计值由表 1给出.由表 1可以看出,延拓结果具有很高的精度.综上所述,数值实验结果进一步表明,本文给出的任意采样点情况下的离散频率计算公式是正确的.
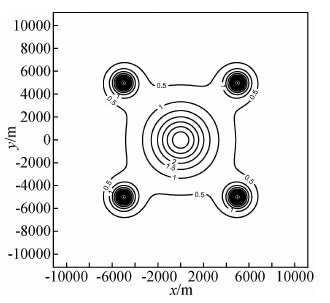 | 图 5 重力数据计算值(z=-200 m) Fig. 5 Computed gravity data (z=-200 m) |
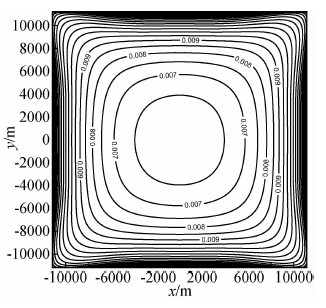 | 图 6 延拓误差 Fig. 6 Continuation error |
|
|
表 1 重力数据(z=-200 m)和延拓误差统计值 Table 1 Statistics of gravity data (z=-200 m) and continuation error |
正确计算离散频率是应用FFT算法解决地球物理问题的一个关键环节,目前已发表文献对该问题研究较少.本文从离散傅里叶变换作为傅里叶变换数值计算逼近的观点,通过分析离散傅里叶变换公式推导过程,给出了任意采样点情况离散频率计算公式,并从物理和数学两方面阐述了离散频率计算公式的含义.以频率域求解重力场延拓问题为例,通过理论模型数值实验,进一步验证了离散频率计算公式的正确性.本文研究结果,为应用任意采样点数FFT算法在频率域求解地球物理场问题,如重磁场的延拓、求导、重磁场正演等,提供一定理论指导.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持! 附录A将式(20)代入式(23),推导可得
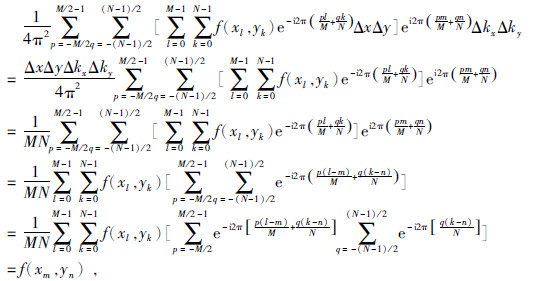
上述推导过程中,利用了如下结论
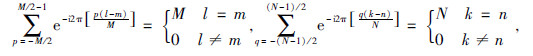
该结论的证明比较简单,在此省略.
推导结果表明,若将式(20)和式(23)作为等式关系看待,则它们是严格数学意义上的正反变换.利用相同思路,可以证明式(20)分别与式(21)、式(22)构成正反变换对,在此省略.
| [1] | Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge:Cambridge University Press. |
| [2] | CAI Zongxi. 2002. Potential Theory in Curved Surface and Its Applications in Geophysics(in Chinese)[M]. Zhengzhou:Henan Science and Technology Press. |
| [3] | CHAI Yupu. 1997. Shift Sampling Theory and Its Application(in Chinese)[M]. Beijing:China Petroleum Industry Press. |
| [4] | Chu S and Burrus C S. 1982. A prime factor FTT algorithm using distributed arithmetic[J]. IEEE Transactions on Acoustic, Speech, and Signal Processing, 30(2):217-227. |
| [5] | Cooley J W, Lewis P A W, Welch P D. 1967. Historical notes on the fast Fourier transform[J]. IEEE Transactions on Audio and Electroacoustics, 15(2):76-79. |
| [6] | Cooley J W, Turkey J W. 1965. An algorithm for the machine calculation of complex Fourier series[J]. Mathematics of Computation, 19(90):297-301. |
| [7] | Cooper G. 2004. The stable downward continuation of potential field data[J]. Exploration Geophysics, 35(4):260-265. |
| [8] | Duhamel P, Hollmann H. 1984. Split-radix FFT algorithm[J]. Electronics Letters, 20(1):14-16. |
| [9] | Duhamel P, Vetterli M. 1990. Fast Fourier transforms:a tutorial review and a state of the art[J]. Signal Processing, 19(4):259-299. |
| [10] | Frigo M, Johnson S G. 2005. The design and implementation of FFTW3[J]. Proceedings of the IEEE, 93(2):216-231. |
| [11] | GUAN Zhining. 2005. Geomagnetic Fields and Magnetic Exploration(in Chinese)[M]. Beijing:Geological Publishing House. |
| [12] | GUO Hong, CAO Xiaoling, HU Xiaoyan. 2011. FFT parallel solver based on JASMIN and applications[J]. Chinese Journal of Computational Physics(in Chinese), 28(4):475-480. |
| [13] | Heideman M T, Johnson D H, Burrus C S. 1984. Gauss and the History of the fast Fourier transform[J]. IEEE ASSP Magazine, 1(4):14-21. |
| [14] | Liu H, Yuan J H, Chen J B, et al. 2006. Theory of large-step wavefield depth extrapolation[J]. Chinese J. Geophys.(in Chinese), 49(6):1779-1793, doi:10.3321/j.issn:0001-5733.2006.06.026. |
| [15] | Liu J Z, Liu L T, Liang X H, et al. 2013. Based on measured gravity anomaly and terrain data to determine the gravity gradients[J]. Chinese J. Geophys.(in Chinese), 56(7):2245-2256, doi:10.6038/cjg20130712. |
| [16] | Lu H Y, Fu L Y, Jiang T. 2010. Wave-equation datuming based on fast Fourier transform[J]. Progr. Geophys.(in Chinese), 25(4):1313-1322, doi:10.3969/j.issn.1004-2903.2010.04.020. |
| [17] | Press W H, Teukolsky S A, Vetterling W T, et al. 1997a. Numerical Recipes in Fortran 77:the Art of Scientific Computing[M]. 2nd ed. Cambridge:Cambridge University Press. |
| [18] | Press W H, Teukolsky S A, Vetterling W T, et al. 1997b. Numerical Recipes in Fortran 90:the Art of Scientific Computing[M]. 2nd ed. Cambridge:Cambridge University Press. |
| [19] | Rader C M. 1968. Discrete Fourier transforms when the number of data samples is prime[J]. Proceedings of the IEEE, 56(6):1107-1108. |
| [20] | Swarztrauber P N. 1982. Vectorizing the FFTs[A].//Rodrigue G ed. Parallel Computations[M]. New York:Academic Press, 51-83. |
| [21] | Wang W Y, Liu J L, Qiu Z Y, et al. 2009. The research of the frequency domain dipole layer method for the processing and transformation of potential field on curved surface[J]. Chinese J. Geophys.(in Chinese), 52(10):2652-2665, doi:10.3969/j.issn.0001-5733.2009.10.026. |
| [22] | Wei B J, Liu Q H. 2007. Fast algorithm for simulating 3-D electromagnetic inverse scattering in horizontally stratified medium via DTA[J]. Chinese J. Geophys.(in Chinese), 50(5):1595-1605, doi:10.3321/j.issn:0001-5733.2007.05.037. |
| [23] | Winograd S. 1976. On computing the discrete Fourier transform[J]. Proceedings of the National Academy of Sciences of the United States of America, 73(4):1005-1006. |
| [24] | Winograd S. 1978. On computing the discrete Fourier transform[J]. Mathematics of Computation, 32(141):175-199. |
| [25] | Xu S Z. 2007. A comparison of effects between the iteration method and FFT for downward continuation of potential fields[J]. Chinese J. Geophys.(in Chinese), 50(1):285-289, doi:10.3321/j.issn:0001-5733.2007.01.035. |
| [26] | Xu S Z, Yu H L. 2007. The interpolation-iteration method for potential field continuation from undulating surface to plane[J]. Chinese J. Geophys.(in Chinese), 50(6):1811-1815, doi:10.3321/j.issn:0001-5733.2007.06.022. |
| [27] | Ye H X, Dai J W, Jin Y Q, et al. 2010. Analytical iterative algorithm for fast computation of scattering from multiple conductive cylinders and the image reconstruction[J]. Chinese J. Geophys.(in Chinese), 53(7):1653-1660, doi:10.3969/j.issn.0001-5733.2010.07.016. |
| [28] | YE Qixiao, SHEN Yonghuan. 2006. Practical Handbook of Mathematics(in Chinese)[M]. 2nd ed. Beijing:Science Press. |
| [29] | ZENG Hualin. 2005. Gravity Field and Gravity Exploration(in Chinese)[M]. Beijing:Geological Publishing House. |
| [30] | Zhang E H, Shi L, Li Y H, et al. 2015. 3D interface inversion of gravity data in the frequency domain using a parabolic density-depth function and the application in Sichuan-Yunnan region[J]. Chinese J. Geophys.(in Chinese), 58(2):556-565, doi:10.6038/cjg20150218. |
| [31] | Zhang J G, Jiao L G, Liu X C, et al. 2013. A study on the characteristics of ULF electromagnetic spectrum before and after the Wenchuan MS 8.0 earthquake[J]. Chinese J. Geophys.(in Chinese), 56(4):1253-1261, doi:10.6038/cjg20130420. |
| [32] | 蔡宗熹. 2002. 曲面上的位场理论及其在地球物理中的应用[M]. 郑州:河南科学技术出版社. |
| [33] | 柴玉璞. 1997. 偏移抽样理论及其应用[M]. 北京:石油工业出版社. |
| [34] | 管志宁. 2005. 地磁场与磁力勘探[M]. 北京:地质出版社. |
| [35] | 郭红, 曹小林, 胡晓燕. 2011. 基于JASMIN框架的FFT并行解法器及其应用[J]. 计算物理, 28(4):475-480. |
| [36] | 刘洪, 袁江华, 陈景波,等. 2006. 大步长波场深度延拓的理论[J]. 地球物理学报, 49(6):1779-1793, doi:10.3321/j.issn:0001-5733.2006.06.026. |
| [37] | 刘金钊, 柳林涛, 梁星辉,等. 2013. 基于实测重力异常和地形数据确定重力梯度的研究[J]. 地球物理学报, 56(7):2245-2256, doi:10.6038/cjg20130712. |
| [38] | 卢回忆, 符力耘, 蒋韬. 2010. 快速Fourier变换波动方程基准面校正方法研究[J]. 地球物理学进展, 25(4):1313-1322, doi:10.3969/j.issn.1004-2903.2010.04.020. |
| [39] | 王万银, 刘金兰, 邱之云,等. 2009. 频率域偶层位曲面位场处理和转换方法研究[J]. 地球物理学报, 52(10):2652-2665, doi:10.3969/j.issn.0001-5733.2009.10.026. |
| [40] | 魏宝君, Liu Q H. 2007. 水平层状介质中基于DTA的三维电磁波逆散射快速模拟算法[J]. 地球物理学报, 50(5):1595-1605, doi:10.3321/j.issn:0001-5733.2007.05.037. |
| [41] | 徐世浙. 2007. 迭代法与FFT法位场向下延拓效果的比较[J]. 地球物理学报, 50(1):285-289, doi:10.3321/j.issn:0001-5733.2007.01.035. |
| [42] | 徐世浙, 余海龙. 2007. 位场曲化平的插值-迭代法[J]. 地球物理学报, 50(6):1811-1815, doi:10.3321/j.issn:0001-5733.2007.06.022. |
| [43] | 叶红霞, 戴俊文, 金亚秋,等. 2010. 随机分布多导体圆柱目标散射的快速计算及其成像模拟[J]. 地球物理学报, 53(7):1653-1660, doi:10.3969/j.issn.0001-5733.2010.07.016. |
| [44] | 叶其孝, 沈永欢. 2006. 实用数学手册[M]. 第2版. 北京:科学出版社. |
| [45] | 曾华霖. 2005. 重力场与重力勘探[M]. 北京:地质出版社. |
| [46] | 张恩会, 石磊, 李永华,等. 2015. 基于抛物线密度模型的频率域三维界面反演及其在川滇地区的应用[J]. 地球物理学报, 58(2):556-565, doi:10.6038/cjg20150218. |
| [47] | 张建国, 焦立果, 刘晓灿,等. 2013. 汶川MS 8.0级地震前后ULF电磁辐射频谱特征研究[J]. 地球物理学报, 56(4):1253-1261, doi:10.6038/cjg20130420. |
 2016, Vol. 31
2016, Vol. 31


