2. 凯里学院, 贵州, 凯里 556011;
3. 江苏省地理信息资源开发与利用协同创新中心, 南京 210023
2. Kaili College, Guizhou, Kaili 556011, China;
3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
Ei Niño(La Niña)事件是全球气候变化研究的热点问题之一,Bierknes(1969)首先提出Ei Niño、La Niña现象是赤道附近的海-气系统相互作用,与发生在热带大气中南方涛动(Southern ocsmatoin)现象有着内在联系,它们共同称为ENSO.许多学者针对它的成因机制、影响因素及预报方法进行研究.如,Wyrtki(1975)提出信风张驰理论,Philander等(1984)、Hirst(1986)提出不稳定海洋波动理论,Suarez和Schopf(1988)和Neelin(1991)提出延迟振子理论,刘式适等(2001)讨论了地球自转速率变化对海气耦合系统的影响,薛峰等研究了外热带大气扰动对ENSO的影响.韩延本等(2000)认为地球自转变慢时,Ei Niño事件较多,当地球自转加快,La Niña事件发生较多.赵佩章等(2001a)、孙熔(2011)认为太阳黑子发生峰年与厄尔尼诺事件具有密切相关性.赵佩章等(1998)、杨学祥(2008)提出日食发生对Ei Niño(La Niña)事件具有重要影响,杨冬红和杨学祥(2008)对日食与Ei Niño、La Niña之间的成因关系进行分析,项月琴和李建京(1989)从日食对太阳辐射能量影响分析了它与Ei Niño、La Niña的关系,林振山等(1998)提出了日食-厄尔尼诺相关预报系数.Ludescher等(2013,2014)基于高质量空气温度数据,对近60年200多个测量点数据进行分析,对太平洋远距站点之间的气候变暖进行研究,提出半年期厄尔尼诺事件预测方法.Cobb等(2013)在science杂志发表文章,他们通过对ENSO活动中心地北莱恩群岛的珊瑚礁化石进行分析,重构了过去7000年ENSO事件发生过程.他们研究结果表明无论是自然或人类造成ENSO被迫改变,都可能非常困难从其环境内部变异性中区分出来,因此厄尔尼诺—南方涛动在整个全新世具高度可变化性.
上述研究虽然各自都能部分地解释Ei Niño(La Niña)的发生和演变特征,但其发生确切原因仍未真正清楚,其发生预报仍然是一个重要而困难的科学问题.地球表面大气活动规律与变化受太阳活动变化、太阳能量到达地球过程显著影响.Ei Niño(La Niña)事件过程与地球表面能量来源变化过程具有非常密切的联系.因而,太阳活动、地球自转速率变化及日食与Ei Niño(La Niña)发生都具有非常直接联系.通过对这些要素发生规律、特征与Ei Niño(La Niña)事件的发生时间、位相等方面进行分析研究,如果它们具有较好一致性,说明其产生机理与这些要素具有密切的联系,并依据它们相互联系与特点,提出与Ei Niño(La Niña)事件的相关系数与预报定理.
1 资料与研究方法1.1 数据与资料地球自转速率变化以国际地球自转服务局(IERS,http://hpiers.obspm.fr/)提供的地球日转时间(LOD)数据来表征地球自转速度的快慢,LOD数据表示地球日长时间实际值与24小时差值.当 LOD 值增大时,表明地球自转速度减慢,反之亦然.国际地球自转服务局(IERS)提供了从1962-2014年共52年的每月平均日长变化,以及更长时间年平均地球自转日长变化数据.
日食数据来源于美国国家航空航天局,包括日食发生纬度、观测时间与范围、类型等详细信息.(http://eclipse.gsfc.nasa.gov/SEcat5/SEcatalog.html#cattab).Ei Niño、 La Niña数据来源于ENSO监测小组(1998)及其他学者(王绍武和龚道溢,1999; 张秀伟和赵景波,2014)的统计资料,划分依据是选取赤道东太平洋范围(0°-10°S、180°-90°W)内的海表温度(SST)资料,以该海域月平均海温距平是否≥0.5 ℃(≤0.5 ℃)作为指标.一次事件长度至少为半年,其中允许有1个月中断.其强度由事件持续时间长度、最大⊿SST(最小⊿SST),以及⊿SST≥1.0(⊿SST≤-1.0)的月数三项综合评价.太阳黑子数据来源于比利时太阳影响数据分析中心(WDC-SILSO,Royal Observatory of Belgium,Brussels),从其获得1945年至2014年每日太阳黑子数量.
1.2 经验模态分解(EMD)经验模态分解(Empirical Mode Decomposition)是Huang等(1998,1999)提出.EMD是对一个信号同时将不同尺度(频率)的波动或趋势逐级分解开来,产生一系列具有不同特征尺度的数据序列称为本征模函数(Intrinsic Mode Function,IMF),并将每一个IMF进行希尔伯特变换,称希尔伯特-黄变换.IMF波动分量具有显著缓变波包特性,不同IMF分量是平稳信号,具有非线性特征,其缓变波包特征味意着不同特征尺度波动的波幅随时间变化,因而也具有时域上的局域化特征.趋势分量则是单调函数或者均值函数,可以代表其长期变化趋势或平均态.EMD最终结果是得到在时域和频域都有较高分辨率特征的谱图.目前,EMD方法已经成功应用于大气科学、地质、生态及社会经济科学等非线性科学领域.
经验模态分解(EMD)方法是将时间信号X(t)分解成一系列本征模态函数IMF,每个IMF分量具有如下特征:①从全局特性上看,极值点数必须和过零点数一致或者至多相差一个;②在某一个局部点,极大值包络和极小值包络在该点的值的算术平均和是零.EMD实际上是一种循环迭代算法,从时间序列实现分解,公式为
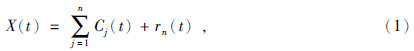
根据EMD提取的地球自转和太阳黑子变化IMF分量,建立动力学模型为
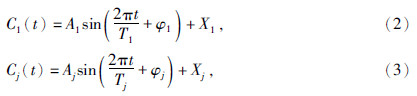
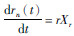 ,对其积分得到:rn(t)=Xrert,式中:Cj(t)地球自转或太阳黑子数初始总量;Xj代表各初始量IMF分量;Xr代表趋势项初始量;t代表时间;Tj代表周期;Aj代表振幅;φj代表相位,r代表太阳黑子数或地球自转变化的年增长率;j是IMF分量的分量数.因此,由EMD分解原理得预测模型为
,对其积分得到:rn(t)=Xrert,式中:Cj(t)地球自转或太阳黑子数初始总量;Xj代表各初始量IMF分量;Xr代表趋势项初始量;t代表时间;Tj代表周期;Aj代表振幅;φj代表相位,r代表太阳黑子数或地球自转变化的年增长率;j是IMF分量的分量数.因此,由EMD分解原理得预测模型为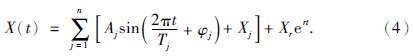
王钟睿等(2002)、冯松和汤懋苍(1997)建立平均温度与太阳黑子峰年值周期长度之间的简单数学模型,拟合近2000a来的温度变化,结果表明太阳活动是影响10a以上尺度气温变化的基本因素,故对1945a-2014a太阳黑子数量变化与Ei Niño(La Niña)事件的多尺度相关性进行分析.
采用EMD方法对1945a-2014a逐月太阳黑子数据进行逐级分解,得到6个IMF分量和趋势分量(图 1).表 1是不同尺度IMF分量所表征不同时间尺度波动的平均周期及方差贡献率.分析6个IMF分量可知,IMF1表示准3月尺度极短周期振荡;IMF2表示准半年尺度极短周期振荡;IMF3表示准1.5年短周期振荡;IMF4表示准6年短周期振荡;IMF5表示准11年周期波动振荡;IMF6表示准22年周期波动振荡.IMF5分解量方差贡献率达78.0384%,其太阳黑子活动准11年的波动振荡周期,与公认太阳活动周期吻合,也表明该EMD分解较为合理.从趋势量分析看,从1945年至今,太阳黑子数量逐年呈减少趋势,表明太阳黑子活动对地球厄尔尼诺现象影响呈减弱趋势.
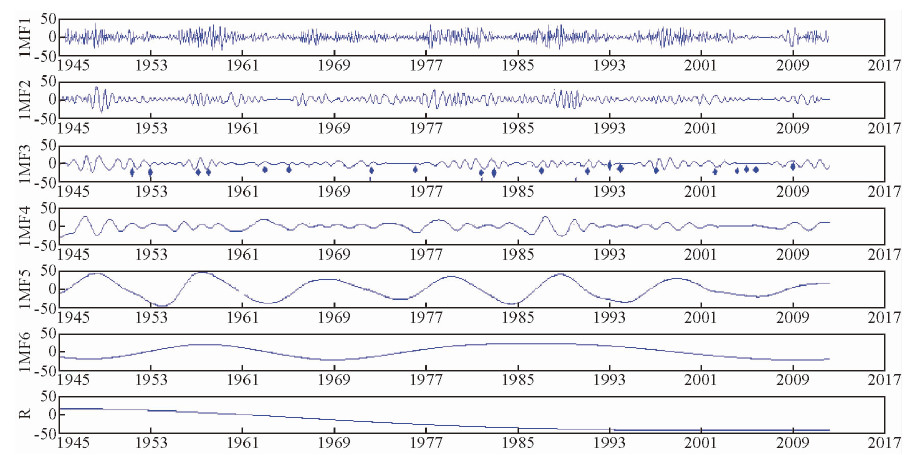 |
图 1 1945a-2014a太阳黑子月均变化的IMF分量及其趋势量 (▲La Niña事件;◆Ei Niño事件) Fig.1 The IMF component and the tendency of sunspot average monthly change from 1945a to 2014a (▲—the La Niña event;◆—the Ei Niño event) |
|
|
表 1 1945a-2014a太阳黑子月均变化IMF分量周期及方差贡献率 Table 1 The IMF period and variance contribution rate of sunspot average monthly change from 1945a to 2014a |
IMF1与 IMF2分解量表示太阳黑子数极短周期内变化,其中1945-2014年期间共有7个高峰值区,而21次太阳活动高峰年,分别在7个太阳活动周期内.第18周期(1944-1954)的1947、1948、1949年;第19周期(1954-1964)的1957、1958、1959年;第20周期(1964-1796)的1967、1968、1969、1970年;第21周期(1976-1986)的1979(中心)、1980、1981年;第22周期(1986-1996)的1989、1990、1991年;第23周期(1996-2008)的2000、2001(中心)、2004年;第24周期(2008-)的2014年.其也存在6个太阳黑子活动数量谷值年区,分别是1952-1955年,1962-1965年,1974-1977年,1985-1987年、2004-2010年.各月及太阳高峰年际间的太阳黑子数变化波动幅度较大,而太阳黑子谷值年的太阳黑子数年际波动变化幅度较小.根据Ei Niño(La Niña)监测资料,从1945-2014年Ei Niño共发生21年次,La Niña发生14年次.其中Ei Niño主要生发年份1951、1953、1957、1985、1963、1965、1972、1976、1982-1983、1987、1991、1993、1994、1997、2002、2004-2005、2006、2009、2014;La Niña主要发生年份1955、1962、1964、1968、1970、1975、1984-1985、1988、1995、1999-2000、2007、2010.
冯博(1989)认为太阳黑子活动高峰年,太阳辐射电磁辐射波变长,其额外加热后使赤道地区海洋吸收更多长波,经过海洋热力作用弛豫过程,可造成对大气运动产生巨大的影响.结合图 1与表 1中IMF5分析可知,Ei Niño主要发生在太阳黑子数量达高峰值年后的1~3年内,而La Niña主要发生在太阳黑子高峰年前1~3年内.因此,太阳黑子高峰值年后Ei Niño事件发生率较高,而在太阳黑子谷值年后La Niña事件发生率较高.结果表明太阳黑子数量变化与Ei Niño(La Niña)事件存在密切联系,与顾节经(1998)、李崇银(2014)等研究结论相同.
2.2 Ei Niño、La Niña与地球自转速率变化多尺度相关分析郑大伟等(1990)、Carter等(1984)认为当地球自转速率变快(LOD值降低),诱发La Niña事件发生;当地球自转速率降低时(LOD值增加)诱发Ei Niño事件发生.任振球和张素琴(1985)研究也获得相同结论.对1962年后地球日长月均变化数据进行EMD分解(图 2、表 2).从各分解量方差贡献率可知,IMF3 1.5年周期方差贡献率3.7464%,IMF6分解量方差贡献率为28.0944%,其周期约为15年,故地球自转速率变化具有一定的长周期性,但短周期性不明显.其中地球自转速率IMF3分解振荡准周期1.5年与太阳黑子数量变化IMF3振荡周期相吻合.叠加Ei Niño(La Niña)事件,可知地球自转速率加快,La Niña发生事件增多;地球自转速率降低,Ei Niño发生事件增多.从趋势量可知,从1962年至今,地球自转速率变化整体处于逐渐增加趋势(日长呈降低趋势),表明地球自转对Ei Niño事件影响呈减弱趋势,对La Niña事件影响则呈增强趋势.
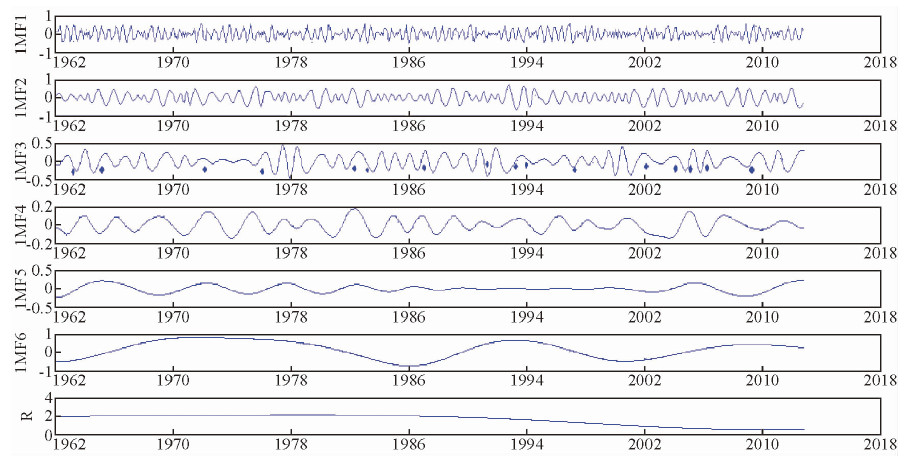 |
图 2 1962a-2014a地球自转月均日长变化的IMF分量及其趋势量 (▲表示La Niña事件;◆Ei Niño事件) Fig.2 The IMF component and the tendency of the LOD average monthly change from 1962a to 2014a (▲—the La Niña event;◆—the Ei Niño event) |
|
|
表 2 1962a-2014a地球自转月均变化分量周期及方差贡献率 Table 2 The IMF period and variance contribution rate of the LOD average monthly change from 1962a to 2014a |
通过对1945a-2014a地球自转年均日长变化及太阳黑子年均数进行距平处理,得到其距平数时间分布图(图 3),并与1950a至2014a的Ei Niño(La Niña)发生年叠加分析它们之间的相关性.在1945a-2014a期间,地球日长变化多年平均值为1.591.当其距平数值小于零,则地球自转速度较快,且其值越小,自转速度越快,反之亦然.太阳黑子数多年平均数为71.0556,如太阳黑子距平数小于零,表示太阳黑子数较少,且其值越小,太阳活动越弱;如距平系数大于零,表示太阳黑子数较多,其值越大,太阳活动越强.
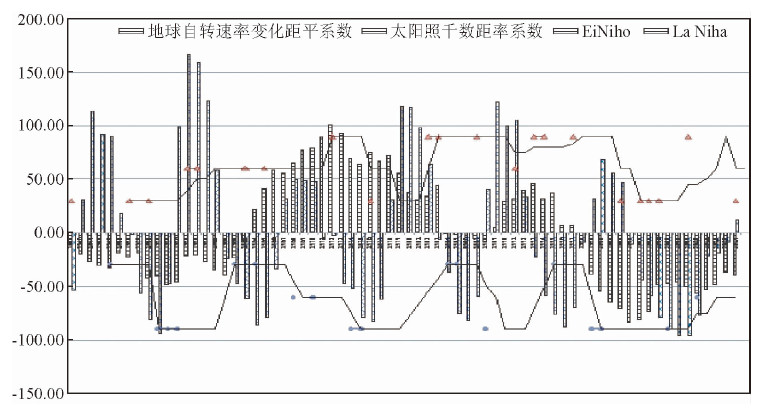 | 图 3 1945a-2014a地球自转日长、太阳黑子距平数与Ei Niño(La Niña)事件 Fig.3 The Anomoly of the LOD and the sunspots, the Ei Niño(La Niña) event from 1945a-2014a |
在Ei Niño事件较强年1957、1958、1972、1981、1982、1993、1997年,期间地球自转速度年际变化由快转慢,且自转速度较低,而太阳黑子活动则处于高峰值年.La Niña较强年分别为1954、1955、1956、1974、1975、1988、1999、2000、2007年,期间地球自转速度年际变化由慢转快且自转速度较快.太阳活动增强,太阳黑子数量增多,引起赤道海区水温增加;地球自转速度减慢,造成赤道带大气和海水获得向东惯性力,促进西太平洋暖水向东流动,东太平洋冷水上翻受阻,因暖水堆积而发生海水增温、海面抬升而诱发Ei Niño.当太阳黑子数量较少时,其对地球影响减弱,与Ei Niño(La Niña)发生的相关性不明显.研究还表明,太阳黑子数量达峰值后约两年后,地球自转速度有加快趋势;太阳黑子数量达谷值年后约2年,地球自转速度呈降低趋势.表明太阳活动与自转速度变化之间有一定的相关性,与罗时芳等(1974)、顾震年(1991)的计算与研究结论基本一致.
3 日食诱发Ei Niño(La Niña)热动力机制日食对Ei Niño(La Niña)事件的影响已经受多数学者所认同,季国良和陈有虞(1980)等认为日食过程的太阳短波辐射量呈线性减弱,长波辐射减弱稍慢;在历时160分钟的日食过程到达地面净能量损失达59.2卡/cm2,若按东经60°-160°,北纬50°以北地区考虑,总面积814.5万km2,总能量损失可达4.8×1018卡.Anderson等(1972)指出日食现象虽然是一个天文现象,但对于地面气象要素如气压、气温等都会产生一定影响.李兴中(1987)研究认为由于日食的影响,地面辐射降低最多可达1.7 μR /h.在众多学者的研究基础上,提出日食诱发Ei Niño(La Niña)的热动力诱发机制:
(1)位能增量
取太阳常数(Q)为8.19 J/(cm2·min),大气比热(c)为1008 J/(kg·℃),赤道一次日全食约2 h,折合完全无光1 h.设大气吸收(R=19%)的100%和海洋陆地吸收(R=51%)的70%,决定了日食区的减温量,则日食区减温为
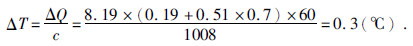
设单位气柱质心高度Zc=5500 m,位能增量和单位质量位能增量分别为ΔE和Δe,因为当Δρ/ρ=ΔT/T=0.3/273=0.11%;ΔE/=gΔMZC/2;则有:Δe/=ΔE/M=gΔTZC/2×273=30(J/kg),式中,e为有效位能,g为重力加速度,ρ为大气密度,M为大气质量.
(2)赤道日食区附近水平对流附加速度V和垂直对流附加速度V⊥,设大气位能增量的有效转化率为p,根据能量守恒定率有:V2/2=ep;
假设大气位能增量的有效转化率取p=15%,则日食区附近水平对流附加速度为
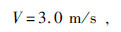
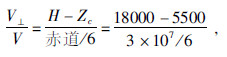
(3)日食区内气柱对外作功时间
由于日食区内平均气温要比外界的低,日食区下垫面将向气柱输送更多的感热和潜热,从而对外作正功.由于实际空气分子的碰撞为非完全弹性碰撞,设气体碰撞的热交换系数为0.75.而对外作功的时间等于气柱质心上升到对流层的时间为t/0.75,公式为
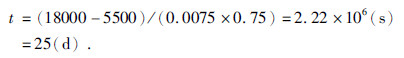
对于极地日食,其日照强度是赤道的cos66.5°=0.4(倍),而大气厚度则是赤道的8/18=0.4(倍),所以极地日食区内气柱对外作功时间为
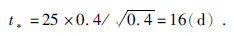
结论1:每次日食对大气环流的平均作用时间为20天左右,每年2~6次的日食将对大气环流产生长期而巨大的影响.
结论2:日食区气柱对外作正功是日食诱发Ei Niño、La Niña的热动力因素.由于日食区内平均气温要比外界的低.日食区下垫面将向日食区气柱输送更多的感热和潜热,从而使日食区内气柱对外作正功诱发Ei Niño、La Niña现象.
结论3:中纬以上连续3~6次同位相减弱赤道东风的代数叠加是日食诱发Ei Niño(La Niña)现象重要因素.由于每次高纬或极区的日食都将使极地下沉气流减弱,从而使赤道东风减弱.而1 a~2 a内在中纬以上地区连续发生3~6次日食,将使赤道东风减弱逐次得到加强,从而诱发Ei Niño(La Niña)现象.
4 日食、太阳黑子及地球自转—Ei Niño(La Niña)相关系数及预测4.1 日食、太阳黑子及地球自转与Ei Niño(La Niña)的相关系数Ei Niño、La Niña是受多种因素影响复杂现象,日食主要有3个周期均不是定数,它们均不具有周期性.因此提出以下假设:
假设1,连续若干次的日食是诱发Ei Niño(La Niña)现象的主要因素之一.
通过分析从1950年以来所有Ei Niño(La Niña)年和日食资料,分析发现日食和厄尔尼诺现象之间存在着以下关系:
A:在极区(南极或北极)连续发生3次或3次以上日食,则当年或次年(发生开始时间)必发生Ei Niño现象.
B:凡一年内在赤道连续发生3次或3次以上日食,则当年或次年(发生开始时间)必发生La Niña现象.
假设2,一年内连续发生多次日食,且当年内同时还处于太阳黑子高峰值年,地球自转速率处于峰值区或谷值区,则它们均是Ei Niño(La Niña)发生的重要影响因素.
通过统计分析1950年以来所有Ei Niño(La Niña)年和地球自转日长变化数据、太阳黑子活动高峰值年数据(认为从大于距平值-20%以上的太阳黑子数均对Ei Niño发生有诱发与促进作用,太阳黑子数越多对Ei Niño增强作用越显著,太阳黑子活动对La Niña没有明显影响),当爆发太阳黑子活动及地球自转变化处于峰值区或谷值区时,它们与Ei Niño(La Niña)事件有以下关系:
C:若地球自转日长大于距平值,其诱发Ei Niño发生(或抑制La Niña),且日长值越大,诱发(或抵抑制)作用越显著;若地球自转日长低于距平值,其诱发La Niña发生(或抑制Ei Niño),且日长值越小,诱发(或抵制)作用越显著;
D:若太阳黑子数量大于距平值-20%,其对Ei Niño发生起诱发增强作用,太阳黑子数越多,其诱发增强作用越显著;若太阳黑子数量小于距平值的-20%,其对Ei Niño(La Niña)的发生没有明显影响.
为进一步证明假设1、2的充分必要性,定义日食—厄尔尼诺系数ei、太阳黑子—厄尔尼诺系数sj、地球自转—厄尔尼诺系数rj;年日食、太阳黑子、地球自转—厄尔尼诺(拉尼娜)系数为E1=ei+sj+rj;累积日食、太阳黑子、地球自转与厄尔尼诺(拉尼娜)系数为E2.设日食中心纬度、日出见食纬度、中午见食纬度、日落见食纬度分别为ψm、ψa、ψn:
则有: ψ=ψn+0.18(ψm+ψa-2ψn).
综合考虑到A和B,定义日食一厄尔尼诺系数ei为
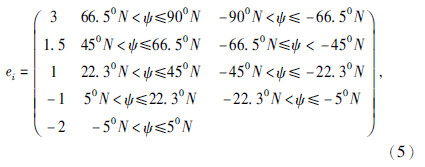
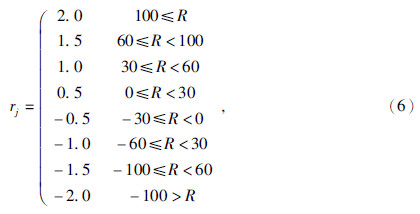
考虑到D,定义太阳黑子-厄尔尼诺系数为sj,按照太阳黑子数距平百分数(S)进行划分为
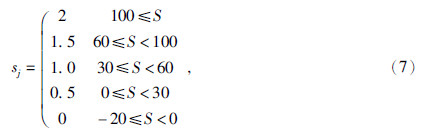
定义累积日食、太阳黑子、地球自转一厄尔尼诺系数E2=∑(∑(eji+e(j+1)i)+rj+rj+1+sj+sj+1,i=1,2,…n,n为1年内发生日食的总次数;j为第某年,从1948-2014年.
4.2 Ei Niño(La Niña)的E1-E2预测定理日食、太阳黑子、地球自转对大气系统影响具有能量传播与转换运动过程,具有较一定驰豫过程,且多数Ei Niño(La Niña)事件是跨年发生,故对大气层影响具有两年振荡期(顾震年,1998).因此,把当年日食、太阳黑子、地球自转—厄尔尼诺(拉尼娜)系数(E1)对当年与次年Ei Niño(La Niña)事件预测,而2年累加系数(E2)则对其次年及后年发生进行预测,提出预测Ei Niño(La Niña)年的R1-R2预测定理:
(1)E1≥ 9(当年或次年发生Ei Niño);
(2)E2≥11(次年或后年发生Ei Niño);
(3)E1<1(当年或次年发生La Niña);
(4)E2≤-1(次年或后年发生La Niña).
4.3 资料检验与预测(1)资料检验:依据公式(5)、(6)、(7)得到1948年以来年日食、太阳黑子、地球自转-厄尔尼诺系数E1和年累积系数E2(表 3),并依据资料检验得到E1-E2的验证结果(表 3).结果表明实际验证正确率达86.75%,其中Ei Niño预测准确率高于La Niña.由于Ei Niño(La Niña)的发生是多因素复杂系统过程,此次预测采用了3个指标,它们对Ei Niño(La Niña)的影响机制尚未完全清楚,其次部份La Niña事件时间较短、活动弱,这都增加了预测难度,但研究结果较高准确率仍然充分表明E1-E2定理具有较好的预测作用.
|
|
表 3 日食、太阳黑子、地球自转与Ei Niña(La Niña)相关系数及E1-E2预测结果表 Table 3 The correlation coefficient between the eclipse, sunspot,earth rotate and Ei Niña(La Niña) and the E1-E2 prediction results |
(2)地球自转和太阳黑子数量变化的动力学预测及E1-E2定理
根据EMD分析,太阳黑子的IMF5分量方差贡献率达78.04%,地球自转IMF6分量方差贡献率28.90%,趋势项方差贡献率48.18%,其他各项方差贡献率较小而忽略.地球自转年均增长为-0.53%,太阳黑子年均增长率为1.254%,分别以2010年为初始量代入动力预测模型(公式4)计算,得到2015年至2025年太阳黑子数量与地球自转日长变化预测值,将预测值按E1-E2定理进行Ei Niño(La Niña)预测(表 3).结果表明2015年E2=11,预测2016年发生Ei Niño;2016年E1=-2,预测2017年发生La Niña;2018年E1=9.5、E2=13,2019年E2=13.5,预测2018、2019、2020年发生Ei Niña;2022年E2=11,预测2023年发生Ei Niña;2023年E1=-1,预测2024年发生La Niña.另外根据Ei Niña与La Niña的相间发生特征,预测2021发生La Niña.
5 结 论5.1 Ei Niña主要发生在太阳黑子数量达高峰值年后,La Niña发生在高峰值年前;太阳黑子峰年与Ei Niña发生有较好关联性;地球自转速率增加,诱发或增强La Niña,抑制Ei Niña现象;地球自转速率降低时,诱发或增强Ei Niña现象,抑制La Niña现象.分析了日食与Ei Niña(La Niña)事件间热动力诱因关系.
5.2 构建日食、太阳黑子、地球自转与Ei Niña(La Niña)之间相关系数,通过E1-E2预测定理对过去60多年Ei Niña(La Niña)事件进行预测验证.其结果准确较高,充分说明日食、太阳黑子、地球自转—Ei Niña(La Niña)系数及E1-E2预测定理具有一定合理性.
5.3 运用动力学模型,预测2015-2025年太阳黑子数量与地球自转日长变化,并依据E1-E2定理对未来10年的Ei Niña(La Niña)事件进行预测,结果是Ei Niña发生年为2016、2018、2019、2020、2023年,La Niña发生年为2017、2021、2024年.
致 谢 本文引用了多位学者研究成果,在此向各位作者表示衷心感谢!感谢编辑和审稿人对本文的编辑审阅!| [1] | Anderson R C, Keefer D R, Myerss O E. 1972. Atmospheric pressure and temperature changes during the 7 march 1970 solar eclipse[J]. Jourual of the Atmosphereic Science, 29(3):583-587. |
| [2] | Bierknes J. 1969. Atmospheric Teleconnections from the equatorial pacific[J]. Mon. Wea. Rev., 97(3):163-172. |
| [3] | Carter W E, Robertson D S, Pettey J E, et al. 1984. Variations in the rotation of the earth[J]. Science, 224(4652):957-961. |
| [4] | Cobb K M, Westphal N, Sayani H R, et al. 2013. Highly variable El Niña-southern oscillation throughout the holocene[J]. Science, 339(6115):67-70. |
| [5] | ENSO Monitoring Group. 1998. The classification standards and index of El Niña[J]. Meteorological Monthly(in Chinese), 15(3):37-38. |
| [6] | Feng Bo. 1989. Solar activity, EI Niña enent and the earth rotation[J]. Publication of Shaanxi Observatory(in Chinese), 12(1-2):38-42. |
| [7] | Feng S, Tang M C. 1997. The solar activity and air temperature fluction in recent 2500 years[J]. Quaternary Science(in Chinese), 17(1):28-36. |
| [8] | Gu J J. 1998. The sunspot activity impact and predicte the EI Niña enents[J]. Liaoning Meteorological(in Chinese),(4):6-7. |
| [9] | Gu Z N. 1991. The effect of solar activity on the terrestrial climate and earth rotation[J]. Progress in Astronomy(in Chinese), 9(1):51-59. |
| [10] | Gu Z N. 1998. On the relation among the activity, the quasi-biennial oseilliation in the eaquatorial stratosphere and EI Niña[J]. Publications of Yunna Observatory(in Chinese),(4):23-29. |
| [11] | Han Y B, Li Z A, Zhao J. 2000. Using the variation of the earth's rotation to predicte El Niña[J]. Progress in Geophysics(in Chinese), 15(3):112-114. |
| [12] | Hirst A C. 1986. Unstable and damped equatorial modes in simple coupled ocean-atmosphere models[J]. J. Atmos. Sci., 43(6):606-630. |
| [13] | Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. R. Soc. Land. A, 454:903-995. |
| [14] | Huang N E, Shen Z, Long S R. 1999. A new view of nonlinear water waves:The Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 31:417-457. |
| [15] | Ji G L, Chen Y Y. 1980. Observation of solar radiation and its changes, during a solar eclipse[J]. Plateau Meteorology(in Chinese), 1(2):69-77. |
| [16] | Li C Y. 2014. More attention should be paid to the variability in solar activity and its impact on the earth's climate[J]. Advances in Meteorological Science and Technology(in Chinese), 4(4):6-8. |
| [17] | Li X Z. 1987. Effect of solar eclipse on cosmicray radiation on the ground[J]. Uranium Geology(in Chinese),(5):319. |
| [18] | Lin Z S, Zhao P Z, Zhao W T. 1999. The solar eclipse-Ei Niña coefficients and its application[J]. Chinese Journal of Geophysics(in Chinese), 42(6):732-739. |
| [19] | Lin Z S, Wang S G. 2004. EMD analysis of northern hemisphere temperature variability during last 4 centuries[J]. Joural of Tropical Meteorology(in Chinese), 20(1):90-96. |
| [20] | Liu S S, Jiang X, Liu S D, et al. 2001. Earth rotation and El Niña:theory of air sea coupling[J]. Chinese J. Geophys.(in Chinese), 44(4):477-489. |
| [21] | Ludescher J, Gozolchiani A, Bogachev M I, et al. 2013. Improved El Niña forecasting by cooperativity detection[J]. Proc. Natl. Acad. Sci. USA, 110(29):11742-11745. |
| [22] | Ludescher J, Gozolchiani A, Bogachev M I, et al. 2014. Very early warning of next El Niña[J]. Proc. Natl. Acad. Sci. USA, 111(6):2064-2066. |
| [23] | Luo S F, Liang S G, Ye S F, et al. 1974. Analysis of the periodicity of the irregular rotation of the earth[J]. Acta Astronomica Sinica(in Chinese), 15(1):79-85. |
| [24] | Neelin J D. 1991. The slow sea surface temperature mode and the fast-wave limit:Analytic theory for tropical interannual oscillations and experiments in a hybrid coupled model[J]. J. Atmos. Sci., 48(4):584-606. |
| [25] | Philander S G H, Yamagata T, Pacanowski R C. 1984. Unstable air-sea interactions in the tropics[J]. J. Atmos. Sci., 41(4):604-613. |
| [26] | Ren Z Q, Zhang S Q. 1985. Decrease of earth rotation and El Niña enents[J]. Chinese Science Bulletin(in Chinese), 30(6):444-447. |
| [27] | Suarez M J, Schopf P S. 1988. A delayed action oscillator for ENSO[J]. J. Atmos. Sci., 45(21):3283-3287. |
| [28] | Sun R. 2011. The response to the sunspots activity on the El Niña and La Niña[C].//The 28 Session Annual Meeting of China Meteorological Society-The Disasters Weather Research and Forecasting(in Chinese). Beijing:Chinese Meteorological Society. |
| [29] | Wang S W, Gong D Y. 1999. ENSO events and their intensity during the past century[J]. Meteorological Monthly(in Chinese), 25(1):9-13. |
| [30] | Wang Z R, Gao X Q, Tang M C. 2002. The air temperature change in the past 2000 years simulated using solar activity indices[J]. Plateau Meteorology(in Chinese), 21(6):552-555. |
| [31] | Wyrtki K. 1975. El Niña-the dynamic response of the equatorial Pacific ocean to atmospheric forcing[J]. J. Phys. Oceanogr., 5(4):572-583. |
| [32] | Xiang Y Q, Li J J. 1989. Influence of solar eclipse on attenuation of energy of solar radiation near ground[J]. Acta Energiae Solaris Sinica(in Chinese), 10(4):351-360. |
| [33] | Xue F, He J X. 2007. The influence of the extratropical atmospheric disturbances on ENSO[J]. Chinese J. Geophys.(in Chinese), 50(5):1311-1318. |
| [34] | Yang D H, Yang X X. 2008. The causes for El Niña and La Niña events and their prediction[J]. Desert and Oasis Meteorology(in Chinese), 2(5):1-10. |
| [35] | Yang X X. 2008. Reason and evidences for El Niña event[J]. Ziran Zazhi(in Chinese), 26(3):151-155. |
| [36] | Zhang X W, Zhao J B. 2014. Effects of El Niña/La Niña events on climate of eastern edge of Erdos Plateau in recent 57 years[J]. Journal of Shanxi Normal University(Natural Science Edition)(in Chinese), 28(1):95-102. |
| [37] | Zhao P Z, Zhao W T, Zhao D X. 1998. Relation between solar eclipses and Ei Niña[J]. Henan Meteorological(in Chinese),(3):25-26. |
| [38] | Zhao P Z, Chen J, Zhao W T. 2001a. The sunspots affect El Niña and La Niña[J]. Progress in Geophysics(in Chinese), 16(3):85-90. |
| [39] | Zhao P Z, Chen J, Zhao W T. 2001b. Relation between solar eclipses and El Niña and La Niña events[J]. Bimonthly of Xinjiang Meteorology(in Chinese), 24(1):1-4. |
| [40] | Zheng D W, Song D X, Luo S F. 1990. To predicte El Niña enent by the length of days observation data[J]. Chinese Science Bulletin(in Chinese),(16):1244-1246. |
| [41] | ENSO监测小组. 1998. 厄尔尼诺事件的划分标准和指数[J]. 气象, 15(3):37-38. |
| [42] | 冯博. 1989. 太阳活动、厄尔尼诺与地球自转[J]. 陕西天文台台刊, 12(1-2):38-42. |
| [43] | 冯松, 汤懋苍. 1997. 2500多年来的太阳活动与温度变化[J]. 第四纪研究, 17(1):28-36. |
| [44] | 顾节经. 1998. 太阳黑子活动对厄尔尼诺的影响和预测[J]. 辽宁气象,(4):6-7. |
| [45] | 顾震年. 1991. 太阳活动对地表气候和地球自转的影响[J]. 天文学进展, 9(1):51-59. |
| [46] | 顾震年. 1998. 太阳活动、赤道平流层中准两年振荡与厄尔尼诺之间的关系[J]. 云南天文台台刊,(4):23-29. |
| [47] | 韩延本, 李志安, 赵娟. 2000. 由地球自转的年际变化预测El Nino事件[J]. 地球物理学进展, 15(3):112-114. |
| [48] | 季国良, 陈有虞. 1980. 日食过程中的太阳辐射观测及其各分量的变化[J]. 高原气候, 1(2):69-77. |
| [49] | 李崇银. 2014. 太阳活动变化及其对地球气候的影响值得关注[J]. 气象科技进展, 4(4):6-8. |
| [50] | 李兴中. 1987. 日食对宇宙射线在地面辐射量的影响[J]. 铀矿地质,(5):319. |
| [51] | 林振山, 赵佩章, 赵文桐. 1999. 日食-厄尔尼诺系数及其应用[J]. 地球物理学报, 42(6):732-739. |
| [52] | 林振山, 汪曙光. 2004. 近四百年北半球气温变化的分析:EMD方法的应用[J]. 热带气象学报, 20(1):90-96. |
| [53] | 刘式适, 蒋循, 刘式达,等. 2001. 地球自转与El Niña-海气耦合理论[J]. 地球物理学报, 44(4):477-489. |
| [54] | 罗时芳, 梁世光, 叶叔华,等. 1974. 地球自转速率变化的周期分析[J]. 天文学报, 15(1):79-85. |
| [55] | 任振球, 张素琴. 1985. 地球自转与厄尼诺现象[J]. 科学通报, 30(6):444-447. |
| [56] | 孙熔. 2011. El Nino和La Nina事件对太阳黑子活动的响应[C].//第28届中国气象学会年会-天气预报灾害天气研究与预报. 北京:中国气象学会. |
| [57] | 王绍武, 龚道溢. 1999. 近百年来的ENSO事件及其强度[J]. 气象, 25(1):9-13. |
| [58] | 王钟睿, 高晓清, 汤懋苍. 2002. 用太阳活动拟合近2000年的温度变化[J]. 高原气象, 21(6):552-555. |
| [59] | 项月琴, 李建京. 1989. 日食对地面太阳辐射能减弱的影响[J]. 太阳能学报, 10(4):351-360. |
| [60] | 薛峰, 何卷雄. 2007. 外热带大气扰动对ENSO的影响[J]. 地球物理学报, 50(5):1311-318. |
| [61] | 杨冬红, 杨学祥. 2008. 厄尔尼诺事件和拉尼娜事件的成因与预测[J]. 沙漠与绿洲气象, 2(5):1-10. |
| [62] | 杨学祥. 2008. 厄尔尼诺事件产生的原因与验证[J]. 自然杂志, 26(3):151-155. |
| [63] | 张秀伟, 赵景波. 2014. 近57年来El Niña、La Niña事件对鄂尔多斯高原东缘气候的影响[J]. 山西师范大学学报, 28(1):95-102. |
| [64] | 赵佩章, 赵文桐, 赵得秀. 1998. 厄尔尼诺现象和日食的关系[J]. 河南气象,(3):25-26. |
| [65] | 赵佩章, 陈健, 赵文桐. 2001a. 太阳黑子对厄尔尼诺、拉尼娜的影响[J]. 地球物理学进展, 16(3):85-90. |
| [66] | 赵佩章, 陈健, 赵文桐. 2001b. 日食与厄尔尼诺、拉尼娜现象[J]. 新疆气象, 24(1):1-4. |
| [67] | 郑大伟, 宋国玄, 罗时芳. 1990. 日长变化观测资料预测El Niña事件[J]. 科学通报,(16):1244-1246. |
 2016, Vol. 31
2016, Vol. 31


