声电效应是指声波在介质中激发的电磁波效应,其本质是介质中机械能与电能相互转换的过程.声电效应可以获得介质性质的丰富信息,在区分油水气的物质成分、渗透率测量及地层参数计算等多方面具有显著优势(关威等,2011).因此,声电效应的研究已经受到广泛的关注与重视.从1994年开始,美国麻省理工学院的Zhu等(1999)等人在实验中观测到了声电信号,并对不同类型的介质中的声电信号进行了考察分析,进一步证明了发声电效应的存在.在国内,石昆法(2001)经过实验研究提出,双相介质的局部体应变发生变换时,其介质密度和介电常数将发生瞬态变化,这种变化会引起介质中电荷密度的变化,从而产生了电流.张欣等人(2006)通过在实验室中建立的冻土模型,研究了E类声电效应,并且野外条件下现场观测了冻土中的震电信号.任士房等(2012)研究了声电效应在隧道地震波场物理模拟中的应用,通过物理模型实验初步验证了声电效应在隧道地质超前预报中应用的可能性.
而针对瑞利面波频散特性的研究,国内外学者主要进行了数值模拟以及现场实验,并且取得了丰硕的成果,但是对面波进行物理模拟试验的研究却很少.在国内,主要有张碧星等人(2000,2002)通过物理模拟实验研究了瑞利面波勘探中“之”字形频散曲线的形成机理,同时用频率-波数法分析了频散曲线.鲁来玉等(2006)利用模型实验研究了层状半空间模型的瑞利面波多模式问题,并进行了瑞利面波高阶模式反演的实验研究.
总体来说,通过物理模型进行面波的频散特性实验具有一定的局限性,因为实验室中的模型不可能很大,要在有限尺寸的模型中进行面波实验,同时又要克服边界的反射等影响,就需要实验中的震源有较高的频率,而过高频率的震源与实际中的地震波不相符.如何解决这些问题,对面波频散特性物理模拟研究有重要影响.通过声电效应实验,研究者们(袁蕾,2009;任士房等,2012)已经认识到用点电极作为点源可以将实验模型小型化,增加实验的精度;同时点电极具有宽带的特征,减弱了窄带声源对信号的影响.因此,利用声电效应的这些特征,将其应用于面波频散特性的研究当中来,具有一定的研究价值.这种应用是否可行,是否有实际的意义,将是本研究的重点.
1 基本理论 1.1 声电效应理论当地震波在充液多孔介质中传播时,引起孔隙液体与固体骨架的相对运动,使液体中的带电离子形成微电流,在不连续边界处将会激发电磁波,与此相反的逆效应亦存在,即当交变电场在充液介质中激发了孔隙液体带电离子的振动,液体与固体骨架的相对运动将会在介质中激发产生地震波(张元中等,2005;苏魏等,2006;王云海等,2007).
国内外公认的声电效应产生的机制主要有两类:当弹性波通过向地下提供稳恒直流电的电极时,震动引起电极附近电阻率发生变化,流过电极的电流强度发生波动,该现象称为第一类声电效应(I效应);在不向地下施加电流情况下,当弹性波通过土壤时,离弹性场源不同距离之间存在电位差,该现象称为第二类声电效应(E效应)(胡恒山等,2003).
E类声电效应的产生与孔隙介质中固-液界面上存在双电层现象有关.由于饱和多孔介质中固液界面的电化学效应,固相表面存在双电层现象,孔隙液体中存在自由电荷.当超声波在介质中传播时,自由电荷的相对位移激发电磁场,该过程称为声电转换.相反地,当外电场激励自由电荷相对固相颗粒移动时,产生压强差,在孔隙流体与固相颗粒间产生弹性波,该过程称为电声转换(Zhu and Toksöz,2003).
研究表明(Zhu and Toksöz,2005),产生压电效应最强的天然石英脉的震电能量转换效率为10-6量级,而含流体多孔介质在一定条件下的震电能量转换效率可达10-3量级.同时,震电耦合机制产生的辐射电磁场在地下介质中以指数衰减,到达地面接收装置的震电信号将变得异常微弱.由此可见,在微弱信号采集困难的条件下,E类声电效应具有研究价值.
1.2 瑞利面波频散理论实际中的地震波虽然不是单一频率的简谐波,但是可以将它认为是由许多个简谐波叠加而成.这些简谐波相遇时会发生相长干涉时和相消干涉,叠加后形成的波的振幅也有所不相同.若将单频简谐波的速度称为相速度,将各简谐波发生相长干涉后形成的波的传播速度称为群速度 U,则相速度与群速度之间关系为(邓乐翔,2010):

其中,λ是简谐波的波长.当dc/dλ≠0,即相速度c随着波长而变化时,我们称之为速度频散.瑞利面波相速度c与其频率f的关系曲线称为瑞利面波的速度频散曲线.在弹性介质中,体波没有速度频散现象.对瑞利面波而言,在均匀介质中传播时,其相速c度与它的频率无关(即dc/dλ=0),瑞利面波不存在速度频散的现象,即其频散曲线为一条直线;在非均匀的介质中传播时,其相速度与频率有关(即dc/dλ≠0),即瑞利面波存在速度频散现象,其频散曲线为一条变化的曲线.本文主要以均匀介质中瑞利面波的频散特性为基础展开相关研究.
2 实验方法 2.1 试验材料本实验主要包括声-声试验和声-电试验两个部分.对于声-声试验,试验材料的选取范围相对广泛,只要满足超声波的传播条件及材料成型较容易即可,因此,本试验中的声-声试验部分主要选择了均匀性良好的有机玻璃,同时由于冻砂成形性比较好,选择有机玻璃和冻砂制作层状介质.但是对于声-电试验,模型材料不仅要符合实际,而且重要的是满足在实验条件下可以观测到声电信号.经试验表明,冻砂介质对声电信号衰减较弱,可以产生较理想的声电效应;同时,与其他各类材料相比,经过筛分的砂颗粒直径较小,能满足相似比条件,而且冻砂模型容易饱和密实,尺度容易控制,制作周期短(Liu et al.,2008;袁蕾等,2009).故根据本实验的特点,将选取冻砂作为主要的模型材料.实验前采用饱和细石英砂置于模具中冷冻24 h,制作成人工均匀半空间模型,并完成材料与换能器的选择及模型尺寸的确定(任士房等,2012).
2.2 试验观测系统本实验采用多道面波观测系统进行试验,试验装置示意图如图 1所示.本研究分别采用了声-声以及声-电两种实验方法,两种方法所采用的实验模型相同,信号发射装置均为超声换能器,声-声观测中的信号接收装置为超声换能器,而声-电观测中的信号接收装置为点电极.同时,由于声电信号为微弱信号,为了使采集的信号具有可分析性,进行声电效应实验时需要利用前置放大器对声电信号进行放大.由于该试验模型简单,试验的可操作性强.在声-声实验中,我们只需要移动接收换能器即可,而在声-电试验中,点电极是固定在接收点的,因此可以在不移动点电极的情况下,对炮点位于不同位置时的同一排列进行声电信号的记录,对同一模型从不同的角度进行观测.此外,还可以将某一道的信号进行多次采集并叠加,从而提高信号的信噪比.
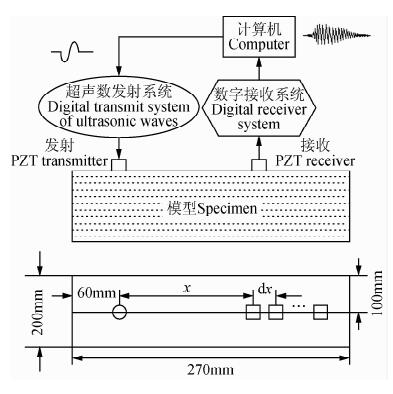 | 图 1 实验装置示意图 Fig. 1 Schematic of experimental device |
实验平台采用基于虚拟仪器技术的观测技术(刘志辉,2007).综合经济及物理因素,测量中采用大功率压电陶瓷窄带超声波换能器,长为5 cm,直径为3 cm,中心频率为48 kHz,激励电压为750 V,发射脉宽为0.03 ms的方波脉冲.声电信号为微弱信号,接受电极要求导电性好、不易极化的、适应大温差变化,故实验中一般采用纯银电极,直径为2~3 mm.并采用前置放大器将声电信号放大10000倍.实验时,信号采用1024次叠加采集,采集频率为1 M,采集时窗长度为1.024 ms.为了消除外界噪声及电磁波的干扰,实验时需关闭不必要的电源,所有实验仪器都应接地,模型利用锡箔纸包裹(张欣等,2009;任士房等,2012).
3 实验数据分析试验数据处理采用Geogiga Seismic专业面波处理软件,处理主要流程见图 2:
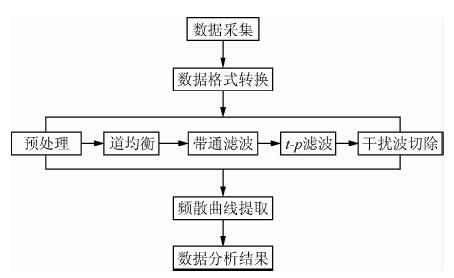 | 图 2 数据处理流程图 Fig. 2 The flowchart of the data processing |
用有机玻璃做成均匀半空间模型,利用实验室现有条件可以测得超声纵、横波在其中传播的速度,经计算可得到理论上瑞利面波在有机玻璃中的传播速度.实验中的有机玻璃模型参数如表 2所示,有机玻璃模型的试验参数如表 3所示.
|
| 表 2 有机玻璃的物理参数 Table 2 Physical parameters of plexiglass |
|
| 表 3 有机玻璃模型声-声试验参数 Table 3 Experimental parameters of acoustic-acoustic in plexiglass |
图 3所示为实验观测到的声-声信号及处理结果.由瑞利面波理论可知,在均匀半无限弹性介质中传播时,瑞利面波不存在速度频散现象,即其频散曲线应该是一条直线.由图 3c可以看出,实验原始信号是窄带的,主频基本位于发射换能器的主频300 K附近,且出现了较多的高频干扰,这是由于发射机发射频率与发射换能器的主频不相匹配造成发射换能器不是在共振状态下工作导致的.利用带通滤波将过高的频率滤除,滤波之后的频谱如图 3d所示.由图 3e和(f)可知,实验所得到的频散曲线近似为一条直线,且由图 3f可得实验中面波的速度约为1217 m/s,而由表 2可得根据理论
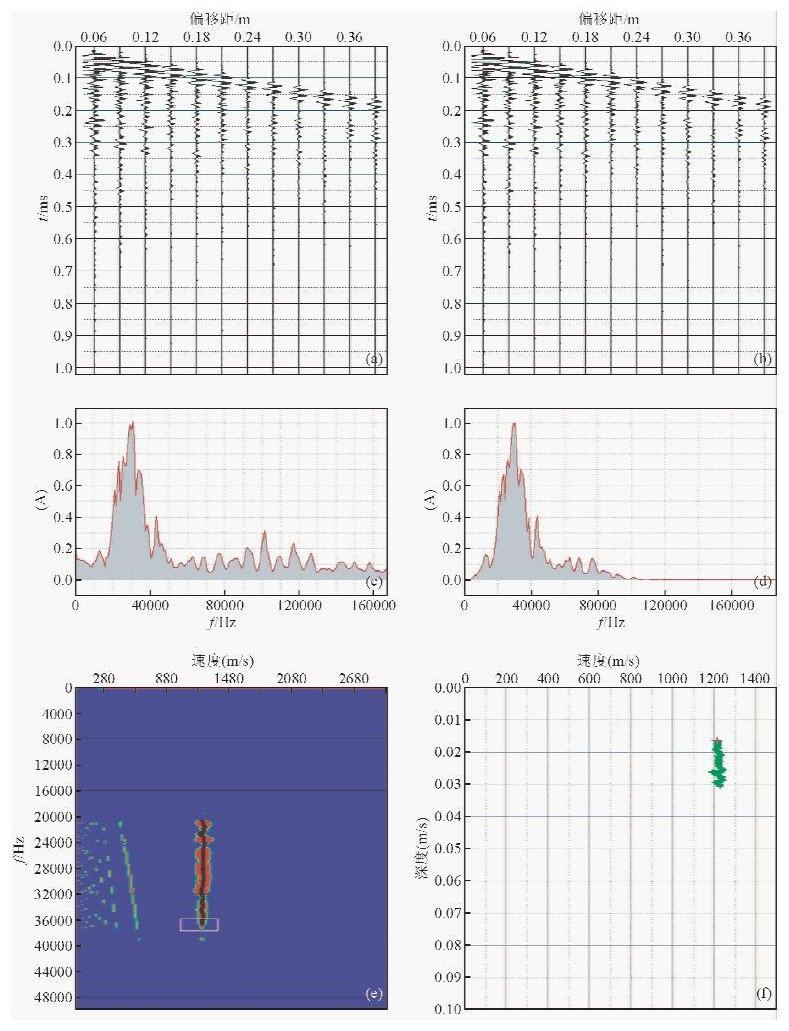 |
图 3 有机玻璃声-声实验记录 (a)t-x域原始记录;(b)带通滤波后的t-x图;(c)原始记录频谱;(d)滤波后频谱; (e)频散曲线提取图;(f)频散曲线. Fig. 3 Experimental records of acoustic-acoustic in plexiglass (a) Original records in t-x domain;(b) Records in t-x domain after bandpass filtering; (c) Original spectrum;(d) Spectrum after bandpass filtering; (e) Picking of the dispersion curves;(f) Dispersion curves. |
公式求得的面波速度为1206 m/s,实验结果仅比理论速度大0.91%.在实验允许误差范围内,可认为实验结果与理论值相一致.综合以上实验结果,初步验证了本实验所采用的实验观测系统和实验方法的可行性和正确性.
3.2 冻砂均匀半空间声-声试验本部分实验所采用的实验观测系统及方法与有机玻璃模型实验室相同.同样在测得模型中纵、横波速度的情况下经理论公式计算可得面波在冻砂模型中的速度.实验中的冻砂模型参数如表 4所示,冻砂模型实验的实验参数如表 5所示.
|
| 表 4 冻砂模型物理参数 Table 4 Physical parameters of frozen sand |
|
| 表 5 冻砂模型声-声试验参数 Table 5 Experimental parameters of acoustic-acoustic in frozen sand |
图 4为实验观测到的声-声原始信号及处理结果.冻砂模型作为均匀半空间介质,瑞利面波在其表面传播不会产生速度频散现象,即其频散曲线应该也是一条直线.由图 4c可以看出,实验原始信号是窄带的,而且其主频与发射换能器的中心频率基本吻合,滤除低频干扰之后的频谱如图 4d所示.由图 4e和图 4f可知,实验所得到的频散曲线近似为一条直线,由于试验所采用的接收换能器窄带的,只能接收到中心频率附近一个小频率范围内的面波信号,拾取的频散曲线也较短.由4f可得实验中面波的速度约为2250 m/s,由表 3可得理论上计算的面波速度为2171 m/s,实验结果仅比理论值大3.51%.在实验允许误差范围内,可认为实验结果与理论值相一致.综合以上实验结果,再次验证了实验观测系统和实验方法的可行性和正确性.
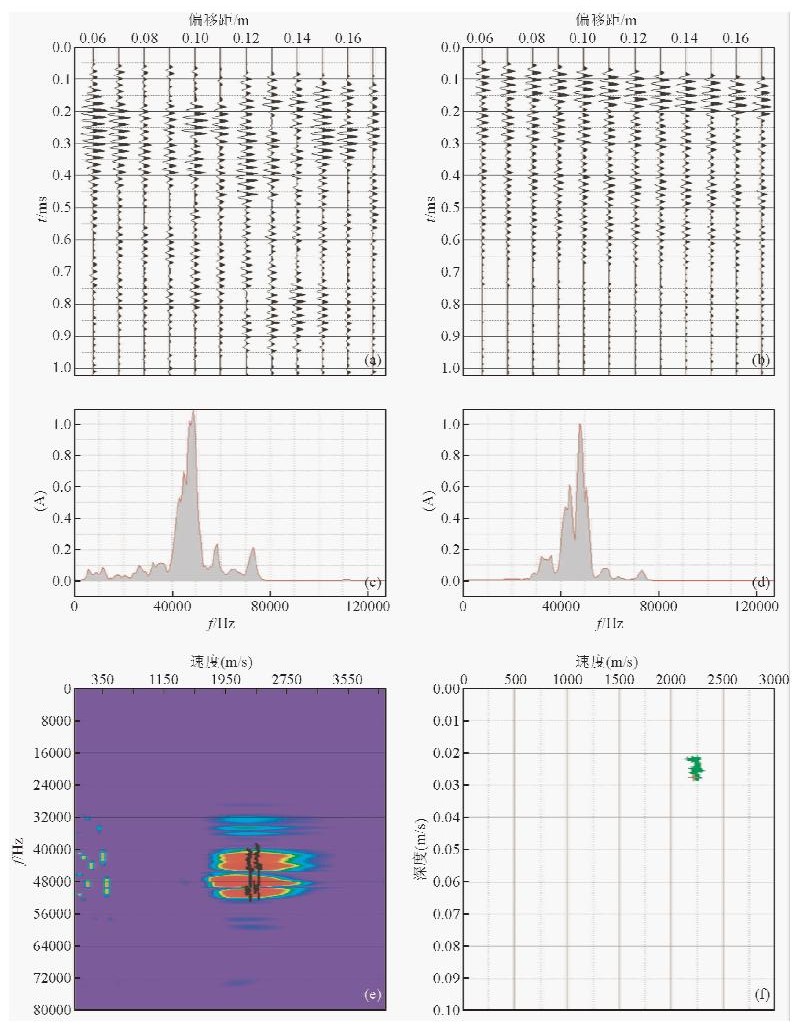 |
图 4 冻砂模型声-声实验记录 (a)t-x域原始记录;(b)经过滤波后的t-x图;(c)原始记录频谱;(d)滤波之后频谱; (e)频散曲线提取图;(f)频散曲线. Fig. 4 Experimental records of acoustic-acoustic in frozen sand (a) Original records in t-x domain;(b) Record in t-x domain after bandpass filtering; (c) Original spectrum;(d) Spectrum after bandpass filtering; (e) Picking of the dispersion curves;(f) Dispersion curves. |
本节主要进行了冻砂均匀半空间模型中的声-电试验,实验模型的制作、实验观测系统及实验方法与声-声实验相同.本实验与声-声实验的主要区别在于信号接收装置的不同,实验中采用点电极接收电信号;同时,由于声点信号十分微弱,需要采用前置放大器将信号进行放大10000倍.本部分实验的目的有两个:(1)验证声电效应在面波频散特性研究中的可能性;(2)在实验条件相同的情况下,将声-电实验结果与声-声实验结果比较,探索声电效应实验相较于传统的超声实验的优越性.
实验中冻砂模型的物理参数见表 4,冻砂模型实验参数如表 5所示.
图 5为实验观测到的声-电实验原始信号及处理结果.从图 5a和图 5c中可以看出,在面波波出现之前,有一个较强的同干扰电磁波信号,由于发射换能器对接收点电极的影响造成的,是本实验实验不可避免的,但是可以通过滤波技术将干扰信号滤除.由图 5c可知,实验接收到的声电信号频带较宽,但其信号的最大能量团仍然集中在发射换能器主频48 K附近,这也证明了接收到的声电信号就是超声波所激励的声电转换信号.
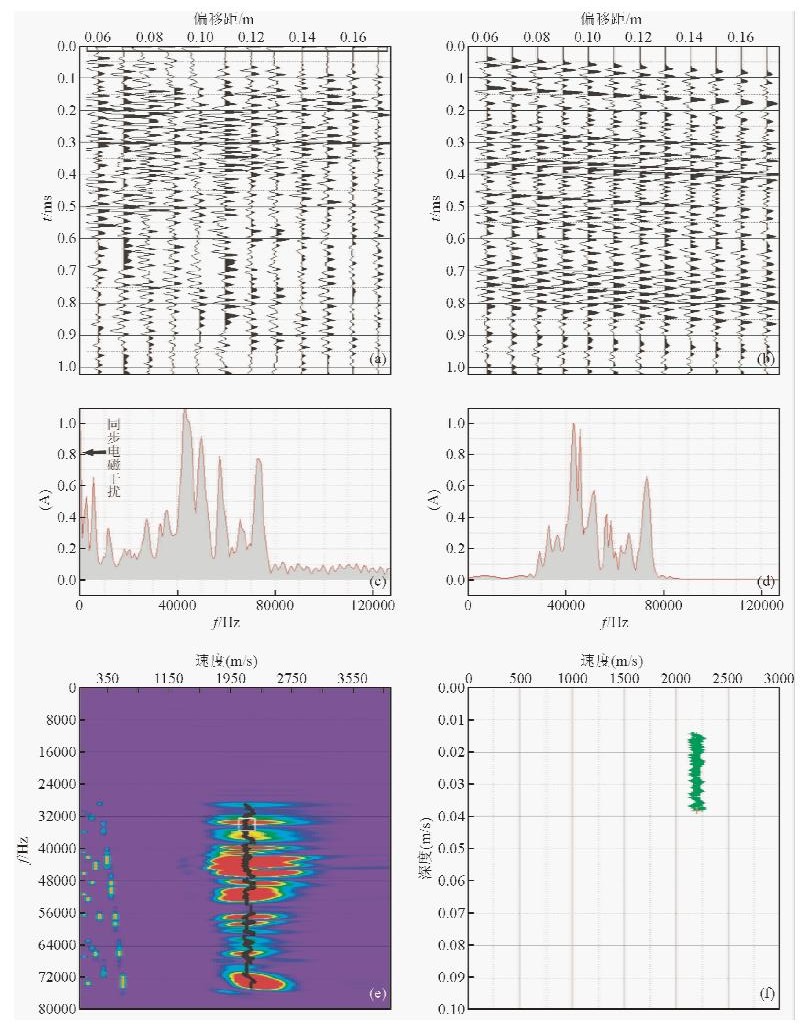 |
图 5 冻砂模型中声-电实验记录 (a)t-x域原始记录;(b)滤波后的t-x图;(c)原始记录频谱;(d)滤波之后频谱; (e)频散曲线提取图;(f)频散曲线. Fig. 5 Experimental records of acoustic-electric in frozen sand (a) Original records in t-x domain;(b) Record in t-x domain after bandpass filtering; (c) Original spectrum;(d) Spectrum after bandpass filtering; (e) Picking of the dispersion curves;(f) Dispersion curves. |
根据均匀半空间介质中的面波理论,面波在此模型中是不产生频散的,即其频散曲线应该为一条直线.由图 5f可知,实验拾取的频散曲线基本为一条直线,且其对应的面波速度约为2180 m/s,与理论上面波的速度2171 m/s值相差0.42%.在实验允许误差范围内,可认为实验结果与理论值相一致.综合以上实验结果,说明实验中接收到的信号确实为声电转换信号,验证了声电效应在多道面波实验中应用的可能性.
4 结 论4.1 对相同冻砂模型中声-声与声-电实验结果进行对比分析.比较两种观测系统下接收到信号的原始频谱图,即图 4c与图 5c,可以看出声-电实验中接收到信号的频带与声-声实验信号相比有明显拓宽.比较图 4e与图 5e可得,声-电实验中面波的可探测频率范围(28000~76000 Hz)约为声-声实验(40000~52000 Hz)的4倍.其直接结果是使提取的频散曲线范围有大幅拓宽,即面波的可探测介质深度范围的增加,由图 4f与图 5f也可看出,其深度范围由声-声实验中的0.02~0.03 m增加到声电实验中的0.15~0.04 m,增加了1.5倍.
4.2 基于冻砂模型中的声-声及声-电实验结果,可以得出以下结论:(1)声电效应实验中,根据实验接收信号的频谱及所提取的频散曲线结果,都可以说明实验中所采集的信号为声电信号,并且为E类声电信号,验证了声电效应在面波频散特性物理模拟中应用的可行性.
(2)与声-声信号相比,声电效应中声-电信号的采集使用的点电极作为点源,其受固有频率的限制小,接收信号的频带有明显拓宽,使面波的探测深度范围明显增大.
(3)声电效应实验中作为接收源的点电极尺寸较小(2~3 mm),远小于超声换能器的尺寸,不仅可以使实验模型小型化,而且增强了接收源与模型的耦合效果,从而提高了实验的观测精度.
致 谢 本课题由国家自然科学基金项目(山区深部岩体结构的瑞利面波椭圆极化特征研究,批准号:41274107)资助完成,感谢本课题组所有成员对本研究所做的支持,感谢审稿人和编辑部为本文的修改提供了非常宝贵的意见.
| [1] | Deng L X. 2009. Rayleigh wave field simulation modeling and frequency dispersion curves of extraction (in Chinese)[M. Sc. thesis]. Xi'an:School of Civil Engineering of Chang'an University. |
| [2] | Guan W, Hu H S, Tang T Z, et al. 2011. The ratio of the acoustoelectric field to the acoustic pressure in a borehole and its dependence on permeability[J]. Chinese Journal of Geophysics (in Chinese), 54(6):1660-1671, doi:10.3969/j.issn.0001-5733.2011.06.026. |
| [3] | Hu H S, Liu J Q, Wang H B, et al. 2003. Simulation of acousto-electric well logging based on simplified Pride equations[J]. Chinese Journal of Geophysics (in Chinese), 46(2):259-264, doi:10.3321/j.issn:0001-5733.2003.02.021. |
| [4] | Liu Z P, Yuan L, Zhang X, et al. 2008. A laboratory seismoelectric measurement for the permafrost model with a froze-unfrozen interface[J]. Geophysical Research Letters, 35(21):L21404, doi:10.1029/2008GL035724. |
| [5] | Lu L Y, Zhang B X. Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes[J]. Chinese Journal of Geophysics (in Chinese), 49(4):1082-1091, doi:10.3321/j.issn:0001-5733.2006.04.021. |
| [6] | Ren S F. 2012. An application research of seismoelectric effect to the tunnel seismic modeling (in Chinese)[M. Sc. thesis]. Chengdu:School of Civil Engineering of Southwest Jiaotong University. |
| [7] | Ren S F, Liu Z P, Xiong Z Y, et al. 2012. An application of seismoelectric effect to the tunnel seismic modeling[J]. Progress in Geophysics (in Chinese), 27(5):2240-2247, doi:10.6038/j.issn.1004-2903.2012.05.052. |
| [8] | Shi K F. 2001. Seismo-electric effect theory and preliminary experimental results[J]. Chinese Journal of Geophysics (in Chinese), 44(5):720-728, doi:10.3321/j.issn:0001-5733.2001.05.016. |
| [9] | Su W, Liu C, Chen C. 2006. Progress of seismoelectric in theory and research[J]. Progress in Geophysics (in Chinese), 21(2):379-385. |
| [10] | Wang Y H, He X Q, Dou L M. 2007. Study on regularity and mechanism of acoustic emission and electromagnetic emission during fracture process of coal samples[J]. Chinese Journal of Geophysics (in Chinese), 50(5):1569-1575. |
| [11] | Yuan L. 2009. Electroseismic effect of in experiment and applications studies of frozen soil dynamics properties (in Chinese)[MSc thesis]. Chengdu:School of Civil Engineering of Southwest Jiaotong University. |
| [12] | Yuan L, Liu Z P, Zhang X, et al. 2009. The acquisition system of acoustic-electric conversions based on virtual instruments and its application to the studies of the permafrost model[J]. Progress in Geophysics (in Chinese), 24(3):1142-1148, doi:10.3969/j.issn.1004-2903.2009.03.048. |
| [13] | Zhang B X, Lu L Y, Bao G S. 2002. A study on zigzag dispersion curves in Rayleigh wave exploration[J]. Chinese Journal of Geophysics (in Chinese), 45(2):263-274, doi:10.3321/j.issn:0001-5733.2002.02.013. |
| [14] | Zhang B X, Xiao B X, Yang W J, et al. 2000. Mechanism of zigzag dispersion curves in Rayleigh exploration and it's inversion study[J]. Chinese Journal of Geophysics (in Chinese), 43(4):557-567, doi:10.3321/j.issn:0001-5733.2000.04.017. |
| [15] | Zhang L. 2009. An approach to the wave-field characteristic analysis and inversion algorithm of Reyleigh surface wave for layered medium (in Chinese)[Ph. D. thesis]. Chengdu:School of Civil Engineering of Southwest Jiaotong University. |
| [16] | Zhang X. 2009. Experimental study of seismoelectric effect with a frost-thawing interface (in Chinese)[M. Sc. thesis]. Chengdu:School of Civil Engineering of Southwest Jiaotong University. |
| [17] | Zhu Z, Haartsen M W, Toksöz M N. 1999. Experimental studies of electrokinetic conversions in fluid-saturated borehole models[J]. Geophysics, 64(5):1349-1356. |
| [18] | Zhu Z, Haartsen M W, Toksöz M N. 2000. Experimental studies of seismoelectric conversions in fluid-saturated porous media[J]. Journal of Geophysical Research, 105(B12):28055-28064. |
| [19] | Zhu Z, Toksöz M N. 2003. Crosshole seismoelectric measurements in borehole models with fractures[J]. Geophysics, 68(5):1519-1524. |
| [20] | Zhu Z, Toksöz M N. 2005. Seismoelectric and seismomagnetic measurements in fractured borehole models[J]. Geophysics, 70(4):F45-F51. |
| [21] | 邓乐翔. 2010.瑞雷波场正演模拟及频散曲线的提取[硕士论文].西安:长安大学土木工程学院. |
| [22] | 关威,胡恒山,汤天知,等. 2011.声电效应测井电声比及其与地层渗透率的关系[J].地球物理学报, 54(6):1660-1671, doi:10.3969/j.issn.0001-5733.2011.06.026. |
| [23] | 胡恒山,刘家琦,王洪滨,等. 2003.基于简化的Pride理论模拟声电效应测井响应[J].地球物理学报, 46(2):259-264, doi:10.3321/j.issn:0001-5733.2003.02.021. |
| [24] | 鲁来玉,张碧星,汪承灏. 2006.基于瑞利波高阶模式反演的实验研究[J].地球物理学报, 49(4):1082-1091, doi:10.3321/j.issn:0001-5733.2006.04.021. |
| [25] | 任士房. 2011.声电效应在隧道地震波场物理模拟中的应用研究[硕士论文].成都:西南交通大学土木工程学院. |
| [26] | 任士房,刘争平,熊自英,等. 2012.声电效应在隧道地震波场物理模拟实验中的应用[J].地球物理学进展, 27(5):2240-2247, doi:10.6038/j.issn.1004-2903.2012.05.052. |
| [27] | 石昆法. 2001.震电效应原理和初步实验结果[J].地球物理学报, 44(5):720-728,doi:10.3321/j.issn:0001-5733.2001.05.016. |
| [28] | 苏魏,刘财,陈晨. 2006.震电效应理论及其研究进展[J].地球物理学进展, 21(2):379-385. |
| [29] | 王云海,何学秋,窦林名. 2007.煤样变形破坏声电效应的演化规律及机理研究[J].地球物理学报, 50(5):1569-1575. |
| [30] | 袁蕾. 2009.震电效应在冻土动力学性质试验中的应用研究[硕士论文].成都:西南交通大学土木工程学院. |
| [31] | 袁蕾,刘争平,张欣,等. 2009.基于虚拟仪器技术的声-电效应观测系统及其在冻土模型研究中的应用[J].地球物理学进展, 24(3):1142-1148, doi:10.3969/j.issn.1004-2903.2009.03.048. |
| [32] | 张碧星,鲁来玉,鲍光淑. 2002.瑞利波勘探中"之"字形频散曲线研究[J].地球物理学报, 45(2):263-274, doi:10.3321/j.issn:0001-5733.2002.02.013. |
| [33] | 张碧星,肖柏勋,杨文杰,等. 2000.瑞利波勘探中"之"形频散曲线的形成机理及反演研究[J].地球物理学报, 43(4):557-566, doi:10.3321/j.issn:0001-5733.2000.04.017. |
| [34] | 张立. 2009.层状介质中瑞利面波波场特征分析和反演方法研究[博士论文].成都:西南交通大学土木工程学院. |
| [35] | 张欣. 2009.冻土冻融界面的震电信号实验研究[硕士论文].成都:西南交通大学土木工程学院. |
| [36] | 张元中,肖立志,楚泽涵,等. 2005.井孔声电效应转换电磁波的特征[J].地球物理学报, 48(2):452-458, doi:10.3321/j.issn:0001-5733.2005.02.032. |
 2015, Vol. 30
2015, Vol. 30

