面波是能量主要集中于距离自由地表约一个波长范围内传播的弹性波.它是体波与自由界面或分层介质的弹性分界面相互作用,以满足物理上的自由边界条件或界面的连续条件而产生的一种弹性波.1887年,英国科学家Rayleigh针对均匀半空间介质预言了它的存在,因此,又称为瑞利(Rayleigh)面波.实际上,对于多层介质而言,还存在另一种形式的面波,称为勒夫(Love)面波,由于不及瑞利波容易激发,其应用也不及瑞利波广泛,多用于全球尺度上为研究介质的各向异性同时对两种不同极化方式的面波进行反演.最近也有人开始研究其在浅层勘探中的应用(Xia et al.,2012;潘雨迪等,2014).本文主要对瑞利波的应用进行评述,大部分流程也适用于勒夫面波.
和体波相比,面波能量主要集中在自由地表附近,且以柱面波扩散的形式传播,所以其传播距离远、衰减慢、能量大,易于在表面接收.因此,面波方法被广泛应用于地球结构探测和工程勘察及各种无损检测中.面波在工程勘察中的应用,主要利用了面波的频散特性,即在均匀水平分层介质中,不同周期的面波以不同的传播速度传播.周期越长其传播速度受到越深的介质属性影响,通过测量不同周期的面波速度(即频散曲线)就可以通过一定的反演方法来推断不同深度介质的属性,从而达到探测的目的.理论上,面波的传播速度受密度、纵波速度、横波速度的影响,然而,根据Xia(1999)等人的研究,这些因素中,对面波速度影响最大的是剪切波速度,因此利用面波获得剪切波速度结构是面波勘探的一个主要目的.工程场地的浅层剪切波速度结构是工程勘察、地震安全性评价、地基处理效果评价的重要参数.目前对剪切波速度结构的测量主要有两种方法:
一是直接测量,通过在场地打地质钻孔,用传感器在不同深度接收地面上激发的剪切波得到不同深度的剪切波到时,然后计算地层的分层与每层的剪切波速;
第二种就是用面波勘探方法测量面波频散曲线,然后反演出测点的剪切波速度结构.面波勘探方法相对于直接测量有以下优势:
1)因为钻孔费用较高一般勘察设计阶段不会设置密集的钻孔,所以场地中地质钻孔数量有限,只能通过直接测试获得个别点的剪切波速度结构,而面波勘探通过测线布置可以获得很好的连续地质剖面;
2)地质钻孔对地层结构有破坏性,而面波勘探是一种无损检测方法,特别是在地基或路基处理效果的评价中面波勘探方法更具优势.
对于面波勘察方法而言,根据震源类型的不同可分为主动源和被动源方法.顾名思义,主动源是采用人工方法激发面波信号,通常的激发手段是锤击、落重、炸药及各种气枪、电火花等震源类型,可以根据探测目的和施工环境来选择不同的激发源.在主动源方法中通常采用线性阵排列接收面波信号,这种排列简单易行,施工效率高,且数据处理简单,但有时对施工场地条件要求较高,比如在复杂的山区、丘陵环境或在繁华的市区就无法提供较大面积的平整施工场地,接收信号受地形和人为干扰较大.对于这种情况被动源不失为一种好的选择.所谓被动源,是指采用检波器直接记录地表的振动,而不需要人工激发.早在1957年,Aki(1957)就提出了一种被动源的面波勘探方法,即SPAC(spatial autocorrelation)方法.SPAC是传统被动源面波勘探中的一种常用方法,后又被扩展为ESPAC方法可以利用多种排列形式进行观测(张维等,2013).早期SPAC方法的提出主要针对工程领域的浅层勘察,比如,徐佩芬等(2012,2013a)利用该方法探测隐伏断裂构造以及地铁工程勘察中的“孤石”.由于其成像原理和地震层析成像类似,该方法现在也被用于较大尺度的地壳S波速度结构反演(徐佩芬等,2013b).反过来,随着背景噪声互相关技术在全球地壳结构层析成像的成功应用,基于背景噪声互相关技术(noise correlation function,NCF)提取格林函数的方法也逐渐被移植到小尺度浅层面波勘探中并获得成功试验(Gouédard et al.,2008c;Picozzi et al.,2009;Nunziata et al.,2009;de Nisco and Nunziata,2011).虽然已有学者证明了SPAC方法和NCF方法的基础理论在物理上是一致的(Yokoi and Margaryan,2008;Tsai and Moschetti,2010),一个是在频率域中的描述,一个是在时间域的描述,但正如本文将要指出的,由于其推导的前提假设和数据处理方法的不同,这两种被动源方法有其特殊的差异.SPAC方法得到的是排列下方整个区域的平均频散曲线,而由NCF通过互相关函数得到的频散曲线是任意两个台站之间路径上的平均效应.因此,可借助大尺度地震层析成像的方法实现小尺度被动源面波三维层析成像.另外,由于NCF方法对于台站位置没有要求,台阵布置形式自由,仅通过两个台站即可提取台站间频散信息,在台站数相当的情况下,可得的射线路径相比于空间自相关法更多,能够更好的覆盖探测区域.因此,基于地震干涉的NCF方法也逐渐成为一种有效的被动源面波浅勘方法. de Nisco和Nunziata(2011)在意大利那不列斯的一处公园布设了间距约440 m左右的台阵,通过NCF获得了面波的频散曲线,成功反演了~100 m左右的S波速度结构.国内也有研究者将背景噪声互相关成功用于小尺度结构研究(Xu et al.,2013;王小龙等,2013;刘影等,2014;李成等,2014).
在国内,面波浅勘的研究开始于20世纪80年代后期,1986年日本的GR-810佐藤稳态式全自动地下勘探系统传入中国,但该设备笨重,价格昂贵.杨成林(1989)较早开展了主动源面波浅层勘探的研究,几乎同期,王振东(1986)将微动的空间自相关法引入中国,推动了微动方法在国内的推广.在上世纪90年代中期,刘云祯和王振东(1996)开发了瞬态面波勘探仪器,大大促进了主动源瞬态面波法在工程中的应用.这些研究主要关注频散曲线的提取,对结果的解释主要利用经验性较强的半波长法、拐点法、极值点法等.同时,一些学者从弹性波理论入手,着重研究模型的计算问题,例如,陈云敏和吴世明(1991)总结改进了前人算法提出了一种既能有效避免高频有效数字损失又提高计算效率的方法,但是该方法不适用于有软硬夹层的情形.张碧星等(2002)讨论了实际勘探中“之”字形频散曲线的形成机理,指出软夹层的存在使高阶能量在某些频段能量较大,引起模式之间的跳跃,使频散曲线呈“之”字形.基于此,鲁来玉等(2006)讨论了高阶模式的反演问题,为软夹层结构的反演提出了可行方法,避免了反演时模式的误判.凡友华等(2002)提出了快速矢量传递算法,该方法各矩阵的元素均为无量纲的实数值,避免了以往方法中各元素的数量级相差较大、出现复数运算的缺陷,提高了精度和稳定性.
在多道面波勘探方面,夏江海等(Xia et al,1999,2002,2012,2013)及其合作者开展了诸多理论与应用研究,在实际应用和方法推广方面起到了较大作用.与此同时,何正勤等(2007),徐佩芬等(2009,2013a,2012,2013b)在微动理论和应用方面开展了卓有成效的工作.
虽然主动源和被动源面波勘探是分别发展的技术,但联合应用的想法和实践已有报道(王振东,1998;Park et al.,2006;张维等,2013).目前,在浅层勘探中,主动源和被动源联合勘探主要是传统的主动源方法与被动源的SPAC方法的联合,联合应用充分利用不同方法对不同频段信息的分辨力,进行不同方法得到频散曲线拼接的方式进行联合勘探(Park et al.,2006;张维等,2013;Hayashi et al.,2013),这种方法有效的扩展了勘探范围.SPAC方法得到的结果是台阵覆盖下介质的平均效应,如果采用该方法获取三维速度,就必须在场地不同位置密集布设多个阵列,将所有结果拼接而成,工作量十分巨大,而且要在场地内无障碍物的情况下才可以实施.而NCF方法,只需把台阵主要布设在场地周边,根据不同路径的频散信息就很容易通过层析成像反演获得地下的三维速度结构,达到事半功倍的效果.因此,将NCF方法和现有的面波勘探方法联合将使面波勘探从传统的二维剖面解释拓展得到三维精细速度结构,有效提高勘探精度而不需要明显的额外代价.
本文基于地震干涉技术的发展,主要对前述主动源与被动源面波方法及相应的理论基础进行评述,侧重对基本原理、物理基础的理解,并分析不同方法的差异.文章也对面波勘探中有关多模性的几个术语进行了介绍,讨论了软夹层结构存在时考虑多模式面波的反演方法,最后评述了面波浅勘方法的几个值得关注的发展方向.
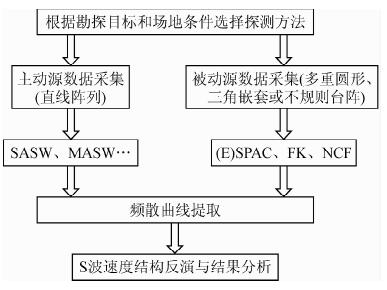
1 面波勘探方法的基本原理无论是主动源和被动源面波勘探,其基本流程都相近,如图 1所示,主要分为数据采集、数据处理并提取频散曲线、对观测结果进行反演,只是工作步骤中的具体做法有所差异.
|
图 1 面波勘探的基本流程 Fig. 1 The principle and processing flow of surface wave exploration |
数据采集时,激发源与接收台阵的布设要根据数据处理方法和勘探目的和场地条件进行设计.首先,要根据所采用的方法布置测线,一般主动源勘探要布置直线型排列,为了能够确定最小偏移距、道间距,一般在正式观测前要进行试验.若采用SPAC方法,一般要布置圆型观测台阵(最简单的为正三角形为内接三角形的三台布置法),理论及实验表明台阵半径与探测深度有关,一般台阵大小由目标深度确定.利用噪声互相关方法,台阵布置就比较自由,保证台阵对的射线分布尽可能均匀即可.扩展的空间自相关(ESPAC)技术可以将台阵布置成L型、线性、多边形、不规则形等,这样SPAC与NCF方法可以利用一组数据记录.
数据采集时参数设置包括采样频率和记录长度,根据采样定理,可分辨的最高频率小于采样频率一半,最低可分辨频率要小于记录长度的倒数.关于时间同步性,目前一般利用GPS进行时间同步校正.此外,在正式采集之前,需要对检波器的一致性进行检测.
1.2 频散曲线提取主动源面波方法常见的频散曲线提取方法有相位差法、倾斜叠加法、频率波数法等,各处理方法通常与勘探方法相对应,各种频散曲线的处理方法与对应方法的物理假设、台阵布设方式、信号的来源特点有关.被动源方法中,SPAC通过计算空间自相关系数(或称相干系数)与第一类零阶贝塞尔函数拟合来提取频散曲线;NCF一般利用时频分析方法结合相位匹配技术进行群速度或相速度提取(Yao et al.,2006;Bensen,2007).随着信号处理技术的发展和计算机应用的普及,地球物理学家和工程师们已经将各种时频分析技术如短时傅里叶变换、Gabor变换、二次型时频分析、小波变换、S变换(袁伟等,2013)等时频分析技术应用于地震信号处理中,并不断完善.
1.3 速度结构的反演早期面波勘探中速度结构的反演多采用经验性的推断,一般是在得到频散曲线后根据剪切波速为瑞利波速的1.1倍,其代表深度为一半波长的经验关系,给出剪切波速度结构.后来引入了定量反演,首先建立一个分层均匀介质的初始模型,然后以层厚和剪切波速为独立变量,依据层状均匀介质中的面波频散方程正演方法来求取理论频散曲线,再将该曲线与观测的频散曲线进行拟合匹配来调整速度模型,当拟合误差在设定范围内时,该模型即为反演结果.
地球物理反演是根据实际需求而发展起来的学科,其内容涉及多种数学理论与思想,特别是最优化理论,目前面波反演中利用的方法主要有两类,一类是基于优化设计的最小二乘方法反演及阻尼最小二乘法反演;第二类是基于全局搜索的算法,如遗传算法、神经网络算法、蒙特卡洛算法等(Tarantola and Valette,1982;王家映,2002).两类算法相比而言,最小二乘法在反演过程要用到导数信息,因此,对初始模型要求较高,而全局算法不需要求导,对初始模型要求不高,但全局搜索会使收敛速度变慢.反演是数据处理的最后一步,其方法的优劣和准确性对结果有较大影响,通常根据勘探目的和对场地先验信息的了解选择合适的反演方法.
2 主动源面波勘探方法面波勘探在工程中的应用最早见于20世纪60年代(Jone,1962;Ballard,1964).主动源面波勘探的发展经历了稳态法到瞬态法的过程,瞬态法中的表面波谱分析法(Spectral Analysis of Surface Wave,SASW)和多道瞬态分析法(Multichannel Analysis of Surface Wave,MASW)在不同时代扮演着重要角色.
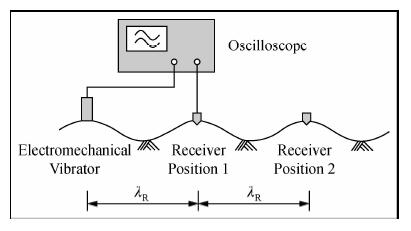
2.1 稳态法稳态法面波勘探是通过激振器激发单一频率的正弦波,利用单个检波器进行接收,通过移动检波器的位置接收信号,当接收距离等于激发频率对应的波长时,示波器将显示相同相位的波形(如图 2).为了提高精度,移动检波器一直到n倍的波长处,对于均匀水平分层介质n个测点连成的时距曲线将是直线,该直线斜率就是对应频率的面波速度,或者直接根据频率与波长的关系计算相速度,公式为
|
图 2 稳态法面波勘探布置(Foti,2000) Fig. 2 The illustration of steady State Rayleigh wave method(from Foti,2000) |

其中,f为激发正弦波频率,λR为测得的波长,VR(f)为对应频率的面波相速度.通过激发不同频率值的正弦信号,并利用时距曲线求得不同频率对应的波长,我们就可以得到一系列频散点,用平滑曲线连接即得到频散曲线.得到频散曲线后根据剪切波速为瑞利波速的1.1倍,以及半波长经验法,给出剪切波速度剖面.20世纪80年代,日本曾研制了专门用于工程勘察的GR810型激振器用于面波工程勘察,然而由于这种激振器笨重,且稳态方法要多次移动检波器,费时费力,不久就被发展起来的瞬态面波勘探法所代替.
2.2 瞬态表面波谱分析法(SASW)通过一次冲击激发,可以获得一个较宽频带的信号,于是瞬态法(刘云祯和王振东,1996)的单次激发就取代了稳态法的多次激发.表面波谱分析法是Nazarian和Stokoe提出的瞬态面波勘探方法(Nazarian and Stokoe,1986a,b).表面波谱分析法(SASW)一般利用大锤或落重激发,利用两个检波器接收的方式布置(如图 3),由于衰减、空间假频、近场效应的影响,一次观测的频带范围有限,为扩大频带分辨力,一般通过调整两接收检波器的距离获得更好观测效果,一般近源检波器与源的距离应大致与道间距相近(Foti,2000).为了消除及判断所勘探区的横向不均匀性、地层倾斜等情况对测试的影响,有时可以采用双边激发,看记录波形差异是否明显,如果差异明显则说明存在水平层状介质假设不符合性,需记录该位置且调整勘探测线重新布置.

|
图 3 SASW方法勘探布置 (单个源激发,同一直线两个检波器接收) Fig. 3 The configuration of SASW method (a single source and two receivers in a line) |
表面波谱分析方法的数据处理多在频率域进行,若两个接收检波器的原始信号记录分别为x1(t)和x2(t),则两个信号的互相关函数为
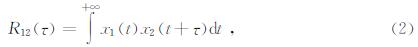
其傅里叶变换为两个信号的互谱
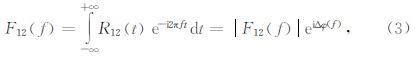
其中,Δφ(f)为对应频率f的相位差.通过上式可以看出,互相关谱的相位就是两接收道间的相位差,那么根据谐波参数关系可按下式计算瑞利波速度频散:

互谱的相位为
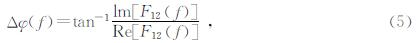
其中,lm表示取虚部,Re表示取实部.通过(5)式计算相位角范围为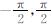 ,因此我们可以通过求取F12(f)实部和虚部的正负号来判断所在象限,如此我们就可以得到(-π,π)的结果.由于反三角函数为多值函数,所计算的相位只能给出相位主值,而实际上的相位为
,因此我们可以通过求取F12(f)实部和虚部的正负号来判断所在象限,如此我们就可以得到(-π,π)的结果.由于反三角函数为多值函数,所计算的相位只能给出相位主值,而实际上的相位为

而n值的判断在频率域很难判断,这就是所谓的“360°卷绕问题(Spurious 360 cycles)”(Al-Hunaidi,1992).实际相位需要进行解卷绕得到,虽然理论上去卷绕问题可以解决,但由于实际观测中噪声的存在,只有当信噪比较高时,才能较为准确的去卷绕,而对于信噪比的估计很大程度依赖于操作者的经验.由(4)式可以看出相位差法假设了面波相速度为频率的单值函数,而根据面波理论面波是具有多模性,因此本方法仅适合能量突出的单一模式频散提取,对于多阶模式频散无法判断.因此,在此方法中非主导模式的面波也成为了干扰波.为了使结果更为准确,在计算过程中可以通过计算相干函数的方法选取高信噪比频带,公式为

其中,F12(f)为两道记录互谱,其复共轭为F12(f),F11(f)和F22(f)分别为两记录的自功率谱.比如,可以选择相干系数大于0.8作为可分辨频率(潘冬明,2009).
2.3 多道瞬态面波分析法(MASW)多道瞬态面波分析,每次激发采用线性排列的检波器阵接收信号,例如,图 4为12道接收的观测系统.这种方法实际依赖于地震勘探仪器技术的发展,目前工程上数据记录仪一般可以记录24道或48道信号.比如,德国生产的主要用于浅勘的Summit仪可以实现任意多道的排列接收,对应于这种直线排列记录需要采用不同于上述两道观测法的数据处理技术.

|
图 4 MASW方法勘探布置(单个源激发,多个检波器位于一条直线接收) Fig. 4The configuration of MASW method (a single source and multi-receivers in a line) |
1987年,频率波数法首次用于提取多模式的瑞利波频散曲线(Gabriels et al.,1987),20世纪90年代由北京水电物探研究所刘云祯和王振东等人研制的SWS瞬态面波勘探仪中的频散提取就是采用的这种方法.该仪器的研制成功大大推动了多道瞬态面波法在我国的发展,国内多家生产和科研单位使用类似方法都取得了较好效果.随着面波勘探技术的迅速发展,2004年国内制定了第一个面波勘探行业标准《多道瞬态面波勘探技术规程》,为工程勘察中面波的应用提供了技术依据.
频率波数法是在时间空间域记录的波场通过二维傅里叶变换(Alleyne and Cawley,1991),在频率-波数域分析信号特征的一种方法(Forchap and Schmid,1998).按照图 4所示的直线排列可以获得一个时空域记录f(x,t),通过傅里叶变换将其变换到频率波数域为
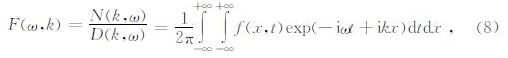
其中,ω为角频率,k为波数,x为空间坐标,t为时间.根据分层介质中的面波理论,面波对应F(k,ω)中极点的留数贡献,留数由D(k,ω)=0决定,因此,在频率-波数域中,对应面波的能量具有极大值,按照振幅极大值的波数与频率就可以根据(9)式计算特定频率的相速度,重复多个频率的这种计算就可以得到对应的频散曲线,公式为

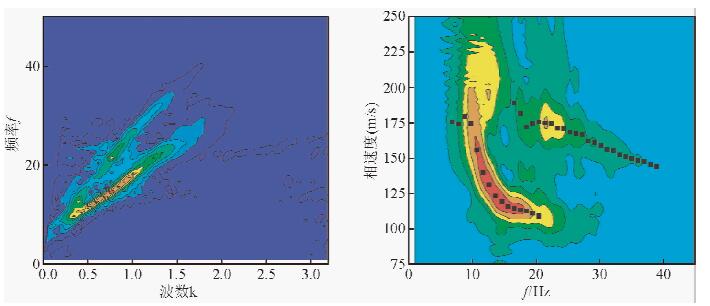
图 5给出某多道瞬态记录的二维振幅谱图,该图显示有两个能量束存在于频率波数域,这两个能量束说明所记录的面波数据有高阶模式存在,但高阶模态信号能量较基阶模态能量明显偏弱,由相速度公式(9),可知两个能量束脊的斜率大小就为相速度,可以看出基阶模式信号速度低于高阶模式速度.
|
图 5 能谱图与频散曲线 左图为某多道面波记录在频率-波数(f-k)域的能谱图,右图为对应在频率-速度(f-v)域的能谱图,黑色点线为提取的频散曲线. Fig. 5Energy spectrum in f-k domain and dispersion curves in f-v domain The left panel is the energy spectrum in frequency-wavenumber domain processed by a multichannel records. The right panel is the dispersion map in frequency-velocity domain. |
1999年,美国堪萨斯地质调查局Park和夏江海等人提出了他们自己的MASW(Multichannel analysis of surface waves)方法(Park et al.,1999).该团队多年来,较为系统的研究了面波勘探的主动源、被动源和联合勘探的方法(Park et al.,2006).Park等在1998年SEG年会提出的多道面波记录提取频散曲线方法称为相移法(Park et al.,1998).该方法可以说是频率-波数法的改进,将记录变换到频率域后表示成振幅项与相位项的乘积,并对振幅项进行归一化处理从而减少衰减的影响,可以较好的提取频散曲线.对于能量谱中某一频率值,沿相速度轴将有一个或几个峰值,可以获得多模式的面波频散曲线.该方法同样利用了能谱分布提取频散曲线,与频率-波数法的不同在于未变换到波数域而直接利用了空间相位信息来计算相速度.
实际数据处理中频散曲线还有很多其他方法如倾斜叠加变换法(τ-p变换法)、拉冬变换法、小波变换等时频分析技术等(McMechan et al,1981;潘冬明,2009;Poggi et al,2012;单娜琳和刘占兴,2013).
3 被动源面波勘探方法被动源勘探指从微动(或背景噪声)信号中提取面波信号的勘探方法.微动是一种在地面随时都存在的一种人感觉不到的微小振动,只有灵敏的地震计才可以记录到.由于微动是各种振动通过地球介质散射而到达接收点的,因此其携带了丰富的介质信息,这是微动勘探的基础.微动主要分为两类,一类是频率1 Hz以上的微动,其主要来源于人类的活动,比如工厂的机械振动、交通工具产生的噪声;另一类是频率低于1 Hz的微动,源于各种自然现象,包括海浪对海岸的冲击、河水运动、气压变化等,这些自然产生的较低频率的微动一般称为脉动(孙勇军等,2009).对于浅层勘探一般要利用较高频率的微动信息,以下将主要介绍利用台阵观测技术的SPAC方法和NCF方法.
3.1 空间自相关法空间自相关方法(SPatial AutoCorrelation,SPAC)是Aki在1957年提出的一种从微动中提取面波频散曲线,从而反演地下剪切波速度结构的一种微动(Microseism)探测方法(Aki,1957,1965).微动(Microseism)是被动源在浅层工程勘察领域的术语,有时也叫地脉动,在大尺度的被动源地震层析成像中称被动源为地震背景噪声(Seismic ambient noise),这些应用于不同尺度范围的被动源方法只是所采用的频带范围、数据处理方法、源的来源与特征不同,其物理思想相同,本文对术语“被动源”不做详细区分,均称为背景噪声场或微动.
Aki(1957)在利用微动信息提取面波频散信息时,假定台阵周围不同方向入射的背景噪声场具有平稳随机特征,在同一频率具有相同的相速度,在此假设下,考察两个距离为r的台站接收到的噪声信号(标量形式或仅考虑垂直向分量)空间坐标的互相关,然后对不同方位相同距离的台站对求方位平均,可以证明,对入射噪声场功率谱密度进行归一后,方位平均后的相关系数为

其中,k=ω/c(ω)为水平方向波数,r为两台站间的距离,ω为角频率,c(ω)为相速度,J0(x)为第一类零阶贝塞尔函数(Bessel Function).
因此,将经方位平均的相关系数与J0(kr)拟合可以求得不同频率的相速度,从而对地下结构进行反演.在实际应用中要对不同方位具有相同台间距的台站对的噪声记录进行互相关运算,然后求取方位平均.“互相关”运算和描述方法本身的术语“空间自相关”,单从字面来看是矛盾的,但注意到时间和空间上背景噪声随机平稳这一假设,当在时间域进行互相关运算时,一个接收位置的记录实际上是另一个接收位置记录的时间延迟,因此不同空间坐标获得的记录是同一个随机平稳信号从一点传播到另一点的结果,因此,实际在时间域或频率域进行的互相关运算,与这种方法称为“空间自相关”并不矛盾.
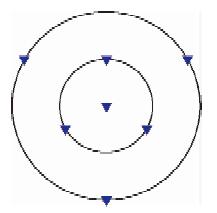
为了提高频散曲线的精度,实际操作时,通常我们布置不同距离R的台站,最后取平均之后的结果,典型的SPAC方法的野外台阵布置如图 6所示.根据最初的理论思路,一般认为在圆周上尽量多的布置测点可以更好的获得自相关系数的方位平均.近些年,多数SPAC方法的研究实例均采用正三角形布置方式.特别是正三角形嵌套的形式在实际工程中也给出了很好的效果(冯少孔,2003;叶太兰等,2004;何正勤等,2007;徐佩芬等,2009).Asten(2004,2006)应用SPAC方法进行地层结构反演时应用圆周上6个测点的布置形式,在数据处理时,不仅利用圆周记录与圆心记录计算互相关系数,还运用多种组合方式,对圆周记录之间的互相关记录做方位平均计算,同一圆形排列便得到不同半径的自相关系数,这样在对相关系数进行Bessel函数拟合时,可以同时得到高阶模式的Bessel函数曲线.虽然在反演时一般仅利用基阶模式(Roberts and Asten,2004;Asten,2004),Asten指出正六边形台阵可以获得比正三角形台阵更多半径值的自相关系数,因此可以促进鉴别高模式能量,并且由于台站对冗余度的增加,提高了频散曲线提取的精度,这为进一步研究SPAC方法的高阶反演提供很好的思路.另外,Asten(2006)还用数值模拟的方法分析了台阵布置形式以及平面波入射范围对测试结果的影响,指出当平面波入射角范围大于60°时,正三角形台阵可以得到较高频信息,并有较好的频带覆盖,而对于平面波入射范围很窄时,三角形台阵仅能得到有限频带信息;正六边形的台阵布设形式,可以对入射范围窄的单一方向信号给出较宽的分辨频带,这实际上隐含考虑了噪声源分布特征对SPAC方法的影响.实际上由于我们并不能判断实际信号的入射范围,所以根据Asten的结论利用正六边形台阵布置可能更为适用.近期在一些地区基于噪声源均匀分布的双台SPAC方法观测实验也获得了成功,更加简化了其应用方法(Hayashi et al.,2013).
|
图 6 嵌套的正三角形SPAC观测台阵示意图 Fig. 6 Schematic diagram of nested triangle SPAC observatory array |
目前,国内研究中基本上用嵌套型三角形布阵形式,台阵半径大小则根据勘探深度来确定.何正勤等(2007)利用半径为300 m,400 m,500 m的同心圆正三角形台阵,在北京朝阳区应用微动的空间自相关法进行地热勘探时,给出了深度3公里内的S波速度结构;在顺义的试验场地,用半径为50 m,100 m,200 m的同心圆正三角型台阵得到了800 m深度内的S波速度结构.Xu等(Xu et al.,2012)应用75到600 m半径的正三角形台阵探测隐伏断层,给出了3公里深度内的地层速度结构.根据这些经验,空间自相关法最大勘探深度约为台阵最大半径的2到7倍之间,在设计时,可以将3到4倍的半径作为勘探深度,为了保持其有效性,布置以该半径为中心,向内和向外分别给予适当小半径和大半径的台阵布置.
空间自相关系数可以在时域和频率域进行计算,时域计算方法源于Aki最初文献中的建议,而频率域计算方法的引入大大加快了计算速度,其结果具有等效性(Koopmans,1974).时域计算步骤为:(1)选取记录良好的原始记录,对每一条记录做归一化处理;(2)对归一化的数据进行取窗和窄带滤波处理,得到(11)式描述的以滤波器中心频率为自变量的近似单色波记录;(3)对单频记录的圆周点与中心点按式(12)计算空间自相关系数;(4)循环第2、3步计算出各个频率值对应其圆周点记录与中心点的空间自相关系数,对所得的两两自相关记录取方位平均,得到用于计算频散的自相关系数式(13),公式(11)-(13)分别为
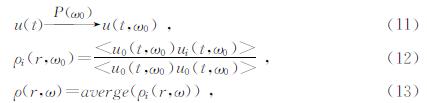
这里符号<>表示整体平均,空间自相关系数的频率域计算公式为
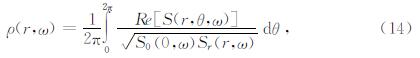
式中,θ为台站方位角,S(r,θ,ω)为圆心记录与圆周记录点的交叉谱,S0(0,ω)和Sr(r,ω)分别为圆心和圆周记录的自功率谱.计算步骤为:选取良好的记录数据,将各道数据做归一化处理,加窗进行傅里叶变换将各个道的数据变换到频率域,在频率域内分别计算各道的功率谱及中心记录与与圆周记录道的互谱,然后根据式(14)计算各个台站对的相关系数,最后计算方位平均.罗松和罗银河(2014)总结了前人用于计算 SPAC系数的6种具体算法,并通过数值模拟对比了各种计算方法的效果,其结果指出对于窄带滤波法,不加时窗法和加时窗法结果均与理论SPAC系数一致,而FFT法加时窗时计算结果与理论SPAC系数一致,其不加时窗法结果与降幅的理论SPAC系数一致.
得到相关系数后,可以利用式(10)将相关系数与第一类零阶贝塞尔函数进行拟合,根据拟合关系求出相速度频散曲线.最初,Aki(1957)所采取的拟合方式是通过寻找自相关系数与贝塞尔函数极大值、零点、极小值的对应关系来求解频散曲线.Asten(2004,2006)和Roberts和Asten(2004)对SPAC方法的一些研究中并未经过利用式(10)提取频散曲线的过程,而是在得出自相关系数后,就直接对自相关系数进行反演,之所以可以这么做是因为在任何给定的分层介质模型中面波正演都可以求得理论频散曲线,也就是可以给出c(ω)与ω的对应关系,于是将该结果代入X=ωr/c(ω),就可以求得该正演模型的理论空间自相关系数,然后直接将反演结果与测量结果进行匹配,最后找出拟合最好的模型作为反演的最后结果.这种方法,不仅省略了一步,而且由于正演计算可以计算出高阶模式频散曲线,所以当遇到某些频段非基阶模态占主导时,可以用某段高阶模态信息来替代匹配不好的基阶频散.虽然利用高阶模态反演的例子还没出现,但高阶模态的应用是SPAC方法的发展方向之一.
Asten(2006)曾通过数值模拟讨论过接收排列和信号入射方位对结果的影响,并根据频率域相干系数虚部的形态,分析了利用相干系数虚部对测试结果进行质量控制的可能性.文成哲(2010)在其博士论文中利用数值模拟方法分析了空间自相关法控制精度问题,特别是其论文中广泛引用前人的研究成果及方法指出信号的方位混叠、非相干噪声的存在、有限时间统计等会影响测试结果的精度,并指出了传统提取频散曲线的方法是利用bessel函数宗量的0.4~3.2范围进行拟合,因此限制了相关系数信息的利用范围,并认为Asten等(Asten,2004;Roberts and Asten,2004)提出的直接反演方法可以更有效的利用观测信息.正是因为受各种因素的影响,所以在某些条件下SPAC方法的假设并不完全成立,甚至由于噪声记录的复杂性很多影响因子至今仍未文发现,所以该方法的应用条件以及合理勘探范围的确定依然更多的依赖于经验性.
3.2 背景噪声互相关函数提取格林函数法(NCF)背景噪声互相关技术属于地震干涉(Seismic interferometry)技术之一,由于其基础数据利用背景噪声而得名,最初,研究人员利用的并不是背景噪声数据,而是地震尾波数据(Campillo and Paul,2003;Paul et al.,2005),后来该方法被广泛用于背景噪声数据的处理,用于地球壳幔结构研究,在世界各地区取得很多成果(Yao et al.,2006;Yang et al.,2007;房立华等,2013;王小龙等,2013).最近几年,已有学者将该方法用于浅层地质结构调查的试验并显示出该方法的可行性(Gouédard et al.,2008c;Picozzi et al.,2009;Nunziata et al.,2009; de Nisco and Nunziata,2011;李成等,2014).
虽然地震干涉理论已经较为广泛的被接受和应用,但是其理论基础并不统一,不同研究者从不同角度给出了不同的证明,如模式均分理论、时间反转理论、稳相近似理论、波动互易理论等.Gouédard等(2008a)给出了白噪声随机分布的任意介质的互相关函数提取两点格林函数的推导,公式为
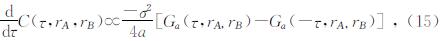
式中,C(τ,rA,rB)表示A、B两点的互相关函数.格林函数Ga(τ,rA,rB)表示在0时刻一个脉冲集中力作用于A点,在τ时刻B点接收的位移记录.根据格林函数的互易性,Ga(-τ,rA,rB)表示在0时刻一脉冲集中力作用于B点,在τ时刻A点接收到的位移记录.σ2是噪声记录的方差,a是A、B两点间介质的衰减因子.该式表明,对于两点间的位移记录的互相关函数对时间的微分与两点间介质格林函数成正比.所以,通过两台站记录的噪声进行互相关计算可以得到格林函数的相位信息.由于时间域中的时间反转,等于频率域中复共轭,时间域的互相关,等于频率域中与复共轭的相乘,因此(15)式在频率域中可以近似表示为
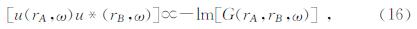
其中u(rA,ω),u(rB,ω)分别是A,B两点的频率记录,<>表示整体平均,[u(rA,ω)u*(rB,ω)]是互相关函数在频率域中的表示.(16)式表明,在频率域中,位移互相关函数,正比于格林函数的虚部.
对于背景噪声互相关技术的处理流程Bensen等(Bensen et al.,2007)给予了详细的总结,目前无论壳幔尺度还是小尺度应用基本的数据处理流程是一样的.背景噪声互相关技术在浅层应用中与大尺度应用中的主要区别就是关注频率更高、台站间距更小,这就要求我们数据的记录有高的采样率,例如,Picozzi等(2009)用了500 Hz的采样率,Nunziata等(2009)用了100 Hz的采样率.
相对于大尺度背景噪声成像,小尺度背景噪声成像需要更高频率的背景噪声源.Gouédard等(2008b)在一个小尺度的噪声成像实验中,围绕传感器步行,以产生高频率的噪声源,其接收阵为线性排列,通过对噪声记录进行互相关运算提取面波信号,用f-k变换法获得了高频面波信号的频散曲线.该实验指出这种方法有3个优点:(a)应用方便,不要严格的台阵排列形状;(b)快速,仅需30 min就可完成布置和记录;(c)简单,不需要对源的激发和各个接收台站阵进行同步处理.这种方法利用不同间距的互相关运算得到了不同到时的面波信号,类似于主动源勘探的多道分析法原始信号,因此,利用f-k变换法即可提取频散曲线.同年,Gouédard等(2008a)对利用数值模拟方法得到的噪声记录分别运用了SPAC方法、高分辨率频率波数法(High-resolution frequency-wavenumber method,HRFK)和噪声互相关方法提取面波后利用倾斜叠加方法给出了Rayleigh面波频散结果.结果显示互相关方法相比另外两种方法可以得到更高频的有效相速度信息,如果路径的方位覆盖较高,将大尺度的面波层析成像方法,移植到小尺度面波勘探中来,可以对小尺度介质实现三维结构成像,相比SPAC方法,具有更高的效率.
3.3 三分量SPAC方法目前SPAC技术主要利用了其竖向分量间的互相关运算.Aki(1957)在最初讨论这种方法时,给出了水平分量的空间自相关系数.根据3.2中,背景噪声互相关函数与格林函数之间的关系,很容易利用瑞利波和勒夫波张量格林函数的表达式,直接利用(16)式求取不同分量之间的空间自相关系数.Yokoi和Margaryan(2008)利用(16)式讨论了不同分量之间的互相关函数表示,这种关系实际也证明了NCF和SPAC物理上的一致性.Haney等(2012)给出了张量形式的空间自相关函数表达式,对于瑞利波有:
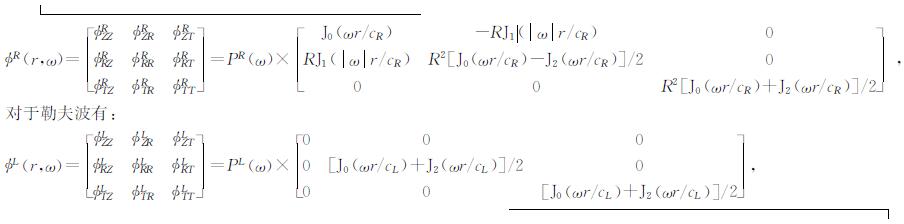
其中,ω为角频率,r为径向距离,cR是瑞利波相速度,cL是勒夫波相速度,R是瑞利波水平方向与竖直方向运动的比率,PR是瑞利波能谱,PL是勒夫波能谱,J0、J1、J2分别为零阶、一阶、二阶bessel函数.Aki(1957)在最初的文献中仅考虑了对角线元素而并未考虑非对角线相关系数的影响,Haney等(2012)利用以上形式中ΦZZR和ΦZRR项,给出了一个例子,得出的频散结果与附近的地质模型极为相近.相比于单分量方法,多分量SPAC分析方法有利于从微动中提取出更多的地质信息.
4 主动源与被动源面波联合勘探这里的面波联合勘探主要指利用主动源激发的面波法与利用被动源的面波法进行同一场地浅层地质结构的调查方法.之所以利用联合勘探,是因为各种方法有着不同的分辨力和勘探效果.主动源对几十米以内深度分辨力较高,且具有一定的横向分辨力,即使加大震源的能量也只能有限的增加勘探深度,特别是现在很多勘察在城市进行,一般不允许使用炸药源,所以勘探深度较浅.被动源勘探中的SPAC法,众多试验证明其勘探深度可达台站半径的数倍到十几倍,勘探深度大,然而相比主动源,被动源对浅层结构信息的反应较为粗糙,这正好可以由主动源对地表浅层的分辨能力来弥补.因此主动源和被动源联合应用,有助于提高勘探深度并与主动源勘探保有同样的精度,目前的主动源和被动源联合应用,主要限于主动源和SPAC的联合,主动源和NCF和SPAC三者的联合应用,还较为少见.而将NCF方法加入被动源勘探可以对较深区域处介质的各向异性给出很好的分辨,对于横向不均匀介质能够有较好的分辨.
4.1 主动源和SPAC方法的结合主动源与被动源方法技术与理论的发展是独立进行的.而在最近应用研究过程中,人们发现两者有着优势互补的作用,这是因为主动源面波方法一般仅能分辨较浅的深度(约30 m),即使加大震源也仅可稍微增加勘探深度,而在当今城市勘探中加大震源会产生较大噪声,很不实用.被动源方法由于其获得信号频率较低(波长更长)所以根据面波理论它可以探测更深的地层,而且不会产生噪声,所以将被动源方法与主动源面波法结合,将两种方法获得的频散曲线进行拼接即可获得更宽频带的频散曲线.已有主动源与被动源结合的试验主要是SPAC方法和主动源方法的结合(Park et al.,2006;张维等,2013).这种联合方法是通过对同一场地进行主动源勘探观测后,再布置SPAC方法的观测系统记录微动信号,然后分别利用前述方法提取两个系统的频散曲线,由于两个系统所得频散的有效频带范围不同,然后对两种方法得到的有效频散曲线进行拼接得到用于反演的频散曲线.对该频散曲线进行反演就获得联合勘探的结果.很多联合勘探试验的结果与地质资料对应良好(Park et al.,2006;张维等,2012,2013),勘探范围明显高于单一方法,说明该方法与单一方法相比有巨大优势,而且由于被动源SPAC方法的数据采集工作量极小,因此,与常规主动源勘探相结合能够起到事半功倍的效果.
4.2 主动源、SPAC和NCF方法的结合随着NCF方法在全球或区域地震层析成像及介质波速变化监测方面的成功应用,众多研究领域的学者开始关注由背景噪声重建系统格林函数这一理论.人们发现这一理论其实可以更早的追溯到Claerbout在1968年关于由透射响应的自相关重建反射响应这一论述,以及这种方法与扩散场空间相干理论之间的关系.除了Aki在1957年关于微动SPAC理论外,在声学领域Cox(1973),Cron和Sherman(1962),Corn等(1965),Balach and ran(1959),Jacobson(1962)等对不同类型的背景噪声场的空间相干进行过研究.现在我们已经知道,对于统计平均的各向同性的噪声场,二维情形下相距为r的两点间归一化的互谱密度为J0(kr,这与SPAC关于标量的结果是一致的.对于三维标量场情况,归一化的互谱密度为sin(kr)/kr=Sinc(kr),对于一维情形则为cos(kr),这里k为波数(Nakahara,2006).背景噪声场的空间相干表达与目前应用的NCF理论,其物理本质是一致的(Yokoi and Margaryan,2008;Tsai and Moschetti,2010),一个是在空间频率域中的描述,一个是在时间域中的描述.Nakahara(2006)曾系统给出了不同维度下,噪声场空间相干与格林函数重建理论之间的系统研究.正是由于这种物理基础的一致性,可以将主动源以及SPAC和NCF方法三者联合应用,使得面波浅层勘探兼具三种方法的优点.
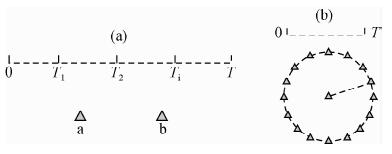
将NCF方法用于浅层勘探中,由于和传统的被动源SPAC方法,在数据处理、成像算法有所不同,因此,这里有必要从简单的理论模型来说明二者在实际应用中的差异.如图 7所示,SPAC方法的观测系统是在一定范围布置圆形(或者嵌套三角形)等排列的台阵,求取不同方位分布的台站对(图中圆周上的不同台站和圆心的台站)空间自相关系数,然后将不同方位分布台阵对相关系数进行方位平均,根据平均后的SPAC系数求取频散曲线,这就意味着由此得到的频散曲线是台阵下方区域的平均效应,反演得到的速度结构是该区域下平均的一维速度结构,如果要用此方法获取二维剖面速度剖面,需要沿测线移动整个台阵,将沿测线的一维速度结构拼接为二维剖面的形式.比如徐佩芬等(2009)在利用SPAC方法探测煤矿陷落柱时,为了得到剖面的信息,沿整个测线移动观测台阵进行观测.
|
图 7NCF(a)和SPAC(b)方法台阵布设和 数值处理示意图 Fig. 7 Illustration of array arrangement and data processing for NCF(a) and SPAC(b)method |
相对而言,NCF方法因其分别利用每个台站对,理论上n个台站可得到n(n-1)/2个路径覆盖.如图 7(a)所示,在NCF中,对于任意台站对ab,将两个台站各自长时间的背景噪声记录,进行分段,然后对每一段进行互相关运算,将不同时间段内的互相关函数进行叠加,得到该路径下两点之间的近似格林函数.这种处理方法意味着,背景噪声源是方位均匀入射的,且每个方向入射的噪声源谱密度相同,对单个台站对,就得到反映该台站对路径下的传播效应.NCF成像方法计算不同路径的频散曲线,得到两两不同路径的频散曲线之后,首先进行纯路径的面波速度反演,得到不同周期的二维速度分布图,然后进行每个成像区域反演,最后得到三维的S波速度结构.因此,对于一个台阵来说,不需要移动台阵的观测结果就可以获得三维的速度结构,这在以前不管是主动源还是被动源面波的浅层勘探方法中都是无法实现的.
所以,三种测试方法的联合应用将给出更加细致的结果,具有较高的浅层分辨力,较高的横向分辨力,及更大的探测深度.联合应用方法设计可考虑如下步骤:
(1)用同一直线排列对主动源和被动源进行记录,然后分别给予解释,主动源方法用相位差法或频率波数法、被动源利用SPAC方法或互相关倾斜叠加法(Gouédard et al.,2008c).
(2)按SPAC方法布置圆形台阵或嵌套正三角型的台阵,或者更为宽松的保证相对均匀的路径覆盖的台阵布设,在数据处理时分别利用背景噪声互相关法和SPAC方法提取频散曲线.
(3)将主动源和SPAC得到的不同频段的频散曲线进行拼接,初步反演地下的平均S波速度结构,进行初步解释.
(4)对NCF方法得到的不同频率的相速度,进行二维纯路径结构反演,然后将步骤3的反演结果作为初始模型,根据纯路径的反演结果反演三维的S波速度结构.另外,如果我们能利用足够多的三分量地震仪进行实验,还可以通过极化分析和F-k分析对实际噪声源分布进行分析,并通过分析不同分量的互相关结果,考虑可能的各向异性反演,因此对这种联合勘探的实验和理论研究具有重大意义和应用潜力.
5 面波的多模性及低速层探测均匀水平分层的层状模型是目前绝大多数面波勘探方法的前提假设,在这样的模型中,对于每一个频率,面波具有多个模式,所谓模式,在空间域上对应体波在每一层之间来回反射的不同路径,正是不同路径的体波与分层模型的边界与界面的条件造成了观测的面波记录.本节以两个例子说明模式的一些概念,以及低速层存在时考虑多模式面波的反演方法.模型参数见表 1,模型1为速度递增的三层介质模型,模型2为含有低速层的三层介质模型.
|
|
表 1 水平均匀分层的层状介质模型 Table 1 The horizontal multi-layered model considered in this paper |
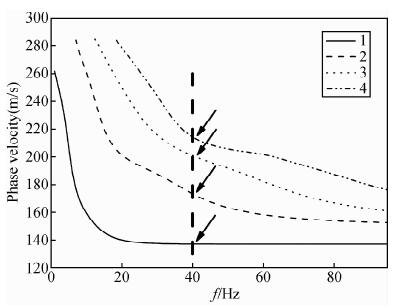
图 8给出了模型1中传播的4个瑞利波模式的频散曲线.由于多层介质瑞利波的频散方程较为复杂,通常采用数值方法,比如二分法,进行求解.在计算频散曲线时,对单个频率进行搜索,将求得的根按大小进行排列,速度从低到高,依次称为基阶(第1阶),第2阶,第3阶等模式.这样得到结果在f-v域中将相应模式的相速度连起来,就得到了图 8所示的多模式频散曲线,这些频散曲线也称为频散枝(Branch).瑞利波的多模性是指在同一频率下,介质允许多个相速度存在,比如在图 8中,给出了40 Hz时的4个模式的相速度在不同频散枝上的位置.
|
图 8 模型1中传播的基阶和3个高阶模式的Rayleigh
面波频散曲线,图中箭头标出了40 Hz频率下的
4 个模式的相速度在频散枝(Branch)上的位置
Fig. 8 The dispersion branch of fundamental and 3
higher modes of Rayleigh wave propagated in Model 1. The location of the phase velocity at frequency 40 Hz are denoted by arrows along dispersion branches |
模型1中,介质速度随深度的增加而递增,对这样的正频散模型来说,记录到的面波能量通常是基阶模式占据主导地位,因此反演时仅考虑基阶模式,本文涉及到的数据处理大多是针对单个模式的.由于高阶模式比基阶模式具有更深的勘探深度,有时也采用高阶模式反演,要获取高阶模式的频散曲线需要一定的数据处理技术,使在时域中叠加在一起的信号分离开来,比如前述的f-k分析(图 5).此时,可以用“多模式面波信号(Multi-mode surface wave)”或“多模式叠加信号”,来描述在时域中接收到的信号,而不是“模式的耦合”,因为均匀水平分层介质中,各模式永远是独立传播的.
模式耦合(mode-coupling)用来表示在水平均匀介质出现横向非均匀体时面波模式之间发生的耦合现象(Maupin,2007),其中一个模式的能量会转化为另一个模式的能量,物理上与均匀水平分层介质中的多模式面波是不同的.在均匀水平分层介质中,所有的模式独立传播,各模式的特征函数在数学上相互正交,这也是面波的理论基础.正是由于其独立传播,才可以将多模式的频散曲线通过数据处理方法分离开来.而横向非均匀介质中,由于模式耦合的存在,这些模式不是独立传播的,对于弱的横向非均匀介质中,可以采用模式耦合方法来计算理论的面波波形.Woodhouse(1974)和Maupin(1988)采用局剖模式耦合,Kennett(1984)采用参考模式耦合来模拟面波波形.模式耦合也可以在考虑散射影响的的有限频成像中,计算三维敏感度核(Sensitivity kernel)(Zhou et al.,2004).如果横向非均匀性很强,或者弱的非均匀体尺度很大,参考模式耦合的方法将失效.这是由于模式的概念来源于均匀水平分层介质,对于强的横向非均匀介质,用参考模型中的模式来描述波场本身是不恰当的.另外,对于水平层状介质面波理论,模式耦合也严格用于表示“交叉枝(Cross-Branch)”之间的耦合(Maupin,2007),或者模式自身的耦合,比如图 8中,40 Hz时不同频散枝上的耦合(箭头所示),或者该频率下,模式自身的耦合,不存在沿某个频散枝(along-branch)的耦合.
因此,对于面波勘探方法来说,除非考虑了横向非均匀体的散射,所有以水平均匀分层模型为前提的正反演方法中,均不存在模式耦合现象,用“模式耦合”描述此模型下记录的时域中多模式叠加信号是不恰当的.
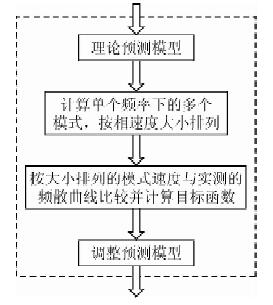
如模型1的速度递增模型,如果在实际勘探过程中,采集信号的信噪比很高,有时可以获得2个或2个以上模式的频散曲线(如图 5),对于只考虑单模式的频散曲线反演,对于给定的初始理论模型,只需选择某个频率下,速度最小的相速度与实测的基阶模式相速度(速度最小)进行比较拟合,依此计算目标函数,调整理论预测模型.如果考虑多模式频散曲线,需将理论模型计算的相速度,按大小依次和实测频散曲线进行比较,其目标函数的计算如图 9所示,这也是传统基阶模式和多模式面波反演方法.
|
图 9 速度递增模型多模式反演方法的 目标函数计算方法 Fig. 9 The method to calculate the objective function in the multimode surface wave inversion for the model |
在传统区域地震学中,由于探测深度较大,几十到上百公里,这时地球模型可近似看作一个速度递增的层状介质,这种条件下面波能量主要集中于基阶模式,我们通过以基阶模式为主的区域面波成像来进行地球结构分析.在浅层勘探中,虽然速度递增型结构依然常见,但有些地层由于各种沉积环境不同、或经过人为改造或其他自然条件的原因会存在低速夹层的情况.例如,一些沉积环境中会有小的透镜体、经过地基处理后地基上部变的密实而下部并没有表层密实,这就出现了软夹层的情况.在众多存在软夹层的实践观测中常出现“之”字形的频散曲线,而不同于大尺度地震学中频散曲线的形态.针对实际中“之”字形观测曲线的出现,张碧星等(2002),鲁来玉(2004),鲁来玉等(2006)通过实验和数值模拟研究,指出这是由于各模式激发能量不同,在不同频段,可能不同模式的能量居于主导地位,以至于提取的频散曲线在模式之间跳跃形成的(Lu et al.,2006,2007).对于不同的处理方法来说,比如SASW方法,认为波速是频率的单值函数,于是给出的结果就是各个模式叠加后的能量变化随频率的变化关系;频率-波数法虽然可以区分模式,但由于模式激发能量在不同频段可能对应不同的模式,因此对于含有低速层的介质而言,实际提取的频散曲线呈现“之”字形结构(刘雪峰和凡友华,2011),对于这样的频散曲线,在反演中仍按图 9中的计算方法,会出现模式的误判(mode-misidentified)(Zhang and Chan,2003),降低反演精度,甚至导致错误的结果.
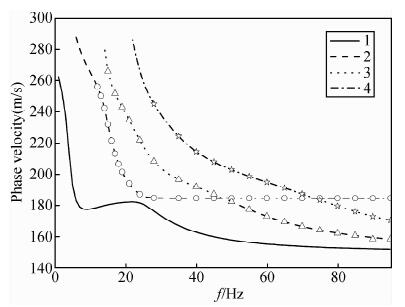
图 10给出了表 1中模型2的前4个瑞利波模式的频散曲线,图中不同线型的频散枝,是根据5.1中的方法,将求得的频散方程的根按从小到大排列,然后依次将不同频率的相速度值连接成一条曲线.事实上,对于这种模型来说,这种划分模式的方法并不是有效的,仅仅是一种数值处理方式.由于频散方程的复杂性,无法直接判断某个频率下求得的根,和相邻频率下求得的根,哪一个具有物理上相同的特征,只能按速度大小来排列,并在f-v域中连线,造成这种所谓的“交叉现象”.根据模式频散曲线的连续性,及其导数特征,如果按图中不同形状所示的连线看成是一个模式,可能在物理上更具有合理性.实际上,如果考察模式的位移分布,按图中不同线型划分的模式,在所谓“交叉点”附近位移曲线并不连续,相反,如果按图中不同形状所示的曲线,看成一个模式,位移曲线具有良好的连续性,并且,图中圆圈所示的模式,在频率超过22 Hz以后,其能量具有绝对的主导地位,这也造成观测的频散曲线在基阶模式和该模式之间的跳跃.在反演时,如果仍按图 9所示的目标函数计算方法,仅考虑速度的大小无法判断由理论模型计算的频散曲线,哪一个模式对应实际观测的频散曲线.根据造成实际观测频散曲线的跳跃是模式激发能量造成的这一实验和模拟结论,我们提出了低速层存在时“之”字形频散曲线的反演方法,如图 11所示.和不含低速层时相比,在计算某个频率下的相速度之后,需要计算其相应的激发能量,然后根据能量大小,判断选择哪一个模式和实测频散曲线进行对比.这种方法,已通过实验模型、数值模型及野外勘测数据进行了验证,可以很好的避免反演中的模式误判问题,其代价是在计算激发能量时,需要更多的计算量,但相对于反演精度的提高,这种代价的付出是值得的(Maraschini et al.,2010;Socco et al.,2010;Tsuji et al.,2012).
|
图 10 模型2中传播的多模式瑞利波的频散曲线 Fig. 10 Multimode dispersion curve of Rayleigh waves in model 2 in which a low-velocity layer is imbedded |

|
图 11 低速层存在时多模式反演目标函数计算方法 Fig. 11 The method to calculate the objective function in the multimode surface wave inversion for the model in which a low-velocity layer is imbedded |
6.1 利用面波方法进行浅层勘探已经兴起几十年,由于该方法效率高、易操作及无破坏性等特点,被广泛用于各种工程勘察领域,比如高速公路的质量检测(刘强,2009),建筑物基础工程勘察(郑柱坚,2012),岩石溶洞探测(杨威,2012),S波速度结构成像(何正勤等,2007),煤矿陷落柱探测(徐佩芬等,2009)及隧道工程勘察(徐佩芬等,2012)等领域.近年来,随着城市建设的发展,由于激震设备及传感器布设的局限性,主动源在市区的应用受到越来越多的限制.同时,伴随着背景噪声互相关技术(NCF)在全球地震层析成像的广泛应用及微动技术的发展,被动源面波勘察方法逐渐成为研究者关注的焦点.浅勘领域的著名期刊“The leading edge”分别在2011年5月及2012年12月出版了两期主题分别为“Interferometry application”和“Passive seismic and microseismic”的专刊,讨论被动源面波技术相关的理论和方法.
6.2 主动源和被动源的主要区别在于源和前期的数据采集和处理有所不同,后期反演解释基本类似,都是基于提取的频散曲线和(或)幅度的衰减,对介质进行反演.传统的基于弹性水平分层介质模型中基阶(或高阶)模式的正反演理论和相应的激发和采集设备及解释软件等发展的相对成熟.伴随地震干涉理论的发展(Wapenaar et al.,2010a,b),以下几个方面是未来面波勘探的理论和方法值得关注的研究方向.
(1)多分量信息的应用
目前,主动源和被动源面波方法集中于瑞利波方法,这主要是因为从信号的激发和接收的角度来说,任意的均匀层状(含半无限)介质,均可以有效激发瑞利波信息,采用垂直分量传感器就可以接收瑞利波垂向分量.勒夫(Love)波的激发需要特定的激发源和分层介质模型,采用水平分量传感器进行接收,这限制了勒夫面波在浅勘应用中的发展.在大尺度地震层析成像中,水平偏振的勒夫波经常和瑞利波一起,用于推断介质的各向异性特征.在浅勘尺度范围,Safani等(2006)和夏江海等(Xia et al.,2009;Xia et al.,2012)都曾开展过Love波的应用研究,和MASW类似,Xia等(2012)提出了基于勒夫波信息的MALW(Multichannel Analysis of Love Wave)方法.伴随地震背景噪声技术的发展,基于被动源的勒夫波方法也得到了发展.Tada等(2009)利用圆形阵列微震技术获取了勒夫波的相速度;García-Jerez等(2010)研究了基于圆形阵列的勒夫波微动技术;Shabani等(2011)将传统的SPAC方法用于水平偏振的背景噪声处理;Behm和Snieder(2013)利用交通产生的背景噪声信息成功提取了Love波相速度.与这些应用相关的被动源干涉理论也得到了发展,Haney等(2012)利用背景噪声互相关函数与系统格林函数之间的关系,给出了交叉分量SPAC系数的张量表示,并考虑了近场对交叉分量干涉的影响(Haney and Nakahara,2014).由于多分量信息相对传统单分量对介质的反演可以提供更多的约束,多分量干涉理论的应用逐渐受到研究者关注.van Wijk等(2011)利用交叉分量的互相关来估计瑞利波的脉冲响应.最近,Takagi等(2014)将交叉分量干涉技术用于分离体波和面波信号.另外,如果介质具有一定的各向异性,将在不同的传播方向和偏振方向有所体现,多分量信息潜在提供了一种反演介质各向异性的方法.随着计算和反演方法的发展,多分量信息的利用将满足未来面波浅勘对介质精细结构探测的需求.
多分量信息在面波工程中的另一个应用是基于水平和垂直分量的振幅比(H/V)来推断沉积层特征及场地的放大效应(Salinas et al.,2014).由于H/V谱比法更多的是基于经验公式来判断,也不是本文关注的对象,这里不对其进行展开叙述.
(2)黏弹性和介质的衰减
目前,成熟的方法和相应的解释软件主要针对完全弹性的介质情形,从传播理论来讲,将弹性介质扩展到黏弹性介质,并不存在困难.如果对介质的衰减或者品质因子进行反演,要求采集的数据,除相位信息外,幅度信息应足够精确地反应波在传播过程中的吸收,还要考虑介质的复杂性引起的散射和几何扩散,这对传感器和数据采集处理技术都提出了更高的要求.同时,反演参数的增加,使反演的稳定性受到影响,因此,在实际应用中对衰减或品质因子的反演,滞后于黏弹性介质中面波的传播理论研究.Lai等(2002)及Xia等(2002,2013)等考虑过对速度和衰减(或品质因子)同时进行反演的研究.Lu等(2011)等基于高频激光超声对混凝土试块的检测实验数据,假定速度和品质因子在深度方向是连续变化的,利用高频面波反演了功能梯度材料的S波速度和品质因子.对于被动源地震干涉技术,对衰减的反演目前主要集中于较大尺度的地球结构反演.Prieto等(2009)基于背景噪声干涉理论,较早开展了这方面的研究.在其研究中,Prieto等(2009)将二维弹性情形下的微震空间相关系数表达式进行了修正,即将衰减介质中的空间自相关系数表示成零阶贝塞尔函数和一个指数衰减因子的乘积,依此来推断介质的衰减,并在大尺度上用于美国西部的衰减成像(Lawrence and Prieto,2011).然而,对于衰减介质,被动源的互相关函数表达高度依赖于背景噪声源的分布,对被动源干涉的衰减成像还存在一定争议(Weaver 2011).Nakahara(2012)对衰减介质的SPAC系数的研究表明,Prieto等(2009)给出的修正表达式,只在衰减很小的情况下近似成立.对于不同的背景噪声源模型,空间相关系数和归一化的不同选择,其干涉表达式是不同的(Tsai,2011),这在一定程度上引起了人们对干涉衰减成像结果的争议,因为这种方法得到的衰减图像和介质的真实衰减有一定的差别.Lawrence等(2013)和Liu和Ben-Zion(2013)通过数值模拟,研究了噪声源的分布对背景噪声互相关函数的影响,对于不同的噪声源模型,衰减在空间相关系数的表达中可以近似地表示成指数衰减形式,因此,在一定假设下,可以近似地用于反演介质的视衰减(Menon et al.,2014).对于浅勘领域的小尺度情形,可以直接借用大尺度的研究结果,对介质衰减或品质因子进行反演.
(3)复杂模型的面波干涉理论
背景噪声成像方法得益于利用背景噪声重建系统格林函数的发展,2001年,Weaver和Lobkis(2001)首先基于简正模式的等分原理,证明了背景噪声的互相关可以重建系统的格林函数,并在一个铝块上,放置两个传感器,基于记录到的热噪声,通过互相关重建了系统的格林函数(Weaver and Lobkis,2002).随后,这一理论被成功应用于全球尺度的地震层析成像,并使不同学科领域的研究者研究并回溯这一理论的发展历程,发现与早期的统计声学(Cook,1955;Cox,1973),微动(Aki,1957)及地震干涉(Claerbout,1968)具有相通之处,从而奠定了被动源干涉方法与微动的SPAC技术一样,可以用于浅勘领域的理论基础.在大尺度成像中,一般只考虑单分量的基阶模式,基于一些简单模型和物理假设的标量波干涉理论就可以对其进行解释.由于面波的多模多分量特征,需要研究面波的干涉理论.多模式面波的干涉理论主要是由Halliday和Curtis(2008,2009a,2009b)发展的,基于均匀分层介质模型,Halliday和Curtis(2008)还研究了源的分布对面波干涉的影响,这些研究都局限于简单模型的数值模拟研究.如果要考虑多模式面波的反演及介质的衰减,需要进一步研究复杂模型下面波的干涉理论,这是从背景噪声中提取多模式面波格林函数及进行模式分离的关键.NCF方法主要基于互相关运算的叠加,来获取系统格林函数,从而提取频散曲线.由于面波的多模性,互相关运算除了同一模式之间的互相关,也包含交叉模式之间的互相关,如果噪声源在表面和一定深度均有分布,由于面波模式的正交特征,互相关运算不会出现不同模式之间的互相关引起的交叉项.然而,实际的背景噪声源受多种因素的影响,此时由互相关重建面波格林函数时,如果缺少一定深度的源的分布,不能完全利用面波模式的正交特征,提取的格林函数具有交叉项干扰.高玲利等(2014)采用拉东变换对干涉引起的交叉项进行分离,然后对单个模式进行互相关运算,再进行求和,这是解决交叉项干扰的一种途径.要正确进行模式分离,并考虑复杂的噪声源及衰减的影响,需要进一步研究对复杂模型下面波的干涉理论.
(4)三维反演方法及面波的散射
目前,主动源面波探测通常采用线性排列,在反演解释时,假定波沿源到检波器连线的路径传播,最终得到的反演解释,比如一维的S波速度剖面,是沿整个测线的平均效应,如果沿测线布置较多的传感器或者做多次测量,最终可将反演得到的一维速度剖面拼接成二维的速度剖面.另外,如果对相邻道采用SASW方法处理,也可以得到类似的二维剖面.与此类似,基于微动技术的SPAC方法,一次微动观测结果视为是整个阵列下方的平均效应,要得到二维的速度剖面,需要移动阵列沿剖面观测.由于NCF方法,不要求严格的阵列布置,因此可以直接移植大尺度面波层析成像的方法,对频散曲线先做纯路径反演,得到不同周期的二维速度分布,然后由不同网格上的面波速度反演S波速度结构,这种方法目前在浅勘中的应用还比较少见,不失为一种简单易行的三维层析成像方法.需要指出,这种三维成像方法,仍然是基于射线理论的,没有考虑实际三维体对面波的散射效应.如果基于波动理论,开展真正的三维面波层析成像,需要研究面波的散射理论.散射面波,在目前的应用中,是作为干扰剔除的,基于散射面波反演三维结构,目前只限于一些简单模型的理论和实验研究(van Wijk et al.,2004;Kaslilar,2007),在反演中对模型做了相当简单的假设,比如Campman和Riyanti(2007)利用散射面波进行成像时,仅考虑了密度的扰动.如果仍然采用基于频散曲线(走时)对三维结构进行成像,三维面波反演需要考虑三维体的扰动引起的面波相位或幅度的灵敏度核(鲁来玉等,2011),除了多模性问题,额外增加了计算量.另一种完全不同的考虑,是跳过频散曲线提取这一步,直接利用全波形进行反演,这在大尺度成像方面有些理论和应用研究,由于利用全波形反演,避免了传统方法中的模式误判等问题,应是面波浅勘领域未来反演方法的一个发展方向(Solano et al.,2014).
致 谢 文中诸多内容受益于和中国地震局地球物理研究所何正勤研究员的多次讨论,在此表示感谢.感谢审稿人对文章初稿提出的意见和建议.
| [1] | Aki K. 1957. Space and time spectra of stationary stochastic waves, with special reference to microtremors[J]. Bull. Earthq. Res. Inst. Tokyo, 35:415-456. |
| [2] | Aki K. 1965. A note on the use of microseisms in determining the shallow structures of the Earth's crust[J]. Geophysics, 30(4):665-666. |
| [3] | Al-Hunaidi M O. 1992. Difficulties with phase spectrum unwrapping in spectral analysis of surface waves nondestructive testing of pavements[J]. Canad. Geotechn. J., 29:506-511. |
| [4] | Alleyne D, Cawley P. 1991. A two-dimensional Fourier transform method for the measurement of propagating multimode signals[J]. J. Acoust. Soc. Am., 89(3):1159-1168. |
| [5] | Asten M W. 2004. Passive seismic methods using the microtremor wave field for engineering and earthquake site zonation[C].//74th SEG Annual Meeting, Denver. |
| [6] | Asten M W. 2006. On bias and noise in passive seismic data from finite circular array data processed using SPAC methods[J]. Geophysics, 71(6):153-162. |
| [7] | Balachandran C G. 1959. Random sound field in reverberation chambers[J]. J. Acoust. Soc. Am., 31(10):1319-1321. |
| [8] | Ballard R F Jr. 1964. Determination of soil shear moduli at depth by in situ vibratory techniques[R].Waterways Experiment Station, Miscellaneous paper No.4-691. |
| [9] | Behm M, Snieder R. 2013. Love waves from local traffic noise interferometry[J]. The Leading Edge, 32(6):628-632, doi:10.1190/tle32060628.1. |
| [10] | Bensen G D, Ritzwoller M H, Barmin M P, et al. 2007, Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophys. J. Int., 169(3):1239-1260. |
| [11] | Campillo M, Paul A. 2003. Long-range correlations in the diffuse seismic coda[J]. Science, 299(5606):547-549. |
| [12] | Campman X, Riyanti C D. 2007. Non-linear inversion of scattered seismic surface waves[J]. Geophys. J. Int., 171(3):1118-1125. |
| [13] | Chen Y M, Wu S M. 1991. A new method to solve characteristic equation of Rayleigh wave in a layer soil[J]. Journal of Zhejiang University (Natural Science) (in Chinese), 25(1):40-82. |
| [14] | Claerbout J F. 1968. Synthesis of a layered medium from its acoustic transmission response[J]. Geophysics, 33(2):264-369. |
| [15] | Cook R K, Waterhouse R V, Berendt R D, et al. 1955. Measurement of correlation coefficients in reverberant sound fields[J]. J. Acoust. Soc. Am., 27(6):1072-1077. |
| [16] | Cox H. 1973. Spatial correlation in arbitrary noise fields with application to ambient sea noise[J]. J. Acoust. Soc. Am., 54(5):1289-1301. |
| [17] | Cron B F, Hassell B C, Keltonic F J. 1965. Comparison of theoretical and experimental values of spatial correlation[J]. J. Acoust. Soc. Am., 37(3):523-529. |
| [18] | Cron B F, Sherman C H. 1962. Spatial-correlation functions for various noise models[J]. J. Acoust. Soc. Am., 34(11):1732-1736. |
| [19] | de Nisco G, Nunziata C. 2011. VS Profiles from Noise Cross Correlation at Local and Small Scale[J]. Pure and Applied Geophysics, 168(3-4):509-520. |
| [20] | Fan Y H, Liu J Q, Xiao B X. 2002. Fast vector-transfer algorithm for computation of Rayleigh wave dispersion curves[J]. Journal of Hunan University (Natural Sciences Edition) (in Chinese), 29(5):25-30. |
| [21] | Fang L H, Wu J P, Wang W L, et al. 2013. Love wave tomography from ambient seismic noise in North-China[J]. Chinese J. Geophys. (in Chinese), 56(7):2268-2279, doi:10.6038/cjg20130714. |
| [22] | Feng S K. 2003. Array microtremor survey and its application to civil engineering[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 22(6):1029-1036. |
| [23] | Forchap E A, Schmid G. 1998. Experimental determination of Rayleigh-wave mode velocities using the method of wave number analysis[J]. Soil Dynamics and Earthquake Engineering, 17(3):177-183. |
| [24] | Foti S. 2000. Multistation methods for geotechnical characterization using surface waves[Ph.D.Thesis]. Italy:Politecnico di Torino. |
| [25] | Gabriels P, Snieder R, Nolet G. 1987. In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh wave[J]. Geophysical Prospecting, 35(2):187-196. |
| [26] | García-Jerez A, Luzón F, Navarro M, et al. 2010. Assessing the reliability of the single circular-array method for love-wave ambient-noise surveying[J]. Bull. Seism. Soc. Am., 100(5A):2230-2249, doi:10.1785/0120090224. |
| [27] | Gouédard P, Stehly L, Brenguier F, et al. 2008a. Cross-correlation of random fields:mathematical approach and applications[J]. Geophysical Prospecting, 56(3):375-393. |
| [28] | Gouédard P, Cornou C, Roux P. 2008b. Phase-velocity dispersion curves and small-scale geophysics using noise correlation slantstack technique[J]. Geophys. J. Int., 172(3):971-981. |
| [29] | Gouédard P, Roux P, Campillo M. 2008c. Small-scale seismic inversion using surface waves extracted from noise cross correlation[J]. J. Acoust. Soc. Am., 123(3):EL26-EL31. |
| [30] | Halliday D, Curtis A. 2008. Seismic interferometry, surface waves and source distribution[J]. Geophys. J. Int., 175(3):1067-1087, doi:10.1111/j.1365-246X.2008.03918.x. |
| [31] | Halliday D, Curtis A. 2009a. Generalized optical theorem for surface waves and layered media[J]. Phys. Rev. E, 79(5):056603, doi:10.1103/PhyRevE.79.056603. |
| [32] | Halliday D, Curtis A. 2009b. Seismic interferometry of scattered surface waves in attenuative media[J]. Geophys. J. Int., 178(1):419-446, doi:10.1111/j.1365-246X.2009.04153.x. |
| [33] | Hayashi K, Martin A, Hatayama K, et al. 2013. Estimating deep S-wave velocity structure in the Los Angeles Basin using a passive surface-wave method[J]. The Leading Edge, 32(6):620-626, doi:10.1190/tle32060620.1. |
| [34] | Haney M M, Mikesell T D, Van Wijk K, et al. 2012. Extension of the spatial autocorrelation (SPAC) method to mixed-component correlations of surface waves[J]. Geophys. J. Int., 191(1):189-206. |
| [35] | Haney M M, Nakahara H. 2014. Surface-wave Green's tensors in the near field[J]. Bull. Seism. Soc. Am., 104(3):1578-1586, doi:10.1785/0120130113. |
| [36] | He Z Q, Ding Z F, Jia H, et al. 2007. To determine the velocity structure of shallow crust with surface wave information in microtremors[J]. Chinese J. Geophys. (in Chinese), 50(2):492-498, doi:10.3321/j.issn:0001-5733.2007.02.021. |
| [37] | Jacobson M J. 1962. Space-time correlation in spherical and circular noise fields[J]. J. Acoust. Soc. Am., 34(7):971-978. |
| [38] | Jones R. 1962. Surface wave technique for measuring the elastic properties and thickness of roads:theoretical development[J]. British J. Appl. Phys., 13(1):21-29. |
| [39] | Kaslilar A. 2007. Inverse scattering of surface waves:imaging of near-surface heterogeneities[J]. Geophys. J. Int., 171(1):352-367. |
| [40] | Kennett B L N. 1984. Guided wave propagation in laterally varying media -I. Theoretical development[J]. Geophys. J. Int., 79(1):235-255. |
| [41] | Koopmans L H. 1974. The Spectral Analysis of Time Series[M]. New York:Academic Press Inc. |
| [42] | Lai C G, R, Rix G J, Foti S, et al. 2002. Simultaneous measurement and inversion of surface wave dispersion and attenuation curves[J]. Soil Dynamics and Earthquake Engineering, 22(9-12):923-930. |
| [43] | Lawrence J F, Denolle M, Seats K J, et al. 2013. A numeric evaluation of attenuation from ambient noise correlation functions[J]. J. Geophys. Res., 118(12):6134-6145, doi:10.1002/2012JB009513. |
| [44] | Lawrence J F, Prieto G A. 2011. Attenuation tomography of the western United States from ambient seismic noise[J]. J. Geophys. Res., 116(B6):B06302, doi:10.1029/2010JB007836. |
| [45] | Liu X, Ben-Zion Y. 2013. Theoretical and numerical results on effects of attenuation on correlation functions of ambient seismic noise[J]. Geophys. J. Int., 194(3):1966-1983. |
| [46] | Liu X F, Fan Y H. 2011. A study on 'jump point' frequencies of zigzag dispersion curves in Rayleigh wave exploration[J]. Chinese J. Geophys. (in Chinese), 54(8):2124-2135, doi:10.3969/j.issn.0001-5733.2011.08.020. |
| [47] | Liu Y Z, Wang Z D. 1996. Data collection and processing system of transient surface wave method and examples of its application[J]. Geophysical #180; Geochemical Exploration (in Chinese), 20(1):28-34. |
| [48] | Lu L Y. 2004. Rayleigh wave pattern analysis in layered medium half space and medium parameters inversion (in Chinese)[Ph. D. thesis]. Beijing:Institute of Acoustic, Chinese Academy of Science. |
| [49] | Lu L Y, Chekroun M, Abraham O, et al. 2011. Mechanical properties estimation of functionally graded materials using surface waves recorded with a laser interferometer[J]. NDT #180; E International, 44(2):169-177. |
| [50] | Lu L Y, Ding Z F, He Z Q. 2011. Analysis of 3D sensitivity kernels of the finite frequency surface wave tomography in shallow subsurface[J]. Chinese J. Geophys. (in Chinese), 54(1):55-66, doi:10.3969/j.issn.0001-5733.2011.01.007. |
| [51] | Lu L Y, Wang C H, Zhang B X. 2006. Experimental analysis of multimode guided waves in stratified media[J]. Appl. Phys. Lett., 88(1):014101. |
| [52] | Lu L Y, Wang C H, Zhang B X. 2007. Inversion of multimode Rayleigh waves in the presence of a low-velocity layer:Numerical and Laboratory study[J]. Geophys. J. Int., 168(3):1235-1246. |
| [53] | Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes[J]. Chinese J. Geophys. (in Chinese), 49(4):1082-1091, doi:10.3321/j.issn:0001-5733.2006.04.021. |
| [54] | Maraschini M, Ernst F, Foti S, et al. 2010. A new misfit function for multimodal inversion of surface waves[J]. Geophysics, 75(4):G31-G43. |
| [55] | Maupin V. 1988. Surface waves across 2-d structures:a method based on coupled local modes[J]. Geophys. J. Int., 93(1):173-185. |
| [56] | Maupin V. 2007. Introduction to mode coupling methods for surface waves[A].//Wu R S, Maupin V, eds. Advances in Wave Propagation in Heterogeneous Earth, Vol 48, Advances in Geophysics[M]. Amsterdam:Elsevier. |
| [57] | McMechan G A, Yedlin M J. 1981. Analysis of dispersive waves by wave field transformation[J]. Geophysics, 46(6):869-874. |
| [58] | Menon R, Gerstoft P, Hodgkiss W S. 2014. On the apparent attenuation in the spatial coherence estimated from seismic arrays[J]. J. Geophys. Res., 119(4):3115-3132, doi:10.1002/2013JB010835. |
| [59] | Nakahara H. 2006. A systematic study of theoretical relations between spatial correlation and Green's function in one-, two-and three-dimensional random scalar wavefields[J]. Geophys. J. Int., 167(3):1097-1105. |
| [60] | Nakahara H. 2012. Formulation of the spatial autocorrelation (SPAC) method in dissipative media[J]. Geophys. J. Int., 190(3):1777-1783. |
| [61] | Nazarian S, Stokoe K H. 1986a. In situ determination of elastic moduli of pavement systems by spectral-analysis-of-surface-waves method (practical aspects)[R]. Research Report 01419314, Center For Transportation Research, The University of Texas at Austin, Austin, Tex. |
| [62] | Nazarian S, Stokoe K H. 1986b. In situ determination of elastic moduli of pavement systems by spectral-analysis-of-surface-waves method (theoretical aspects)[R]. Research Report 00473174, Center For Transportation Research, The University of Texas at Austin, Austin, Tex. |
| [63] | Nunziata C, de Nisco G, Panza G F. 2009. S-waves profiles from noise cross correlation at small scale[J]. Engineering Geology, 105(3-4):161-170. |
| [64] | Pan D M. 2009. Dispersion analysis of Rayleigh surface waves and application (in Chinese)[Ph. D. thesis]. Beijing:China University of Mining and Technology. |
| [65] | Park C B, Miller R D, Xia J. 1998. Imaging dispersion curves of surface waves on multi-channel record[C].//68th Ann. Mtg. of SEG, in SEG Expanded Abstracts, 1377-1380. |
| [66] | Park C B, Miller R D, Xia J H. 1999. Multichannel analysis of surface waves[J]. Geophysics, 64(3):800-808. |
| [67] | Park C B, Miller R D, Ryden N, et al. 2006. Combined use of active and passive surface waves[J]. Journal of Environmental & Engineering Geophysics, 10(3):323-334. |
| [68] | Paul A, Campillo M, Margerin L, et al.2005. Empirical synthesis of time-asymmetrical Green functions from the correlation of coda waves[J]. J. Geophys. Res., 110(B8), doi:10.1029/2004JB003521. |
| [69] | Picozzi M, Parolai S, Bindi D, et al. 2009. Characterization of shallow geology by high-frequency seismic noise tomography[J]. Geophys. J. Int., 176(1):164-174. |
| [70] | Poggi V, Fah D, and Giardini D. 2012. Time-frequency-wavenumber analysis of surface waves using the continuous wavelet transform[J]. Pure Appl. Geophys., 170(3):319-335. |
| [71] | Prieto G A, Lawrence J F, and Beroza G C. 2009. Anelastic Earth structure from the coherency of the ambient seismicfield[J]. J. Geophys. Res., 114(B7):B07303, doi:10.1029/2008JB006067. |
| [72] | Roberts J C, Asten M W. 2004. Resolving a velocity inversion at the geotechnical scale using the microtremor (passive seismic) survey method[J]. Exploration Geophysics, 35(1):14-18. |
| [73] | Safani J, O'Neill A, Matsuoka T, et al. 2006. Applications of love wave dispersion for improved shear-wave velocity imaging[J]. Journal of Environmental & Engineering Geophysics, 10(2):135-150, doi:10.2113/JEEG10.2.135. |
| [74] | Salinas V, Luzón F, García-Jerez A, et al. 2014. Using diffuse field theory to interpret the H/V spectral ratio from earthquake records in Cibeles Seismic Station, Mexico City[J]. Bull. Seism. Soc. Am., 104(2):995-1001, doi:10.1785/0120130202. |
| [75] | Shabani E, Eskandari-Ghadi M, Mirzaei N. 2011. The SPAC Method for 1Finite M-Station Circular Array Using Horizontally Polarized Ambient Noise[J]. Bull. Seism. Soc. Am., 101(2):544-557, doi:10.1785/0120090213. |
| [76] | Shan N L, Liu Z X. 2012. Application of τ-p Transformation to High and Order Mode in Surface Wave Separetion[J]. Journal of Guilin University of Technology (in Chinese), 33(3):413-419. |
| [77] | Socco L V, Foti S, Boiero D. 2010. Surface-wave analysis for building near-surface velocity models-Established approaches and new perspectives[J]. Geophysics, 75(5):75A83-75A102. |
| [78] | Solano C A P, Donno D, Strobbia C, et al. 2014. Imaging the shallow subsurface with surface waves:dispersion curve analysis versus full waveform inversion[C].//EGU Geophysical Research Abstracts 16:EGU2014-12088-1, Vienna, Austria. |
| [79] | Sun Y J, Xu P F, Ling S Q, et al. 2009. Microtremor survey method and its progress[J]. Progress in Geophysics (in Chinese), 24(1):326-334. |
| [80] | Tada T, Cho I, Shinozaki Y. 2009. New circular-array microtremor techniques to infer love-wave phase velocities[J]. Bull. Seism. Soc. Am., 99(5):2912-2926, doi:10.1785/0120090014. |
| [81] | Takagi R, Nakahara H, Kono T, et al. 2014. Separating body and Rayleigh waves with cross terms of the cross-correlation tensor of ambient noise[J]. J. Geophys. Res., 119(3):2005-2018, doi:10.1002/2013JB010824. |
| [82] | Tarantola A, Valette B. 1982. Generalized nonlinear inverse problems solved using the least squares criterion[J]. Reviews of Geophysics, 20(2):219-232. |
| [83] | Tsai V C, Moschetti M P. 2010. An explicit relationship between time-domain noise correlation and spatial autocorrelation (SPAC) results[J]. Geophys. J. Int., 182(1):454-460. |
| [84] | Tsai V C. 2011. Understanding the amplitudes of noise correlation measurements[J]. J. Geophys. Res., 116(B9):B09311, doi:10.1029/2011JB008483. |
| [85] | Tsuji T, Johansen T A, Ruud R O, et al. 2012. Surface-wave analysis for identifying unfrozen zones in subglacial sediments[J]. Geophysics, 77(3):EN17-EN27. |
| [86] | van Wijk K, Komatitsch D, Scales J A, et al. 2004. Analysis of strong scattering at the micro-scale[J]. J. Acoust. Soc. Am., 115(3):1006-1011. |
| [87] | van Wijk K, Mikesell T D, Schulte-Pelkum V, et al. 2011. Estimating the Rayleigh-wave impulse response between seismic stations with the cross terms of the Green tensor[J]. Geophys. Res. Lett., 38(16):L18301, doi:10.1029/2011GL047442. |
| [88] | Wang J Y. 2002. Inverse Theory in Geophysics (Second Ed.) (in Chinese)[M]. Beijing:Higher Education Press. |
| [89] | Wang X L, Ma S L, Guo Z, et al. 2013. S-wave velocity of the crust in Three Gorges Reservoir and the adjacent region inverted from seismic ambient noise tomography[J]. Chinese J. Geophys. (in Chinese), 56(12):4113-4124, doi:10.6038/cjg20131216. |
| [90] | Wang Z D. 1986. The micromotional spatial autocorrelation method and its practical technique[J]. Geophysical & Geochemical Exploration (in Chinese), 10(2):123-133. |
| [91] | Wang Z D. 1998. Double source surface wave exploration conception[J]. Chinese Geology (in Chinese), (4):47-48. |
| [92] | Wapenaar K, Draganov D, Snieder R, et al. 2010a. Tutorial on seismic interferometry:Part 1-Basic principles and applications[J]. Geophysics, 75(5):75A195-75A209. |
| [93] | Wapenaar K. Slob E, Snieder R, et al. 2010b. Tutorial on seismic interferometry:Part 2-Underlying theory and new advances[J]. Geophysics, 75(5):75A211-75A227. |
| [94] | Weaver R L. 2011. On the amplitudes of correlations and the inference of attenuations, specific intensities and site factors from ambient noise[J]. Comptes Rendus Geoscience, 343(8-9):615-622. |
| [95] | Weaver R L, Lobkis O I. 2001. On the emergence of the Green's function in the correlations of a diffuse field[J]. J. Acoust. Soc. Am.109(5):2410. |
| [96] | Weaver R L, Lobkis O. 2002. On the emergence of the Green's function in the correlations of a diffuse field:pulse-echo using thermal phonons[J]. Ultrasonics, 40(1-8):435-439. |
| [97] | Wen C Z. 2010. Study on the feasibility of the SPAC method using microseism in the exploration of underground structure (in Chinese)[Ph. D. thesis]. Changchun:Jilin University. |
| [98] | Woodhouse J H. 1974. Surface waves in a laterally varying layered structure[J]. Geophys. J. Int., 37(3):461-490. |
| [99] | Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 64(3):691-700. |
| [100] | Xia J H, Miller R D, Park C B, et al. 2002. Determining Q of near-surface materials from Rayleigh waves[J]. J. Appl. Geophys., 51(2-4):121-129. |
| [101] | Xia J H, Cakir R, Miller R D, et al. 2009. Estimation of near-surface shear-wave velocity by inversion of Love waves[C].//79th Annual International Meeting, SEG, Expanded Abstracts, 1390-1394. |
| [102] | Xia J H, Xu Y X, Luo Y H, et al. 2012. Advantages of using multichannel analysis of Love waves (MALM) to estimate near-surface shear-wave velocity[J]. Survey in Geophysics, 33(5):841-860. |
| [103] | Xia J H, Yin X F, Xu Y X. 2013. Feasibility of determining Q of near-surface materials from Love waves[J]. Journal of Applied Geophysics, 95:47-52. |
| [104] | Xu P F, Li C J, Ling S Q, et al. 2009. Mapping collapsed columns in coal mines utilizing Microtremor Survey Methods[J]. Chinese J. Geophys. (in Chinese), 52(7):1923-1930, doi:10.3969/j.issn.0001-5733.2009.07.028. |
| [105] | Xu P F, Ling S Q, Li C J, et al. 2012. Mapping deeply-buried geothermal faults using microtremor array analysis[J]. Geophys. J. Int., 188(1):115-122. |
| [106] | Xu P F, Li S H, Ling S Q, et al. 2013. Application of SPAC method to estimate the crustal S-wave velocity structure[J]. Chinese J. Geophys. (in Chinese), 56(11):3846-3854, doi:10.6038/cjg20131126. |
| [107] | Xu P F, Li S H, Du J G, et al. 2013. Microtremor survey method:A new geophysical method for dividing strata and detecting the buried fault structures[J]. Acta Petrologica Sinica (in Chinese), 29(5):1841-1845. |
| [108] | Xu P F, Shi W, Ling S Q, et al. 2012. Mapping spherically weathered 'Boulders' suing 2D microtremor profiling method:a case study along subway line 7 in Shenzhen[J]. Chinese J. Geophys. (in Chinese), 55(6):2120-2128, doi:10.6038/j.issn.0001-5733.2012.06.034. |
| [109] | Xu Y H, Shen C, Xu Y X. 2013. Near-surface shear-wave velocities and quality factors derived from high-frequency surface waves[J]. The Leading Edge, 32:612-618, doi:10.1190/tle32060612.1. |
| [110] | Yang C L. 1989. The principle and application of Rayleigh wave exploration method[J]. Geophysical & Geochemical Exploration (in Chinese), 13(6):465-468. |
| [111] | Yang W. 2012. Application research of Rayleigh wave in the karst exploration (in Chinese)[Master thesis]. Changsha:Central South University. |
| [112] | Yang Y J, Ritzwoller M H, Levshin A L, et al. 2007. Ambient noise Rayleigh wave tomography across Europe[J]. Geophys. J. Int., 168(1):259-274. |
| [113] | Yao H J, van der Hilst R D, de Hoop M V. 2006. Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-I. Phase velocity maps[J]. Geophys. J. Int., 166(2):732-744, doi:10.1111/j.1365-246X.2006.03028.x. |
| [114] | Ye T L. 2004. The exploration technique for microtremor array and its application[J]. Earthquake Research in China (in Chinese), 20(1):47-52. |
| [115] | Yokoi T, Margaryan S. 2008. Consistency of the spatial autocorrelation method with seismic interferometry and its consequence[J]. Geophysical Prospecting, 56(3):435-451. |
| [116] | Zhang B X, Lu L Y, Bao G S. 2002. A study on zigzag dispersion curves in Rayleigh wave exploration[J]. Chinese J. Geophys. (in Chinese), 45(2):263-274, doi:10.3321/j.issn:0001-5733.2002.02.013. |
| [117] | Zhang S X, Chan L S. 2003. Possible effects of misidentified mode number on Rayleigh wave inversion[J]. Journal of Applied Geophysics, 53(1):17-29. |
| [118] | Zhang W, He Z Q, Hu G, et al. 2012. Detect the velocity structure of shallow crust with artificial and nature source Rayleigh wave technology[J]. Technology for Earthquake Disaster Prevention (in Chinese), 7(1):26-36. |
| [119] | Zhang W, He Z Q, Hu G, et al. 2013. Detection of the shallow velocity structure with surface wave prospection method[J]. Progress in Geophysics (in Chinese), 28(4):2199-2206, doi:10.6038/pg20130467. |
| [120] | Zheng Z J. 2012. Application of multi-channel transient rayleigh-wave method on dynamic consolidation foundation[J]. Journal of Yunnan University (in Chinese), 34(S2):291-295. |
| [121] | Zhou Y, Dahlen F, Nolet G. 2004. Three-dimensional sensitivity kernels for surface wave observables[J]. Geophys. J. Int., 158(1):142-168. |
| [122] | 陈云敏,吴世明. 1991.成层地基的Rayleigh波特征方程的解法[J].浙江大学学报(自然科学版), 25(1):40-52. |
| [123] | 凡友华,刘家琦,肖柏勋. 2002.计算瑞利波频散曲线的快速矢量传递算法[J].湖南大学学报(自然科学版), 29(5):25-30. |
| [124] | 房立华,吴建平,王未来,等. 2013.华北地区勒夫波噪声层析成像研究[J].地球物理学报, 56(7):2268-2279, doi:10.6038/cjg20130714. |
| [125] | 冯少孔. 2003.微动勘探技术及其在土木工程中的应用[J].岩石力学与工程学报, 22(6):1029-1036. |
| [126] | 高玲利,夏江海,潘雨迪. 2014.高分辨线性拉东变换进行模式分离提取面波格林函数[C].//2014年中国地球科学联合会学术年会.北京:中国地球物理学会, 1452. |
| [127] | 何正勤,丁志峰,贾辉等. 2007.用微动中的面波信息探测地壳浅部的速度结构[J].地球物理学报, 50(2):492-498, doi:10.3321/j.issn:0001-5733.2007.02.021. |
| [128] | 李成,姚华健,方洪健. 2014.基于背景噪声方法的合肥城市近地表速度结构研究[C].//2014年中国地球科学联合会学术年会——专题14:地下介质结构及其变化的地震面波、背景噪声及尾波研究论文集.北京:中国地球物理学会, 745. |
| [129] | 刘强. 2009.基于瑞雷波理论的公路无损检测方法研究[博士论文].西安:长安大学. |
| [130] | 刘雪峰,凡友华. 2011. Rayleigh波勘探中"之"字形频散曲线"起跳点"频率研究[J].地球物理学报, 54(8):2124-2135, doi:10.3969/j.issn.0001-5733.2011.08.020. |
| [131] | 刘影,张海江,姚华健. 2014.中国西南某页岩气开采区域近地表面波噪声成像研究[C].//中国地球科学联合会学术年会——专题20:岩石物理与非常规油气勘探开发论文集.北京:中国地球物理学会, 1315. |
| [132] | 刘云祯,王振东. 1996.瞬态面波法的数据采集处理系统及其应用实例[J].物探与化探, 20(1):28-34. |
| [133] | 鲁来玉. 2004.分层介质半空间瑞利波模式分析和介质参数反演[博士论文].北京:中国科学院声学研究所. |
| [134] | 鲁来玉,张碧星,汪承灏. 2006.基于瑞利波高阶模式反演的实验研究[J].地球物理学报, 49(4):1082-1091, doi:10.3321/j.issn:0001-5733.2006.04.021. |
| [135] | 鲁来玉,丁志峰,何正勤. 2011.浅层有限频率面波成像中的3D灵敏度核分析[J].地球物理学报, 54(1):55-66, doi:10.3969/j.issn.0001-5733.2011.01.007. |
| [136] | 罗松,罗银河. 2014. SPAC系数计算方法研究[C].//中国地球科学联合会学术年会——专题14:地下介质结构及其变化的地震面波、背景噪声及尾波研究论文集.北京:中国地球物理学会, 755. |
| [137] | 潘冬明. 2009.瑞雷面波频散分析与应用[博士论文].北京:中国矿业大学. |
| [138] | 潘雨迪,夏江海,高玲利. 2014.三维勒夫波多道分析方法[C].//中国地球科学联合会学术年会论文集——专题24:浅地表地球物理进展论文集.北京:中国地球物理学会, 1450. |
| [139] | 单娜琳,刘占兴. 2013.分离高阶模态面波的τ-p变换方法[J].桂林理工大学学报, 33(3):413-419. |
| [140] | 孙勇军,徐佩芬,凌甦群,等. 2009.微动勘查方法及其研究进展[J].地球物理学进展, 24(1):326-334. |
| [141] | 王家映. 2002.地球物理反演理论(第2版)[M].北京:高等教育出版社. |
| [142] | 王小龙,马胜利,郭志,等. 2013.利用地震背景噪声成像技术反演三峡库区及邻近地区地壳剪切波速度结构[J].地球物理学报, 56(12):4113-4124, doi:10.6038/cjg20131216. |
| [143] | 王振东. 1986.微动的空间自相关法及其实用技术[J].物探与化探, 10(2):123-133. |
| [144] | 王振东. 1998.双源面波勘探构想[J].中国地质, (4):47-48. |
| [145] | 文成哲. 2010.微震空间自相关法在地下空间探测中的可行性研究[博士论文].长春:吉林大学. |
| [146] | 徐佩芬,李传金,凌甦群,等. 2009.利用微动勘察方法探测煤矿陷落柱[J].地球物理学报, 52(7):1923-1930, doi:10.3969/j.issn.0001-5733.2009.07.028. |
| [147] | 徐佩芬,李世豪,杜建国,等. 2013a.微动探测:地层分层和隐伏断裂构造探测的新方法[J].岩石学报, 29(5):1841-1845. |
| [148] | 徐佩芬,李世豪,凌甦群,等. 2013b.利用SPAC法估算地壳S波速度结构[J].地球物理学报, 56(11):3846-3854, doi:10.6038/cjg20131126. |
| [149] | 徐佩芬,侍文,凌苏群,等. 2012.二维微动剖面探测"孤石":以深圳地铁7号线为例[J].地球物理学报, 55(6):2120-2128. |
| [150] | 杨成林. 1989.瑞雷波法勘探原理及其应用[J].物探与化探, 13(6):465-468. |
| [151] | 杨威. 2012.瑞雷波在岩溶勘查中的应用研究[硕士论文].长沙:中南大学. |
| [152] | 叶太兰. 2004.微动台阵探测技术及其应用研究[J].中国地震, 20(1):47-52. |
| [153] | 袁伟,周洪生,刘成东,等. 2013.短时傅立叶变换和广义S变换用于提取面波频散曲线效果对比研究[J].物探化探计算技术, 35(1):54-59. |
| [154] | 张碧星,鲁来玉,鲍光淑. 2002.瑞利波勘探中"之"字形频散曲线研究[J].地球物理学报, 45(2):263-274, doi:10.3321/j.issn:0001-5733.2002.02.013. |
| [155] | 张维,何正勤,胡刚,等. 2012.用人工源和天然源面波联合探测浅层速度结构[J].震灾防御技术, 7(1):26-36. |
| [156] | 张维,何正勤,胡刚,等. 2013.用面波联合勘探技术探测浅部速度结构[J].地球物理学进展, 28(4):2199-2206, doi:10.6038.pg20130467. |
| [157] | 郑柱坚. 2012.多道瞬态面波法在强夯地基处理工程的应用[J].云南大学学报(自然科学版), 34(S2):291-295. |
 2015, Vol. 30
2015, Vol. 30


