2. 中海油研究总院, 北京 100027
2. CNOOC Research Institute, Beijing 100027, China
Huang等(1998)提出一种适应于非线性非平稳信号的时频分析新方法—希尔伯特-黄变换(HHT),在信号处理研究中受到广泛关注,该方法的核心技术是经验模态分解(Empirical Mode Decomposition,EMD),EMD能将复杂信号分解为一系列被称为固有模态函数(Intrinsic Mode Function,IMF)的子信号,每个IMF有着不同的频率分量,可对输入信号进行不同尺度的描述,经希尔伯特变换后可获得有明显物理意义的瞬时属性,指示不同的地质与地层信息.同时EMD具有正交性、完备性和自适应性等特点,对非平稳信号分析有很大的优势.然而,当信号中某个频段的分量不连续或存在间断信号、噪声干扰时,EMD会出现模态混叠现象,破坏每个IMF所蕴含的物理意义,降低分解的准确性,这使得基于EMD的地震数据处理方法很难得到推广.
为克服EMD的模态混叠效应,Wu和Huang(2009)提出了一种噪声辅助信号分析方法—总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD),利用高斯白噪声频谱均匀分布的统计特性,向原始信号中加入不同的白噪声,使得信号在不同尺度上具有连续性,但是该方法不具有完备性,虽提高加总平均次数可以降低重构误差,但这是以增加计算成本为代价的.为解决EEMD存在的问题,Yeh等(2010)提出了一种完备总体经验模态分解(Complete Ensemble Empirical Mode Decomposition,CEEMD),该方法以正负成对的形式向原始信号中加入辅助白噪声,这样能够很好地消除重构信号中的残余辅助噪声,而且噪声实现次数可以较低,提高了计算效率.Torres等(2011)也对EEMD方法做了进一步改进,提出了自适应噪声的CEEMD,它是在分解的每一阶段添加一个特定白噪声,并计算一个唯一残差以得到每个IMF,该方法能够提供原始信号的精确重构,更好的模态频谱分离以及更低的计算成本.
高频噪声压制是高分辨率地震数据处理中提高信噪比的关键性问题.不少学者(杜修力等,2007;汤井田等,2008;史恒等,2011;李雪英等,2011,2012;Chen et al.,2012;李月等,2013;贾瑞生等,2015)利用EMD、EEMD或者与其他方法(如小波阈值去噪、独立分量分析)相结合进行噪声的去除,取得了一定的效果.然而,在EMD、EEMD、CEEMD三种分解方法中,CEEMD不仅受模态混叠影响最小,计算成本较低,而且能够完美重构原信号,因此其最具优越性.考虑到小波去噪方法中小波基和阈值函数的参数选择不确定,选取最优参数困难易造成有效信号损失,以及CEEMD直接舍弃高频IMF分量去噪易导致随机噪声压制不完全或高频有效信号损失的问题,本文尝试将Torres等提出的CEEMD与小波变换技术相结合,提出一种基于CEEMD的小波阈值去噪方法,通过互补方式解决上述去噪中的这些问题.经模型和实际地震资料处理,证明了该方法能够更好地压制随机噪声,并且减少有效信号的损失.
1 基本原理1.1 CEEMD方法与EEMD一样,CEEMD也是一种噪声辅助分析方法 .首先定义算子Ej(·),当给定一个信号,通过EMD求得第j个模态;ωi(n)表示单位方差的零均值高斯白噪声N(0,1);i=1,...,I;εk系数允许在每个阶段选择信噪比.设x(t)为目标信号,则CEEMD的步骤如下描述(刘爽,2014):
1)IMF1(t)的求取方法与EEMD方法相同,即使用不同的噪声实现通过EMD重复分解过程I次,计算加总平均值并将其定义为目标信号x(t)的IMF1(t),公式为

2)对k=1,计算一阶残差r1(t),公式为

3)EMD实现r1(t)+ε1E1(ωi(t)),直到满足第一个IMF(t)条件,并定义总体平均值为IMF2(t),公式为

4)对k=2,...,K,计算k阶残差rk(t),公式为

5)提取rk(t)+εkEk(ωi(t))的IMF1(t)分量,计算它们的总体平均值得目标信号的IMF(k+1)(t),公式为
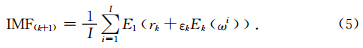
6)重复步骤(4)(5),直到残差不能再被分解为止,则得到最终残差R(t)为


通过合成信号对EMD、EEMD及CEEMD进行算法比较,以证明CEEMD的优势.图 1是各组分信号及其合成信号,自上而下分别是100 Hz的Morlet子波(0.2 s处)、20 Hz(0~1 s)和10 Hz(1~2 s)余弦信号、50 Hz间歇性余弦信号、合成信号.图 2是采用EMD对图 1中合成信号进行分解的结果,由图可见,EMD分解的IMF存在着明显的模态混叠问题:IMF1没有单独提取出高频分量,掺杂了低频的分量.同样的,在其他IMF中也混合了其他分量.这使得信号分析变得复杂化,很难识别出各IMF中的确切分量.
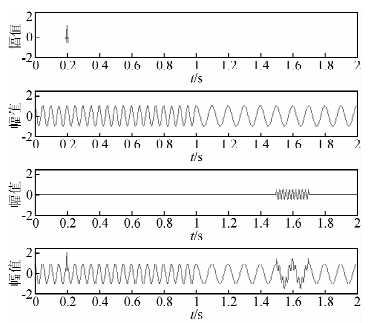 | 图 1 合成信号及各组分信号 Fig. 1 Synthetic signal and each component of the signal |
 | 图 2 经验模态分解结果 Fig. 2 The results of EMD |
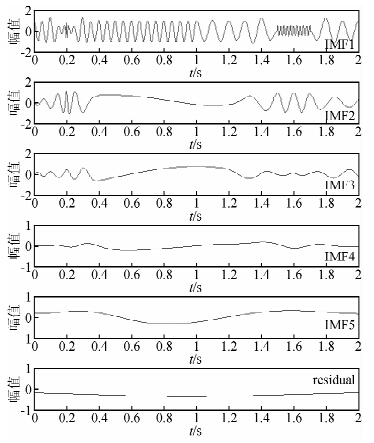
图 3是EEMD的分解结果(噪声实现次数或加总平均次数为500),图中只列出了前6个IMF,从图中可以看出,EEMD已经在一定程度上改善了模态混叠现象,10 Hz、20 Hz的余弦信号分别在IMF3和IMF2中完全被提取出来,100 Hz的高频Morlet子波在IMF1中被完全地恢复.然而,IMF1和IMF2也包含了50 Hz的余弦分量,这说明模态混叠现象仍有存在,但与EMD结果相比,有了较为明显的降低水平.
 | 图 3 总体经验模态分解结果(前6个分量) Fig. 3 The results of EEMD (the first six IMFs) |
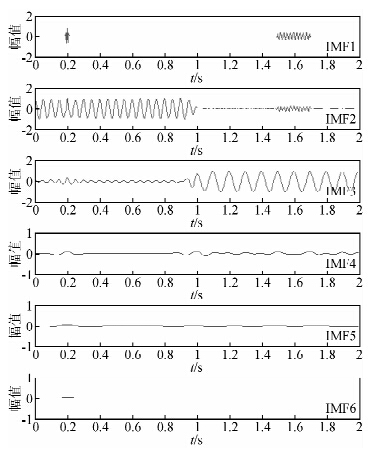
图 4是CEEMD的分解结果(加总平均次数为100),图中也只列出了前6个IMF,能量主要分布在前4个IMF分量,IMF1完全地恢复了100 Hz的高频子波分量,IMF2、IMF3、IMF4分别将50 Hz、20 Hz、10 Hz的简谐波分量完全地提取出来.由此可见,三种方法中CEEMD结果受模态混叠影响最小,而且相较于EEMD已大大降低了计算成本.
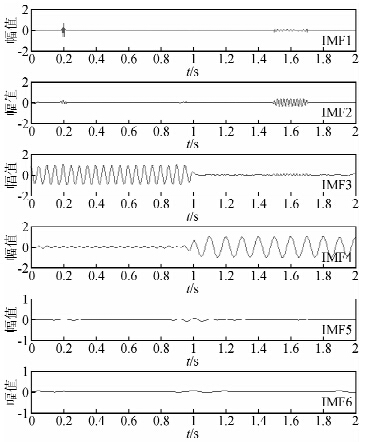 | 图 4 完备总体经验模态分解结果(前6个分量) Fig. 4 The results of CEEMD (the first six IMFs) |
图 5a、图 5b、图 5c分别是EMD、EEMD、CEEMD的重构误差.通过对比可见,EEMD没有完美重构原始信号,总能量重构误差不可忽视; 而CEEMD完美保持了EMD的完备性,其误差数量级为10-15,接近机械精度,可忽略不计.
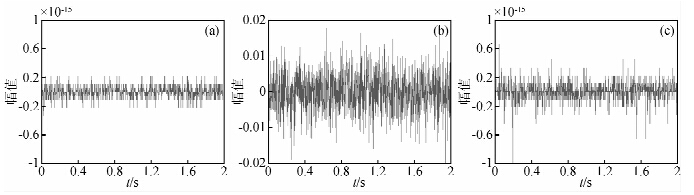 |
图 5 EMD、EEMD、CEEMD的重构误差对比 (a)EMD的重构误差;(b)EEMD的重构误差;(c)CEEMD的重构误差. Fig. 5 The comparison of the reconstruction errors of EMD、EEMD and CEEMD (a) EMD reconstruction error; (b) EEMD reconstruction error; (c) CEEMD reconstruction error. |
CEEMD也保持了EMD的二进滤波特性,分解出的IMF分量满足从高频到低频的系列分布,前几个IMF分量是高频成分,一般随机噪声会分布其中.常规的CEEMD去噪一般是直接舍弃含噪的高频IMF分量,但这会造成高频有效信号损失或随机噪声去除不彻底的问题.故本文尝试将3种分解方法中最具优越性的CEEMD与小波阈值去噪方法相结合进行随机噪声的去除研究.
1.2 小波阈值去噪在地震数据去噪中,小波阈值去噪以其优秀的去噪效果和较高的计算效率,受到普遍青睐(To et al.,2009).小波阈值去噪方法的实现步骤为:①将原始信号变换到小波域,求取小波系数;②设置一个阈值,小于该阈值的小波系数被认为是由噪声产生的,并将其去掉;③利用处理后的小波系数进行小波重构就可得到去噪后的信号.阈值函数包括硬阈值函数和软阈值函数.硬阈值函数表达式为


 为处理后的小波系数;λ表示阈值.
为处理后的小波系数;λ表示阈值.
小波阈值去噪方法中,小波基和阈值的选取目前主要是通过经验,没有理论依据,而不适当的小波基和阈值直接影响降噪的质量(李振兴和徐洪洲,2009).硬阈值保留较大小波系数的值,能够保持信号有效部分的特征;而软阈值对其作了改变,不能完全保持原始信号的特征.
1.3 基于CEEMD的小波阈值去噪当含噪地震信号中包含较小幅度的有效信息时,直接进行小波阈值降噪会在压制大部分噪声的同时,也去除掉这些小幅度的有效信号,这是由小波阈值去噪的本身特性所决定的;而采用CEEMD直接舍弃高频IMF分量去噪又会造成高频噪声压制不完全或高频有效信号损失的问题.鉴于此,本文将CEEMD与小波阈值降噪方法相结合,通过互补的方式解决上述去噪中的这些问题.基于CEEMD的小波阈值去噪方法的实现步骤如下描述:
1)对原始信号进行小波阈值降噪处理,选定一个合适的阈值.
2)对原始信号进行CEEMD分解,分解出的IMF分量满足从高频到低频的系列分布.前几个分量是高频成分,随机噪声往往分布在这些高频IMF分量中.
3)采用自相关法分析各个分量,确定出前几个分量中需要进行小波阈值降噪的含噪IMF分量.
4)对确定出的含噪的高频IMF分量进行小波阈值降噪处理,获得降噪后的数据与不含噪声的低频IMF分量一起重构原信号,得去噪后的信号.由于小波阈值去噪仅仅作用于含噪的高频IMF分量,而不是整个信号,在很大程度上克服了小波阈值降噪的缺陷.
2 模型试算设计了一个模拟地震数据进行方法测试(图 6a),它为一模拟地震信号的重复显示,共10道,每道加入标准差为原始信号标准差15%的各不相同的高斯白噪声(如图 6b).分别采用CEEMD直接去噪、小波阈值去噪和本文方法对图 6b所示的含噪模拟数据进行处理.
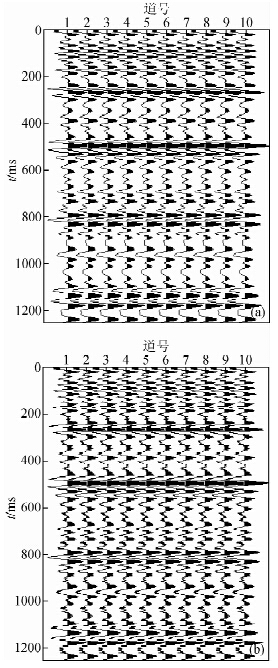 |
图 6 模拟数据及加入随机噪声后的数据 (a)模拟数据;(b)含随机噪声的数据. Fig. 6 Simulated data and the data with the random noise (a) Simulated data; (b) Noisy data. |
随机噪声主要分布在CEEMD分解出的前几个高频模态分量中,但至于哪几个高频IMF分量,很难直观确定.考虑到随机噪声的自相关是一个尖脉冲,而有效信号的自相关主瓣具有子波形状且有一定的宽度,当IMF分量含噪声较多时,主瓣会比较窄,为此本文采用自相关法分析各个分量,依据这个经验判定选取需要进行小波阈值降噪处理的IMF分量,一般选择自相关曲线中主瓣宽度小于有效信号主瓣宽度的IMF.图 7a、图 7b分别为随机噪声和含噪信号的的自相关曲线,图 7c至图 7g分别为CEEMD分解出的前5个IMF分量的自相关曲线.从图 7b中可识别出有效信号的主瓣宽度约为32 ms,由图 7c至图 7g可见只有IMF1和IMF2的主瓣宽度小于32 ms,说明含随机噪声比较多,故本文方法只须选取IMF1和IMF2作为小波阈值去噪的对象.
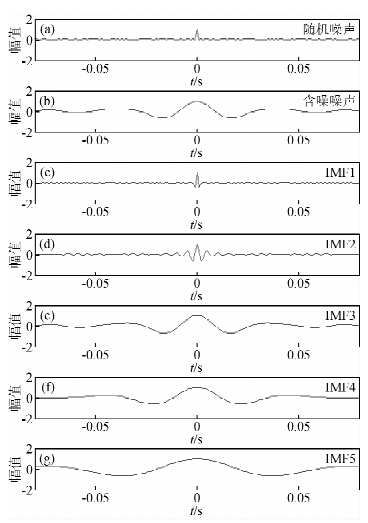 |
图 7 随机噪声、含噪信号及CEEMD分解出的前5个IMFs的自相关曲线 (a)随机噪声; (b)含噪信号; (c)IMF1; (d) IMF2; (e) IMF3; (f) IMF4; (g) IMF5. Fig. 7 The comparison of autocorrelation curves (a) Random noise; (b) Noisy signal; (c) IMF1; (d) IMF2; (e) IMF3; (f) IMF4; (g) IMF5. |
本文采用信噪比SNR衡量各种方法的去噪效果,值越高,表明信号中残留的噪声越小,计算公式为

 ;
; ;x(i)为无噪的原始模拟数据;
;x(i)为无噪的原始模拟数据; 为降噪后的数据.图 7b含噪数据的信噪比SNR≈15.03.
为降噪后的数据.图 7b含噪数据的信噪比SNR≈15.03.
图 8a为CEEMD分解后舍弃IMF1分量后重构的结果;图 8b为CEEMD分解后舍弃IMF1和IMF2分量后重构的结果;图 8c为小波阈值降噪的结果;图 8d为本文方法的去噪结果.各种方法去噪后数据按式(10)计算的信噪比SNR分别约为:18.90,20.81,19.96,21.52.
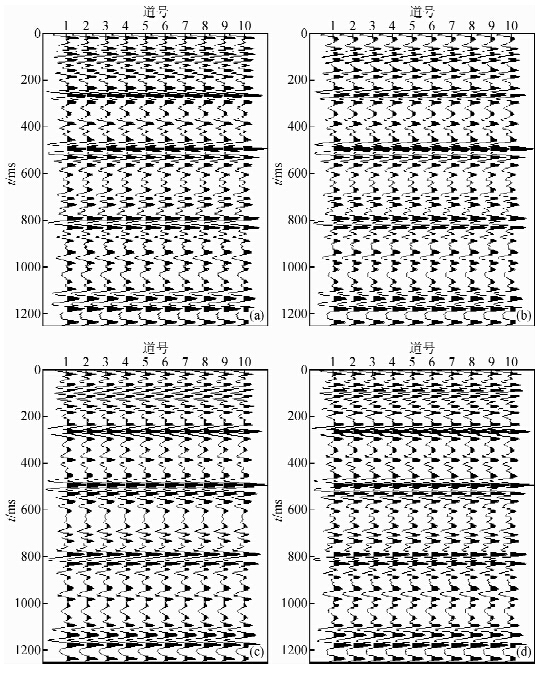 |
图 8 各种去噪方法对图7b含噪数据的去噪效果对比 (a)CEEMD直接舍弃IMF1后重构结果;(b)CEEMD直接舍弃IMF1和IMF2后重构结果; (c)小波阈值去噪结果;(d)本文方法去噪结果. Fig. 8 The comparison of several methods’ denoising effects on noisy seismic data in Fig.7b (a) CEEMD reconstruction result after removing IMF1; (b) CEEMD reconstruction result after removing IMF1 and IMF2; (c) The result of wavelet threshold denoising; (d) The denoised result of our proposed denoising method. |
对比分析各种方法去噪后剖面的信噪比和分辨率,可见:
(1)CEEMD直接舍弃IMF1分量去噪时,尽管浅层信号分辨率较高,但随机噪声压制不完全,致使信噪比较低(图 8a).
(2)CEEMD直接舍弃IMF1和IMF2分量去噪时,虽然完全压制了随机噪声,提高了信噪比,但同时也损失了高频有效成分,导致分辨率较低(如图 8b中0~200 ms范围内).
(3)小波阈值去噪方法压制噪声的效果较好,但由于该方法的本身特性,使得弱能量的有效信息损失较严重(如图 8c中600~700 ms及850~1100 ms范围内).
(4)本文方法去噪后剖面不但信噪比较高,而且浅层分辨率也没有太大的损失(图 8d).综合分析对比可见,CEEMD直接舍弃高频IMF分量去噪方法容易导致随机噪声残留较多或高频有效信息损失;小波阈值去噪存在着小幅度有效信号损失的问题;而本文方法在有效压制随机噪声的同时,能够有效地保持有效信号,是一种相对保幅的去噪方法.
3 实际资料处理选取某实际地震资料的叠后剖面(图 9a)进行不同去噪方法的应用效果对比.图 9b、图 9c分别为CEEMD分解的IMF1分量剖面和IMF2分量剖面;图 9d为CEEMD直接舍弃IMF1分量去噪的结果;图 9e为小波阈值去噪结果;图 9f为本文方法去噪后的结果.图 9a的估计信噪比SNR为1.15,抽取几道含随机噪声的数据进行CEEMD分解及自相关分析,发现分解后的信号随机噪声主要分布在IMF1剖面上(图 9b),IMF2剖面(图 9c)除了含高频有效信息外,也包含较多的噪声,故采用CEEMD直接去噪时只能舍弃IMF1分量(结果见图 9d,SNR≈3.26),因为若同时也舍弃IMF2分量,则会损失有效高频信号;而采用本文方法去噪时需要对IMF1和IMF2分量进行小波阈值降噪处理,然后与不含噪声的其他IMF分量一起重构原信号(如图 9f所示,SNR≈6.04);小波阈值去噪处理的结果如图 9e所示,SNR≈4.18.通过对比分析各种方法去噪后剖面及信噪比估算结果可见,CEEMD直接舍弃高频IMF1分量去噪结果中,随机噪声压制不完全,残留较多(图 9d);小波阈值去噪压制噪声效果虽然较好,但损失了部分弱幅度有效信号且仍存有少许随机噪声(图 9e);而本文方法去噪结果信噪比最高,剖面上噪声残留较少,而且有效信息也最丰富,同相轴相对更加清晰,去噪效果相对比较理想(图 9f).
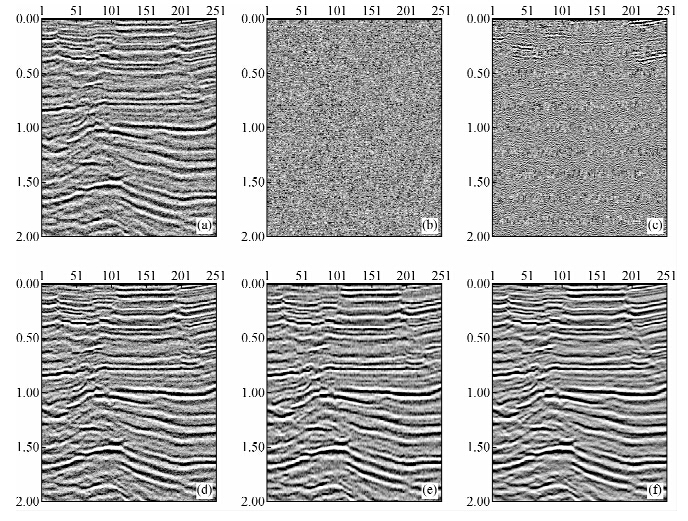 |
图 9 实际资料叠后剖面、CEEMD分解的IMF1和IMF2剖面以及各种方法去噪后的剖面对比 (a)实际叠后地震剖面;(b)CEEMD分解的IMF1剖面;(c)CEEMD分解的IMF2剖面; (d)CEEMD舍弃IMF1直接去噪的结果;(e)小波阈值去噪的结果;(f)本文方法去噪的结果. Fig. 9 The post-stack section of real data, IMF1 and IMF2 profiles of CEEMD and the denoised sections of several methods (a) Real post-stack seismic profile; (b) IMF1 profile of CEEMD; (c) IMF2 profile of CEEMD; (d) The denoised section of CEEMD after abandoning IMF1; (e) The section after wavelet threshold denoising; (f) The denoised profile of this paper’ method. |
图 10显示了实际地震资料去噪前剖面的振幅谱(图 10a)和不同方法去噪后剖面的振幅谱,通过对比可以看出,CEEMD直接舍弃IMF1分量去噪后依然含有大量的高频噪声成分,去噪不彻底(图 10b);小波阈值去噪结果中一些弱幅度有效信号被压制,且有效频带较窄(图 10c);而本文方法能够去除绝大部分高频噪声,同时也保持了较宽的频带(图 10d).
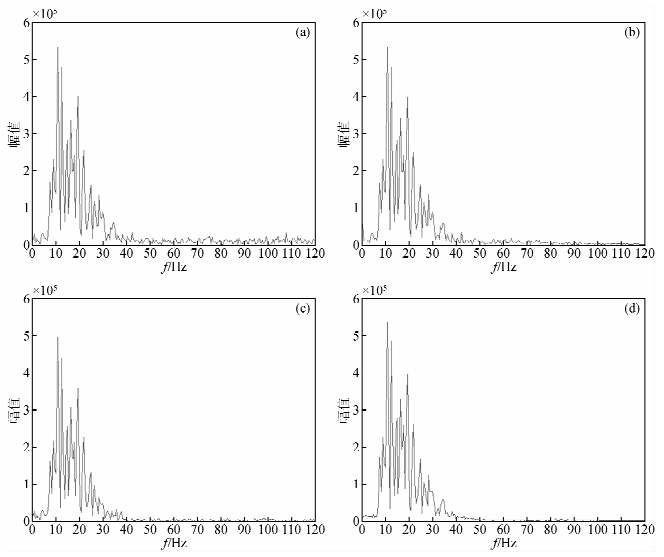 |
图 10 实际地震资料去噪前、后的剖面振幅谱对比 (a)实际地震资料去噪前剖面的振幅谱;(b)CEEMD直接舍弃IMF1分量后剖面的振幅谱; (c)小波阈值方法去噪后剖面的振幅谱;(d)本文方法去噪后剖面的振幅谱. Fig. 10 The contrast of amplitude spectra of real seismic profile before and after denoising (a) The amplitude spectrum of profile before denoising; (b) The amplitude spectrum after CEEMD denoising directly removing IMF1; (c) The amplitude spectrum after wavelet threshold denoising; (d) The amplitude spectrum after applying our denoising method. |
4.1 去噪是地震数据处理中必不可少的步骤.考虑到地震信号的非平稳性和去噪方法对非平稳信号的适应性,针对CEEMD直接舍弃高频IMF分量去噪方法以及小波阈值去噪方法存在的不足,本文将CEEMD分解与小波阈值去噪相结合,提出了基于CEEMD的小波阈值去噪方法.该方法首先利用自相关曲线判别出含噪较多的高频IMF分量,然后对CEEMD直接去噪要舍弃的这些含噪高频分量进行小波阈值降噪,以保留这些分量中的高频有效信息,最后与不含噪声的低频IMF分量一起重构原信号.该方法达到既能有效压制高频噪声,又能保持原信号中的高频有效成分和弱信号信息不受损失目的.理论和实际资料试算表明,基于CEEMD的小波阈值去噪方法的去噪效果优于CEEMD直接舍弃高频分量的去噪方法和小波阈值去噪方法,去噪效果对比证明了本文方法的有效性和优越性.
4.2 还有一些亟待解决的问题:如针对不同地质条件下的不同噪声类型,如何选择合适的IMF分量进行重构滤波;去噪时如何针对不同数据更加合理地选取阈值已达到更好的去噪效果,仍是今后需要注意和改进的地方.
4.3 由于地震数据是多维信号,若按单道进行处理,往往会忽略剖面横向上的结构特征,将一维CEEMD算法延拓到二维,然后把二维CEEMD与小波阈值去噪方法相结合,并应用于地震数据噪声压制中,去噪后的剖面横向连续性可能会更好,能量分布更均匀,整体效果比较可观,这也有可能成为今后地球物理领域比较热门的一个研究方向.
致 谢 感谢审稿专家提出宝贵的修改意见和编辑部老师的帮助.
| [1] | Chen W, Wang S X, Chuai X Y, et al. 2012. Random noise reduction based on ensemble empirical mode decomposition and wavelet threshold filtering[C].//82th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 3887-3890. |
| [2] | Du X L, He L Z, Hou W. 2007. A study of wavelet threshold denoising based on empirical mode decomposition(EMD)[J]. Journal of Beijing University of Technology (in Chinese), 33(3):265-272. |
| [3] | Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. R. Soc. Lond.A, 454:903-995. |
| [4] | Jia R S, Zhao T B, Sun H M, et al. 2015. Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis[J]. Chinese J. Geophys. (in Chinese), 58(3):1013-1023, doi:10.6038/cjg20150326. |
| [5] | Li X Y, Kong D, Hou X H, et al. 2011. Comparison of generalized S transform and empirical mode decomposition in high frequency seismic noise suppression[J]. Progress in Geophysics (in Chinese), 26(6):2039-2045, doi:10.3969/j.issn.1004-2903.2011.06.019. |
| [6] | Li X Y, Kong X Q, Hou X H. 2012. High frequency noise suppression by empirical mode decomposition in the frequency-spatial domain based on high-pass filter[J]. Progress in Geophysics (in Chinese), 27(3):1070-1077, doi:10.6038/j.issn.1004-2903.2012.03.030. |
| [7] | Li Y, Peng J L, Ma H T, et al. 2013. Study of the influence of transition IMF on EMD do-noising and the improved algorithm[J]. Chinese J. Geophys. (in Chinese), 56(2):626-634, doi:10.6038/cjg20130226. |
| [8] | Li Z X, Xu H Z. 2009. A wavelet threshold de-noising algorithm based on empirical mode decomposition[J]. Computer Simulation (in Chinese), 26(9):325-328. |
| [9] | Liu S. 2014. A study and application of seismic data processing based on CEEMD (in Chinese)[Master thesis]. Jilin:Jilin University. |
| [10] | Shi H, Li G L, Wang W, et al. 2011. Random noise attenuation based on ensemble empirical mode decomposition[J]. Progress in Geophysics (in Chinese), 26(1):71-78, doi:10.3969/j.issn.1004-2903.2011.01.007. |
| [11] | Tang J T, Hua X R, Cao Z M, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J. Geophys.(in Chinese), 51(2):603-610. |
| [12] | To A C, Moore J R, Glaser S D. 2009. Wavelet denoising techniques with applications to experimental geophysical data[J]. Signal Processing, 89(2):144-160. |
| [13] | Torres M E, Colominas M A, Schlotthauer G, et al. 2011. A complete ensemble empirical mode decomposition with adaptive noise[C].// 2011 International Conference on Acoustics, Speech and Signal Processing (ICASSP).Prague:IEEE, 4144-4147. |
| [14] | Wu Z H, Huang N E. 2009. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 1(1):1-41. |
| [15] | Yeh J R, Shieh J S, Huang N E. 2010. Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2(2):135-156. |
| [16] | 杜修力,何立志,候伟. 2007.基于经验模态分解(EMD)的小波阈值除噪方法[J].北京工业大学学报, 33(3):265-272. |
| [17] | 贾瑞生,赵同彬,孙红梅,等. 2015.基于经验模态分解及独立成分分析的微震信号降噪方法[J].地球物理学报, 58(3):1013-1023, doi:10.6038/cjg20150326. |
| [18] | 李雪英,孔丹,侯相辉,等. 2011.基于广义S变换、经验模态分解叠前去噪方法的比较[J].地球物理学进展, 26(6):2039-2045, doi:10.3969/j.issn.1004-2903.2011.06.019. |
| [19] | 李雪英,孔祥琦,侯相辉. 2012.基于高通滤波的频率-空间域经验模态分解压制高频噪声[J].地球物理学进展, 27(3):1070-1077, doi:10.6038/j.issn.1004-2903.2012.03.030. |
| [20] | 李月,彭蛟龙,马海涛,等. 2013.过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法[J].地球物理学报, 56(2):626-634, doi:10.6038/cjg20130226. |
| [21] | 李振兴,徐洪洲. 2009.基于经验模态分解的小波阈值降噪方法研究[J].计算机仿真, 26(9):325-328. |
| [22] | 刘爽. 2014.基于CEEMD的地震数据处理研究与应用[D].长春:吉林大学. |
| [23] | 史恒,李桂林,王伟,等. 2011.基于总体经验模式分解的地震信号随机噪声消除[J].地球物理学进展, 26(1):71-78, doi:10.3969/j.issn.1004-2903.2011.01.007. |
| [24] | 汤井田,化希瑞,曹哲民,等. 2008. Hilbert-Huang变换与大地电磁噪声压制[J].地球物理学报, 51(2):603-610. |
 2015, Vol. 30
2015, Vol. 30

