2. 中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室, 武汉 430074;
3. 中国地震局第一监测中心, 天津 300180
2. Hubei Subsurface Multi-scale Imaging Key Laboratory China University of Goesciences, Wuhan 430074, China;
3. First Crust Deformation Monitoring and Application Center, CEA, Tianjin 300180, China
在实际勘探工作中,我们测量得到的位场数据通常是地下不同规模、不同形态和不同埋深的不均匀地质体的综合响应,通过测量获取的位场资料存在着混叠效应:它既包括区域异常,又存在局部异常,这些观测数据具有多源性、非线性、非稳态性特点.在位场资料处理中,研究者根据研究目标的不同,力求从观测异常中提取研究对象产生的异常,即进行异常的分离.因此,如何从这些多源混合性、非线性和非平稳性位场数据中提取有用的异常信息是位场数据处理中的关键环节.
傅里叶变换、小波变换等分析方法通常被用来处理复杂信号,且取得了一定的效果,但具有一定的局限性.傅里叶变换对于线性、平稳信号而言,是一个强有力的工具,而对于非线性、非平稳信号,则具有一定局限性;而小波变换本质上是一种窗口可调的傅里叶变换,并没有摆脱傅里叶变换的束缚,且不具有分解的自适应性,分解效果取决于小波基函数的选取,在信号的分析处理中仍有一定的局限性(Huang et al.,1998).
为了解决这一问题,Huang等(1998,1999)提出一种处理非线性、非平稳信号的分析方法——经验模态分解(Empirical Mode Decomposition,EMD),它将复杂信号分解成若干个从高频到低频排列的固有模态函数(Intrinsic Mode Function,IMF)和一个剩余分量(Residue,Res).该方法不仅具有多分辨率的特性,而且具有自适应性,其对非线性、非平稳信号处理的优势在语音分析、机械故障诊断、信号去噪和地震信号分析等众多领域得到体现.Nunes等(2003a,b,2005)在一维EMD的基础上,提出了一种用于提取图像多尺度特征或空间频率的算法——二维经验模态分解(Bidimensional Empirical Mode Decomposition,BEMD).BEMD方法提出以后,国内外学者尝试将该方法运用到图像处理领域,并在纹理分割、图像融合、边缘检测和数字图像水印分析等方面取得很好的成果.
在地球物理勘探中,所采集到的位场数据是地下不同场源在观测平面的综合反映,具有多源性,非平稳特征,基于此特点,国内外学者将EMD和BEMD方法应用到位场数据处理和异常的提取中,并取得了很好的效果(Hassan and Pierce,2005; 曾琴琴和刘天佑,2009,2010,2011; Cooper et al.,2010; 黄静宁等,2010; 周文纳等,2010; 陈建国等,2011; 何丽娟等,2011; 王林松等,2011; 陈永清和赵彬彬,2011; 陈永清等,2012; Hou et al.,2012; 菅贞贞等,2012; Pei et al.,2012).本文首先介绍了BEMD的基本原理,探讨了其在分解过程中的关键技术,然后将BEMD方法应用到位场数据去噪和分离中,实现了位场数据的多尺度分解,并利用径向对数功率谱来估计了各级模态函数所反映的场源似深度,最后通过对各级模态函数重构实现分场,与传统常规分场方法进行比较分析,证明了BEMD是一种有效的位场分离方法.
1 二维经验模态分解BEMD方法能够有效地将信号的各种频率成分以固有模态函数的形式从二维信号中分离出来,这个分解过程可以解释为尺度滤波过程,每个模态函数分量都反映了信号的尺度特征,代表着信号的非线性、非平稳信号的内在模态特征.该方法是基于信号局部特征实现的,因此具有较强自适应以及对数据类型没有限制的特点.BEMD方法处理非线性、非平稳信号是有效的,且其保持了小波多分辨率特性,能够实现信号多尺度分解.
1.1 方法原理Nunes等人(2003a)成功地将EMD方法推广到二维,开辟了EMD新的应用领域.BEMD的原理与EMD的原理类似,它将一维EMD中对线的筛分拓展为对面的筛分,最终得到若干二维固有模态函数(Bidimensional Intrinsic Mode Function,BIMF)和一个剩余分量(Residue,Res).设存在一个二维信号
sori(x,y)(x=1,2,…,m;y=1,2,…,n)(其中m,n为正整数),那么,二维信号的分解具体步骤如下:
(1)初始化:Res0=sori(x,y).
(2)提取第j级二维固有模态函数BIMF,其中j为分解得到的固有模态函数个数,初始值j=1,步骤为
① fi-1(x,y)=Resj-1(x,y),初始值i=1;
② 查找fi-1(x,y)的局部极大值点和极小值点;
③ 利用局部极大值点和极小值点分别进行插值计算,得到上、下包络面Eup,i-1(x,y)和Elow,i-1(x,y);
④ 计算上、下包络面的均值为
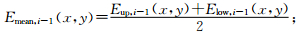
⑤ 计算fi-1(x,y)曲面减去上、下包络曲面的均值得到一个新的曲面,记作fi(x,y)为
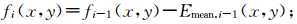
⑥ 计算终止条件——标准偏差(St and ard Deviation,SD),若SD<ε(ε为阈值,可预先设定一个较小的数),则第j级固有模态函数BIMFj(x,y)=fi(x,y),否则i=i+1,重复步骤②~⑥.
(3)计算剩余值:
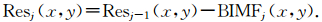
(4)j=j+1,重复步骤(2)、(3)直到Resj(x,y)极大值点和极小值点个数小于K(K为较小的整数)或极大值和极小值的数值近似相等.
最后,二维信号sori(x,y)(x=1,2,…,m;y=1,2,…,n)通过BEMD方法分解得到K个二维固有模态函数BIMF和一个剩余分量Res,即:
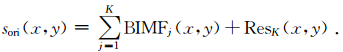
BEMD方法在进行信号分解的过程中受到许多因素的影响,其中影响分解过程的关键技术包括:
(1)局部极大值点和极小值点提取方式,包括邻近窗口法与数学形态学重建法等.
(2)包络曲面的插值方法,包括基于Delaunay三角剖分和三次样条插值、基于径向基函数插值等.
(3)筛分过程中的停止准则,Nunes等(2005)利用标准偏差SD作为EMD筛分终止判断条件,将其拓展应用到二维,当SD小与某一阈值ε则停止筛分,为获得丰富的细节信息,ε可取较小的值,反之,ε可取相对较大的值,当然,可在传统筛分终止准则的基础上,可提出新的筛分准则以满足实际应用需要.
(4)BEMD终止准则,分解终止准则决定何时终止整个分解过程,分解终止准则包括:① 极大值和极小值点个数小于M(M为较小的正整数);② 极小值点和极大值点数值都近似相等;③ 筛分得到的第j级BIMF小于期望值;④ 剩余分量Res为线性变化;⑤ 人为设定固定的分解层数K.
然而,在利用曲面插值方法进行边界拟合的过程中,边界会出现发散和失真的情况,再经过插值过程的多次迭代会向内部发散污染整个数据,使分解结果面目全非,如何更好地处理边界效应是BEMD分解成败的关键因素.同时,当筛分条件和终止条件过于苛刻、数据量较大时,可能导致分解耗时过长,降低分解效率.
本文为了获得较为理想的分解结果,在进行筛分之前进行了扩边处理,采用了邻近窗口法来提取极值点、插值较为准确的径向基函数进行包络曲面的插值计算、标准偏差SD作为筛分终止条件、极大值和极小值点个数小M(M取3)作为分解终止条件.
2 实际应用2.1 位场数据去噪野外实测位场数据是地下地质异常体物性特征、分布特征和构造特征等多种地质信息的综合反映.通过对这些数据的处理,可以确定异常体的几何参数、物性参数、物性分界面的深度与起伏和密度分布.然而,在采集位场数据时,可能会受不同因素的干扰,包括测量仪器的精度、仪器受外界环境的干扰和操作人员的操作不当等,使得所测的数据带有干扰噪声.若利用带有噪声的数据直接用于数据处理,得到的结果可能不准确甚至严重偏离真实情况.从干扰背景中提取有用信息、提高位场实测资料的信噪比是位场数据处理的必要环节.因此,进行数据的预处理是非常有必要的,通过预处理可以有效地去除干扰噪声,提取有效的数据信息并进行后续的相关处理,得到的结果才能真实地反映异常体的地质信息.下面利用BEMD方法进行尺度滤波,该算法即为简单地去掉一个或多个BIMF分量之后,对其他的BIMF和剩余分量进行重组以实现滤波.
为了验证利用BEMD方法进行去噪的可行性,我们建立了一个水平长方体模型(模型参数见表 1),对正演得到的重力异常中添加2%的高斯白噪声,就得到了带有噪声的重力异常(如图 1a).由于添加噪声幅值较小,为了获得更多的细节信息,在筛分过程中可选择较小阈值,这里阈值取ε=10-7,对带有噪声的重力异常进行二维经验模态分解,得到三组重力异常数据,分别为第一级固有模态函数(BIMF1)、第二级固有模态函数(BIMF2)和剩余分量(Res),分别如图 1b~d所示.
|
|
表 1 水平长方体模型参数 Table 1 The parameters of horizontal rectangle model |
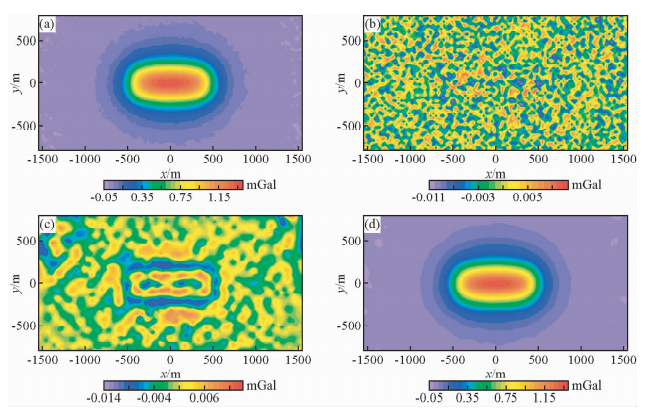 |
图 1 带噪声的重力异常及其BEMD分解结果 (a) 带噪声重力异常;(b) BIMF1;(c) BIMF2;(d) Res. Fig. 1 The decomposition results of gravity anomaly with noise by BEMD |
由于分解得到的固有模态函数的频率范围是从高到低变化的,BIMF1比较凌乱,为高频噪声异常,BIMF2和Res中带有长方体的异常信息,为有用异常信息.因此,可将BIMF1作为高频噪声、BIMF2和Res相加作为去噪后的重力异常,重构结果如图 2所示.图 2a表示是高频噪声,图 2b表示去噪后的结果,仍含有少许噪声残留,去噪结果较为粗糙、不够圆滑.
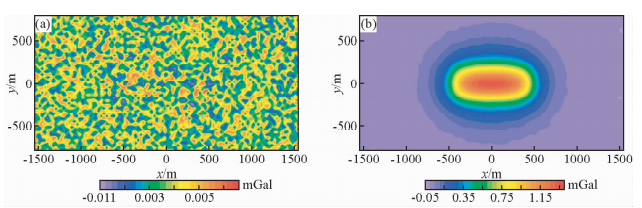 |
图 2 带噪声重力异常经BEMD分解后的重构结果 (a) 高频噪声(BIMF1);(b)去噪结果(BIMF2+Res). Fig. 2 The reconstruction of decomposition results of gravity anomaly with noise by BEMD |
简单地去掉一个或多个BIMF分量后,然后对其他的BIMF和剩余分量进行重组,这种BEMD滤波方法可能导致相应分量上的有用信号一起被删除掉,导致信号的失真,因此,它是一种粗糙的去噪方法.故尝试用BEMD和小波阈值方法相结合来实现基于BEMD的小波阈值滤波,该方法要对分解的BIMF分量和剩余分量Res选择一种阈值确定准则进行各个分量上的阈值估计,然后选择一种阈值函数,结合各个分量上的阈值估计值进行去噪计算,得到去噪后的BIMF分量和剩余分量Res,最后以去噪后的各个分量来重构信号,该信号即为去噪后的信号.利用该方法对上述带噪声的重力异常进行处理,结果如图 3a所示,从图中可以看出去噪较为彻底,能在保留有效信息的基础上实现圆滑去噪,且异常幅值保持去噪之前的水平.同样地,选取了二次曲面平滑去噪(图 3b),该方法较好地保留了有效信息,去除了数据中的噪声,但仍存在稍许残留,且去噪后异常幅值没有恢复到去噪之前的水平,因此,运用基于BEMD的小波阈值方法进行位场去噪的优势愈发明显,它可以最大限度的保留异常数据中的有效信息的同时,较好地去除了数据中的噪声,是一种有效的位场去噪方法.
 |
图 3 不同去噪方法的去噪效果对比 (a) 基于BEMD的小波阈值去噪;(b) 四十九点二次曲面平滑处理去噪. Fig. 3 The comparison of the de-noising results of two kinds of methods |
由于空间分布的位场异常是由地下各种场源综合作用的结果,它既包括区域异常,又存在局部异常.若能从叠加的位场异常中分离得到目标地质体的异常,实现位场的分离,进而可以以此进行位场异常的反演和地质解释工作,最终实现运用地球物理方法研究区域构造、局部构造,达到间接或直接找矿的目的.
位场分离方法总体上可以分为两大类:(1)空间域位场分离法;(2)频率域位场分离法.常用空间域位场分离方法包括:函数逼近、平均场法、趋势分析法、统计分析法、插值切割法等;常用频率域位场分离方法包括:解析延拓、匹配滤波、维纳滤波、小波分析、方向滤波等.上述方法由于数学原理不同,应用前提也不尽相同,因而都具有针对性和选择性,如何恰当地使用好现有这些方法对于位场数据处理尤为关键.
利用BEMD方法可以实现位场异常数据的多尺度分解,不需要预先参数设置,且分解具有自适应性.位场数据经分解可得到若干个固有模态函数和一个剩余分量.高频的固有模态函数可能是地表或者地下浅层异常体的反映,低频的固有模态函数可能是地层起伏、结晶基底变化的反映.将一个或多个短波长固有模态函数相加,可重构出位场局部异常;将长波长的固有模态函数和剩余分量相加,可重构出位场区域异常.
本文选取三峡地区作为研究对象,该地区地貌以大巴山、巫山山脉为骨架,形成以震旦系至三叠系碳酸盐岩组成的褶皱山地,属于以侵蚀为主兼有溶蚀作用的中山峡谷间夹低山宽谷的地貌景观.山脉总体为近东西向,局部为南北向.由于长江多斜切或横切,因而河谷多为斜向或横向.由于该区域的地质与地球物理背景复杂,几十年来,受到国内外科学家的关注,围绕该地区进行了地质、水文与灾害防治等多方面的调查与研究.
由于重力数据在反映地质构造特征上具有较高的横向分辨率,因此利用布格重力异常(图 4)对三峡地区的区域构造特征进行研究.由于重力异常存在叠加效应,需将其分解到不同尺度下进行剖析研究.为了在分解过程中获得较多的异常细节信息,选取阈值ε=0.001,运用BEMD方法对三峡地区布格重力异常进行多尺度分解,得到六组重力异常数据,如图 5a~f所示.
 | 图 4 三峡地区的布格重力异常 Fig. 4 The Bouguer gravity anomaly of the Three Gorges area |
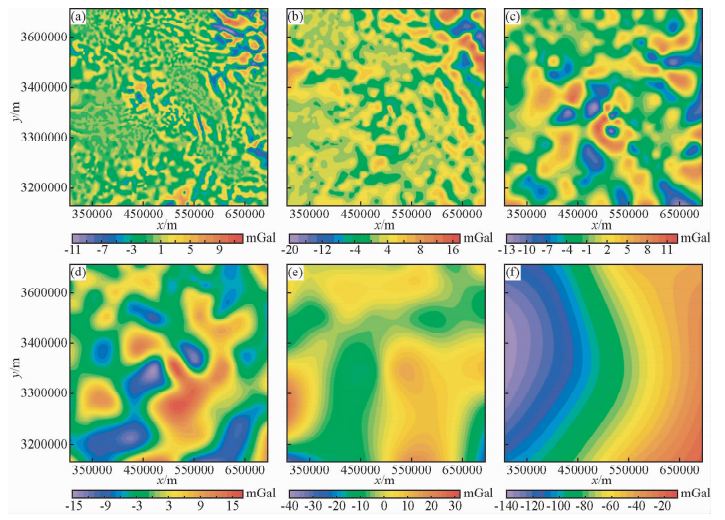 |
图 5 三峡地区布格重力异常的BEMD分解结果 (a) BIMF1;(b) BIMF2;(c) BIMF3;(d) BIMF4;(e) BIMF5;(f) Res. Fig. 5 The decomposition results of the Bouguer gravity anomaly of the Three Gorges area by BEMD |
从BEMD分解结果来看,BIMF1、BIMF2和BIMF3表现为高频的局部重力异常,异常分布零散,分布范围相对较小,其可能反映了三峡地区岩体、构造、地质异常体的物性和产状变化等;BIMF4、BIMF5和Res表现为低频的区域重力异常,异常分布较集中,分布范围较广,其可能反映了三峡地区区域岩矿石密度的变化以及地层、基底界面起伏变化.
此外,位场数据处理研究中一个重要问题是对研究区域场源似深度进行估计,从而可以对异常的反演和解释提供重要参考.由BEMD方法得到的各级固有模态函数,可利用径向对数功率谱(Spector and Grant,1970; Bhattacharyya and Leu,1975)来估计引起该异常的场源似深度,进而可以了解其所蕴含的地质信息.在对数功率谱值和频率值构成的对数功率谱曲线上,需要画出拟合谱中最低波数斜线,利用直线斜率来估算场源埋深(贺日政等,2007; 邱宁等,2007; 郑洪伟等,2010; 刘彦等,2012),可以得到各级固有模态函数的反映的地下构造体的似深度.每级固有模态函数所对应的对数功率谱曲线如图 6所示,其中直线为最低波数斜线.
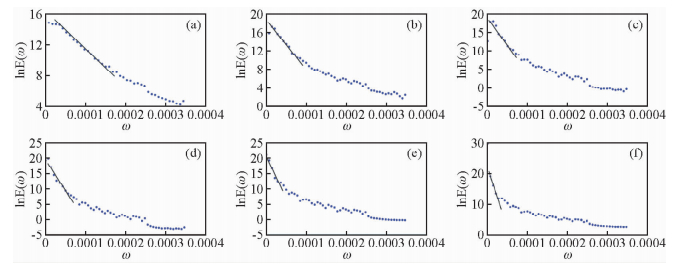 |
图 6 各级固有模态函数的径向对数功率谱曲线 (a) BIMF1;(b) BIMF2;(c) BIMF3;(d) BIMF4;(e) BIMF5;(f) Res. Fig. 6 The radial logarithmic power spectrum curve of bidimensional intrinsic mode function at all levels |
对上述曲线进行最小二乘拟合,将拟合得到的最低波数直线斜率代入计算公式估算平均深度,各级固有模态函数的估计的深度分别为:7.3 km、16.7 km、25.8 km、45.3 km、52.7 km、71.3 km.由前文分析可知,二维EMD对位场数据经过多尺度分解得到异常,异常波长与其反映的场源深度随着分解阶次的增加而增大.BEMD方法分离出不同场源产生的异常,结合谱分析方法来估算出场源的大致深度,有利于反演和地质解释.
与此同时,对分解出来的六组重力数据进行重构,将BIMF1、BIMF2和BIMF3相加作为局部重力异常;BIMF4、BIMF5和Res相加作为区域重力异常,重构局部重力异常和区域重力异常如图 7a、b所示.运用匹配滤波方法对布格重力异常进行位场分离,得到的局部异常和区域异常分别如图 8a、b所示.对比匹配滤波分场结果,BEMD方法进行重力异常分离得到的局部异常中细节分布范围基本一致,它是岩石圈密度分布不均匀的反映;区域异常的整体趋势是一致的,能够呈现出基底起伏特征.因此,BEMD方法可作为一种有效的位场分离方法.局部重力异常和区域重力异常共同组成了该地区的布格重力异常.局部重力异常主要反映了该地区地壳内部主要密度分界面的起伏和密度横向不均一的分布特征;区域重力异常主要反映了该地区莫霍面的起伏和上地幔密度的不均匀.
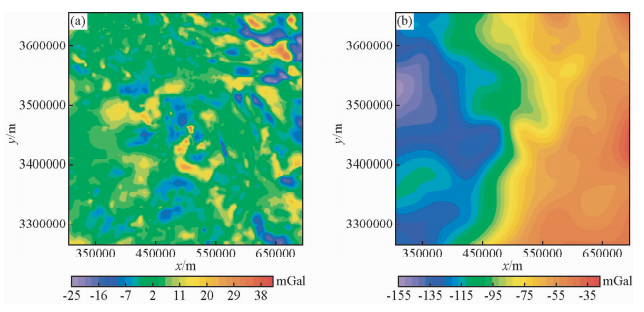 |
图 7 布格重力异常BEMD分解的重构结果 (a) 局部异常(BIMF1+BIMF2+BIMF3);(b) 区域异常(BIMF4+BIMF5+Res). Fig. 7 The reconstruction of decomposition results of the Bouguer gravity anomaly by BEMD |
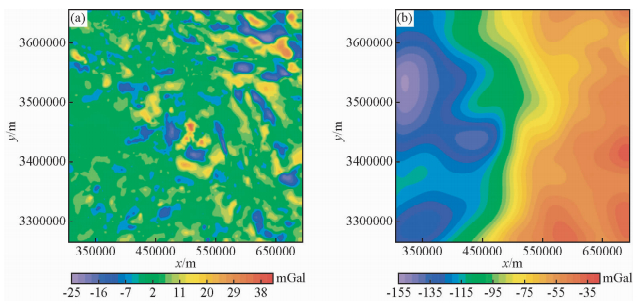 |
图 8 匹配滤波得到的局部异常和区域异常 (a) 局部异常;(b) 区域异常. Fig. 8 The local and regional gravity anomaly by matched filtering method |
3.1 利用BEMD方法的多分辨率的特性,对位场数据进行了多尺度分解,实现了位场去噪和分离.BEMD方法分解得到的各级固有模态函数对应着不同深度场源的地质信息,可以从不尺度上来分析和了解异常特征,比空间延拓、滤波、导数运算等传统位场数据处理方法具有较高的分辨率,可以定性或半定量地将实测异常分解为地下不同深度场源产生的异常,较好地揭示了场源赋存的地质信息.
3.2 虽然BEMD方法在位场数据处理中取得了一定的应用效果,但是在理论上和拓展应用过程中依然存在一些问题仍需要进一步探究,例如:(1)由位场数据经BEMD得到的各级固有模态函数可通过径向对数功率谱估计地下场源的似深度,在一定程度上可以大致了解地质体的几何特征,但其所反映的地质意义仍需深入研究;(2)位场局部异常和区域异常的重构只凭借个人主观臆断,重构准则需要进一步量化,方可获得较为准确的分场结果.
致 谢 感谢国家重点基础研究发展计划(973)(2012CB416800),湖北省自然科学基金(2014CFB170),教育部科技项目第50批留学回国人员科技启动基金和物化探研究所中央级公益性科研院所基本科研业务费专项资金资助项目(WHS201210,WHS201211)对本文的联合资助.
| [1] | Bhattacharyya B K, Leu L K. 1975. Spectral analysis of gravity and magnetic anomalies due to two-dimensional structures[J]. Geophysics, 40(6):993-1013. |
| [2] | Chen J G, Xiao F, Chang T. 2011. Gravity and magnetic anomaly separation based on bidimensional empirical mode decomposition[J]. Earth Science-Journal of China University of Geosciences (in Chinese), 36(2):327-335. |
| [3] | Chen Y Q, Zhao B B. 2011. The application of both singular value decomposition and bi-dimensional empirical mode decomposition in extraction of gravity anomalies associated with gold mineralization[J]. Geological Bulletin of China (in Chinese), 30(5):661-669. |
| [4] | Chen Y Q, Zhao B B. 2012. Extraction of gravity anomalies associated with gold mineralization:A comparison of singular value decomposition and bi-dimensional empirical mode decomposition[J]. Advanced Materials Research, 455-456:1567-1577. |
| [5] | Cooper S M, Liu T Y, Mbue I N. 2010. The Empirical Mode Decomposition (EMD), a new tool for potential field separation[J]. Journal of American Science, 6(7):183-187. |
| [6] | Hassan H H, Pierce J W. 2005. Empirical Mode Decomposition (EMD) of potential field data:airborne gravity data as an example[C].//2005 Annual Meeting, SEG Expanded Abstracts, 24:704. |
| [7] | He L J, Zhang Y, Zhang Y. 2011. Study on application of bidimensional empirical mode decomposition in processing geophysical and geochemical data[J]. Contributions to Geology and Mineral Resources Research (in Chinese), 26(3):311-315. |
| [8] | He R Z, Gao R, Zheng H W, et al. 2007. Matched-filter analysis of aeromagnetic anomaly in mid-western Tibetan Plateau and its tectonic implications[J]. Chinese Journal of Geophysics (in Chinese), 50(4):1131-1140, doi:10.3321/j.issn:0001-5733.2007.04.020. |
| [9] | Hou W S, Yang Z J, Zhou Y Z, et al. 2012. Extracting magnetic anomalies based on an improved BEMD method:A case study in the Pangxidong area, South China[J]. Computers & Geosciences, 48:1-8. |
| [10] | Huang J N, Zhao B B, Chen Y Q, et al. 2010. Bidimensional Empirical Mode Decomposition (BEMD) for extraction of gravity anomalies associated with gold mineralization in the Tongshi gold field, Western Shandong uplifted block, Eastern China[J]. Computers & Geosciences, 36(7):987-995. |
| [11] | Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. Roy. Soc. London. A, 454(1971):903-995. |
| [12] | Huang N E, Shen Z, Long S R. 1999. A new view of the nonlinear water waves:the Hilbert spectrum[J]. Annu. Rev. Fluid Mech., 31(1):417-457. |
| [13] | Jian Z Z, Chen Y Q, Zhao B B. 2012. The application of bidimensional empirical mode decomposition (BEMD) to the extraction of Pt and Pd anomalies in eastern Yunnan Province[J]. Geological Bulletin of China (in Chinese), 31(5):799-806. |
| [14] | Liu Y, Yan J Y, Wu M A, et al. 2012. Exploring deep concealed ore bodies based on gravity anomaly separation methods:A case study of the Nihe iron deposit[J]. Chinese Journal of Geophysics (in Chinese), 55(12):4181-4193, doi:10.6038/j.issn.0001-5733.2012.12.030. |
| [15] | Nunes J C, Bouaoune Y, Delechelle E, et al. 2003a. Image analysis by bidimensional empirical mode decomposition[J]. Image and Vision Computing, 21(12):1019-1026. |
| [16] | Nunes J C, Guyot S, Deléchelle E. 2005. Texture analysis based on local analysis of the bidimensional empirical mode decomposition[J]. Machine Vision and Applications, 16(3):177-188. |
| [17] | Nunes J C, Niang O, Bouaoune Y, et al. 2003b. Bidimensional Empirical Mode Decomposition modified for texture analysis[C].//Image Analysis. Springer Berlin Heidelberg, 2749:171-177. |
| [18] | Pei Y, Wu Y G, Jia D C. 2012. Gravity anomaly separation based on bidimensional empirical mode decomposition[J]. Research Journal of Applied Sciences, Engineering and Technology, 4(21):4227-4236. |
| [19] | Qiu N, He Z X, Chang Y N. 2007. Ability of improving gravity anomaly resolution based on multiresolution wavelet analysis and power spectrum analysis[J]. Progress in Geophysics (in Chinese), 22(1):112-120, doi:10.3969/j.issn.1004-2903.2007.01.015. |
| [20] | Spector A, Grant F S. 1970. Statistical models for interpreting aeromagnetic data[J]. Geophysics, 35(2):293-302. |
| [21] | Wang L S, Chen C, Liang Q, et al. 2011. The application of bidimentional empirical mode decomposition in the multiscale decomposition of satellite magnetic anomaly in China and its adjacent region (in Chinese)[C].//Proceedings of the Chinese Geophysical Society 27th Annual Meeting, 502. |
| [22] | Zeng Q Q, Liu T Y. 2009. Potential field separation based on the empirical mode decomposition and its application[C].//2nd International Congress on Image and Signal Processing, 1-4. |
| [23] | Zeng Q Q, Liu T Y. 2010. A potential field separation method based on empirical mode decomposition[J]. Oil Geophysical Prospecting (in Chinese), 45(6):914-917. |
| [24] | Zeng Q Q, Liu T Y. 2011. EMD of gravity and magnetic anomalies and its application for iron deposit exploration in Zhangfushan, Eastern Hubei[J]. Progress in Geophysics (in Chinese), 26(4):1409-1414, doi:10.3969/j.issn.1004-2903.2011.04.036. |
| [25] | Zheng H W, Meng L S, He R Z, et al. 2010. The matched-filter analysis of Bouguer gravity anomaly in Qinghai-Tibet Plateau and its tectonic implications[J]. Geology in China (in Chinese), 37(4):995-1001. |
| [26] | Zhou W N, Zeng Z F, Du X J, et al. 2010. Gravity anomaly separation based on empirical mode decomposition[J]. Global Geology (in Chinese), 29(3):495-502. |
| [27] | 陈建国,肖凡,常韬. 2011.基于二维经验模态分解的重磁异常分离[J].地球科学-中国地质大学学报, 36(2):327-335. |
| [28] | 陈永清,赵彬彬. 2011.应用奇异值分解与二维经验模型分解提取金矿化致矿重力异常[J].地质通报, 30(5):661-669. |
| [29] | 何丽娟,张毅,张焱. 2011.二维EMD方法在物化探数据处理中的应用研究——以云南个旧地区为例[J].地质找矿论丛, 26(3):311-315. |
| [30] | 贺日政,高锐,郑洪伟,等. 2007.青藏高原中西部航磁异常的匹配滤波分析与构造意义[J].地球物理学报, 50(4):1131-1140, doi:10.3321/j.issn:0001-5733.2007.04.020. |
| [31] | 菅贞贞,陈永清,赵彬彬. 2012.应用二维经验模态分解(BEMD)法提取滇东Pt、Pd元素地球化学异常[J].地质通报, 31(5):799-806. |
| [32] | 刘彦,严加永,吴明安,等. 2012.基于重力异常分离方法寻找深部隐伏铁矿——以安徽泥河铁矿为例[J].地球物理学报, 55(12):4181-4193, doi:10.6038/j.issn.0001-5733.2012.12.030. |
| [33] | 邱宁,何展翔,昌彦君. 2007.分析研究基于小波分析与谱分析提高重力异常的分辨能力[J].地球物理学进展, 22(1):112-120, doi:10.3969/j.issn.1004-2903.2007.01.015. |
| [34] | 王林松,陈超,梁青,等. 2011.二维经验模态方法在中国及邻区卫星磁异常多尺度分解中的应用[C].//中国地球物理学会第二十七届年会论文集, 502. |
| [35] | 曾琴琴,刘天佑. 2010.一种基于经验模态分解(EMD)的位场分离方法[J].石油地球物理勘探, 45(6):914-917. |
| [36] | 曾琴琴,刘天佑. 2011.重、磁异常的经验模态分解及其在鄂东张福山铁矿勘探中的应用[J].地球物理学进展, 26(4):1409-1414, doi:10.3969/j.issn.1004-2903.2011.04.036. |
| [37] | 郑洪伟,孟令顺,贺日政,等. 2010.青藏高原布格重力异常匹配滤波分析及其构造意义[J].中国地质, 37(4):995-1001. |
| [38] | 周文纳,曾昭发,杜晓娟,等. 2010.基于经验模态分解的重力异常分离[J].世界地质, 29(3):495-502. |
 2015, Vol. 30
2015, Vol. 30


