2. 青岛海洋地质研究所, 青岛 266071;
3. 中国科学院地质与地球物理研究所, 北京 100029
2. Qingdao Institute of Marine Geology, Qingdao 266071, China;
3. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 10029, China
压制噪声、提高地震数据的信噪比是地震数据处理中的重要任务,但多分量地震数据相对于常规纵波数据信噪比更低,各个分量上的波场比较复杂,使得有效信号在低频带与面波有重叠的部分.欲得到满足地质解释需要的处理成果,有效地识别和压制噪声显得格外重要.多分量处理中常规的噪声压制方法有:f-k滤波(Melo et al.,2009),维纳滤波(李月等,2010),radon变换(Wang,2002),极化滤波(Chen et al.,2013)等方法.这些方法在面波压制方面都有了一定的效果,但也有其不足之处.如:f-k滤波是基于傅里叶变化的方法,去除面波的同时会造成子波畸变和有效信号的损失;radon变换压制过程由于反变换过程中“边界效应”会使得面波的边界部分残留;极化滤波是基于不同波的偏振方向不同而进行波场分量,但是体波和面波不总是线性和椭圆轨迹,以至有效波的信息也会损失.
希尔伯特黄变换(HHT)是处理复杂的非线性、非平稳随机信号(地震信号)的一种全新的工具(Huang,1996;Huang et al.,1998,2003).对于地震信号,Fourier分析理论已经不能人们的需要,于是处理此类信号的时频分析方法应运而生,比如说:短时Fourier变换、小波变换等.短时Fourier变换从本质上来说还是Fourier变换,只是加了窗函数的处理,它对不同的信号没有适应性;小波变换是近几年比较常用的处理非平稳信号的分析工具(陈文超等,2009).然该方法对不同信号有适应性,但是在小波变换分解过程中最佳小波基的选择是一个难题.而HHT变换的多尺度性和自适应特点很好的解决了这个问题,经过发展也逐步形成了独立的理论体系.在地球物理应用方面,首先国外学者开始将HHT方法用于地震资料的分析(Loh et al.,2001;Huang and Wu,2008)、电法的属性参数提取(Neukirch and Garcia,2014);然后国内有人利用该方法提取地震信号的动力特征并与Fourier分析、小波分析结果进行了比较(吴琛和周瑞忠,2006;毕明霞等,2012),显示了HHT方法的优越性.基于HHT的时频分析特点,对地震信号进行时频分析和属性提取也有了很多研究(杨培杰等,2007;侯斌等,2009;曹思远等,2013);同时应用该方法在地震资料的去噪处理方面有了初步进展(刘庆敏等,2009;李月等,2013;王德营等,2014).
本文主要根据HHT变换的自适应特性和多分辨率,利用多分量数据特点,提出一种压制面波的方法.其思路是EMD分解得到不同频率尺度的特征信号,利用信号与噪声的特征尺度不同进一步剔除分离出来的IMF成分,进而提取出单频剖面在量化的频域通道进行信号重构来压制面波.对于面波和有效信号有重叠的部分,做进一步的瞬时属性分析,通过阈值处理压制残留的噪声成分.从而得到信噪比品质较好的资料.
1 Hilbert-Huang变换原理Hilbert-Huang变换是一种两步骤信号处理方法.首先用EMD分解获得有限数目的固有模态函数(IMF),然后再利用Hilbert变换和瞬时频率方法获得信号的时-频谱(Hilbert谱).由于瞬时频率方法只能对单分量信号才有意义,对于地震领域的应用,我们所获取的信号一般都不能满足单分量信号的要求,因此必须对信号进行近似的处理.EMD方法就是通过对信号进行分解,使之能够表示为许多单分量信号之和,也就是分解成含有不同尺度信息的信号.
1.1 EMD分解过程对于给定的信号,Huang所介绍的EMD方法是:首先找到信号的极大值和极小值,通过三次样条拟合对所有的极值点进行插值,从而获得信号的上包络曲线Xmax(t)和下包络曲线Xmin(t);然后计算上下包络曲线在每一点上的平均值,从而获得平均值曲线m1(t).设分析信号为X(t),则:
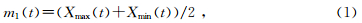
再用X(t)减掉m1(t)得到h1(t)为

对于不同的信号,h1(t)可能是一个IMF分量,也可能不是.一般来讲,它并不完全满足IMF所需的条件,此时把h1(t)当做一个新的信号,重复上述步骤,即得:

式中,m11(t)是h1(t)的上、下包络线的均值.若h11(t)不是IMF分量,则继续上面的步骤,重复上面的方法k次,可以得到第k次循环的数据h1k(k)为
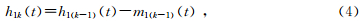
h1k(k)满足筛选终止条件的要求,则h1k(k)为第一阶IMF,记为c1(t),即

从原信号中减去c1(t)得到剩余信号,即残差r1(t)为

这里,第一个被分离出来的固有模态函数,也是频率最高的分量;然后,把r1(t)作为一个新的原序列,按照上面的步骤,依次提取出第二、第三、…,直至第n个固有模态函数;最后,我们得到的rn(t)是单调的函数,不能再被分解了.通过这样我们得到了原始序列X(t)为
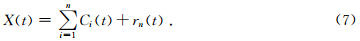
EMD分解过程其实是就是一个“筛选”的过程.在“筛选”的过程中,在消除了模态波形叠加的影响的情况下,更使得波形轮廓对称更好.EMD分解方法从特征时间尺度来说,首先分离出来的是信号中特征尺度最小的固有模态分量;然后是特征时间尺度较大的固有模态;最后分离出来的是特征时间尺度最大的固有模态分量,因此我们可以把EMD方法看成是一个高通滤波器(钱昌松等,2010).同时这种EMD分解方法是自适应的,这也是它相比于小波变换做信号分析的一大优点.
EMD分解为多分量地震资料面波压制提供了理论基础,去噪过程其实就是一个波场分离的过程.从(7)式中我们可以得知,整个地震数据我们能把它分解成不同分辨率的信号,面波成分一定存在于低频带的有限个的IMF分量中,于是从数据中分离出有效波就能达到压制面波的效果.
1.2 希尔伯特变换和希尔伯特谱希尔伯特变换(Hilbert)变化是信号处理分析中重要的工具.复信号是频谱的实部与虚部的关系,通常是希尔伯特变换的关系.对给定的连续时程曲线X(t),其中Hilbert变换定义为
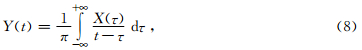
我们引入了解析函数Z(t),则有:

Z(t)可写为

其中
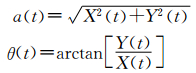
瞬时频率可定义为

可见,瞬时频率w(t)也是时间的函数.
信号X(t)通过EMD分解得到一系列的IMF分量及残余项后,对X(t)的n阶IMF分量分别进行Hilbert变换后,构造解析函数H(t)表示为
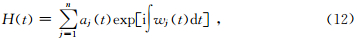
其中,aj(t)是第j阶固有模态函数cj(t)的解析信号的幅值,对照(12)式可看出,这里省略残余函数,Re表示取实部,展开后,则称为Hilbert幅值谱,简称Hilbert谱.记作
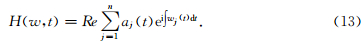
从上面的公式中我们可以看出,Hilbert谱是一种加权的联合时间—频率—幅值三维的显示,能比较清晰的刻画出信号的局部信息.在Hilbert谱中,能得到“三瞬”的信息,基于有效波和面波的瞬时属性的差异,我们可以进行进一步的面波压制,以达到更好的去噪效果.
2 仿真信号实验用已知信号的EMD分解及其由此产生的一系列固有模态函数IMF重构是检验EMD方法实际应用效果的一种最简单、直观、有效的方法.为此我们由信号x1=4×cos(100×pi×t1)、x2=cos(50×pi×t1)、x3=8×cos(200×pi×t1)合成复杂信号x=x1+x2+x3.
经过合成后的信号X(t)是多分量信号.按照EMD变换的分解步骤,第一步是对信号的包络极值点进行搜寻和确定,接下来对确定的极值点坐标进行样条插值.本文中采用三次样条函数对整个信号进行插值(陈林和宋海斌,2008),分解得到的结果如下图所示:
图 1中横坐标为时间t,纵坐标为振幅.从图中可以看出多尺度信号X(t)中的三个分量被清晰地分解出来,分解得到的每个IMF成分都是比较干净的.而且分解得到的IMF分量是按频率尺度从高到低依次分解出的.结果表明,利用经验模态分解方法的多尺度滤波特征,可以有效保留信号中局部属性,从而验证了HHT方法的理论可行性.
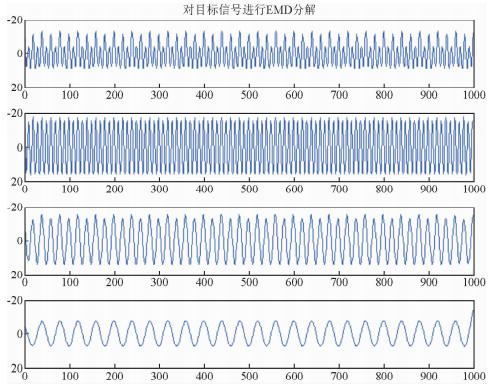 | 图 1 信号x(t)的EMD分解结果 Fig. 1 Signal x(t) of the EMD decomposition results |
本文主要研究的是该方法对多波地震数据进行去面波应用.由于在多波资料一般信噪比比较低,波场较复杂.为了测试方法在多分量地震去噪中面波的的压制效果,我们采用复杂地区黄土塬浅地层的模拟地震数据.其中深度为2000毫秒,震源子波主频为30赫兹,采样间隔为2 ms,道数为351道.表 1为整个地质模型的具体参数.
|
|
表 1 模型参数 Table 1 Model parameters |
图 2是通过波场模拟得到的三分量数据.基于面波和有效波的特性作对比分析(王德营等,2014).X、Z分量上只包含了浅地层的信息.即指包含直达波、面波、多次波、 多次折射波等信息.我们可以在图中指示的部分,看出模拟得到的X、Z分量上的地震数据近偏移距上存在面波,而且能量是比较强的.
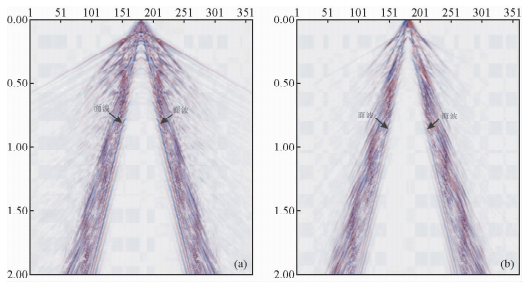 |
图 2 模拟的三分量数据 (a)Z分量;(b)X分量. Fig. 2 The simulation of three-component data (a)Z component; (b)X component. |
对整个地震剖面做EMD处理和对信号做EMD处理过程是一致的.我们只需要对道进行循环做EMD分解即可,同样能得到有限阶的IMF分量.在这里显示为地震剖面的形式,而且上一阶的IMF比下一阶的IMF主频要低,不同的尺度的IMF包含的主要信号的信息不同.对于EMD方法中,对应的每一种波都有相对应的一个尺度去近似.因此我们可以根据面波在哪个合适的尺度对它进行压制,或者通过大尺度的IMF重组得到去面波的地震剖面.我们也可以把EMD对地震信号的分解过程,理解对信号的多分辨率滤波的过程.这也验证EMD具有多分辨率的特性,这是相比于传统的滤波方法的优点(张军华等,2006).
根据面波相应的特征,分析得到图 2指示处存在很强的面波成分.图 3是经过EMD处理过的去除面波后的地震剖面.我们可以看出在大部分面波成分得到了去除,Z分量上比X分量去除的比较干净.这是因为Z分量波场相对于X量的波场比较简单,Z分量上大部分都是纵波的成分;而X分量上波场复杂,同时转换波和面波有重叠的部分,使得在X分量上分离信号不如Z分离效果好.这也是多波勘探的难点之一.因为Y分量跟X分量处理是一样的,在这里不做讨论.
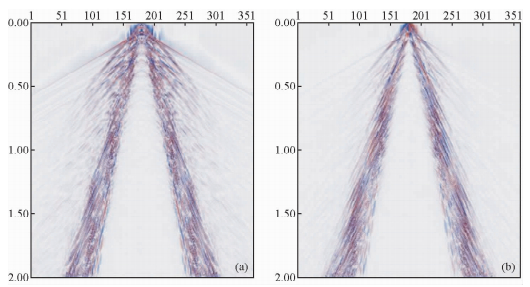 |
图 3 EMD去面波后的数据 (a) Z component; (b) X component. Fig. 3 The data after suppressing surface wave by EMD (a)Z component; (b)X component. |
接下来我们对模拟得到的地震数据和去面波后的地震数据进行频谱分析,图 4是Z分量数据面波去除前后的频谱对比.左边是原始地震记录的频谱,右边是去除面波后的频谱图,主频大概在24 Hz左右.图 5是X分量数据去面波去除前后的频谱对比.从两图的标记的部分可以看出,原始地震剖面的频谱在低频部分有很强的能量,经过EMD后,低频的面波部分得到了压制;同时我们也能看出在高频的部分没有损伤,也就说我们需要的有效的反射信号没有被破坏,有利于对地震资料进行高分辨率处理(袁艳华等,2013).同时验证了HHT在地震去噪方面的可行性.
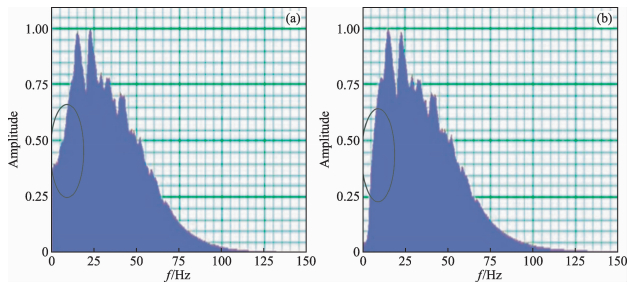 |
图 4 Z分量去面波前后频谱对比 (a)去面波前频谱;(b)去面波后频谱. Fig. 4 The spectral contrast between original and denoised spectrum in Z component (a)Spectrum before suppress surface wave; (b)Spectrum after suppress surface wave. |
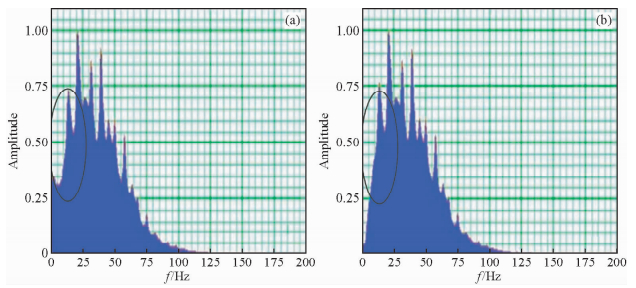 |
图 5 X分量去面波前后频谱对比 (a)去面波前频谱;(b) 去面波后频谱. Fig. 5 The spectral contrast between original and denoised spectrum in X component (a)Spectrum before suppress surface wave; (b)Spectrum after suppress surface wave. |
实际资料是来自川西地区采集到的三分量地震数据,从图 6中标记的部分可以看出该处含有很强的面波成分.首先从中提取该地震剖面的第100道地震信号进行相应的EMD分解,得到如图 7所示的结果.
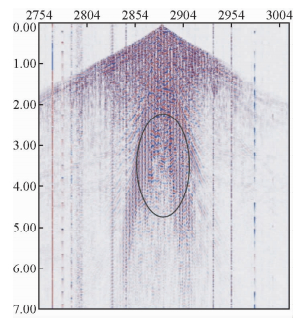 | 图 6 实际地震资料剖面 Fig. 6 The seismic data profiles |
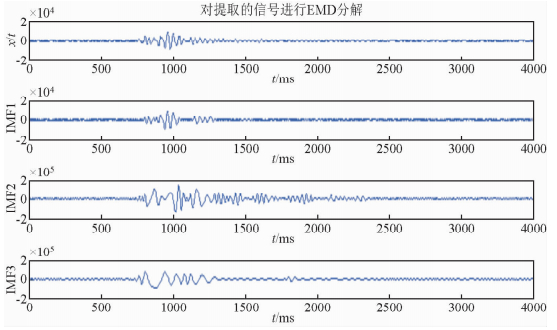 | 图 7 对提取的道数进行EMD分解的结果 Fig. 7 The results of EMD decomposition to the extracted trace |
为了验证每个IMF分量的尺度差异,对其做FFT变换,求得它们的频谱如图 8所示.从图中可以看出,对地震数据某一道信号进行EMD分解,得到频率大小不一样的、具有不同尺度的固有模态函数IMF,它们的主频是依次降低的,从第一个IMF分量的主频15 Hz到IMF3的主频是大概4 Hz左右.正如EMD原理所述,对地震信号进行EMD分解,也是自适应的,同时在低频段存在有不同尺度,为本文中压制面波提供了有效的途径.接下来对整个实际多波多分量地震剖面做去面波处理.
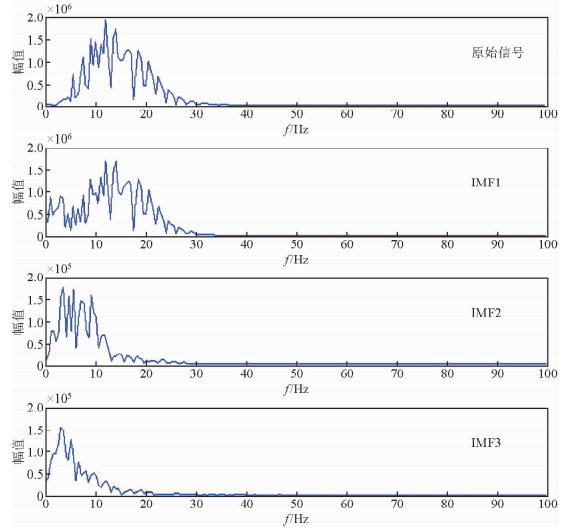 | 图 8 原信号和EMD分解得到的IMF分量的频谱 Fig. 8 The spectrum of original signal and spectrum of IMF components by EMD |
根据模拟地震资料进行EMD分解的过程,现在将这种流程应用于整个地震数据剖面.但是实际的多波地震数据相对于模拟的地震数据,信噪比相对较差.为了得到满意的效果,做了更详细的处理.首先对原始的数据做频谱分析,得到频谱图 10a和图 12a,该数据主频大概在16~18 Hz之间,为了不损害有效反射信号,我们给含有面波的地震剖面加一个窗函数;然后在窗函数里依次提取该数据剖面中的每一道并对其进行EMD分解.为了对所有地震道信号进行统一的分解,并为了分解之后的IMF分量更加方便地分析,强制分解后的固有模态函数数目为10个(为了得到足够多的频带);接下来依次对分解所得的分量作FFT变换,来进行相应的频谱分析.如果遇见频带比较宽的话,说明分解得不是很彻底,里面含有多个尺度的固有模态函数,因此把个别的分量拿出来再进一步做EMD分解处理,把具有面波形态以及具有低频的部分分离处理,这就是我们分离出来的面波成分;最后,将剩下的所有经过处理的模态函数分量进行信号的重构得到压制面波的地震剖面.
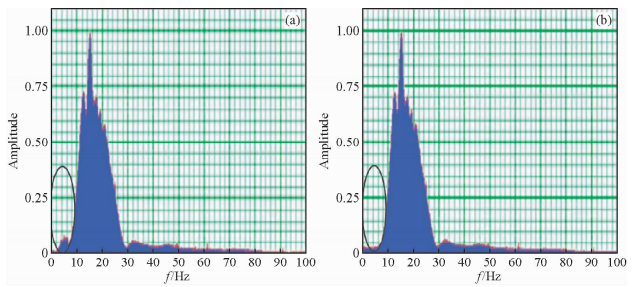 |
图 12 X分量去面波前后频谱对比结果 (a)去面波前频谱;(b)去面波后频谱. Fig. 12 The contrast between original spectrum and denoised spectrum in X component (a)Spectrum before suppress surface wave; (b)Spectrum after suppress surface wave. |
图 9a和图 11a是川西新场地区实际三分量地震数据的Z、X分量的数据,用上文所述的方法对每个分量的数据进行相关压制面波处理(王赟等,2005;孙岐峰和杜启振,2011).
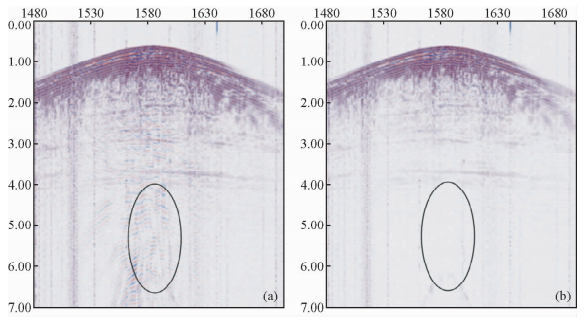 |
图 9 Z分量去面波前后剖面对比结果 (a)去面波前;(b) 去面波后. Fig. 9 The contrast between original section and denoised section in Z component (a)Before suppress surface wave; (b)After suppress surface wave. |
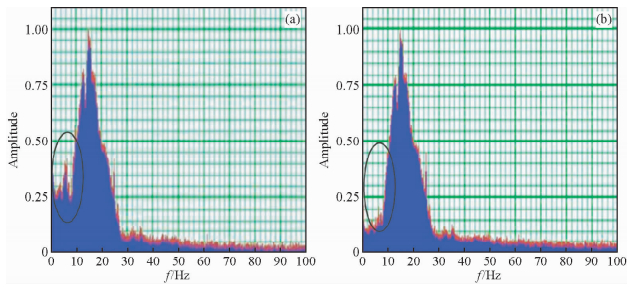 |
图 10 Z分量去面波前后频谱对比结果 (a)去面波前频谱;(b) 去面波后频谱. Fig. 10 The contrast between original spectrum and denoised spectrum in Z component (a)Spectrum before Suppress surface wave; (b)Spectrum after Suppress surface wave. |
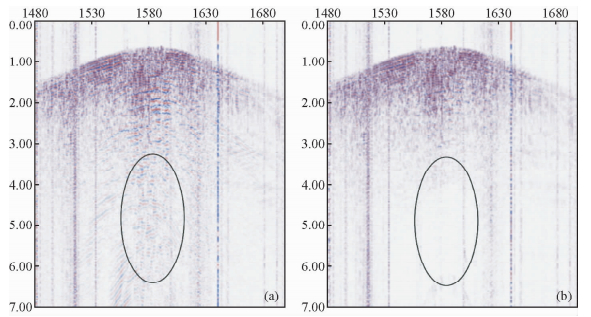 |
图 11 X分量去面波前后剖面对比结果 (a)去面波前;(b)去面波后. Fig. 11 The contrast between original section and denoised section in X component (a)Before suppress surface wave; (b)After suppress surface wave. |
由于方法的一些局限性,EMD处理过后的地震剖面对于面波的去除不是很彻底,尤其是在X分量上,因此下一步工作是:对EMD过后的地震剖面进行希尔伯特变换,求得整个地震剖面的瞬时频率剖面,基于面波和有效波瞬时频率的大小的差别(瞬时频率是信号出现的概率的大小,反应的是信号局部的信息)进行残留的面波的压制.在本文中主要以瞬时频率数据为依据,利用中值滤波对其做进一步的滤波处理,得到去噪效果更好的地震剖面.
图 9b和图 11b是经过EMD去除面波以后的多波地震资料,从图中标记的部分我们能清晰的看出面波得到了比较好的去除.从对应压制面波前后的频谱上也能清楚的看出,低频的面波部分得到了压制.剖面质量有了改进,同时保护了有效波成分,地震资料的信噪比得到了提高.
5 结 论5.1 HHT中 EMD分解方法在整个分解过程是属于直接和自适应的,基函数直接从信号本身去产生,它能从时域和频域的分辨特性去识别噪声和有效波跟传统的滤波方法来比,HHT方法对地震资料进行去噪处理,实际上是特征提取和低通滤波的综合应用,因此能更彻底的分解出面波部分.
5.2 相对于常规地震资料,三分量地震数据能量弱,信噪比更差,转换波频率较低且与面波干扰有很大的重叠.因此本文利用HHT变换中分解的多尺度的特性,可以更好的对面波进行压制.同时我们可以利用HHT的局部时频分析能力,对地震处理解释做进一步的探索.
5.3 在处理多分量中X分量中,由于其波场更加复杂,信噪比比较低的情况,同时算法本身存在一定缺陷,选择适当长度的信号或加入适量的白噪声进行EMD,也有可能提高最终信号处理的质量.将一维的HHT算法延拓到三维上,可能成为地球物理领域更加热门的研究方向.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Bi M X, Huang H M, Bian Y J, et al. 2012. Study on seismic signal features extraction based on EMD[J]. Progress in Geophys. (in Chinese), 27(5):1890-1896, doi:10.6038/j.issn.1004-2903.2012.05.008. |
| [2] | Cao S Y, Bing P, Lou J T, et al. 2013. Seismic data time-frequency analysis by the improved Hilbert-Huang transform[J]. Oil Geophysical Prospecting (in Chinese), 48(2):246-254. |
| [3] | Chen H F, Li X Y, Qian Z P, et al. 2013. Robust adaptive polarization analysis method for eliminating ground roll in 3C land seismics[J]. Applied Geophysics, 10(3):295-304, doi:10.1007/s11770-013-0386-0. |
| [4] | Chen L, Song H B. 2008. Seismic instantaneous attribute extraction based on empirical mode decomposition[J]. Progress in Geophysics (in Chinese), 23(4):1179-1185. |
| [5] | Chen W C, Gao J H, Bao Q Z. 2009. Based on the continuous wavelet transform adaptive surface wave suppression[J]. Chinese Journal of Geophysics (in Chinese), 52(11):2854-2861. |
| [6] | Hou B, Gui Z X, Hu M, et al. 2009. Time-frequency spectral analysis of seismic data based on Hilbert-Huang transform[J]. Progress in Exploration Geophysics (in Chinese), 32(4):248-251, 290. |
| [7] | Huang N E. 1996. Computer implicated empirical mode decomposition method, apparatus, and article of manufacture[P]. Patent US 6311130 B1. |
| [8] | Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society A, 454(1971):903-995. |
| [9] | Huang N E, Wu M L, Long S R, et al. 2003. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceeding of the Royal Society A, 459(2037):2317-2345. |
| [10] | Huang N E, Wu Z H. 2008. A review on Hilbert-Huang transform:Method and its applications to geophysical studies[J]. Rev. Geophys., 46(2):RG2006, doi:10.1029/2007RG000228. |
| [11] | Li Y, Ma H T, Lin H B, et al. 2010. The research of principal-component wiener filtering method based on kernel function[J]. Chinese J. Geophys. (in Chinese), 53(5):1226-1223. |
| [12] | Li Y, Peng J L, Ma H T, et al. 2013. Study of influence of transition IMF on EMD do-noising and the improved algorithm[J]. Chinese J. Geophys. (in Chinese), 56(2):626-634, doi:10.6038/cjg20130226. |
| [13] | Liu Q M, Yang W Y, Tian L Y, et al. 2009. Application of Hilbert-Huang transformation to noise elimination of seismic data[J]. Xinjiang Petroleum Geology (in Chinese), 30(3):333-336. |
| [14] | Loh C H, Wu T C, Huang N E. 2001. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses[J]. Bulletin of the Seismological Society of America, 91(5):1339-1357. |
| [15] | Melo P E M, Porsani M J, Silva M G. 2009. Ground-roll attenuation using a 2D time-derivative filter[J]. Geophys. Prospect., 57(3):343-353. |
| [16] | Neukirch M, Garcia X. 2014. Nonstationary magnetotelluric data processing with instantaneous parameter[J]. J. Geophys. Res., 119(3):1634-1654, doi:10.1002/2013JB010494. |
| [17] | Nie P F, Li Y, Zeng Q, et al. 2012. Ground-roll attenuation using the directional derivative trace transform[J]. Chinese J. Geophys. (in Chinese), 55(6):2035-2043, doi:10.6038/j.issn.0001-5733.2012.06.025. |
| [18] | Qian C S, Liu D Z, Liu Z G, et al. 2010. EMD based on recursive high-pass filter and its application on seismic signal analysis[J]. Chinese Journal of Geophysics (in Chinese), 53(5):1215-1225, doi:10.3969/j.issn.0001-5733.2010.05.024. |
| [19] | Sun Q F, Du Q Z. 2011. A review of the multi-component seismic data processing[J]. Petroleum Exploration and Development (in Chinese), 38(1):67-73. |
| [20] | Wang D Y, Li Z C, Huang J P, et al. 2014. A scale of surface wave suppression methods[J]. Acta Petrolei Sinica (in Chinese), 35(2):303-309. |
| [21] | Wang Y, Xing D, Xing C Y. 2005. Some key problems towards practicability of multicomponent seismic technology[J]. Progress in Exploration Geophysics (in Chinese), 28(3):174-177. |
| [22] | Wang Y H. 2002. Antialiasing conditions in the delay-time Radon transform[J]. Geohpys. Prospect., 50(6):665-672. |
| [23] | Wu C, Zhou R Z. 2006. Application of Hilbert-Huang transform in extracting dynamic properties of seismic signals[J]. Earthquake Engineering and Engineering Vibration (in Chinese), 26(5):41-46. |
| [24] | Yang P J, Yin X Y, Zhang G Z. 2007. Seismic signal time-frequency analysis and attributes extraction based on HHT[J]. Progress in Geophysics (in Chinese), 22(5):1585-1590, doi:10.3969/j.issn.1004-2903.2007.05.037. |
| [25] | Yuan Y H, Wang Y B, Liu Y K, et al. 2013. Non-dyadic Curvelet transform and its application in seismic noise elimination[J]. Chinese J. Geophys. (in Chinese), 56(3):1023-1032, doi:10.6038/cjg20130330. |
| [26] | Zhang J H, Lv N, Tian L Y, et al. 2006. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics (in Chinese), 21(2):546-553, doi:10.3969/j.issn.1004-2903.2006.02.033. |
| [27] | 毕明霞,黄汉明,边银菊,等. 2012.基于经验模态分解的地震波特征提取的研究[J].地球物理学进展, 27(5):1890-1896, doi:10.6038/j.issn.1004-2903.2012.05.008. |
| [28] | 陈林,宋海斌. 2008.基于经验模态分解的地震瞬时属性提取[J].地球物理学进展, 23(4):1179-1185. |
| [29] | 曹思远,邴萍萍,路交通,等. 2013.利用改进希尔伯特-黄变换进行地震资料时频分析[J].石油地球物理勘探, 48(2):246-254. |
| [30] | 陈文超,高静怀,包乾宗. 2009.基于连续小波变换的自适应面波压制方法[J].地球物理学报, 52(11):2854-2861. |
| [31] | 侯斌,桂志先,胡敏,等. 2009.基于希尔伯特-黄变换的地震信号时频谱分析[J].勘探地球物理进展, 32(4):248-251, 290. |
| [32] | 李月,彭蛟龙,马海涛,等. 2013.过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法[J].地球物理学报, 56(2):626-634, doi:10.6038/cjg20130226. |
| [33] | 李月,马海涛,林红波,等. 2010.基于核函数主分量的维纳滤波方法研究[J].地球物理学报, 53(5):1226-1223. |
| [34] | 刘庆敏,杨午阳,田连玉,等. 2009.希尔伯特-黄变换在地震资料去噪中的应用[J].新疆石油地质, 30(3):333-336. |
| [35] | 聂鹏飞,李月,曾谦,等, 2012.方向导数迹变换面波压制[J].地球物理学报, 55(6):2035-2043, doi:10.6038/j.issn.0001-5733.2012.06.025. |
| [36] | 钱昌松,刘代志,刘志刚,等. 2010.基于递归高通滤波的经验模态分解及其在地震信号分析中的应用[J].地球物理学报, 53(5):1215-1225, doi:10.3969/j.issn.0001-5733.2010.05.024. |
| [37] | 孙岐峰,杜启振. 2011.多分量地震数据处理技术研究现状[J].石油勘探与开发, 38(1):67-73. |
| [38] | 王德营,李振春,黄建平,等. 2014.一种分尺度的面波压制方法[J].石油学报, 35(2):303-309. |
| [39] | 王赟,滕殿波,邢春颖. 2005.多分量地震技术实用化的一些关键问题[J].勘探地球物理进展, 28(3):174-177. |
| [40] | 吴琛,周瑞忠. 2006. Hilbert-Huang变换在提取地震信号动力特性中的应用[J].地震工程与工程振动, 26(5):41-46. |
| [41] | 杨培杰,印兴耀,张广智. 2007.希尔伯特-黄变换地震信号时频分析与属性提取[J].地球物理学进展, 22(5):1585-1590, doi:10.3969/j.issn.1004-2903.2007.05.037. |
| [42] | 袁艳华,王一博,刘伊克,等. 2013.非二次幂Curvelet变换及其在地震噪声压制中的应用[J].地球物理学报, 56(3):1023-1032, doi:10.6038/cjg20130330. |
| [43] | 张军华,吕宁,田连玉,等. 2006.地震资料去噪方法技术综合评述[J].地球物理学进展, 21(2):546-553, doi:10.3969/j.issn.1004-2903.2006.02.033. |
 2015, Vol. 30
2015, Vol. 30

