波动方程数值模拟在油气勘探过程中一直发挥着非常重要的作用.它不仅可以帮助研究人员深入了解地震波的传播规律,认识复杂地质条件下的地震响应特征,还能够合成各种类型的地震观测记录,为资料处理技术方法的研究提供定量分析的基础数据(Carcione et al.,2002; Martin,2004; 薛昭等,2014).然而,复杂模型的波动方程数值模拟计算量和存储量都很大,特别是对三维复杂构造模型的模拟,至今仍然没有得到很好的解决.如何有效提高波动方程数值模拟的计算效率是广大科研工作者共同探寻的目标.
波动方程数值模拟需要高性能的计算机.早在2006年以前,计算机性能的提升还主要是靠提高CPU主频来实现的.随着CPU主频的不断提高,发热量也在不断增加.当主频高达3.8 G的Pentium4处理器问世以后,再通过提高主频来获得的性能提升已变得非常有限,随之而来的CPU发热问题却愈来愈不可控制,稳定性开始降低.“高频高能”的路子走到了尽头,世界各主要CPU制造商纷纷转向发展多核处理器,即在一个物理CPU内植入多个计算核心,通过多核并行处理来提升计算机的总体性能.至此,计算机的发展开始进入一个新纪元.
当前,双核、四核计算机已经十分普遍,CPU也在朝着众核方向快速发展.然而,现有的波动方程模拟及偏移程序基本都是采用MPI实现并行计算的(张文生等,2001,2015; 朱振宇等,2003; 赵景霞等,2006; 宋若龙等,2010; 李焱等,2012; 宋国杰等,2012).这种进程级粒度的并行计算方式在PC-Cluster之类的分布式计算机上效果很好,可是在单个节点上却受内存限制,往往只能使用少数几个甚至一个计算核心,多核处理器的效能难以得到有效发挥(谢桂生等,2005).本文将占据波动方程模拟主要计算时间的递推公式分解为矩阵-向量乘法、向量对应元素乘法和向量对应元素减法等基本运算,通过MEX文件机制,在MATLAB中引入OpenMP多线程并行计算,解决了MPI进程级并行在内存使用受限的情况下,多核CPU利用效率低的问题,即在进程中实现多线程并行,多个线程共享内存,并行计算,有效提高多核处理器的计算能力.
1 MATLAB编程的优势计算机程序设计语言有很多种,经过不间断淘汰,仍然被广泛使用的都在特定领域保持着优势,如C语言适合写系统,FORTRAN语言适合数值计算,正所谓“尺有所短,寸有所长”.MATLAB较传统的计算机编程语言(FORTRAN和C)主要有以下优势:
(1)编程简单高效.MATLAB编程不需要声明变量类型,由系统自动完成动态内存的分配和释放,并提供了如lu、eig、inv、sort、fft等大量计算效率很高的函数直接调用.这非常有助于研究者将有限的时间和精力专注于如何解决问题,而非实现细节.因此,MATLAB是非常适合科学研究的计算机编程工具,尤其是用它快速实现设计方法的原型.
(2)程序调试方便,可视化功能强.MATLAB是一种解释性语言,解释器按顺序逐条执行每个语句,用分号即可控制计算结果的显示输出.系统提供的Profiler程序性能分析工具,通过统计各条语句的执行次数和运行时间,能帮助程序员快速锁定计算热点(计算热点是程序中计算最集中最费时的代码段,也是优化改进的焦点).此外,MATLAB很容易在程序运行过程中实时的数据成图,数据分析方便直观.图 1是Marmousi模型正演模拟的一幅波场快照.震源激发的地震波场(前景)叠合在速度模型(背景)之上,能够清晰的观察到地震波的透射、反射和干涉,地震波沿高速层传播产生的折射波,强界面间的多次波,以及断层对地震波的影响.类似这种直观的数据分析方式非常有利于加深对地震波传播规律的理解,而这些可视化技术却是让普通程序员用C或Fortran等传统计算机编程语言难以实现的.
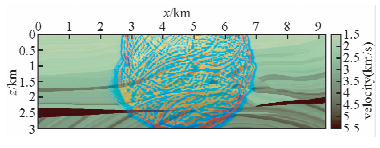 | 图 1 Marmousi模型正演模拟波场快照 Fig. 1 Marmousi model forword modeling wavefield snap |
(3)程序性能随MATLAB版本升级获得提升.MATLAB针对不同的处理器架构进行了优化,并及时更新BLAS、LAPACK、FFTW、MKL等基础库.自版本R2007a以 后,引入支持多线程的内置函数,使得如sin、exp、det、lu、 A\b、fft等众多函数都能在多核计算机上并行运算.自版本R2010b以后,又在其Parallel Computing Toolbox中 引入GPU并行计算,追赶更高的计算效率.由于各版本函数接口保持一致,原程序几乎不需要修改就可以随MATLAB软件升级得到比较大的性能提升.相对而言,目前C和FORTRAN程序仅靠编译器升级带来的性能提升则非常有限.
同时也要指出,由于MATLAB是解释性语言,每当程序运行时解释器才逐条翻译并执行语句,而解释器的翻译工作也要耗费CPU时间,因此,相比FORTRAN和C等编译型语言的程序执行效率要低(编译型语言的程序经编译器编译成机器代码后即可直接运行).特别是当循语句中循环次数很大,而单个循环的计算量又很小时,此时翻译工作量比重相对较高,MATLAB程序的运行效率会明显降低,这正是许多人认为MATLAB不适合搞大型计算的主要原因.不过针对这个问题,MATLAB也给出了如循环向量化、MEX文件改写循环代码等技术策略,可以得到很好的解决(MATLAB Programming & Fundamentals,2015).
2 波动方程外推公声波方程或弹性波方程经空间域半离散化后,用Galerkin法可以导出对应的有限元方程.经单元合成后,二者的有限元方程可以统一写为(Marfurt,1984; 监凯维奇,1985; 王勖成,2003)

其中,M是全局质量矩阵,C是全局阻尼矩阵,K是全局刚度矩阵,αt是t时刻计算网格上的波场向量,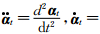
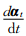 ,Q t是t时刻计算网格上的震源向量.
,Q t是t时刻计算网格上的震源向量.
在中心差分中,

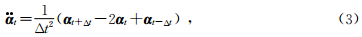
将(2)、(3)两式代入方程(1)得
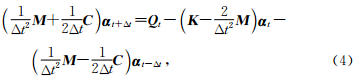
若已经求得 α t-Δt和α t,通过上式可以进一步求出 α t+Δt,(4)式即为波动方程中心差分法显式时间外推公式.当采用集中质量矩阵和集中阻尼矩阵时,(4)式左端的系数矩阵是一个对角线矩阵,它的逆就是对角线元素取倒,可以简化线性方程组的求解.
在波动方程正演计算中,除去系数矩阵的计算与合成,以及必要的数据I/O,(4)式几乎占据全部的计算量.只要式能够实现并行运算,整个正演程序的计算效率就能显著提高.递推式是典型的数据依赖,不能采用任务并行的并行方式.然而,离散化形成的全局系数矩阵都是大规模稀疏矩阵(阶次一般都在106量级以上),一次外推的计算量十分可观.因此,可以在每次波场外推时采用SPMD(单程序多数据)的并行方式提高计算效率.图 2是两个向量对应元素相乘的SPMD并行计算示意图.A和B是两个长度相等的向量,A×B表示两个向量的对应元素相乘.在多核计算机上,可以先根据CPU核数将A、B两个向量按照同样的方式拆分为长度大致相等的几块,再让CPU的每个核选择其中的一块数据做对应元素的乘法运算,多个核心同时计算,提高计算效率.
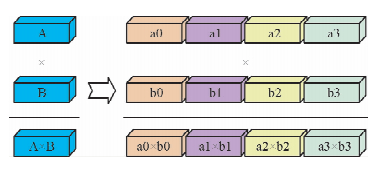 | 图 2 SPMD并行模式实现两个向量的对应元素相乘 Fig. 2 Tow vector elements multiply in SPMD parallel mode |
MEX文件是用C或FORTRAN语言按一定规则编写的,能够在MATLAB环境下运行的动态链接库.MEX文件调用MATLAB提供的API函数接口操作数据,对用户而言,它就像是一个MATLAB的内置函数.MATLAB通过MEX文件机制解决了两个关键问题,一是可以在MATLAB中调用已有的C和FORTRAN程序,二是可以将低效率的MATLAB代码用C或FORTRAN改写.所以,在MEX文件中引入OpenMP就可以实现用户热点代码的多线程并行.
如前所述,波动方程数值模拟的计算量集中在式(4).若令
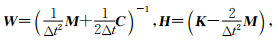
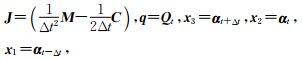
则(4)式可改写为

(5)式的计算分为两步,首先计算方程的右端项,再解线性方程组.实际运算包括矩阵-向量乘法,向量对应元素的相乘和相减,都可以用OpenMP按数据分割的并行方式实现多线程并行计算(如图 2).图 3是两个向量对应元素相乘的OpenMP多线程并行MEX文件C源码示例.其中,第2和第13行是为引入OpenMP多线程并行而加入的.第2行告诉编译器OpenMP的函数声明,第13行告诉编译器后面的for循环要并行执行,同时指定各个变量的作用域(Chapman et al.,2007; 周伟明,2009).除去这两行剩余的代码是一个普通的串行MEX文件C源码.关于具体的MEX文件编写规则和API函数说明可以参考MATLAB文档(MATLAB External Interfaces,2015).
 | 图 3 向量对应元素相乘的OpenMP多线程并行MEX文件C源码 Fig. 3 The C code of two vectors' elements multiply in MATLAB MEX file with OpenMP |
MATLAB默认的MEX文件编译环境并不支持OpenMP多线程并行.要让加入OpenMP编译语句后的MEX文件编译链接通过,还必须正确配置编译环境.下面以64位系统C语言MEX文件的编译环境设置为例:
Windows环境下:
①安装Visual C++编译器.需Visual Studio 2005以上版本才支持OpenMP.为编译64位应用程序,安装时要选择完全安装.
②运行mex -setup,为MATLAB指定MEX文件的编译器.
③修改步骤②中MATLAB系统更新的mexopts.bat文件,在编译参数中添加/openmp,使编译器支持OpenMP语句.
Linux环境下:
①安装gcc编译器.gcc需要4.2以上版本才支持OpenMP.
②运行mex -setup,为MATLAB指定MEX文件的编译器.
③修改步骤②中MATLAB系统更新的mexopts.bat文件,在编译参数中添加-fopenmp,使编译器支持OpenMP语句.
5 并行计算实例如图 4所示二维均匀弹性介质模型,模型范围8 km×8 km,在4 km深处存在一个水平弹性界面,界面上方介质vp=3200 m/s,vs=2000 m/s,界面下方介质vp=4000 m/s,vs=2500 m/s.采用纵波震源,放置于(x=4000 m,z=3000 m)处,震源函数为25 Hz主频的Richer子波,子波延迟40 ms.检波器置于地表接收.
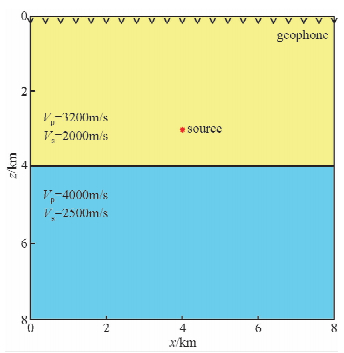 | 图 4 计算模型 Fig. 4 The elastic geologic model |
计算采用2.5 m网格距,15度吸收边界条件.图 5是几个时刻的波场快照,u代表水平分量,w代表垂直分量,从中可以观察到界面附近产生的转换横波.计算过程中形成的全局系数矩阵的阶数达到了4×107量级.在四核计算机上,当采用串行程序模拟6 s记录时,正演计算共耗时35901 s,其中波场外推式共执行12980次,计算右端项累计耗时32346 s,解方程累计耗时2891 s;当改用四核并行计算以后,正演计算共耗时12005 s,其中右端项累计耗时9592 s,解方程累计耗时1732 s.表 1列出了多核并行计算的加速比.可以看到,右端项计算平均加速3.37倍,解对角线方程平均加速1.66倍,整个波场外推式的计算平均加速3.11倍.虽然,本文只针对波场外推式的计算实现了多核并行,但由于它在正演计算中占主要的计算量,这也使得正演计算的总体计算速度提高了近3倍.
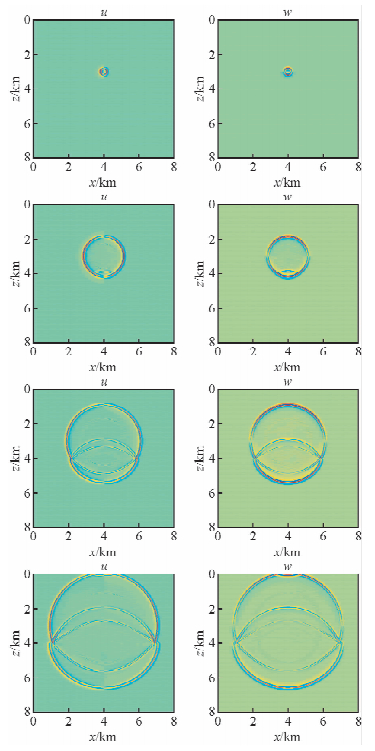 |
图 5 二维弹性波方程数值模拟波场快照 u代表水平分量,w代表垂直分量. Fig. 5 The elastic wavefield snap u is horizontal component, w is vertical component. |
|
|
表 1 四核计算机上的加速比测试 Table 1 Speed-up on 4-core computer |
本文基于MATLAB科学计算平台构建波动方程数值模拟并行算法,有以下结论:
(1)由于波动方程数值模拟耗费的存储量大,目前以MPI方式实现的“进程级”并行计算,在计算节点上要将可用的内存均分给该节点上的每个进程,因而受内存大小限制,常常不能利用节点上的全部计算核心;
(2)以OpenMP方式实现的“线程级”并行计算,所有线程共享内存,因此在相同的内存大小情况下,可以使用全部计算核心,提高并行效率;
(3)虽然波动方程时间递推式是典型的数据依赖,不能采用任务并行的并行方式.但是,每次外推的计算量都很大,可以针对构成外推式的矩阵-向量乘法、向量对应元素相乘和相减等运算,采用多线程数据并行的方式提高计算效率,此为本文的一个创新;
(4)通过MATLAB的MEX文件机制,在MATLAB中引入OpenMP多线程并行计算,是本文的另一个创新.
致 谢 感谢本文匿名审稿人和编辑给予的帮助!
| [1] | Carcione J M, Herman G C, ten Kroode A P E. 2002. Seismic modeling[J]. Geophysics, 67(4):1304-1325. |
| [2] | Chapman B, Jost G,van der Pas R. 2007. Using OpenMP:Portable Shared Memory Parallel Programming[M]. Cambridge:The MIT Press. |
| [3] | Li Y, Hu X Y, Yang W C, et al. 2012. A study on parallel computation for 3D magnetotelluric modeling using the staggered-grid finite difference method[J]. Chinese J.Geophys.(in Chinese), 55(12):4036-4043, doi:10.6038/j.issn.0001-5733.2012.12.015. |
| [4] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 49(5):533-549. |
| [5] | Martin G S. 2004. The marmousi2 model, elastic synthetic data, and an analysis of imaging and AVO in a structurally complex environment[Ph. D. Thesis]. Houston:University of Houston. |
| [6] | MATLAB® External Interfaces. 2015. http://www.mathworks.com/help/pdf_doc/matlab/apiext.pdf. |
| [7] | MATLAB Programming &Fundamentals. 2015. http://www.mathworks.com/help/pdf_doc/matlab/matlab_prog.pdf. |
| [8] | Song G J, Yang D H, Tong P, et al. 2012. Parallel WNAD algorithm for solving 3D elastic equation and its wavefield simulations in TI media[J]. Chinese J.Geophys.(in Chinese), 55(2):547-559, doi:10.6038/j.issn.0001-5733.2012.02.017. |
| [9] | Song R L, Liu J X, Yao G J, et al. 2010. Parallel finite difference modeling of acoustic fields in nonaxisymmetric cased hole[J]. Chinese J.Geophys.(in Chinese), 53(11):2767-2775, doi:10.3969/j.issn.0001-5733.2010.11.026. |
| [10] | Wang X C. 2003. Finite Element Method (in Chinese)[M]. Beijing:Tsinghua University Press. |
| [11] | XIE Gui-Sheng, LIU Hong, ZHAO Lian-Gong. 2005. Parallel algorithm based on the multithread technique for pseudospectal modeling of seismic wave[J]. ProgressinGeophys. (in Chinese), 20(1):17-23,doi:10.3969/j.issn.1004-2903.2005.01.004. |
| [12] | Xue Z, Dong L G, Li X B, et al. 2014. Discontinuous Galerkin finite-element method for elastic wave modeling including surface topography[J]. Chinese J.Geophys.(in Chinese), 57(4):1209-1223, doi:10.6038/cjg20140418. |
| [13] | Zhang W S, Guan Q, Song H B. 2001. Prestack depth migration by hybrid method with high precision and its parallel implementation[J]. Chinese J.Geophys., 44(4):542-551,doi:10.3321/j.issn:0001-5733.2001.04.013. |
| [14] | Zhang W S, Luo J, Teng J W. 2015. Frequency multiscale full-waveform inversion[J]. Chinese J. Geophys. (in Chinese), 58(1):216-228, doi:10.6038/cjg20150119. |
| [15] | Zhao J X, Zhang S L, Sun P Y, et al. 2006. 3-D parallel prestack depth migration of synthetic source records[J]. Chinese J.Geophys.(in Chinese), 49(1):225-233, doi:10.3321/j.issn:0001-5733.2006.01.029. |
| [16] | Zhou W M. 2009. Multi-Core Computing and Programming(in Chinese)[M]. Wuhan:Huazhong University of Science and Technology Press. |
| [17] | Zhu Z Y, Liu H, Li Y M. 2003. Application of equation prestack depth migration and parallel computing in South Yellow Sea area[J]. Progress inGeophys. (in Chinese), 18(2):302-305, doi:10.3969/j.issn.1004-2903.2003.02.019. |
| [18] | Zienkiewicz O C. 1985. The Finite Element Method (in Chinese)[M]. Yin Z Y, Jiang B N Trans. Beijing:Science Press. |
| [19] | 监凯维奇O C. 1985.力学名著译丛-有限元法[M].尹泽勇,江伯南译.北京:科学出版社. |
| [20] | 李焱,胡祥云,杨文采,等. 2012.大地电磁三维交错网格有限差分数值模拟的并行计算研究[J].地球物理学报, 55(12):4036-4043, doi:10.6038/j.issn.0001-5733.2012.12.015. |
| [21] | 宋国杰,杨顶辉,童平,等. 2012.求解3D弹性波方程的并行WNAD方法及其TI介质中的波场模拟[J].地球物理学报, 55(2):547-559, doi:10.6038/j.issn.0001-5733.2012.02.017. |
| [22] | 宋若龙,刘金霞,姚桂锦,等. 2010.非轴对称套管井中声场的并行有限差分模拟[J].地球物理学报, 53(11):2767-2775, doi:10.3969/j.issn.0001-5733.2010.11.026. |
| [23] | 王勖成. 2003.有限单元法[M].北京:清华大学出版社. |
| [24] | 谢桂生,刘洪,赵连功. 2005.伪谱法地震波正演模拟的多线程并行计算[J].地球物理学进展, 20(1):17-23, doi:10.3969/j.issn.1004-2903.2005.01.004. |
| [25] | 薛昭,董良国,李晓波,等. 2014.起伏地表弹性波传播的间断Galerkin有限元数值模拟方法[J].地球物理学报, 57(4):1209-1223, doi:10.6038/cjg20140418. |
| [26] | 张文生,关泉,宋海斌. 2001.高精度混合法叠前深度偏移及其并行实现[J].地球物理学报, 44(4):542-551, doi:10.3321/j.issn:0001-5733.2001.04.013. |
| [27] | 张文生,罗嘉,滕吉文. 2015.频率多尺度全波形速度反演[J].地球物理学报, 58(1):216-228, doi:10.6038/cjg20150119. |
| [28] | 赵景霞,张叔伦,孙沛勇,等. 2006.三维并行合成震源记录叠前深度偏移[J].地球物理学报, 49(1):225-233, doi:10.3321/j.issn:0001-5733.2006.01.029. |
| [29] | 周伟明. 2009.多核计算与程序设计[M].武汉:华中科技大学出版社. |
| [30] | 朱振宇,刘洪,李幼铭. 2003.波动方程叠前深度偏移及并行计算在南黄海地区的应用[J].地球物理学进展, 18(2):302-305, doi:10.3969/j.issn.1004-2903.2003.02.019. |
 2015, Vol. 30
2015, Vol. 30

