瞬变电磁法(TEM)是一种有效的寻找良导电金属矿的地球物理方法，应用广泛，有许多成功的找矿实例.定源回线装置主要用于详查阶段，确定目标地质体的较为准确的埋深、边界等几何参数(蒋邦远，1998；李貅，2002;牛之琏，2007).定源回线装置在实际测量中常使用边长数百米的矩形发射回线，在垂直于矩形长边的测线(包括框内、框外)上观测瞬变响应.发射源可以固定放置于靠近回线边的某个位置，可以用大功率发射.因此，其场源具有发射磁矩大，场较为均匀及随距离衰减慢等特点，适合于深部矿产勘查工作(蒋邦远，1998).

定源回线装置瞬变电磁场计算的国内外研究成果较多，Lee给出了阶跃波激发条件下大回线装置层状大地感应电动势的表达式(Lee and Lewis，1974).Poddar将回线边分割为小的电流段，以小电流段作为电偶极子沿回线进行线积分，给出了层状大地表面矩形回线源频域场表达式(Poddar，1983).Raiche采用电偶极子线积分的方法，给出了层状大地多边形回线源的瞬变电磁场的算法(Raiche，1987).Goldman利用水平电偶极源激发的电磁场推导出矩形回线在两层介质表面激发的电磁场(Goldman and Fitterman，1987).Wang将Dufort-Frankel有限差分格式应用于回线源激发瞬变电磁场的三维数值模拟(Wang and Hohmann，1993).殷长春利用并矢格林函数理论和积分方程方法计算两层大地中三维异常体的频率域电磁响应，并利用反余弦变换方法将其转换为时间域电磁响应(殷长春和刘斌，1994).Singh利用超几何分布函数化简了圆形发射回线电磁场表达式中的贝塞尔函数的乘积，从而求解出圆形回线在任意点激发的频率域电磁场(Singh and Mogi，2005).丁燕飞采取早、中、晚期分别计算的方式实现了均匀半空间表面大定源瞬变电磁响应的快速算法(丁艳飞等，2012).李建慧实现交错网格有限差分法和有限体积法对回线源瞬变电磁法的三维正演(李建慧等，2013).孙怀凤对Wang与Hohmann的经典时域算法做了改进，实现了考虑关断时间的回线源激发TEM三维时域有限差分正演(孙怀凤等，2013).以上研究成果对于定源回线装置瞬变电磁法的正演理论的完善起到了重要的作用.

目前多数商品化的瞬变电磁仪器可实现三分量数据采集.然而对于定源回线装置的解释理论研究目前仅为一维反演和视电阻率成像，并且大多只利用单分量数据，三分量有用数据还未充分利用.目前还缺少实用快速的实现三维三分量反演的有效方法.薛国强对大回线源瞬变电磁成像进行了理论分析及数值计算，采用电偶极子迭加方法解决了回线源非中心点视电阻率计算问题(薛国强等，2004，2007，2010)；李建平将电偶极子积分转变为求和，获得了任意形状回线源瞬变电磁全区视电阻率公式(李建平等，2007).张成范利用了电偶极子求和的方法，获得了矩形回线的全区视电阻率公式(张成范等，2009).熊彬利用逆样条插值计算方法获得了大回线瞬变电磁法全区视电阻率计算方法(熊彬，2005).石显新将大定源回线定义的视电阻率应用于实际资料解释中获得了良好的效果(石显新等，2009年).李貅、戚志鹏、武军杰等等定义了定源回线瞬变电磁法的水平分量全区视电阻率和约束条件下的一维反演(戚志鹏等，2011，2014；武军杰等，2012，2013).

Barnett认为定源回线装置瞬变电磁法激发的导电薄板中产生的涡流可以等效为电流环，从而提出了等效电流环的方法，并加以证实(Barnett，1984).之后Duncan和Eadie将等效电流环应用于地-井瞬变电磁法的资料解释中，但是由于受限于单分量探头而在解释中只利用了Z分量(Duncan，1987；Eadie and Staltari，1987).以上研究对于瞬变电磁方法的反演解释起到了重要的作用，但是目前还缺少实用快速的解决定源回线装置瞬变电磁法三维三分量反演的有效方法.

本文借鉴了Barnett的方法，将等效电流环应用于地面定源回线三分量的数据解释中，提出了基于等效电流环的三分量纯异常三维反演方法.首先根据实测曲线特征估算定源回线TEM三分量背景场，进而近似求得自由空间三分量感应磁场的纯异常场.在自由空间建立电流环模型，并以电流环产生的三个分量磁场拟合由实测数据获得的纯异常场，最终通过系列电流环的参数来综合确定异常体的几何参数.

本文中介绍了等效电流环的基本原理，对于提取纯异常和纯异常反演的理论进行了论述.文中对模型和实测数据分别进行了反演验证.理论模型和实测数据反演结果表明，等效电流环反演结果能够较好确定导电体的中心位置、半径、埋深、倾向、倾角等几何参数.本文提出的基于等效电流环的解释方法同时利用三个分量数据，计算快速、可靠、使反演结果更加合理，为定源回线装置瞬变电磁法提供了一种有效的解释方法.

设导电薄板位于均匀一次场中，当发射回线中的电流突然关断，一次场瞬间消失时，根据法拉第定律，为了维持导体内原来的均匀磁场，板体内立即感应出涡流，导电薄板上感应涡流的磁矩总是垂直薄板(蒋邦远，1998).感应涡流在板内将形成与导电板体形状相似的电流环分布，早期是集中在板的边缘，然后向导体中心扩散(Barnett，1984).短时间间隔后，这一电流分布达到了一种准平衡状态，然后做简单地振幅衰减.由理论和数值模拟可以证明，不仅在晚期，即便在较早期，这一电流分布也可以用一个等效电流环表示(Barnett，1984)，如图 1所示.

图 1

Fig. 1

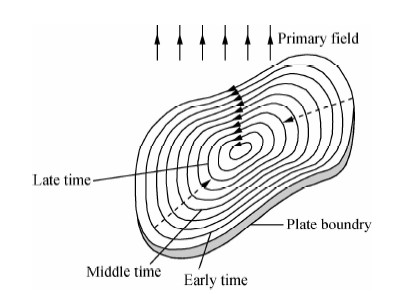图 1 导电薄板涡旋电流分布示意图 (据Barnett C. T,1984) Fig. 1 The diagram of eddy in conductive plate (Barnett，1984)

同样地，如果均匀的一次场中存在一个导电球体，当发射回线中的电流突然关断，一次场瞬间消失时，按法拉第电磁感应定律为了维持球内原来的均匀磁场，会立即感应出涡流，并仅仅分布在球体的表面，之后球体内的环形电流的分布则受这些电流引起的磁场相互影响所支配，向球内移动.此时电流不仅向内移动而且因热损耗而减弱.最后电流的分布不再随时间而改变，靠近球心电流密度沿半径的距离线性地增加，在二分之一半径内相对均匀分布，并向球边缘微微地减弱.此后电流和相应的外部磁场开始以某一时间常数呈指数衰减，直到消失(蒋邦远，1998)，如图 2所示.

图 2

Fig. 2

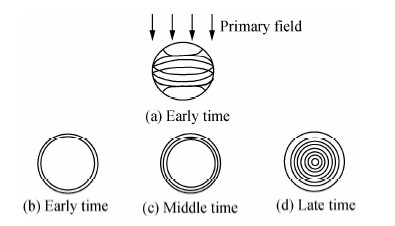图 2不同时期球体中涡流的分布(据McNeill,1980) (a)早期涡流在球体表面的分布;(b)-(d)不同时期 球赤道平面上的涡流分布. Fig. 2 The distribution of eddy in sphere at different time (McNeill,1980) (a) Surface distribution of eddy at the early time; (b)-(d) Surface distribution of eddy at the different time in the equatorial plane.

通过以上理论可知，矿体受激发所产生的涡流可以用矿体内流动的“等效电流环”的场相等效.圆型电流环能够很好地反映透镜状的导电体.描述圆形电流环模型的参数有7个：中心位置(X、Y、Z)、半径、电流值、倾向、倾角.

自由空间建立笛卡尔坐标系，定义Z分量方向向上，电流环位于X-Y平面内，中心与坐标原点重合，半径为R，电流强度为I.

由图 3可以看出：

图 3

Fig. 3

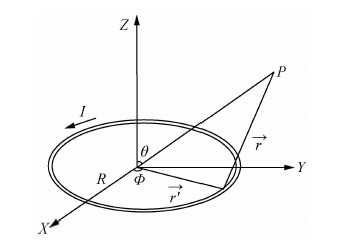图 3自由空间电流环 Fig. 3 Current circle in free space

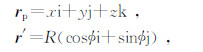
由矢量运算规则可知：

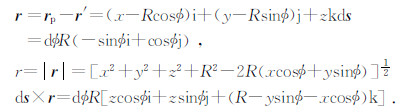
根据毕奥-萨伐尔定律可知：

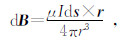
则电流环产生的磁场各分量表达式为

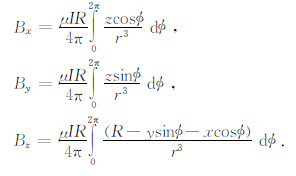
2 纯异常场提取

等效电流环产生的磁场各分量表达式是在自由空间，而实测数据是在半空间中，并且为感应电动势，因此在实际数据处理中还需在实测数据中提取纯异常，即消除地层、地形、装置等的影响，只保留异常体产生的瞬变响应，再转换为感应磁场值.

对于如均匀半空间中低阻板状体理论模型，则其纯异常可以通过分别计算均匀半空间背景和总体响应，相减并积分获得异常场值.而对于实测的三分量感应电动势，则可以利用约束条件来构建围岩地电模型，求取背景场值，并与实测值比较，采用人机交互的方式获得异常场数据.根据实测和背景曲线对比情况，结合收集到的地质、物探、物性、测井、地质编录等信息实时调整模型参数，获得合适的背景值.在求取感应电动势的纯异常值后，只需对时间积分即可获得相应的纯异常感应磁场值.

3 三分量纯异常三维反演

圆形电流环产生的三个分量的磁场的公式并不复杂，因此可以通过不断调整电流环参数，根据公式计算等效电流环产生的磁场同时拟合三分量实测数据，达到反演的目的.利用最小二乘方法即可实现.构建的目标函数为

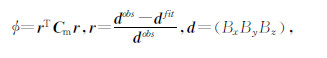
其中 C _m为方差矩阵.

在实际数据处理中需要根据实测时间道反演一组电流环来分别拟合不同道实测数据.实测数据的点数一般应大于参数的个数，如果测点数不足以求出参数，则需要在反演中对某些参数进行约束.

为验证基于等效电流环的TEM反演解释方法，建立系列理论模型进行正演计算. 装置选择定源回线装置，在均匀半空间中建立不同倾角三维薄板低阻体，模拟低阻薄板的瞬变响应三分量曲线.正演软件使用EM Vision.反演计算使用本文提出的基于等效电流环的TEM反演解释方法.

低阻薄板模型、发射框与测线位置关系如图 4所示.测线长度800 m，线距100 m，点距50 m，起止点号均为-400~400.发射框1000 m×1000 m，中心点位置(0，0).均匀半空间电阻率1000 Ω·m，低阻薄板电导率50 S，薄板倾角0°，尺寸为300 m×300 m，中心点位置(0，0)，埋深150 m.

图 4

Fig. 4

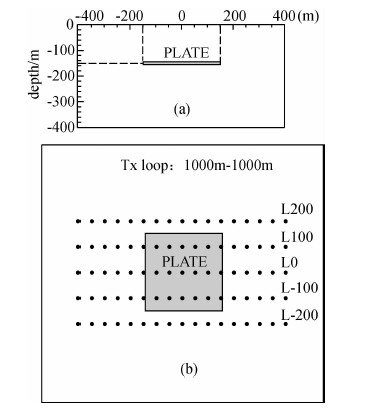图 4 理论模型、发射框及测点图 (a)断面图; (b) 平面图. Fig. 4 The plate model and survey lines (a)Section figure; (b)Plan figure.

图 5为反演结果不同视角显示对比图.图中显示了反演电流环在透视、俯视、正视和侧视视角下的形态.透视图中可以看出反演电流环的空间形态，俯视图中显示了电流环与测线在平面上的位置关系，正视和侧视图则显示电流环的倾向和倾角.

图 5

Fig. 5

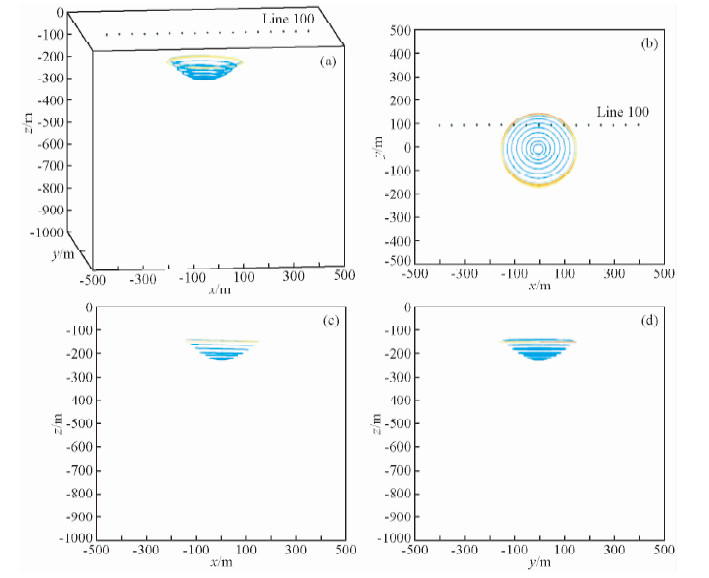图 5 L100线反演结果不同视角对比图 (a)透视图;(b)俯视图;(c)正视图;(d) 侧视图. Fig. 5 The inversion results figure with different view angle of line100 (a) Perspective view;(b)Vertical view;(c) Front view;(d) Side view.

表 1为L100线反演不同时刻电流环的参数.表中列举了从173 μs到18.875 ms 12道采样窗口的反演结果，包括电流环的半径、幅值、中心位置、倾向、倾角.可以看出，0.173~5.607 ms反演结果与理论模型较为吻合，电流环的半径、位置与理论值误差不超过5%，这是因为在涡旋电流在早期主要分布在导电板体的边缘部分，并且幅值较强.而自6.669 ms开始电流环半径、电流值开始逐步减小，不断向板体中心聚拢.说明涡旋电流自导电板体的边缘开始向中心传播，并最终消失.随着时间增加，反演所得板体的埋深逐渐增大，这是由于纯异常提取不完全造成的.目前纯异常提取一般是自总体响应中减掉背景场的响应.而实际上TEM响应并非完全等于异常体和围岩的响应之和.晚期道数值较小，受此影响相对较大，因此在晚期道中电流环的深度偏大.电流环中心点的平面位置与理论值自始至终对应很好.

表 1(Table 1)

表 1 L100线不同时间道反演电流环参数表 Table 1 Inversion filament parameters of different time channel of line 100 t(ms) 半径(m) 电流(mA) X(m) Y(m) Z(m) 倾向(°) 倾角(°) 0.173 152.31 -1787.5 0.50 -1.77 -150.54 0.50 0.00 0.414 151.47 -1772.5 0.69 -2.19 -150.54 0.83 0.00 0.990 150.35 -1383.5 0.92 -1.30 -150.54 0.73 0.00 2.356 144.71 -661.23 0.48 -4.00 -153.85 0.73 1.46 5.607 143.92 -132.82 0.50 -3.40 -154.20 1.13 1.42 6.669 125.94 -115.87 -0.40 -1.12 -163.95 0.00 1.39 7.931 107.30 -95.91 -1.41 0.43 -182.14 0.00 1.62 9.434 86.75 -78.59 -1.62 2.21 -198.93 0.32 1.18 11.221 65.97 -60.49 -1.75 2.87 -209.19 0.08 0.60 13.345 48.10 -44.62 -1.86 0.06 -218.76 0.04 0.00 15.872 31.03 -35.37 -1.80 -0.53 -222.56 0.57 0.00 18.875 19.07 -27.86 -1.70 -1.63 -225.22 0.85 0.00

表 1 L100线不同时间道反演电流环参数表 Table 1 Inversion filament parameters of different time channel of line 100

图 6为五条测线总体反演结果，反演中仅使用了早、中期道数据.可以看出，不同位置的五条测线的反演结果基本重合在一起，反演结果很好地反映了理论模型的平面中心、尺寸、埋深和倾角.

图 6

Fig. 6

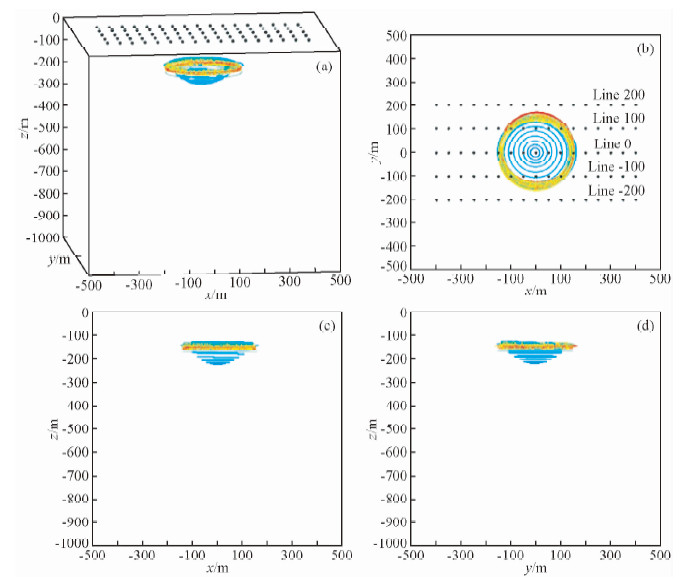图 6 五条测线线反演结果不同视角对比图 (a)透视图；(b)俯视图；(c)正视图；(d) 侧视图. Fig. 6 The inversion results figure with different view angle of 5 lines (a)Perspective view；(b)Vertical view；(c)Front view；(d)Side view.

低阻薄板模型、发射框与测线位置关系如图 7所示.测线、发射框、均匀半空间参数同上例.低阻薄板电导率50S，倾向180°(沿测线向右为0°)，倾角30°，尺寸为300 m×300 m，板体中心点位置为(20，0，-225)，顶界面埋深150 m.

图 7

Fig. 7

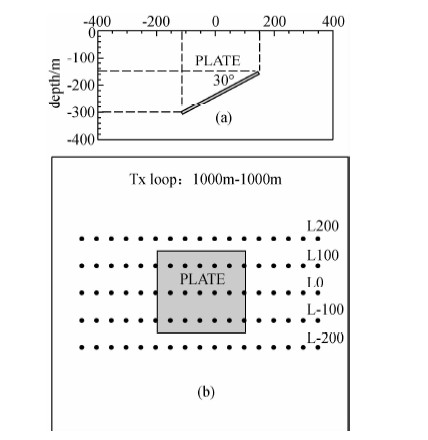图 7理论模型、发射框及测点图 (a)断面图；(b) 平面图. Fig. 7 The plate model and survey lines (a) Section figure; (b) Plane figure.

表 2为五测线在0.990 ms反演获得的电流环的参数.表中列举了L-200、L-100、L0、L100、L200五条测线的反演结果.可以看出不同位置测线的反演结果大体一致，与理论模型基本符合.由于在反演中采用的时间道较早，反演的电流环半径与理论值相符，反映的是板体边界.

表 2(Table 2)

表 2 不同测线0.990 ms时间道反演电流环参数表 Table 2 Inversion filament parameters of different lines at time channel 0.990ms 测线 半径 (m) 电流(mA) X (m) Y (m) Z (m) 倾向 (°) 倾角 (°) L-200 137.166 -1303.80 11.98 -2.22 -230.84 179.63 25.22 L-100 143.78 -1090.71 8.98 -0.29 -216.00 176.04 22.90 L0 143.18 -1263.27 12.00 3.00 -233.39 180.00 30.00 L100 145.77 -1431.93 6.13 4.32 -217.47 182.07 20.25 L200 154.25 -1304.08 10.52 -11.10 -256.18 180.00 27.97

表 2 不同测线0.990 ms时间道反演电流环参数表 Table 2 Inversion filament parameters of different lines at time channel 0.990ms

图 8为五条测线总体反演结果.图中可以看出五条测线的反演结果基本重合在一起，反演结果较准确地反映了理论模型的中心、尺寸、埋深和倾角.

图 8

Fig. 8

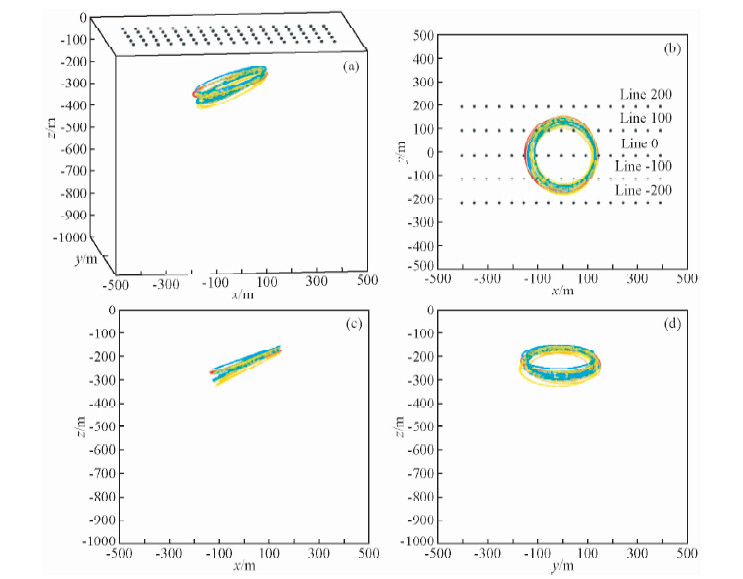图 8五条测线线反演结果不同视角对比图 (a)透视图;(b)俯视图;(c)正视图;(d) 侧视图. Fig. 8 The inversion results figure with different view angle of 5 lines (a) Perspective view;(b) Vertical view;(c) Front view;(d) Side view.

夏日哈木铜镍矿区位于青海省祁漫塔格整装勘查区，地处柴达木盆地西南缘，是东昆仑成矿带新发现的一处超大型岩浆熔离型铜镍硫化物矿床(李世金等，2012).

在HS26异常区开展了定源回线瞬变电磁法的野外试验.测线(L9、L11、L13、L15、L17)与地质勘探线重合.试验发射框600 m×600 m，发射电流20 A，发射基频6.25 Hz.接收使用PEM探头(10 kHz)，接收面积3850 m²，测量三分量数据.实测中定义Z分量向上为正，X分量以向北为正，Y方向以向西为正.

图 9为5条测线测点分布平面示意图.实际完成了L9、L11、L13、L15、L17五条测线的三分量数据采集工作，各测线11号点与发射线框重合，实际测量时向南偏离测线20 m.

图 9

Fig. 9

图 9 发射框及测点分布图 Fig. 9 Transmit loop and station distribution

限于篇幅，本文中仅列出L11线实测曲线与地质断面对比图，如图 10所示.L11线地质断面图中可以看出，L11线已被钻孔控制，钻孔间距40 m，矿体整体范围在8-18号点之间，叠加厚度较大，深度范围约为几十米到300 m.

图 10

Fig. 10

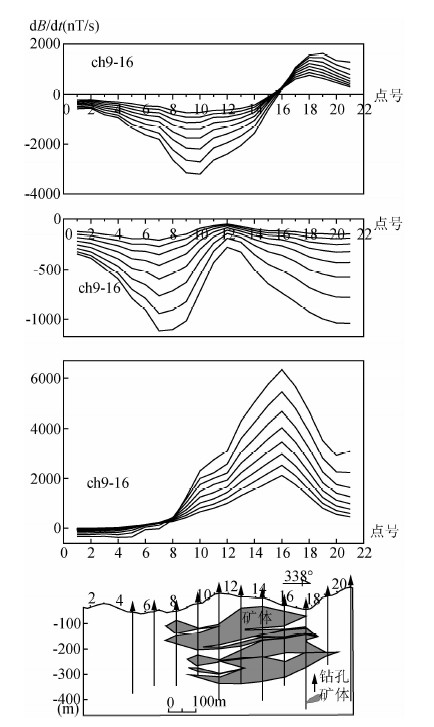图 10 L11线三分量TEM曲线及地质断面图 (a) X分量;(b) Y分量;(c) Z分量; (d) 地质剖面. Fig. 10 Three-component TEM response curves and geological section of line 11 (a) X component; (b) Y component; (c) Z component; (d) Geological section.

图 10中列出了三分量瞬变响应中期道(9-16)曲线与地质断面图对比情况.可以看出X分量曲线呈“S”型，并以16号点为界呈左负右正特征，这与X分量正方向的确定有关.9、18号点对应的负、正二峰值分别与矿体的边界位置相对应.Y分量整体为负(Y分量正方向定义引起的)，在12号点处出现异常显示.Z分量曲线为正异常，峰值对应16号点，且南缓北陡.

可以看出由于装置为定源回线装置，并且测线在框内、框外均有布置，实测曲线中即包含了装置引起的异常还包括矿体引起的异常显示.直接分析实测曲线很难获得足够的矿体信息.

图 11为五测线反演结果综合对比图，图中显示了5条测线不同时间道的电流环反演结果.5测线反演结果基本一致，矿体中心平面位置均在L11线15号点附近.电流环的半径平均约为200 m，X方向边界分别在10和19点，电流环深度范围40~300 m，略向南倾，这与实际矿体是符合的.可以看出，对于实测数据，反演结果能够为矿体的解释提供可靠有效的信息.

图 11

Fig. 11

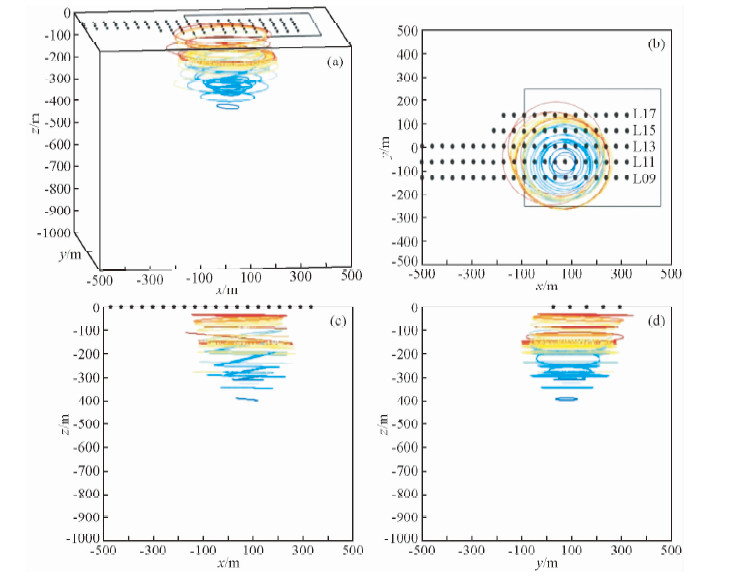图 11实测数据反演结果不同视角对比图 (a)透视图; (b)俯视图; (c)正视图; (d) 侧视图. Fig. 11 The inversion results figure with different view angle of field data (a) Perspective view; (b) Vertical view; (c) Front view; (d) Side view.

定源回线瞬变电磁方法应用越来越广泛，但是三分量解释方法不能满足目前的生产需求，需要研究快速实用的解释方法.文中针对定源回线装置瞬变电磁法提出的基于等效电流环的三分量纯异常三维反演方法，可以获得导电体所产生涡流的几何分布，从而近似确定导电地质体的中心、尺寸、倾角等几何参数.该方法计算快速、可靠，能够满足目前的勘查需求.