2. 中国海洋大学海洋地球科学学院, 青岛 266100
2. College of Marine Geosciences, Ocean University of China, Qingdao 266100, China
地震勘探是通过人工激发、观测和分析在地层中传播的地震波,查明地下地层的形态和性质.地震波在地层中传播的速度是地震勘探领域最重要的参数之一,对高精度地震成像以及储层岩性的刻画起着非常重要的作用.确定地层速度是地震勘探的核心内容之一.随着地震勘探条件复杂程度不断加剧,对估计地层速度的精度要求越来越高.叠前深度偏移成像质量极大地依赖于地层速度模型的精度.传统的偏移速度分析方法(Biondi and Symes,2004)和走时层析反演方法(Zhu et al.,1989;Schuster and Quintus-Bosz,1993;Zhang et al.,2014)都只能得到宏观速度场,即速度的低频成分,难以得到高分辨率的速度模型.
Tarantola(1984)提出的基于广义最小二乘的全波形反演方法,对地震反演理论的发展产生了深刻影响.全波形反演直接利用地震波形信息,可以得到高精度的地下速度模型,能够满足当前复杂构造成像方法对速度参数的要求.全波形反演既可以在时间域又可以在频率域和Laplace域实现.时间域全波形反演能够灵活地对地震数据进行必要的预处理和选择所需要的特征波,且时间域波场模拟对内存要求较小.但时间域资料是连续的,反演使用的是全频波场数据,这样做会增强全波形反演过程中解的非唯一性,使得迭代求解过程很容易收敛于局部极小,且在分频多尺度策略中需要引入低通滤波器,对反演结果产生影响.频率域全波形反演直接在频率域求解,容易实现低频数据到高频数据的多尺度反演,且仅需几个离散的频率数据即可完成高分辨率的速度建模,但三维频率域正演所需的巨大内存,在很大程度上限制了三维频率域全波形反演的应用(Pratt et al.,1988,1998;Sirgue and Pratt,2004;Operto et al.,2007;Brossier et al,2009;李国平等,2011;Kim and Min,2014;Innanen,2014;Liu,2014;Adamczyk et al.,2014,Castellanos et al.,2015).Laplace域全波形反演可以较好地解决时间域、频率域反演中低频波场数据的不可靠问题,得到速度模型中的长波长信息,但在反演精度上无法达到时间域和频率域全波形反演那么高的精度(Shin and Cha,2008;Pyun et al.,2008,Shin and Ha,2008;Shin and Cha,2009;孙晓琳等,2011; Ha et al.,2012;Ha and Shin,2012;Shin et al.,2013;Son et al.,2014).这三类全波形反演方法各有优缺点,都在不断的被研究和发展.
本文主要介绍了日渐成熟的时间域全波形反演方法的研究进展,着重论述了时间域全波形反演研究中地震波场模拟、震源子波的处理、目标泛函的建立、优化反演、梯度预处理等关键环节和方法,指出了当前时间域全波形反演方法的主要发展方向.
1 时间域全波形反演发展历程在20世纪80年代,全波形反演首先在时间域提出,且以线性波形反演为主,Lailly(1983)、Tarantola(1984a,1984b)、Nowack和Aki(1986)等对线性波形反演进行了初步研究.Tarantola(1984a)首先提出了基于广义最小二乘的时间域全波形反演方法,奠定了时间域全波形反演的理论基础.然而,在线性地震波形反演中,实际地震数据和速度的关系被近似线性化,但只有当地下地质构造不是很复杂或对背景速度场有较好的先验信息时,这种线性化的反演方法才是合理的,而当地下介质复杂时,线性波形反演难以解决速度模型的长波长分量问题.
针对线性波形反演的不足,Gauthier等(1986)、Tarantola(1986)、Mora(1987,1989)、Pica等(1990)等率先对时间域完全非线性波形反演进行了详细研究.Mora(1989)证明了在正常勘探条件下,采用完全非线性地震波形反演方法,地震速度场的所有频率分量都是可观测的.Pica等(1990)采用基于逆时偏移的梯度下降法,对实测海洋地震资料试算得到了很好的反演结果,展示了时间域全波形反演方法的应用潜力.但是,由于完全非线性反演算法采用最速下降法、共轭梯度法等梯度类迭代方法和牛顿法、高斯牛顿法等牛顿类迭代方法,尽管收敛速度快,但反演结果强烈依赖于初始模型和反演问题本身的非线性程度.初始模型选取不恰当或非线性程度严重都有可能使反演过程收敛于局部极值,反演结果往往不尽人意.
为了克服收敛于局部极值问题,许多学者提出了一些解决方法.首先是将全局最优化方法引入到全波形反演当中,如Sen和Stoffa(1991)和Stoffa和Sen(1991)等针对一维非线性反演的多极值问题,将模拟退火算法、遗传算法等全局优化方法引入到波形反演中;Jin和Madariaga(1994)用蒙特卡洛法进行反演.虽然这些基于全局优化的反演方法不需要一个适当的初始模型,不会陷入局部极值,但在处理实际地下复杂地质构造时,反演收敛速度过慢,对计算机性能要求很高.为解决局部极值以及反演收敛速度问题,人们开始将尺度分解的思想应用于波形反演中. Bunks et al.(1995)提出了时间域多尺度全波形反演方法,对于复杂地质模型的实验得到了很好的效果,并且提高了反演的计算速度. Boonyasiriwat等(2009,2010)和Dagnino等(2014)等也实现了时间域多尺度的全波形反演算法.
针对时域全波形反演的应用研究,是全波形反演发展的必然. Pecher等(1996)将全波形反演方法应用于秘鲁近海似海底反射波的反演. Sirgue等(2010)率先对挪威北海Valhall油田OBC数据实现了三维全波形反演,极大地鼓舞了全波形反演的研究热潮. Ma等(2012)对2D海底OBC数据进行了具有成像导向的全波形反演. Plessix和Perkins(2010)、Fichtner和Tramper(2011)和Hu等(2012)等也实现了全波形反演技术对海面三维实测资料的应用.壳牌公司与东方地球物理公司合作研究了二维陆上低频大偏移距观测系统地震资料的全波形反演方法,验证了陆上地震资料全波形反演的良好效果(Plessix et al.,2012).
我国对时域全波形反演研究起步相对较晚,除了宋海斌等(2003)研究了天然气水合物似海底反射层的全波形反演等少数工作之外,大部分方法和应用研究都是近年来开展的,并已初步应用于实际资料. 董良国等(2013)研究了声波全波形反演的目标函数,王薇等(2013)提出了波形反演的非线性稀疏约束正则化方法,刘玉柱等(2014)研究了基于Born波路径的高斯束初至波波形反演,魏哲枫等(2014)研究了基于非规则网格声波正演和分尺度反演方法,张文生等(2015)提出了基于不同尺度的频率数据的“逐级反演”策略.石玉梅等(2014)将基于声学的时间域全波形反演应用于我国西部某致密砂岩气藏的二维地震成像中,其有效性被钻井结果证实.张猛等(2014)实现了基于CPU/GPU异构平台的时间域全波形反演,对胜利油田某探区实际地震资料的试处理取得了初步的效果.这些研究极大地推动了我国时间域全波形反演方法及其应用的进展.此外,刘国峰等(2012)、曹书红和陈景波(2012,2014)、张衡等(2014)等对频率域地震全波形反演进行了研究,王兆磊等(2007)、丁亮等(2012)、吴俊军等(2014)、周辉等(2014)在探地雷达全波形反演方法上也取得了一定进展.
尽管时间域地震全波形反演不断取得进展,但仍然存在反演非唯一性、对噪声的敏感性、强列依赖于初始模型、且易陷入局部极值、计算量大等问题,制约着其实际应用.为此,根据实际应用需要,对时域全波形反演中的正演和反演各关键环节进行优化和改进成为近年来的研究重点.
2 时间域全波形反演方法进展时间域全波形反演主要流程如图 1所示.近些年来,时间域全波形反演在各个环节的主要问题,如波场正演模拟方法、震源子波处理方式、目标泛函的建立方式、优化反演方法、梯度预处理方式等方面都取得了重要进展.
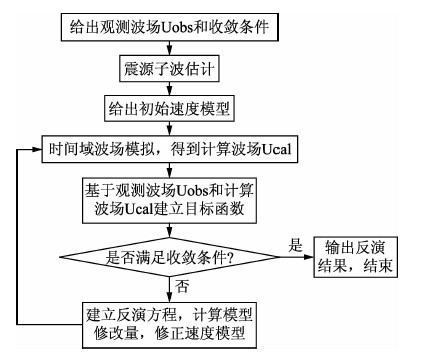 |
图 1 时间域全波形反演流程图 Fig. 1 The flow chart of time-domain full waveform inversion |
地震波场正演模拟是反演的基础,正演的精度和效率在很大程度上决定了反演的精度和效率.有限差分法是应用最广泛的时间域波场模拟方法,且由起初的规则网格有限差分方法(Tarantola,1986;Bunks et al.,1995;丁继才等,2007)发展为模拟复杂模型更为精确地交错网格有限差分方法(Sheen et al.,2006;Boonyasiriwat et al.,2009;Tran and McVay,2012).近年来,一些学者(Zhang et al.,1999;徐义和张剑锋,2008;魏哲枫等,2014)在时间域地震波场正演模拟中使用格子法,结合有限元、有限差分法的优点,采用非规则、非结构化三角网格,精细刻画复杂构造,且内存需求小,计算效率与常规差分法相当.此外,Wang等(2013)在波场模拟中考虑各向异性及衰减效应,使模型更接近于实际地下介质,模拟的波场更精确.
地震全波形反演是一种迭代反演方法,而迭代过程需要不断的进行正演计算,所以在保证地震波场正演模拟精度的同时,如何提高正演计算效率也是当前研究的热点.Berkhout(2008)提出的同时激发震源技术,将不同空间位置的多个震源按照随机线性编码方式激发组成超级炮. Krebs等(2009)、张生强等(2013)在全波形反演过程中使用了同时激发震源技术,其优势是使用同时激发震源技术取代每炮独立的正演工作,这样可以在单炮记录里同时模拟多炮的波场,大大提高有限差分算法多炮正演模拟的计算效率,同时可以用更多的炮对地下进行照明. 刘玉柱等(2014)利用高斯束计算格林函数和正演波场,减少了正演计算量.
因此,在今后地震勘探条件复杂程度逐渐加剧情况下,能更精确模拟复杂构造的非规则、非结构化网格的有限差分法将是地震波场模拟采用的主要方法,在提高地震波场模拟效率上,基于震源编码的同时激发震源技术将是今后的主流方法.
2.2 震源子波处理方式震源子波估计也是全波形反演的重要环节,尤其是在处理实际资料过程中,震源子波正确与否是反演能否取得理想结果的关键之一.早期人们对全波形反演做理论研究时,都是固定震源子波,即将计算地震数据的震源子波与观测地震数据的震源子波保持一致,未考虑震源子波不准对全波形反演的影响.近些年来,很多学者对震源子波对全波形反演的影响的研究表明,震源子波相位变化引起波形的变化,会严重影响全波形反演中的梯度计算;在全波形反演中采用的子波主频,比观测数据子波主频过大或过小都会给反演结果带来误差;子波的振幅变化对反演的影响不是特别敏感,但是当振幅过大时,部分信息会严重干扰梯度的求取.为了克服震源子波的影响,许多学者提出了不依赖于震源子波的全波形反演方法.在频率域卷积波场和反卷积波场方法(Lee et al.,2003;Zhou and Greenhalgh,2003;Choi et al.,2005;Cheong et al.,2006;Xu et al.,2006)提出之后,Choi和Alkhalifah(2011)、Tran和McVay(2012)将交叉卷积波场方法应用于时间域全波形反演方法中,即将观测波场与计算波场的一个参考道记录卷积,将计算波场与观测波场的一个参考道记录卷积,建立目标函数为
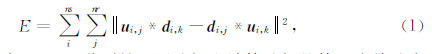
其中,d i,k、 u i,k分别是观测波场和计算波场的第k个检波点的记录.将波场用格林函数和震源子波的卷积形式表示,(1)式为
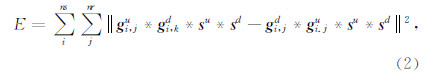
从(2)式可以看出,相减的两个项都含有计算的震源子波与实际震源子波的卷积,从而避免震源子波估计不准对反演结果的影响.这种不依赖于精确震源子波的全波形反演方法在今后全波形反演方法中将会得到广泛应用.
2.3 目标泛函的建立方式在全波形反演方法发展的很长一段时间内,假设地震数据中的噪音服从高斯分布,一般选用观测波场与模拟波场的L2范数(Jannane et al.,1989; Bunks et al.,1995;Boonyasiriwat et al.,2009; 董良国等,2013)建立反演的目标泛函.当噪音不服从高斯分布时,采用L1范数形式的目标函数对数据噪音不敏感,反演结果更加稳定. L1泛函比L2泛函的抗噪性更强,但在波场残差接近于零时会存在不稳定性问题,因此,近些年来使用在L1泛函和L2泛函之间能进行自动切换的混合L1/L2范数的Huber函数建立目标函数(Bube and Nemeth,2007; Ha et al.,2009;卞爱飞等,2010;吕晓春等,2013):
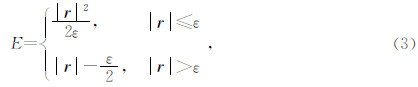
其中,r 为波场残差,为选择L1范数或L2范数的阈值.这样做不但增强了抗噪性,而且避免了L1泛函在波场残差接近于零时出现的不稳定问题.
在目标函数选择时除了基于不同的范数形式,还可基于不同的函数类型.Shin and Min(2006)在频率域提出了基于自然对数波场的反演目标函数、幂型和积分型目标函数.此外,Sheen等(2006)和Asnaashari等(2013)等将先验信息作为最优化的惩罚项加入到反演目标函数中,增加反演问题的稳定性. 董良国等(2013)分析了声波全波形反演的不同的目标函数随不同物性参数摄动尺度的变化形态,以及对反演效果的影响. 因此,如何建立合适的目标泛函也是未来全波形反演研究的一个重要问题.
2.4 优化反演方法全波形反演优化寻优算法是影响全波形反演效果和效率的一个重要因素,寻求收敛速度快而又不显著增加计算量的优化算法一直是全波形反演研究的热点.目前主要有梯度类局部寻优方法以及局部和全局结合的混合寻优方法.
2.4.1 梯度类的局部寻优方法 p>在全波形反演算法中使用最为广泛的是梯度类局部寻优方法.在过去几十年里,多数学者采用了共轭梯度法(Tarantola,1986; Mora,1987;Crase et al.,1990;Shin and Min,2006;Boonyasiriwat et al.,2009;Liu,2014;Son et al.,2014等),在有适当的先验信息约束下,共轭梯度法可以避免陷入局部极值,且收敛速度快,计算量小.Tarantola(1987)将牛顿法应用到时间域全波形反演算法中.在初始模型接近于全局极值时,牛顿法收敛速度要优于共轭梯度法,且反演稳定,但Hessian矩阵的计算量大,通常需要避免这类大型矩阵的直接求逆,尤其是对全波形反演这种强非线性问题.
Sheen等(2006)、王守东(2011)、Tran和McVay(2012)、Joo等(2013)、Pakravan和Kang(2014)等应用高斯-牛顿法进行时间域全波形反演. 高斯-牛顿法收敛速度优于共轭梯度法,但它的一个显著缺点是在每次迭代过程中都需要在内存中存储Hessian矩阵的逆近似,当矩阵规模很大时,对计算机的内存要求较高,因此不适合求解大规模优化问题.
在实际应用中,为减少存储量和计算量,Brossier等(2009)、魏哲枫等(2014)、王义和董良国(2014)、Dagnino等(2014)和Castellanos等(2015)等采用一种拟牛顿优化算法—L-BFGS(Nocedal,1980).L-BFGS算法的核心是利用目标函数及其梯度来构建近似Hessian阵,避免了近似Hessian的计算,其公式为
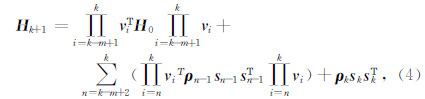
其中,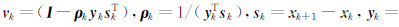
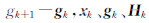 分别是第k次反演迭代时的模型参数、梯度和近似Hessian阵,H 0选择为一正定对角阵即可.复杂模型试验结果表明,L-BFGS算法大大节省了内存,减少了计算量,并且加快了收敛速度.
分别是第k次反演迭代时的模型参数、梯度和近似Hessian阵,H 0选择为一正定对角阵即可.复杂模型试验结果表明,L-BFGS算法大大节省了内存,减少了计算量,并且加快了收敛速度.
Ma和Hale(2010,2011)利用投影Hessian矩阵修改BFGS算法,减少了计算耗时和内存占用量,还将影像引导插值技术应用到全波形反演中,通过减少模型参数的个数加快收敛速度. 但是常规拟牛顿法在构造近似Hessian矩阵的逆时,只考虑了目标函数的梯度和模型参数,忽视了目标函数本身的数值. Zhang等(1999)(Zhang and Xu,2001)推导了新的拟牛顿条件,在构造近似Hessian的逆的同时,利用了目标函数梯度和其本身数值,得到了修正的BFGS公式. 刘璐等(2013)将Zhang等(1999)(Zhang and Xu,2001)提出的修正拟牛顿条件引入到全波形反演中,说明了修正BFGS算法由于综合考虑了梯度、模型参数和目标函数本身信息,更能逼近Hessian矩阵的逆,在保证全波形反演精度的前提下加快收敛速度,减少反演耗时.
2.4.2 联合局部寻优与全局寻优的混合优化方法考虑到全局优化算法对初始模型不敏感的特性以及局部优化算法的快速收敛特性,一些学者在全波形反演中提出了混合优化反演方法.邢文军(2006)在时间域全波形反演算法中联合了模拟退火法与共轭梯度法.首先随机产生初始模型用模拟退火法进行反演,等到搜索到全局最小附近时换用共轭梯度法,把模拟退火反演结果作为共轭梯度法的初始模型,既解决了初始模型问题,又避免了陷入局部极值.朱童等(2013)在频率域全波形反演算法中联合了全局随机非线性粒子群算法(师学明等,2009;岳碧波等,2009)和局部寻优的梯度法,在算法迭代之初,选择多个初始模型用粒子群算法迭代找到较好的初始模型,然后利用局部收敛特性较好的梯度类算法寻找最优解.
无论在时间域还是频率域,在实际资料低频信息缺失或传统速度建模方法无法得到较好初始模型的情况下,采用这种局部寻优与全局寻优结合的混合优化方法,将不失为一种较好的选择.
2.5 梯度预处理方式在时间域全波形反演算法中,使用最为广泛的是梯度类寻优方法.但是,由于几何扩散效应、焦散效应等影响,在使用梯度类寻优方法时,即使当浅层模型参数被很好的确定时,深部模型参数却难以得到很好的重建.为了解决深部模型和加速收敛问题,需要对梯度做预处理.
Gauthier等(1986)研究时间域全波形反演方法在距离震源点不同位置处的反演效果时,发现远处的反演效果要比近处的反演效果差,于是,在计算各处梯度时,引入了与震源的距离参数,使远处的反演结果得到了改善.其梯度预处理格式为

其中,g(x)n为目标函数的梯度,g(x)wn为预处理后的梯度. 该式增加了一个计算点到炮点的距离因子项,这种简单预处理对于复杂实际问题的效果一般.Pratt等(1998)随后用近似Hessian矩阵的对角线元素进行梯度预处理,反演迭代格式为
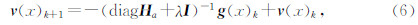
其中,diag表示取矩阵的对角阵,I 为单位阵,λ为可调节正则化因子.Shin等(2001)、Choi et al.(2008)和成景旺等(2013)从计算量方面考虑用伪Hessian来做梯度预处理,比近似Hessian的计算量小,但缺点是缺失几何扩散相关的因子.任浩然等(2013)在全波形反演中提出了偏移距域Hessian算子,加快了全波形反演迭代过程的计算速度.
Zhang等(2011)提出了基于地震波能量的梯度预处理方法,即使用炮点处正向传播的波场和检波点处数据残差逆向传播的波场对梯度进行预处理,公式为

式中,g(x)为梯度,g(x)w为预处理之后的梯度,W s、 W r分别为对炮点正向传播波场的预条件算子、对检波点处数据残差逆向传播波场的预条件算子,且
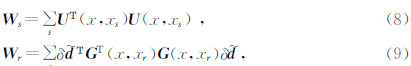
其中,U(x,xs)是正向传播波场散度 ▽ · u(x,xs)的一个离散时间序列,G(x,xr)是格林函数散度 ▽ · green(x,xr)的一个离散时间序列,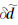 为检波点处数据残差.复杂模型实验结果表明这种方法加速了收敛、改善了对深部模型的反演效果.考虑到检波点处数据残差不仅包含了几何扩散效应,而且包含了散射信息,用其对梯度预处理会放大异常扰动点附近的假象,减缓收敛速度或收敛于一个错误的解,Zhang等(2012)使用检波点处的地震记录代替数据残差逆向传播波场来对梯度进行预处理,即在上式中取
为检波点处数据残差.复杂模型实验结果表明这种方法加速了收敛、改善了对深部模型的反演效果.考虑到检波点处数据残差不仅包含了几何扩散效应,而且包含了散射信息,用其对梯度预处理会放大异常扰动点附近的假象,减缓收敛速度或收敛于一个错误的解,Zhang等(2012)使用检波点处的地震记录代替数据残差逆向传播波场来对梯度进行预处理,即在上式中取
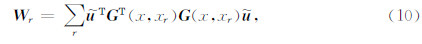
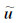 是检波点处接收到的地震记录.
是检波点处接收到的地震记录.
如图 2所示是基于不同梯度预处理的共轭梯度法对一个复杂理论模型的试验结果,表明改进后的基于地震波能量的梯度预处理方法收敛更快,能更好地重建深部模型,但需要比改进前的方法多做一次波场模拟.可见,梯度预处理对于梯度类全波形反演方法来说是非常重要的,直接影响对模型深部的反演效果.因此,对于梯度类反演方法,仍然需要寻求在不显著增加计算量前提下的梯度预处理方法.
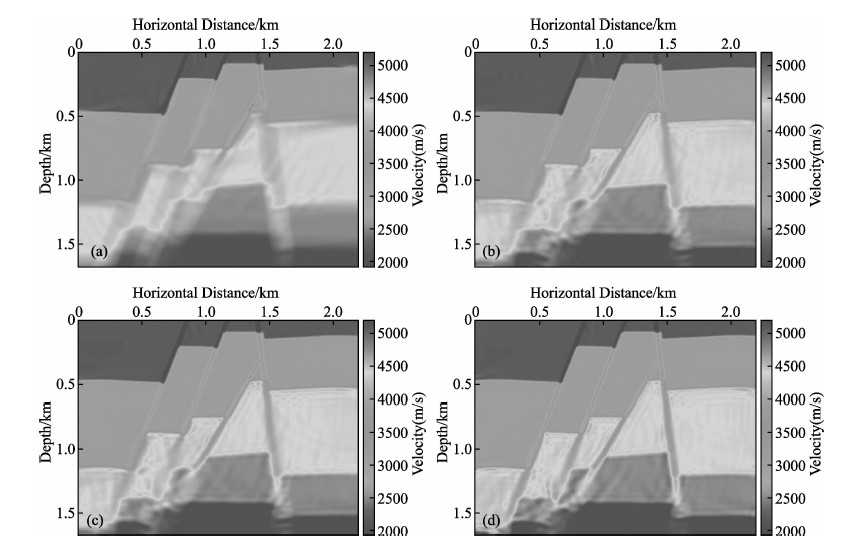 |
图 2不同梯度预处理方法的共轭梯度法反演结果 (a)未做梯度预处理,(b)用伪Hessian算子做梯度预处理,(c)原基于地震波能量预处理方法, (d)改进的基于地震波能量预处理方法.(Zhang et al.,2012) Fig. 2 The results of full waveform inversion using the conjugate gradient method without gradient preprocessing(a),with the pseudo-Hessian method(b),the wave-energy-weighted gradient preprocessing method(c),and the new wave-energy-based gradient preprocessing method(d) |
时间域多尺度反演就是把观测数据和地震子波分解成不同频带的观测数据和子波成分,然后由低频带到高频带逐带反演,并把低频带反演结果作为高频带反演的初始模型,保证了反演过程的稳定性,而且,低频带反演一般采用大网格和大时间采样间隔,提高了计算效率. Boonyasiriwat等(2009,2010)、魏哲枫等(2014)针对Bunks等(1995)提出的时间域多尺度全波形反演策略做了进一步优化,使用了滤波效果更好的Wiener滤波器分离不同频带数据,计算公式为
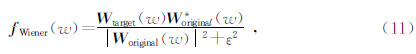
其中,f Wiener为Wiener滤波器,W target为低频目标震源子波,W original为原始震源子波,ε为控制数值溢出的因子. 图 3所示是由图 4d理论模型模拟的地震观测数据及其用Wiener滤波器得到的低频观测数据.
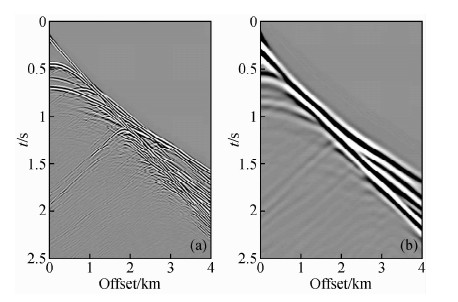 |
图 3(a)正演模拟地震记录,(b)Wiener滤波
得到的低频数据 Fig. 3 Seismic records modeled with the original wavelet(a),the low frequency data from the seismic records obtained by the Wiener filter(b).(Boonyasiriwat et al.,2009) |
张文生等(2015)提出了基于不同尺度的频率数据的“逐级反演”策略的时间域全波形反演方法,即先基于低频尺度的波场信息进行反演,得出合理的初始模型,然后再利用其他不同尺度频率的波场进行反演,并且用前一尺度的迭代反演结果作为下一尺度反演的初始模型,并实现了这种逐级反演的MPI并行计算,对Marmous模型试验得到较好的反演效果.
图 4是对一复杂理论模型数据的时间域多尺度反演结果.可以看出,低频带全波形反演可以很好的恢复速度模型的低波数成分,高频带反演可以很好的恢复速度模型的高波数成分;与走时反演结果相比,多尺度全波形反演对复杂模型尤其是局部异常体的反演效果更好.因此,多尺度的策略在以后全波形反演方法中会得到越来越多的重视.
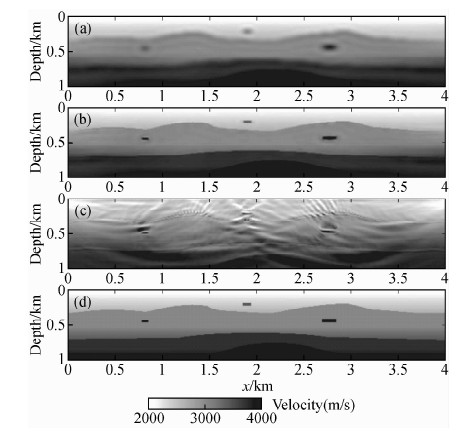 |
图 4理论和反演速度模型,(a)用走时反演结果做低频
带全波形反演初始模型反演结果,(b)用低频带反演结果
做高频带初始模型反演结果,(c)单尺度全波形反演结果,
(d)理论模型.(Boonyasiriwat et al.,2009) Fig. 4 The results of model test,the inversion results of the low frequency b and which the initial model used by the results of the travel time tomography(a),the inversion results of the high frequency b and which the initial model used by the inversion results of the low frequency b and (b), the inversion results of the single multiscale waveform inversion(c),and the true model(d) |
全波形反演在频率域的波场正演模拟需占用很大内存,且难以实现并行计算,特别是三维频率域正演问题更突出,制约了三维频率域全波形反演的发展,也因此促进了频率域反演与时间域正演的混合域全波形反演方法的发展(Hu,2012;Xu and McMechan,2014).这种在时间域进行正演、在频率域进行反演的全波形反演方法,既节约了存储空间、便于实现多尺度算法,又可以灵活地对地震数据进行预处理,且适用于大规模并行计算,能最大程度地提高全波形反演方法的计算效率.可以预见,混合域反演方法将有力促进三维全波形反演方法的实际应用.
3 时间域全波形反演研究展望3.1 全波形反演是建立高分辨率速度模型的有效手段,成为近年来地球物理学领域一个研究热点.时间域全波形反演方法可以灵活地对数据进行预处理、方便地选取部分波场进行反演,而且时间域波场模拟相对于频率域可以节省很大内存.近期,时间域全波形反演方法将在这些方面得到进一步发展:非规则、非结构化网格的有限差分法将是提高复杂模型地震波场模拟精度的主要方法;基于震源编码的同发震源技术将是提高地震波场正演模拟效率的有效方法;不依赖于精确震源子波的全波形反演方法将是今后的主流研究方向;既增强抗噪性又避免L1泛函在波场残差接近于零时不稳定的混合L1/L2泛函形式的目标泛函,在全波形反演中将会得到越来越多的应用;分频分尺度、联合局部寻优与全局寻优方法、联合时间域正演与频率域反演等多种技术的有效结合将是全波形反演的发展方向.
3.2 对理论模型数据和某些实际资料的反演结果初步显示了时域全波形反演方法的应用潜力.但是对于目前实测的海洋及陆地地震勘探资料,全波形反演还受到一些限制:常规的反射波勘探观测系统,偏移距小,波路径正交程度较差,很大程度上限制了全波场信息的获取;实际观测数据中低频信息缺失,没有低频数据与初始模型很好耦合,使反演问题较容易收敛于局部极小;波传播的动力学信息对噪声异常敏感,数据预处理在消除噪音干扰的同时,又破坏了地震波的动力学特征;对大规模数据的应用仍然需要高性能的计算设备.可以预见,随着全波场和宽频带等观测技术、数据预处理保真技术、全波形反演理论和技术、以及计算机软硬件技术的发展与进步,全波形反演方法必将在不远的将来被广泛地应用于生产.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Adamczyk A, Malinowski M, Malehmir A. 2014. High-resolution near-surface velocity model building using full-waveform inversion-a case study from southwest Sweden[J]. Geophys. J. Int., 197(3):1693-1704. |
| [2] | Asnaashari A, Brossier R, Garambois S, et al. 2013. Regularized seismic full waveform Inversion with prior model information[J]. Geophysics, 78(2):R25-R36. |
| [3] | Berkhout A J. 2008. Changing the mindset in seismic data acquisition[J]. The Leading Edge, 27(7):924-938. |
| [4] | Bian A F, Yu W H, Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophys. (in Chinese), 25(3):982-993, doi:10.3969/j.issn.1004-2903.2010.03.037. |
| [5] | Biondi B, Symes W W. 2004. Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging[J]. Geophysics, 69(5):1283-1298. |
| [6] | Boonyasiriwat C, Valasek P, Routh P, et al. 2009. An efficient multiscale method for time-domain waveform tomography[J]. Geophysics, 74(6):WCC59-WCC68. |
| [7] | Boonyasiriwat C B, Schuster G T, Valasek P, et al. 2010. Applications of multiscale waveform inversion to marine data using a flooding technique and dynamic early-arrival windows[J]. Geophysics, 75(6):R129-R136. |
| [8] | Brossier R, Operto S, Virieux J. 2009. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion[J]. Geophysics, 74(6):WCC105-WCC118. |
| [9] | Bube K P, Nemeth T. 2007. Fast line searches for the robust solution of linear systems in the hybrid l1/l2 and Huber norms[J]. Geophysics, 72(2):A13-A17. |
| [10] | Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion[J]. Geophysics, 60(5):1457-1473. |
| [11] | Cao S H, Chen J B. 2012. A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation[J]. Chinese J. Geophys. (in Chinese), 55(10):3440-3449, doi:10.6038/j.issn.0001-5733.2012.10.027. |
| [12] | Cao S H, Chen J B. 2014. Studies on complex frequencies in frequency domain full waveform inversion[J]. Chinese J. Geophys. (in Chinese), 57(7):2302-2313, doi:10.6038/cjg20140724. |
| [13] | Castellanos C, Métivier L, Operto S, et al. 2015. Fast full waveform inversion with source encoding and second-order optimization methods[J]. Geophys. J. Int., 200(2):718-742. |
| [14] | Cheng J W, Gu H M, Liu C C, et al. 2013. Full waveform inversion for velocity structure from reflected wave seismic data in the frequency domain[J]. Earth Science-Journal of China University of Geosciences (in Chinese), 38(2):391-397. |
| [15] | Cheong S, Pyun S, Shin C. 2006. Two efficient steepest-descent algorithm for source signature-free waveform inversion[J]. Journal of Seismic Exploration, 14(4):335-348. |
| [16] | Choi Y, Alkhalifah T. 2011. Source-independent time-domain waveform inversion using convolved wavefields:application to the encoded multisource waveform inversion[J]. Geophysics, 76(5):R125-R134. |
| [17] | Choi Y, Shin C, Min D -J, et al. 2005. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion:An amplitude approach[J]. Journal of Computational Physics, 288(2):455-468. |
| [18] | Crase E, Pica A, Noble M, et al. 1990. Robust elastic nonlinear waveform inversion:Application to real data[J]. Geophysics, 55(5):527-538. |
| [19] | Dagnino D, Sallares V, Ranero C R. 2014. Scale-and parameter-adaptive model-based gradient pre-conditioner for elastic full waveform inversion[J]. Geophys. J. Int., 198(2):1130-1142. |
| [20] | Ding J C, Chang X, Liu Y K, et al. 2007. Layer by layer waveform inversion of seismic reflection data[J]. Chinese J. Geophys. (in Chinese), 50(2):574-580. |
| [21] | Ding L, Han B, Liu R Z. 2012. Inversion imaging method for concrete non-destructive testing based on GPR[J]. Chinese J. Geophys. (in Chinese), 55(1):317-326, 10.6038/j.issn.0001-5733.2012.01.032. |
| [22] | Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion[J]. Chinese J. Geophys. (in Chinese), 56(10):3445-3460, doi:10.6038/cjg20131020. |
| [23] | Fichtner A, Tramper J. 2011. Resolution analysis in full waveform inversion[J]. Geophys. J. Int., 187(3):1604-1624. |
| [24] | Gauthier O, Virieux J, Tarantola A. 1986. Two-dimensional nonlinear inversion of seismic waveforms:Numerical results[J]. Geophysics, 51(7):1387-1403. |
| [25] | Ha T, Chung W, Shin C. 2009. Waveform inversion using a back-propagation algorithm and a Huber function norm[J]. Geophysics, 74(3):R15-R24. |
| [26] | Ha W, Chung W, Park E, et al. 2012. 2-D acoustic Laplace-domain waveform inversion of Marine field data[J]. Geophys. J. Int., 190(1):421-428. |
| [27] | Ha W, Shin C. 2012. Laplace-domain full-waveform inversion of seismic data lacking low-frequency information[J]. Geophysics, 77(5):R199-R206. |
| [28] | Hu G H, Etienne V, Castellanos C, et al. 2012. Assessment of 3D acoustic isotropic full waveform inversion of wide-azimuth OBC data from Valhall[C].//SEG Technical Program Expanded Abstracts, 1-6. |
| [29] | Innanen K A. 2014. Seismic AVO and the inverse Hessian in precritical reflection full waveform inversion[J]. Geophys. J. Int., 199(2):717-734. |
| [30] | Jannane M, Beydoun W, Crase E, et al. 1989. Wavelengths of Earth structures that can be resolved from seismic reflection data[J]. Geophysics, 54(7):906-910. |
| [31] | Jin S, Madariaga R. 1994. Nonlinear velocity inversion by a two-step Monte-Carlo method[J]. Geophysics, 59(4):577-590. |
| [32] | Joo Y, Seol S J, Byun J. 2013. Acoustic full-waveform inversion of surface seismic data using the Gauss-Newton method with active constraint balancing[J]. Geophysical Prospecting, 61(1):166-182. |
| [33] | Kim W -K, Min D -J. 2014. A new parameterization for frequency-domain elastic full waveform inversion for VTI media[J]. Journal of Applied Geophysics, 109:88-110. |
| [34] | Krebs J R, Anderson JE, Hinkley E, et al. 2009. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 74(6):WCC177-WCC188. |
| [35] | Lailly P. 1983. The seismic inverse problem as a sequence of before stack migrations[C].//Conference on Inverse Scattering. Theory and Application. Society for Industrial and Applied Mathematics, Expanded Abstracts, 206-220. |
| [36] | Lee K H, Kim H J. 2003. Source-independent full-waveform inversion of seismic data[J]. Geophysics, 68(6):2010-2015. |
| [37] | Li G P, Yao F C, Shi Y M, et al. 2011. Pre-stack wave equation inversion and its application in frequency domain[J]. Oil Geophysical Prospecting (in Chinese), 46(3):411-416. |
| [38] | Liu G F, Liu H, Meng X H, et al. 2012. Frequency-related factors analysis in frequency domain waveform inversion[J]. Chinese J. Geophys. (in Chinese), 55(4):1345-1353, doi:10.6038/j.issn.0001-5733.2012.04.030. |
| [39] | Liu L, Liu H, Zhang H, et al. 2013. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese J. Geophys. (in Chinese), 56(7):2447-2451, doi:10.6038/cjg20130730. |
| [40] | Liu Y. 2014. An optimal 5-point scheme for frequency-domain scalar wave equation[J]. Journal of Applied Geophysics, 108:19-24. |
| [41] | Liu Y Z, Xie C, Yang J Z. 2014. Gaussian beam first-arrival waveform inversion based on born wavepath[J]. Chinese J. Geophys. (in Chinese), 57(9):2900-2909, doi:10.6038/cjg20140915. |
| [42] | Lü X C, Gu H M, Cheng J W. 2013. The frequency domain full waveform inversion based on Huber function[J]. Geophysical Prospecting for Petroleum (in Chinese), 52(5):544-552. |
| [43] | Ma Y, Hale D. 2010. Full waveform inversion with image-guided gradient[C].//80th Annual International Meeting, SEG, Expanded Abstracts 29:1003-1007. |
| [44] | Ma Y, Hale D. 2011. A projected Hessian matrix for full waveform inversion[C].//81th Annual International Meeting. SEG, Expanded Abstracts 30:2401-2405. |
| [45] | Ma Y, Hale D, Gong B, et al. 2012. Image-guided sparse-model full waveform inversion[J]. Geophysics, 77(4):R189-R198. |
| [46] | Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 52(9):1211-1228. |
| [47] | Mora P. 1989. Inversion=migration+tomography[J]. Geophysics, 54(12):1575-1586. |
| [48] | Nocedal J. 1980. Updating quasi-Newton matrices with limited storage[J]. Mathematics of Computation, 35(151):773-782. |
| [49] | Nowack R L, Aki K. 1986. Iterative inversion for velocity using waveform data[J]. Geophys. J. Int., 87(3):701-730. |
| [50] | Operto S, Virieux J, Amestoy P, et al. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver:a feasibility study[J]. Geophysics. 72(5):SM195-SM211. |
| [51] | Pakravan A, Kang J W. 2014. A Gauss-Newton full-waveform inversion for Material profile reconstruction in 1D PML-truncated solid media[J]. KSCE Journal of Civil Engineering, 18(6):1792-1804. |
| [52] | Pecher I A, Minshull T A, Singh S C, et al. 1996. Velocity structure of a bottom simulating reflector offshore Peru:Results from full waveform inversion[J]. Earth and Planetary Science Letters, 139(3-4):459-469. |
| [53] | Pica A, Diet J P, Tarantola A. 1990. Nonlinear inversion of seismic reflection data in a laterally invariant medium[J]. Geophysics, 55(3):284-292. |
| [54] | Plessix R -é, Baeten G, de Maag J W, et al. 2012. Full waveform inversion and distance separated simultaneous sweeping:a study with a land seismic data set[J]. Geophysical Prospecting, 60(4):733-747. |
| [55] | Plessix R -é, Perkins C. 2010. Full waveform inversion of a deep water ocean bottom seismometer dataset[J]. First Break, 28(4):71-78. |
| [56] | Pratt R G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space domain seismic waveform inversion[J]. Geophys. J. Int., 133(2):341-362. |
| [57] | Pratt R G, Worthington M H. 1988. The application of diffraction tomography to cross-hole seismic data[J]. Geophysics, 53(10):1284-1294. |
| [58] | Pyun S, Shin C, Lee H. 2008. 3D elastic full waveform inversion in the Laplace domain[C].//Expanded Abstracts of 78th Annual Internat SEG Mtg, 1976-1980. |
| [59] | Ren H R, Huang G H, Wang H Z, et al. 2013. A research on the Hessian operator in seismic inversion imaging[J]. Chinese J. Geophys. (in Chinese), 56(7):2429-2436, doi:10.6038/cjg20130728. |
| [60] | Schuster G T, Quintus-Bosz A. 1993. Wavepath eikonal traveltime inversion:Theory[J]. Geophysics, 58(9):1314-1323. |
| [61] | Sen M K, Stoffa P L. 1991. Nonlinear one-dimensional seismic waveform inversion using simulated annealing[J]. Geophysics, 56(10):1624-1638. |
| [62] | Sheen D -H, Tuncay K, Baag C -E, et al. 2006. Time domain Gauss-Newton seismic waveform inversion in the elastic media[J]. Geophys. J. Int., 167(3):1373-1384. |
| [63] | Shi X M, Xiao M, Fan J K, et al. 2009. The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J]. Chinese J. Geophys. (in Chinese), 52(4):1114-1120, doi:10.3969/j.issn.0001-5733.2009.04.029. |
| [64] | Shi Y M, Zhang Y, Yao F C, et al. 2014. Methodology of seismic imaging for hydrocarbon reservoirs based on acoustic full waveform inversion[J]. Chinese J. Geophys. (in Chinese), 57(2):607-617, doi:10.6038/cjg20140224. |
| [65] | Shin C, Cha Y H. 2008. The direct-removal method of waveform inversion in the Laplace inversion for deep-sea environments[J]. Geophys. J. Int., 173(3):922-931. |
| [66] | Shin C, Cha Y H. 2009. Waveform inversion in the Laplace-Fourier domain[J]. Geophysical Journal International, 177(3):1067-1079. |
| [67] | Shin C, Ha W. 2008. A comparison between the behavior of objective functions for waveform inversion in the frequency and Laplace domains[J]. Geophysics, 73(5):VE119-VE133. |
| [68] | Shin C, Min D J. 2006. Waveform inversion using a logarithmic wavefield[J]. Geophysics, 71(3):R31-R42. |
| [69] | Shin C, Yoon K, Marfurt K J, et al. 2001. Efficient calculation of a partial-derivative wavefield using reciprocity for seismic imaging and inversion[J]. Geophysics, 66(6):1856-1863. |
| [70] | Shin J, Kim Y, Shin C, et al. 2013. Laplace-domain full waveform inversion using irregular finite elements for complex foothill environments[J]. Journal of Applied Geophysics, 96:67-76. |
| [71] | Sirgue L, Barkved O I, Dellinger J, et al. 2010. Full waveform inversion:the next leap forward in imaging at Valhall[J]. First Break, 28(4):65-70. |
| [72] | Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J]. Geophysics, 69(1):231-248. |
| [73] | Son W, Pyun S, Shin C, et al. 2014. Laplace-domain wave-equation modeling and full waveform inversion in 3D isotropic elastic media[J]. Journal of Applied Geophysics, 105:120-132, doi:10.6038/cjg20140525. |
| [74] | Song H B, Osamu M, Shin'ichi K. 2003. Full waveform inversion of gas hydrate-related bottom simulating reflectors[J]. Chinese J. Geophys. (in Chinese), 46(1):42-46. |
| [75] | Stoffa P L, Sen M K. 1991. Nonlinear multiparameter optimization using genetic algorithms; Inversion of plane-wave seismograms[J]. Geophysics, 56(11):1794-1810. |
| [76] | Sun X L, Gao J, Xue B. 2011. Waveform inversion in the Laplace domain with frequency-varying damping constant[J]. Journal of Shandong University of Science and Technology (Natural Science), (in Chinese), 30(1):11-15. |
| [77] | Tarantola A. 1984a. Linearized inversion of seismic reflection data[J]. Geophysical Prospecting, 32(6):998-1015. |
| [78] | Tarantola A. 1984b. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 49(8):1259-1266. |
| [79] | Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 51(10):1983-1903. |
| [80] | Tarantola A. 1987. Inverse Problem Theory:Methods for Data Fitting and Parameter Estimations[M]. New York:Elsevier Science Publ. Co. |
| [81] | Tran K T, McVay M. 2012. Site characterization using Gauss-Newton inversion of 2-D full seismic waveform in the time domain[J]. Soil Dynamics and Earthquake Engineering, 43:16-24. |
| [82] | Wang C, Yingst D, Bai J Y, et al. 2013. Waveform inversion including well constraints, anisotropy, and attenuation[J]. The Leading Edge, 32(9):1056-1062. |
| [83] | Wang S D. 2011. Total variation regularization waveform inversion of crosswell seismic data[J]. Geophysical Prospecting for Petroleum (in Chinese), 50(3):234-240. |
| [84] | Wang W, Han B, Tang J P. 2013. Regularization method with sparsity constraints for seismic waveform inversion[J]. Chinese J. Geophys. (in Chinese), 56(1):289-297, doi:10.6038/cjg20130130. |
| [85] | Wang Y, Dong L G. 2014. Selection strategy of the initial matrix for L-BFGS method in time domain full waveform inversion[J]. Geophysical Prospecting for Petroleum (in Chinese), 53(5):545-555. |
| [86] | Wang Z L, Zhou H, Li G F. 2007. Inversion of ground-penetrating radar data for 2D electric parameters[J]. Chinese J. Geophys. (in Chinese), 50(3):897-904, doi:10.3321/j.issn:0001-5733.2007.03.031. |
| [87] | Wei Z F, Gao H W, Zhang J F. 2014. Time-domain full waveform inversion based on an irregular-grid acoustic modeling method[J]. Chinese J. Geophys. (in Chinese), 57(2):586-594, doi:10.6038/cjg20140222. |
| [88] | Wu J J, Liu S X, Li Y P, et al. 2014. Study of cross-hole radar tomography using full-waveform inversion[J]. Chinese J. Geophys. (in Chinese), 57(5):1623-1635, doi:10.6038/cjg20140525. |
| [89] | Xing W J. 2006. Research on the methods and application of waveform inversion (in Chinese)[D]. Qingdao:China University of Petroleum (East China). |
| [90] | Xu K, Greenhalgh S A, Wang M Y. 2006. Comparison of source-independent methods of elastic waveform inversion[J]. Geophysics, 71(6):R91-R100. |
| [91] | Xu K, McMechan G A. 2014. 2D frequency-domain elastic full-waveform inversion using time-domain modeling and a multistep-length gradient approach[J]. Geophysics, 79(2):R41-R53. |
| [92] | Xu Y, Zhang J F. 2008. An irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling[J]. Chinese J. Geophys. (in Chinese), 51(5):1520-1526. |
| [93] | Yue B B, Peng Z M, Hong Y G, et al. 2009. Wavelet inversion of pre-stack seismic angle-gather based on particle swarm optimization algorithm[J]. Chinese J. Geophys. (in Chinese), 52(12):3116-3123, doi:10.3969/j.issn.0001-5733.2009.12.021. |
| [94] | Zhang H, Liu H, Liu L, et al. 2014. Frequency domain acoustic equation high-order modeling based on an average-derivative method[J]. Chinese J. Geophys. (in Chinese), 57(5):1599-1611, doi:10.6038/cjg20140523. |
| [95] | Zhang J Z, Deng N Y, Chen L H. 1999. New quasi-Newton equation and related methods for unconstrained optimization[J]. Journal of Optimization Theory and Applications, 102(1):147-167. |
| [96] | Zhang J F, Liu T L. 1999. P-S V-wave propagation in heterogeneous media:Grid method[J]. Geophys. J. Int., 136(2):431-438. |
| [97] | Zhang J Z, Shi T -K, Zhao Y S, et al. 2014. Static corrections in mountainous areas using Fresnel-wave path tomography[J]. Journal of Applied Geophysics, 111:242-249. |
| [98] | Zhang J Z, Xu C X. 2001. Properties and numerical performance of quasi-Newton methods with modified equations[J]. Journal of Computational and Applied Mathematics, 137(2):269-278. |
| [99] | Zhang M, Wang H Z, Ren H R, et al. 2014. Full waveform inversion on the CPU/GPU heterogeneous platform and its application analysis[J]. Geophysical Prospecting for Petroleum (in Chinese), 53(4):461-467. |
| [100] | Zhang S Q, Liu C C, Han L G, et al. 2013. Frequency multi-scale full waveform inversion based on L-BFGS algorithm and simultaneous sources approach[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 43(3):1004-1012. |
| [101] | Zhang W S, Luo J, Teng J W. 2015. Frequency multiscale full-waveform velocity inversion[J]. Chinese J. Geophys. (in Chinese), 58(1):216-228, doi:10.6038/cjg20150119. |
| [102] | Zhang Z G, Huang L J, Lin Y Z. 2012. A wave-energy-based precondition approach to full-waveform inversion in the time domain[C].//81st Annual International Meeting, SEG, Expanded Abstracts, 1-5. |
| [103] | Zhang Z G, Lin Y Z, Huang L J. 2011. Full-waveform inversion in the time domain with an energy-weighted gradient[C].//81st Annual International Meeting, SEG, Expanded abstracts, 2772-2776. |
| [104] | Zhou B, Greenhalgh S A. 2003. Crosshole seismic inversion with normalized full-waveform inversion amplitude data[J]. Geophysics, 68(4):1320-1330. |
| [105] | Zhou H, Chen H M, Li Q Q, et al. 2014. Waveform inversion of ground-penetrating radar data without needing to extract exciting pulse[J]. Chinese J. Geophys. (in Chinese), 57(6):1968-1976, doi:10.6038/cjg20140627. |
| [106] | Zhu T, Li X F, Wang W S, et al. 2013. PSO-gradient algorithm and its application to seismic waveform inversion for velocity structure in frequency domain[J]. Progress in Geophys. (in Chinese), 28(1):180-189, doi:10.6038/pg20130119. |
| [107] | Zhu X H, McMechan G A. 1989. Estimation of a two-dimensional seismic compressional-wave velocity distribution by iterative tomographic imaging[J]. International Journal of Imaging Systems and Technology, 1(1):13-17. |
| [108] | 卞爱飞,於文辉,周华伟. 2010.频率域全波形反演方法研究进展[J].地球物理学进展, 25(3):982-993, doi:10.3969/j.issn.1004-2903.2010.03.037. |
| [109] | 曹书红,陈景波. 2012.声波方程频率域高精度正演的17点格式及数值实现[J].地球物理学报, 55(10):3440-3449, doi:10.6038/j.issn.0001-5733.2012.10.027. |
| [110] | 曹书红,陈景波. 2014.频率域全波形反演中关于复频率的研究[J].地球物理学报,57(7):2302-2313,doi:10.6038/cjg20140724. |
| [111] | 成景旺,顾汉明,刘春成,等. 2013.频率域反射波全波形速度反演[J].地球科学-中国地质大学学报. 38(2):391-397. |
| [112] | 丁继才,常旭,刘伊克,等. 2007.反射地震数据的逐层波形反演[J].地球物理学报, 50(2):574-580. |
| [113] | 丁亮,韩波,刘润泽,等. 2012.基于探地雷达的混凝土无损检测反演成像方法[J].地球物理学报, 55(1):317-326, 10.6038/j.issn.0001-5733.2012.01.032. |
| [114] | 董良国,迟本鑫,陶纪霞,等. 2013.声波全波形反演目标函数性态[J].地球物理学报, 56(10):3445-3460, doi:10.6038/cjg20131020. |
| [115] | 李国平,姚逢昌,石玉梅,等. 2011.频率域叠前波动方程反演及其应用[J].石油地球物理勘探, 46(3):411-416. |
| [116] | 刘国峰,刘洪,孟小红,等. 2012.频率域波形反演中与频率相关的影响因素分析[J].地球物理学报, 55(4):1345-1353, doi:10.6038/j.issn.0001-5733.2012.04.030. |
| [117] | 刘玉柱,谢春,杨积忠. 2014.基于Born波路径的高斯束初至波波形反演[J].地球物理学报, 57(9):2900-2909, doi:10.6038/cjg20140915. |
| [118] | 刘璐,刘洪,张衡,等. 2013.基于修正拟牛顿公式的全波形反演[J].地球物理学报, 56(7):2447-2451, doi:10.6038/cjg20130730. |
| [119] | 吕晓春,顾汉明,成景旺. 2013.基于Huber函数的频率域全波形反演[J].石油物探, 52(5):544-552. |
| [120] | 任浩然,黄光辉,王华忠,等. 2013.地震反演成像中的Hessian算子研究[J].地球物理学报, 56(7):2429-2436, doi:10.6038/cjg20130728. |
| [121] | 师学明,肖敏,范建柯,等. 2009.大地电磁阻尼粒子群优化反演法研究[J].地球物理学报, 52(4):1114-1120, doi:10.3969/j.issn.0001-5733.2009.04.029. |
| [122] | 石玉梅,张研,姚逢昌,等. 2014.基于声学全波形反演的油气藏地震成像方法[J].地球物理学报, 57(2):607-617, doi:10.6038/cjg20140224. |
| [123] | 宋海斌, Osamu M, Shin'ichi K. 2003.天然气水合物似海底反射层的全波形反演[J].地球物理学报, 46(1):42-46. |
| [124] | 孙晓琳,高建,薛冰. 2011.拉普拉斯域频变衰减常数波形反演方法[J].山东科技大学学报(自然科学版), 30(1):11-15. |
| [125] | 王守东. 2011.井间地震资料全变差正则化波形反演[J].石油物探, 50(3):234-240. |
| [126] | 王义,董良国. 2014. L-BFGS法时间域全波形反演中初始矩阵的选择方法[J].石油物探, 53(5):545-555. |
| [127] | 王薇,韩波,唐锦萍. 2013.地震波形反演的稀疏约束正则化方法[J].地球物理学报, 56(1):289-297, doi:10.6038/cjg20130130. |
| [128] | 王兆磊,周辉,李国发. 2007.用地质雷达数据资料反演二维地下介质的方法[J].地球物理学报, 50(3):897-904, doi:10.3321/j.issn:0001-5733.2007.03.031. |
| [129] | 魏哲枫,高红伟,张剑锋. 2014.基于非规则网格声波正演的时间域全波形反演[J].地球物理学报, 57(2):586-594, doi:10.6038/cjg20140222. |
| [130] | 吴俊军,刘四新,李彦鹏,等. 2014.跨孔雷达全波形反演成像方法的研究[J].地球物理学报, 57(5):1623-1635. |
| [131] | 邢文军. 2006.波形反演方法与应用研究[D].青岛:中国石油大学(华东). |
| [132] | 徐义,张剑锋. 2008.地震波数值模拟的非规则网格PML吸收边界[J].地球物理学报, 51(5):1520-1526. |
| [133] | 岳碧波,彭真明,洪余刚,等. 2009.基于粒子群优化算法的叠前角道集子波反演[J].地球物理学报, 52(12):3116-3123, doi:10.3969/j.issn.0001-5733.2009.12.021. |
| [134] | 张衡,刘洪,刘璐等. 2014.基于平均导数方法的声波方程频率域高阶正演[J].地球物理学报, 57(5):1599-1611, doi:10.6038/cjg20140523. |
| [135] | 张猛,王华忠,任浩然. 2014.基于CPU/GPU异构平台的全波形反演及其实用化分析[J].石油物探, 53(4):461-467. |
| [136] | 张生强,刘春成,韩立国,等. 2013.基于L-BFGS算法和同时激发震源的频率多尺度全波形反演[J].吉林大学学报(地球科学版), 43(3):1004-1012. |
| [137] | 张文生,罗嘉,滕吉文. 2015.频率多尺度全波形速度反演[J].地球物理学报, 58(1):216-228, doi:10.6038/cjg20150119. |
| [138] | 周辉,陈汉明,李卿卿,等. 2014.不需要提取激发脉冲的探地雷达波形反演方法[J].地球物理学报, 57(6):1968-1976, doi:10.6038/cjg20140627. |
| [139] | 朱童,李小凡,汪文帅,等. 2013.粒子群-梯度算法在频率域地震波形反演中的应用[J].地球物理学进展, 28(1):180-189, doi:10.6038/pg20130119. |
 2015, Vol. 30
2015, Vol. 30


